On the performance of Spin Diffusion NMR Techniques in Oriented Solids: Prospects for Resonance Assignments and Distance Measurements from Separated Local Field Experiments

Abstract

NMR spin diffusion experiments have the potential to provide both resonance assignment and internuclear distances for protein structure determination in oriented solid-state NMR. In this paper, we compared the efficiencies of three common spin diffusion experiments: proton-driven spin diffusion (PDSD), cross-relaxation driven spin diffusion (CRDSD), and proton-mediated proton transfer (PMPT). As model systems for oriented proteins, we used single crystals of N-acetyl-L-¹⁵N-leucine (NAL) and N-acetyl-L-¹⁵N-valyl-L-¹⁵N-leucine (NAVL) to probe long- and short distances, respectively. We demonstrate that for short ¹⁵N/¹⁵N distances such as those found in NAVL (3.3 Å), the PDSD mechanism gives the most intense cross-peaks, while for longer distances (> 6.5 Å), the CRDSD and PMPT experiments are more efficient. The PDSD was highly inefficient for transferring magnetization across distances greater than 6.5 Å (NAL crystal sample), due to small ¹⁵N/¹⁵N dipolar couplings (< 4.5 Hz). Interestingly, the mismatched Hartmann-Hahn condition present in the PMPT experiment gave more intense cross-peaks for lower ¹H and ¹⁵N spinlock field strengths (32 and 17 kHz, respectively) rather than higher values (55 and 50 kHz), suggesting a more complex magnetization transfer mechanism. Numerical simulations are in good agreement with the experimental findings, suggesting a combined PMPT and CRDSD effect. We conclude that in order to assign SLF spectra and measure short and long-range distances, the combined use of homonuclear correlation spectra, such as the ones surveyed in this work, are necessary.

Introduction

Oriented solid-state NMR is an important technique that allows anisotropic NMR parameters such as chemical shift (CS) and dipolar coupling (DC) to be measured directly.¹ This methodology has been important in resolving the orientation and structure of liquid crystalline molecules as well as in the determination of the structure and topology of membrane proteins within lipid bilayers.^1–11 To accurately probe membrane protein topology, separated local field (SLF) experiments such as PISEMA,^{12, 13} SAMPI4,¹⁴ HIMSELF,¹⁵ and their sensitivity-enhanced variants^16–18 are used to measure DC and CS. These observables are then incorporated into structural refinement protocols essentially as dihedral angle restraints.^{7, 19–21}

For membrane proteins, SLF-type spectra are assigned using selectively and/or uniformly labeled samples that rely on the periodic nature of the DC and CS (polar index slant angle, PISA, wheel pattern,^{22, 23}) that results from the periodicity of secondary structures (helices and sheets) commonly present in membrane proteins.^{24, 25} While this has been useful in assigning resonances for structural restraints, this approach heavily relies on the assumption of helix ideality (e.g., ideal dihedral angles for α-helices) as well as the use of several selectively labeled samples. Although membrane helix ideality has been shown to constitute a good approximation,²⁶ deviations can lead to incorrect assignments and a general bias toward ideal structures. Therefore, sequential assignment strategies such as those employed in solution NMR or magic angle spinning (MAS) techniques are preferred.^27–29 Unfortunately, membrane protein dynamics and mosaic spread³⁰ in mechanically aligned lipid bilayer samples result in severe inhomogenous line-broadening (10–15 ppm in ¹⁵N linewidths).^{31, 32} The implementation of magnetically aligned lipid bicelles have overcome many of the limitations in glass plate samples such as a maintaining a constant level of hydration,^{2, 5, 33, 34} which has substantially decreased mosaic spread and led to increases in signal to noise and sample reproducibility.

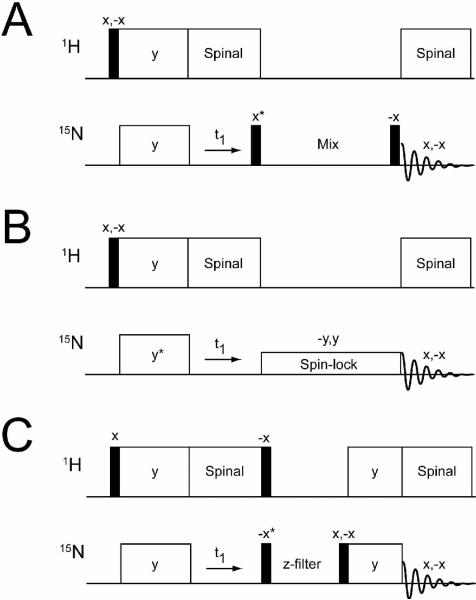
There are three NMR experiments currently used to correlate internuclear distances in oriented solid-state NMR: proton driven spin diffusion (PDSD),^{35, 36} cross-relaxation driven spin diffusion (CRDSD),³⁷ and proton-mediated proton transfer (PMPT)³⁸ (Figure 1). The preparation periods (90° and cross-polarization) and t₁ chemical shift evolution of these pulse sequences are identical (Figure 1), with the only difference occurring in the mixing elements used for spin diffusion. The PDSD contains a mixing element with no RF fields applied to either nuclei. This experiment has had limited application to membrane proteins mechanically aligned on glass plates,^{39, 40} and are widely believed to be too inefficient for resonance assignment. For these reasons, two exchange sequences, CRDSD³⁷ and PMPT³⁸ (similar to PAR experiments in MAS^41–43) were developed. The mixing period for the CRDSD experiment utilizes a weak spinlock field on ¹⁵N to drive the spin diffusion among the ¹⁵N nuclei, while the PMPT sequence, in addition to the Z-filter, contains a cross-polarization element mismatched with respect to the perfect Hartmann-Hahn condition. The PMPT experiment was recently shown to be useful in assigning SLF spectra for Pf1 phage coat protein.⁴⁴

FIGURE 1.

Pulse sequences used to correlate ¹⁵N/¹⁵N: A) proton driven spin diffusion (PDSD), B) cross-relaxation driven spin diffusion (CRDSD), and C) proton-mediated proton transfer (PMPT). Asterisks indicate pulses that were adjusted by 90° to acquire phase-sensitive data in the indirect dimension (ω1).

In oriented solid-state NMR, there has not been a parallel comparison of the three spin diffusion methods on the same system. The CRDSD experiment was tested with a single crystal of the dipeptide N-acetyl-L-¹⁵N-valyl-L-¹⁵N-leucine (NAVL), while PMPT was originally evaluated using a crystal of N-acetyl-L-¹⁵N-leucine (NAL). These crystals differ in the nearest interatomic distances between ¹⁵N spins: 3.3 and 6.5 Å for NAVL and NAL, respectively. In this study we systematically assessed the efficiency of PDSD, CRDSD and PMPT with both NAL and NAVL crystals. We found that the PDSD is the most efficient for short distances and for assignment, while CRDSD and PMPT are more suitable for longer distance correlations.

Experimental Methods

NMR Spectroscopy

¹⁵N labeled single crystals of NAL and NAVL were prepared by slow evaporation from H₂O as previously described.⁴⁵ NMR experiments were conducted on a VNMRS Varian system operating at a ¹H Larmor frequency of 700 MHz. The two crystals were placed in arbitrary orientations with respect to the magnetic field in order to maximize the dispersion of ¹⁵N resonances. All spin diffusion experiments were conducted on the same crystal orientations using a double resonance low-E probe.⁴⁶ For all experiments, including the PISEMA, PDSD, CRDSD, and PMPT (see Figure 1), 4 or 16 scans (NAL or NAVL, respectively) were acquired for each t₁ increment with a 3 sec recycle delay between experiments. The spectral widths for the homonuclear ¹⁵N/¹⁵N spectra were 10 and 50 kHz for the indirect and direct dimensions with a total acquisition time of 4 and 10 ms, respectively. For the PDSD experiments, we employed mixing periods from 1 to 30 sec for NAL and 1 to 20 sec for NAVL. The ¹⁵N radiofrequency driven spin diffusion (RFDSD)^{47, 48} experiments were conducted by varying the ¹⁵N spinlock field (ω_s/2π) from 0 to 50 kHz with no proton spinlock. The CRDSD experiments³⁷ were then performed by adjusting the mixing time from 1 to 20 msec using a ¹⁵N spinlock of 21 kHz (optimized value). For the PMPT experiments,³⁸ three variables were adjusted. First, spectra were acquired by varying the ¹H spinlock field (ω_I/2π) during mismatch-Hartmann-Hahn (mmHH) from 0 to 70 kHz at three ¹⁵N spinlock fields (ω_s/2π = 21, 37.5, and 52.5 kHz) at a mixing time of 10 msec. The ¹H spinlock fields that gave the most intense cross-peaks were used when performing mixing time build-up curves from 1 to 20 msec. All 2D experiments were acquired in a pseudo-3D interleaved fashion to minimize experimental errors.

Numerical Simulations

PMPT and CRDSD experiments were simulated by considering 12 spins (two ¹⁵N, spin S and 10 ¹H nuclei, spin I). The rotating frame Hamiltonian in the presence of on-resonance RF pulses on I and S spins is given by:

$$\begin{array}{cc}\hfill H=& {\omega }_s(S_{1x}+S_{2x})+{\omega }_1\sum _{i=1}^N{I}_{ix}+H_{IS}+H_{II}+H_{SS}\hfill \\ \hfill H_{IS}& =\sum _{i=1}^N[d_{1i}{S}_{1z}{I}_{iz}+d_{2i}{S}_{2z}{I}_{iz}]\hfill \\ \hfill H_{II}& =\sum _{i<j}^N{b}_{1i}[I_{iz}{I}_{jz}-\frac{1}{4}(I_{+i}{I}_{-j}+I_{-i}{I}_{+j})]\hfill \\ \hfill H_{SS}& =b_{12}[S_{iz}{S}_{2z}-\frac{1}{4}(S_{+1}{S}_{-2}+S_{-1}{S}_{+2})]\hfill \end{array}$$ (1)

H_IS is the heteronuclear dipolar Hamiltonian, H_II and H_SS are the homonuclear dipolar Hamiltonians, ω_I and ω_S are RF amplitudes for spins I and S, and d_ij and b_ij are the hetero and homonuclear dipolar couplings between nuclei i and j, respectively. The simulations were carried out with N = 10. In order to calculate all d_ij and b_ij values for NAL, we performed a PISEMA experiment to measure CS and DC values for the four unique ¹⁵N sites. These observables were then used to rotate the crystal coordinate file of NAL (CCDC 624793) to best match the experimental values. After optimization, two ¹⁵N nuclei were chosen that had the closest distances in the crystal (6.5 Å), corresponding to a ¹⁵N/¹⁵N dipolar coupling of 3.2 Hz. In addition, 10 protons were selected that had > 30 Hz dipolar couplings with both ¹⁵N nuclei. All dipolar couplings used for the simulation are given in the Supplementary Table II. In order to calculate the transfer efficiency between the two ¹⁵N spins, G(t), we evaluate the following equation in Matlab for several mixing times (t) ranging from 0–40 msec (1 msec intervals):

$$G\left(t\right)=\mathit{Trace}\left(S_{1x}{e}^{-iHt}{S}_{2x}{e}^{iHt}\right)$$ (2)

PMPT and CRDSD experiments were simulated by varying the ¹H spin-lock field strength (ω_I) from 0–70 kHz (in 2.5 kHz intervals) for each of three ¹⁵N spin-lock fields (ω_S = 17.5, 33, and 50 kHz). Note that for the simulation of the CRDSD experiment, ω_I = 0. The complete Hamiltonian in Eq. 1 was used in Eq. 2, with no motional processes or relaxation accounted for in the simulation.

Results

Spin Diffusion Between ¹⁵N/¹⁵N Distances in NAL and NAVL

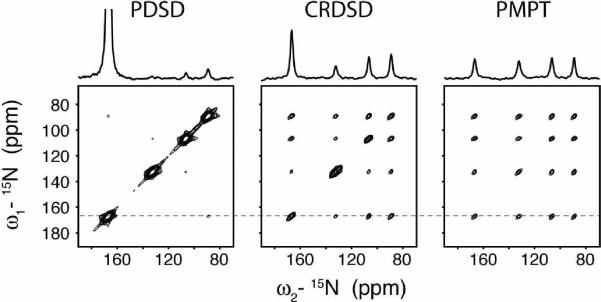
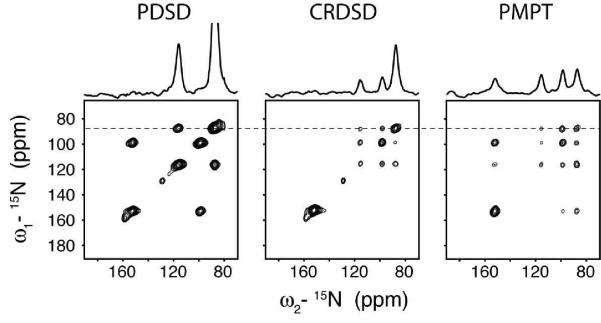
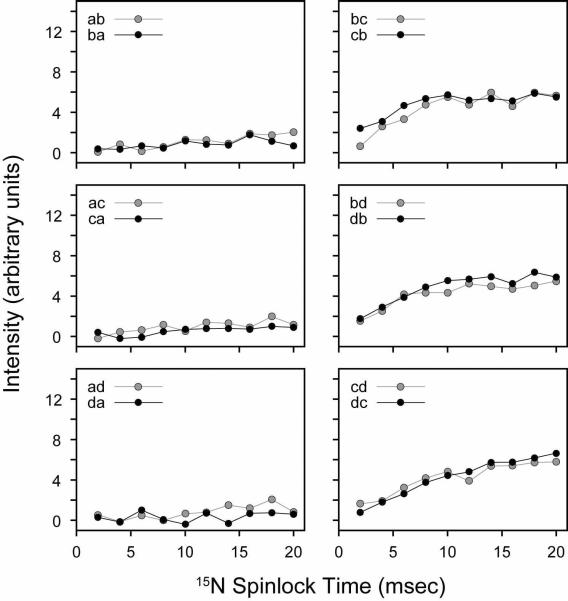
The single crystals of NAL and NAVL were placed at an arbitrary orientation and kept in this position for all of the measurements. The nearest distance between ¹⁵N nuclei in NAVL and NAL are 3.3 and 6.5 Å, which are good mimics of i, i+1 and i, i+4 ¹⁵N/¹⁵N distances in an ideal α-helix (~3 and ~6 Å). Both NAL and NAVL gave four unique ¹⁵N resonances, therefore allowing for 12 total cross-peaks in each homonuclear 2D ¹⁵N/¹⁵N correlation spectrum. Figure 2 shows the results from 2D spectra acquired using PDSD, CRDSD and PMPT experiments. The noise floor in Figures 2 (NAL) and 3 (NAVL) is the same for all three spectra, so the cross-peak intensities for the three pulse sequences can be directly compared. For NAL, the PDSD experiment was found to be the most inefficient, with very weak cross-peaks. In contrast, the CRDSD and PMPT experiments both were quite efficient for long ¹⁵N/¹⁵N distances found within NAL, resulting in observation of all cross-peaks. This result supports previous experiments in which ¹⁵N/¹⁵N distances up to 8.5 Å were detected.^{38, 49} For the NAVL crystal, the PDSD experiment gave significantly more intense cross-peaks than the NAL crystal. In fact, the intensities were larger than those detected using either the CRDSD or PMPT experiment. In the following sections, we compare the three experiments systematically, adjusting the experimental parameters that need to be optimized for strong cross-peaks in ¹⁵N/¹⁵N (or ¹³C/¹³C) correlation spectra for both short and long distances in oriented molecules (e.g., mixing times and spinlock field strengths). All of the intensity units for experiments conducted on NAL and NAVL have been normalized to make the intensities directly comparable between the PDSD, CRDSD, and PMPT experiments (i.e., same noise floor).

FIGURE 2.

Comparison of spin diffusion experiments on NAL. Note that the peak naming convention (peaks a, b, c, d) is from the most downfield (peak a) to the most upfield (peak d). For example, the cross-peak at ω₂ = 167 ppm and ω₁ = 133 ppm is referred to as ab. The PDSD experiment utilized a 3 sec mixing time, the CRDSD experiment used a ¹⁵N spinlock field of 21 kHz, and the PMPT experiment used a Z-filter of 3 sec and ¹H and ¹⁵N spinlock fields of 30 kHz and 21 kHz, respectively. The CRDSD and PMPT experiment used a mixing time of 10 msec. 1D sections are taken from the dotted line in the 2D spectra. All 2D spectra are shown at the same contour level, allowing for a direct comparison of peak intensities.

FIGURE 3.

Comparison of spin diffusion experiments on NAVL. Note that the peak naming convention (peaks a, b, c, d) is from the most downfield (peak a) to the most upfield (peak d). For example, the cross-peak at ω₂ = 152 ppm and ω₁ = 99 ppm is referred to as ac. The PDSD experiment utilized a 3 sec mixing time, the CRDSD experiment used a ¹⁵N spinlock field of 21 kHz, and the PMPT experiment used a Z-filter of 3 sec and ¹H and ¹⁵N spinlock fields of 65 kHz and 55 kHz, respectively. The CRDSD and PMPT experiment used a mixing time of 10 msec. 1D sections are taken from the dotted line in the 2D spectra. All 2D spectra are shown at the same contour level, allowing for a direct comparison of peak intensities.

Note that another spin diffusion experiment referred to as CHHC or NHHN has shown to be quite useful in MAS solid-state NMR experiments.⁵⁰ While we were able to observe ¹⁵N/¹⁵N cross-peaks in NAL using NHHN, the signal to noise was only a fraction of that observed with the other experiments, and we therefore did not further pursue this pulse sequence as a viable alternative to PDSD, CRDSD or PMPT for oriented systems. Proton-proton mixing has, however, been shown to be useful in some oriented solid-state NMR experiments.⁵¹

Proton Driven Spin Diffusion

The PDSD experiment has been reported to be too inefficient as a transfer mechanism for detecting ¹⁵N/¹⁵N correlations in proteins.³⁷ This is expected due to the dependence of the spin diffusion probability (Ω) on the dipolar coupling strength between the two nuclei (ω_ij), given by Fermi's golden rule.^{36, 52}:

$$\Omega =\frac{1}{2}\pi F_{ij}\left(0\right){\omega }_{ij}^{2}t$$ (3)

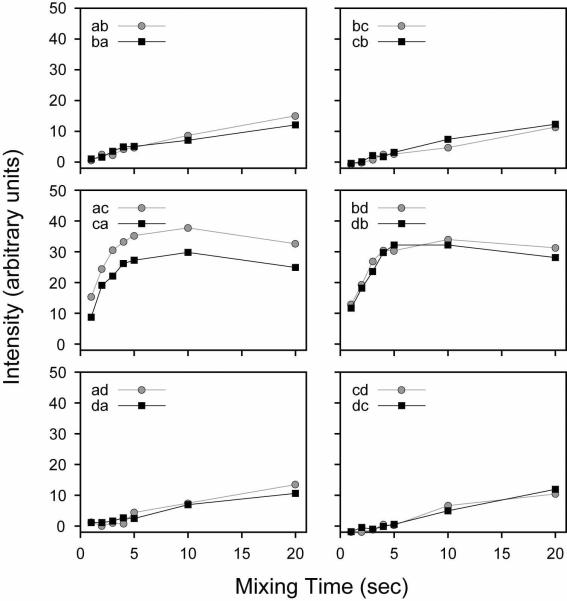
F_ij(0) is the zero-quantum lineshape and t is the time for spin diffusion to take place. Since the dipolar coupling is proportional to $r_{ij}^{-3}$ (r is the distance between nuclei), the probability for a transition between two ¹⁵N nuclei is quite small for r_ij > 6.5 Å and t < 5 sec (i.e., ¹⁵N/¹⁵N dipolar couplings < 4.5 Hz). For the NAL crystal, where the nearest ¹⁵N/¹⁵N distances are 6.5, 6.7, and 8.5 Å, the build-up of magnetization as a function of mixing time is highly inefficient (Figure 4 and Supplementary Figure 15). At a mixing time of 30 sec, the cross-peak displaying the most efficient transfer rate (cross-peak intensity divided by diagonal peak intensity) approaches only 20% (Supplementary Figure 15), echoing the spin diffusion probability expected from Fermi's golden rule.

FIGURE 4.

PDSD experiments on the NAL single crystal. All 12 cross-peaks are shown from the spectra are shown in arbitrary intensity units. All experiments from the NAL crystal (Figures 6, 8, 10 and 11) are shown in the same relative units (i.e., same noise floor).

For the NAVL single crystal, the results (Figure 5 and Supplementary Figure 16) agree well with the theoretical ω_ij² dependence in Eq. 3, showing an efficient transfer of magnetization for intramolecular ¹⁵N sites (a/c and b/d) and a substantially more inefficient transfer for intermolecular ¹⁵N nuclei. Due to the shorter intra-molecular distance between ¹⁵N spins of 3.3 Å (¹⁵N/¹⁵N dipolar couplings < 35 Hz),⁴⁵ the magnetization was almost completely transferred at ~10 sec with ~50% efficiency at ~3–4 sec (Supplementary Figure 16). In contrast, at mixing times of 20 sec the transfer efficiency is only 40% between intermolecular sites, indicating that the PDSD has a clear distance dependence consistent with Fermi's golden rule. While a mixing time of 5–10 sec is somewhat long, the relaxation in the PDSD experiment is dominated by T₁, which is very long for ¹⁵N magnetization, leading to strong cross-peaks in NAVL.

FIGURE 5.

PDSD experiments on the NAVL single crystal. All 12 cross-peaks are shown from the spectra are shown in arbitrary intensity units. All experiments from the NAVL crystal (Figures 7, 9 and 12) are shown in the same relative units (i.e., same noise floor).

Cross-Relaxation Driven Spin Diffusion

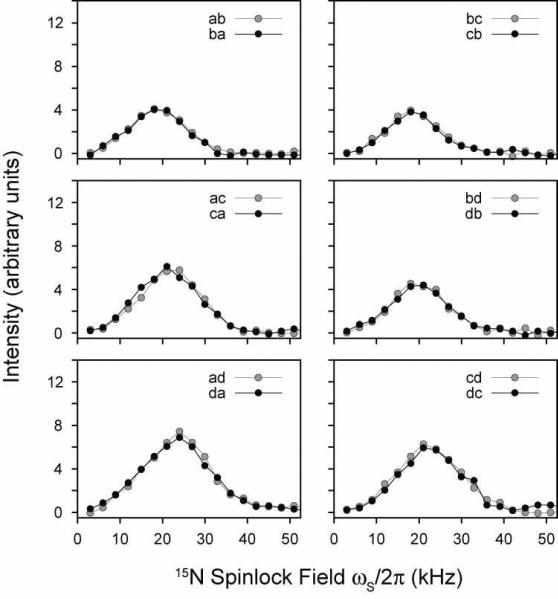
The CRDSD mechanism has been reported to be a highly efficient mechanism of transferring magnetization in the NAVL crystal.³⁷ Unlike the PDSD experiment (Figure 1), there are two variables that need to be independently optimized to achieve the most favorable transfer: 1) the ¹⁵N spinlock field strength and 2) the mixing time. Figure 6 shows changes in the cross-peak intensities in NAL upon variation of the ¹⁵N spinlock field for a 10 msec mixing time. Due to relaxation during the spinlock (from multiple relaxation channels), we plot the absolute intensity of the cross-peaks rather than the normalized cross-peak intensity.^{53, 54} The maximum intensity of all cross-peaks occurs for ω_s/2π = 17–22 kHz (Figure 6). A similar range was found to give maximal cross-peak heights in the NAVL dipeptide crystal,³⁷ which is in quantitative agreement with our measurements (Figure 7).

FIGURE 6.

CRDSD experiments on the NAL single crystal. The ¹⁵N spinlock field was varied while keeping the mixing time fixed at 10 msec. The intensities are expressed in arbitrary units. All experiments were acquired in an interleaved manner to avoid potential differences in the experiments, and are therefore relevant to compare within each figure.

FIGURE 7.

CRDSD experiments on the NAVL single crystal. The ¹⁵N spinlock field was varied while keeping the mixing time fixed at 10 msec. The intensities are expressed in arbitrary units.

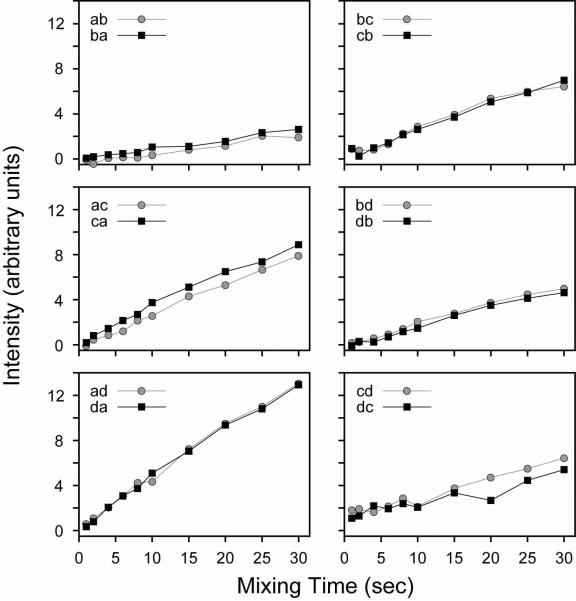
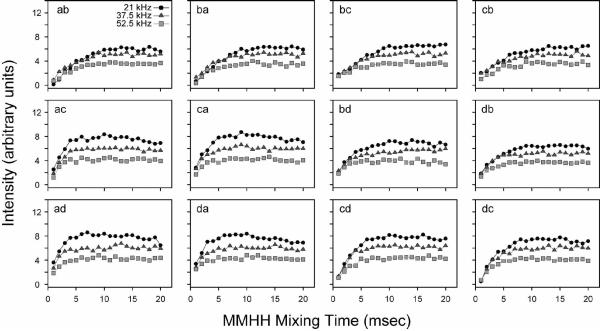
We also performed a systematic build-up of the NAL and NAVL cross-peaks by varying the mixing time at a fixed ¹⁵N spinlock field of 21 kHz. From the series of 2D spectra acquired at different mixing times, it is apparent that the magnetization has reached a maximum for all NAL cross-peaks between 5–15 msec (Figure 8). Therefore, the magnetization transfer is much more efficient in the CRDSD than the PDSD experiment. In Figure 9, we plot the cross-peak intensities as a function of the mixing time from the NAVL sample, which are consistent with those previously reported³⁷ (even the crystal orientation is similar). The results obtained for NAL and NAVL suggest that both intra- and inter-molecular magnetization transfers proceed essentially at the same rate (Figures 8 and 9). Since the internuclear distances in the crystals are strikingly different, 3.3 vs. 6.5 Å, there is a potential problem for using these experiments to sequentially assign resonances. Ideally, for a walk through the backbone ¹⁵N residues (i.e., sequential resonance assignment) one would only want to correlate residue i with the adjacent i±1. Due to the tightly coupled proton network, the CRDSD mechanism, while relying on the presence of direct ¹⁵N/¹⁵N couplings, reduces and/or in some cases essentially removes the distance dependence of the cross-peak intensities.

FIGURE 8.

CRDSD experiments on the NAL single crystal. The ¹⁵N spinlock field was fixed at 21 kHz, while the mixing time was varied between 1–20 msec. The cross-peak intensities are plotted in arbitrary units.

FIGURE 9.

CRDSD experiments on the NAVL single crystal. The ¹⁵N spinlock field was fixed at 21 kHz, while the mixing time was varied between 1–20 msec. The cross-peak intensities are plotted in arbitrary units.

Proton-Mediated Proton Transfer Mechanism

Unlike the PDSD and CRDSD pulse schemes, there are three experimental parameters that need to be optimized for the PMPT experiment: 1) ¹⁵N spinlock, 2) ¹H spinlock (mismatch condition), and 3) the mixing time. It is noted that the PMPT experiment is essentially the oriented solid-state NMR version of the proton assisted recoupling (PAR) experiment used in MAS experiments.^41–43

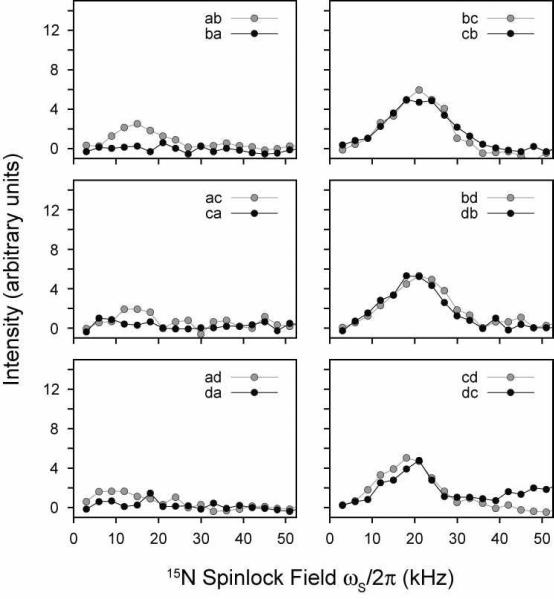
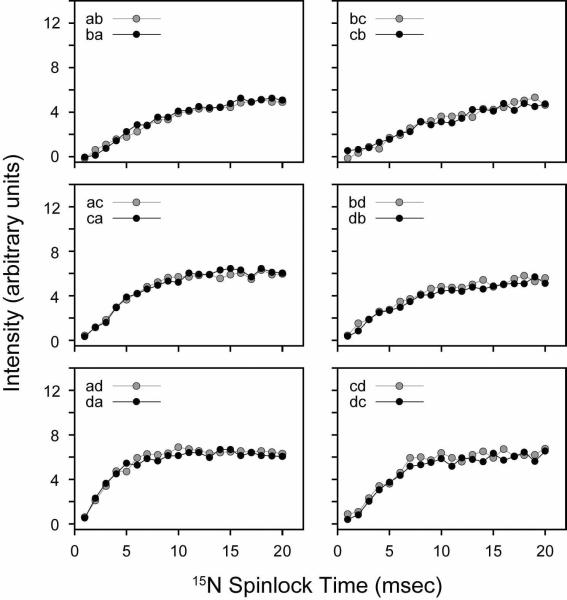
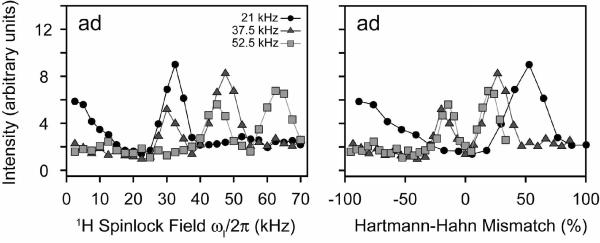
For our analysis of PMPT, we first set the mixing time to 10 msec, and adjusted the ¹H spinlock field at three different ¹⁵N spinlock values (ω_s = 21, 37.5, and 52.5 kHz). Figure 10 shows the experimental results for NAL. The PMPT mechanism has previously been reported to be most efficient in NAL when the ¹H RF field is mismatched by 110% from that of the ¹⁵N spinlock.^{38, 49} When the ¹H spinlock approaches the Hartmann-Hahn match,⁵⁵ part of the magnetization is transferred back to the protons, depleting the observable ¹⁵N magnetization. Therefore, there is a trade-off between the efficiency of the proton-mediated transfer mechanism and the Hartmann-Hahn match. Figure 10 shows the cross-peak intensities as a function of the ¹H spinlock field. We found that two of the curves (¹⁵N spinlocks of 37.5 and 52.5 kHz) each have two relative maxima that are located above and below the Hartmann-Hahn match. For the 21 kHz ¹⁵N spinlock curve, there is only one maximum, which is present above the Hartmann-Hahn matching condition (32 kHz ¹H spinlock or 155% of the ¹⁵N spinlock value). Interestingly, we found that the absolute cross-peak intensities were actually higher at a lower ¹⁵N spinlock value (and therefore ¹H spinlock field) for a mixing time of 10 msec. To further investigate this, we performed a systematic build-up of the mixing time for the three ¹⁵N spinlock values and the optimized ¹H mismatch values determined from Figure 10. As with the CRDSD mechanism, all of the cross-peaks were observed with a maximum intensity reached at 5–10 msec (see Figure 11). As suggested by the data in Figure 10, the ¹⁵N spinlock at the lowest value of 21 kHz gave the most intense cross-peaks (Figure 11). Therefore, this suggests that the mechanism is a combination of both direct ¹⁵N/¹⁵N couplings (the CRDSD mechanism), as well as the proton-mediated effect (PMPT mechanism).

FIGURE 10.

PMPT experiments on the NAL single crystal. The ¹H spinlock field was varied between 0–70 kHz for three different ¹⁵N spinlock fields (21, 37.5, and 52.5 kHz). The values are also plotted as the Hartmann-Hahn mismatch percentage. The mixing time was fixed at 10 msec for all points. Cross-peak intensities are plotted in arbitrary units. The dip in the curves is due to the Hartmann-Hahn match. The other cross-peaks are essentially the same as that plotted for the cross-peak ad. All other curves are shown in Supplementary Figures 17 and 18.

FIGURE 11.

PMPT experiments on the NAL single crystal. The ¹H spinlock field was set to 32.5, 47.5 and 62.5 kHz for 21, 37.5 and 52.5 kHz ¹⁵N spinlock, respectively, based on the results shown in Figure 10. The mismatched Hartmann-Hahn (MMHH) mixing time was varied from 1–20 msec. The cross-peak intensities are in arbitrary units (i.e., not divided by the diagonal peak intensity).

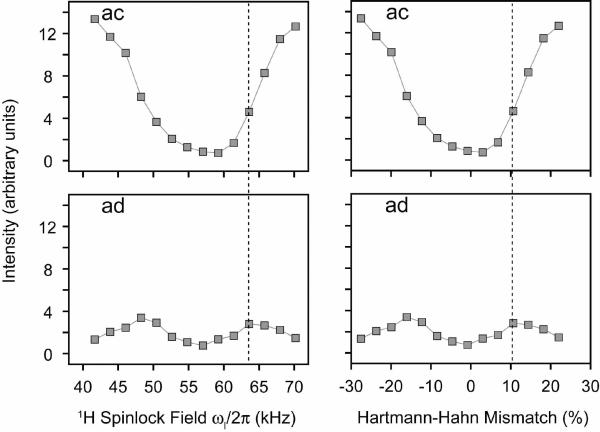
We repeated the PMPT experiments using NAVL. We found that the most efficient transfer for intramolecular ¹⁵N nuclei was due to the 3 sec Z-filter element used in the pulse sequence (see Figure 1). In fact, the removal of the MMHH element from the PMPT experiment makes the pulse sequence identical to the PDSD experiment, which was shown to give strong intramolecular cross-peaks in 3 sec for NAVL (Figure 3). Finally, we analyzed the cross-peak build-up at a ¹⁵N spinlock field of 57.5 kHz as a function of the ¹H spinlock field. The cross-peak intensity profiles for intermolecular ¹⁵N/¹⁵N correlations are nearly identical to those found in NAL (compare intermolecular cross-peaks ad in Figures 10 and 12). However, for intramolecular ¹⁵N/¹⁵N transfer, the MMHH condition decreased the cross-peak intensity (Figure 12). The dotted line in Figure 12 indicates the most optimal ¹H spinlock field for the PMPT mechanism, and this does not give the maximum intensity for the intramolecular¹⁵N/¹⁵N peak ad, indicating the PMPT mechanism only depleted the signal by the transfer of magnetization to ¹H (i.e., the Hartmann-Hahn mechanism). These results suggest a more efficient transfer between short distances from using the PDSD experiment rather than either PMPT or CRDSD.

FIGURE 12.

PMPT experiments on the NAVL single crystal. The ¹H spinlock field was varied for a ¹⁵N spinlock of 57.5 kHz. The mixing time was fixed at 10 msec for all points. The curves plotted are for crosspeaks ac (intramolecular ¹⁵N/¹⁵N, 3.3 Å) and ad (intermolecular ¹⁵N/¹⁵N, > 6 Å). Intensities are plotted in arbitrary units. The dip in the curves is due to the Hartmann-Hahn match. The dotted line indicates the best transfer ¹H spinlock value for intermolecular transfer in NAVL. The optimal value for intermolecular transfer results in less magnetization transfer for intramolecular sites. The other cross-peaks are essentially the same as those plotted for the cross-peaks ac and ad. All other curves are shown in Supplementary Figures 18 and 19.

Simulations

To validate the results above, we performed numerical simulations of the PMPT and CRDSD experiments for NAL. The DC values used in the simulations were obtained by rotating the NAL crystal coordinates to maximize the agreement with the experimental DCs and CSs measured from a PISEMA experiment. The principal values for the ¹⁵N chemical shift tensor were δ₁₁=64, δ₂₂=77, and δ₃₃=217 ppm.⁵⁶ From this crystal orientation, we calculated all relevant angles relative to the magnetic field, and therefore all dipolar coupling frequencies (b_ij and d_ij from Eq. 1; Supplementary Table I).

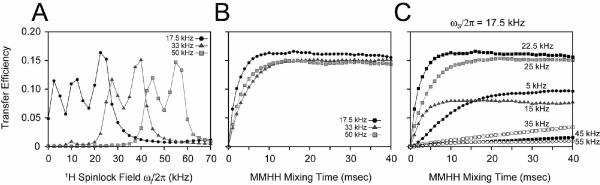
The results from the simulation are reported in Figure 13. We set the ¹⁵N spinlock field at values similar to those used in the experiments on NAL (17, 33, and 50 kHz). The ¹H spinlock field was varied from 0–70 kHz, and the time of the transfer from 0–40 msec. In Figure 13A, the transfer efficiencies are plotted as a function of the ¹H spinlock at a mixing time of 20 msec. The simulations at three different spinlock fields clearly show that at a small ¹⁵N spinlock value, the magnetization transfer is more efficient than those obtained at larger spinlock fields. Additionally, the CRDSD experiment (¹H spinlock = 0 kHz) is reproduced by the simulations: a smaller ¹⁵N spinlock of 17.5 kHz gives efficient transfer, while larger ¹⁵N spinlock fields (33, 50 kHz; RFDSD experiment) result in little or no transfer.^{37, 47} The reason for this observation is that a low ¹⁵N spin-lock field (17 kHz) is unable to completely decouple ¹⁵N nuclei from ¹H, whereas, a larger spin-lock field does sufficiently decouple the heteronuclear dipolar coupling.

FIGURE 13.

Twelve-spin simulations of the PMPT and CRDSD experiments on the NAL single crystal. A) Varying the spinlock field on the ¹H spinlock field for three different ¹⁵N spinlock fields (17.5, 33, and 50 kHz) at a MMHH mixing time of 20 msec. Note that for a ¹H spinlock field of 0 kHz, this is the CRDSD experiment for a 17.5 kHz ¹⁵N spin-lock and the RFDSD experiment for larger ¹⁵N spin-locks. B) Build-up for the most optimal transfer efficiencies in panel A. For ¹⁵N spinlocks of 17.5, 33, and 50 kHz, the ¹H spinlock field was maximal at 22.5, 40, and 55 kHz, respectively. C) Several mixing time build-up curves for different ¹H spinlock fields when the ¹⁵N spinlock was set to 17.5 kHz.

For the PMPT experiment, the HHMM fields that give optimal transfer are 29, 21, and 10% for ¹⁵N spinlocks of 17.5, 33, and 50 kHz, respectively, which is in good agreement with the experimental values of 55, 27, and 19% for NAL. The small deviations from experiment can be accounted for by offset dependencies at smaller spin-lock fields, small errors in the calculation of the experimental spinlock fields, and the approximation of only 12 spins in the simulation. The simulations also show that the transfer efficiencies plotted as a function of the mixing time were in close agreement with those found experimentally. At ~10 msec the transfer efficiencies (Figure 13B) in the simulation reached a maximum, which agrees closely with those reported experimentally in Figures 8 and 11. Taken together, these simulations show that the magnetization in NAL (long distances) is more efficiently transferred with PMPT and CRDSD than PDSD.

Discussion

In this work, we present a comparison of the spin diffusion experiments currently available for oriented solid-state NMR experiments. While SLF experiments are the most reliable method to directly probe anisotropic structural restraints (DC and CS), no definitive sequential assignment schemes are currently used to accurately and efficiently assign the spectra.

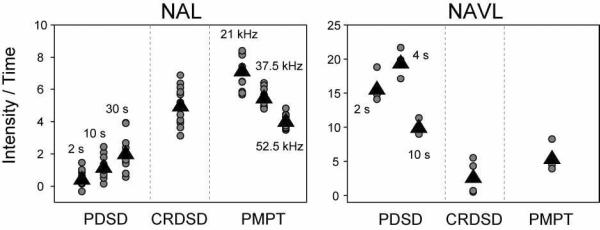
In pursuit of an assignment strategy, we compared the efficiencies of three spin diffusion methods with model compounds that are mimics of short and long range distances in proteins (NAL and NAVL). In addition, the ability to detect long-range connectivities in proteins will be important for implementing structural restraints. In order to directly compare the intensities observed for NAL between the PDSD (Figure 4), CRDSD (Figure 8), and PDSD (Figure 11) experiments, we need to normalize the PDSD data to account for the increased experimental data acquisition time due to the mixing period. The results are plotted in Figure 14 (values in Table I), and show that the PMPT experiment carried out with low spinlock fields (¹H 32.5 kHz, ¹⁵N 21 kHz) gives on average a factor of 34 greater intensity per unit time than PDSD (30 sec mixing time) and a factor of 1.4 more signal than the CRDSD experiment. Therefore, both the CRDSD and PMPT experiments are highly efficient mechanisms for transferring magnetization at distances up to 8 Å with modest spinlock fields (17–30 kHz) and mixing times (~10 msec). For the PMPT experiment, we found that the mismatched Hartmann-Hahn condition is most efficient in transferring magnetization at weaker spinlock fields for ¹H and ¹⁵N (Figure 14 and Table I). The latter is an important point, since it is always preferable to use lower powers in experiments to minimize the stress to NMR hardware. While the probes have improved to handle large spinlock fields (approaching 100 kHz) for 20 msec under low electric field conditions,^{46, 57} sample heating still occurs, which is more pronounced at high magnetic fields.

Figure 14.

Comparison of PDSD, CRDSD, and PMPT experiments for NAL and NAVL normalized for the mixing time in the PDSD experiment. Since a 3 sec recycle delay was used for every experiment, normalization was done by dividing the PDSD 2D peak intensities by 1.29, 1.53, 2.08, and 3.32 to account for 2, 4, 10, and 30 sec mixing times, respectively. Although the PMPT experiment used a 3 sec Z-filter time, no normalization was done for this experiment due to the fact that a much shorter time can be used that would only marginally influence the experimental acquisition time.⁴⁴ For NAVL, much of the magnetization created in the PMPT experiment originated from the 3 sec Z-filter time. Circles represent all cross peaks observed in the NAL spectra and only intramolecular ¹⁵N/¹⁵N cross-peaks in the NAVL crystal (i.e., peaks ac, ca, bd, and db). Triangles represent the average of the cross-peak intensities shown (values in Table I). The CRDSD experimental cross-peaks are from the spectra using a 10 msec mixing time with a ¹⁵N spinlock of 21 kHz (both NAL and NAVL). The PMPT experimental cross-peaks are from the 10 msec mixing time with the indicated ¹⁵N spinlock for NAL and the optimized ¹H spinlock used in Figure 11. For NAVL, the PMPT experiment used the 10 msec mixing time with ¹H and ¹⁵N spinlocks of 65.8 and 57.5 kHz, respectively (same as in Supplementary Figure 19). It is not appropriate to compare the intensities between NAL and NAVL, as the crystal sizes were different.

Table I.

The average of intensity values per unit time for NAL and NAVL as plotted in Figure 14. The third column shows the data further normalized to 1.0 for the experiment that gave the most intensity / time in NAL and NAVL.

NAL	Intensity / Time	Normalized
PDSD (2 sec)	0.5	0.0069
PDSD (10 sec)	1.2	0.017
PDSD (30 sec)	2.1	0.029
CRDSD	50.1	0.70
PMPT (21 kHz)	72.0	1.0
PMPT (37.5 kHz)	55.1	0.77
PMPT (52.5 kHz)	40.6	0.56

NAVL	Intensity / Time	Normalized
PDSD (2 sec)	15.7	0.81
PDSD (4 sec)	19.5	1.0
PDSD (10 sec)	10.1	0.52
CRDSD	2.8	0.14
PMPT	5.5	0.28

From the prospective of the sequential resonance assignment in SLF experiments such as PISEMA, HIMSELF or SAMPI4 the most useful ¹⁵N/¹⁵N correlations are i, i+1. This will make the assignments unambiguous and directly amenable to implementing DC and CS restraints in calculating membrane protein structure and topology. A direct comparison of the cross-peak intensity observed for PDSD, CRDSD, and PMPT is observed in Figures 5, 9, and 12, respectively. As for NAL, we calculated the normalized intensity per unit time, with the results shown in Figure 14 (values in Table I). We find that on average, PDSD with a 4 sec mixing time results in the most signal. It gives a factor of 3.5 more signal than the PMPT experiment and a factor of 7 more signal than the CRDSD experiment. Importantly, unlike PDSD, the CRDSD and PMPT sequences essentially erase the distance dependence, making all ¹⁵N/¹⁵N correlations from 3.3 to 8 Å observable with similar cross-peak intensity. In fact, we found that the PMPT experiment with a 3 sec Z-filter element (acting like a PDSD experiment) significantly reduced cross-peak intensities observed between intramolecular ¹⁵N nuclei spaced 3.3 Å apart. Although this might be attractive for long-range distances (e.g., i, i+4 distances), it is likely to be problematic for resonance assignments. Recently, a paper by Nevzorov and co-workers introduced the PMPT scheme for assigning membrane proteins. While this method is very promising for measuring long-range distances, the observation of correlations other than i, i+1, makes this scheme cumbersome for assignment purposes.⁴⁴

A final consideration is that spinlock experiments such as CRDSD and PMPT result in magnetization that decays with T_1ρ (from multiple relaxation channels), whereas the magnetization in the PDSD experiment decays with T₁. Since T₁ in solids is relatively long for ¹⁵N spins, the PDSD experiment still might be the most sensitive experiment available for unambiguous resonance assignment of membrane proteins (i.e., correlating only i, i+1 resonances). Since its first application in oriented experiments on glass plates, there have been no reported uses of this pulse sequence for assignment purposes, presumably due to the significant inhomogenous line-broadening present in the spectra, leading to poor signal to noise. Bicelle technology will likely allow these experiments to be usable for sequential assignment (PDSD) and long-range distance restraints (CRDSD and PMPT).⁴⁴