Abstract
Calcium is a key intracellular signal that controls manifold cellular processes over a wide temporal range. The development of calcium-sensitive fluorescent dyes and proteins revolutionized our ability to visualize this important second messenger and its complex signalling characteristics. The subsequent advent of high throughput plate-based fluorescence readers has resulted in the calcium assay becoming the most widely utilized assay system for the characterization of novel receptor ligands. In this review we discuss common approaches to calcium assays, paying particular attention to the potential issues associated with interpretation of receptor pharmacology using this system. Topics covered include dye saturation and forced-coupling of receptors to the calcium pathway, but special consideration is given to the influence of non-equilibrium conditions in this rapid signalling system. Modelling the calcium transient in a kinetic mode allows the influence of ligand kinetics, receptor reserve and read time to be explored. This demonstrates that observed ligand pharmacology at very early time points can be quite different to that determined after longer incubations, even resulting in reversal of agonist potency orders that may be misinterpreted as agonist biased signalling. It also shows that estimates of antagonist affinity, whether by Schild analysis or inhibition curves, are similarly affected by hemi-equilibrium conditions. Finally we end with a discussion on practical approaches to accurately estimate the affinity of insurmountable antagonists using calcium assays.
Keywords: calcium assay, equilibrium, hemi-equilibrium, antagonist, agonist, modelling and simulation, receptor theory, drug discovery
Historically, drug discovery was performed using tissue preparations and whole animal models. This had the clear advantage that drugs were studied in a physiologically relevant system, but co-expression of related family members made the task of characterizing the pharmacology of a drug at a specific receptor complex and at times impossible. It certainly was not quick. In the last part of the twentieth century several important innovations combined to radically change the way the pharmacology of new receptor ligands was assessed (Rang, 2006). First, advances in molecular biology enabled recombinant receptors to be expressed in immortalized host cell backgrounds to produce a ‘cleaner’ (arguably too sterile) environment. This allowed the activation of specific receptor subtypes to be studied at a cellular level. Many G protein-coupled receptors (GPCRs) can trigger an increase in cytosolic calcium concentration, most commonly by initiating a cascade of events involving G proteins, phospholipase C (PLC), inositol 1,4,5-trisphosphate (InsP3) and InsP3-sensitive calcium channels on the endoplasmic reticulum that stores calcium in the cell (Berridge et al., 2003). To exploit this, calcium-sensitive fluorescent dyes were used in conjunction with fluorimeters to assess receptor activation. At this stage the experiments were still labour-intensive, with fluorescence measurements made one at a time using cuvette-based fluorimeters. But it was the development of fluorescence imaging plate readers, particularly the FLIPR from Molecular Devices, that hailed the advent of high throughput pharmacology (Schroeder and Brad, 1996; Sullivan et al., 1999). These plate readers, coupled with refined high emission calcium-sensitive fluorescent dyes, enabled the kinetics of intracellular calcium levels to be measured from 96 wells simultaneously, increasing the number of data points a single scientist could generate in a day by two orders of magnitude (Chambers et al., 2003). Since then, technology has advanced at an incredible rate, with machines capable of simultaneously imaging 1536 wells (Hodder et al., 2004) and high content imaging devices able to measure calcium flux in single cells in a plate format (Richards et al., 2006). It is now relatively simple for one scientist to generate full IC50 curves for hundreds of compounds a day. This has undoubtedly helped speed up the process of testing novel compounds, but in our drive for increased efficiency we run the risk of overlooking the detail in the large quantities of data we generate. In this article we review the use of the calcium assay in drug discovery and show that although it may be one of the most convenient assay systems available, care must be taken to not misinterpret the pharmacology of novel receptor ligands.
The complexity of calcium signalling
Elevation of cytosolic calcium concentration is one of the most universal, yet functionally diverse intracellular signals (Berridge et al., 2003). Calcium can trigger extremely rapid events, such as neurotransmitter release (Augustine, 2001), but also act over much longer periods of time to promote gene transcription and cell proliferation (Berridge, 2005; Greer and Greenberg, 2008). The functional consequences of increased intracellular calcium levels are largely governed by the temporal profile of calcium signalling, which can range from short, intense ‘sparks’ in smooth muscle cells (Jaggar et al., 2000) to long periods or ‘plateaus’ of raised calcium in vascular endothelial cells (Faehling et al., 2002). Many G protein-coupled receptors (GPCRs) can trigger an increase in cytosolic calcium. Although there are several examples where GPCRs can regulate calcium influx through voltage-dependent ion channels via the G protein Go (Hescheler et al., 1987), the large majority increase intracellular calcium levels by activating phospholipase C (PLC) via Gαq or Gi-derived βγ subunits. This results in the generation of the soluble intracellular messenger inositol 1,4,5-trisphosphate (InsP3), that diffuses to the endoplasmic reticulum, opening InsP3-sensitive calcium channels to release stored calcium into the cytosol. The result is a rapid peak in intracellular calcium levels that, in the absence of extracellular calcium, is transient (Berridge et al., 2003). Typically, however, this peak is followed by an influx of extracellular calcium that results in a more sustained second phase of signalling. In many different cell types, this process repeats to form calcium oscillations that can vary in both frequency and amplitude (Berridge, 1990). Figure 1A shows an example of the kinetics of calcium signalling for a range of concentrations of methacholine at the M3 receptor recombinantly expressed in CHO cells (CHO-M3 cells).
Figure 1.
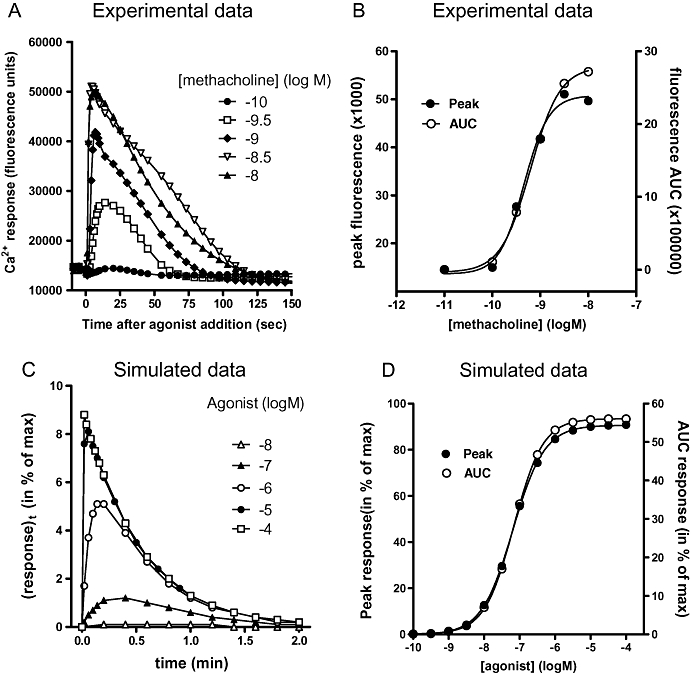
(A) Methacholine-induced intracellular calcium responses in CHO cells expressing the recombinant M3 muscarinic receptor (data re-drawn from Sykes et al., 2009). (B) Concentration-response curves generated from the data in panel A using either peak calcium or area under the curve as the measure of response. (C) Simulated calcium signals (in % of maximal response of the system) generated by increasing concentrations of an agonist (with k1= 1 107 M−1·min−1 and k2= 1 min−1) as a function of the post-agonist administration time in a system with low cellular amplification (τ= 0.1) and k3= 2 min−1. (D) Simulated agonist concentration-response curves obtained by simulating calcium signal peak levels (in % of maximal response of the system) and area under the curve values (AUC, in % of total plot area) in a system with high cellular amplification (τ= 10). Rate constants are the same as in panel C. Parameters of the curves are given in Table 1. AUC, area under the curve; CHO cells, Chinese hamster ovary cells.
This complexity presents an important question: How do we quantify calcium signalling for the purpose of assessing receptor activation? For simplicity, the majority of researchers use the peak calcium response, but the entire calcium transient can also be quantified using area under the curve (AUC). In many systems, however, the resulting concentration-response curves are similar, as shown in Figure 1B where the concentration-response data from Figure 1A are analysed using both the peak and AUC as measurements of response. The frequency of calcium oscillations can also vary between agonists, but as the majority of plate readers measure the response from the entire well, only fully synchronous oscillations can be detected using these instruments. This can be overcome using single-cell imaging, but this is still not feasible if reasonable throughput is required.
Calcium indicators
The development of fluorescent calcium indicator dyes has revolutionized our ability to measure the functional consequence of GPCR activation and a bewildering array of options are available. For a more thorough discussion see reviews by Takahashi et al. (1999) and Paredes et al. (2008). Each dye has a different affinity (Kd) for calcium and they are usually split into high- and low-affinity dyes. The low affinity dyes have Kd values in the range of 1–100 µM and are good for imaging calcium in compartments such as endoplasmic reticulum where the calcium concentration can be around 200 µM (Hofer et al., 1995). The high affinity dyes typically have Kd values between 1 and 500 nM and are more widely used for investigating cytosolic calcium concentration, which is normally between 10–100 nM at resting, but can increase by over 100-fold at peak stimulation in certain cell types. Fluo-3 and the higher emission Fluo-4 are most routinely utilized in modern receptor pharmacology labs (Gee et al., 2000). These are high affinity, high emission indicators that are very sensitive to small calcium changes so have become very popular for assay development to achieved good signal: noise ratios. Change in fluorescence is, however, only linear with change in calcium over a narrow range, meaning that a calcium concentration of less than 0.1-fold will not be detected and at a calcium concentration greater than 10-fold Kd, the dye will saturate. Thus, although high affinity dyes might be more sensitive to small changes, in cells that generate large changes in calcium concentration the dye may become saturated and underestimate the magnitude of signal. Such observations were made in a study of glutamate-induced calcium signalling in neurons where the maximal response detected was higher for low affinity dyes than high affinity dyes (Mulligan and MacVicar, 2005). This is important as it may result in an overestimation of agonist potency for full agonists and efficacy for partial agonists. It may also result in steeper concentration-response curves.
The fluorescent properties of ratiometric calcium dyes (e.g. Fura-2) shift on binding to calcium, allowing quantification of bound and unbound dye and therefore calcium concentration (once Kd is established). They are often, however, not as bright as single wavelength indicators. In addition, the first generations of calcium imaging plate readers did not support ratiometric measurements, so the use of single wavelength indicators has become widespread, and it is usual to express calcium levels as change in fluorescence units (ΔF). It is possible to estimate the calcium concentration from ΔF of single wavelength dyes using the following equation:
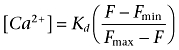 |
(1) |
where Kd is the dissociation constant of the dye for calcium, F is the experimentally measured fluorescence value, Fmin is the fluorescence in the absence of calcium and Fmax is the fluorescence at saturating calcium, achieved using permeabilized cells (Takahashi et al., 1999). In practice, however, this is seldom performed and can become an issue when the incorrect dye is chosen for a particular application. For this reason it is important to at least check for dye saturation and choose the appropriate dye for the system of interest. Another consideration is that many compounds can directly influence the signal from fluorescent dyes via quenching or auto-fluorescence, generating false positive or false negative hits in a screening campaign. High throughput screening falls outside the scope of this review, so readers are referred to alternative sources for information on compound interference (Comley, 2003; Inglese et al., 2007).
An alternative method for detecting calcium signals utilizes photoproteins, such as the jellyfish-derived aequorin. These biosensors can be recombinantly expressed in a variety of cell types and even targeted to specific organelles (e.g. mitochondria) to investigate sub-cellular localization of calcium signalling (Rizzuto et al., 1992). Aequorin requires a substrate, coelenterazine, to generate a signal. When calcium binds to aequorin (Kd∼ 10 µM), coelenterazine is oxidized to coelenteramide, emitting light in the blue range that can be detected using a charge-coupled device (CCD). The result is an extremely efficient system with high signal: noise ratios, although the slower reaction kinetics mean it is not suitable for measuring complex calcium transients in real-time. As the aequorin response is not directly correlated to calcium concentration, methods have also been described for quantifying intracellular calcium concentrations from a luminescence signal (Blinks, 1989). This is, however, more complex and error-prone than calibration of fluorescent dyes. Regeneration of the aequorin molecule requires low calcium concentrations, meaning the reaction is effectively irreversible during elevated calcium levels. This results in a progressive depletion of the biosensor and short-term sequestration of calcium. Considering only low expression levels of aequorin are normally required for a high signal, this can significantly blunt the fraction of total calcium that can be detected. More recently, Photina® has been developed specifically to improve upon the issues associated with the use of aequorin in high throughput screens (Bovolenta et al., 2007). This novel chimeric photoprotein has slower kinetics and a larger luminescent intensity than aequorin.
An alternative family of fluorescence resonance energy transfer (FRET)-based biosensors have been developed using chimeras of green fluorescent proteins (GFPs) with calcium binding proteins. The cameleons consist of two modified GFPs linked by calmodulin and the calmodulin binding domain of myosin light chain (Miyawaki et al., 1997). Calcium binding to calmodulin results in a conformational change that increases the FRET signal. Circularized versions of these biosensors, the camgaroos or pericams, have also been developed that have a higher affinity for calcium and increased fluorescent output (Baird et al., 1999). All of these FRET-based calcium indicators are fully and rapidly reversible, meaning that unlike aequorin they can be used to continuously monitor changes in intracellular calcium concentrations over time (e.g. oscillations). They do, however, suffer from the same type of interference described above for the fluorescent dyes. See Eglen and Reisine (2009) for a more thorough review on the variety of calcium-sensitive photoproteins available.
It is clear from the discussion above that there are a large number of alternative options for the monitoring of intracellular calcium concentration, all of which exhibit particular strengths and weaknesses. As there is no single solution, careful selection is required to identify the most appropriate calcium indicator for any given situation.
Forced and facilitated coupling to the Gαq pathway
The relative simplicity of measuring calcium signalling has resulted in its widespread exploitation for receptor pharmacology studies. However, although a large number of GPCRs coupling to Gαq, the majority do not efficiently stimulate a rise in intracellular calcium concentrations, hindering the universal application of this method. This has been particularly important in the field of receptor de-orphanization, where the G protein coupling preference of a new receptor can not be predicted, complicating the interpretation of failed ligand fishing campaigns. For these reasons, efforts have been made to force the coupling of Gαi and Gαs-preferring receptors to the calcium pathway, even if they do not naturally activate PLC. The most common approaches involve utilizing promiscuous G proteins. There are several naturally occurring G proteins (e.g. Gα16, Gα15) that are members of the Gαq family and can couple many receptors to the PLC pathway. In addition, a series of chimeric G proteins have been developed that efficiently couple Gαi-preferring receptors the PLC (Conklin et al., 1993). Studies have shown that as predicted, Gα16 is more efficient at coupling Gαs-preferring receptors to calcium and the chimeric Gαqi5 G protein more efficiently couples to the Gαi-preferring receptors (Kostenis, 2001). This suggests there is unlikely to be a single, universal G protein adaptor. To overcome this problem, experimenters have in the past transfected a cocktail of promiscuous G proteins to increase the probability of coupling newly identified receptors to the calcium pathways. This might not always be advised, due to potential dominant negative effect of promiscuous G proteins on coupling to natural, endogenous subtypes. For example, the S1P3 receptor couples efficiently to endogenous Gαq (and therefore calcium) in HEK 293 cells, but overexpression of either Gα16 or the myristillated form of Gαqi5 reduces the effectiveness of S1P to increase calcium (Kostenis, 2001). In addition, overexpression of Gαq alone may generate a highly sensitive system that will overestimate the potency of receptor agonists relative to physiological systems. For this reason it may be more appropriate to utilize parallel cell lines rather than a cocktail of promiscuous G proteins. An alternative method for improving the coupling efficiency of Gαi-preferring receptors to the calcium pathway is to ‘prime’ the system using a Gαq-coupled receptor. Cross-talk between second messenger pathways appears relatively common, with Gαq-coupled receptors able to modulate the responses at Gαi-coupled receptors, and vice versa (Selbie and Hill, 1998). With respect to calcium signalling, the prior addition of ATP or an alternative Gαq agonist can enable Gαi-coupled receptors to stimulate a calcium response (Werry et al., 2002), even in situations where there was no response in the absence of the priming agent (Rosethorne et al., 2004). This method appears to retain the natural G protein-coupling characteristics of the receptor in question, but because crosstalk can occur at a number of levels in the signal transduction pathway it may complicate interpretation of data with of novel ligands of unknown selectivity. Finally, as GPCR and Gα protein densities may differ considerably from one cell type to another, influencing the cellular response to a given agonist, efforts have been undertaken to construct GPCR-Gα fusion proteins (Wurch and Pauwels, 2001). By this way, a fixed 1:1 stoichiometry between both is achieved irrespective of the cell system and of the absolute expression level. While the proponents of this approach claim that it should allow an accurate comparison of experimental data obtained in different laboratories, a number of critical considerations have been raised, including potential attenuation of the Gα–βγ interactions and the ability of such fusion proteins to still activate endogenous Gα proteins (Wenzel-Seifert and Seifert, 2000; Vauquelin and von Mentzer, 2007).
The rapid and transient nature of calcium responses
Agonist-generated calcium responses are transient in nature; the cytoplasmic calcium concentration typically reaches a maximum after a few seconds and then declines to attain a longer-lasting plateau of variable height. The time to this peak response is variable and depends upon the degree of receptor activation, with higher agonist concentrations achieving peak responses more rapidly. Due to the rapid and complex nature of the calcium signal, the system is unlikely to reflect equilibrium binding conditions. In addition, it is common to determine the agonist-induced response at peak calcium level regardless of the time take to reach that point, exacerbating the non-equilibrium conditions. Despite this, many investigators apply pharmacological methods that assume equilibrium binding to their calcium studies (e.g. Schild analysis). We have chosen to demonstrate the influence of non-equilibrium conditions on apparent pharmacology using a series of computer-aided simulations. The model we have used is adapted from that described by Christopoulos et al. (1999), with one important difference. The Christopoulos model states that the calcium response fades as a consequence of receptor desensitization, yet is not always the case in experimental situations. For example, while angiotensin II produces a sharp and short (<1 min) rise in the cytoplasmic calcium levels in recombinant AT1-receptor expressing Chinese Hamster Ovary (CHO) cells, the level of inositol triphosphate molecules continues to rise unabated for almost 10 min (Vanderheyden et al., 1999). To better describe such a situation, we developed an alternative scheme in where it is not [AR] that ‘desensitizes’ but KE that increases with the rate k3 (Scheme 1A). This corresponds to a ‘desensitization’ of τ (τ=[R]total/KE, see below). As the agonist-bound receptors themselves were considered unable to desensitize within the short time frame a calcium signal is usually recorded, receptor ‘recycling’ was disregarded. This variant model produces more rapid peak times than the original, in line with experimental data (see below). Computer-assisted simulations were obtained by integrating the differential equations (Equations 2 to 4) as previously described (Vauquelin et al., 2001; Vauquelin and Van Liefde, 2006) and allowed the calcium signal (response) to be simulated as a function of time.
Scheme 1.
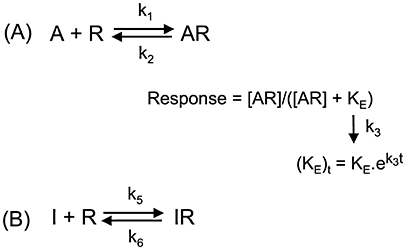
(A) Description of transient calcium response kinetics by a dynamic model adapted from that described by Christopoulos et al. (1999). In this model, binding of the agonist molecules (A) to free receptors (R) proceeds according to a reversible bimolecular reaction so that the amount of occupied receptors [AR] obeys the law of mass-action. The corresponding association and dissociation rate constants are referred to as k1 and k2 respectively. Agonist binding generates/favours an active receptor conformation that serves as the ‘stimulus’ for initiating a cascade of intracellular events leading to the response of interest. While the stimulus-response relationship could be linear in certain cases, this only seldom so (especially in recombinant receptor over-expressing cell systems; Brink et al., 2000) because of the limited capacity of some intervening cellular processes to cope with the upstream ‘demand’. Therefore, receptor occupancy-response relationships are commonly described by a logistic rectangular hyperbolic function where KE (=[R]total/τ) is an efficacy term (Black and Leff, 1983). Finally, to deal with the transient nature of the calcium response, KE is set to increase time-wise with the first-order rate constant k3. (B) Binding of competitive antagonist molecules (I) to free receptors also proceeds according to a reversible bimolecular reaction with association and dissociation rate constants denoted as k5 and k6 respectively.
| (2) |
| (3) |
| (4) |
At each time point (t) the (response)t=[AR]t/([AR]t+ (KE)t). These differential equations yield changes in KE as well as the percentage of free and occupied receptors after a very small time interval (t, typically 10 000 times less than t′, the total time lapse of the measurement).
Figure 1C shows an example of such simulated calcium signals as a response to increasing agonist concentrations as a function of the post-agonist administration time. When the agonist concentration increases, the response peak level is higher and occurs sooner. Such simulations represent a close approximation to real-life calcium transients such as those initiated upon addition of methacholine to CHO-M3 cells (Figure 1A). As described previously for this experimental system (Figure 1B), simulated agonist concentration-response curves based on peak levels may also closely mirror those based on AUC determinations (Figure 1D). As previously described, it is most commonly the peak calcium levels that are used to construct agonist concentration-response curves from which the maximal response (or intrinsic activity; Ariens, 1954), and potency (EC50) can be derived. However, because of the positive influence of the cellular amplification thereon, such values provide little information about the agonist's actual interaction with its receptor (Vauquelin and von Mentzer, 2007). Additionally, the recorded peak heights are unlikely to reflect equilibrium binding of the agonist because of the very small time lapse between its emergence and the agonist administration. In the ensuing sections we show step by step how these different phenomena might affect agonist concentration – calcium signal response curves.
The bimolecular binding process
Even in the case of a simple bimolecular ligand (L)-receptor interaction, one needs already to be alert to the potential interference of non-equilibrium situations when analysing radioligand saturation binding data in terms of affinity (defined by the equilibrium dissociation constant, Kd). As illustrated in Figure 2A, this is due to the fact that ligands need appreciably more time to reach equilibrium binding at low concentrations than at higher concentrations. The association curves are mono-exponential with a pseudo-first order rate constant, kobs (=0.69/apparent association t1/2). Yet, kobs is not truly a constant as, besides being function of the genuine rate constants, it is also positively related to the ligand concentration: i.e. kobs= k2+ k1.[L]. Hence, the apparent association t1/2 is negatively related to the ligand concentration. It is rather obvious that kobs should be positively related to k1 but less intuitive is that this is also the case with respect to k2. This forms a rationale for many observations showing that slow dissociating ligands also associate slowly and the definition by Motulsky and Mahan (1984) that equilibrium is reached when incubation exceeds four times the dissociation t1/2 of LR (or the slowest dissociating one when more than one ligand is present). After short incubation periods, non-equilibrium binding will be more prominent at the lowest ligand concentrations. As a result, while the amount of binding/response may already reflect a close-to-equilibrium situation at the highest ligand concentrations, it may still be far less than expected at the lowest concentrations. This will result in a steep saturation curve (i.e. nH > 1; Figure 2B) and the half-maximal binding (BC50) values may also be appreciably higher than expected for an equilibrium situation.
Figure 2.
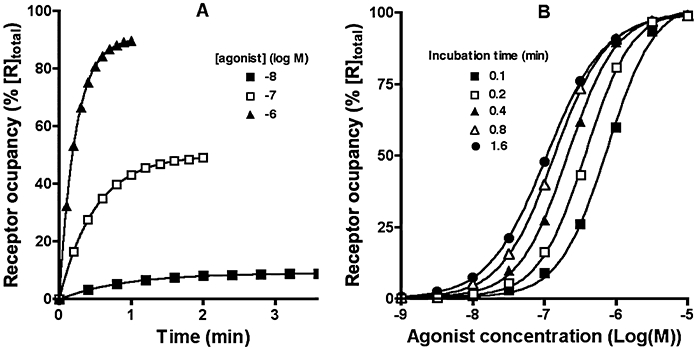
(A) Simulated receptor occupancy as a function of time at 10 nM, 100 nM and 1 µM of a ligand (with k1= 107 M−1·min−1 and k2= 1 min−1). Half-maximal binding is attained at 0.63, 0.35 and 0.16 min respectively. (B) Simulated receptor occupancy at different concentrations of the same ligand when measured after 0.1, 0.2, 0.4, 0.8 and 1.6 min. p(BC50) values are 6.17, 6.44, 6.68, 6.86 and 6.96 and slope factors (nH) of the curves are 1.38, 1.35, 1.27, 1.16 and 1.06 respectively.
Adding intrinsic efficacy and cellular amplification of the signal
In the ‘operational model’ from Black and Leff (1983) KE is an efficacy term that is inversely proportional to the ability of the agonist to generate/favour an active receptor conformation or, in other words, the stimulus. This ability is given by the ‘intrinsic efficacy, ε’ of the agonist in question (Furchgott, 1966). KE is also inversely related to the cellular amplification of the resulting signal. Being positively related to ε and the cellular amplification, it is more intuitive to use the transducer ratio term, τ (τ=[R]total/KE) than KE itself for describing the efficiency by which receptor occupancy is transduced to a biological effect (Black and Leff, 1983). Hence, τ will be adopted as the descriptor further on. For the same response and cellular system, τ reflects the agonist's intrinsic efficacy. Alternatively, for the same agonist, τ reflects the degree of cellular amplification. As τ decreases with time in the calcium assays (with the rate constant k3), only its initial value (i.e. at the time of agonist addition) is provided in the corresponding descriptions and figure legends.
Inspection of the operational model sheds light on three interesting facts. First, to obtain a near-linear receptor occupancy-response relationship at all ligand concentrations, τ must be very small so that only a minute response is generated even at full receptor occupancy. Next, Emax can be approached when τ is very large, but never attained. Finally, due to the hyperbolic nature of the relationship, the response is advantaged at low receptor occupancy, especially when τ is large. This will result in a τ-dependent leftward shift the agonist concentration-response curves or, in other words, increase the agonist's potency. As shown in Figure 3A and Table 1, this shift as well as the ‘intrinsic activity’ of the agonist is positively related to τ, not only for equilibrium binding situations but also for non-equilibrium situations in where the response is recorded after a short incubation time. It is only for small values of τ that the EC50 values come close to the BC50 values (Table 1). In the case of the theoretical equilibrium situation the slope of the agonist concentration-response curves remained the same as for the saturation binding curves (i.e. nH = 1) at all τ values examined. Yet, for the short-incubation non-equilibrium situations, the concentration-response curves became steeper (Figure 3A) especially at high τ (Table 1). Taken together, increasing the agonist's intrinsic efficacy and/or cellular amplification will cause the maximal response and agonist potency (i.e. the BC50/EC50 ratio) to increase in equilibrium as well as in short-incubation non-equilibrium situations and, in the latter situation, it will even affect the slope of the agonist concentration-response curves.
Figure 3.
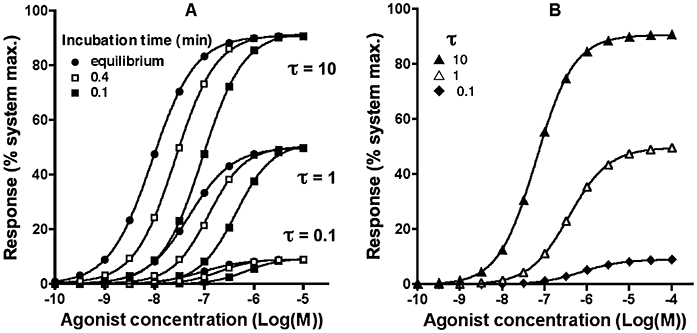
Simulated agonist concentration-response curves: (A) Effect of τ on agonist-mediated responses recorded after a brief, fixed-time incubations (0.1 and 0.4 min) and at equilibrium. Agonist kinetic parameters are: k1= 107 M−1·min−1 and k2= 1 min−1. (B) Effect of τ on calcium signal peak values for the same agonist and k3= 2 min−1. Time dependencies of the calcium signal at selected agonist concentrations are shown in Figure 1C for τ= 0.1. Parameters of the curves are given in Table 1.
Table 1.
Parameters obtained by analysis (variable slope) of the concentration- response curves shown in Figure 3A
| Time (min) | τ | pEC50 or pBC50* | Slope (nH) | Maximal response by agonist (% of maximal response by system) |
|---|---|---|---|---|
| Equilibrium | 10 | 8.04 | 1.00 | 91 |
| Equilibrium | 1 | 7.30 | 1.00 | 50 |
| Equilibrium | 0.1 | 7.04 | 1.00 | 9 |
| Equilibrium | R occupancy | 7.00* | 1.00 | |
| 0.1 | 10 | 7.03 | 1.04 | 92 |
| 0.1 | 1 | 6.36 | 1.18 | 52 |
| 0.1 | 0.1 | 6.15 | 1.27 | 10 |
| 0.1 | R occupancy | 6.12* | 1.29 | |
| 0.4 | 10 | 7.58 | 1.06 | 92 |
| 0.4 | 1 | 6.91 | 1.19 | 50 |
| 0.4 | 0.1 | 6.70 | 1.27 | 9 |
| 0.4 | R occupancy | 6.68* | 1.27 | |
| Peak | 10 | 7.20 | 0.97 | 91 |
| Peak | 1 | 6.43 | 0.93 | 50 |
| Peak | 0.1 | 6.14 | 0.91 | 9 |
| AUC | 10 | 7.17 | 1.05 | 56 |
| AUC | 1 | 6.70 | 1.04 | 17 |
| AUC | 0.1 | 6.52 | 1.01 | 2.3 |
Peak corresponds to peak values of the calcium response (Figure 3B). AUC corresponds to area under the calcium response curve (in % of total plot area, i.e. maximal response during 2 min).
pBC50 (given for the sake of comparison) corresponds to the half-maximal receptor occupancy by the same agonist (curves shown in Figure 2B).
AUC, area under the curve.
Adding the variable time to peak calcium response
In contrast to other assay formats (e.g. inositol triphosphate or cAMP accumulation measurements), the kinetic read-out of calcium levels allows the peak response to be accurately determined. It is unlikely, however, that equilibrium is achieved between receptor and agonist during the short time lapse between the administration of agonist and attainment of the peak (Figure 2). The agonist concentration- calcium (peak level) response curve will further be affected by the apriori unknown intrinsic efficacy of the agonist and cellular amplification of the signal (Figure 3A). In addition, it is also likely to be affected by the potential differences in time lapse at which the peak emerges at low and high agonist concentrations (Figure 1A and C) and the complex mechanisms that are responsible or the transient nature of the signals (Scheme 1). Simulations such as those shown in Figure 3B were performed to explore the impact of this additional level of complexity on the concentration- calcium peak response curves. Compared with the single time point non-equilibrium situations (Figure 3A), only relatively small changes are noticed when focussing on the effect of τ on the agonist's maximal response and potency (Table 1). In particular, while the potency remains less than expected from an equilibrium binding situation at low τ, this tendency can be reversed upon increasing τ (Leff and Martin, 1986). Very similar potencies and variations thereof are obtained by analysing the AUC rather than peak values.
Interpretation of assay-dependent agonist pharmacology – agonist-biased signalling?
As described above, many factors including the degree of receptor activation, the cellular amplification of the signal and transient nature of the calcium response may affect the maximal response and potency of the agonist as well as the slope of its concentration-response curve. This can significantly complicate the interpretation of agonist pharmacology, particularly when comparing transient responses to those measured at longer time points. To illustrate this point, we have compared the concentration-response curves of two agonists in two different assay systems. The agonists have identical intrinsic efficacy but 10-fold difference in potency and 100-fold difference in off-rate. The first assay mimics a calcium peak response in case of a very large system amplification (τ= 100). The second assay system mimics a [35S]GTPγS binding assay with little amplification (τ= 1) and where agonist has been allowed to equilibrate for 60 min prior to initiation of functional effect by addition of [35S]GTPγS for a further 60 min. Figure 4A shows that at equilibrium with the [35S]GTPγS binding assay, the agonists have the expected 10-fold difference in potency. When the response is observed at the peak calcium concentration however, the agonists behave very differently (Figure 4B). The lower affinity (Kd= 100 nM), fast onset agonist is highly potent (EC50= 1.5 nM), as would be expected in a system with higher receptor reserve. In contrast, the higher affinity (Kd= 10 nM), slowly equilibrating agonist is less potent (EC50= 5.5 nM), due to the transient nature of this read-out. Such reversal in agonist potency orders at different pathway read-outs has been suggested as evidence of agonist-directed trafficking of receptor signalling (Kenakin, 1995), whereby different agonists may trigger/stabilize distinct receptor conformations modulating the receptor's preference for certain G proteins/responses (Hermans, 2003). In line with some critical considerations in Urban et al. (2007), it is advisable that any data used in support of this hypothesis should first be assessed for kinetic artifacts. As developed in the next section, these complex, non-equilibrium-based recordings could also interfere with the study of antagonist-receptor interactions.
Figure 4.

Simulated concentration-response curves for two agonists (with kinetic properties specified in the figure) measured in the following experimenal systems. (A) [35S]GTPγS binding assay in a system with low cellular amplification (τ= 1). Membranes are pretreated for 60 min with increasing concentrations of the agonists. Then [35S]GTPγS is added and its binding is measured after an additional 60 min incubation. (B) Calcium signal peak values for the same agonists in a cellular readout system with very high amplification (τ= 100) and with k3= 2 min−1. Response values are expressed in per cent of the maximal response produced by each agonist in question.
Calcium signals for the study of antagonist-receptor interactions – impact of hemi-equilibrium
In functional experiments, antagonist-receptor interactions are typically investigated indirectly by evaluating their ability to decrease agonist-mediated responses. One of the most robust pharmacological methods available for determining antagonist affinity is that described by Arunlakshana and Schild (1959), which calculates the concentration of antagonist required to shift the agonist concentration-response curve by twofold. The resulting value is termed the equilibrium dissociation constant (Kd) and is equal to the concentration of antagonist required to bind 50% of available receptors at equilibrium. Equilibrium is attained between the antagonist and receptor by ensuring a sufficient pre-equilibration time before addition of the agonist (Leff and Martin, 1986). It is not possible to achieve equilibration after agonist addition, however, because of the very short time lapse between the administration of the agonist and the attainment the calcium peak level. This situation was termed ‘hemi-equilibrium’ by Paton and Rang (1965). This can result in a reduction in the maximal response elicited by the agonist, even with competitive antagonists that should be fully surmountable (Vauquelin et al., 2002a, b;). This phenomenon, known as ‘insurmountable’ antagonism, has historically been associated with binding of irreversible antagonists which results in a permanent reduction of receptor number. However, insurmountability will also be observed when pre-formed antagonist-receptor complexes are reversible but dissociate so slowly that only part of the receptors can be liberated and, hence, occupied/stimulated by the subsequently added agonist molecules before the response is measured. This situation will readjust with time until ultimately, both the agonist- and the antagonist- receptor interactions reach competitive equilibrium. Therefore, the insurmountability of slow dissociating antagonists is only ‘apparent’ and can theoretically be overcome by measuring the response after a sufficient time lapse. Yet, this is not possible with calcium response measurements and, because of the much shorter delay between these measurements and the agonist administration when compared with other experimental paradigms, even otherwise ‘surmountable’, quite fast dissociating competitive antagonists may display insurmountable behaviour. To illustrate this assertion, simulations presented in Figure 5 explore the effect of pre-administered antagonists with different dissociation rates on the agonist concentration-dependent calcium peak levels. For these simulations, some differential equations have to be added or adapted. As for the agonist, the antagonist (I)-receptor interactions are described as a reversible bimolecular binding process with the bimolecular association rate constant, k5, and the monomolecular dissociation rate constant, k6 (Scheme 1). The antagonists are competitive so that agonist and antagonist binding is mutually exclusive. While Equations 3 and 4 are still valid, Equation 2 has to be extended (to Equation 5) and an additional equation has to be to included (Equation 6) to incorporate antagonist binding: i.e.
Figure 5.
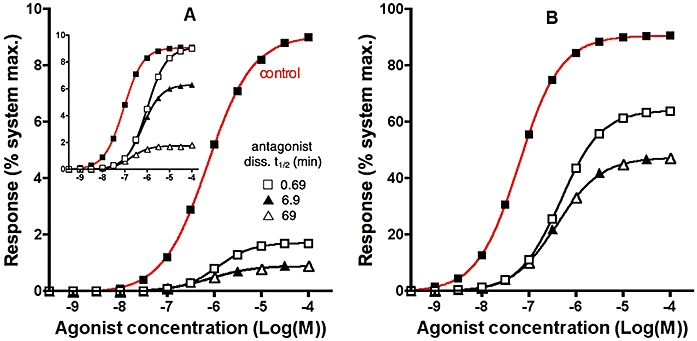
Simulated agonist concentration- calcium peak response curves in a system with τ= 0.1 (A) or 10 (B) without pretreatment (control, red curve) or after pretreating the cells with a fast, medium- or slow dissociating antagonist (rates specified in the figure and k5= 108 M−1·min−1 for all). Pretreatment lasts until equilibrium binding (91% receptor occupancy for [I]= 10.Kd) is reached. Then different concentrations of agonist (with k1= 107 M−1·min−1 and k2= 1 min−1) are added and calcium peak levels are recorded. Other parameters are: k3= 2 min−1. Insert of panel A. Same conditions as for the main panel except that τ remains steady (k3= 0 min−1) and that the response is only measured after a fixed, 10 min incubation with the agonist.
| (5) |
| (6) |
Figure 5 shows simulated calcium peak levels after addition of different agonist concentrations to naïve receptors (control curve) or after pretreatment with antagonists with different dissociation rates. For the sake of comparison, antagonist binding has reached equilibrium at the moment of agonist administration and the same fraction of receptors (91%) are occupied. All the antagonists produce a significant depression of the maximal response by the agonist, i.e. they show insurmountable behaviour. In this respect, it is remarkable that even the fast dissociating antagonist (k6= 1, corresponding to dissociation t1/2= 0.69 min) is insurmountable in this experimental setting albeit to a lesser degree than the slower dissociating ones. Of note is that increasing τ dampens the insurmountable behaviour of the antagonists (compare Figure 5B to 5A). This is because the agonist is able to generate a response at lower receptor occupancy (see above). That even the fast-dissociating antagonist shows some insurmountability in the calcium response paradigm can merely be attributed to the very short time lag between the administration of the agonist end the manifestation of the calcium peak. This is clearly illustrated by the fact that such an antagonist no longer displays insurmountability when another response (but with the same receptor occupancy – response relationship) is measured after a much longer incubation time (10 min) with the agonist (compare the insert and main panel of Figure 5A). Insurmountable antagonism can also be a hallmark of allosteric inhibition of receptor signalling (May et al., 2007). The fact that even competitive antagonists can show insurmountability of calcium responses largely precludes the use of this assay system for ascribing compound mechanism of action.
Although Schild analysis is arguably the most appropriate method to determine antagonist affinity from functional experiments, it is far more common to perform inhibition (IC50) experiments where the antagonist is titrated against a fixed concentration of agonist. Provided the agonist- and (at all concentrations) antagonist-receptor interactions are competitive and at equilibrium, antagonist potency ratios are inversely related to their IC50-ratios, and the equilibrium dissociate constant (Kd) can be calculated using the functional form of the Cheng and Prusoff correction (Cheng and Prusoff, 1973; Leff and Dougall, 1993). Although this last condition is more or less obeyed for such assays that permit a sufficiently long incubation time before the response is measured, this is again not the case in calcium assays. While co-incubation experiments clearly reflect a non-equilibrium situation, experiments in where the antagonist was allowed to equilibrate with the receptor before addition of the agonist are at best in hemi-equilibrium. The profound effect of this hemi-equilibrium is illustrated in Figure 6, where inhibition curves of competitive antagonists are simulated at different agonist concentrations (abscissa) and the antagonist IC50 values (expressed as pIC50) are calculated by analysing the curves according to a variable-slope one-site competition model. The different curves in each panel correspond to antagonists with different dissociation rates. With a low ‘receptor reserve’ or a weak partial agonist (i.e. a small value of τ, Figure 6A), the pIC50s of the three antagonists investigated varied only marginally, even upon a 100-fold increase in the agonist concentration. This may inadvertently lead to the false conclusion that the antagonists in question were non-competitive/allosteric (Christopoulos and Kenakin, 2002). For a larger value of τ (Figure 6B), the most rapidly dissociating antagonist exhibits the relationship expected from a normal competitive ligand. However, even with this large receptor reserve the pIC50s vary little with the slowest dissociating antagonist.
Figure 6.
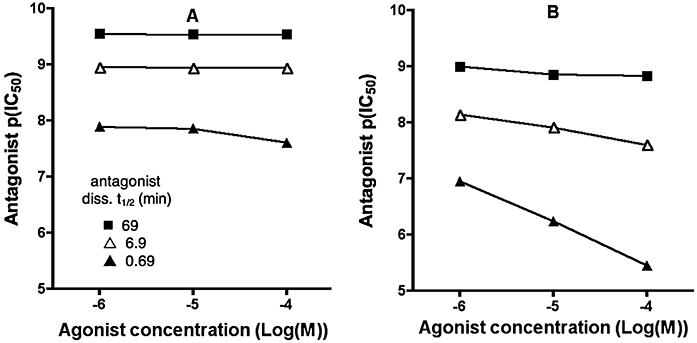
Antagonist pIC50 values from simulated inhibition curves when calcium responses are measured at different agonist concentrations (abscissa) in a system with τ= 0.1 (A) or 10 (B). In the simulations, receptors were pretreated for 30 min with medium alone or with different concentrations of a fast, medium- or slow dissociating antagonist (specified in the figure and k5= 1 108 M−1·min−1 for all) and then challenged with agonist (with k1= 107 M−1·min−1 and k2= 1 min−1). Other parameters are: k3= 2 min−1. The antagonist IC50 values (expressed as pIC50) are calculated by analysing the so-obtained inhibition curves (not shown) according to a variable-slope one-site competition model.
So, rather than being constant, the Kd value of an antagonist calculated using the Cheng Prusoff correction are dependent upon its dissociation rate, the agonist's intrinsic efficacy and the cellular amplification of the signal (Figure 6). Even more extreme situations could be encountered when comparing antagonist IC50 values obtained from calcium assays with those obtained from other functional assays requiring a much longer, e.g. 10-min incubation with the agonist. As illustrated in Figure 7, the slow-dissociating antagonist is apparently less potent in the calcium assay (panel A) whereas the fast-dissociating antagonist appears to be less potent in the alternative assay (panel B). Comparable assay-related antagonist potency inversions have already been observed for, e.g. the CCK2 receptor in CHO cells (Pommier et al., 1999). Note that shallow inhibition curve of the fast dissociating antagonist in the calcium assay (solid squares in panel A) results from the combination of a high value of τ and the partial liberation of the receptors by the antagonist before the measurement of the peak. Similar behaviour has also been observed before in the case of partially insurmountable AT1 angiotensin receptor antagonism (Fierens et al., 1999). However, at first impression, one could be tempted to advance that the agonist triggers the calcium response by activating two distinct receptors, and that they display quite different affinity for the fast dissociating antagonist and comparable affinity for the slow dissociating antagonist. Such observations may also be mistaken as evidence for receptor-specific conformations. Alternatively, if the two read-outs were from different tissues, it might be concluded that the antagonist displays tissue-selectivity.
Figure 7.
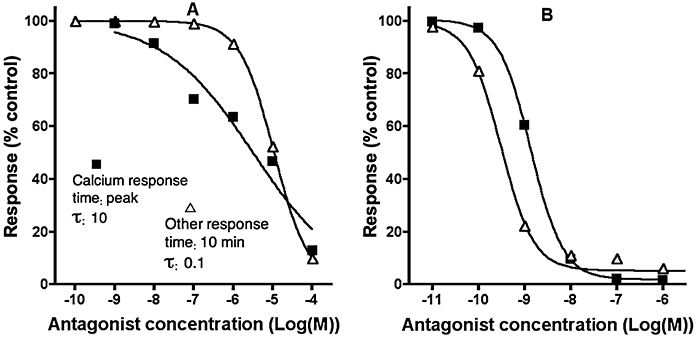
Simulated inhibition curves of a fast- (panel A: dissociation t1/2= 0.69 min) and slow dissociating antagonist (panel B: dissociation t1/2= 69 min) by measuring distinct responses by the same agonist. Receptors are pretreated for 30 min with different concentrations of both antagonists. Then a high concentration (100 µM) of agonist (with k1= 107 M−1.min−1 and k2= 1 min−1) is added and calcium peak levels are recorded in a system with high cellular amplification (τ= 10) and k3= 2 min−1. Alternatively, responses are recorded after 10 min incubation in a system with low and steady cellular amplification (τ= 0.1 and k3= 0 min−1). Other parameters are: k5= 108 M−1·min−1.
Positive aspects of calcium signalling
To this point we have largely focussed on the confounding issues and potential bias associated with using calcium assays to investigate the affinity and mechanism of action of new receptor ligands. There are, however, several qualities that might make it the assay format of choice for a number of different applications. First, calcium assays are often highly sensitive. A large degree of signal amplification can be achieved in high receptor expression systems (Sykes et al., 2009), making it one of the most sensitive pathways for high throughput screening to discover new agonists. This does tend to skew the apparent potency and efficacy, so it is important to also use an alternative system (preferably primary human cells) that more closely resembles the physiological setting in order to properly characterize the compounds. Providing low concentrations of agonist are used, calcium assays can also be a very sensitive tool for discovering new antagonists, where hemi-equilibrium conditions (particularly in low expression cell lines) can make the pre-equilibrated antagonist appear much higher affinity than would be expected if it was left to reach equilibrium with the agonist (discussed above). Thus, providing the appropriate secondary assays are in place to determine mechanism of action, calcium assays are very useful for the discovery of new GPCR ligands.
Second, many physiological processes involve rapid receptor-mediated calcium signalling, such as cardiac muscle contraction. If the receptor under study was responsible for such transient signalling, it could be argued that the ‘apparent’ pharmacology observed in a calcium assay is actually more relevant and predictive of in vivo behaviour than that observed at equilibrium. For example, a competitive compound with slow dissociation kinetics that appears insurmountable in the calcium assay would be likely to also exhibit this profile in vivo, reducing the maximal agonist-induced response rather than shifting its potency. The important consideration here is that the mechanism of insurmountability would not be obvious from the original experiment using calcium assays. Indeed, in situations in where the receptors are pre-incubated with antagonist before their challenge with agonist, it is difficult to determine whether such compounds bind an allosteric site at the receptor or simply display slow dissociation kinetics. Analysis of agonist concentration-response curves under antagonist co-incubation conditions could solve this issue as, under this condition, competitive antagonists should merely produce a rightward shift of the agonist concentration-response curve (Vauquelin et al., 2002a, b;) This has been observed for AT1 angiotensin receptor antagonists in inositol phosphate accumulation measurements (Fierens et al., 1999; Le et al., 2007). Yet, because of the fast emergence of calcium peak levels, such rightward shifts may only become perceptible at very high antagonist concentrations, especially if they dissociate slowly from the receptor.
Moving forward – how should we interpret data at hemi-equilibrium?
We have described in detail the potential bias associated with non-equilibrium conditions in calcium assays, but have also established that there are clear technical and practical benefits to using this assay format. With this quandary in mind, is there a way forward that enables the estimation of antagonist affinity at hemi-equilibrium? As can be seen from the simulations described above, the influence of hemi-equilibrium is less apparent where there is a significant amplification in the response (large τ-value). In practical terms, this large receptor reserve can be achieved by high receptor expression in recombinant systems, efficient receptor coupling and high efficacy agonists, or a combination of the three. In these systems, even non-competitive antagonists will shift the concentration response curve of an agonist to the right, until the point where spare receptors are no longer available. In these situations it is possible to estimate the affinity of insurmountable antagonists by calculating the pA2 from dose ratios at low agonist responses, as described by Kenakin et al. (2006). This can be demonstrated by examining the relationship between pA2 and pKB of an insurmountable antagonist (Equation 7),
| (7) |
where [A] is the control agonist concentration at which the dose ratio (DR) is calculated. This equation shows that at low agonist occupancy (i.e. [A]<<KA) the pA2 will tend towards the pKB, but at high occupancy the pA2 will overestimate the true affinity of the antagonist. A practical solution to estimate the affinity of an insurmountable antagonist would therefore be to use a system with high receptor reserve and calculate the pA2 (using pA2= log(DR-1)-log[B]) by determining the DR at low agonist responses. This can be exemplified using the data in Figure 5B for the most slowly dissociating compound (t1/2= 69 min) which has a pKB of 10 (see Figure 8). If the DR is calculated at the 10% response level (green arrow), the estimated pA2 is reasonably accurate at 10.08. If, however, the DR is calculated at the 40% response level (red arrow), the resultant pA2 overestimates the true affinity by fivefold at 10.69.
Figure 8.
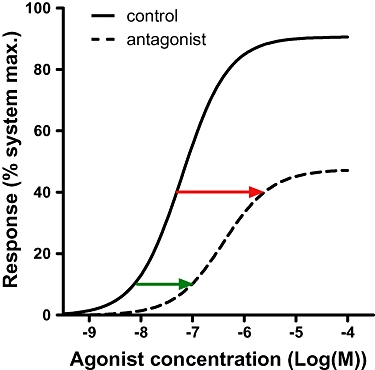
Illustration of the optimal agonist response levels at which to determine the dose ratio (DR) of an insurmountable antagonist. Data are reproduced from Figure 5A for the most slowly dissociating antagonist (t1/2= 69 min). Red and green arrows illustrate the DR at 40% and 10% response respectively.
Conclusions
The calcium assay remains one of the most widely utilized experimental systems to characterize the pharmacology of novel G protein-coupled receptor ligands. In this review we have described a number of factors that may complicate the interpretation of calcium response data, focussing in particular on the influence of rapid response kinetics on observed potency, efficacy and affinity of receptor ligands. We have also highlighted the potential danger of misinterpreting kinetic artefacts as evidence for a number of topical concepts, including agonist-biased signalling, tissue selective antagonism and allosteric mechanisms of action. Despite this, the calcium assay has significant practical benefits and is also a highly relevant readout for drug targets that utilize this pathway physiologically. We suggest that, providing the common artefacts are fully appreciated and data are analysed appropriately, the calcium assay remains an important tool for characterizing the pharmacology of novel receptor ligands.
Glossary
Abbreviations
- AUC
area under the curve
- BC50
ligand concentration producing half-maximal receptor occupancy
- CHO cells
Chinese hamster ovary cells
- CHO-M3
Chinese hamster ovary cells recombinantly expressing the M3 muscarinic receptor
- DR
dose ratio
- EC50
agonist concentration producing half-maximal response
- FLIPR
fluorescence imaging plate reader
- GFP
green fluorescent protein
- GPCR
G protein-coupled receptor
- HEK cells
human embryonic kidney cells
- InsP3
inositol 1,4,5-trisphosphate
- Kd
equilibrium dissociation constant, equivalent to the concentration of ligand required to bind 50% of the available receptor sites at equilibrium
- kobs
pseudo first-order rate constant for ligand-receptor association. Other kinetic constants are specified in Scheme 1
- KE
parameter describing the efficiency by which receptor occupancy is transduced to a biological effect
- nH
hill coefficient
- PLC
phospholipase C enzyme
- τ
[R]total/KE where [R]total is the total receptor concentration
Conflicts of interest
None.
References
- Ariens EJ. Affinity and intrinsic activity in theory of compepitive inhibition. Part I. Problems and theory. Arch Int Pharmacodyn. 1954;99:32–49. [PubMed] [Google Scholar]
- Arunlakshana O, Schild HO. Some quantitative uses of drug antagonists. Br J Pharmacol. 1959;14:48–58. doi: 10.1111/j.1476-5381.1959.tb00928.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augustine GJ. How does calcium trigger neurotransmitter release? Curr Opin Neurobiol. 2001;11:320–326. doi: 10.1016/s0959-4388(00)00214-2. [DOI] [PubMed] [Google Scholar]
- Baird GS, Zacharias DA, Tsien RY. Circular permutation and receptor insertion within green fluorescent proteins. Proc Natl Acad Sci USA. 1999;96:11241–11246. doi: 10.1073/pnas.96.20.11241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berridge MJ. Calcium oscillations. J Biol Chem. 1990;265:9583–9586. [PubMed] [Google Scholar]
- Berridge MJ. Calcium signalling and cell proliferation. Bioessays. 2005;17:491–500. doi: 10.1002/bies.950170605. [DOI] [PubMed] [Google Scholar]
- Berridge MJ, Bootman MD, Roderick HL. Calcium signalling: dynamics, homeostasis and remodeling. Nat Rev Mol Cell Biol. 2003;4:517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- Black JW, Leff P. Operational models of pharmacological agonism. Proc R Soc Lond B Biol Sci. 1983;220:141–162. doi: 10.1098/rspb.1983.0093. [DOI] [PubMed] [Google Scholar]
- Blinks JR. Use of calcium-regulated photoproteins as intracellular Ca2+ indicators. Methods Enzymol. 1989;172:164–203. doi: 10.1016/s0076-6879(89)72015-2. [DOI] [PubMed] [Google Scholar]
- Bovolenta S, Foti M, Lohmer S, Corazza S. Development of a Ca(2+)-activated photoprotein, Photina, and its application to high-throughput screening. J Biomol Screen. 2007;12:694–704. doi: 10.1177/1087057107301497. [DOI] [PubMed] [Google Scholar]
- Brink CB, Wade SM, Neubig RR. Agonist-directed trafficking of porcine alpha(2A)-adrenergic receptor signaling in Chinese hamster ovary cells: l-isoproterenol selectively activates G(s) J Pharmacol Exp Ther. 2000;294:539–547. [PubMed] [Google Scholar]
- Chambers C, Smith F, Williams C, Marcos S, Liu ZH, Hayter P, et al. Measuring intracellular calcium fluxes in high throughput mode. Comb Chem High Throughput Screen. 2003;6:355–362. doi: 10.2174/138620703106298446. [DOI] [PubMed] [Google Scholar]
- Cheng Y, Prusoff WH. Relationship between the inhibition constant (K1) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem Pharmacol. 1973;22:3099–3108. doi: 10.1016/0006-2952(73)90196-2. [DOI] [PubMed] [Google Scholar]
- Christopoulos A, Kenakin T. G protein-coupled receptor allosterism and complexing. Pharmacol Rev. 2002;54:323–374. doi: 10.1124/pr.54.2.323. [DOI] [PubMed] [Google Scholar]
- Christopoulos A, Parsons AM, Lew MJ, El-Fakahany EE. The assessment of antagonist potency under conditions of transient response kinetics. Eur J Pharmacol. 1999;382:217–227. doi: 10.1016/s0014-2999(99)00550-6. [DOI] [PubMed] [Google Scholar]
- Comley J. Assay interference, a limiting factor in HTS? Drug Discov World. 2003;4:91–98. [Google Scholar]
- Conklin BR, Farfel Z, Lustig KD, Julius D, Bourne HR. Substitution of three amino acids switches receptor specificity of Gq alpha to that of Gi alpha. Nature. 1993;363:274–276. doi: 10.1038/363274a0. [DOI] [PubMed] [Google Scholar]
- Eglen RM, Reisine T. Photoproteins: important new tools in drug discovery. Assay Drug Dev Technol. 2009;6:659–671. doi: 10.1089/adt.2008.160. [DOI] [PubMed] [Google Scholar]
- Faehling M, Kroll J, Föhr KJ, Fellbrich G, Mayr U, Trischler G, et al. Essential role of calcium in vascular endothelial growth factor A-induced signaling: mechanism of the antiangiogenic effect of carboxyamidotriazole. FASEB J. 2002;16:1805–1807. doi: 10.1096/fj.01-0938fje. [DOI] [PubMed] [Google Scholar]
- Fierens FLP, Vanderheyden PML, De Backer J-P, Vauquelin G. Insurmountable angiotensin II AT1 receptor antagonists: the role of tight antagonist binding. Eur J Pharmacol. 1999;372:199–206. doi: 10.1016/s0014-2999(99)00205-8. [DOI] [PubMed] [Google Scholar]
- Furchgott RF. The use of β-haloalkylamines in the differentiation of receptors and in the determination of dissociation constants of receptor-agonist complexes. Adv Drug Res. 1966;3:21–55. [Google Scholar]
- Gee KR, Brown KA, Chen WN, Bishop-Stewart J, Gray D, Johnson I. Chemical and physiological characterization of fluo-4 Ca(2+)-indicator dyes. Cell Calcium. 2000;27:97–106. doi: 10.1054/ceca.1999.0095. [DOI] [PubMed] [Google Scholar]
- Greer PL, Greenberg ME. From synapse to nucleus: calcium-dependent gene transcription in the control of synapse development and function. Neuron. 2008;59:846–860. doi: 10.1016/j.neuron.2008.09.002. [DOI] [PubMed] [Google Scholar]
- Hermans E. Biochemical and pharmacological control of the multiplicity of coupling at G-protein-coupled receptors. Pharmacol Ther. 2003;99:25–44. doi: 10.1016/s0163-7258(03)00051-2. [DOI] [PubMed] [Google Scholar]
- Hescheler J, Rosenthal W, Trautwein W, Schultz G. The GTP-binding protein, Go, regulates neuronal calcium channels. Nature. 1987;325:445–447. doi: 10.1038/325445a0. [DOI] [PubMed] [Google Scholar]
- Hodder P, Mull R, Cassaday J, Berry K, Strulovici B. Miniaturization of intracellular calcium functional assays to 1536-well plate format using a fluorometric imaging plate reader. J Biomol Screen. 2004;9:417–426. doi: 10.1177/1087057104264038. [DOI] [PubMed] [Google Scholar]
- Hofer AM, Schlue WR, Curci S, Machen TE. Spatial distribution and quantitation of free luminal [Ca] within the InsP3-sensitive internal store of individual BHK-21 cells: ion dependence of InsP3-induced Ca release and reloading. FASEB J. 1995;9:788–798. doi: 10.1096/fasebj.9.9.7601343. [DOI] [PubMed] [Google Scholar]
- Inglese J, Johnson RL, Simeonov A, Xia M, Zheng W, Austin CP, et al. High-throughput screening assays for the identification of chemical probes. Nat Chem Biol. 2007;3:466–479. doi: 10.1038/nchembio.2007.17. [DOI] [PubMed] [Google Scholar]
- Jaggar JH, Porter VA, Lederer WJ, Nelson MT. Calcium sparks in smooth muscle. Am J Physiol Cell Physiol. 2000;278:C235–C256. doi: 10.1152/ajpcell.2000.278.2.C235. [DOI] [PubMed] [Google Scholar]
- Kenakin T. Agonist-receptor efficacy. II. Agonist trafficking of receptor signals. Trends Pharmacol Sci. 1995;16:232–238. doi: 10.1016/s0165-6147(00)89032-x. [DOI] [PubMed] [Google Scholar]
- Kenakin T, Jenkinson S, Watson C. Determining the potency and molecular mechanism of action of insurmountable antagonists. J Pharmacol Exp Ther. 2006;319:710–723. doi: 10.1124/jpet.106.107375. [DOI] [PubMed] [Google Scholar]
- Kostenis E. Is Galpha16 the optimal tool for fishing ligands of orphan G-protein-coupled receptors? Trends Pharmacol Sci. 2001;22:560–564. doi: 10.1016/s0165-6147(00)01810-1. [DOI] [PubMed] [Google Scholar]
- Le MT, Pugsley M, Vauquelin G, Van Liefde I. Molecular characterisation of the interactions between olmesartan and telmisartan and the human angiotensin II AT1 receptor. Br J Pharmacol. 2007;151:952–962. doi: 10.1038/sj.bjp.0707323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leff P, Dougall IG. Further concerns over Cheng-Prusoff analysis. Trends Pharmacol Sci. 1993;14:110–112. doi: 10.1016/0165-6147(93)90080-4. [DOI] [PubMed] [Google Scholar]
- Leff P, Martin GR. Peripheral 5-HT2-like receptors. Can they be classified with the available antagonists? Br J Pharmacol. 1986;88:585–593. doi: 10.1111/j.1476-5381.1986.tb10239.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May LT, Leach K, Sexton PM, Christopoulos A. Allosteric modulation of G protein-coupled receptors. Annu Rev Pharmacol Toxicol. 2007;47:1–51. doi: 10.1146/annurev.pharmtox.47.120505.105159. [DOI] [PubMed] [Google Scholar]
- Miyawaki A, Llopis J, Heim R, McCaffery JM, Adams JA, Ikura M, et al. Fluorescent indicators for Ca2+ based on green fluorescent proteins and calmodulin. Nature. 1997;388:882–887. doi: 10.1038/42264. [DOI] [PubMed] [Google Scholar]
- Motulsky HJ, Mahan LC. The kinetics of competitive radioligand binding predicted by the law of mass action. Mol Pharmacol. 1984;25:1–9. [PubMed] [Google Scholar]
- Mulligan SJ, MacVicar BA. Monitoring intracellular Ca2+ in brain slices with fluorescent indicators. In: Zamponi G, editor. Voltage-Gated Calcium Channels. New York: Kluwer Academic; 2005. pp. 12–26. [Google Scholar]
- Paredes RM, Etzler JC, Watts LT, Zheng W, Lechleiter J. Chemical calcium indicators. Methods. 2008;46:143–151. doi: 10.1016/j.ymeth.2008.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton WD, Rang HP. The uptake of atropine and related drugs by intestinal smooth muscle of the guinea-pig in relation to acetylcholine receptors. Proc R Soc Lond B Biol Sci. 1965;163:1–44. doi: 10.1098/rspb.1965.0058. [DOI] [PubMed] [Google Scholar]
- Pommier B, Da Nascimento S, Dumont S, Bellier B, Million E, Garbay C, et al. The cholecystokininB receptor is coupled to two effector pathways through pertussis toxin-sensitive and -insensitive G proteins. J Neurochem. 1999;73:281–288. doi: 10.1046/j.1471-4159.1999.0730281.x. [DOI] [PubMed] [Google Scholar]
- Rang HP. The receptor concept: pharmacology's big idea. Br J Pharmacol. 2006;147:S9–S16. doi: 10.1038/sj.bjp.0706457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards GR, Jack AD, Platts A, Simpson PB. Measurement and analysis of calcium signaling in heterogeneous cell cultures. Methods Enzymol. 2006;414:335–347. doi: 10.1016/S0076-6879(06)14019-7. [DOI] [PubMed] [Google Scholar]
- Rizzuto R, Simpson AW, Brini M, Pozzan T. Rapid changes of mitochondrial Ca2+ revealed by specifically targeted recombinant aequorin. Nature. 1992;358:325–327. doi: 10.1038/358325a0. [DOI] [PubMed] [Google Scholar]
- Rosethorne EM, Leighton-Davies JR, Beer D, Charlton SJ. ATP priming of macrophage-derived chemokine responses in CHO cells expressing the CCR4 receptor. Naunyn Schmiedebergs Arch Pharmacol. 2004;370:64–70. doi: 10.1007/s00210-004-0932-7. [DOI] [PubMed] [Google Scholar]
- Schroeder KS, Brad DN. FLIPR: a new instrument for accurate, high throughput optical screening. J Biomol Screen. 1996;1:75–80. [Google Scholar]
- Selbie LA, Hill SJ. G protein-coupled-receptor cross-talk: the fine-tuning of multiple receptor-signalling pathways. Trends Pharmacol Sci. 1998;19:87–93. doi: 10.1016/s0165-6147(97)01166-8. [DOI] [PubMed] [Google Scholar]
- Sullivan E, Tucker EM, Dale IL. Measurement of [Ca2+] using the Fluorometric Imaging Plate Reader (FLIPR) Methods Mol Biol. 1999;114:125–133. doi: 10.1385/1-59259-250-3:125. [DOI] [PubMed] [Google Scholar]
- Sykes DA, Dowling MR, Charlton SJ. Exploring the mechanism of agonist efficacy: a relationship between efficacy and agonist dissociation rate at the muscarinic M3 receptor. Mol Pharmacol. 2009;76:543–551. doi: 10.1124/mol.108.054452. [DOI] [PubMed] [Google Scholar]
- Takahashi A, Camacho P, Lechleiter JD, Herman B. Measurement of intracellular calcium. Physiol Rev. 1999;79:1089–1125. doi: 10.1152/physrev.1999.79.4.1089. [DOI] [PubMed] [Google Scholar]
- Urban JD, Clarke WP, von Zastrow M, Nichols DE, Kobilka B, Weinstein H, et al. Functional selectivity and classical concepts of quantitative pharmacology. J Pharmacol Exp Ther. 2007;320:1–13. doi: 10.1124/jpet.106.104463. [DOI] [PubMed] [Google Scholar]
- Vanderheyden PML, Fierens FLP, De Backer J-P, Fraeyman N, Vauquelin G. Distinction between surmountable and insurmountable selective AT1 receptor antagonists by use of CHO-K1 cells expressing human angiotensin II AT1 receptors. Br J Pharmacol. 1999;126:1057–1065. doi: 10.1038/sj.bjp.0702398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vauquelin G, Morsing P, Fierens FLP, De Backer JP, Vanderheyden PML. A two-state receptor model for the interaction between angiotensin II AT1 receptors and their non-peptide antagonists. Biochem Pharmacol. 2001;61:277–284. doi: 10.1016/s0006-2952(00)00546-3. [DOI] [PubMed] [Google Scholar]
- Vauquelin G, Van Liefde I. From slow antagonist dissociation to long- lasting receptor protection. Trends Pharmacol Sci. 2006;27:355–359. doi: 10.1016/j.tips.2006.05.001. [DOI] [PubMed] [Google Scholar]
- Vauquelin G, Van Liefde I, Birzbier BB, Vanderheyden PML. New insights in insurmountable antagonism. Fundam Clin Pharmacol. 2002a;16:263–272. doi: 10.1046/j.1472-8206.2002.00095.x. [DOI] [PubMed] [Google Scholar]
- Vauquelin G, Van Liefde I, Vanderheyden P. Models and methods for studying insurmountable antagonism. Trends Pharmacol Sci. 2002b;23:514–518. doi: 10.1016/s0165-6147(02)02081-3. [DOI] [PubMed] [Google Scholar]
- Vauquelin G, von Mentzer P. In: In G-Protein Coupled Receptors: Molecular Pharmacology. Vauquelin G, von Mentzer P, editors. Chichester, UK: John Wiley & Sons Ltd; 2007. pp. 53–64.pp. 185–191. [Google Scholar]
- Wenzel-Seifert K, Seifert R. Molecular analysis of beta(2)-adrenoceptor coupling to G(s)-, G(i)-, and G(q)-proteins. Mol Pharmacol. 2000;58:954–966. doi: 10.1124/mol.58.5.954. [DOI] [PubMed] [Google Scholar]
- Werry TD, Christie MI, Dainty IA, Wilkinson GF, Willars GB. Ca(2+) signalling by recombinant human CXCR2 chemokine receptors is potentiated by P2Y nucleotide receptors in HEK cells. Br J Pharmacol. 2002;135:1199–1208. doi: 10.1038/sj.bjp.0704566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wurch T, Pauwels PJ. Analytical pharmacology of G protein-coupled receptors by stoichiometric expression of the receptor and G(alpha) protein subunits. J Pharmacol Toxicol Methods. 2001;45:3–16. doi: 10.1016/s1056-8719(01)00126-5. [DOI] [PubMed] [Google Scholar]


