Kinetics of the Reverse Mode of the Na⁺/Glucose Cotransporter

Abstract

This study investigates the reverse mode of the Na⁺/glucose cotransporter (SGLT1). In giant excised inside-out membrane patches from Xenopus laevis oocytes expressing rabbit SGLT1, application of α-methyl-d-glucopyranoside (αMDG) to the cytoplasmic solution induced an outward current from cytosolic to external membrane surface. The outward current was Na⁺ - and sugar-dependent, and was blocked by phlorizin, a specific inhibitor of SGLT1. The current-voltage relationship saturated at positive membrane voltages (30–50 mV), and approached zero at − 150 mV. The half-maximal concentration for αMDG-evoked outward current ($K_{0.5}^{\mathrm{\alpha }\text{MDG}}$) was 35 mM (at 0 mV). In comparison, $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ for forward sugar transport was 0.15 mM (at 0 mV). $K_{0.5}^{\text{Na}}$ was similar for forward and reverse transport (≈35 mM at 0 mV). Specificity of SGLT1 for reverse transport was: αMDG (1.0) > d-galactose (0.84) > 3-O-methyl-glucose (0.55) > d-glucose (0.38), whereas for forward transport, specificity was: αMDG ≈ d-glucose ≈ d-galactose > 3-O-methyl-glucose. Thus there is an asymmetry in sugar kinetics and specificity between forward and reverse modes. Computer simulations showed that a 6-state kinetic model for SGLT1 can account for Na⁺/sugar cotransport and its voltage dependence in both the forward and reverse modes at saturating sodium concentrations. Our data indicate that under physiological conditions, the transporter is poised to accumulate sugar efficiently in the enterocyte.

Introduction

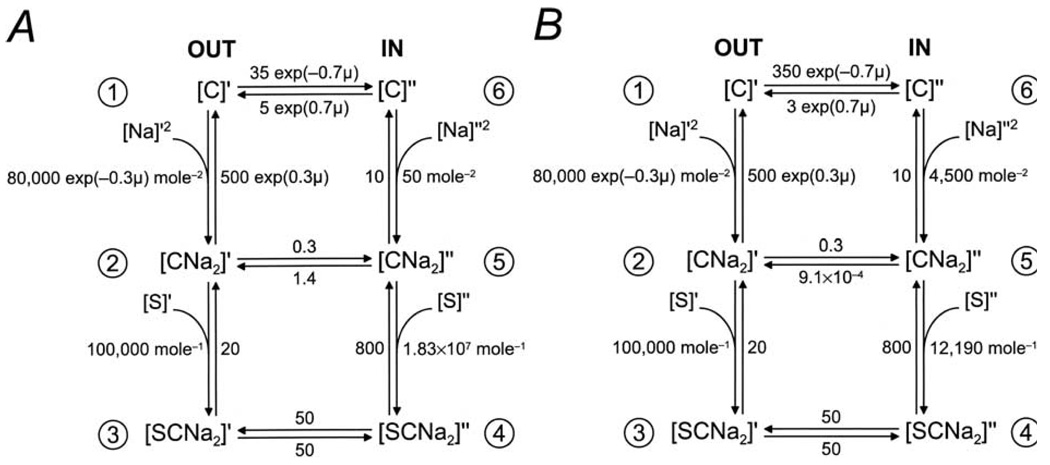
Glucose is accumulated across the apical membrane of the small intestine and proximal tubular kidney cells by Na⁺-glucose cotransporters (SGLTs). The cloning of SGLT1 and its over-expression in Xenopus laevis oocytes allowed for a detailed characterization of the kinetics of cotransport (Hediger et al., 1987; Parent et al., 1992a,b; Loo et al., 1993; Hazama et al., 1997; Loo et al., 1998). Electrophysiological and tracer uptake experiments in intact oocytes expressing SGLT1 focused on the forward mode, where the substrates are transported from the extracellular to intracellular compartments. These studies have revealed that SGLT1 is electrogenic, with a stoichiometry of 2 Na⁺:1 glucose (e.g., Chen et al., 1995; Mackenzie, Loo & Wright, 1998; Meinild et al., 2002). Cotransport occurs via an alternating access mechanism. Two external Na⁺ ions bind to the cotransporter before glucose, and the substrates are transported simultaneously across the membrane (Parent et al., 1992b). A 6-state kinetic model (see Fig. 6) has been proposed for SGLT1 that accounts for the presteady-state and steady-state kinetics of the transporter operating in the forward mode (Parent et al., 1992b; Hazama et al. 1997; Meinild et al., 2002).

Fig. 6.

Parameters for the 6-state ordered kinetic model for SGLT1. (A) Six-state ordered kinetic model for Na⁺/sugar cotransport (modified from Parent et al., 1992b). There are 6 states, the ligand-free (C₁, C₆), the Na⁺-bound (C₂, C₅), and the fully loaded (C₃, C₄) transporter on both sides of the membrane. Two external Na⁺ ions bind to the protein before glucose. The fully loaded transporter undergoes a conformational change to expose the bound substrates to the interior of the cell. The ligand-free transporter returns to the outside for another cycle. Membrane voltage influences the conformational change of the empty transporter and Na⁺ binding. The rate constants for rabbit SGLT1 were from Parent et al. (1992b), with the corrected value for k₅₄ (1.83 × 10⁷ M⁻¹s⁻¹, Parent et al., 1992c). All rate constants are expressed as per second (s⁻¹). (B) The rate constants were revised taking into consideration the experimental data obtained in this study for the reverse mode. When k₆₅, k₁₆, and k₆₁ were changed to 4500 M⁻²s⁻¹, 350 s⁻¹, and 3 s⁻¹ respectively, microscopic reversibility (Parent et al., 1992b) required that k₅₄ and k₅₂ be decreased to 12190 M⁻¹s⁻¹ and 9.1 × 10⁻⁴ s⁻¹. The reduced potential (μ) is defined by μ = FV_m/RT, where F is the Faraday’s constant, V_m is the membrane potential, R is the gas constant, and T is the absolute temperature. Simulations of the model for reverse transport are shown by the curves in Figs. 2, 3A and 4. The revised parameters predict that the sugar (αMDG) and Na⁺ dissociation constants (K_D,s) at the cytoplasmic surface are 66 and 47 mM. On the external surface, the measured K_0.5 Values ($K_{0.5}^{\mathrm{\alpha }\text{MDG}}=330\mathrm{\mu }\mathrm{M}$ at 100 mm [Na⁺]_o and $K_{0.5}^{\text{Na}}=54\text{mM}$ at 1 mM [αMDG]_o, from Parent et al., 1992b) are close to the K_D values (200 µM and 79 mM).

The goal of this study is to critically examine the kinetic model for sugar transport by measuring the kinetics of SGLT1 in the reverse mode. The kinetic model and the set of kinetic parameters obtained for rabbit SGLT1 (Parent et al., 1992b, see also Fig. 6A) predicted that transport is reversible. Computer simulations of the model indicate that when the Na⁺ gradient is reversed (10 mm [Na⁺]_o and 100 mm [Na⁺]_i), the transporter generates an outward current with half-maximal concentrations for Na⁺ and αMDG $(K_{0.5}^{\text{Na}},\text{ and }{K}_{0.5}^{\alpha \text{MDG}})$ of 410 mM and 25 µM (at 0 mV). The goal of this study is to obtain direct information on reverse sugar transport by SGLT1, and to define the kinetic constants on the internal membrane surface. The giant excised patch technique was used to control the composition of the internal compartment (cytoplasm). The kinetics of reverse sugar transport were measured under driving forces similar to transport in the forward mode, i.e., saturating internal Na⁺ (500 mm), low external Na⁺ (10 mm), sugar-free external solutions, and membrane potentials from + 50 to − 150 mV. This facilitated a direct comparison of the kinetic parameters for reverse and forward transport. The results indicate that the affinity of SGLT1 for sugars in the internal membrane surface is 250-fold less than that on the external surface. In addition, there is a difference in sugar specificity between the two membrane surfaces. Computer simulations indicate that the 6-state model for SGLT1 can largely account for the steady-state kinetics of both forward and reverse modes. A preliminary account of this study has been presented (Eskandari, Loo & Wright, 1999), and since then a similar preliminary study has been reported (Sauer et al., 2000).

Materials and Methods

OOCYTE PREPARATION

Mature Xenopus laevis oocytes were collected from adult female frogs anaesthetized with 0.1% Tricaine. Frogs were killed with an overdose of anesthetic (Nembutal) after the final collection of oocytes. These protocols were approved by the UCLA Animal Research Committee, and meet all the NIH guidelines for the humane treatment of animals used for research. The oocytes were defolliculated, injected with 50 ng of rabbit SGLT1 cRNA, and maintained in Barth’s medium (in mm: 88 NaCl, 1 KCl, 0.33 Ca(NO₃)₂, 0.41 CaCl₂, 0.82 MgSO₄, 2.4 NaHCO₃, 10 HEPES, pH 7.4) supplemented with 5 µg/ml gentamycin at 18°C for 3–8 days until use (Birnir, Loo & Wright, 1991; Parent et al., 1992a; Loo et al., 1993).

SUGAR TRANSPORT

For transport in the forward direction, we used the two-electrode voltage clamp on intact oocytes and the sugar-dependent currents were measured as previously described (Birnir et al., 1991; Parent et al., 1992a; Loo et al., 1993). The oocytes were normally bathed in a NaCl buffer (in mm: 100 NaCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.5). Sugar transport was determined by the addition of αMDG (α-methyl-d-glucopyranoside, a non-metabolizable sugar analogue) to the external solution. The majority of the oocytes used in the present study had maximal whole-cell sugar (αMDG)-induced currents (I_max) of 600 to 1000 nA (at Vm of − 50 mV). The whole-cell oocyte capacitance ranged from 400 to 550 nF.

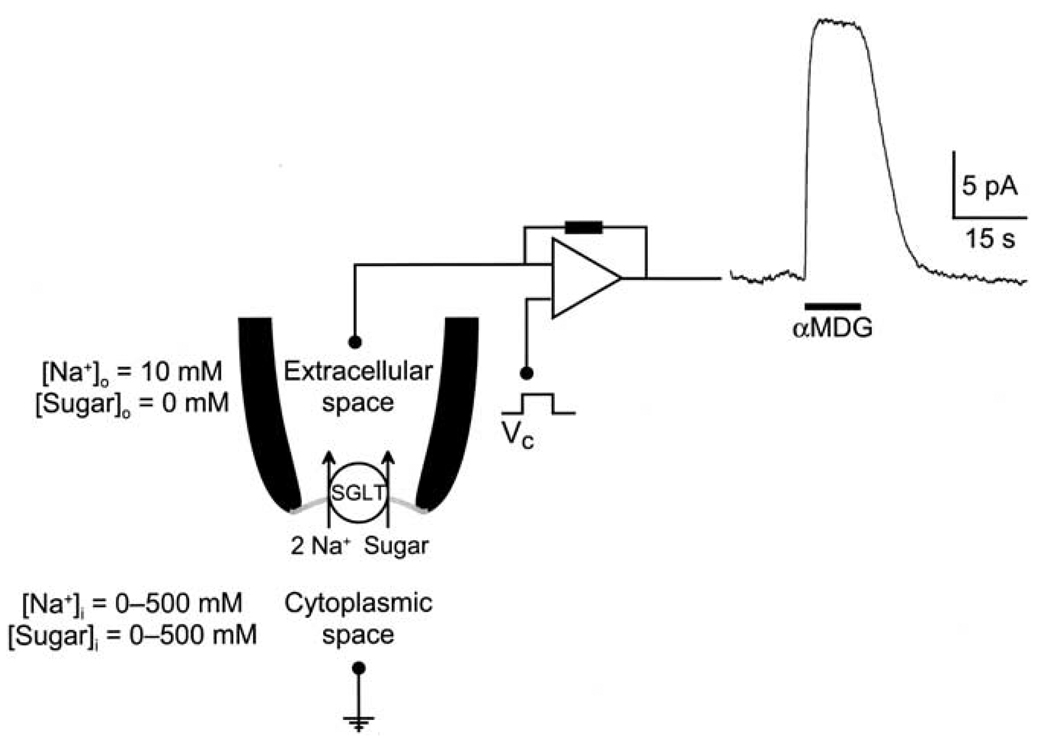
Reverse sugar transport was studied using the giant excised patch (Hilgemann, 1995) after confirming the level of SGLT1 expression in the oocyte with the 2-electrode voltage clamp. The vitelline membrane of the oocyte was manually removed, high electrical resistance seals (between 1–10 GΩ) were made, and the patches were excised into the inside-out configuration. Patch pipettes were pulled from borosilicate glass and had a tip inner diameter ranging from 25 to 40 µm, with an access resistance of < 200 kΩ measured before seal formation in the bathing solution. Capacitance of the giant patches ranged from 5 to 10 pF, and assuming a specific membrane bilayer capacitance of 1 µF/cm², the surface area of patches was between 500–1000 µm². Electrophysiological experiments were performed using an Axopatch 1B amplifier equipped with an IHS-1 integrating headstage and pClamp software (Axon Instruments, Union City, CA). Current records were low-pass filtered at 500 Hz. The giant-patch experiments were especially challenging and the success rate for obtaining giant excised patches was less than 10%. However, once obtained, excised patches were stable for periods ranging between 30 min to 1 h, and this allowed us to carry out up to 30 solution changes in some experiments. The membrane voltage was usually maintained at 0 mV. For reverse transport, the pipette (external) solution contained (in mm): 10 NaCl, 90 cholineCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.5, and bath (internal or cytoplasmic) solution normally contained (in mm): 500 NaCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.2. During experiments, the bath solution was continuously perfused with the 500 mm NaCl buffer. The kinetics of Na⁺ - and sugar-activation of SGLT1 were studied by varying the concentrations of NaCl (0–500 mm) and αMDG (0–500 mm) in the bath solution. The osmotic difference between the external and internal solutions had no effect on the results since sugar-evoked outward currents were not observed in non-injected oocytes, and in SGLT1-expressing oocytes the sugar-evoked outward current showed a specificity for sugars, and mannitol, which does not interact with SGLT1 on the external surface, did not induce an outward current. All experiments were performed at room temperature (20–22°C).

The voltage dependence of sugar transport was studied using a pulse protocol where the membrane was stepped from the holding potential (− 50 mV in intact cells, and 0 mV in excised patches) to a series of voltages, starting at + 50 mV and ending at − 150 mV, in 20 mV decrements. The convention is that downward deflections of the current traces (negative currents) represent inward currents, due to the influx of cations from the external compartment into the cell. Thus, reverse transport would result in an outward current, and upward deflection of the current trace.

The sugar-induced current was obtained by subtracting the current in the absence of sugar from the total currents with sugar added to the bath solution. The sugar-induced currents were fitted (using Sigmaplot, SPSS Inc., Chicago, IL) to the equation (1): I = (I_max [S])/(K_0.5 + [S]), where [S] is the αMDG concentration in the intracellular surface, I_max is the maximal current, and K_0.5 is the half-maximal sugar concentration. Reported errors represent the standard error of the mean obtained from data from several patches.

Simulations of the steady-state properties of the 6-state kinetic model (Fig. 6) were performed by generating the current vs. voltage relations (using Eqn. A50 of Parent et al., 1992b) from the steady-state distribution of transporter states (Eqns. A44–A49 of Parent et al., 1992b), solved numerically by Gauss-Jordan elimination (Press et al., 1986). At each membrane voltage, the predicted half-maximal concentrations for Na⁺ and sugar $(K_{0.5}^{\text{Na}},K_{0.5}^{\alpha \text{MDG}})$ were obtained by fitting the simulated dose-response relations (current vs. [αMDG] or [Na⁺]) to hyperbolic (for sugar activation) or sigmoidal (for Na⁺ activation) relations.

Results

A current record from an excised inside-out patch demonstrating outward Na⁺/sugar transport by rabbit SGLT1 is depicted in Fig. 1. The Na⁺ concentration gradient across the membrane has been reversed: the pipette and bath solutions, representing the external and internal membrane compartments, contained 10 and 500 mm Na⁺, respectively. With the membrane potential held at 0 mV, when 100 mm αMDG was applied to the cytoplasmic surface of the membrane, there was an immediate (half time t_½≈150–200 ms) outward current (I_out) of ≈20 pA. The evoked outward current returned to baseline when sugar was removed from the bath solution. In control experiments, sugar-induced outward currents were not observed in membranes patches from non-injected oocytes.

Fig. 1.

Outward Na⁺/sugar cotransport by rabbit SGLT1. Continuous current record of an excised inside-out patch. The membrane potential (V_m) was clamped at 0 mV, and at the time shown by the bar, 100 mm αMDG was added to the external superfusing solution (internal surface of SGLT1). Sugar induced an upward deflection of the current trace, signifying an outward current (20 nA). Pipette (or external) solution contained (in mm): 10 NaCl, 90 cholineCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.5, and bath (or internal) solution contained (in mm): 500 NaCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.2.

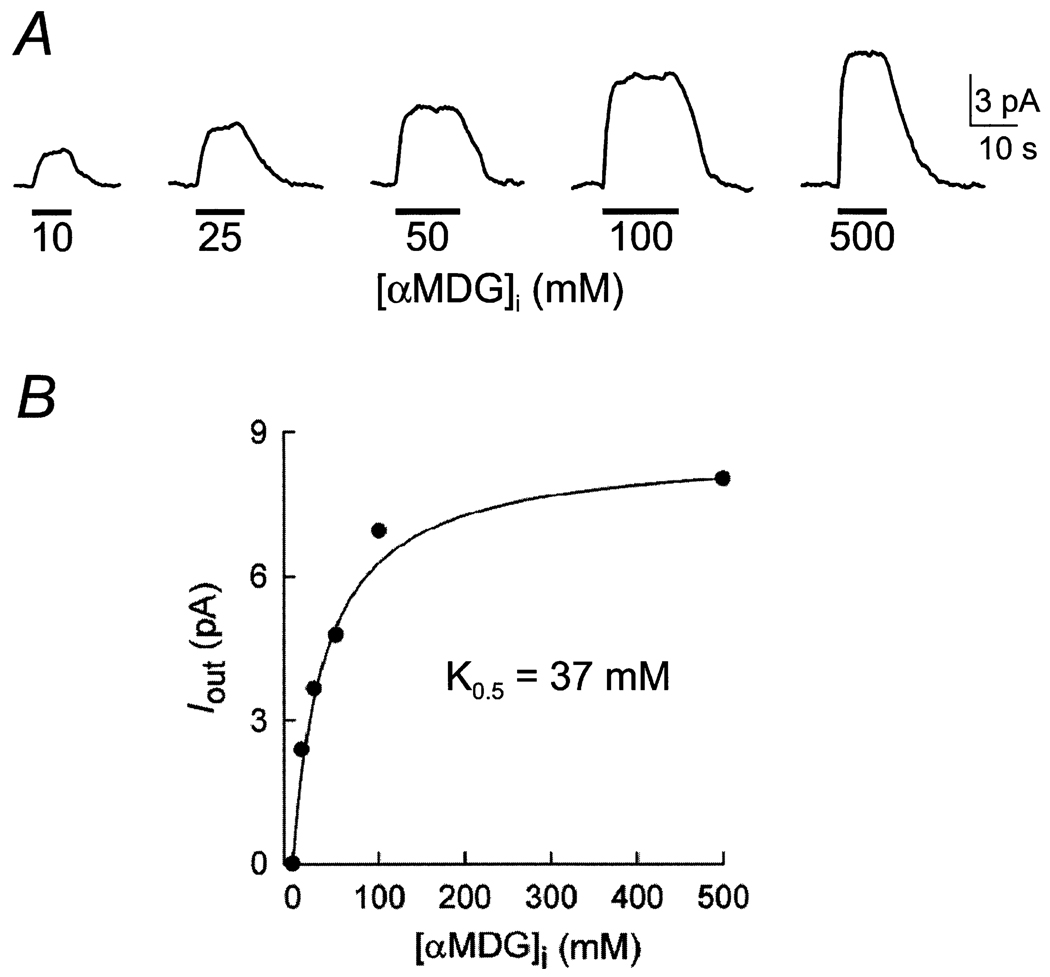
The dependence of the reverse mode on internal sugar (αMDG) concentration is illustrated in Fig 2A. Outward sugar-induced currents were measured as internal [αMDG] was varied from 0 to 500 mm while the membrane potential was maintained at 0 mV. The Na⁺ concentration gradient was constant (500 mm [Na]_i/10 mm [Na]_o). The sugar-induced outward current (I_out) was saturable and followed a simple hyperbolic relationship. For the data shown in Fig. 2B, the half-maximal concentration for αMDG ($K_{0.5}^{\mathrm{\alpha }\text{MDG}}$) was 32 mM. From five experiments on rabbit SGLT1, $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ was 32 ± 8 mM. The solid line in Fig. 2B is the predicted dose-response curve with a K_0.5 of 37 mM obtained from simulation of the kinetic parameters of Fig. 6B (see below).

Fig. 2.

Dependence of the outward current on internal sugar (αMDG) concentration. (A) Shown are current records in the same patch as various concentrations of αMDG were added to the bath solution. The experiment was performed on an oocyte expressing rabbit SGLT1. Pipette and bath solutions contained 10 and 500 mm Na⁺ as in Fig. 1. Membrane potential was 0 mV. (B) Relationship between the αMDG-induced outward current (I_out) and [αMDG]_i. Data are from the experiment of Fig. 2A. The data followed a hyperbolic relation (Eq. 1) with a half-maximal concentration (K_0.5) for αMDG of 32 ± 5 mM (standard error of the fit). The population average was 32 ± 8 mM (n = 5). The curve is the prediction of the model with the set of kinetic parameters shown in Fig. 6B with a K_0.5 of 37 mM.

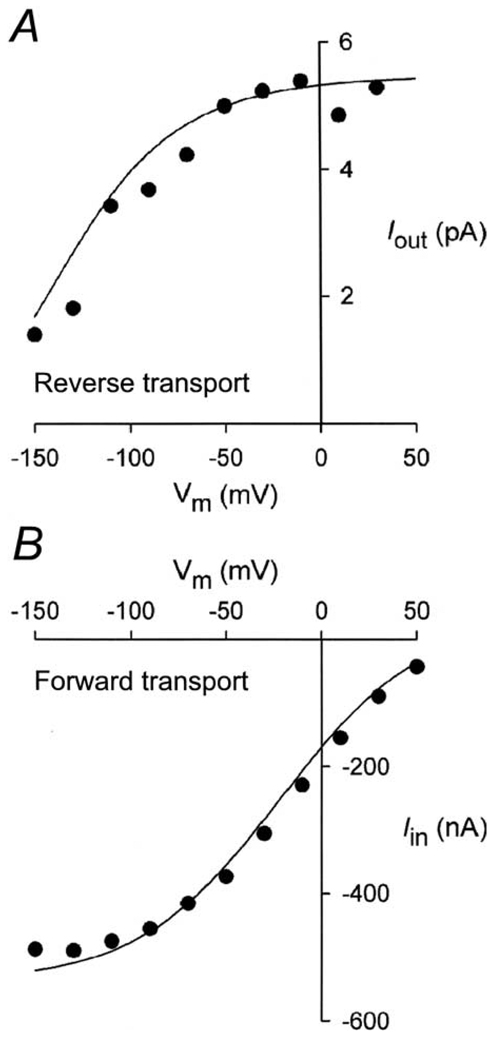
The voltage-dependence of the sugar-induced outward current was obtained with a pulse protocol where the membrane potential was stepped (from the holding potential, 0 mV) to a series of test values (V_m). The current-voltage relationships were obtained by subtracting the total current in the absence of sugar from the total currents in the presence of sugar (100 mm αMDG) in the cytoplasmic surface of the membrane (Fig. 3A). The I/V curve saturated at positive V_m (30–50 mV), and approached zero at − 150 mV. This relationship contrasts sharply with that determined for Na⁺/sugar transport in the forward mode in intact oocytes, where the I/V curve saturated with hyperpolarizing voltages (Fig. 3B). A major difference between the two I/V curves was that at 0 mV, the current for the reverse mode was saturated, but was only 40% of the maximum for the forward mode.

Fig. 3.

Current-voltage (I/V) relationships of the inward and outward sugar-evoked currents mediated by rabbit SGLT1. (A) I/V relation for outward current (reverse Na⁺/glucose cotransport). External and internal [Na⁺] were 10 and 500 mm, respectively. The sugar-induced current was obtained by subtracting the current in the absence of sugar from that in the presence of sugar ([αMDG]_i, = 100 mm). A similar I/V relationship was obtained in four patches. (B) I/V relation for the inward current (forward Na⁺/glucose cotransport) from whole-cell currents using the two-electrode voltage clamp. Bath solution was the 100 mm NaCl buffer. The inward current was generated by 10 mm αMDG. The curves were model predictions from Fig. 6B scaled for the appropriate number of transporters (7 × 10¹⁰ transporters for Fig. 3B). The simulations were performed with the rate constants: k₁₆ = 350 s⁻¹ and k₆₁ = 3 s⁻¹ in A ([Na⁺]_o = 10 mm); and k₁₆ = 35 s⁻¹ and k₆₁ = 5 s⁻¹ in B ([Na⁺]_o = 100 mm).

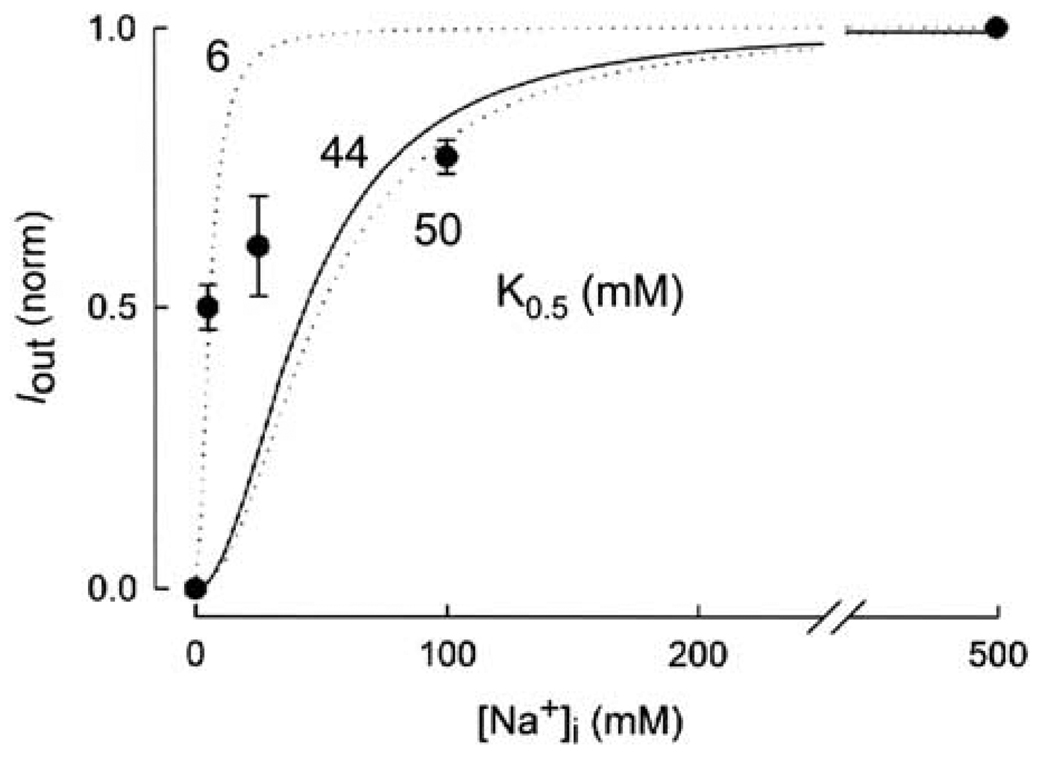
The dependence of the reverse currents on internal Na⁺ was studied with the membrane potential maintained at 0 mV. The outward currents induced by 100 mm αMDG were determined as internal [Na⁺] was varied from 0 to 500 mm. Fig. 4 shows a composite of the dose-response curves from four oocytes. The reverse current increased as internal [Na⁺] was increased. At 5 mm Na⁺, the current was ≈50% of that at 500 mm (Fig. 4). However, the current did not saturate at 100 mm Na⁺, and was 82% of that at 500 mm Na⁺. When the dose-response curve was fitted with a hyperbolic function (not shown), the K_0.5 for Na⁺ ($K_{0.5}^{\text{Na}}$) was 10 ± 5 mM. Since 2 Na⁺ ions are transported with each glucose molecule (Mackenzie et al., 1998), we anticipate a sigmoidal relationship. The two dashed lines were drawn according to the Hill equation (with a Hill coefficient of 2) for K_0.5 of 6 and 50 mM. The solid line in Fig. 4 is the model prediction with a K_0.5 of 44 mM and a Hill coefficient of 2 obtained from simulation of Fig. 6B (see below).

Fig. 4.

Dependence of the outward sugar-induced currents on internal Na⁺ concentration. The normalized dose-response (I_out vs. [Na⁺]_i) curve is the composite of data from four experiments with each data point representing the mean ± the standard error of 2 to 4 values. The data at 5and 500 mm Na⁺ were from 4 experiments. Membrane potential was clamped at 0 mV, and internal [αMDG] was maintained at 100 mm. The outward currents were measured as the internal [Na⁺] was increased from 0 to 500 mm. [Na⁺] in the pipette (external) solution was 10 mm. When the data set was fitted with a hyperbolic equation (Eq. 1), the K_0.5 for Na⁺ was 10 ± 5mm. The two dashed lines were drawn with the Hill equation with K_0.5 of 6 and 50 mM, and a Hill coefficient of 2.0. The solid curve was the model prediction using the kinetic parameters shown in Fig. 6B. The model predicted a K_0.5 of 44 mM for Na⁺ and a Hill coefficient of 2.

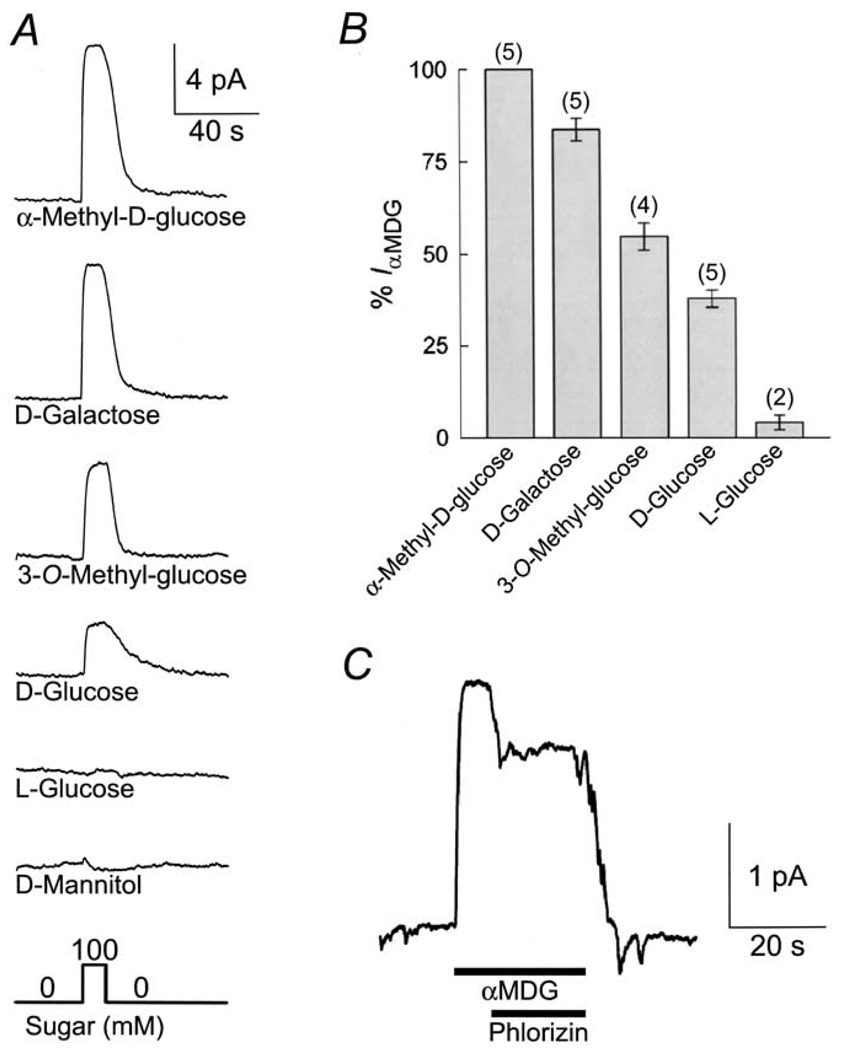
The sugar selectivity of SGLT1 in the reverse mode was examined by applying various sugars (100 mm) to the cytoplasmic surface of the membrane in the same patch (Fig. 5A and B). The sugars induced outward currents of different magnitudes. The relative magnitude of the outward current generated by the various sugars was: αMDG (1.0) > d-galactose (0.84 ± 0.03; n = 5 ) > 3-O-methyl-glucose (0.55 ± 0.04; n = 4) > d-glucose (0.38 ± 0.02; n = 5) (Fig. 5B). l-Glucose induced a very small outward current (4 ± 2% of that evoked by αMDG), whereas d-mannitol did not induce an outward current (Fig. 5B and C).

Fig. 5.

Sugar specificity of the sugar-evoked outward current mediated by rabbit SGLT1. (A) Outward current (I_out) was measured at 0 mV in the same patch, as various sugars (100 mm) were added to the cytoplasmic surface. Pipette and bath solutions contained 10 and 500 mm Na⁺, respectively. (B) Comparison of the magnitude of the outward currents induced by the different sugars. The currents have been normalized to the current generated by 100 mm αMDG, and the number of experiments is indicated above the bars. No outward current was induced by d-mannitol. (C) Phlorizin (1 mm), a specific blocker of SGLT1, led to a 34 ± 3% (n = 3) inhibition of the outward current evoked by 100 mm αMDG.

Phlorizin is a specific high-affinity competitive inhibitor of Na⁺/glucose cotransport from the external membrane surface, with an apparent inhibitory constant K_i ≈ 10 µM and a true K_i of 0.76 µM (Umbach, Coady & Wright, 1990; Birnir et al., 1991; Parent et al., 1992a; Hazama et al., 1997; Hirayama et al., 1996). Fig. 5C shows that sugar transport in the reverse mode was also sensitive to phlorizin. Addition of phlorizin (1 mm) to the bath solution blocked the reverse current induced by αMDG (100 mm) by 25%. In three patches, 1 mm phlorizin inhibited the outward current evoked by 100 mm αMDG by 34 ± 4%. The limited solubility of phlorizin in aqueous solutions did not allow us to examine higher concentrations of phlorizin. We estimate an apparent K_i > 1 mM and the true K_i to be ≈0.5 mM (using Eqn. III-5 of Segal (1975), with the assumption that phlorizin is also a competitive inhibitor on the internal membrane surface). Addition of phlorizin (1 mm) to the bath solution in the absence of sugar did not induce any changes in steady-state current (not shown).

Discussion

The present study shows that SGLT1 is reversible. The protein will cotransport Na⁺ and glucose in and out of the cell depending on the direction of the driving force. Negative membrane voltages increase transport in the forward mode, and positive voltages increase transport in the reverse mode. There is significant asymmetry with respect to the apparent affinity constant for sugar. The apparent affinity constant for sugar is 250-fold higher for the reverse mode than that for the forward mode (at 0 mV, $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ is 0.15 mM for the forward, and 35 mM for the reverse mode). The asymmetry in sugar affinity is accompanied by a similar loss of affinity for phlorizin between both membrane surfaces: the true K_i for phlorizin increased from 0.76 µM on the external surface (Hirayama et al., 1996) to ≈ 0.5 mM on the internal surface. Sugar specificity also differs between the forward and reverse modes. However, the half-maximal concentration for Na⁺-activation of the currents ($K_{0.5}^{\text{Na}}$ ≈ 40 mM at 0 mV) is similar for the forward and reverse modes.

The I/V curves for forward and reverse sugar transport differed. Forward sugar transport saturated with hyperpolarizing voltages, and decreased with depolarizing voltages, while reverse sugar transport saturated with depolarizing voltages and decreased with hyperpolarizing voltages. Despite the fact that the driving forces for forward and reverse transport were comparable, the two I/V curves are not mirror images. At 0 mV, current was maximal for reverse transport, but was only 40% of the maximum for forward transport (Figs. 3A and B).

In addition to the asymmetry in the apparent sugar affinity, there also appears to be a difference in sugar selectivity. The relative outward currents generated by the addition of 100 mm sugars to the cytosolic side of the membrane is shown in Fig. 5. Assuming that the maximum rate for Na⁺/sugar cotransport in the outward direction is identical for these sugars, as is the case for cotransport in the forward direction (Birnir et al, 1991; Hirayama, Loo & Wright, 1997; Díez-Sampedro, Wright & Hirayama, 2001), the relative affinities (for rSGLT1) are αMDG > d-galactose > 3-O-methyl-glucose > d-glucose > > l-glucose. Similar results were obtained for sugar competition of αMDG uptake into inside-out membrane vesicles expressing hSGLT1 (αMDG > 3-O-methyl-glucose ~ d-galactose > d-glucose; Quick & Tomasevic & Wright, 2003). In contrast, the relative affinities for sugar cotransport in the forward direction by rabbit, rat and human isoforms of SGLT1 is αMDG ~ d-glucose ~ d-galactose > 3-O-methyl-glucose (Ikeda et al., 1989; Birnir et al., 1991; Panayatova-Heiermann, Loo & Wright, 1995; Hirayama et al., 1996; 1998; Díez-Sampedro et al., 2001). The differences in sugar affinity and selectivity for cotranport in the two directions under the same driving forces suggest differences in the architecture of the outward- and inward-facing sugar binding sites. This is different from lac permease where it appears that there is one lactose-binding site that is alternatively exposed to the two sides of the plasma membrane (Abramson et al., 2003; Guan & Kaback, 2004).

Reverse sugar transport has also been studied for rabbit SGLT1 using the giant excised patch (Sauer et al., 2000). For sugar activation, the $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ obtained in the present study (32 ± 8 mM) is higher than 7.0 ± 0.8 mM obtained by Sauer et al. (2000) under slightly different conditions (Na⁺-free external solutions). Our value is similar to that obtained for human SGLT1 (56 ± 9 mM) expressed in E. coli using inside-out membrane vesicle preparations with Na⁺-free external solutions (Quick et al., 2003). Thus it is unlikely that the high internal sugar K_0.5 is due to trans-inhibition by external Na⁺. In fact, model simulations (see below) confirm that the presence or absence of 10 mm NaCl in the external solution has no effect on either the internal $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ or the maximum rate of reverse transport over the voltage range − 100 to + 50 mV. In a previous oocyte study, it was reported that the internal $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ for hSGLT1 was between 25 and 50 mM with symmetrical Na⁺ concentrations (50 mm) on each side of the plasma membrane (Chen et al., 1995). There is one additional report on the functional asymmetry of SGLT1 using a microsomal fraction from yeast expressing the transporter but the results are questionable as the authors were unable to find Na⁺-dependent, phlorizin-sensitive, d-glucose uptake into the vesicles (Firnges, Lin & Kinne, 2001).

Reverse sugar transport was Na⁺-dependent with a half-maximum rate of transport at 5 mm NaCl (Fig. 4), and this is comparable with that (12 mm) for sugar uptake into inside-out membrane vesicles from E. coli expressing hSGLT1 (Quick et al., 2003). In our giant-patch experiments the cotransporter currents did not saturate at 100 mm NaCl, as the current was only 82% of that obtained at 500 mm NaCl (Fig. 4). Fitting of the data to a hyperbolic function gave an internal $K_{0.5}^{\text{Na}}$ of 10 ± 5 mM, whereas fitting with a Hill equation with a Hill coefficient of 2 gives $K_{0.5}^{\text{Na}}$ between 6 and 50 mM (Fig. 4). In the Sauer et al. (2000) study they normalized the currents to 110 mm NaCl and estimated a $K_{0.5}^{\text{Na}}$ of 70 ± 13 mM. The currently available data (Fig. 4; Sauer et al., 2000; and Quick et al., 2003) may be fitted equally well with Hill coefficients of 1 or 2 and, therefore, the degree of co-operativity between the two internal binding sites remains to be resolved. Since the SGLT1 coupling of Na⁺ to sugar transport stoichiometry is 2 (Parent et al. 1992 a,b; Chen et al., 1995; Mackenzie et al., 1998), the most conservative interpretation of the results is that there is low co-operativity between the two Na⁺ binding sites at the internal surface of the transporter. As yet there is no evidence about the order of ligand binding at the internal surface of SGLT1.

The present finding of a high apparent K_i (> 1 mM) for phlorizin on the intracellular surface is in agreement with Sauer et al. (2000). Phlorizin also inhibited Na⁺/sugar transport into inside-out membrane vesicles (Quick et al., 2003) but only with a slow half-time (≈ 5 minutes).

We have proposed a 6-state kinetic model for Na⁺/glucose cotransport by SGLT1 based on an alternating access mechanism (Fig. 6, Parent et al., 1992b). The model is supported by a wealth of experimental data and it, in turn, quantitatively predicts the steady-state kinetics of Na⁺/glucose cotransport in the forward direction, and qualitatively the presteady-state kinetic behavior of the transporter (Parent et al., 1992a,b; Loo et al., 1993, 1998, 2002; Hazama et al., 1997; Meinild et al., 2002). In this model, the protein is negatively charged (valence − 2) with 6 kinetic states, consisting of the empty (C₁, C₆), the Na⁺-bound (C₂, C₅) and the Na⁺- and sugar-bound (C₃, C₄) forms on the external and internal membrane surfaces. In a transport cycle, 2 external Na⁺ ions bind to the transporter before glucose. Na⁺ and sugar are transported via a conformational change (C₃ to C₄), and sugar is released before Na⁺ on the internal membrane surface. Membrane voltage influences the conformational change of the empty transporter (between C₁ and C₆), and Na⁺ binding/dissociation (between C₁ and C₂). Computer simulations of forward sugar transport have yielded sets of rate constants that account for the presteady-state and steady-state kinetics of rabbit and human SGLT1 (Parent et al., 1992b; Loo et al., 1993, 2002; Panayotova-Heiermann, 1995; Hirayama et al., 1996; Hazama et al., 1997).

A simplifying assumption of the 6-state model involves the binding of the two Na⁺ ions in a single step (Fig. 6). This one-step approximation at high external [Na⁺] is supported by the observation of high co-operativity between the two Na⁺ binding sites (Parent et al., 1992b; Falk et al., 1998; Mackenzie et al., 1998; Meinild et al., 2002). However, at low external Na⁺ concentrations, the model fails to account for the presteady-state kinetics (Hazama et al., 1997). Specifically, Falk et al. (1998) suggested that replacing the two Na⁺ binding steps by a single step results in Na⁺-dependent pseudo-rate constants k₁₆, k₆₁, k₁₂ and k₆₅ (Fig. 6A).

The kinetic constants of Fig. 6A (from Parent et al., 1992b, c) predicted a $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ of 25 µM and $K_{0.5}^{\text{Na}}$ of 410 mM (at 0 mV) for reverse transport. Compared to our experimental data $(K_{0.5}^{\mathrm{\alpha }\text{MDG}}32\text{mM and}{K}_{0.5}^{\text{Na}}6–50\text{mM})$, the predicted $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$ was 3 orders of magnitude too low, and the predicted $K_{0.5}^{\text{Na}}$ an order of magnitude too high.

Simulations were repeated using the 6-state kinetic model taking into consideration that k₁₆ and k₆₁ were pseudo-rate constants dependent on external (and internal) Na⁺ and the higher observed sodium affinity at the cytoplasmic surface $(K_{0.5}^{\text{Na}}\approx 35\text{mM})$. For the reverse mode, where the Na⁺ gradient was reversed, k₁₆ was increased to 350 s⁻¹ and k₆₁ decreased to 3 s⁻¹. The increase in k₁₆ is suggested by the dependence of k₁₆ on 1/[Na⁺]_o (Eqn. 18, Falk et al., 1998), and the decrease in k₆₁ (from 5 s⁻¹ to 3⁻¹) compensates for overestimation of the flux from C₁ to C₂ at low [Na⁺]₀ (Eqn. 19, Falk et al., 1998). A set of rate constants whose predictions are compatible with our data is shown in Fig. 6B.

The results of the simulations for the reverse mode are shown by the curves in Fig. 2 for $K_{0.5}^{\mathrm{\alpha }\text{MDG}}$, in Fig. 3A for the I/V curve, and Fig. 4 for $K_{0.5}^{\text{Na}}$. The simulations for the forward mode were performed with k₁₆ = 35 s⁻¹ and k₆₁ = 5 s⁻¹ since the experiments were performed in 100 mm [Na⁺]_o. The curve in Fig. 3B is the predicted I/V curve for forward sugar transport using the kinetic parameters of Fig. 6B. The fits for the sugar affinity and the I/V curves are excellent, whereas the fit for the internal sodium activation is poor. Our simulations also indicated that the revised parameter set of Fig. 6B predicted virtually the same steady-state kinetics (I/V relation, K_0.5 for Na⁺ and αMDG) for the forward mode as previously proposed by Parent et al. (1992b; shown in Fig. 6A). Thus the 6-state kinetic model, together with the requirement that k₁₆ and k₆₁ are pseudo-rate constants, can largely account for the kinetic properties of both forward and reverse modes of sugar transport by SGLT1. Two points still to be determined experimentally are the degree of co-operativity of the two Na⁺ binding sites, and the order of ligand binding at the internal surface.

The simulations predicted that the maximal transport rate (I_max) is the same between the forward and reverse modes. Are the experimental results consistent with this prediction? In our experiments, the patch capacitance was 5–10 pF. The whole-cell sugar-evoked inward current was 600–1000 nA (at − 50 mV), and the oocytes that were studied had whole-cell capacitances of 400–550 nF. Using mid-range values, we anticipate the currents in the giant-patch experiments to be ≈10 pA (800 nA × 7.5pF/475nF). In agreement with this prediction, the majority of our giant patches had sugar-induced outward currents between 4 and 10 pA (the range was 1–18 pA), indicating that the I_max’s for outward and inward sugar transport were similar. For the γ-aminobutyric acid transporter GAT1, the maximal transport rates are also similar for the forward and reverse modes of transport (Wang et al., 2003).

Simulations showed that the asymmetry of the I/V curves between forward and reverse modes is due to the distribution of the empty or ligand-free transporter between states C₁ and C₂. The median voltage of the I/V relation, i.e., the voltage at 50% I_max (maximal sugar-induced current) shifted from − 10 mV for forward mode to − 110 mV for reverse mode (Fig. 3). This shift of 100 mV is the same as the shift of the median voltage of the distribution of SGLT1 between states C₂ and C₆ when external [Na⁺] is reduced from 100 to 10 mm (see Fig. 3D of Hazama et al., 1997). Since the I/V curve for reverse sugar transport can be accounted for by the voltage dependence of the empty transporter alone (Fig. 3A), this indicates that the voltage dependency of the internal Na⁺ interaction is negligible. There is also a difference in the distribution of conformations of SGLT1 between forward and reverse modes under saturating Na⁺/sugar transport conditions. For forward transport (at − 150 mV, Fig. 3B), the transporter is predominantly in state C₅ with a probability of 0.93. For reverse transport, at saturation (+ 50 mV, Fig. 3A) the pre-dominant conformations are C₃, C₄ and C₅ with probabilities of 0.29, 0.41 and 0.28. Thus, the partial reactions on the cytoplasmic surface are rate-limiting for both forward and reverse transport.

Under normal conditions ([Na⁺]_o = 100 mm, [Na⁺]_i = 10 mm), the revised set of kinetic parameters (Fig. 6B) predicted that the internal glucose generates a maximal outward current that is only 3% of the maximal inward Na⁺/glucose current. The revised model also predicts an inhibition of forward Na⁺/glucose transport by internal Na⁺ in the absence of internal glucose (trans-Na⁺ inhibition) with a K_0.5 (57 mM at 0 V) that is similar to that reported by Kaunitz & Wright, 1984 (54 mM at 0 mV). There is a predicted inhibition of forward transport by internal glucose in the absence of internal Na⁺ (trans-sugar inhibition) with a K_0.5 of 62 mM (at 0 mV) that is similar to that (≈50 mM at 0 mV) reported by Kessler & Semenza (1983). Thus, the revised model can predict: 1) the difference in the I/V relations between the forward and reverse modes; 2) the K_0.5 values for Na⁺ and sugar for both forward and reverse modes; and 3) trans-inhibition of forward sugar transport by internal Na⁺ and glucose. In contrast, the model of Parent et al. (1992b) predicted that under normal conditions, no outward current is generated by SGLT1, and the model could not predict the trans-inhibition by Na⁺ and by glucose without adjusting the parameters to fit the experimental data (see Figs. 11 and 12 of Parent et al., 1992b). Note that the model in the present form cannot be used to predict isotope effects, e.g., the effect of trans Na⁺ and sugar on sugar uptake (see Kessler & Semanza, 1993).

In summary, in this study we have for the first time: 1) accounted for the apparent K_m for sugar in the reverse direction (Fig. 2); 2) accounted for the I-V curves for SGLT1 operating in the forward and reverse directions (Fig. 3). Our I-V relations for forward and reverse sugar transport provide strong first evidence that external Na binding and conformational change of the empty transporter between inside- and outside-facing conformations are the only significant voltage-dependent steps; 3) provided experimental evidence in support of the theoretical study of Falk et al. (1998) that postulated the sodium dependence of the rate constants for the conformational changes of the empty transporter (k₁₆ and k₆₁) in the simple 6-state kinetic model for SGLT1; 4) provided direct information about the asymmetry in sugar specificity between forward and reverse Na/sugar transport and the affinity for phlorizin at the internal surface; and 5) demonstrated that our simple model accounts for Na/glucose cotransporter kinetics, forward and reverse directions, at normal sodium concentrations. Finally, while SGLT1 can mediate sugar efflux, given the very low affinity for glucose at the cytosolic surface, under physiological conditions, there would be little or no sugar efflux mediated by SGLT1. The consequence of the functional asymmetry is that the transporter is poised to accumulate sugars in the intestine and kidney with high efficiency. This transporter behavior is suited to the function of the absorptive epithelial tissues in which it is found.