Hair-Cell Versus Afferent Adaptation in the Semicircular Canals

Abstract

The time course and extent of adaptation in semicircular canal hair cells was compared to adaptation in primary afferent neurons for physiological stimuli in vivo to study the origins of the neural code transmitted to the brain. The oyster toadfish, Opsanus tau, was used as the experimental model. Afferent firing-rate adaptation followed a double-exponential time course in response to step cupula displacements. The dominant adaptation time constant varied considerably among afferent fibers and spanned six orders of magnitude for the population (~1 ms to >1,000 s). For sinusoidal stimuli (0.1–20 Hz), the rapidly adapting afferents exhibited a 90° phase lead and frequency-dependent gain, whereas slowly adapting afferents exhibited a flat gain and no phase lead. Hair-cell voltage and current modulations were similar to the slowly adapting afferents and exhibited a relatively flat gain with very little phase lead over the physiological bandwidth and dynamic range tested. Semicircular canal microphonics also showed responses consistent with the slowly adapting subset of afferents and with hair cells. The relatively broad diversity of afferent adaptation time constants and frequency-dependent discharge modulations relative to hair-cell voltage implicate a subsequent site of adaptation that plays a major role in further shaping the temporal characteristics of semicircular canal afferent neural signals.

INTRODUCTION

Sensory hair cells of the inner ear are exquisitely sensitive to small-amplitude ciliary displacements and are often tuned to respond maximally to a particular frequency of hair-bundle movement. Sensitivity and frequency selectivity rely on the biophysical properties of mechano-transduction channels located near the apical tips of the cilia (Hudspeth et al. 2000; Martin et al. 2003; Ricci et al. 2002) and on the dynamics of basolateral ionic currents (Art et al. 1986; Brichta et al. 2002; Fettiplace and Fuchs 1999; Pitchford and Ashmore 1987; Ramanathan and Fuchs 2002). These features underlie membrane potential tuning in response to sinusoidal stimuli and adaptation in response to hair-bundle step displacements. Together with modulations attributable to pre- and postsynaptic processes (Bao et al. 2003; Ishiyama et al. 2002; Lysakowski and Goldberg 1997; Maison et al. 2002; Smith and Goldberg 1986; von Gersdorff 2001), this sensory cascade specifies the temporal properties of the neural code transmitted to the brain.

Significantly, individual afferents in the population innervating one end organ respond with a relatively wide range of temporal dynamics. In semicircular canal afferents, this diversity is apparent in frequency-dependent responses to sinusoidal stimuli and in adaptation to steps of angular acceleration (Boyle and Highstein 1990b; Brichta and Goldberg 1996; Dickman and Correia 1989a; Fernandez and Goldberg 1971; Goldberg and Fernandez 1971b). It has been proposed that adaptation of hair-cell mechano-transduction currents contributes to the adaptation of afferent discharge in the otolith organs (Corey and Hudspeth 1983a,b; Eatock 2000; Eatock et al. 1987). There are both slow and fast components of hair-cell transduction current adaptation (Fettiplace and Ricci 2003). In the present work, we focus on stimuli within the physiological range of the organ—relatively slow stimuli where the sub-millisecond fast transduction current transient would be expected to be fully adapted. In contrast, the slow component of transduction-channel adaptation occurs at rates consistent with adaptation in a subset of vestibular afferents (Brichta et al. 2002; Crawford et al. 1989; Eatock 2000; Eatock et al. 1987; Fernandez and Goldberg 1971, 1976; Goldberg and Fernandez 1971b; Holt et al. 2002). This slow transduction-channel adaptation is dependent upon a myosin-based motor that adjusts the transducer operating point to compensate for static shifts in hair-bundle position (Crawford et al. 1989; Evans and Kros 2001; Frank et al. 2002; Garcia et al. 1998; Gillespie 1997; Holt et al. 2002; Howard and Hudspeth 1987; Hudspeth and Gillespie 1994; Strassmaier and Gillespie 2002; Vollrath and Eatock 2003; Zhao et al. 1996). At a subsequent stage, basolateral ionic currents also contribute to adaptation and response dynamics of hair-cell membrane potentials (Armstrong and Roberts 2001; Baird 1994a,b; Baird and Schuff 1994; Eatock et al. 2002; Holt et al. 1997; Holt et al. 1999; Masetto et al. 1995). In particular, regional differences in K⁺ and Ca²⁺ currents may play a role in shaping regional differences in afferent temporal responses (Masetto et al. 1994, 1996). Evidence from the turtle canals, however, indicates that basolateral currents cannot explain the full repertoire of temporal response characteristics of afferents (Brichta et al. 2002; Goldberg and Brichta 2002). Indeed, a causal link between hair-cell and afferent response dynamics has yet to be established. Toward that end, the present study evaluated the relationship between hair-cell current/voltage temporal response dynamics and afferent discharge modulation in the crista ampullaris for physiological stimuli in vivo.

METHODS

Toadfish (Opsanus tau; ~500 g, either gender) obtained from the Marine Biological Laboratory (Woods Hole, MA) were anesthetized by immersion in MS 222 (25 mg/l sea water, 3-aminobenzoic acid ethyl-ester methane sulphonate; Sigma, St. Louis, MO), partially immobilized by intramuscular injection of pancuronium bromide (0.05 mg/kg), and secured in a lucite tank filled with fresh seawater (10–15°C) covering all but the dorsal surface of the animal as previously described (Boyle and Highstein 1990b). A dorsal craniotomy was made lateral to the anterior canal, allowing direct access to the horizontal canal nerve and ampulla to a distance of ~1.1 cm posterior to the ampulla. A bolus of fluorocarbon (FC75, 3M) was injected into the cranial opening, partially filling the dorsal perilymphatic vestibule, to provide insulation during electrocauterization of the ampulla and prevent perilymph evaporation and tissue dehydration. Normal perilymph bathed the labyrinth and canal nerve throughout the experiments.

In some experiments, the endolymphatic duct of the membranous horizontal canal was occluded by compression against the bone using a ~1.2-mm-diam glass rod tipped with malleable wax (Takiwax; Cenco). Plugs were situated 1 cm (⁺0.2) from the crista as measured along the curved centerline of the canal. Maintained cupular displacements were generated by applying controlled mechanical indentation to the duct in the region between the cupula and the plug (Fig. 1A). Afferent nerve responses to sinusoidal stimulation were continuously monitored while compressing the canal to ensure that the plugging procedure did not impair transduction (Rabbitt et al. 1999, 2001). After each experiment; a saturated solution of Alcian green was injected into the ampulla to confirm canal blockage.

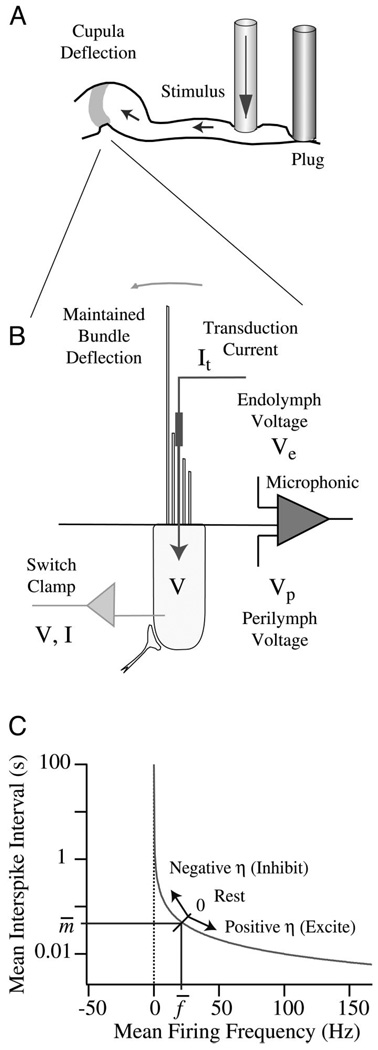
FIG. 1.

Experimental set-up. The horizontal canal was plugged along its slender course and stimulated by piezoelectric mechanical indentation to induce controlled volumetric displacements of the cupula (A). One micrometer of mechanical indentation generates ~0.002 rad of angular hair-bundle displacement. Results are reported re: displacement of the stimulus rod. Afferent discharge, hair-cell voltage/current, and the endolymphatic microphonic (V_e − V_p) were recorded for step and sinusoidal stimuli (B) in patent and plugged-canal conditions. Adaptation of the interspike interval (instantaneous mean) was modeled as a dynamic process that modulates the value of the state variable η on the basis of input stimuli (C).

Experimental set-up

Glass microelectrodes were used for extracellular and intra-axonal afferent nerve recordings from the right horizontal canal nerve ~1 mm from the ampulla. Conventional bridge amplification and external spike discrimination were employed. Access to hair cells was achieved by electrocauterizing a small fistula in the utricular side of the ampullary wall using a 25-µm-diam tungsten electrode and a 3-W pure cutting waveform (Valley Labs, SSE4). Sharp quartz electrodes (125–350 mΩ; 2 M KCH₃SO₄) were lowered through the fistula under visual guidance to impale individual hair cells. A single-electrode switch clamp (NPI, SEC05L) was used in voltage- and current-clamp modes to record receptor currents and potentials in the cells. The clamp switch frequency was ~25 kHz with analog current and voltage low-pass filters set at 2000 and 1000Hz, respectively, and sampled at 4,000 Hz (Fig. 1B).

Stimulation of the canal duct was achieved using a 1.2-mm-diam glass rod attached to a micro-actuator (Burleigh PZL 060-11) as described previously (Dickman and Correia 1989a; Dickman et al. 1988; Rabbitt et al. 1995) with the caveat that the canal was plugged (unless otherwise noted) to force the fluid displacement caused by indentation to move toward the cupula, generating a prescribed volumetric displacement of the cupula. The endolymph volumetric displacement generated by this form of stimulation is detailed by Rabbitt et al. (1995) and, in the mid-band patent condition, generates ~0.002 rad of angular hair-bundle deflection for each micrometer of canal indentation (Damaino and Rabbitt 1996; Rabbitt et al. 2004). This angular deflection is equivalent to a linear deflection of the cilia of ~20 nm when measured at a distance of 10 µm above its insertion into the cell body. Displacement of the stimulating rod was continuously monitored using a linear variable differential transformer (LVDT; Schaevitz DEC-050) mounted in-line with the actuator. A waveform generator (Tektronix AFG 5102) and high-voltage amplifier (TrigTek 207A, Los Angeles, CA) provided input to the microactuator to deliver sinusoidal and step stimuli.

Semicircular canal microphonics were recorded by cutting the anterior canal at its dorsal extreme, isolating the cut ends in air, and inserting an endolymph-filled glass microelectrode into the rostral limb. The electrode was lowered through the anterior canal ampulla and into the utricular vestibule just medial to the horizontal canal ampulla. Voltages were preamplifed (10¹² Ω input impedance, custom) and recorded in quadrature relative to the mechanical stimulus using a lock-in amplifier (Stanford Research Systems, SR830). In a subset of experiments, the endolymph voltage was polarized re: perilymph using a voltage-passing electrode in the dorsal limb of the anterior canal and a voltage-recording pipette in the anterior canal ampulla as described previously (Highstein et al. 1996).

Stimuli were restricted to magnitudes <10 µm (equivalent to ~40°/s angular head rotation) where afferents respond nearly linearly (Boyle and Highstein 1990b; Rabbitt et al. 1995). Hair-cell transduction currents were relatively small (~10–50 pA) and in the range where nonlinearity of the transduction current would be expected to produce <10% harmonic distortion.

Digital data acquisition (Cambridge Electronic Design 1401Plus, Apple Macintosh interface) was used to record externally discriminated spike times, displacement of the indenter (LVDTs), hair-cell voltage and hair-cell current. Analog signals were filtered below the Nyquist frequency and externally amplified to span the 12-bit range of the A/D. Stimulus trigger-signals and externally discriminated spikes were recorded to a resolution of 0.08 ms.

Analysis was done off-line using a custom interactive analysis procedure (IgorPro, Wave Metrics, Lake Oswego, OR). For sinusoidal stimuli, the first-harmonic gain and phase were computed for five or more consecutive stimulus cycles by manually selecting portions of the record and averaging the results. Individual spike times (t_n) were discriminated using a constant level crossing, numbered sequentially (n = 1, 2, …), and interpolated with straight-line segments to define a continuous floating-point function [n(t)] giving the number of spikes versus time. Spike times were averaged relative to the stimulus trigger (occurring at times t = T_k) using J = 100 bins/cycle phase histograms. For each cycle (k = 1, 2, …, K) of the stimulus, the spike count occurring in each bin was determined using a central difference c_jk = n(t_j+1/2 + T_k) − n(t_j−1/2 + T_k), where t_{j+1/ 2} = (j + 1/2) (T_k+1 − T_k)/J and t_j−1/2 = (j − 1/2)(T_k+1 − T_k)/J. The cycle-averaged instantaneous discharge rate (spikes/s vs. bin number j) was estimated using ${\overline{c}}_j=\frac{1}{K}{\displaystyle \sum _{k=1}^K{c}_{\mathit{\text{jk}}}\mathit{\text{ Jf}}}$, where f (Hz) is the stimulus frequency. The histogram was fit with a sinusoid in quadrature using linear least-squares to define the first harmonic modulation (Wave-Metrics, Lake Oswego, OR). Empty bins were ignored in the afferent fitting procedure and the average rate was constrained to be >0. The complex-valued first-harmonic afferent response was then divided by the complex-valued first-harmonic of the stimulus to determine the first harmonic gain (spikes · s⁻¹ · µm⁻¹) and phase (degree, re: peak indentation). The relationship of gain and phase for indentation stimuli re: angular head rotation has been reported previously (Dickman and Correia 1989a; Dickman et al. 1988; Rabbitt et al. 1995). For step and square-wave stimuli, afferent firing rates were fit using both single- and double-exponent curves constrained to asymptote to the spontaneous discharge rate. Time constants and amplitudes obtained by this fitting procedure were subsequently used as initial estimates in a simple nonlinear adaptation model. The rise time of the step stimulus was ~8 ms (time constant ~2.7 ms) with a holding time ranging from 2 to 150 s.

Useful data were obtained from 59 fish, as follows: afferent nerve firing rates (n = 93 units, 47 fish), HC receptor currents/potentials (n = 73 cells, 19 fish), and endolymphatic microphonics (5 fish). The experiments were approved by the Institutional Animal Care and Use Committees at the Marine Biological Laboratory and the University of Utah.

Modeling methods

A simple empirical model was formulated to describe afferent discharge adaptation. The model is based on the observation that applied stimuli modulate the statistical moments of interspike interval distribution in a quasi-steady process. We are interested here only in modulation of the mean value of this distribution. At rest, the afferent has a mean interspike interval m̄ and corresponding mean instantaneous spike frequency f̄. Stimuli cause the state of the afferent to deflect from the mean value along the curve illustrated in Fig. 1C. Two state variables, η₁ and η₂, are introduced to track dynamic adaptation. These variables are zero at rest, and in response to stimuli follow the dynamic

$$\frac{\mathrm{d}{\eta }_k}{\mathrm{d}t}+\frac{1}{{\tau }_k}{\eta }_k=g_k^o\frac{\mathrm{d}s}{\mathrm{d}t}+\frac{g_k^{\mathrm{\infty }}}{{\tau }_k}s$$ (1)

where τ_k is the adaptation time constant, $g_k^o$ is the instantaneous gain (adapted part), $g_k^{\mathrm{\infty }}$ is the gain at infinite time (nonadapted part), and s is the input (i.e., hair-cell voltage perturbation). The index k = 1 denotes the slow adaptation while k = 2 denotes the fast adaptation. Equation 1 is a first-order linear adaptation operator relating an input (independent variable s on the right-hand side) to an output (dependent variable η on the left hand side). To track afferent discharge modulation, we define a combined state variable η as a sum of the slow η₁ and fast η₂ state variables according to

$$\eta ={\eta }_1+{\eta }_2·r({\eta }_2)$$ (2)

where the function r(x) accounts for the nonlinear excitatory/inhibitory asymmetry observed in the fast adaptation. If the stimulus is maintained at a constant value, the slow and fast adaptation operators cause η to recover to zero over time thereby adapting the response back to the spontaneous discharge rate. To account for the inhibitory-excitatory asymmetry, we used r(x) = 1 for x > 0 and r(x) = 0.2 for x < 0. This caused the recovery to the spontaneous discharge to be dominated by the slow time constant for inhibitory stimuli (η < 0). The combined state variable along the curved trajectory (Fig. 1C) is related to the instantaneous frequency f and instantaneous interspike-interval m by dη² = dm² + df². Integrating this provides

$$\eta ={\displaystyle {\int }_{{-}_f}^f\sqrt{1+{\zeta }^{-4}}\mathrm{d}\zeta }$$ (3)

where f̄ is the resting background discharge rate. This formula can be inverted numerically to arrive at the firing frequency as a function of the state variable, f = f(η), as shown in Fig. 1C. With this, the instantaneous firing frequency is

$$f=f({\eta }_1+{\eta }_2·r({\eta }_2))$$ (4)

It is important to note that this approach automatically accounts for the nonlinearity of inhibitory cut-off and rate saturation through the relationship between the state variable, interspike interval, and discharge frequency. The equations were solved numerically using a fourth-order Runge-Kutta method with the cupular displacement and hair-cell membrane potential modulation taken to be proportional to mechanical indentation of the plugged canal (i.e., s in Eq. 1 was proportional to indentation). Application to non-plugged preparations would require an additional transfer function to describe the elasto-hydrodynamics leading to cupular displacements (Rabbitt et al. 1995, 1999, 2003).

RESULTS

Double-exponential afferent discharge adaptation

The discharge patterns of two representative afferent nerves (A and B) in response to excitatory and inhibitory step (square wave) stimuli (A and B) are shown in Fig. 2. For excitatory stimuli, the time course of adaptation could be described by a double-exponential curve with two time constants—a relatively fast adaptation (τ_f) immediately after onset of the step, followed by a slow adaptation (τ_s). The two-time-constant response for excitatory steps is easily seen in Fig. 2A, where the afferent discharge rate exhibits rapid adaptation (τ_f) followed by a slow recovery adaptation (τ_s) to prestimulus discharge levels. The unit in 2B clearly exhibited inhibitory cut-off (0 firing region) where the firing rate decreased to zero. Adaptation was not symmetric for excitatory vs inhibitory stimuli (e.g., Fig. 2A). Adaptation during inhibitory stimuli followed a single-exponential curve with a time constant equal to the slow adaptation observed during excitatory stimulation (Fig. 2A, τ_s). This asymmetric nonlinearity reflects a fast adaptation process in response to excitatory stimuli that was absent, or obscured, during inhibitory stimulation. Some units were driven into inhibitory cut-off and did not discharge during the inhibitory stimulus (Fig. 2B).

FIG. 2.

Afferent adaptation. Sample records showing slowly adapting (dots, A) and rapidly adapting (dots, B) afferent discharge in response to step stimuli (solid) in the plugged-canal condition. Afferent discharge adaptation for excitatory stimuli was fit using a double-exponential curve (slow and fast time constants τ_s, τ_f) and using a single exponential for inhibitory stimuli (slow time τ_s). (C) histograms and log-normal probability density functions of the fast (solid) and slow (dotted) adaptation times. Afferent adaptation times spanned ~6 orders of magnitude with a most probable fast adaptation of ~0.53 s and a most probable slow adaptation of ~13s.

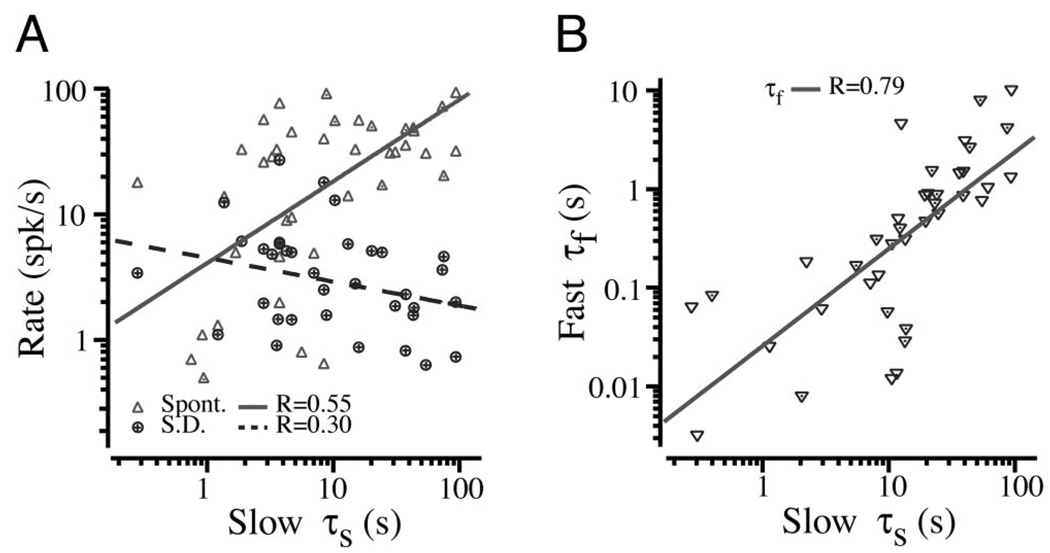
Adaptation time constants: correlates

The time constants for fast and slow afferent adaptation are summarized in Fig. 2C. They were well described by lognormal distributions with the total times spanning approximately six orders of magnitude (~10⁻³s–10³s; n = 46). In a small subset of afferents, the fast adaptation time constant was approximately equal to the stimulus rise-time constant. This also occurred in the weakly nonlinear model due to the dependence of discharge probability on both the stimulus and the rate of change of the stimulus (see model results in following text). The most probable discharge-rate adaptation times were τ_f = 0.53 s (range: 0.004–46 s) and τ_s = 13.4 s (range: 0.07 to >600 s). Although the most probable times were clearly identifiable, we were not able to determine the slowest adaptation in the population tail due to the technical difficulty associated with holding units for extended periods of time. We stress that, because the canal lumen was plugged, these adaptation times are not associated with the mechanical time constant of the canal—the displacement of the cupula was nearly constant during the adaptation. The spontaneous discharge rate of these neurons averaged 30.8 spikes/s (range: 0–113; n = 46). Adaptation times showed only a weak correlation with mean spontaneous discharge rate (Fig. 3A, R = 0.55) and standard deviation of the discharge rate (R = 0.30). The nondimensional regularity cv* defined by Goldberg and Frenandez (1971b) was not computed because some units are silent at rest and therefore would need to be excluded from the computation, and because regularity does not correlate with response dynamics in the toadfish (Boyle and Highstein 1990b; Boyle et al. 1992; Goldberg and Fernandez 1971a). The fast and slow adaptation times did correlate reasonably well with each other (Fig. 3B, R = 0.79).

FIG. 3.

A: the very weak correlation between mean background discharge rate (▵, —, R = 0.55) ± SD (○, - - -, R = 0.30) with adaptation time constant (n = 46) B: the correlation between the fast and slow afferent adaptation time constants (R = 0.79; n = 46).

Afferent two-time constant validation in time domain

We also evaluated to what extent adaptation time constants for step stimuli could predict afferent nerve discharge patterns observed during more complex stimuli. Step stimuli were used to determine parameters of a simple empirical model (see METHODS) and then model responses based on the step stimuli were compared to data collected during sinusoidal and complex stimuli. Figure 4 provides direct examples comparing predictions of the model to the empirical data for two afferent nerve responses. Stimuli consisting of a combination of sinusoidal and step indentations of plugged canals are shown in Fig. 4, A and B, bottom. The corresponding neural responses (dots) and model simulations (solid gray lines) are shown in the top traces for both afferents. Because the canal lumen was plugged, these responses show the influence of neural adaptation and not canal hydrodynamics. There was excellent agreement between the observed discharge rates and the predicted responses for sinusoidal, step, and transient stimuli. The measured stimuli (Fig. 4, bottom traces) were then fed directly into the time-domain model, so all features of the stimuli were used to compute the results. It is notable that the model captures the difference in the time course of recovery to step stimuli for inhibitory versus excitatory stimuli as well as nonlinear inhibitory cut-off. This asymmetry is visible by eye in B, where the fast adaptation during excitatory steps is not present during inhibitory steps. This nonlinearity is also manifest in the responses to sinusoidal stimuli. For example, the apparent downward drift in the firing rate evident over the initial ~30 s (Fig. 4B) is a direct result of the asymmetric nonlinearity. This induces a stimulus-dependent slow “DC” shift during sinusoidal stimuli. The offset was not present in the stimulus (Fig. 4B, bottom) and therefore was not present in the input to the model equations. Nevertheless, the model predictions closely follow the observed responses. These results strongly indicate that this behavior arises from the inherent asymmetry (nonlinearity) attribute in afferent adaptation.

FIG. 4.

Model predictions vs. observed discharge patterns. Responses of 2 representative afferents (dots; A, and B) are shown for stimuli consisting of a combination of sinusoidal and step indentations (solid). Numerical simulations based on the simple 2-time constant model (METHODS) are shown for each afferent superimposed on the afferent discharge. The model captures the inhibitory saturation (A) and nearly linear superposition (A,*) as well as the difference in adaptation rate for excitatory vs. inhibitory stimuli (B).

Steps versus sinusoids

To investigate the strength of this nonlinearity, we compared gain and phase recorded in response to sinusoidal stimuli to model predictions based on adaptation to step stimuli. Gain and phase were computed using constrained fits accounting for cut-off responses as described in METHODS. The comparison was done by first adjusting the model parameters to fit the data obtained using excitatory and inhibitory step stimuli and subsequently comparing predicted responses to the experimental data for sinusoidal simulations. Figure 4 provides a qualitative example of this procedure and illustrates the comparison for step and/or sinusoidal stimuli. Quantitative comparisons of model-based predictions and experimental data for gain and phase of response are provided in Fig. 5. There was excellent agreement between the gain predicted on the basis of step responses and that measured using sinusoidal stimuli (Fig. 5A, R = 0.98). This indicates that the two-time constant adaptation model with a weak nonlinearity captures the main features underlying gain. Although there was greater variability in comparisons of phase, the correlation was nevertheless quite high (Fig. 5B, R = 0.80). Some of this scatter was due to the fact that we fixed the ratio of the fast time constant to the slow time constant in fitting the step data (using the most probable value τ_f = 0.0396* τ_s). This was done in order to reduce the number of fitted parameters and simplify the model. Use of a fixed ratio was also motivated by the nearly linear correlation obtained between the fast and slow time constants (see Fig. 3B). Results shown in Figs. 4 and 5 demonstrate that Bode plots of gain and phase provide reasonable measures of afferent discharge even though the adaptation process is nonlinear. This is supported by the fact that the Bode plots are consistent with, and can be extracted from, the nonlinear two-time-constant adaptation responses. However, the Bode form of gain and phase depiction does not convey quantitative aspects of the excitatory/inhibitory response asymmetry that is clearly observed in the time domain responses (see Fig. 4). The linear Bode description also fails to describe changes in the time-averaged discharge (DC) rate induced by oscillatory (AC) stimuli. For example, the slow downward drift in the time-averaged discharge rate shown in Fig. 4B (dots over the 1st ~30 s) is not predicted by a linear Bode analysis, but is captured by the weakly nonlinear model (Fig. 4B, solid curve).

FIG. 5.

Steps vs. sinusoids. The gain (A) and phase (B) of afferent discharge predicted on the basis of adaptations to step stimuli are compared to the gain and phase determined by direct curve-fitting of sinusoidal responses. —, ideal responses expected for a linear system; - - -, fits to the present data. The close correspondence between the linear case and data illustrate that nonlinearity of afferent adaptation is relatively weak for these stimuli. This comparison accounts for the inhibitory saturation because it was present to equal extents when curve-fitting both the simulated and actual sinusoidal responses (see METHODS).

Hair-cell responses

Hair-cell transduction currents and receptor potentials were recorded in addition to afferent spike trains to compare the time course of adaptation in semicircular canal hair cells to the nerve. Example responses in the plug-canal condition are shown in Fig. 6. A and B show entry into a hair cell along with voltage and current responses to mechanical stimulation. Electrode penetration into the cell (arrow I) was characterized by a sudden drop in voltage accompanied by an increase in resistance and capacitance (note RC voltage perturbation resulting from current pulses present after penetration). Sinusoidal modulation of the receptor potential was immediately detectable upon dropping into the hair cell. An expanded view of the voltage modulation at a later time in the record is shown in Fig. 6B. The gain of this example hair cell was ~0.8 mV/µm of mechanical indentation at 2 Hz. It is important to note that the mechanical stimulus generates ~0.002 rad of angular hair-bundle deflection for each micrometer of indentation. The amplifier was switched into voltage-clamp mode (arrow III) to record the transduction current. Current modulation for this hair cell was ~1.5 pA/µm of mechanical indentation. The hair-cell voltage modulation was in phase with the mechanical stimulus (arrow II) and the hair-cell current modulation was 180° out of phase relative to the stimulus (arrow IV). C and D provide example data for step stimuli recorded in voltage-clamp (C) and current-clamp (D) modes. In most cases, it was not possible to record from hair cells for a sufficiently long time to observe exponential adaptation using step stimuli and therefore straight-line segments to determine the initial slope of a presumed exponential adaptation (using a Taylor series expansion, e^−t/τ~1 − t/τ + …). The phase relations and adaptation time constants exemplified by these cells (Fig. 6) are representative of the population recorded (reported in the following text). Example data provided in Figs. 6 and 2 indicate, at least for these cells, that afferent discharge may exhibit substantially more adaptation than hair-cell voltage. This difference was explored further using sinusoidal stimuli as described in the following text.

FIG. 6.

Hair-cell current and voltage. A: example hair-cell voltage recorded in current-clamp during sinusoidal mechanical stimuli (Note: mechanical stimuli generate ~0.002 rad of angular hair-bundle deflection for each micrometer of indentation). The resting membrane potential re: endolymph upon entering the cell was near −54 mV (I) and the whole cell resistance was 302 MΩ (pulse). B: same cell at a later time showing the voltage modulation in phase with indentation (II) and the switch from current-clamp to voltage-clamp mode (III). Inward transduction currents are associated with negative deflections of the current trace. Note that the peak receptor potential was nearly in phase (II) re: the mechanical stimulus while the peak current was ~180° out of phase (IV). C and D: example hair-cell responses to step mechanical stimuli in voltage-clamp (C) and current-clamp modes (D).

Responses to sinusoidal stimuli were quantified in the form of first-harmoinic gain and phase (i.e., Bode plots). This approach does not address nonlinear components of the responses, and therefore it is important to quantify the relative importance of the nonlinearity. As detailed in the preceding text, although afferent responses were nonlinear, first-harmonic gain and phase (Bode plots) indeed capture the major features of afferent discharge modulation. Hair-cell responses also exhibited nonlinear responses, most obvious in an excitatory-inhibitory asymmetry and manifested in the odd harmonic responses. Excitatory responses were slightly larger and more peaked relative to inhibitory responses. The nonlinearity, however, was relatively small in comparison to the first harmonic of interest here. Nonlinear distortion measured by the third harmonic, for example, was only 8.9 ± 5.4% re: the fundamental in current clamp and 12.9 ± 4.1% in voltage clamp (statistics over all data presented herein). The magnitude of the third harmonic did not correlate well with the amplitude of the stimulus (R < 0.18 in current clamp and R < 0.14 in voltage clamp, data grouped over all cells). Results show that the major component of the hair cell response to sinusoidal stimuli is captured by the first-harmonic modulation (Bode plots), at least for the dynamic range and bandwidth of stimuli tested here.

Hair cell versus afferent adaptation times

It is of interest to note that we were unable to estimate the adaptation times in seven of the hair cells due to a positive initial slope. This implies an absence of adaptation, very small adaptation gains, or adaptation times outside of our recording range. Excluding these “non-adapting” cells, the Taylor series estimate yielded an average transduction current adaptation of 166 s (14 s minimum, >647 s maximum recorded) and average voltage adaptation of 275 s (11 s minimum, >775 s maximum recorded). Grouped together, adaptation times of all hair cells were well described by a log-normal distribution with a mean of 112 ± 3.16 (SD) s, skewness of 1.1, and kurtosis of 0.10. This distribution is compared with the afferent adaptation times in Fig. 7. It is notable that adaptation times of hair cells and afferent nerves both followed log-normal distributions, but the present population of hair cells had a mean at least two orders of magnitude slower than that of the afferent nerve fibers.

FIG. 7.

Hair-cell voltage vs. afferent discharge adaptation time constants. Probability density functions showing hair-cell voltage adaptation time constants and afferent adaptation time constants, both in response to step stimuli in the plugged-canal condition. Note the rapid adaptation times <1 s were present in the nerve but absent in the population of hair cells recorded.

Hair-cell Bode responses for sinusoidal stimuli

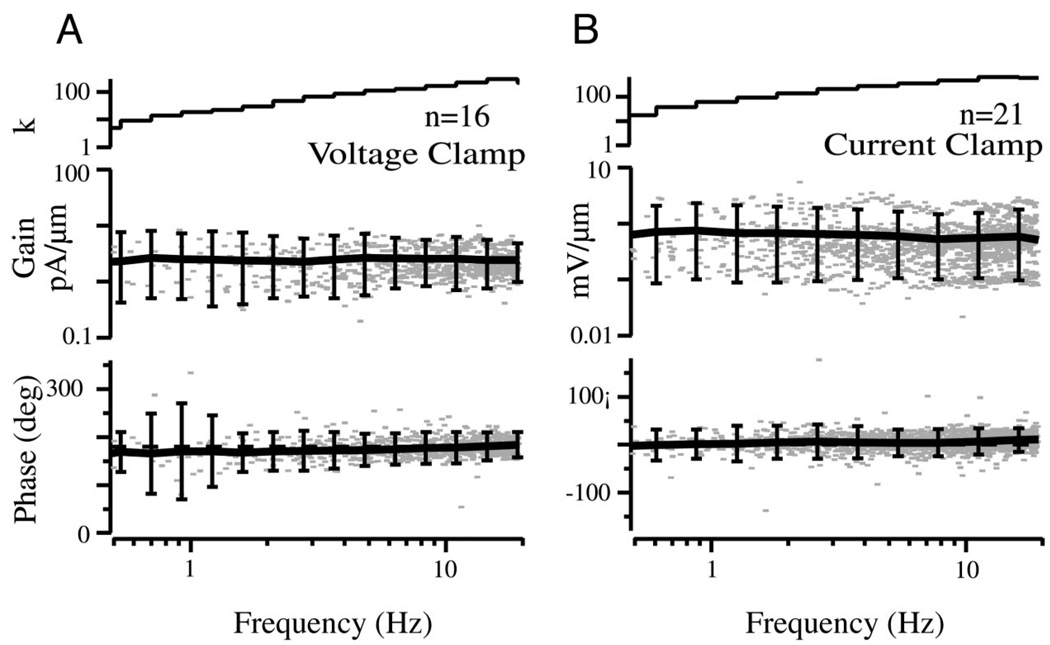
Slow sweeps of sinusoidal stimulation were used to further examine hair-cell dynamic responses. The frequency sweeps were limited to <20 Hz, specifically to avoid the high-frequency/vibrational components of the stimulus that could be present to some extent during the step. Frequency domain results are for patent canals and are therefore limited to frequencies above the lower corner (>0.1 Hz) where mechanical adaptation is not present (Rabbitt et al. 2003). Figure 8 provides a population summary in Bode form of hair-cell receptor currents (A) and potentials (B) for sinusoidal stimuli for the subset of cells recorded near the zero-current potential. Voltage-clamp Bode plots (Fig. 8A) show data from n = 16 cells clamped to the zero-current potential of −46 + 9 mV re: resting endolymph (DC current averaged −3 + 30 pA; average resistance 328 MΩ in 28 cells; all hair-cell data reported re: endolymph, see Fig. 10 for enolymph resting potential re: perilymph). The current gain and phase were both relatively flat over the entire frequency range tested. The same frequency insensitivity was found when hair-cell voltage modulations were recorded in current-clamp mode (Fig. 8B). Current-clamp Bode plots (Fig. 8B) show data from n = 21 cells having an average membrane potential of −43 + 6 mV re: resting endolymph (DC current averaged −37 + 60 pA). The relatively flat gain and nearly zero phase of the hair cell Bode plots are consistent with adaptation results using step stimuli in that a single transfer function reproduces both responses.

FIG. 8.

Hair-cell receptor currents (A) and potentials (B) for sinusoidal sweep stimuli. Results are shown for the patent canal condition. Voltage-clamp data are summarized in the form of Bode plots: gain (A, pA/µm indent) and phase re: peak indentation (°). Error bars show the 90% confidence interval for binned data based on a 2-tailed t-test, n indicates the number of cells, and k indicates the number of records within each frequency bin. Current-clamp data are also summarized in Bode form: gain (B, mV/µm) and phase re: peak indentation (°). The current was 180° out of phase re: the voltage due the sign conventions used for membrane potential and transduction current (defined re: electrode). The relatively flat gain and phase are notable.

FIG. 10.

Semicircular canal microphonic. First-harmonic modulation of the endolymph voltage re: perilymph is shown as a function of sinusoidal mechanical stimulus frequency in Bode form: gain (A, µV/µm) and phase (B, °) for the patent canal condition. Thick black curves (A and B) show averages across fish, and error bars indicate the 90% confidence interval based on a 2-tailed t-test. Example results for individual fish are shown as dotted and dashed curves. C and D: sensitivity of the microphonic gain (C, normalized) and phase (D, °) as functions of endolymph polarization voltage re: perilymph. The gain of the microphonic approached 0, and the phase reversed at the transduction current reversal potential, thus indicating that the microphonic reflects the whole-organ transduction current.

Gain versus phase probability density functions

The difference between responses of the present population of hair cells versus afferents for sinusoidal stimuli is summarized in Fig. 9 in the form of probability density functions for each population. Contour plots show the probability of recording a cell with a specific gain and phase during hair-cell voltage clamp (A) and hair-cell current clamp (B) and for single-afferent units (C). Maximum likelihood gain and phase values are indicted by dashed lines in each panel. Curves on the right show probability density functions for the gain (obtained by integrating left to right over all phases). In all cases, the gains are well described by single or multimodal log-normal distributions. However, it is critical to note the increased variance of the afferent gain responses in comparison with those of the hair cells. When viewed in terms of dynamic range, this corresponds to an expanded range for the afferent gains, approximately three orders of magnitude, whereas that of the hair cells spanned approximately one to two orders of magnitude. Even more striking differences were observed in the phase probability density functions (Fig. 9D, obtained by integrating from top to bottom over all gains). The most probable phase of the hair cell current modulation lagged the stimulus by 8°, whereas the most probable hair-cell voltage led the stimulus by 13°, and the most probable afferent discharge led the stimulus by 47°. These differences in mean phase were statistically significant (>99.99%, t-test). The phase advance in the modulation of hair cell voltage re: current is consistent with processing by voltage-sensitive basolateral ionic currents (Brichta et al. 2002; Goldberg and Brichta 2002). The additional phase advance present at the level of the afferents, in contrast, is much more significant and cannot be explained by hair-cell current or voltage. It is interesting to compare the phase advance of afferents and hair cells shown in Fig. 9D for sinusoidal stimuli to adaptation time constants shown in Fig. 7 for step stimuli. Both experiments find nearly identical distributions, both indicating a rapid adaptation process present in the response of afferents but absent in hair-cell voltage/current responses.

FIG. 9.

Summary: hair cell vs. afferent gain and phase for sinusoidal stimuli. Contour plots (A–C) show probability density functions providing the likelihood of recording a cell with a specific gain and phase for hair-cell voltage clamp (A), hair-cell current clamp (B), and single-unit afferent discharge (C). Data are grouped over all frequencies tested with n denoting the number of cells and k denoting the total number of data points recorded at various frequencies. White indicates 0 probability and black indicates the highest probability (values indicated by short dashed lines). The phase of the current (A) has been shifted 180° re: Fig. 8 to facilitate comparison to voltage and afferent discharge. Note the increased dynamic range (vertical extent of gain) and bandwidth (horizontal extent of phase) of afferent responses (C) relative to hair-cell responses (A and B). Differences in temporal responses are highlighted in D showing clear differences between the probability density functions for the phases of hair-cell and afferent populations recorded.

Microphonic Bode plot and voltage dependence

Further evidence was obtained by recording the frequency dependence of the semicircular canal microphonic in response to sinusoidal mechanical stimulation of the canal-limb. Figure 10, top, provides the Bode gain (A; µV/µm) and phase (B; °) as functions of stimulus frequency. Note that the microphonic gain and phase were relatively flat across the frequency range—Bode plots that are quite similar to hair-cell transduction currents recorded in the present population (Figs. 8 vs. 10). This led us to hypothesize that the microphonic primarily reflects hair-cell transduction currents in this preparation. To test this, the magnitude and phase of the microphonic was recorded while polarizing the endolymph relative to the perilymph. Fig. 10, bottom, clearly show that the microphonic decreased as the endolymph voltage was polarized in the negative direction and reversed phase as the endolymph voltage was polarized beyond −63 mV re: perilymph. Individual data points show results at four different test frequencies with gains normalized to 1 at the semicircular canal resting endolymphatic potential (vertical dashed line, −11 mV). The microphonic reversal potential was −52-mV polarization re: endolymph and approximately −62 mV re: perilymph. It is highly notable that the reversal also corresponds to the voltage that nulls the membrane potential acting across the apical surfaces of the hair cells and is nearly the same potential where the transduction current reverses (hair-cell 0-current potentials reported above are relative to endolymph). The dashed curves show the voltage dependence of the microphonic gain (Fig. 10A) and phase (B) that would be expected on the basis of reversal of hair-cell transduction currents. The data show a slower transition in phase and incomplete nulling of the gain consistent with 10% heterogeneity (solid curves), presumably arising from either from the population of hair-cell transduction currents and/or baslolateral currents responsible for the whole-organ microphonic. The precise origin of this heterogeneity, however, is not germane to the present focus. The critical observation is that the whole-organ microphonic Bode plots were nearly identical to the hair cell Bode plots, thus building confidence in the hair-cell recordings and also indicating that the hair-cell data may indeed reflect the overall population.

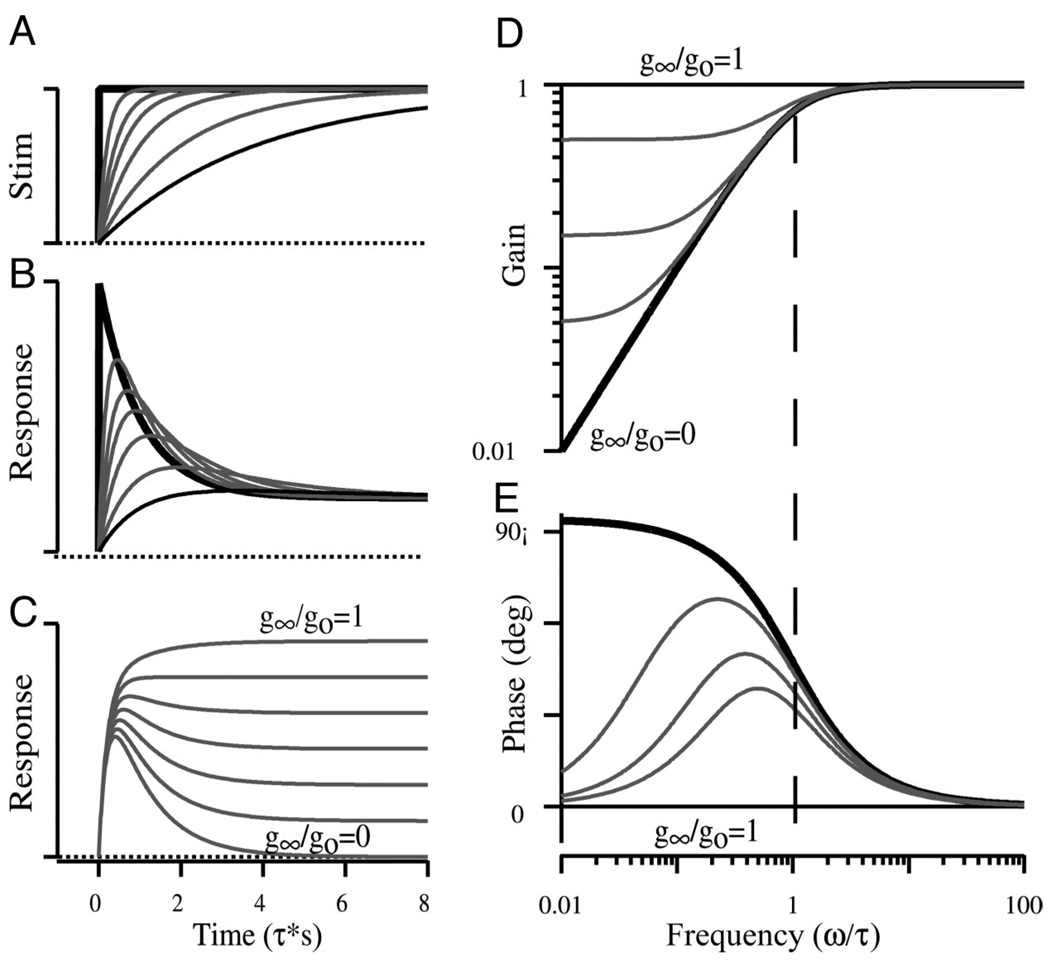
Ideal adaptation

For the purpose of discussion, a conceptual framework incorporating key properties of ideal adaptation, as predicted by the simple first-order model (Eq. 1 alone), is illustrated in Fig. 11 for step stimuli (A–C) and sinusoidal stimuli (D and E). Ideal adaptation for step stimuli (Fig. 11A) is characterized by a rapid increase (B) in the response followed by a period of recovery that returns the response toward the prestimulus level. Ideal responses are shown for a perfect step as thick black curves and for a slowly rising step as thin black curves. It is important to note that adaptation is lost if the stimulus rise time is too slow (Fig. 11 A and B, thin black curves). Adaptation can be also be obscured if the process itself is incomplete. This is illustrated as a series of curves from 0 to 100% complete (Fig. 11C) for the perfect step stimulus. Thin curves red curves show partial adaptations (0, 5, 15, and 50%). The same features are shown for sinusoidal stimuli in the Bode form of gain and phase as functions of frequency (Fig. 11 D and E). Note that the gain and phase are flat for sinusoidal stimuli above the ideal adaptation corner frequency (Fig. 11, D and E; vertical dashed line). For frequencies below the corner frequency, ideal adaptation (thick solid curves) causes a 90° increase in phase, and roll-off in magnitude. Stimuli constrained to the right of the corner frequency will not reveal the adaptation process. Incomplete adaptation flattens the gain and forces the phase to zero at low frequencies. Hence, with incomplete adaptation, stimuli constrained to the left of the corner frequency will not reveal the adaptation process. These simple relationships are critical in evaluating the efficacy of a particular stimulus in revealing an adaptation process and are critical to the proper interpretation of adaptation data. The absence of adapting responses does not argue against the presence of the process itself but rather brackets the process as either slow relative to the stimuli used or fast relative to the stimuli used but incomplete in extent.

FIG. 11.

Characteristic features of ideal adaptation. Adapting responses are shown in the time domain (B and C) for step stimuli (A) and in the frequency domain (D and E) for sinusoidal stimuli (Eq. 1, METHODS). Thick solid curves (A and B) show ideal adaptation for a perfect step stimuli. Thin curves in B illustrate the influence of the stimulus rise time (A, τ_r), and curves in C illustrate the influence of the nonadapting portion of the response (g_∞/g_o) for a fixed stimulus rise time. D and E: the influence of the adaptation time constant and the nonadapting portion of the response (g_∞/g_o) for sinusoidal stimuli in the form of magnitude (D) and phase (E). The frequency axis has been scaled by the adaptation time constant yielding a nondimensional corner frequency of 1. Results range from 100% complete adaptation (g^∞/g^o = 0) to 0% adaptation (g^∞/g^o = 1).

DISCUSSION

In the present study, striking differences were observed in the temporal responses of semicircular canal hair-cells versus primary afferent neurons for both step and sinusoidal stimuli. Sampling bias was not a factor in the afferent recordings, based on comparisons of the data with numerous previous reports in toadfish (Boyle and Highstein 1990a,b; Rabbitt et al. 1995, 1999). Because this is the first report of semicircular canal hair-cell recordings under these conditions, it is necessary to entertain the possibility of sampling bias or unforeseen artifact in the hair-cell data. Sampling bias or systematic error, however, seems unlikely owing to the close correspondence of hair-cell Bode plots with whole-organ microphonics. The microphonic data alone, even in the absence of hair cell data, point to a substantial difference between the temporal response of whole-organ current versus temporal modulations of afferent spike trains.

The diverse temporal responses of afferents versus the more uniform responses of hair cells and the whole-organ microphonics suggests the presence of substantial signal processing late in the transduction process. The existence of this process in the semicircular canals has been recognized for years (Fernandez and Goldberg 1971; Goldberg and Fernandez 1971a,b), but the origin was attributed to early stages of transduction, e.g., micro-mechanics and/or mechano-transduction (Brichta et al. 2002; Goldberg and Brichta 2002; Highstein et al. 1996). The present data support the hypothesis that post-receptor-potential mechanisms, rather than mechano-transduction, constitutes the major sources of adaptation in the semicircular canals.

Adaptation of hair-cell current and voltage

Whole cell transduction currents recorded from cochlear hair cells of the turtle reveal a fast adaptation process that, for step hair bundle displacements, rapidly reduces the transduction current to zero (Fettiplace and Fuchs 1999; Ricci et al. 2000, 2002). The adaptation time constant ranges from −1 to 4 ms and is sensitive to endolymph [Ca²⁺] and the anatomical location of the hair cell within the cochlea. A fast transient of similar time course has also been reported in vestibular hair cells from the otolith organs (Holt et al. 2002; Howard and Hudspeth 1987; Hudspeth et al. 2000; Martin et al. 2003; Vilfan and Duke 2003). Fast adaptation in vestibular hair cells is incomplete and reaches a level-dependent plateau for maintained bundle displacements. This is not surprising because vestibular hair cells sense the direction of gravity and low-frequency motion stimuli, physiological stimuli that animals can sense for ≥10⁵ times longer than required to adapt fast component in hair-cell transduction currents. Physiological stimuli (and those used in the present experiments) are too slow to allow studies of fast adaptation (see Fig. 11). Should a fast adaptation process exist in the semicircular canal hair cells, it could contribute to the steady state gain but would not be expected to underlie the adaptation time constants (Fig. 7) or relative phase (Fig. 9D) reported here.

Hair-cell adaptation recorded in the present population appeared to be slower than the myosin-mediated adaptation commonly observed during voltage clamp of otolith hair cells (Eatock et al. 1987, 2002; Gillespie 2002; Holt et al. 2002; Howard and Hudspeth 1987; Hudspeth et al. 2000; Kros et al 2002; Shepherd and Corey 1994; Vollrath and Eatock 2003). The present adaptation data for step stimuli (Fig. 6) and sinusoidal sweep stimuli evoked tonic transduction currents with relatively flat gain and flat phase over the entire frequency bandwidth tested (Figs 8 and 9)—data consistent with the transepithelial microphonic (Fig. 10). The tonic response of the present hair cell data relative to previous work in otolith hair cells was somewhat surprising because canal hair cells operate over similar frequencies as otolith hair cells and face the same challenge in adapting the operating point of the transduction channels. Part of the difference is likely to be due to experimental conditions. It has been suggested that the extent of slow adaptation may decrease as the stimulus magnitude is reduced to the physiological range (Holt et al. 1997; Shepherd and Corey 1994). In fact, the present experiments were performed in vivo using stimuli restricted to physiologically relevant levels. These stimuli evoked transduction current modulations on the order of 25 pA, ~5–10 times less than typically reported in studies of isolated hair cells and 20–50 times less than saturating levels. A second contributing factor may be the impedance of the coupling between the external stimulus and the hair bundle. In the present experiments, the impedance of this coupling was dictated by the physiological interactions between the hair bundles and the anisotropic, hydrated cupula. This relatively compliant coupling in vivo may partially mask the influence of myosin-mediated adaptation relative to stiff probe experiments in vitro, such that the relatively fast components of adaptation observed in vitro might be fully adapted and/or undetectable using physiological stimuli in vivo (Crawford et al. 1991; Holt et al. 1997; Howard and Hudspeth 1987; Ricci et al. 2002; Vollrath and Eatock 2003).

Hair-cell basolateral currents, particularly a K⁺-selective outward rectifying conductance (Armstrong and Roberts 2001; Eatock et al. 2002; Holt et al. 1999), may also contribute to adaptation and response dynamics of the hair-cell receptor potential in some vestibular end organs (Baird 1994b). Such conductances are present with regional variability in the crista ampullaris of frog (Masetto et al. 1994, 1995; Prigioni et al. 1996). However, our findings in toadfish are consistent with previous work in turtle showing that basolateral currents are not likely to be a major factor underlying this aspect of signal processing present in the nerve (Brichta et al. 2002; Goldberg and Brichta 2002).

Adaptation of afferent discharge

The contrast between hair cells and afferent responses is most clearly illustrated by the adaptation times for step stimuli summarized in Fig. 7, and the relative phases for sinusoidal stimuli are summarized in Fig 9D. Only pure angular-velocity sensitive afferents had adaptation time constants similar to the hair cells. These low-gain velocity-sensitive fibers (Boyle and Highstein 1990b) have response dynamics analogous to those of regularly discharging afferents in the squirrel monkey that do not require an adaptation operator to describe their dynamics (Fernandez and Goldberg 1971; Goldberg and Fernandez 1971b; Hullar et al. 2002). The very existence of velocity-sensitive afferents implies that a significant subset of hair cells apparently do not exhibit appreciable adaptation to physiological stimuli, as demonstrated in the present report. In fact, a generalized prediction can be drawn from the observations that reptiles, aves, and fish all have non-adapting as well as adapting semicircular canal afferents, similar to those of the toadfish (Boyle and Highstein 1990b; Brichta and Goldberg 1996; Dickman and Correia 1989b; Honrubia et al. 1989; O’Leary and Dunn 1976). Adaptation time constants in mammalian semicircular canal afferents are lower, on average, but quite significant in irregularly discharging afferents (Baird et al. 1988; Fernandez and Goldberg 1971; Goldberg and Brichta 1998; Goldberg and Fernandez 1971b; Goldberg et al. 1990; Hullar et al. 1999, 2002). Hence features of semicircular canal afferent adaptation reported here have broad relevance across species.

Origins of afferent adaptation

Present data indicate that a major site of adaptation is interposed between the hair-cell voltage and the afferent discharge, implicating synaptic mechanisms and/or the afferent spike generator as possible sites for this process. Afferent spike generation in the semicircular canals, however, results in relatively tonic spike trains in response to steps of current injection (Highstein and Baker 1985) and is not likely to introduce the type of adaptation reported here (Schmich and Miller 1997; Smith and Goldberg 1986). This leads to the hypothesis that hair-cell/afferent complexes are the primary sites for adaptation in vestibular afferents. This finding has a parallel in the auditory system where hair-cell receptor potentials do not exhibit the adaptive properties of afferent nerve discharge (Russell and Sellick 1978; Smotherman and Narins 2000; Weiss and Rose 1988).

Traditionally, synaptic transmission by auditory and vestibular hair cells has been attributed to an excitatory amino-acid such as glutamate (Ottersen et al. 1998; Usami et al. 2001). This transmitter generally elicits relatively short excitatory postsynaptic potentials that summate, directly conferring the time course of afferent discharge modulation. This description is consistent with the conditional discharge statistics of auditory afferents and, in some cases, with a component of adaptation arising from presynaptic transmitter depletion (Furukawa et al. 1972, 1978). Presynaptic depletion, however, can not explain the present data in the semicircular canals where superimposed stimuli sum in a nearly linear fashion (e.g. Fig. 4, epoch denoted * and excellent correspondence to a nearly linear model).

Although depletion is unlikely to be a key factor, recent data from turtle semicircular canal afferents do indicate that at least part of the adaptation is associated with presynaptic mechanisms controlling the timing of quantal release from hair cells (Holt et al. 2004). The presynaptic component corresponds well with responses of a subset of afferents but may not fully account for the bandwith and extent of adaptation in the acceleration-sensitive afferents described here. The presence of GABA has recently been reported in a subset of crista hair cells (Holstein et al. 2004), and it is possible that this plays a role in afferent response dynamics and adaptations reported here. In toadfish, cells staining for GABA are concentrated in the central region of the crista, exactly where the highly adapting, acceleration-sensitive afferents project (Boyle et al. 1991; Boyle and Highstein 1990b). In fact, it has also been shown that the highly adapting afferents form synaptic contacts with both glutamatergic and GABAergic hair cells, whereas nonadapting afferents contact glutamatergic hair cells only (Holstein et al. 2004b). Systemic administration of GABA_B antagonists indeed reduce the extent of adaptation in semicircular canal afferents, thus indicating that at least part of the afferent adaptation reported here is likely due to the convergent action of multiple transmitters and receptors (Holstein et al. 2004b). This finding, however, is not adequate to fully account for the complete transformation from hair-cell voltage to afferent discharge. Results implicate the presence of an additional site of adaptation involving the hair-cell/afferent synaptic complex that further shapes the temporal characteristics of semicircular canal afferent neural signals.