Objective sequence-based subfamily classifications of mouse homeodomains reflect their in vitro DNA-binding preferences

Abstract

Classifying proteins into subgroups with similar molecular function on the basis of sequence is an important step in deriving reliable functional annotations computationally. So far, however, available classification procedures have been evaluated against protein subgroups that are defined by experts using mainly qualitative descriptions of molecular function. Recently, in vitro DNA-binding preferences to all possible 8-nt DNA sequences have been measured for 178 mouse homeodomains using protein-binding microarrays, offering the unprecedented opportunity of evaluating the classification methods against quantitative measures of molecular function. To this end, we automatically derive homeodomain subtypes from the DNA-binding data and independently group the same domains using sequence information alone. We test five sequence-based methods, which use different sequence-similarity measures and algorithms to group sequences. Results show that methods that optimize the classification robustness reflect well the detailed functional specificity revealed by the experimental data. In some of these classifications, 73–83% of the subfamilies exactly correspond to, or are completely contained in, the function-based subtypes. Our findings demonstrate that certain sequence-based classifications are capable of yielding very specific molecular function annotations. The availability of quantitative descriptions of molecular function, such as DNA-binding data, will be a key factor in exploiting this potential in the future.

INTRODUCTION

With the momentous growth in the body of protein sequence data, the availability of computational methods for reliably inferring protein function has become a critical factor. The most widely used methods transfer functional annotations on the basis of sequence similarity to proteins stored in databases. These methods range in sophistication from pairwise sequence comparisons (1), to procedures involving sequence profiles (2), hidden Markov models (HMMs) (3,4) and kernel methods (5). The pairwise methods are effective in identifying closely related proteins, whereas the profile- and kernel-based procedures identify more distant homologs.

Classification of protein domains into families at both the sequence and tertiary-structure levels (6,7)—has also been very helpful in revealing sequence signatures associated with functional properties and providing insight into protein evolution (8). The Pfam database has pioneered such domain-based classifications on a large scale using HMMs (9), and more recently, structure-based HMMs classifications have also been derived (10,11). However, since HMMs are capable of identifying distantly related proteins, classifications based on these models tend to group domains from rather diverse proteins carrying out a range of molecular and cellular functions. Methods have, therefore, been developed for further subdividing protein families into smaller groups, or subfamilies, whose members display higher sequence similarity and are therefore likely to share more specific functional properties.

There are essentially two types of subfamily classification methods: those which cluster proteins on the basis of pairwise sequence similarity [InParanoid (12), OrthoMCL and TribeMCL (13,14), Ncut (15), CD-HIT (16,17)] and those that do so by cutting a phylogenetic or hierarchical dendogram [RIO (18), Orthostrapper (19), SECATOR (20) and SCI-PHY (21,22)]. In all these methods, the coarseness of the classification, or clustering granularity, is governed by adjustable parameters. The values of these parameters are usually set by requiring that identified clusters maximize the recall of protein subtypes identified by experts (23) or of conserved clades detected using standard phylogenetic tree analysis. Yet, in the absence of quantitative measures of functional properties across family members, it has not been possible so far to evaluate the extent to which subfamily classifications by any of these methods actually reflect the functional specialization of the corresponding proteins.

An unprecedented opportunity to investigate this important issue has been offered recently by the systematic analysis of Berger et al. (24) of the DNA-binding specificities of the ∼60-amino-acid homeodomains (HDs) from mouse. These specificities were derived from data on DNA binding collected using protein-binding microarrays (PBMs). The latter contained 41 944 60-mers in which all possible 8-base sequences are represented in 32 different contexts, thereby providing a robust estimate of the binding preference of each HD to all possible 8-mers (25–27). These estimates enabled the authors to group a total of 178 mouse transcription factors into 64 sub-types with distinct DNA-binding preferences, revealing rich and complex patterns of sequence specificity at the DNA level. However, this grouping was manually adjusted, considering additional information on DNA-binding motifs derived from the target 8-mers binding data, as well as sequence similarity relationships deduced from a ClustalW dendogram.

In this work, we approached the problem of classifying the mouse HDs of (24) using completely automatic methods. We took the Berger et al. DNA-binding preferences of the HDs as a quantitative measure of their functional specificity and used these preferences to group the different HD into subtypes with distinct binding specificities. We then investigated to what extent automatic subfamily-classification methods that are based on sequence information alone are able to segregate the HDs into subfamilies that are consistent with these subtypes.

The ∼60-amino-acid HDs, which play an important role in regulating many specific processes, are well suited for such analysis. Individual HDs are believed to have distinct protein- or DNA-binding activities. Although protein–protein interactions seem to play a role in target definition (28), it has been well established that the sequence specificity of domain monomers does contribute to target specificity (29). Confirming prior work (25), Berger et al. (24) have also shown that the DNA-binding motifs tend to vary among different HD subtypes.

To group the mouse HDs into subtypes considering only the DNA-binding data, we built a graph that links HDs on the basis of the similarity between their DNA-binding profiles. The Markov clustering (MCL) procedure (30) was then used to partition the graph into nontrivial clusters of HDs (larger than singletons and pairs) with most similar binding profiles. This approach groups the 178 mouse HDs into a similar number of subtypes and subtype membership as the manually adjusted classification of Berger et al. Comparison with classifications of the closely related human HDs, derived from a standard phylogenetic tree analysis (31–33), shows that the subdivision afforded by the DNA-binding data is much finer than the commonly cited class level defined in these classifications, in agreement with the conclusions of Berger et al. (24).

To classify the same HDs on the basis of sequence information, we used a total of five different procedures. Four of these are established subfamily classification methods from the two categories mentioned above: SECATOR, TribeMCL, CD-HIT and SCI-PHY. In addition, the HDs were grouped by three variants of a novel procedure. This procedure involves straightforward pruning of the pairwise sequence similarity graphs on the basis of an objectively defined pruning threshold.

To evaluate the sensitivity of the different methods to the HD data set composition, we applied them to two different datasets: the 178 mouse domains of Berger et al., which, except for 21 duplicates with identical sequences, are rather diverse (∼30% sequence identity on average), and a larger data set of 559 sequences. The latter contains 381 HDs from 86 different organisms in addition to the 178 mouse HDs.

We found that the four established methods produce coarse HD groupings. These groupings differ significantly from one another, and from the HD subtypes defined on the basis of the DNA-binding data. On the other hand, the objective pruning procedures and a nonstandard mode of the SCI-PHY algorithm produce much finer and remarkably similar classifications. These classifications feature HD subfamilies with closely related domains (78–80% sequence identity). These subfamilies show good correspondence with the DNA-binding data and with the HD subtypes derived from these data alone.

Our study provides evidence that sequence information alone can be used to identify protein/domain subtypes with distinct functional properties that are measured on a quantitative basis. It is of particular significance that these properties pertain to the DNA recognition specificity of the domains, which represents one specialized aspect of their molecular function. The implications of our findings for the annotation of molecular function from sequence are discussed.

MATERIALS AND METHODS

HD data sets

Mouse HDs

This data set comprises 178 HDs from mouse, comprising the ∼60-amino-acid regions involved in DNA binding, for which in vitro DNA-binding affinities were measured using PBMs (24). This dataset, denoted as mH178, includes 157 unique HD sequences and 21 duplicate ones (see Supplementary Table S1 for the full list). Eleven of the duplicates originated from different genes coding for the same HD as one already in the list (but with different flanking residues), and another ten were from the same genes expressed in different aliquots or alternate constructs. These duplicates were used as control in order to evaluate the error in experimental binding scores (24).

HDs from different organisms: To test the effects of introducing additional homologous sequences into the data, the sequence-based subfamily classifications (see below) were performed using additionally a larger dataset containing a total of 559 HD sequences, also comprising the ∼60 amino acid regions involved in DNA binding as defined in Pfam (9). This dataset is denoted as H559. It includes 381 non-identical HDs, of which 26 are from mouse and 355 from other organisms (34), to which we added the 178 mouse HDs sequences mentioned above (see Supplementary Figure S1 for the full list).

The 381 HDs were derived from a larger set of 465 HDs by removing identical sequences. This larger set included 27 HDs with high resolution structures deposited in the PDB, 175 HD sequences from InterPro (35) that matched the homeobox signature in Pfam (9) and 254 HD sequences retrieved from the database of expressed sequence tags (EST) PartiGeneDB (36) (see Supplementary Methods for details).

In vitro DNA-binding data

DNA-binding data for the mouse HDs are those measured from PBMs as reported in ref. 24. These arrays contained 41 944 60-mers in which all possible 8-base sequences are represented in 32 different contexts, thereby providing a robust estimate of the binding preference of each protein to all possible 8-mers (37). The arrays also contained 32 instances of all gapped 8-mers up to a width of 12 bases, in order to enable the detection of longer motifs.

Binding data determined in ref. 24 were expressed in terms of the so-called enrichment score (E-score), which is a modified form of the Wilcoxon–Mann–Whitney statistic, providing a measure of the significance of the binding to an 8-mer for a given HD. This score varies between −0.5 and 0.5 and a cutoff of 0.45 was determined as a lower threshold for identifying significant binding interactions (24). The E-score was shown to vary in a nonlinear fashion with the normalized median binding intensity for each 8-mer, as well with the association constant K_a of the domain, when the latter was known (25). Its advantage lies in the fact that 8-mer E-score ranks are the most highly reproducible of any other tested measures and facilitate comparisons between different experiments. The experimental data contains 2585 8-mers that show an E-score above the cutoff for at least one HD. This set of 8-mers defines the E-scores (binding) profile of each of the 178 mouse HDs. In addition, a position weighted matrix (PWM) was built in (24) for each transcription factor, representing the most likely DNA-sequence profile it binds to.

Pairwise similarity measures for HD binding preferences

In order to objectively quantify the similarity in binding preferences of different mouse HD proteins, two main measures were used. One is the pairwise Pearson Correlation (PC) coefficient between the binding profiles of two different HD, with each profile being defined by the corresponding E-score values measured for the set of 2585 thresholded 8-mers defined above (24).

The second measure quantifies the similarity between the DNA-binding sites of the two HD proteins. It is computed as the maximum normalized overlap, i.e. the maximum cosine, between the PWMs of the two HDs. The normalized overlap between two PWMs is computed as the scalar product of the two matrices, maximized over all possible alignments (without gaps) of the two profiles considering both DNA strands, and divided by the Euclidean norm of both matrices.

Comparing partitions of the HD data set

Two measures were used in order to quantify the differences between HD groupings obtained using various methods and parameters. One is the variation of information (VI) distance between two partitions P and P* (38):

(1)

Where is the partition consisting of the set of all pairwise intersections between clusters from P and clusters from. 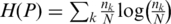is the Shannon entropy associated with the cluster-size distribution of a given partition P, with 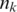being the size of cluster k, and N the total number of HDs. The VI distance is a measure of the information needed to transform one partition into another and takes up values from 0 to log N. When using logarithms of base 2, it expresses the number of bits needed to encode the difference between two partitions. H(P) measures the granularity of a partition with values ranging from zero, when all HDs are grouped into one single cluster, to log N, where N is the number of singleton clusters.

The second measure of similarity between partitions of the HD dataset is the so-called Purity score. Given a pair of ‘target’ and ‘reference’ partitions, the Purity score p is defined as in (21):

(2)

where 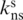is the number of nonsingleton clusters in the target partition that exactly match, or are subsets of, clusters in the reference partition; and 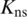is the total number of nonsingleton clusters in the target partition. This score does not differentiate whether the target partition is identical to or an exact refinement of the reference partition. In both situations p = 1.

To enable comparisons between the partitions of a smaller mH178 set of mouse HDs to those of a larger H559 set of HDs from mouse and other organisms, the classifications of the larger dataset were postprocessed to retain only subfamilies containing members of the mH178 set and discarding all other TFs.

Subfamily classification methods

Objective single-linkage

In this method, the sequence similarity graph was pruned by thresholding the pairwise similarity metric, such that the resulting partition was robust with respect to small changes in the threshold value. This robust partition (consisting of a set of sub-graphs) was then taken to represent the subfamily classification. Subfamilies or clusters obtained in this way were defined by the single-linkage criterion: any two groups of TFs in which at least two TFs, one from each group, displayed sequence similarity equal or above the threshold, were merged into the same cluster.

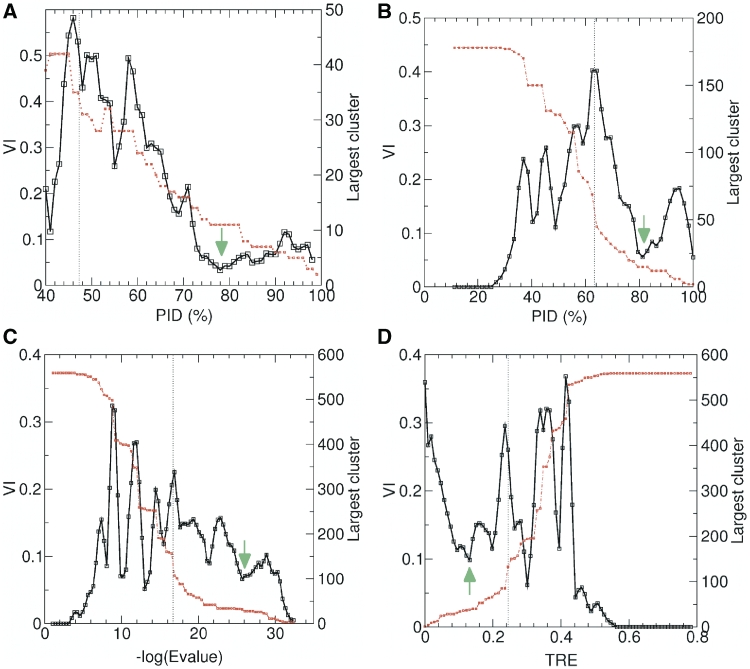
The added value of our approach is that it defines the pruning threshold in an objective fashion, as follows. A wide range of threshold values was sampled at constant intervals. The sampling interval was defined objectively as the smallest interval that leads to the pruning of at least one additional (or one less) edge of the graph at any given step. At each interval we computed the average VI distance of the resulting partition to the four flanking partitions (two on each side), and this distance was plotted as a function of the threshold value (Figure 1b–d).

Figure 1.

Objective subfamily classifications of mouse HD by CD-HIT and the three graph pruning procedures. Two curves are plotted on each panel. One is the variation of the largest cluster size as a function of the threshold for pruning the sequence similarity/dissimilarity graph (red dots), and the other is the average variation of information distance (VI) between a partition (subfamily classification) at a given threshold and those of its four flanking partitions. The dotted vertical line indicates the pruning threshold value at which the entropy of the resulting partition equals half its maximum value (ln N). The selected robust partition corresponds to the lowest local minimum in the VI curve found after that midpoint (indicated by an arrow). Shown are four plots computed using two methods, applied to different similarity/dissimilarity graphs; PID stands for percent sequence identity; TRE stands for total relative entropy. (A) and (B) were derived from the mH178 data set; (C) and (D), from the H559 data set. (A) Plots for CD-HIT; robust partitions identified at PID = 78%. (B) Plots for OSL_PID, robust partition identified at PID =81%. (C) Plots for OSL_E-val, robust partition identified at BLAST log E-values = –25.7. (D) Plots for OSL_TRE,; robust partition identified at TRE = 0.1317. The direction of this plot is reversed relative to the three others, as TRE is a dissimilarity measure.

To select a meaningful minimum from this plot, we monitored the entropy H(p) of the generated partitions p, as a function of the pruning threshold. As already mentioned, H(p) reflects the granularity of these partitions and varies from zero to ∼log N. Its variation is characterized by a sharp transition region, where the partition granularity changes most dramatically as a function of the applied threshold (Figure 1b–d). The pruning threshold corresponding to the midpoint of this transition was then defined as the value at which H(p) is half its maximum size. Finally, the optimal robust partition was selected as the lowest minimum in the average VI plot located after the transition midpoint of the H(p) curve. When several minima of similar magnitude are identified, the one closest to the transition midpoint was selected.

In a related approach, the optimal partition is defined by selecting the threshold value at which the largest subfamily reaches half its maximum size (39). This typically results in much coarser partitions, whose correspondence with the DNA-binding data is poorer, as shown in this work.

The approach outlined above was applied to graphs built using three different sequence-similarity metrics: pairwise sequence identity (PID), the BLASTP log E-value (1) and the Total Relative Entropy (TRE) (21), with the corresponding procedures referred to as OSL_PID, OSL_E-value and OSL_TRE, respectively. All three procedures were applied to both the mH178 and the H559 HD data sets. BLAST E-values are very dependent on the query sequence length and the database size. This is the case for the present datasets, where mouse HDs Tcf1 and Tcf2, which introduce a long insertion in the multiple sequence alignment (MSA), give rise to an outlying smaller E-value. Hence, this value was ignored when defining the optimal sampling step.

Figure 1 illustrates the identification of robust subfamily classifications by applying the three objective graph-pruning methods (OSL_PID OSL_E-value OSL_TRE) to either the mH178 or the H559 dataset. The robust partition identified by OSL_PID (Figure 1b) is obtained with a PID threshold of ∼81%, which yields subfamilies containing at most ∼15 members. The PID normalization used is the average sequence length. The robust partitions and corresponding thresholds obtained with the other two OSL procedures are illustrated in Figures 1c and d.

SCI-PHY

This procedure takes as input a multiple sequence alignment and proceeds in two steps (21). First, it builds a dendogram based on a symmetrized version of Kullbak–Leibner distance measuring the total relative entropy (TRE) between two sequence profiles, and on Dirichlet mixture priors. Next, it partitions the dendogram into groups of sequences (clusters) by optimizing a scoring function.

Two distinct scoring functions were used here. One is the default function of the SCI-PHY software (22), termed Encoding Cost (EC) in (21):

(3)

where N is the number of sequences, S the number of subfamilies for a given cut of the tree, i is the position along the protein sequence, 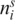is the frequency of any of the 20 amino acids at position i in cluster s and α is the Dirichlet mixture density. The first term penalizes a classification that is too fine-grained, while the second term is maximized when the sequences within each subfamily are very similar to each other (22). The dendogram is partitioned by minimizing the expression in Equation (3).

The second scoring function, denoted here as the entropy function E, also available in SCI-PHY but not commonly used, is:

(4)

The sums in Equation (4) run over all positions i of the multiple sequence alignment, all subfamilies s and all amino acids a present in each cluster, respectively, and 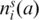is the frequency of the observed amino acids in each cluster. The dendogram is partitioned by maximizing the expression in Equation (4).

Both scoring functions were applied to dendograms built by SCI-PHY for the mH178 and H559 data sets. To run SCI-PHY, the HD sequences were multiply aligned using ClustalW (40). Tests were also performed using more recent multiple-sequence alignment procedures [MUSCLE (41) and MAFFT (42); see Supplementary Methods] without finding significant differences.

For the alignment of larger HD data set of 559 proteins, the following two-step procedure was used [see (34) and Supplementary Methods for details]. First, a multiple structural alignment of the 27 high-resolution structures of HD representatives from the Protein Data Bank [PDB; (43)] was performed using the software MALECON (44). This produced a structure-based sequence profile to which the 429 HD sequences from InterPro and PartiGeneDB were aligned using the sequence-to-profile option of ClustalW (40), yielding a multiple sequence alignment of all 381 proteins. Finally, the 178 Mouse HD sequences from (24) were aligned to this larger set using ClustalW.

SECATOR

SECATOR identifies subfamilies by constructing and analyzing a hierarchical tree. It takes as input a multiple sequence alignment and builds a phylogenetic tree based on percent sequence identities (PIDs) using BIONJ (45). It then uses a sequence-dissimilarity measure to define the optimal cut of the tree. We applied it to the mH178 and H559 data sets using default settings.

TribeMCL

The TribeMCL algorithm operates on the sequence-similarity graph built using the logarithm of the pairwise BLAST E-values (2) as edge weights. The results depend on the E-value threshold used for the initial pruning of the graph, and on the value of the inflation parameter I of the MCL algorithm (14). MCL is an unsupervised graph-clustering algorithm that simulates random flow through the graph to find clusters of highly interconnected vertices (30). Unlike other clustering procedures, such as the classical K-means (46), MCL is a deterministic algorithm (yielding identical results in different runs on the same data), and several studies have shown it to be more efficient than a number of competing procedures in clustering noisy graphs (47,48).

Rather than applying empirically derived thresholds for the MCL parameters, as was done in previous studies (13), we defined them on an objective basis, using a similar approach to that described above for the OSL procedures. We scanned all integer powers of 10 between −1 and −40 for the E-value threshold (-log E-value). For each threshold, the MCL inflation parameter I, which controls the granularity of the obtained partitions, was tabulated between 1.2 and 4.8 with increments of 0.4, covering the range recommended in the MCL documentation. Higher values of the E-value threshold remove weaker edges from the input network, whereas higher inflation values tend to break weaker flow paths.

We then identified the appropriate parameter combinations by looking for MCL partitions that are robust with regard to small changes in the parameter values. Such partitions were identified by considering each MCL partition obtained within the surveyed parameter range, computing its average VI distance to the eight flanking partitions (with a one-step perturbation in either direction in inflation I and/or log E-value), and selecting those with the smallest average distance.

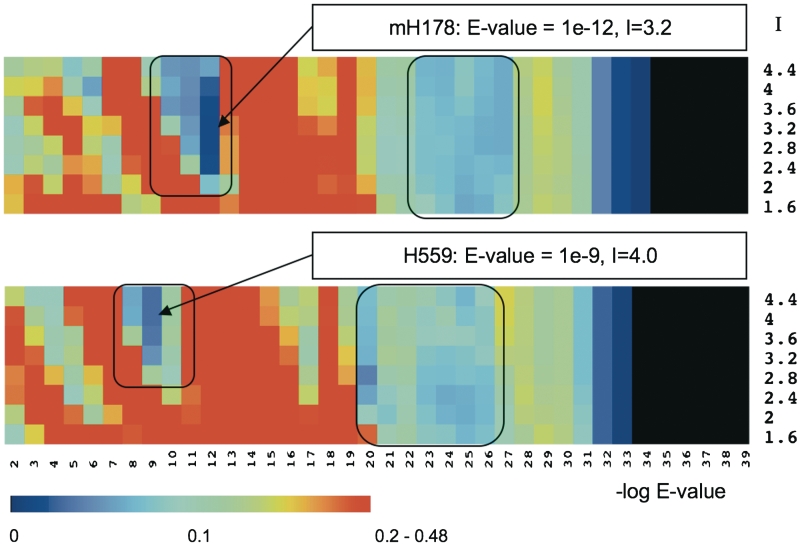
The position of the robust partitions in the TribeMCL landscape covered by the surveyed parameter range is illustrated in Figure 2. In each case, the first robust region contains the most robust non-trivial solutions, as indicated by the smallest VI distance. Notably, this region corresponds to typical TribeMCL parameters used in literature (E-values between 10⁻⁸ and 10⁻¹²). The second robust region (E-values between 10⁻²⁰ and 10⁻²⁷) represents a local minimum in the VI distance that is both broader and less pronounced than in the first case. It contains TribeMCL partitions that, upon examination, are almost entirely determined by the initial network pruning, and are thus very similar to the corresponding OSL_E-Value partitions. Finally, the black regions on the right side of Figure 2 (E-values ≤10⁻³⁵) correspond to excessive pruning that breaks the partitions almost completely into singleton clusters (except for one pair Tcf1-Tcf2). The parameter values yielding the most robust partitions for the mH178 and H559 data sets are E-value = 10⁻¹², I = 3.2 and E-value = 10⁻⁹, I = 4, respectively. Further details, such as the number of clusters and the largest cluster size, are provided in Table 1.

Figure 2.

Identification of robust TribeMCL mouse HD classifications based on sequence information. Heat plot displays the average VI distance of each TribeMCL partition to its eight immediate-neighbor partitions for the mH178 (top) and H559 (bottom) datasets. The horizontal values are the negative powers of 10 used as the BLAST E-value thresholds. Vertical values are for the MCL inflation parameter I. The immediate-neighbor partitions are determined by one-step perturbation of the –log E-value (±1, horizontal axis) and/or I (±0.4, vertical axis) parameters. The distance between partitions is computed using the Variation of Information (VI) metric, and follows the depicted color scale. Robust regions are shown within black rectangles, with the most robust solutions indicated by arrows (see ‘Materials and Methods’ section).

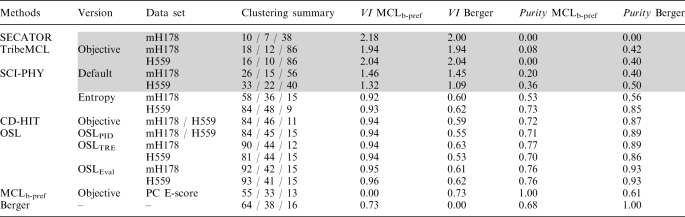
Table 1.

Summary of the mouse HD classifications derived on the basis of sequence information

The listed classifications were derived using five different methods using either default, or optimized settings. SECATOR was applied using default settings. Highlighted in gray are the coarser grained classifications, which display poor overlap with HD groups derived on the basis of the DNA-binding data.

SCI-PHY was applied using the Default and Entropy modes, respectively.

For the remaining methods thresholds and parameter values were objectively defined as those yielding classifications that are robust against small changes in these values (see ‘Materials and Methods’ section).

The Objective Single Linkage (OSL) procedure was applied to three different sequence-similarity graphs built using the pairwise sequence identity (PID), the BLASTP log E-value (E-value) and the Total Relative Entropy (TRE) as sequence-similarity measures.

‘MCL_b-pref’ is the classification derived using the MCL clustering algorithm applied to the graph built from the pairwise Pearson Correlation (PC) of the measured DNA-binding profiles (E-scores; see ‘Materials and Methods’ section).

‘Berger’ is the manually adjusted classification of Berger et al. (24).

All the sequence-based classifications were applied to the mH178 and H559 data sets (column 3). The ‘clustering summary’ (column 4) lists the total number of subfamilies, the number of subfamilies with at least two members and the number of HDs in the largest subfamily.

Columns 5 and 6 list the Variation of Information (VI) distance of the sequences based classifications to the HD subtypes derived here from the DNA-binding data (MCL_b-pref) and to the manually adjusted Berger classification, respectively.

The last two columns list the purity scores of the subfamilies relative to the same two classifications. In performing the Purity score calculations, the MCL_b-pref and Berger et al. classification were used as ‘reference’ partitions.

CD-HIT

CD-HIT (Cluster Database at High Identity with Tolerance) (16) has originally been designed to produce a set of families (or subfamilies) composed of very closely related proteins, starting from a larger set of more diverse sequences. It uses a fast greedy procedure to cluster sequences with similarity above a specified PID (percent identity) threshold by applying short word filters.

Application of CD-HIT, with the default identity threshold of 90% to the mH178 data set, yielded an overtly refined classification with a total of 108 subfamilies, of which 62 were composed of single HDs (singletons). We therefore tested a range of sequence identity thresholds (40–99% in 1% intervals) and looked for CD-HIT partitions with the highest robustness, along the lines of the OSL approach. The robust partition for mH178 dataset was identified at a PID value of 78% as shown in Figure 1a.

Grouping HDs on the basis of their DNA-binding preferences

To group together HD proteins with most similar DNA-binding preferences, we first built a weighted graph with a total of 178 nodes, where each node represented one mouse HD protein and edge weights were the pairwise PC coefficients of their binding profiles defined above.

Next, we applied the MCL algorithm to partition the graph into highly interconnected regions. Preliminary tests indicated that this graph was too densely connected to be readily amenable to clustering using MCL or several other algorithms that we tested (see Supplementary Methods for details). We therefore set out to prune the graph before applying the MCL algorithm. To this end, we set to zero edge weights corresponding to negative PC values and raised the remaining weights to a power of γ, with values of γ varying between 2 and 250 in steps of 2. The resulting edge weights were rounded off to four decimal places, which is the default in the MCL clustering software. This power-based procedure has a similar effect to straightforward thresholding, except that it also modifies the values of the remaining edges so as to further enhance differences in magnitude between them. This in turn facilitates the partitioning of the graph by MCL (see Supplementary Methods).

In addition to considering different starting graphs produced by applying different power functions, we also varied the MCL Inflation parameter. Similar to the procedure used for TribeMCL, we surveyed Inflation values between 1.2 and 4.8 in steps of 0.4, covering the recommended parameter range.

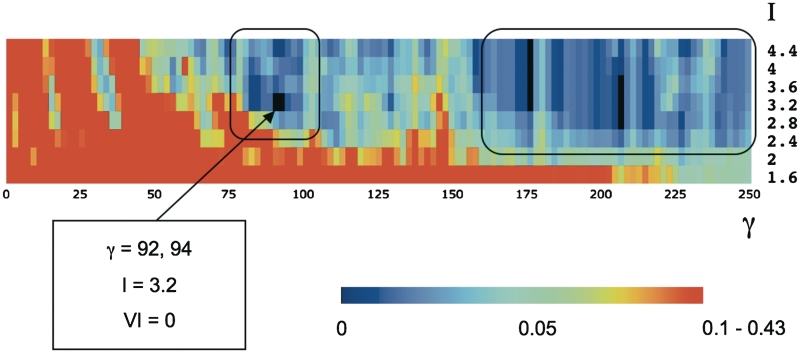
Varying the power and Inflation parameters produced a total of 1250 MCL partitions of the set of 178 mouse HDs into clusters, based on the in vitro DNA-binding preferences. This landscape was then searched for optimal combinations of the γ and I values, defined as those corresponding to MCL clustering solutions that show the highest robustness against small changes in these values, while, at the same time, being well balanced between having too few large clusters and too many singletons. To identify such solutions we considered each MCL partition obtained within the surveyed parameter range and computed its average VI distance to the eight neighboring partitions, defined by the parameter-sampling intervals δγ (±2) and/or δI (±0.4).

Figure 3 illustrates the landscape of the surveyed MCL partitions. It reveals two distinct regions of robust solutions. The first region contains well-balanced partitions. We were able to ascertain the meaningful character of these solutions by examining how several properties of the corresponding MCL solutions, such as the size of the largest clusters, the average cluster size, the standard deviation in cluster sizes, the total number of clusters and the number of nonsingleton clusters, behave as the γ and I parameters are varied (see Supplementary Figure S2). Among these solutions we identified the one at γ = 94, I = 3.2 as the most robust and representative solution. The second region, at much higher γ values, turned out to represent trivial solutions containing a majority of singletons and only a few clusters with three or more HDs.

Figure 3.

Identification of robust MCL partitions for the mH178 data set based on the in vitro DNA-binding profiles. The heat plot displays the average distance of each MCL partition of the mH178 data set to its eight immediate-neighbor partitions, each obtained with one-step perturbation of the γ (±2, horizontal axis) and/or I (±0.4, vertical axis) parameters (see ‘Results’ section for details). The distance between partitions is computed using the Variation of Information (VI) metric, and follows the depicted color scale. Robust partitions (<VI> = 0) are depicted in black and the most different partitions (VI between 0.1 and 0.43), in red. Two regions showing higher than average robustness are highlighted by black rectangles: one representing non-trivial clustering solutions (including MCL_b-pref at γ = 92–94, I = 3.2), and a larger region (γ > 160) representing trivial solutions consisting of a large number of singletons clusters.

RESULTS

Mouse HD subtypes derived on the basis of their DNA-binding preferences

The collection of mouse HD subtypes derived from the DNA-binding preferences using the MCL clustering is denoted as MCL_b-pref. It contains 55 clusters, with three members per cluster on average. Of these, 33 clusters contain at least two members (nonsingletons) and the largest cluster comprises 13 HDs (see Supplementary Table S3). These characteristics are similar to those of the classification by Berger et al. (24) derived for the same HDs by combining information from the ClustalW dendogram of the corresponding domain sequences, their DNA-binding motifs and the measured DNA-binding preferences (Table 1 and Supplementary Table S2). The two HD groupings display a relatively small VI distance of 0.73. We also see that the slightly more refined Berger et al. solution has a respectable Purity score of 0.68 against MCL_b-pref (Table 1), indicating that a high fraction of nonsingleton clusters in Berger et al. partition exactly match, or are subsets of, clusters in the MCL_b-pref partition (see ‘Materials and Methods’ section).

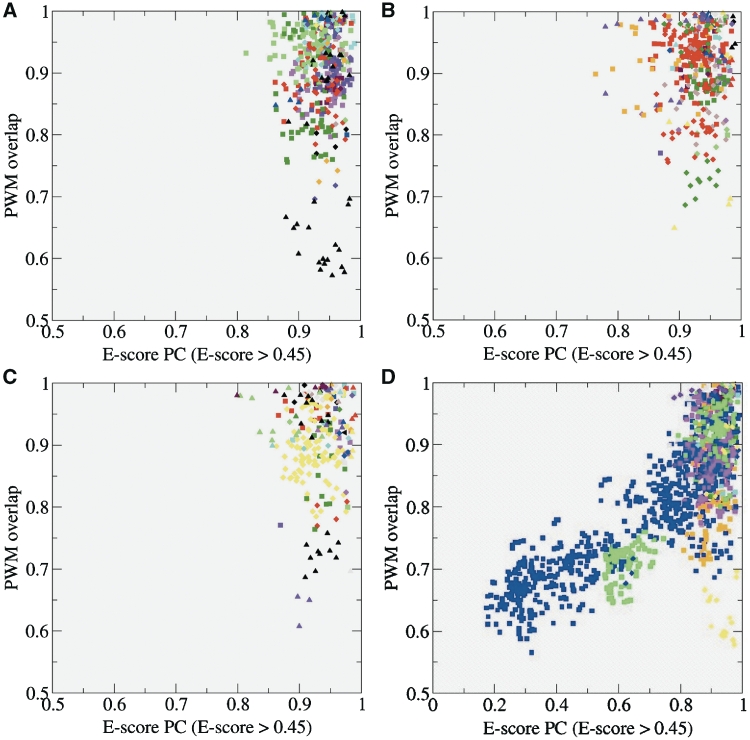
The outstanding differences between the two classifications can be assessed by systematically comparing individual clusters from the two types of classifications, as will be discussed in subsequent sections (see also Supplementary Figures S8–S13). These differences are readily rationalized by the fact that the robust MCL_b-pref partition generated here is solely based on the DNA-binding data, whereas the Berger et al. classification incorporates additional information. This is illustrated by mapping information derived from the DNA-binding data onto the HD groups from the two classifications, as follows. We plotted the PC of the profiles of the 8-mer binding scores (E-scores) (24) against the PWM overlap score, which quantifies the similarity between the DNA sequence motifs recognized by two HDs (see ‘Materials and Methods’ section). The corresponding scatter plots for the MCL_b-pref and the Berger et al. solutions are shown in Figure 4a and b, respectively. Each point in these plots represents a pair of HDs within the same subfamily; thus, only nonsingleton subfamilies are shown.

Figure 4.

Information on binding preferences mapped onto the sequence-based subfamilies derived using the Default- and Entropy- SCI-PHY modes. Scatter plots of the PWM overlap score, which quantifies the similarity between the DNA-binding sites of two homeodomains (see ‘Materials and Methods’ section) (vertical axis), against the pairwise Pearson Correlation (PC) of the 8-mer DNA-binding scores (E-scores) from (24) (horizontal axis). Both quantities are computed for individual HD pairs belonging to the same subfamily, and points representing pairs from different subfamilies are colored differently. (A) Scatter plots for pairs within the 55 subfamilies of the binding-data based MCL_b-pref classification. (B) Scatter plots for pairs within the subfamilies derived by Berger et al. including all 178 mouse homeodomains (Supplementary Table S2). (C) Scatter plots for pairs within the 84 subfamilies of the OSL_PID classification. (D) Scatter plots for pairs within the 33 mouse HD subfamilies of the Default-H559 classification.

We see that the Berger classification displays a slightly wider dispersion in the intra-subfamily PC values than the objective MCL_b-pref grouping. On the other hand, the differences in PWMs between family members, which the manually adjusted classification seeks to minimize as well, are smaller in the latter than in the MCL_b-pref grouping.

Taken together, these results demonstrate that meaningful definitions of HD subtypes can be derived from the DNA-binding data alone using a fully automatic procedure. Furthermore, they confirm that these data reveal a very fine subdivision of the HD data set. This subdivision agrees much better with the one defined by phylogenetic analyses at the Family level than at the coarser class level (31–33). As objective subtype definitions such as those proposed here are solely based on quantitative measures of binding preferences, they represent a valuable reference against which sequence-based classifications can be compared and ultimately calibrated.

Sequence-based subfamilies versus subtypes derived from binding preferences

In order to partition the mouse HDs into subfamilies on the basis of their amino acid sequence, a total of five different procedures were tested. These procedures comprise four well-known subfamily classification methods: SCI-PHY, SECATOR, CD-HIT and the TribeMCL algorithm. In addition, we generated subfamilies using OSL with three different metrics, referred to as OSL_PID, OSL_E-Value and OSL_TRE (see ‘Materials and Methods’ section). These procedures were applied to the 178 mouse HD proteins (mH178 data set) for which the binding data are available, as well as to a larger data set totaling 599 proteins, denoted as H559.

Table 1 summarizes the classification results obtained using these methods and corresponding optimized settings, whenever applicable. Interestingly, we see that the classifications fall into two main categories in terms of the number and size of the subfamilies: a set of coarse HD classifications that differ significantly from one another, and a set of fine-grained very similar classifications, as detailed below.

Coarse-grained classifications

Five coarser classifications were obtained with SECATOR, SCI-PHY and TribeMCL in their default settings. They were derived from either the mH178 or H559 data sets, with individual classifications comprising between 10 and 33 subfamilies of which one is usually quite large (e.g. 40–56 members for Default-SCI-PHY, and 86 members for TribeMCL). The TribeMCL classifications correspond to robust partitions obtained with E-value thresholds similar to those used in the literature (14) (see ‘Materials and Methods’ section). The coarser granularity of these classifications results in large VI distances and very poor Purity scores relative to the HD subtypes derived from the DNA-binding data, or to those of Berger (Table 1). Another indication that the corresponding subfamilies poorly reflect the DNA-binding specificities is the wide spread of the intra-subfamily binding score correlations, as illustrated for one of the default SCI-PHY classifications (Figure 4d).

Furthermore, we see that various coarse-grained classifications also tend to differ greatly from one another (see Supplementary Table S9). Among these classifications, those produced by SCI-PHY show the closest correspondence with expert-based HD classes reported in the literature (31–33). This is consistent with the fact that this method, like a number of others, was designed to maximize the recall of various expert-based classifications of a number of protein systems, which tend to be coarser (21,23). We find, for example, that the largest 56-member subfamily of the Default mH178 partition (Supplementary Table S10), contains many of the proteins of the Antennapedia (ANTP) class (32), including some Hox proteins. However, the majority of the Hox proteins are segregated into two separate subfamilies of 15 members each. The second largest subfamily in Default-mH178 comprises 27 members mainly from the Paired (PRD) gene class, whereas proteins from the smaller LIM and POU classes appear as distinct subfamilies.

Fine-grained classifications

Eight fine-grained classifications were obtained by SCI-PHY in the Entropy mode, by the objective CD-HIT version that optimizes the sequence identity threshold, and by the three OSL procedures. They were likewise derived from either of the two HD data sets.

Table 1 reveals that these classifications share common trends that clearly distinguish them from the partitions of the coarse category. They feature lower VI distances than their coarser counterparts to the HD classification derived from the DNA-binding data (0.94 ± 0.02) and to that of Berger (VI = 0.58 ± 0.05). With one exception, their purity scores relative to the same two partitions are also significantly higher (p = 0.73 ± 0.03 and 0.89 ± 0.04, relative to the binding-based MCL_b-pref subtypes and Berger’s, respectively). The outlier is the Entropy mH178 classification by SCI-PHY. It is somewhat coarser (with 36 nonsingleton subfamilies, compared to 44 ± 4 for the remaining seven classification) and displays correspondingly lower Purity scores of ∼0.54 against the DNA binding-based and manually adjusted classifications (Table 1).

The much improved correspondence of the seven fine-grained classification with the DNA-binding data is further confirmed by the narrower spread of intra-subfamily binding score correlations, as illustrated in the scatter plot of Figure 4c obtained for one of these classifications (OSL_PID). We also note that the objective CD-HIT version and OSL_PID each yielded exactly the same HD subfamilies from mH178 or the H599 data set, the latter containing additional HD sequences from other organisms (Table 1). The effect of these additional sequences on the other OSL versions is minor. This was not the case with Entropy SCI-PHY, which produced a coarser classification than the other methods only when applied to mH178.

The high degree of similarity between the seven fine-grained classifications is clearly evident from their small pairwise VI distances (0.09–018) (Table 2), and their very high mutual Purity scores (Table 3). All seven classifications represent a perfect refinement (Purity Score = 1) of the coarser Entropy-mH178 by SCI-PHY. The nearly identical classifications produced by the objective CD-HIT version and OSL_PID indicate that the CD-HIT short-word filtering algorithm is quite effective. It is also interesting that SCI-PHY and OSL_TRE, both of which are based on the Total Relative Entropy metric but use a completely different scoring function and dendogram, produced virtually identical classifications when applied to H559.

Table 2.

Pairwise comparisons of different mouse HD classifications: VI distances

	SCI-PHYEntropy mH178	SCI-PHYEntropy H559	CD-HIT	OSLPID	OSLTRE mH178	OSLTRE H559	OSLEval mH178	OSLEval H559
SCI-PHYEntropy mH178	0.00	0.53	0.50	0.46	0.56	0.41	0.55	0.56
SCI-PHYEntropy H559		0.00	0.13	0.14	0.11	0.14	0.18	0.19
CD-HIT			0.00	0.09	0.10	0.11	0.15	0.16
OSLPID				0.00	0.10	0.05	0.10	0.10
OSLTRE mH178					0.00	0.15	0.09	0.10
OSLTRE H559						0.00	0.14	0.15
OSLEval mH178							0.00	0.01
OSLEval H559								0.00

Summary of the pairwise similarity levels, in terms of Variation-of-Information (VI) distances, between the seven different fine-grained sequence-based classifications.

These classifications were derived from the mH178 or H559 data set, as indicated (see ‘Materials and Methods’ section for details), using three different methods: SCI-PHY in the Entropy mode, CD-HIT and the three Objective Single Linkage (OSL) procedures. OSL_PID, and CD-HIT each produced exactly the same classification when applied to either of the 2 HD data sets.

Relatively high VI values corresponding to poor similarity levels between the listed classifications are shown as underlined italic.

Table 3.

Pairwise comparisons of different mouse HD classifications: purity scores

	SCI-PHYEntropy mH178	SCI-PHYEntropy H559	CD-HIT	OSLPID	OSLTRE mH178	OSLTRE H559	OSLEval mH178	OSLEval H559
SCI- PHYEntropy mH178	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
SCI- PHYEntropy H559	0.53	1.00	0.91	0.96	0.98	0.93	0.98	0.98
CD-HIT	0.53	0.92	1.00	0.96	0.98	0.91	0.98	0.98
OSLPID	0.56	0.94	0.96	1.00	1.00	0.93	1.00	1.00
OSLTRE mH178	0.50	0.85	0.85	0.89	1.00	0.82	0.95	0.95
OSLTRE H559	0.56	0.98	0.98	1.00	1.00	1.00	1.00	1.00
OSLEval mH178	0.50	0.79	0.80	0.84	0.91	0.77	1.00	1.00
OSLEval H559	0.50	0.79	0.80	0.82	0.89	0.77	0.98	1.00

Summary of the pairwise Purity scores (as defined in ‘Materials and Methods’ section) between the seven different fine-grained sequence-based classifications. Classifications listed along columns were considered as ‘target’ partitions, whereas those listed along rows were used as ‘reference’ partitions. See Table 2 for information on these classifications.

Low Purity values, underlined (column 2), indicate a poor correspondence between the target classifications in columns 1 and the SCI-PHY_entropy mH178 classification used as reference.

In all other cases, the target classifications represent near perfect subdivisions of the reference partitions.

Most importantly, we find that our seven fine-grained sequence-based mouse HD subfamilies and those derived by Berger et al. show a very similar level of overlap with the HD subtypes derived here from the DNA-binding data. In fact, the pairwise VI distances and Purity score values listed in Table 1, indicate that the three classifications are roughly equidistant from one another, although the sequence-based and Berger subfamilies overlap somewhat better with one another, than with the MCL_b-pref subtypes. This is a very encouraging result considering that our classifications were derived by an automatic approach solely on the basis of sequence information. In contrast, the Berger et al. HD grouping was manually adjusted after combining information from DNA-binding preferences, amino acid sequence similarity and DNA-binding motifs (24).

Memberships of HD subfamilies and functional subtypes are highly consistent

In this section, we further illustrate the good correspondence between the sequence-based subfamilies with those of the HD subtypes objectively derived from the DNA-binding preferences. Taking as example the Entropy-H559 SCI-PHY sequence-based classification we compare the composition of its subfamilies with that of the robust MCL_b-pref partition derived from the DNA-binding preferences.

Figure 5 illustrates the detailed compositions of the Entropy-H559 subfamilies and how members of individual clusters of the MCL_b-pref partition map onto them. Rows in Figure 5 correspond to the SCI-PHY subfamilies and the colors correspond to MCL_b-pref clusters (singleton clusters are shown in white). Out of the 48 nonsingleton sequence-based subfamilies, 35 are either exactly identical to an MCL_b-pref cluster (12 subfamilies) or are entirely contained within such cluster (23 subfamilies), whereas the remaining 13 subfamilies group HDs from more than one MCL_b-pref clusters.

Figure 5.

Correspondence between the Entropy-SCI-PHY classification of the H559 data set and the robust MCL_b-pref partition derived from the in-vitro DNA-binding profiles. Shown is the correspondence in terms of membership in individual subfamilies, for the pair of partitions MCL_b-pref (γ = 94, I = 3.2) and the Entropy-H559 classification. The 84 Entropy-H559 subfamilies are listed in rows, in order of decreasing size (1–48 for the 48 nonsingleton subfamilies), with the 36 singleton subfamilies grouped in the bottom row. Individual homeodomains are colored according to their membership in the 55 mouse clusters from the MCL_b-pref clustering solution, which contains 33 nonsingleton clusters and 22 singletons. Different colors correspond to different clusters in the MCL_b-pref classification. Singleton MCL_b-pref clusters are colored in white. Out of the 48 nonsingleton SCI-PHY subfamilies, 35 are either exactly identical to an MCL_b-pref cluster (12 subfamilies: #2, 7, 9, 12, 16, 19, 25, 26, 28, 37, 40, 42, 44), or are entirely contained within such cluster (23 subfamilies: #5, 8, 10, 11, 13, 14, 15, 17, 18, 20, 22, 23, 27, 31, 32, 35, 36, 38, 39, 41, 45, 48), whereas the remaining 13 subfamilies group HDs from more than one MCL_b-pref clusters (see text).

In five of the latter cases this is likely due to noise in the DNA-binding data. In particular, for HDs with identical sequences—which should, under ideal conditions, show a perfect correlation of their DNA-binding profiles (PC = 1) measured by Berger et al. (24) had PC values as low as 0.86 (for Six6; see Supplementary Figure S4). As the majority of the duplicate pairs have a pairwise PC above that value, this does not appear to be a systematic bias, but rather reflects the inaccuracies of the experimental measures. We therefore took PC = 0.86 as the lower bound for considering two binding profiles as indistinguishable. Hence, in such cases, HDs were not necessarily grouped together by the MCL_b-pref clustering. For example, duplicate clones of Six6, Cutl1 and Irx3 are segregated into different MCL_b-pref clusters. Likewise, for Gbx1 and Gbx2, as well as for Irx2, that is separated from the other Irx proteins despite having the same sequence as Irx5.

The remaining seven mismatches involve the separation by the MCL_b-pref partition of Dbx1 from Dbx2, Tcf1 from Tcf2, Tgif1 from Tgif2, Hoxa1 from Hoxd1, Prrx1 from Prrx2, Alx3 from Alx4 and Obox1 and Obox3 from the remaining Oboxs. In all of the above cases, the Entropy-H559 classification places each of these closely related HD pairs or groups together (Figure 5), which seems to be justified. On the other hand, the MCL_b-pref classification splits in two the largest SCI-PHY subfamily, separating the Hox5 group from the Hox6 and Hox7 groups, which goes one step further than the SCI-PHY classification toward separating the Hox proteins into the individual paralog groups (49,50).

Quite remarkably, we thus see that 35 out of the 48 (73%) nonsingleton mouse HDs subfamilies derived from Entropy-H559 reflect well the grouping of these HDs performed independently on the basis of their in vitro DNA-binding preferences. Of this subset, 12 subfamilies faithfully recall the functional grouping for the corresponding HDs, whereas the remaining 23 subfamilies that are entirely contained in an MCL_b-pref cluster represent a perfect refinement of the function-based grouping of the same domains, which is fully consistent with it.

If one also considers the 5 Entropy-H559 subfamilies where the discrepancies with the binding-based MCL_b-pref classification can clearly be attributed to noise in the experimental data, the number of subfamilies correctly reflecting DNA-binding preferences rises to 40 out of 48, representing 83% of the sequence-based groups. This may still be an underestimate of the ability of the sequence-based HD classification to reflect DNA-binding preferences, if at least some of the remaining seven mismatches discussed above are also due, as we suspect, to inaccuracies in the experimental data, or to our manipulations of the original PC correlation graph (see Supplementary Methods for details). A very similar picture was obtained when clusters of the same MCL_b-pref partition were mapped onto the subfamilies derived by CD-HIT and the various types of the OSL (see Supplementary Figures S8–S11).

DISCUSSION

In this work, we showed that HD proteins from an organism, in this case mouse, can be grouped into subfamilies on the basis of amino acid sequence information alone. This grouping was found to reflect quite accurately in vitro DNA-binding preferences of these domains as measured using PBM (24). An important finding of our study is that this result was obtained with several subfamily classification methods and was conditional on the fact that the parameter settings of these methods were either objectively defined, or nonstandard (in the case of SCI-PHY). Under these conditions, as many as five different methods generated very similar fine-grained partitions of the mouse HDs, from either the mH178 or the larger H559 data set. These partitions typically contain 81–93 subfamilies, of which 41–48 are nonsingletons, and none with more than 15 members.

Another significant observation is that the majority of the tested sequence-based classification methods, when applied using default parameters recommended by their authors, consistently yielded more coarse-grained subfamily descriptions. The latter differ from one another, with the total number of subfamilies ranging between 10 and 33. Such coarser subfamilies, in particular those derived using Default SCI-PHY, are in good agreement with expert-derived functional classes (21,22), including those for the HDs analyzed here (31–33), but agree poorly with those defined on the basis of the DNA-binding preferences.

These results taken together highlight the fact that the DNA-binding data afford a more fine-grained description of functional specificity, than that usually derived by experts. Expert-based descriptions are commonly based on physiological, biochemical, sequence and structural information, and in the case of enzymes, often by considering conserved chemical mechanisms as represented by the Enzyme Commission (EC) classification. These features tend to represent high-level, and often qualitative, measures of functional specificity that usually lead to coarser subtype descriptions. However, these are the descriptions that subfamily classification methods have so far been calibrated against.

In contrast, the PBM-derived DNA-binding preferences represent direct quantitative measures of functional specificity that enable finer subtype subdivisions. For enzymes, this would amount to further subdividing those with the same four EC digits on the basis of binding affinities or catalytic efficiencies measured for a given set of substrates.

Such fine-grained subtype descriptions are a completely new benchmark for sequence-based subfamily classification procedures, and we have shown here that several different procedures can perform well in this new context when their parameters are optimized to yield classifications that are robust against small changes in parameter values. This optimization is entirely self-consistent and uses no information on the DNA-binding data, which the classifications aim in principle at matching. It involves plotting the robustness of classifications generated using a wide range of parameter values, and selecting the most robust nontrivial ones (not primarily composed of very small subfamilies containing pairs and single domains) in the plot (see ‘Materials and Methods’ section). Robust fine-grained classifications were identified in this fashion using CD-HIT and the three graph-pruning procedures.

With all five methods, these results were produced by thresholding the sequence similarity graph at rather high levels (80 ± 2% sequence identity, or equivalently, given the data sets used, E-value of ∼10^−25.7). We verified, furthermore, that HDs in different subfamilies display on average ∼40% sequence identity.

These findings are in excellent agreement with a recent report that 80% domain sequence identify is required for safe function transfer for both enzymes and non-enzymes from the CATH-Gene3D catalog (51), indicating moreover, that our results have a wider applicability in the prediction of protein function from sequence.

The degree to which sequence features reflect binding preferences clearly varies between HD subfamilies (Supplementary Tables S7 and S8), due in part to the fact that some HDs tend to display much broader specificities than others. For some HD subtypes, such as the Hoxs, sequence features reflect their DNA-binding preferences to a very fine level of detail, as profiles of individual domains are more highly correlated (average PC∼ 0.94) for different Hox clusters (A–D) within the same paralog group (1–13) (50) than for those in different positions of the same clusters (average PC ∼0.86; see Supplementary Figure S14).

Overall the fine-grained classifications derived here segregate the mouse HDs extremely well into groups that carry out distinct cellular functions, in agreement with suggestions made on theoretical grounds (52). Taking as example the OSL_PID-m178 classification (Supplementary Table S4), we observed that the vast majority of the sub-families with two or more members contain HDs with very similar cellular function, as annotated in the GO ontology (53), and based on information collected using the iHOP resource (54). Notably, the Hox domains are grouped into seven sub-families, each containing only these domains. The largest one with 15 members comprises the Hox paralogous groups 4–8 (50), annotated as involved in anterior/posterior pattern formation and skeletal system development. The remaining Hoxs are grouped into six clusters, each containing Hox domains with distinct roles. For example, the four-member Hox13 subfamily comprises domains involved in prostate gland epithelium morphogenesis, whereas the domains in the three-member Hox11 subfamily are involved more generally in the regulation of organ formation. All five Dlx domains, of which four are implicated in neurogenesis, make up one subfamily. This is also the case for the three Mlx HDs involved in signaling; the Pitx subfamily implicated in hind limb morphogenesis; the four very closely related Obox HDs, whose functional role is currently not well known; and several other HD groups.

Not too surprisingly, the singleton HDs in the OSL_PID-m178 classification are much more functionally diverse. For instance, Otp, Hlx1, Isx, Shox2 are involved in neuropeptide secretion, regulation of colony stimulation, Vitamin A metabolism, and differentiation of cardiac pacemaker cells, respectively (54).

Unfortunately, despite recent efforts (55), not enough is known about the transcriptional regulation network and protein interactions involving the HDs analyzed here. For example, Hox genes act at many levels of the regulatory hierarchy. They regulate effector genes both directly, and indirectly at the ‘executive’ level. But only a very small subset of these regulatory relationships is currently documented. These and other HDs also often associate with each other to form protein complexes, most likely indicating that members of the same complex exert a combined regulatory action.

Lastly, we observe that the binding specificities as measured by the PWMs display poorer agreement with the sequence-based classification than the E-score based binding profiles. This is evident from the wider dispersion in the PWM overlap values (∼0.58–1) than in E-core-based PC values (∼0.8–1) within subfamily members (Figure 4). This suggests that PWMs, which represent the DNA-binding site motifs specific to each TF, may be a less sensitive measure of the HD binding preferences. This is clearly reflected by the shapes of the PWM overlap distributions for HDs within and between the Entropy-H559 SCI-PHY subfamilies respectively (Supplementary Figure S6). The inter-subfamily distribution (inset Figure S6) features a much wider shape than the distribution of the inter-subfamily PC values (Supplementary Figure S5), indicating that the sequence-based subfamily classification poorly discretizes the HDs in terms of the features of their cognate DNA sequence motifs. This fuzzier functional fingerprint of the PWMs likely stems from the fact that the PWMs have been derived from the E-score binding data in (24) using a number of assumptions, and therefore represent the binding preferences of HDs more indirectly than the E-score based profiles themselves. Shortcomings in PWM models have been pointed out in previous analysis of in vitro studies of DNA-binding preferences (56–59), including a recent study of a set of diverse DNA-binding proteins (56). However, it is unclear at this point whether these observations can be generalized to DNA-binding motifs derived from in vivo experimental analyses (60–62), which are customarily used to characterize TF binding specificity.

On the basis of these various considerations we can safely conclude that sequence-based subfamily classification protocols are capable of teasing out key features of the HD amino acid sequences that faithfully reflect very specific aspects of their molecular function. Clearly, the availability of quantitative experimental measures of molecular function specificity, such as the DNA-binding preferences for the mouse HDs, offers completely new opportunities for further fine tuning these protocols and developing new ones.

As it becomes feasible to produce such measures for other transcription factor families (56), and for major signaling domains (SH3, PDZ and others), approaches of the types outlined in this study should be very useful for deriving meaningful domain subtypes from the experimental measures, and for exploiting information from sequence-based subfamily classifications to prioritize the experimental screenings.

In the future these approaches could be generalized and improved to the point of yielding reliable predictions of specialized molecular function from sequence information. This will require, among other things, devising protocols that afford higher precision of the experimental data, notably by programming a large enough number of replicate experiments.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Canadian Institutes of Health Research (MOP#82940); Sickkids Foundation (to S.J.W.); Ontario Research Fund (to S.J.W.); National Science Foundation (to M.F.B.); National Institutes of Health/National Human Genome Research Institute (R01 HG003985 to M.L.B.). SJW is Canada Research Chair, Tier 1. Funding for open access charge: Canadian Institute of Health Research (MOP#82940).

Conflict of interest statement. None declared.