Abstract
Five strategies for pre-processing intensities from Illumina expression BeadChips are assessed from the point of view of precision and bias. The strategies include a popular variance stabilizing transformation and model-based background corrections that either use or ignore the control probes. Four calibration data sets are used to evaluate precision, bias and false discovery rate (FDR). The original algorithms are shown to have operating characteristics that are not easily comparable. Some tend to minimize noise while others minimize bias. Each original algorithm is shown to have an innate intensity offset, by which unlogged intensities are bounded away from zero, and the size of this offset determines its position on the noise–bias spectrum. By adding extra offsets, a continuum of related algorithms with different noise–bias trade-offs is generated, allowing direct comparison of the performance of the strategies on equivalent terms. Adding a positive offset is shown to decrease the FDR of each original algorithm. The potential of each strategy to generate an algorithm with an optimal noise–bias trade-off is explored by finding the offset that minimizes its FDR. The use of control probes as part of the background correction and normalization strategy is shown to achieve the lowest FDR for a given bias.
INTRODUCTION
Background correction and normalization are important pre-processing steps that must be applied to microarray data before downstream analysis can be done. Illumina whole-genome BeadChips have become increasingly popular for expression profiling during the past few years, but without any consensus yet regarding the pre-processing steps. Illumina BeadChips have some unique features compared with other microarray platforms. Each array includes an unusually large number of positive and negative control probes, and each probe is replicated on each array in the form of a random number of beads. The negative control probes can be taken to represent the behavior of non-expressed probes (1). Raw data from BeadChips usually takes the form of probe summary profiles exported by BeadStudio software, meaning that bead-level intensities are already summarized into probe-level values, although extracting bead-level data is also possible (2). BeadStudio also exports intensity summaries for a variety of positive and negative control probes. In this study, we assume that no prior background correction or normalization has been done, so all raw intensities are non-negative.
The pre-processing of data from any single-channel microarray platform typically involves the three major steps of background correction, between-array normalization and data transformation. Most strategies for pre-processing Illumina data share some features with the robust multi-array analysis (RMA) algorithm, which has become well accepted for Affymetrix GeneChip data (3–5). RMA consists of a model-based background correction step, followed by quantile normalization, 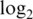 transformation and probe-set summarization. The normal-exponential (normexp) convolution model used by RMA for background correction has been adapted to normalize two-color microarrays (6,7). RMA estimates the unknown parameters in the normexp model by an ad hoc method, but maximum likelihood estimation has been used in the two-color context after the development of appropriate numerical algorithms (7).
transformation and probe-set summarization. The normal-exponential (normexp) convolution model used by RMA for background correction has been adapted to normalize two-color microarrays (6,7). RMA estimates the unknown parameters in the normexp model by an ad hoc method, but maximum likelihood estimation has been used in the two-color context after the development of appropriate numerical algorithms (7).
A number of strategies have been proposed for pre-processing BeadChip data. A relatively simple approach is to quantile normalize then log-transform the raw intensities, without any explicit background correction (8,9). The same normalization and transformation steps have been used but preceded by maximum likelihood normexp background correction (10). Normexp background correction has been also adapted to take advantage of Illumina negative control probes (11–13). Ding et al. (11) proposed a joint likelihood function for both negative control and regular probes in order to estimate the normexp parameters. Xie et al. (12) improved the computational procedures for maximizing the joint likelihood, and also suggested a non-parametric approach in which the background normexp parameters are estimated purely from the negative control probes. Alternatively, a variance-stabilizing transformation (vst) has been proposed that is estimated from the bead-level standard deviations (14). Vst is a generalized log2-transformation that has the effect of background correcting and transforming at the same time. It is followed usually by either quantile normalization or robust spline normalization (15).
In this study, we conducted an assessment of five pre-processing algorithms representative of the major strategies for pre-processing BeadChip data (Table 1). Two variants of vst are included. Two variants of normexp, using or ignoring control probes, are included. The normexp by control (neqc) algorithm uses the non-parametric background correction from Xie et al. (12) followed by quantile normalization with both control and regular probes (13,16). The simplest pre-processing strategy without background correction is also included. Our results show that these five algorithms have quite different behaviors, so that they are not easily comparable. Some tend to maximize precision (minimize noise) while some minimize bias. A special feature of our work is that we use each of five base algorithms to generate a continuum of related algorithms with different noise–bias trade-offs, by offsetting the unlogged intensities away from zero. Our study is not limited to the behavior of the base algorithms as originally proposed, rather we consider the potential of the base algorithms to generate an algorithm with an optimal noise–bias compromise.
Table 1.
Pre-processing strategies assessed in this study
| Name | Bg correction | Transformation | Normalization |
|---|---|---|---|
| logq | None | Log2 | Quantile |
| vstq | Vst (implicit) | Vst | Quantile |
| vstr | Vst (implicit) | Vst | Robust spline |
| neq | Normexp (mle) | Log2 | Quantile |
| neqc | Normexp | Log2 | Quantile |
| (using negative controls) | (including controls) |
For logq, neq and neqc, background correction is performed first, then between-array normalization, then transformation. For vstq and vstr, transformation is performed first followed by between-array normalization.
The idea of offsetting intensity data has been discussed previously as an approximate variance-stabilizing strategy in the context of two-color microarray data (6,17), and has also been used for Illumina data (9,10,13,16). Adding an offset to the intensities before log transformation not only was found to lower the variance (improve precision) but also to compress the fold-change range and increase bias. In other words, offsets decrease noise but increase bias. One of our observations is that each pre-processing algorithm can be viewed as having an effective offset, which tells us a lot about the noise–bias trade-off characteristic of that algorithm. We measure the effective offset for each algorithm by the typical unlogged intensity value assigned by that algorithm to non-expressed probes. This serves to calibrate the amount of shrinkage of normalized log-intensity values. Each base pre-processing algorithm has an innate offset, which we can increase or decrease in our study, moving each pre-processing strategy along the noise–bias spectrum. This provides major insight into the relationships between the different strategies, and also enables us to tune each strategy in an optimal fashion.
There is little agreement in the literature regarding how best to evaluate the performance of pre-processing strategies. Biological results have been used for the comparison (11), but this is subjective and does not dissect the specific aspects of each algorithm's behavior that contribute to its performance. We view the use of suitable calibration data sets containing objective truth as the most objective `gold standard' approach to assessing different strategies. Four data sets are used in this study. Two of them are from spike-in experiments and two from mixture experiments. A mixture experiment mixes two pure samples at different proportions. Spike-in data sets enable us to evaluate the strategies by comparing observed to spiked-in fold changes. Mixture data sets enable us to estimate false discovery rates (FDRs) in assigning differentially expressed (DE) genes by comparing the list of test DE and non-DE genes obtained from the comparison between mixed samples to the list of `true' DE and non-DE genes obtained from the comparison between pure samples.
Our five pre-processing strategies are compared by using metrics for precision, bias and false discovery rate. Precision is evaluated by calculating standard deviations between replicate arrays. Bias can be measured by comparing observed to known fold changes for spike-in probes. Bias is also apparent by observing the range of fold changes across all the probes on the arrays, because the algorithms with greatest bias are those which most shrink the fold-changes. Estimated FDR are used to evaluate the trade-off between precision and bias.
We compare the pre-processing strategies in a number of ways by varying the offsets. We can compare strategies by way of FDR for a given level of bias, or by way of bias for a given FDR. Alternatively, and perhaps most informatively, we can select the offset that minimizes the FDR for each algorithm, and then compare the minimized FDRs. Our results show that normexp background correction using control probes (neqc) gives the best gain in precision for minimum shrinkage. It presents the least biased fold changes for a given FDR.
MATERIALS AND METHODS
Data sets
Four calibration data sets were used in this study:
Mixture data (M1) (1). Two pure samples, MCF7 and Jurkat, were mixed in six different proportions: 100% MCF7 (A1), 94% MCF7/6% Jurkat (A2), 88% MCF7/12% Jurkat (A3), 76% MCF7/24% Jurkat (A4), 50% MCF7/50% Jurkat (A5), 100% Jurkat (A6). Each sample has two replicates, making up 12 arrays in total. Two HumanWG-6 version 1 BeadChips were used.
MAQC data (M2) (18). Two pure samples, Universal Human Reference RNA (UHRR) and Human Brain Reference RNA (HBRR), were mixed in four different proportions: 100% UHRR (A), 100% HBRR (B), 75% UHRR/25% HBRR (C), 25% UHRR/75% HBRR (D). Each sample has five replicates, making up 20 arrays in total. The data used were from test site 2 in the MAQC-I project. Four HumanWG-6 version 1 BeadChips were used.
Spike-in data (S1) (19,20). There were 33 spike-in probes and 12 spike-in concentrations (1000, 300, 100, 30, 10, 3, 1, 0.3, 0.1, 0.03, 0.01, 0). Each spike-in concentration was repeated on four arrays, making up 48 arrays in total. Eight MouseWG-6 version 1 BeadChips were used.
Spike-in data (S2) (21). There were 34 spike-in probes and 12 spike-in concentrations (1000, 300, 100, 30, 10, 3, 1, 0.3, 0.1, 0.03, 0.01, 0). Each spike-in concentration was repeated on four arrays, making up 48 arrays in total. Eight HumanWG-6 version 2 BeadChips were used.
Data input and normalization
Probe summary profile files and control probe summary were exported from BeadStudio, without background correction or normalization. Output columns included detection P-values scores and bead-level standard deviations for each array. The input function read.ilmn in the Bioconductor package limma (22) was used to read the data into R. The neqc function in limma implements the neqc pre-processing strategy. Data pre-processing by the logq and neq strategies was performed using the backgroundCorrect and normalizeBetweenArrays functions in limma. Data pre-processing by the vstq and vstr strategies was performed using the lumiT and lumiN functions in the Bioconductor package lumi (15).
Probe filtering
For each probe on each array, the BeadStudio detection P-value is the proportion of negative control probes, which have intensity greater than that probe on that array. Probes were judged to be non-expressed if they failed to achieve a detection P-value of 0.01 or less for any array in a data set. Normalization was undertaken on all probes, whether expressed or not.
Estimating the proportion of DE probes
A convex decreasing density estimate on a list of P-values was used to estimate the proportion of DE probes (23). Using normalized intensities from logq, differential expression between the pure samples in the mixture data sets was tested using moderated t-statistics (24). The proportion of DE probes in the data set was then estimated from the associated P-values and the convest function in the limma package.
Area under receiver operating curve
Area under receiver operating curve (AUC) was computed to summarize the FDR receiver operating curve across all possible P-value cutoffs. Using mixture data M1, lists of nominally `true' DE and non-DE probes were obtained by comparing samples A1 and A6. Probes were then ranked by P-value for each of the comparisons A2 versus A3, A3 versus A4 and A4 versus A5. Comparing each ranked list to the true list yielded an AUC value, using the auROC function of the limma package. Averaging the AUC values from the three test comparisons gave the final value. The AUC value was calculated in the same way for data set M2, except that there was only one test list that compared samples C and D. The entire AUC calculation was repeated, including the derivation of `true' DE and non-DE probes, for each pre-preprocessing algorithm and each offset.
Added offsets and optimal added offset
Offsets from 0 to 4000 at steps of 20 were added to the unlogged intensities and AUC values were calculated for each added offset. Offsets were added after background correction step but before between-array normalization and transformation. Offsets could not be added for the vstq and vstr strategies because they do not have a separate background correction step.
The optimize function in R (http://www.r-project.org/) was used to find the optimal added offset, which maximizes the AUC value for each pre-processing strategy (25).
Normexp-by-control background correction
Illumina whole genome expression BeadChips include a set of negative control probes with randomly generated sequences (26). The number of negative control probes ranges from 750 to 1600 for BeadChips from different generations and different species. Previous studies by ourselves and others showed that these negative control probes provide a good measurement of the background noise (1,11,12). These negative controls should therefore be useful for the background correction of BeadChip data.
It is widely accepted that for high-density oligonucleotide arrays, the signal can be usefully modeled as an exponential distribution and the background noise as a normal distribution, for the purpose of background correct. The popular RMA algorithm, originally developed for pre-processing Affymetrix GeneChips (3,5), and adapted to two-color microarrays (6,7), fits a normal + exponential convolution model to the expression data. The convolution model involves three unknown parameters which must be estimated from the data, namely the mean μ and standard deviation σ of the background intensities and the mean α of the signal intensities. Estimation algorithms using kernel density estimators (3,5), saddle-point approximations (6) or maximum likelihood (7) have been proposed to estimate these parameters.
Xie et al. (12) proposed three approaches to estimate the normexp parameters. Their `nonparametric estimator' sets 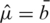 ,
, 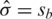 and
and 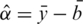 , where
, where 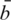 and sb are the mean and standard deviation of the negative control probe intensities and
and sb are the mean and standard deviation of the negative control probe intensities and 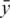 is the mean intensity of the regular probes for a particular BeadChip. The non-parametric estimator was found to perform very competitively (12), and is much faster to compute than other normexp algorithms due to its arithmetic simplicity.
is the mean intensity of the regular probes for a particular BeadChip. The non-parametric estimator was found to perform very competitively (12), and is much faster to compute than other normexp algorithms due to its arithmetic simplicity.
For some data sets, it is possible that some of the negative control probes are subject to cross-hybridization with expression transcripts and hence do not truly reflect background intensity. To allow for this possibility, we provide the option of robust estimation of the background mean and variance in our public software. If this option is chosen, 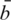 and sb are replaced by estimators which are robust on the log scale (27).
and sb are replaced by estimators which are robust on the log scale (27).
Quantile normalization with control probes
We propose a simple extension of quantile normalization, in which control and regular probes are quantile normalized together, including both positive and negative controls. This serves to make quantile normalization more robust against violations of the assumption that total mRNA production is equal in all the samples. The neqc pre-processing strategy presented in this study uses the normexp-by-control background correction described above followed by quantile normalization with control probes.
RESULTS
Precision versus compression
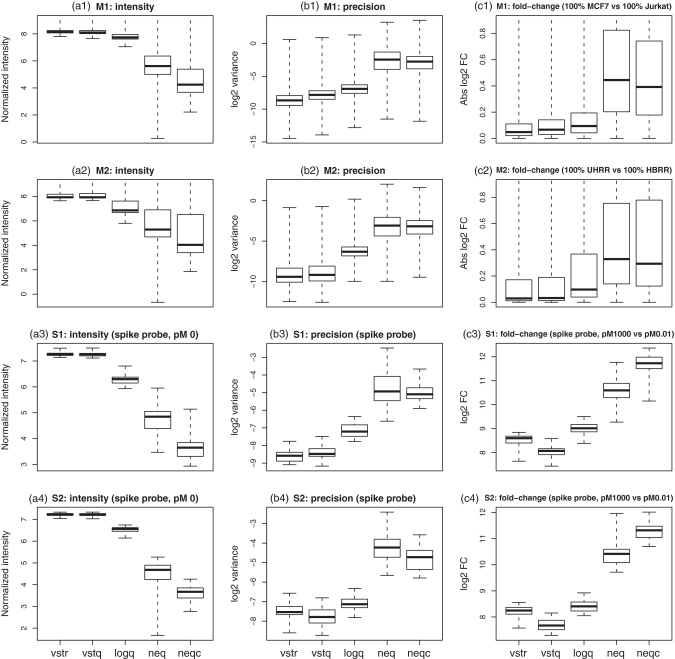
We compare the performance of the five pre-processing strategies using four calibration data sets. Two of the data sets (M1 and M2) are based on mixtures of two RNA samples, and two are spike-in experiments (S1 and S2) for two versions of human WG-6 BeadChips. Figure 1 gives an overall view of the broad properties of the five pre-processing strategies in their base form. The middle column of the figure shows pooled sample variances between replicates, a surrogate for precision. This shows that the two vst algorithms have easily the best precision (lowest variance), whereas the two normexp strategies have the worst (highest variance). However, precision is far from the whole story. The first column of the figure shows that the vst algorithms give most of the probes of the arrays virtually the same 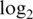 -expression value, whereas the normexp algorithms produce a much greater range of values. The third column of the figure shows that the vst algorithms tend to produce very small fold changes, whereas the normexp algorithms yield a much greater range of fold changes. In fact, the 90% percentile
-expression value, whereas the normexp algorithms produce a much greater range of values. The third column of the figure shows that the vst algorithms tend to produce very small fold changes, whereas the normexp algorithms yield a much greater range of fold changes. In fact, the 90% percentile 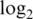 -fold change produced by normexp strategies is 2–4 times that of the vst strategies for data sets M1 and M2 (Table 2). It would appear that the high precision of the vst algorithms has been bought at the cost of a loss of signal. We need to somehow put the algorithms on the same terms before we can compare them meaningfully. In the following sections, we devise a strategy to do that.
-fold change produced by normexp strategies is 2–4 times that of the vst strategies for data sets M1 and M2 (Table 2). It would appear that the high precision of the vst algorithms has been bought at the cost of a loss of signal. We need to somehow put the algorithms on the same terms before we can compare them meaningfully. In the following sections, we devise a strategy to do that.
Figure 1.
Operating characteristics of each pre-processing strategy. Shown are boxplots of normalized 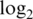 intensities (a1–a4),
intensities (a1–a4), 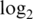 sample variances (b1–b4) and absolute
sample variances (b1–b4) and absolute 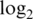 fold changes (c1–c4) for each pre-processing strategy applied to each data set. Each boxplot shows the spread of values across microarray probes for a particular strategy applied to a particular data set. The vertical axis has been truncated in some cases to better show the main body of the boxplots. The first and second rows show results for mixture data sets M1 and M2, respectively. Panels c1-c2 show fold changes for comparing pure samples. The third and fourth rows show results for spike-in data sets S1 and S2, respectively. Only results for spike-in probes are shown (note that spike-in probes and array probes were normalized together). Panels a3–a4 show intensities for probes for which the spike-in concentration is actually 0. Panels c3–c4 show fold changes from the comparison between spike-in concentrations 1000 pM and 0.01 pM. In the left column (a1–a4), longer boxes indicate a good range of normalized values. In the middle column (b1–b4), lower boxes indicate higher precision. In the third column (c1–c4), longer and higher boxes indicate a greater range of fold changes.
fold changes (c1–c4) for each pre-processing strategy applied to each data set. Each boxplot shows the spread of values across microarray probes for a particular strategy applied to a particular data set. The vertical axis has been truncated in some cases to better show the main body of the boxplots. The first and second rows show results for mixture data sets M1 and M2, respectively. Panels c1-c2 show fold changes for comparing pure samples. The third and fourth rows show results for spike-in data sets S1 and S2, respectively. Only results for spike-in probes are shown (note that spike-in probes and array probes were normalized together). Panels a3–a4 show intensities for probes for which the spike-in concentration is actually 0. Panels c3–c4 show fold changes from the comparison between spike-in concentrations 1000 pM and 0.01 pM. In the left column (a1–a4), longer boxes indicate a good range of normalized values. In the middle column (b1–b4), lower boxes indicate higher precision. In the third column (c1–c4), longer and higher boxes indicate a greater range of fold changes.
Table 2.
Innate offset, precision and bias of each pre-processing strategy on mixture data sets M1 and M2
| Strategy | M1 |
M2 |
||||
|---|---|---|---|---|---|---|
| Innate offset |
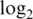 var var |
90% logFC | Innate offset |
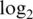 var var |
90% logFC | |
| vstr | 269 | −8.7 | 0.40 | 235 | −9.4 | 0.72 |
| vstq | 259 | −7.8 | 0.45 | 234 | −9.2 | 0.75 |
| logq | 196 | −6.9 | 0.53 | 103 | −6.3 | 1.11 |
| neq | 32 | −2.5 | 1.37 | 26 | −3.1 | 1.61 |
| neqc | 13 | −2.8 | 1.36 | 11 | −3.2 | 1.91 |
Innate offset is on the raw scale. 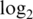 var is the median
var is the median 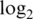 probe-wise variance. 90% logFC is the 90th percentile of absolute
probe-wise variance. 90% logFC is the 90th percentile of absolute 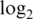 -fold-changes between pure samples. The best value in each subcolumn is bold.
-fold-changes between pure samples. The best value in each subcolumn is bold.
Bias
We can confirm that compressed fold changes correspond to bias by examining results for spike-in probes. To emphasize this, we examined 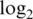 -fold-changes between the two most extreme non-zero spike-in concentrations (Figure 1 panels c3–c4, Table 3). The true
-fold-changes between the two most extreme non-zero spike-in concentrations (Figure 1 panels c3–c4, Table 3). The true 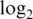 -fold-change here is
-fold-change here is 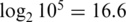 . All the pre-processing strategies underestimate the true fold change, but the normexp strategies do so far less than the vst or logq strategies. We also examined fold changes between progressive spike-in concentrations (Supplementary Figure S1). All pre-processing strategies underestimated fold changes at very low or very high concentrations, but the normexp strategies are least biased overall. The vst strategies were particularly biased at low concentration, giving
. All the pre-processing strategies underestimate the true fold change, but the normexp strategies do so far less than the vst or logq strategies. We also examined fold changes between progressive spike-in concentrations (Supplementary Figure S1). All pre-processing strategies underestimated fold changes at very low or very high concentrations, but the normexp strategies are least biased overall. The vst strategies were particularly biased at low concentration, giving 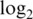 -fold-changes hardly different from zero.
-fold-changes hardly different from zero.
Table 3.
Innate offset, precision and bias of each pre-processing strategy on spike-in data sets S1 and S2
| Strategy | S1 |
S2 |
||||||
|---|---|---|---|---|---|---|---|---|
| Innate offset |
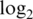 var var |
Max logFC | Slope | Innate offset |
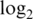 var var |
Max logFC | Slope | |
| vstr | 155 | −8.6 | 8.5 | 0.59 | 150 | −7.5 | 8.2 | 0.58 |
| vstq | 153 | −8.4 | 8.0 | 0.57 | 150 | −7.7 | 7.7 | 0.55 |
| logq | 78 | −7.1 | 9.0 | 0.64 | 93 | −7.1 | 8.4 | 0.61 |
| neq | 27 | −4.7 | 10.6 | 0.75 | 23 | −4.2 | 10.4 | 0.74 |
| neqc | 13 | −5.0 | 11.7 | 0.83 | 13 | −4.8 | 11.3 | 0.80 |
Innate offset is average raw intensity of 0-concentration spike-in probes. 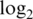 var is mean
var is mean 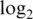 variance for spike-in probes. Max logFC is mean
variance for spike-in probes. Max logFC is mean 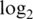 -fold-change between spike-in concentrations 1000 and 0.01 pM (true value is 16.6). Slope is the slope of the regression of
-fold-change between spike-in concentrations 1000 and 0.01 pM (true value is 16.6). Slope is the slope of the regression of 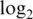 intensities on the true
intensities on the true 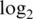 concentrations (ideal value is 1). The best value in each subcolumn is bold.
concentrations (ideal value is 1). The best value in each subcolumn is bold.
The ability of each pre-processing strategy to track to the true concentrations can be summarized by computing the regression slope of normalized 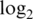 -intensities on the nominal spiked-in
-intensities on the nominal spiked-in 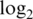 -concentrations. If the normalized intensities were proportional to the spike-in concentrations, then the regression slope would be one (21). All pre-processing strategies give regression slopes less than one, meaning that they tend to damp down the fold changes. This is true for both spike-in data sets S1 and S2 (Table 3). However the normexp strategies are the best, with least damping, whereas the vst strategies are the worst.
-concentrations. If the normalized intensities were proportional to the spike-in concentrations, then the regression slope would be one (21). All pre-processing strategies give regression slopes less than one, meaning that they tend to damp down the fold changes. This is true for both spike-in data sets S1 and S2 (Table 3). However the normexp strategies are the best, with least damping, whereas the vst strategies are the worst.
Innate offsets
The results above show that the pre-processing algorithms with best precision have worst bias and vice versa. A good pre-processing strategy should strike a balance between the precision and bias, yet each algorithm appears to give more emphasis to one or the other. This raises some interesting and important questions. Can we characterize the position of each pre-processing algorithm on the noise–bias (or precision–bias) spectrum in a quantitative way? Can we modify the relative weight that each algorithm gives to precision and bias, thus moving it along the noise–bias spectrum? If so, does this allow us to compare the basic pre-processing strategies on a more equal and meaningful footing?
The left panel in Figure 1 shows the distribution of normalized intensities for each pre-processing strategy. The vstq and vstr strategies offset the data substantially, in that even the smallest unlogged intensities are well above zero. Adding a large offset to the intensities before log transformation will lower the variance (as seen in the center panel of Figure 1), but will also compress the range of both intensities and fold changes (seen in the left and right panels). This motivated us to use the offset to adjust the balance of precision and bias.
We introduce the concept of `innate offset' to measure the offset introduced by a pre-processing strategy in its base form. For the mixture data sets, we define innate offset as the first quartile of the normalized probe intensities. For spike-in datasets, innate offset can be defined as the mean normalized intensity of probes with spike-in concentration zero. All algorithms except vstr use quantile normalization, so the innate offset as just defined is identical across all arrays of an experiment. For vstr, the innate offset may vary slightly between arrays; for simplicity, we present the innate offset obtained from the first array of each dataset as representative of vstr results.
The innate offset is intended to reflect the typical intensity a pre-processing algorithm will assign to non-expressed transcripts. We have shown elsewhere that the proportion of expressed probes in data sets M1 and M2 is ∼50% (1). This supports our choice of the first quartile as the innate offset, because the 25% quantile of the the intensities should be approximately the median of the non-expressed probes.
The vst strategies have by far the largest innate offsets, about 8–21 times (Table 2) or 6–12 times (Table 3) those of the normexp strategies. In general, the order of pre-processing strategies ranked by innate offset is the reverse of their order ranked by variance, fold change, or regression slope (Tables 2 and 3). The only exception is neqc which has better precision than neq even though it has smaller offset. This improvement is presumably due to the extra information gained from using control probes in the background correction and normalization processes.
Added offsets
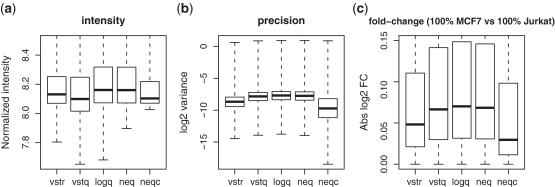
We speculated that if the offsets introduced by different strategies could be aligned, then the differences in precision and bias would not be as remarkable as observed in Figure 1, and the strategies could be compared on more equal terms. To test this idea, extra offsets were added prior to normalization for the logq, neq and neqc strategies to try to match the total resulting offsets of these strategies to the innate offset of vstr strategy (Extra offsets cannot be added to the vstq and vstr strategies because they do not have a separate background correction step). Figure 2 confirms for data set M1 that, after equalizing the offsets in the above way, differences in precision and fold change range between strategies were much less pronounced. Differences in typical absolute fold change were also reduced (data not shown).
Figure 2.
Operating characteristics of pre-processing strategies when total offsets are forced equal. Shown are boxplots of (a) normalized 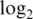 intensities, (b) log
intensities, (b) log variances and (c) absolute
variances and (c) absolute 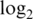 fold changes. Results shown are for data set M1, with added offsets of 73, 237 and 256 for the logq, neq and neqc strategies, respectively.
fold changes. Results shown are for data set M1, with added offsets of 73, 237 and 256 for the logq, neq and neqc strategies, respectively.
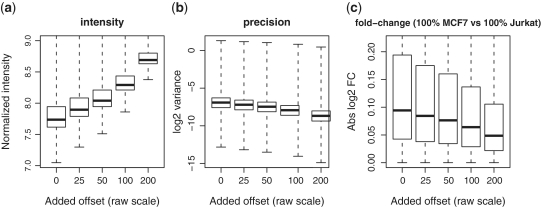
To further demonstrate the role that the offset plays in calibrating the noise–bias trade-off, we consider a simple case in which increasing offsets are added to a data set and the data set is normalized by the logq strategy. Precision steadily improves and the fold change range steadily decreases as more offset is added (Figure 3). This clearly demonstrates that the offset does play an important role in controlling the precision and bias of the normalized data.
Figure 3.
Operating characteristics of the logq pre-processing strategy for different added offsets. Shown are boxplots of (a) normalized 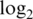 intensities, (b)
intensities, (b) 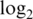 variances and (c) absolute
variances and (c) absolute 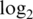 fold changes for comparing pure samples. Results shown are for data M1.
fold changes for comparing pure samples. Results shown are for data M1.
With the ability to move the pre-processing strategy in the noise–bias spectrum, we are able to determine the optimal trade-off between noise and bias for a pre-processing strategy and perform an unbiased comparison for alternative strategies, which are described in the next section.
Estimating the FDR
Differential expression analysis was performed to compare the pure samples in the mixture data sets (i.e. A1 versus A6 in data set M1 and A versus B in M2). A moderated t-statistic was calculated for each probe and each data set (24). We chose the top 30% of absolute t-statistics to designate `true' DE probes, and the bottom 40% to designate `true' non-DE probes. The proportion of DE probes was estimated to be 27% and 41% for datasets M1 and M2, respectively, supporting our choice of cut-off for selecting DE probes. The `true' DE probes and non-DE probes were generated for each pre-processing strategy separately.
Differential expression analysis was then carried out to compare heterogeneous samples. We compared A2 versus A3, A3 versus A4 and A4 versus A5 in data set M1 and C versus D in data set M2. For each comparison, probes were ordered from largest to smallest by absolute moderated t-statistic. The ranking of the `true' DE and non-DE probes in these lists yielded a FDR and an AUC value for each comparison. AUC was used as an overall summary of FDR that is independent of the cutoff used to select DE genes. For data set M1, AUC for the three sample comparisons were then averaged.
The vst strategies were found to have the lowest FDR (highest AUCs) and the normexp strategies to have the highest (lowest AUCs) (Table 4). AUC generally increased with innnate offset.
Table 4.
The innate offset and FDR for each pre-processing strategy
| Dataset | Strategy | Innate offset | AUC |
|---|---|---|---|
| M1 | vstr | 269 | 0.63 |
| vstq | 259 | 0.60 | |
| logq | 196 | 0.57 | |
| neq | 32 | 0.53 | |
| neqc | 13 | 0.55 | |
| M2 | vstr | 235 | 0.935 |
| vstq | 234 | 0.942 | |
| logq | 103 | 0.939 | |
| neq | 26 | 0.923 | |
| neqc | 11 | 0.931 |
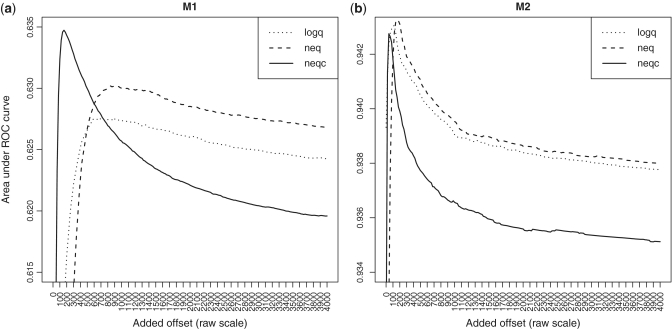
Optimizing the FDR
We next used AUC as a criterion to be optimized in order to determine the best trade-off between precision and bias. Offsets from 0 to 4000 were added to the background corrected data for the neq and neqc strategies and to raw data for the logq strategy to examine changes in FDR. Figure 4 shows that the AUC value does not always increase when the offset increases. Instead, each strategy reaches its AUC peak with its own optimal added offset and then its AUC value decreases. The best AUC of the neqc strategy is comparable, or better than those of logq and neq strategies, and neqc achieves this by using a much smaller added offset in both data sets M1 and M2 (Table 5 and Figure 4). This small offset is highly desirable in that it keeps the total offset and fold change shrinkage to a minimum (Table 5). The neqc strategy also clearly outperforms vstq and vstr strategies in terms of the best AUC value and the typical absolute fold change.
Figure 4.
AUC as a function of added offset for the logq, neq and neqc strategies. Panel (a) is for data set M1, (b) for data set M2.
Table 5.
Optimal added offset for each strategy in terms of FDR
| Dataset | Strategy | Optimal added offset | AUC | Total offset | 90% logFC |
|---|---|---|---|---|---|
| M1 | vstr | – | 0.629 | 269 | 0.40 |
| vstq | – | 0.600 | 259 | 0.45 | |
| logq | 681 | 0.628 | 877 | 0.22 | |
| neq | 922 | 0.630 | 954 | 0.21 | |
| neqc | 156 | 0.635 | 169 | 0.58 | |
| M2 | vstr | – | 0.9350 | 235 | 0.72 |
| vstq | – | 0.9420 | 234 | 0.75 | |
| logq | 108 | 0.9430 | 211 | 0.86 | |
| neq | 171 | 0.9434 | 197 | 0.88 | |
| neqc | 46 | 0.9430 | 57 | 1.32 |
The total offset is essentially the sum of the innate and added offsets.
We then compared different strategies by forcing them to have the same AUC values. Offsets were added to the data as appropriate to ensure that the logq, neq and neqc strategies gave the same AUC value as the better of the two vst strategies. The neqc strategy was found to achieve this AUC with much larger fold changes and smaller total offsets than the other strategies (Table 6), a highly desirable property. The other strategies gave fold changes often only a third or a half as large as neqc, as measured by the 90% quantile of the absolute fold changes.
Table 6.
Comparing different strategies when FDRs are forced equal
| Dataset | Strategy | Added offset | Total offset | AUC | 90% logFC |
|---|---|---|---|---|---|
| M1 | vstr | – | 269 | 0.629 | 0.40 |
| vstq | – | 259 | 0.600 | 0.45 | |
| logq | 681 | 877 | 0.628 | 0.22 | |
| neq | 623 | 655 | 0.629 | 0.27 | |
| neqc | 78 | 91 | 0.629 | 0.74 | |
| M2 | vstr | – | 235 | 0.935 | 0.72 |
| vstq | – | 234 | 0.942 | 0.75 | |
| logq | 26 | 129 | 0.942 | 1.03 | |
| neq | 96 | 122 | 0.942 | 1.04 | |
| neqc | 21 | 32 | 0.942 | 1.52 |
Note that the best AUC the logq strategy can achieve in data set M1 is 0.628, which is less than the consensus AUC value (0.629) chosen from the vstr strategy.
Finally, we compared the five strategies by forcing them to have the same total offset, equal to that of the vst strategy with best AUC value. This made the strategies more similar than in any other comparison. On this level playing field, the neqc strategy showed a modest but noticeable edge on all performance measures, namely precision (Supplementary Figure S2), AUC and fold change (Table 7). Only for data set M2, did neqc not yield the best AUC value, but here all strategies gave high and almost identical AUC values.
Table 7.
Comparing different strategies when total offsets are forced equal
| Data set | Strategy | Added offset | Total offset | AUC | 90% logFC |
|---|---|---|---|---|---|
| M1 | vstr | – | 269 | 0.629 | 0.399 |
| vstq | – | 259 | 0.600 | 0.446 | |
| logq | 73 | 269 | 0.596 | 0.459 | |
| neq | 237 | 269 | 0.602 | 0.459 | |
| neqc | 256 | 269 | 0.634 | 0.461 | |
| M2 | vstr | – | 235 | 0.935 | 0.722 |
| vstq | – | 234 | 0.942 | 0.748 | |
| logq | 131 | 234 | 0.943 | 0.829 | |
| neq | 209 | 234 | 0.943 | 0.828 | |
| neqc | 224 | 234 | 0.940 | 0.837 |
Probe filtering
Filtering out probes that were not expressed has been found previously to improve statistical power to detect DE genes (9,28,29). To explore the effect of this on our results, we filtered out probes which failed to show good evidence of expression for any array.
Comparisons between the different pre-processing strategies were largely unaffected by filtering. Vst still had the highest precision and smallest fold change range of all the strategies (Supplementary Figure S3). The precisions of the normexp strategies improved slightly after filtering whereas those of the vst strategies became worse (Supplementary Table S1). This suggests that the normexp strategies produce a decreasing mean–variance relationship, so that filtering removes more variable probes, whereas the vst strategies produce an increasing relationship, so that filtering removes probes with low variances. Evidently, the vst algorithms do not entirely succeed in stabilizing the variance across the intensity range.
As with the full dataset, AUC values of the logq, neq and neqc strategies first increased with the added offset and then decreased after reaching their peaks. The neqc strategy is now found to have the best AUC values in both data sets M1 and M2 (Supplementary Figure S4). The total offset used by neqc when achieving its best AUC value is also much smaller than those used by other strategies (data not shown). Comparing the five strategies by fixing AUC values or total offsets also shows the superiority of the neqc strategy (Supplementary Tables S2 and S3).
DISCUSSION
This study has demonstrated that offsets provide a means to measure and manipulate the noise–bias trade-off of pre-processing algorithms for Illumina BeadChip data. This is the first study that explores the role of offsets in a systematic way. The precision and bias of the algorithms were found to be determined more by their total offset than by any other property. To a first approximation, all the algorithms can be placed on a (nearly one-dimensional) continuum in terms of noise bias trade-off. This approach constitutes a step forward in understanding the relationships between existing algorithms, because it allows algorithms to be compared on equivalent terms. The potential of each of the base algorithms to generate an algorithm with an optimal noise–bias compromise was examined. This showed that adding a positive offset to most of the algorithms can result in a substantial reduction in the FDR. The improvements achieved in this way were greater than the differences between the original algorithms.
This study is the first to make comparisons between the popular vst algorithm and algorithms of the normexp family, and the first to evaluate the algorithms with respect to their noise–bias trade-offs. The algorithms were evaluated using a suite of calibration data sets with genomic-level known truth. One finding of the study is that the very well-respected vst algorithm has operating characteristics very similar to that of normexp background correction (with or without controls) when an offset in the range of 200–300 is added (Figure 2). This unifies a number of, apparently disparate, proposals (6,14,12), and shows that the best performing algorithms differ mainly in the relative emphasis given to precision and bias.
We show that vst has high precision but also high bias, with fold changes substantially understated. A practical conclusion of this study is that researchers can achieve much of the precision of the vst algorithm while avoiding much of the bias by using normexp background correction with a small to modest added offset. The optimal offset to minimize the FDR varied from about 50 to nearly 1000 (Table 5), but any added offset resulted in some improvement compared to not adding an offset (Figure 4). For practical use, we feel that total offsets larger than about 200 are undesirable because of the degree of compression of the fold changes, regardless of the FDR benefits. Neqc was the only algorithm tested with optimal offset values smaller than this. In general, the amount of bias that is introduced for a given gain in precision was smaller for neq than logq, and smaller again for neqc. This supports the use of control probes to tune the normexp parameters (11,12). For routine practical use, we recommend modest offsets for Illumina data in the range of 10–50, which minimize the bias while still delivering a benefit in terms of FDR. Offsets of 16–50 have been used in a number of biological studies (10,13,16). These results remain essentially unchanged whether or not control probes are used in the normalization step of neqc, although the version with control probes used in this study does slightly better on data sets M1 and S2 (data not shown).
The default background correction method used by Illumina's proprietary BeadStudio software is global background correction, whereby the mean intensity of the negative control probes for each array is subtracted from the intensities of the regular probes for that array. Global background correction was not included in this study because it has been shown elsewhere to introduce variability for probes with low intensities and to behave poorly in differential expression analyses (19). More specifically, global background correction is inappropriate in conjunction with the log algorithm, because it introduces negative intensities and hence undefined values after log-transformation. The neqc algorithm also requires intensities which have not been global background corrected, because that would put the regular probes on a different scale to the negative control probes. The two vst algorithms and neq should give similar results whether or not the regular probes have been global background corrected. They are nearly, although not entirely, invariant to this correction (data not shown).
Our neqc software includes a robust version of neqc, intended to allow the possibility that some of the negative control probes are subject to cross-hybridization with expression transcripts and hence do not truly reflect background intensity (19). For the data sets considered here, robust neqc has a slightly lower innate offset than ordinary neqc but has nearly the same optimized FDR, precision and bias (data not shown).
Illumina BeadChips include around 30 replicate beads for each probe on each array. We analyzed the Illumina BeadChip data at the probe-level using standard Illumina output files, but analysis of the bead-level data is also possible (2,19). In principle, the neqc strategy should be just as effective for pre-processing bead level data as it is for probe-level data. Its computational simplicity would be especially valuable at the bead level.
Our results may have implications for other microarray platforms. Affymetrix GeneChips include a MM (mismatch) probe for each PM (perfect match) probe. The MM probe differs from the corresponding PM probe by only one base (the 13th base in the 25-mer sequence). It has been reported that these MM probes contain signals from target RNA (30), so MM probes do not provide a direct measure of background noise. On the other hand, a variety of recent commercial microarray platforms do include sizeable numbers of negative control probes. These include Agilent Whole Genome Oligo Microarrays and recent Affymetrix products such as exon and microRNA arrays. If the negative control probes are representative of background noise, then the neqc pre-processing strategy should be applicable to these microarray platforms as well.
The neqc pre-processing algorithm is implemented in the freely available open source Bioconductor software package limma (22). The default offset is 16, which seems generally to give good results on recent versions of human and mouse Illumina arrays. A case study, with complete R commands, using the neqc algorithm to normalize Illumina BeadChip data is included in Supplementary Data. This approach has been used successfully in some recent biological studies (13,16). Our experience in these applied studies is that neqc, neq and vst give roughly similar numbers of DE genes on the basis of P-value alone, but neqc yields fold changes 3–4 times as large as those from logq and nearly five times as large as vstq or vstr. Therefore, neqc yields more DE genes when both fold change and P-value thresholds are used. Limited experience with PCR validation suggests that the larger fold changes returned by neqc are closer to the truth, agreeing with the results reported here with spike-in data sets.
CONCLUSION
This study conducts a comprehensive comparison of five alternative pre-processing strategies with regard to precision, bias and FDR. The algorithms are found to differ mainly in the degree to which they offset intensities away from zero and the degree of compression they apply to the fold changes. When this noise–bias trade-off was adjusted, the five algorithms had broadly similar performance. Vst was found to have high precision but also high bias. Adding a positive offset is found to improve the FDRs of the log and normexp algorithms. The normexp algorithm using control probes (neqc) was found to achieve the best precision for a given bias. This strategy is therefore recommended, in conjunction with a modest offset, for pre-processing Illumina BeadChip data.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Funding for open access charge: National Health and Medical Research Council (490037 to G.K.S.).
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Andrew Holloway and Dileepa Diyagama for preparing the M1 mixture samples, Leming Shi for providing the complete raw MAQC-I Illumina data, Rafael Irizarry, Matthew McCall and Mark Dunning for making their spike-in data sets publicly available and Matthew Ritchie for the help on data retrieval.
REFERENCES
- 1.Shi W, de Graaf CA, Kinkel SA, Achtman AH, Baldwin T, Schofield L, Scott HS, Hilton DJ, Smyth GK. Estimating the proportion of microarray probes expressed in an RNA sample. Nucleic Acids Res. 2010;38:2168–2176. doi: 10.1093/nar/gkp1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dunning MJ, Smith ML, Ritchie ME, Tavare S. beadarray: R classes and methods for Illumina bead-based data. Bioinformatics. 2007;23:2183–2184. doi: 10.1093/bioinformatics/btm311. [DOI] [PubMed] [Google Scholar]
- 3.Irizarry RA, Hobbs B, Collin F, Beazer-Barclay YD, Antonellis KJ, Scherf U, Speed TP. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4:249–264. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- 4.Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res. 2003;31:e15. doi: 10.1093/nar/gng015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bolstad BM, Irizarry RA, Astrand M, Speed TP. A comparison of normalization methods for high density oligonucleotide array data based on bias and variance. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- 6.Ritchie ME, Silver J, Oshlack A, Holmes M, Diyagama D, Holloway A, Smyth GK. A comparison of background correction methods for two-colour microarrays. Bioinformatics. 2007;23:2700–2707. doi: 10.1093/bioinformatics/btm412. [DOI] [PubMed] [Google Scholar]
- 7.Silver J, Ritchie ME, Smyth GK. Microarray background correction: maximum likelihood estimation for the normal-exponential convolution model. Biostatistics. 2009;10:352–363. doi: 10.1093/biostatistics/kxn042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Barnes M, Freudenberg J, Thompson S, Aronow B, Pavlidis P. Experimental comparison and cross-validation of the Affymetrix and Illumina gene expression analysis platforms. Nucleic Acids Res. 2005;33:5914–5923. doi: 10.1093/nar/gki890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shi W, Banerjee A, Ritchie M, Gerondakis S, Smyth GK. Illumina WG-6 BeadChip strips should be normalized separately. BMC Bioinformatics. 2009;10:372. doi: 10.1186/1471-2105-10-372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lim E, Vaillant F, Wu D, Forrest NC, Pal B, Hart AH, Asselin-Labat M, Gyorki DE, Ward T, Partanen A, et al. Aberrant luminal progenitors as the candidate target population for basal tumor development in BRCA1 mutation carriers. Nat. Med. 2009;15:907–913. doi: 10.1038/nm.2000. [DOI] [PubMed] [Google Scholar]
- 11.Ding LH, Xie Y, Park S, Xiao G, Story MD. Enhanced identification and biological validation of differential gene expression via Illumina whole-genome expression arrays through the use of the model-based background correction methodology. Nucleic Acids Res. 2008;36:e58. doi: 10.1093/nar/gkn234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xie Y, Wang X, Story M. Statistical methods of background correction for Illumina beadarray data. Bioinformatics. 2009;25:751–757. doi: 10.1093/bioinformatics/btp040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lim E, Wu D, Pal B, Bouras T, Asselin-Labat ML, Vaillant F, Yagita H, Lindeman GJ, Smyth GK, Visvader JE. Transcriptome analyses of mouse and human mammary cell subpopulations reveal multiple conserved genes and pathways. Breast Cancer Res. 2010;12:R21. doi: 10.1186/bcr2560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin SM, Du P, Huber W, Kibbe WA. Model-based variance-stabilizing transformation for Illumina microarray data. Nucleic Acids Res. 2008;36:e11. doi: 10.1093/nar/gkm1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Du P, Kibbe WA, Lin SM. lumi: a pipeline for processing Illumina microarray. Bioinformatics. 2008;24:1547–1548. doi: 10.1093/bioinformatics/btn224. [DOI] [PubMed] [Google Scholar]
- 16.Asselin-Labat ML, Vaillant F, Sheridan JM, Pal B, Wu D, Simpson ER, Yasuda H, Smyth GK, Martin TJ, Lindeman GJ, et al. Control of mammary stem cell function by steroid hormone signalling. Nature. 2010;465:798–802. doi: 10.1038/nature09027. [DOI] [PubMed] [Google Scholar]
- 17.Rocke DM, Durbin B. Approximate variance-stabilizing transformations for gene-expression microarray data. Bioinformatics. 2003;19:966–972. doi: 10.1093/bioinformatics/btg107. [DOI] [PubMed] [Google Scholar]
- 18.MAQC Consortium. The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat. Biotechnol. 2006;24:1151–1161. doi: 10.1038/nbt1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dunning MJ, Barbosa-Morais NL, Lynch AG, Tavare S, Ritchie ME. Statistical issues in the analysis of Illumina data. BMC Bioinformatics. 2008;9:85. doi: 10.1186/1471-2105-9-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dunning MJ, Ritchie ME, Barbosa-Morais NL, Tavare S, Lynch AG. Spike-in validation of an Illumina-specific variance-stabilizing transformation. BMC Res. Notes. 2008;1:18. doi: 10.1186/1756-0500-1-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McCall MN, Irizarry RA. Consolidated strategy for the analysis of microarray spike-in data. Nucleic Acids Res. 2008;36:e108. doi: 10.1093/nar/gkn430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smyth GK. Limma: linear models for microarray data. In: Gentleman R, Carey V, Dudoit S, Irizarry R, Huber W, editors. Bioinformatics and Computational Biology Solutions Using R and Bioconductor. New York: Springer; 2005. pp. 397–420. [Google Scholar]
- 23.Langaas M, Ferkingstad E, Lindqvist B. Estimating the proportion of true null hypotheses, with application to DNA microarray data. J. Roy. Stat. Soc., Ser. B. 2005;67:555–572. [Google Scholar]
- 24.Smyth GK. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Gen. Mol. Biol. 2004;3 doi: 10.2202/1544-6115.1027. article 3. [DOI] [PubMed] [Google Scholar]
- 25.Brent R. Algorithms for Minimization without Derivatives. 1973. Prentice-Hall Englewood Cliffs N.J. [Google Scholar]
- 26.Illumina. BeadStudio Gene Expression Module User Guide. 2008. www.illumina.com (16 November 2009, date last accessed) [Google Scholar]
- 27.Huber PJ. Robust statistics. New York: Wiley; 1981. [Google Scholar]
- 28.Archer KJ, Reese SE. Detection call algorithms for high-throughput gene expression microarray data. Brief Bioinform. 2010;11:244–252. doi: 10.1093/bib/bbp055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hackstadt AJ, Hess AM. Filtering for increased power for microarray data analysis. BMC Bioinformatics. 2009;10:11. doi: 10.1186/1471-2105-10-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wu Z, Irizarry RA, Gentleman R, Martinez-Murillo F, Spencer F. A model-based background adjustment for oligonucleotide expression arrays. J. Am. Stat. Assoc. 2004;99:909–917. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.