Abstract
Tracking moving objects is a fundamental attentional operation. Here we ask which coordinate system is used to track objects: retinal (retinotopic), scene-centered (allocentric), or both? Observers tracked three of six disks that were confined to move within an imaginary square. By moving either the imaginary square (and thus the disks contained within), the fixation cross, or both, we could dramatically increase the disks' speeds in one coordinate system while leaving them unchanged in the other, so as to impair tracking in only one coordinate system at a time. Hindering tracking in either coordinate system reduced tracking ability by an equal amount, suggesting that observers are compelled to use both coordinate systems and cannot choose to track only in the unimpaired coordinate system.
Introduction
In a world without moving objects, attention could simply be directed to locations. However, because objects do move, they first need to be tracked before they can be attended (Pylyshyn 1989). Tracking is thus a fundamental attentional operation and, to some extent, the limits of object-based attention are determined by the limits of tracking. Humans can track only a limited number of objects (Pylyshyn and Storm 1988). The faster the objects move, the fewer can be tracked (Alvarez and Franconeri 2007). An object's speed is therefore a critical factor in determining whether an object can be tracked and consequently attended (Horowitz et al. 2004).
However, speed can be defined only with respect to a coordinate system. For example, in an allocentric (scene-based) coordinate system, speed would be defined as the rate at which the object moves through the environment. This definition makes intuitive sense and, in fact, an allocentric coordinate system is implicitly assumed by most researchers, since fixation is rarely monitored in MOT studies. Given that observers often make eye movements during tracking (Fehd and Seiffert 2008; Zelinsky and Neider 2008), a major advantage of this coordinate system is that the coordinates of the tracked objects would not change every time the observer moves his/her eyes.
Alternatively, in a retinotopic coordinate system, an object's speed would be defined as the rate at which its image moves over the observer's retina. Such a coordinate system would also make intuitive sense. Since a stimulus enters the visual system in a retinotopic coordinate system, in some respects this is the computationally simplest option.
Knowing the coordinate system used for tracking would be fundamental to understanding how we track moving objects. However, there has been surprisingly little work on this question. Liu et al. (2005) proposed that tracking occurs in allocentric coordinates. In their study, objects moved in three dimensions (simulated on a computer monitor) within a wire-frame box. The box itself could rotate, zoom, and translate across the screen. This movement was designed to cause the retinotopic coordinates of the objects to vary rapidly, which would be expected to impair tracking in the retinotopic coordinate system, while leaving the allocentric coordinates of the objects (i.e. the coordinates of the objects measured relative to the wire-frame box) unchanged. Because this manipulation generally had little effect on tracking, Liu et al. concluded that tracking did not occur in retinotopic coordinates, so instead must occur in allocentric coordinates. Consistent with this conclusion they found that when the stimulus was projected onto a convex surface so that the wire-frame box was no longer perceived as rigid, thereby disrupting the allocentric coordinate system, tracking ability deteriorated.
Huff et al. (in press) confirmed these findings. They used a simulated 3D display to compare tracking performance in three conditions: one in which the observer's viewpoint remained constant; one in which the viewpoint rotated smoothly by 30°; and one in which the viewpoint rotated abruptly by 30°. Using the same logic as above, the viewpoint rotation should have disrupted tracking if tracking utilized retinotopic coordinates, but not if tracking utilized allocentric coordinates. Similar to Liu et al. (2005), they found that smooth viewpoint changes did not cause a significant drop in tracking accuracy (providing that the targets were always visible), indicating that tracking occurred in allocentric coordinates.
As an aside, Huff et al. (in press) also compared the effects of abrupt viewpoint changes to the effects of smooth viewpoint changes and found that abrupt viewpoint changes did reduce tracking ability (see also Seiffert 2005; Huff et al. 2009). However, this does not indicate that, for abrupt viewpoint changes, tracking is necessarily achieved by a retinotopic coordinate system. Rather, the abrupt transitions themselves might be hindering tracking. For example, immediately after an abrupt viewpoint change, the allocentric coordinates of the tracked objects are temporarily undefined. Only after the observer deduces the new orientation of the scene can the allocentric coordinates of the objects be determined. Consequently, even if tracking occurred purely in allocentric coordinates, abrupt viewpoint changes might still be disruptive. Similarly, saccades per se might have a disruptive effect on tracking independent of any effect on the coordinate system. To avoid these potential complications, in the experiments presented here, we avoided abrupt transitions. In particular, in our experiments, the display and/or the fixation cross always translated in a smooth manner.
In contrast to Liu et al. (2005) and Huff et al. (in press), Seiffert (2005) proposed that tracking is accomplished in retinotopic coordinates. In her study, objects moved within a two dimensional ring while observers fixated a colored square. In the Display Move condition, the ring rotated around the fixation square, while in the Fixation Move condition, the fixation square rotated around the ring. Both of these manipulations hindered tracking, relative to static control conditions. Interestingly, the effect of moving fixation was somewhat larger than the effect of moving the display, even though the latter manipulation adds speed in both coordinate systems, while the former adds speed only in the retinal coordinate system. This effect may be due to the difficulty of pursuing the moving fixation square, a possibility we had to take into account when designing our study.
The studies described above implicitly assumed that tracking was either retinotopic or allocentric (though Seiffert 2005 concedes that an “object-centered” representation might be involved). However, there is another logical possibility: that tracking uses both retinotopic and allocentric coordinate systems. Previous fMRI studies have demonstrated that a number of brain areas are active when an observer tracks multiple moving objects (Culham et al. 1998; Culham et al. 2001; Jovicich et al. 2001). At least one of these areas, MT, has a well-defined retinotopic coordinate system (Huk et al. 2002; Gardner et al. 2008). The other areas occur later in the visual processing pathway and their coordinate systems are more allocentric (Saygin and Sereno 2008). Since tracking requires these areas to interact with each other (Howe et al. 2009), this suggests that tracking might involve both allocentric and retinotopic coordinate systems.
Note that the Liu et al. (2005), Seiffert (2005) and Huff, et al. (in press) studies all employed a condition designed to disrupt the retinotopic representation while preserving the allocentric representation. However, none of these studies employed the reverse condition, one designed to disrupt the allocentric representation while preserving the retinotopic representation. The logic of this design is that if impairing the retinotopic representation impairs tracking, then tracking must solely rely on that representation, while if the manipulation has no effect, then tracking must be solely allocentric. However, once we admit the possiblity that both coordinate systems might be involved, then we need both of these conditions. This was the approach we took in the current study.
We asked observers to track multiple moving objects while maintaining gaze on a fixation cross. We measured the speed at which observers could track all three targets correctly on 75% of the trials. For simplicity, we assumed that the allocentric coordinates of an object were simply its coordinates relative to the computer monitor (we discuss alternative assumptions in the Discussion section) and the retinotopic coordinates of an object were simply its coordinates relative to the fixation cross. Consider the five conditions cartooned in Figure 1. In the both-preserved condition neither the fixation cross nor the imaginary square moved relative to the computer monitor, so tracking was preserved in both coordinate systems. In the retinotopic-preserved condition, both the fixation cross and the imaginary square underwent circular motion such that their relative separation remained constant. This would impair tracking in the allocentric coordinate system but not in the retinotopic coordinate system. In allocentric-preserved condition, the fixation cross rotated around the imaginary square, thereby hindering tracking in the retinotopic coordinate system but not in the allocentric coordinate system. In the both-impaired-stationary condition, the fixation cross was stationary and the imaginary square rotated around the fixation cross, thereby hindering tracking in both coordinate systems. In the both-impaired-moving condition, both the fixation cross and the imaginary square rotated around the center of the screen, following the same path. Thus, from the perspective of the retinotopic coordinate system, the imaginary square rotated around the fixation cross at the same rate and at the same radius as it did in condition both-impaired-stationary condition. Similarly, the allocentric coordinate system was hindered equally in both conditions. The key difference is that observers had to move their eyes with the fixation cross in the latter condition.
Figure 1.
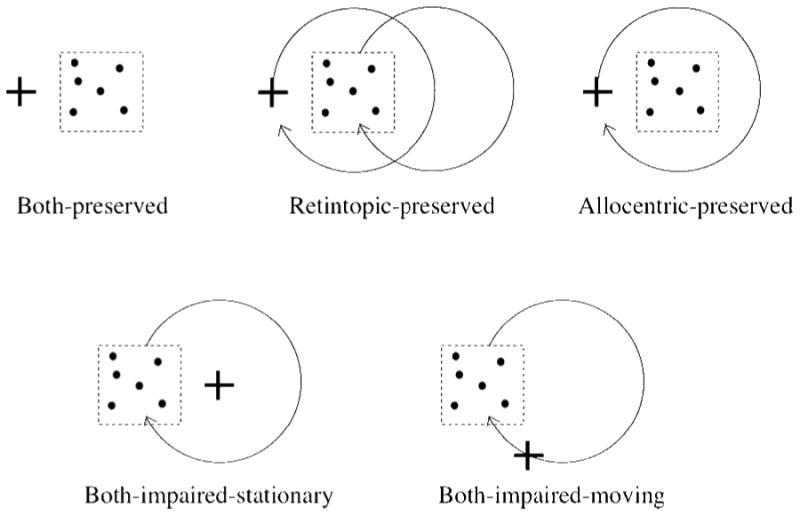
The five stimulus conditions used in the experiment. In all cases the disks were confined to move within an imaginary square. Both-preserved: Neither the fixation cross nor the imaginary square moved relative to the computer monitor, so tracking is preserved in both coordinate systems. Retinotopic-preserved: Both the fixation cross and the imaginary square underwent circular motion such that their relative separation remained constant. This would hinder tracking in the allocentric coordinate system but not in the retinotopic coordinate system. Allocentric-preserved: The fixation cross rotated around the imaginary square, thereby hindering tracking in the retinotopic coordinate system but not in the allocentric coordinate system. Both-impaired-stationary: The imaginary square rotated around the fixation cross, thereby impairing tracking in both coordinate systems. Both-impaired-moving: Same as previous condition, except that the fixation cross also rotated.
In these conditions, the speeds of the disks can be measured in three ways. They can be measured relative to the retinotopic coordinate system, relative to the allocentric coordinate system or relative to the imaginary square. Henceforth, we shall refer to these three speeds as SR, SA, and SI respectively.
Let us first consider these five conditions under the assumption that tracking occurs in an allocentric coordinate system. Since, in this coordinate system, locations are defined relative to the computer monitor, the imaginary square is stationary in the both-preserved and allocentric-preserved conditions but moves along a circular path in the other three conditions. Because the disks are constrained to remain within the imaginary square and all continue to move at the same speed relative to the imaginary square, the circular movement of the imaginary square increases SA(assuming SI is held constant). Because tracking accuracy decreases with increasing object speed (Alvarez and Franconeri 2007), at least when trial duration is held constant (Franconeri et al. in press), for tracking accuracy to be equal in all four conditions, SI would need to be reduced in the conditions retinotopic-preserved, both-impaired-stationary and both-impaired-moving relative to the conditions both-preserved and allocentric-preserved, so that SA would then be the same in all five conditions.
Now we consider the five conditions under the assumption that tracking occurs in a retinotopic coordinate system. From this perspective, the imaginary square is stationary in the both-preserved and retinotopic-preserved conditions but is moving in the other three conditions. Because this circular movement increases SR (again assuming SI is held constant), for tracking accuracy to be equal in all five conditions, SI would need to be reduced in the allocentric-preserved, both-impaired-stationary and both-impaired-moving conditions, relative to the both-preserved and retinotopic-preserved conditions, so that SR would then be the same in all five conditions.
As described above, we also consider a third alternative: that both coordinate systems are needed to track the disks. For tracking to occur in the allocentric coordinate system, SI needs to be reduced in the retinotopic-preserved, both-impaired-stationary and both-impaired-moving conditions relative to the both-preserved condition. Similarly, for tracking to occur in the retinotopic coordinate system, SI needs to be reduced in conditions allocentric-preserved, both-impaired-stationary and both-impaired-moving relative to the both-preserved condition. Combining these restrictions we find that, for tracking to be able to occur in both coordinate systems, SI needs to be reduced in all conditions except the both-preserved condition.
More generally, we might imagine that tracking utilizes both coordinate systems, but may rely more heavily on one than the other. Another way to put this would be to assume that the inputs from the allocentric and retinotopic coordinate systems are weighted. In this framework, the allocentric hypothesis can be restated as the assumption that the weight on allocentric information is 1, and the weight on retinotopic information is 0, while the retinotopic hypothesis assumes the converse.
To preview our results, our data was consistent only with the third alternative. Specifically, we found that SI was reduced in latter four conditions relative to the both-preserved condition and, more importantly, was equal in the retinotopic-preserved and allocentric-preserved conditions. This indicates that both retinotopic and allocentric coordinate systems are of roughly equal importance in tracking. Our data also imply that observers cannot choose to track in only one coordinate system so as to avoid the difficulties in tracking in the other coordinate system. Use of both coordinate systems would appear to be mandatory.
Methods
Participants
There were 12 observers and their ages ranged from 18-54 (mean = 30.2), 8 were female. None were colorblind and they had either normal or corrected-to-normal visual acuity. All observers provided informed consent as approved by the Brigham and Women's Hospital Institutional Review Board.
Apparatus and stimuli
Stimuli were presented on a 21-inch Mitsubishi Diamond Pro monitor at a refresh rate of 75 Hz and at a resolution of 1280 × 960, using Psychophysics toolbox (version 3) for MATLAB® (Brainard 1997; Pelli 1997). The observer's head was supported by a combined head and chin rest and his/her gaze was monitored by an Arrington Research eye tracker. The display subtended 40° × 30°. In all conditions there was a fixation cross (0.5° × 0.5°) and six disks, each of which had a diameter of 0.4°. The disks were restricted to move within an imaginary 8° × 8° square. Relative to the imaginary square, the disks all moved at the same speed and in straight lines except when they bounced off the sides of the imaginary square or each other. The disks were surround by imaginary buffers so that the center-to-center separation of two disks could never be less than 1.5°. The fixation cross was always 5.7° from the center of the imaginary square. In some of the conditions, either the fixation cross, the imaginary square or both would move around a circular path of radius 5.7° at a rate of one complete rotation every 5 seconds, in a direction that was randomly chosen on each trial. Note that when the imaginary square moved, the disks moved in straight lines relative to the imaginary square, but there trajectories were curved relative to the monitor. The luminance of the background was 58 cd/m2 and the luminance of the disks was less than 0.5 cd/m2.
Because the spatial resolution of attention is slightly less in the upper hemifield than in the lower hemifield (Intriligator and Cavanagh 2001), we would expect tracking ability to also be slightly worse in the upper hemifield. For this reason, the angle of the initial offset of the imaginary square relative to the fixation cross was randomly chosen for each trial, so that the imaginary square was located equally often in the upper and lower hemifields.
Procedure
In all conditions, observers were required to fixate the fixation cross. Their fixation was monitored by an eye tracker and if at any point it deviated by more than 2° from the fixation cross, the trial was aborted and redone. The eye tracker was recalibrated after every 40 trials, or sooner if there was any evidence that it had become uncallibrated, such as repeated fixation errors. At the start of the trial, three of disks would turn red for 2 seconds to indicate that these were the targets to be tracked. The trial would then continue for a total of 7 seconds and at the end of which the observer was asked to use the mouse to indicate the three target disks. If the observer made any errors, the entire trial was labeled “incorrect”.
The experiment started with 10 practice trials, followed by 40 trials for each of the five conditions. These 200 trials were interleaved in a random order. The QUEST routine was used to find, for each condition, the speed of the disks that would result in all three disks being tracked correctly on 75% of the trials (Watson and Pelli 1983; King-Smith et al. 1994). To place all the observers on an equal footing, each observer's data was normalized with respect to their performance in the both-preserved condition. For this condition, averaging across the observers, the mean threshold speed was 1.9 deg/s.
Results
The results are shown in Figure 2. To avoid biasing our results towards one of the coordinate systems, Figure 2 reports the disk speed relative to the imaginary square (SI). This was the speed required for all three disks to be tracked correctly on 75% of the trials. We performed four planned t-tests. 1) We found that performance in the both-preserved condition was significantly greater than performance in the retinotopic-preserved condition, t(11)=10.2, p=3.0×10-7, one-tailed. 2) We found that performance in the both-preserved condition was significantly greater than performance in the allocentric-preserved condition, t(11)=11.0, p=1.4×10-7, one-tailed. 3) We found that performance in the both-impaired-stationary condition was significantly greater than the performance in the both-impaired-moving condition, t(11)=1.90, p=0.042, one-tailed. 4) We found that the performance in the retinotopic-preserved and allocentric-preserved conditions were not significantly different, t(11)=0.21, p=0.84, two-tailed. Importantly, the average fixation error was essentially identical for these two conditions, in both cases being 1.8°.
Figure 2.
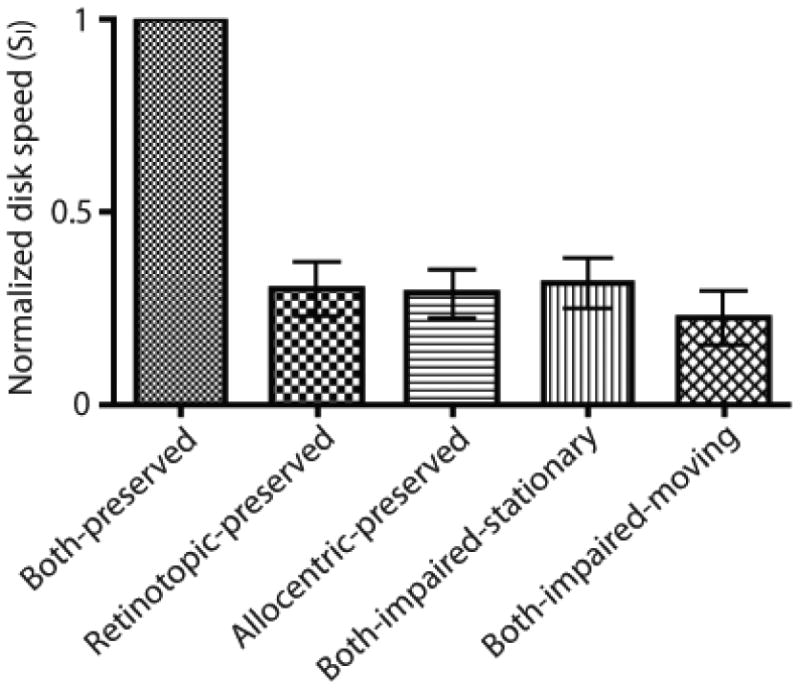
The graph shows the disk speed relative to the imaginary square (SI) that allowed for all three targets to be tracked correctly on 75% of the trials. To make the data for different observers comparable, for each observer the speeds for the five conditions was divided by the speed in the both-preserved condition. Error bars represent one standard error of the mean.
Discussion
The fact that tracking performance, as measured by normalized disk speed, was significantly less in the retinotopic-preserved and allocentric-preserved conditions than in the both-preserved condition shows that our manipulations were strong enough to hinder tracking. The fact that performance was not significantly different in the conditions retinotopic-preserved and allocentric-preserved shows that observers have to track in both coordinate systems and cannot choose to track in only one coordinate system so as to avoid difficulties associated with tracking in the other coordinate system. Use of both coordinate systems would appear to be mandatory.
One possible concern with the above findings is that in the retinotopic-preserved and allocentric-preserved conditions observers had to perform a second task in addition to tracking the three target disks. Specifically, in the retinotopic-preserved condition, observers needed to track a fixation cross and in the allocentric-preserved condition it could be argued that observers needed to track the imaginary square. Conversely, in the both-preserved condition, no secondary tracking task needed to be performed as neither the fixation cross nor the imaginary square were moving. A pertinent question is therefore to what extent did performing a secondary tracking task (i.e. tracking a fixation cross or an imaginary square) decrease the observers' performance on the primary tracking (i.e. tracking the three target disks)?
The comparison of the both-impaired-stationary and both-impaired-moving conditions addresses this issue. In both conditions, both coordinate systems were hindered and this impairment was the same for both conditions. Because the conditions differed only in whether or not the observer was required to track a fixation cross, a comparison of these conditions reveals the cost of tracking the fixation cross. While the above results show that there was indeed a significant cost to tracking the fixation cross, the difference between the both-impaired-stationary and both-impaired-moving conditions was much less than the difference between the both-preserved and retinotopic-preserved conditions or the difference between the both-preserved and allocentric-preserved conditions. This shows that the performance drop from both-preserved to retinotopic-preserved and from both-preserved to allocentric-preserved cannot be attributed solely (or even largely) to a secondary tracking task being performed in the retinotopic-preserved and allocentric-preserved conditions.
Why are the differenced between the retinotopic-preserved and both-impaired-moving conditions and between the allocentric-preserved and both-impaired-moving conditions not larger? In all three of these conditions, observers had to perform a secondary tracking task (i.e. tracking the fixation cross or the imaginary square) in addition to the primary tracking task (i.e. tracking the three target disks). However, in the conditions retinotopic-preserved and allocentric-preserved only one coordinate system was hindered where as in the both-impaired-moving condition both coordinate systems were hindered. Should not hindering both coordinate systems cause a much larger decrement in tracking performance? This question assumes that the two coordinate systems are statistically independent, such that hindering tracking in one system has no effect on tracking in the other. Given such an architecture, we would expect that observers could compensate for a degraded allocantric representation by using information from the retinotopic system, and vice versa, such that hindering both systems would lead to a much more substantial impairment than just hindering one.
However, if the two systems are not statistically independent, then hindering both systems might be only modestly worse than hindering one or the other. Recent work suggests that targets are most likely to be lost when they pass close to distractors and that tracking accuracy decreases as the number of such close passes increases (Franconeri et al. 2009; Franconeri et al. in press). Such close passes will, of course, happen simultaneously in both coordinate systems which would mean that there would be a tendency for targets to be lost simultaneously in both coordinate systems. In the limit that tracking performance was completely non-independent in the two coordinate systems, one would expect performance in the both-impaired-moving condition to be equal to the minimum performance in the retinotopic-preserved and allocentric-preserved conditions. The fact that performance in the both-impaired-moving condition is slightly less than the performance in the retinotopic-preserved and allocentric-preserved conditions is consistent with tracking being only quasi-independent in the allocentric and retinotopic coordinate systems.
Finally, it could be argued that there is a distinction between “updating” and “tracking”. For example, it could be argued that our data is consistent with the hypothesis that objects are tracked only in an allocentric coordinate system but for tracking to be successful their representations need to be updated in a retinotopic coordinate system. Thus, while tracking would utilize both coordinate systems, tracking per se would occur in only one of them.
Alternative allocentric coordinate systems
We have assumed that a disk's allocentric coordinates are simply its coordinates defined relative to the computer monitor (or, equivalently, relative to the observer's head/body, as his/her head/body was held fixed relative to the computer monitor). We made this assumption because the edges of the monitor were clearly visible and intuitively appeared to define a stable coordinate system. However, in principle, it is possible to use alternative definitions. For example, one could define the fixation cross as the center of the scene, which would make the allocentric coordinate system equivalent to the retinotopic coordinate system. According to this definition, the imaginary square moves in the condition previously labeled allocentric-preserved but is stationary in the retinotopic-preserved condition. Thus, for tracking accuracy to be the same in both conditions, SI would need to be less in the condition previously labeled allocentric-preserved than in the retinotopic-preserved condition. This was not the case, suggesting that the brain does not define the allocentric coordinate system in this manner.
Alternatively, one could define the allocentric coordinate system relative to the imaginary square (which is closer to the definition used by Liu et al. 2005), or perhaps the center of mass of the disks, which are roughly equivalent formulations. Under this assumption, we would expect SI to be the same in all conditions. This was also found not to be the case.
Relation to previous work
As we noted in the introduction, Liu et al. (2005) and Huff et al. (in press) provided convincing evidence that tracking occurs in an allocentric coordinate system, at least when the coordinates of the objects were changed smoothly, as was the case in our study, while Seiffert (2005) provided equally convincing evidence that tracking occurs in a retinotopic frame. How can our findings be reconciled with these previous studies? We will begin with the two studies that concluded in favor of an allocentric representation.
One important point is that these studies (Liu et al. 2005; Huff et al. in press) based their conclusions on whether or not they observed an effect of moving the scene relative to the observer. Essentially, by changing the observer's viewpoint, both studies increased the objects' speeds in the retinotopic coordinate system, while preserving the objects' speeds in the allocentric coordinate system, and asked whether tracking was impaired. They reported that this manipulation did not impair tracking and thus concluded that tracking must occur in allocentric coordinates.
An alternative explanation is that their manipulations may not have been large enough to engender a decrement in tracking performance. For example, while our simple translation was a superficially less drastic manipulation than Liu et al.'s “wild ride”, the ratio of the speed of the reference frame to the speed of the tracked objects was actually larger in our study. In Liu et al.'s “slow” condition, for the items near the center of the reference frame, the maximum ratio was 2.4:1, and only 3.4:1 in their “fast” condition (where “slow” and “fast” refer to the speed of the reference frame). In comparison, in our study, in the allocentric-preserved condition, the mean ratio of the speed of the reference frame to the speed of the tracked objects exceeded 19:1 for the disks near the center of the imaginary square. Thus, the disruption to the retinotopic representations would have been much greater in our study. Similar reasoning applies to the Huff et al. (in press) study. In that study, the viewpoint underwent only a rotation, which would not have altered the retinotopic coordinates of the objects near the center of the checkerboard reference frame.
A second possible reason why we obtained a different result from these two previous studies is that we used the adaptive QUEST routine to ensure that, for each observer, the task was sufficiently difficult that the observer's performance would avoid ceiling effects, but not so difficult that floor effects would occur. This increased the chance that we would detect any differences in relative difficulty between conditions.
How can our findings be reconciled with the evidence from Seiffert (2005), which suggested a retinotopic representation for tracking? Recall that Seiffert's study effectively employed three conditions: a static control condition; a Display Move condition, in which the ring rotated around the fixation square; a Fixation Move condition, in which the fixation square rotated around the ring. Since both Display and Fixation Move conditions moved the ring on the retina, and both hindered tracking relative to the static controls, Seiffert concluded that tracking ocurred in retinotopic coordinates. In order to understand the relationship between Seiffert's study and ours, it helps to redescribe her conditions in our terminology: her static control conditions correspond to our both-preserved condition; her Fixation Move condition corresponds to our allocentric-preserved condition; and her Display Move condition corresponds to our both-impaired-stationary condition. As noted above, Seiffert observed that the allocentric-preserved and both-impaired-stationary conditions reduced performance relative to the both-preserved condition, with the former having a slightly larger effect than the latter. If we look at Figure 2, we can see that this is precisely the same pattern that we observed. Our findings therefore replicate those of Seiffert.
The primary difference between the two studies is that we included two additional conditions, the retinotopic-preserved condition and the both-impaired-moving condition. The retinotopic-preserved condition is the most important here: we see that tracking is equally affected by impairing the allocentric coordinates as it is by impairing the retinopic coordinates. The both-impaired-moving condition, meanwhile, provides a useful control for the demands of smooth pursuit of the fixation cross, which we can see has a rather minor effect on tracking the targets, relative to the disruption of either coordinate system (see also Jin et al. 2010). Thus, while our data replicate Seiffert (2005), our additional control conditions lead us to a different interpretation of those data.
These data also have implications outside the study of MOT per se. Recent studies of transsaccadic perception have proposed that, rather than remapping the entire visual field, the visual system uses attention (Wurtz 2008), or at least abstract attentional pointers (Knapen et al. 2009), to select only relevant or salient objects for remapping (Melcher 2009). Our findings can be interpreted as showing that the converse is also true: that attentionally tracking objects requires continuous registration between retinopic and allocentric representations. This is consistent with the notion that tracking is accomplished by mental pointers that point at each tracked object (Pylyshyn and Storm 1988; Alvarez and Franconeri 2007). Indeed, Pylyshyn (2007) suggests that the pointers that enable multiple object tracking serve to reduce the computational complexity of translating across different frames of reference, by restricting the computation to relevant objects. On this view, we would predict that only targets are represented in both coordinate frames, whereas unattended objects might be represented only retinotopically.
More broadly, if we think of tracking as a sort of recurrent spatial memory task (following Cavanagh and Alvarez 2005), then our data are also consistent with recent developments in spatial memory, in which allocentric and egocentric representations are computed in parallel (Burgess 2006). This suggests that it might be interesting to study the relationship between the brain systems involved in tracking and navigation. In particular, our current results are based on 2D displays, whereas navigation typically occurs in a 3D environment. It is possible that 2D and 3D scenes may be processed differently by the brain.
Conclusions
Our results suggest that the brain utilizes both a retinotopic and an allocentric coordinate system when tracking objects. Although this is a novel suggestion in the MOT context, it makes sense from a physiological perspective. Tracking involves a number of different brain areas (Culham et al. 1998; Culham et al. 2001; Jovicich et al. 2001; Howe et al. 2009). Some of these utilize primarily retinotopic coordinates (e.g. MT; Huk et al. 2002; Gardner et al. 2008), whereas others are organized more in an allocentric fashion (Saygin and Sereno 2008). Thus, one would expect the brain to track objects in both coordinate systems.
Acknowledgments
NIH MH65576 to TSH.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Piers D. L. Howe, Email: PiersDouglasHowe@gmail.com.
Yair Pinto, Email: yair.pinto@gmail.com.
Todd S. Horowitz, Email: toddh@search.bwh.harvard.edu.
References
- Alvarez GA, Franconeri SL. How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. Journal of Vision. 2007;7(13):14, 11–10. doi: 10.1167/7.13.14. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spatial Vision. 1997;10(4):433–436. [PubMed] [Google Scholar]
- Burgess N. Spatial memory: how egocentric and allocentric combine. Trends Cogn Sci. 2006;10(12):551–557. doi: 10.1016/j.tics.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Cavanagh P, Alvarez GA. Tracking multiple targets with multifocal attention. Trends in Cognitive Sciences. 2005;9(7):349–354. doi: 10.1016/j.tics.2005.05.009. [DOI] [PubMed] [Google Scholar]
- Culham JC, Brandt SA, et al. Cortical fMRI activation produced by attentive tracking of moving targets. J Neurophysiol. 1998;80(5):2657–2670. doi: 10.1152/jn.1998.80.5.2657. [DOI] [PubMed] [Google Scholar]
- Culham JC, Cavanagh P, et al. Attention response functions: characterizing brain areas using fMRI activation during parametric variations of attentional load. Neuron. 2001;32(4):737–745. doi: 10.1016/s0896-6273(01)00499-8. [DOI] [PubMed] [Google Scholar]
- Fehd HM, Seiffert AE. Eye movements during multiple object tracking: Where do participants look? Cognition. 2008;108(1):201–209. doi: 10.1016/j.cognition.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franconeri S, Sumeeth J, et al. Tracking multiple objects is limited only by object spacing, not speed, time or capacity. Psychological Scicence. doi: 10.1177/0956797610373935. in press. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Jonathan SV, et al. Tracking multiple objects is limited only by interobject crowding, and not object speed. Psychomoic Society Annual Meeting.2009. [Google Scholar]
- Gardner JL, Merriam EP, et al. Maps of visual space in human occipital cortex are retinotopic, not spatiotopic. J Neurosci. 2008;28(15):3988–3999. doi: 10.1523/JNEUROSCI.5476-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horowitz TS, Holcombe AO, et al. Attention pursuit is faster than attentional saccades. Journal of Vision. 2004;4(7):583–603. doi: 10.1167/4.7.6. [DOI] [PubMed] [Google Scholar]
- Howe PD, Horowitz TS, et al. Using fMRI to distinguish components of the multiple object tracking task. Journal of Vision. 2009;9:1–11. doi: 10.1167/9.4.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huff M, Jahn G, et al. Tracking multiple objects across abrupt viewpoint changes. Visual Cognition. 2009;17(3):297–306. [Google Scholar]
- Huff M, Meyerhoff HS, et al. Tracking multiple invisible objects across viewpoint changes. Attention, Perception and Psychophysics. doi: 10.3758/APP.72.3.628. in press. [DOI] [PubMed] [Google Scholar]
- Huk AC, Dougherty RF, et al. Retinotopy and functional subdivision of human areas MT and MST. J Neurosci. 2002;22(16):7195–7205. doi: 10.1523/JNEUROSCI.22-16-07195.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognitive Psychology. 2001;43(3):171–216. doi: 10.1006/cogp.2001.0755. [DOI] [PubMed] [Google Scholar]
- Jin Z, Watamaniuk S, et al. Integration Of Motion Information For Smooth Pursuit During Multiple Object Tracking (MOT) [abstract] Journal of Vision. 2010;10:26, 439. [Google Scholar]
- Jovicich J, Peters RJ, et al. Brain areas specific for attentional load in a motion-tracking task. J Cogn Neurosci. 2001;13(8):1048–1058. doi: 10.1162/089892901753294347. [DOI] [PubMed] [Google Scholar]
- King-Smith PE, Grigsby SS, et al. Efficient and unbiased modifications of the QUEST threshold method: theory, simulations, experimental evaluation and practical implementation. Vision Res. 1994;34(7):885–912. doi: 10.1016/0042-6989(94)90039-6. [DOI] [PubMed] [Google Scholar]
- Knapen T, Rolfs M, et al. The reference frame of the motion aftereffect is retinotopic. Journal of vision. 2009;9(5):16, 11–17. doi: 10.1167/9.5.16. [DOI] [PubMed] [Google Scholar]
- Liu G, Austen EL, et al. Multiple-object tracking is based on scene, not retinal, coordinates. Journal of Experimental Psychology: Human Perception and Performance. 2005;31(2):235–247. doi: 10.1037/0096-1523.31.2.235. [DOI] [PubMed] [Google Scholar]
- Melcher D. Selective attention and the active remapping of object features in trans-saccadic perception. Vision Res. 2009;49(10):1249–1255. doi: 10.1016/j.visres.2008.03.014. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spatial Vision. 1997;10(4):437–442. [PubMed] [Google Scholar]
- Pylyshyn ZW. The role of location indexes in spatial perception: a sketch of the FINST spatial-index model. Cognition. 1989;32(1):65–97. doi: 10.1016/0010-0277(89)90014-0. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW. Things and places: How the mind connects with the world. Cambridge, MA: MIT Press; 2007. [Google Scholar]
- Pylyshyn ZW, Storm RW. Tracking multiple independent targets: evidence for a parallel tracking mechanism. Spatial Vision. 1988;3(3):179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Saygin AP, Sereno MI. Retinotopy and attention in human occipital, temporal, parietal, and frontal cortex. Cereb Cortex. 2008;18(9):2158–2168. doi: 10.1093/cercor/bhm242. [DOI] [PubMed] [Google Scholar]
- Seiffert AE. Attentional tracking across display translations (abstract) Journal of Vision. 2005;5(8):643a. [Google Scholar]
- Watson AB, Pelli DG. QUEST: a Bayesian adaptive psychometric method. Percept Psychophys. 1983;33(2):113–120. doi: 10.3758/bf03202828. [DOI] [PubMed] [Google Scholar]
- Wurtz RH. Neuronal mechanisms of visual stability. Vision Res. 2008;48(20):2070–2089. doi: 10.1016/j.visres.2008.03.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelinsky GJ, Neider MB. An eye movement analysis of multiple object tracking in a realistic environment. Visual Cognition 2008 [Google Scholar]


