Directional decisions during neutrophil chemotaxis inside bifurcating channels^,

Abstract

The directional migration of human neutrophils in classical chemotaxis assays is often described as a “biased random walk” implying significant randomness in speed and directionality. However, these experiments are inconsistent with in vivo observations, where neutrophils can navigate effectively through complex tissue microenvironments towards their targets. Here, we demonstrate a novel biomimetic assay for neutrophil chemotaxis using enclosed microfluidic channels. Remarkably, under these enclosed conditions, neutrophils recapitulate the highly robust and efficient navigation observed in vivo. In straight channels, neutrophils undergo sustained, unidirectional motion towards a chemoattractant source. In more complex maze-like geometries, neutrophils are able to select the most direct route over 90% of the time. Finally, at symmetric bifurcations, neutrophils split their leading edge into two sections and a “tug of war” ensues. The competition between the two new leading edges is ultimately resolved by stochastic, symmetry-breaking behavior. This behavior is suggestive of directional decision-making localized at the leading edge and a signaling role played by the cellular cytoskeleton.

Introduction

During inflammation, human neutrophils are capable of moving rapidly and navigating through complex tissues to specifically target inflammation sites. Without this capability, humans would quickly succumb to the invasion of fungi and bacteria and would not survive more than a few days in their regular habitat.¹ In this respect, neutrophils are some of the most impressive cells in terms of migration speed and orientation, which they have evolved in response to the selective pressure from microorganisms in the environment.² It is somewhat paradoxical that although neutrophils are quite effective at navigating complex and heterogeneous environments in vivo,^3,4 they appear to be less efficient when investigated using simple in vitro assays. For example, when neutrophils moving across a flat surface are exposed to a chemoattractant gradient (from a micropipette or generated by a Zigmond or Dunn chamber), they take a rather tortuous path that can be characterized as a biased random walk, with frequent divagations from a straight line and frequent stops.⁵ Even in the presence of stable, well controlled chemoattractant gradients in microfluidic devices, chemotaxing neutrophils display significant variability in directionality and speed.^6–9 Resolving this paradox requires the development of in vitro assays that can replicate key features of in vivo microenvironments.

Here, we demonstrate a novel approach for studying the migration of human neutrophils using non-planar, enclosed microenvironments of increasing complexity, from straight channels, to channels with posts and simple mazes. The cross-section of the channels is smaller than the human neutrophils, so that cells are mechanically confined and allowed to move only along the axis of the channels. These neutrophils are able to move at nearly constant speed for long periods of time and make robust directional decisions. Our results challenge current paradigms of signaling in neutrophils during chemotaxis and support new models for decision making in moving cells in which the cytoskeleton plays critical signaling roles.

Materials and methods

Microfluidic device manufacturing and setup

Microfluidic devices were fabricated using standard micro-fabrication technologies. Briefly, two layers of polydimethyl-siloxane (PDMS, Dow Corning), one 100 μm thin and one 4 mm thick, were cast on two silicon wafers with matching photolithographic features. The two layers, representing a control layer (thick) and a microfluidic network layer (thin), were aligned and bonded to each other and to a glass slide, as previously described.¹⁰ Air filled syringes were used to control the opening and closing of microfluidic valves on the chip. Syringes with buffer and chemoattractant solutions were handled using a syringe pump (Nemesys, Cetoni, Germany) that produced a stable flow rate of 0.5 μl/min.

A solution of 100 nM formylated peptide (Formyl-methionyl-leucyl-phenylalanine, fMLP, Sigma-Aldrich, St. Louis, MO) was used as chemoattractant and fluorescein (Sigma-Aldrich) was added during some experiments to check for the stability of the gradient throughout the duration of the experiments. The buffer used was 0.2% human serum albumin (HSA, Sigma-Aldrich) in Hanks Buffered Salt Solution (HBSS, ATCC, Manassas, VA). Syringes (1 mL, Hamilton Syringes, Reno, NV) filled with the buffer and chemoattractant solutions were connected to the device using tygon tubing (Small Parts, FL, USA). To promote neutrophil adhesion inside the channels, the device was primed with human-fibronectin solution (0.1%, Sigma-Aldrich) for about 20 min. After incubation, the device was washed with phosphate buffer solution (PBS, Fisher Scientific) and primed with 0.2% HSA in HBSS.

Neutrophil isolation off the chip

Neutrophils were separated from blood samples by centrifugation in hypertonic solution Polymorphoprep (Nycomed, The Netherlands). Briefly, 2 mL of EDTA-treated peripheral blood was laid over 2 mL of Polymorphoprep in a 5 mL tube (Fisher Scientific). Tubes were then centrifuged at 500 g for 25 min. The neutrophil band was removed from the tube by aspiration in a pipette and re-suspended in hypotonic PBS to normalize the final osmolarity of the neutrophil suspension.

Microscopy and image analysis

Neutrophils were introduced into the microfluidic device and captured mechanically at the entrance of the maze. After introducing the chemoattractant, cell motility was recorded on a Nikon 2000TE inverted microscope with a heated stage set at 37 °C. Individual frames recorded at 10 s intervals were analyzed using ImageJ (http://rsb.info.nih.gov/ij/) and the manual tracking plugin.

To measure the velocity of neutrophil migration through straight channels, images were imported into Metamorph (Molecular Devices Software) and cells tracked automatically using the tracking function. To improve the contrast of the images and better identify the moving cells, the initial frame was subtracted from all subsequent frames. The accuracy of automated tracking was verified by manually tracking ten neutrophils in straight channels, following either the leading or the trailing edge. No significant differences were found when cell velocities from various methods were compared.

To measure the speed of neutrophil migration through channels with posts, the leading edge of the neutrophils were manually tracked. The leading edge was tracked from the time of entering the channels until touching the first post, in between the posts, and from the last post until exiting the channels.

Statistical analysis

The statistical significance of the differences between observed and predicted behavior of neutrophils interacting with the posts and the branching channels, was tested using Chi-square analysis. Differences were considered significant at 95% confidence level. The time intervals for leading edge protrusion and collapse in the presence of channels with different geometries were compared using an independent t-test. Differences were considered significant at 95% confidence level.

Results

Microfluidic devices were fabricated with parallel arrays of small channels with cross section (3 × 6 μm) smaller than the average size of the human neutrophils and comparable to the critical dimension of the pores in low density matrices.¹¹ A stable chemoattractant gradient was produced from two streams, one of buffer and one of chemoattractant (fMLP, 100 nM), flowed at the two ends of the array.¹² The streams were balanced by temporary contact and symmetrical splitting inside the microfluidic device (Fig. 1a), such that there was no convective flow in the migration channels and the chemoattractant reached the cells solely by diffusion.¹² The continuous replenishment of buffer and chemoattractant at the channel end ensured constant boundary conditions. The mechanical confinement of neutrophils in channels limited the neutrophil migration along a single axis. The inclusion of symmetrical or asymmetrical bifurcations forced the neutrophils to make binary directional decisions along their uniaxial migration path.

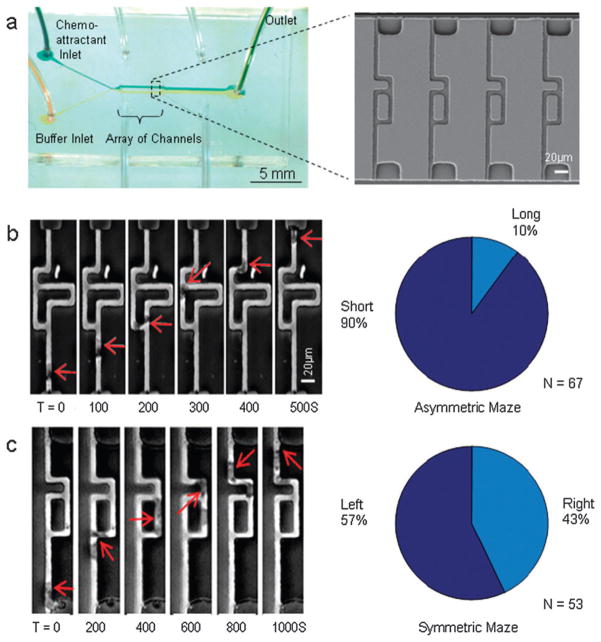
Fig. 1. Chemotaxis assay for neutrophil migration and directional decision making in bifurcating channels.

(a) Overall image of the microfluidic device. Buffer and chemokine were introduced from the left and split symmetrically on the two sides of the array. This created the conditions for an exclusively diffusion-driven gradient along the channels in array. A detail of the channel array, imaged using scanning electron microscope is presented. (b) Inside asymmetric mazes, human neutrophils chose the shorter path towards the source of fMLP 100 nM in the top channel in 90% of the observations (red outline). (c) In control experiments, human neutrophils showed no significant preference for path in symmetric mazes. The position of the neutrophils in the images is indicated by the red arrow, and displayed at 100 or 200 s intervals.

Human neutrophil migration through asymmetrically bifurcating channels

To investigate the possibility of externally biasing the orientation of human neutrophils, the behavior of neutrophils was examined when presented with bifurcations towards branches of different length (Fig. 1b). The steeper chemoattractant gradient through the shorter branch was expected to create conditions for asymmetric stimulation of moving neutrophils. Indeed, calculations indicate that neutrophils at the junction will experience a faster transient increase in chemokine concentration and temporarily larger absolute chemoattractant concentrations at the shorter branch. These differences were expected to bias neutrophil directional decisions at the bifurcations.

The first neutrophil to enter the asymmetric maze consistently chose the shorter (70 μm) vs. the longer (120 μm) of the two branches in 90% of observations (60 out of 67 observed neutrophils, p < 0.01, Movie 1^‡). If other neutrophils were present inside one of the branches, subsequent neutrophils chose to take the alternative, empty branch in 83% of cases (45 out of 54 observed neutrophils, p < 0.01). In control experiments, neutrophils migrating through a symmetrical maze (Fig. 1c, Movie 2^‡) chose randomly between the two branches (57% left vs. 43% right, N = 53 neutrophils observed, p > 0.05). Remarkably, at the second bifurcation point where the two branches recombine, close to 100% of the neutrophils migrated directly towards the source of chemokine rather than back toward the entrance of the channel (210 out of 211 observed neutrophils, p < 0.01).

The effect of contact guidance mechanisms¹³ on the directional decision-making of neutrophils was evaluated by observing the migration through the maze from bottom-to-top, then applying a gradient in the opposite direction so that migration occurred from top-to-bottom. When cells were moving up, they encountered the shorter channel at a right angle from the direction of migration, which would be less preferable if contact guidance mechanisms dominated. When cells were moving down, the shorter channel was in direct continuation of the direction of migration. Nevertheless, neutrophils moving alone and up through the channels chose the shorter path in 60 of 67 observations and 13 of 19 observations when coming from the top. This result indicates that the direction of the branches has little or no effect on the directional decision in moving neutrophils. No significant difference in the decision making between the two situations could be calculated (p = 0.7). These results are consistent with migration through the symmetrical maze, when cells chose between the two branches with equal frequencies (Fig. 1c).

Human neutrophil migration through channels with posts

Since neutrophils exhibited a clear preference for the most direct path under asymmetric conditions, it was intriguing to examine how neutrophils behaved when presented with a choice between two identical paths. Symmetrical bifurcations were implemented using three 6 μm diameter posts, placed successively at 30 μm spacing along the center axis of the channels. Immediately after reaching the posts, the leading edge of moving neutrophils split into two fronts (Fig. 2a–b). Remarkably, both fronts continued to extend and move towards the chemoattractant source at the same speed as the original leading edge, causing an increase in total length of the neutrophils. This “tug of war” between the two leading edges was ultimately resolved when one of the two edges rapidly collapsed to become the “tail” of the cell and the neutrophil moved forward, passing the post either on the left or on the right (Fig. 2b, Movie 3^‡).

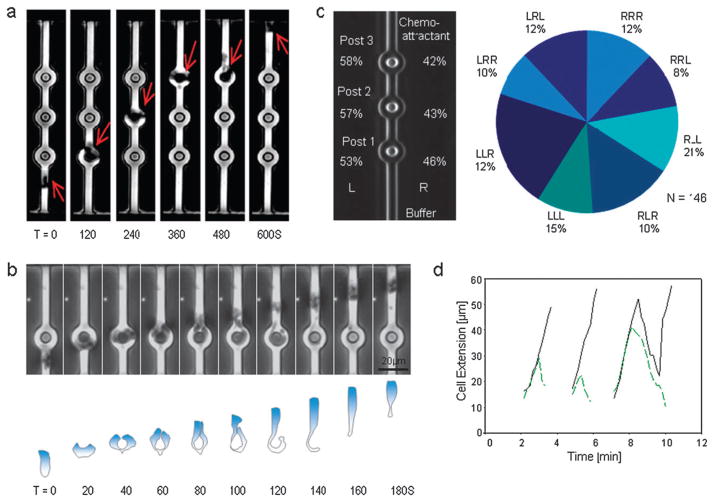
Fig. 2. Human neutrophil chemotaxis through channels with posts.

(a) Time sequence of images showing one human neutrophil migrating through a channel with 6 μm posts placed symmetrically inside the channel at 30 μm separation, toward a source of fMLP 100 nM. Individual frames at 120 s intervals are grouped in a montage. (b) Time sequence montage showing successive images of one neutrophil migrating through a channel with posts. After first touching the post, the leading edge of the neutrophil split into two leading edges that extended on either side of the posts. One of the protrusions rapidly retracted and the neutrophil passed the post on the other side. The contour of the neutrophil moving around the post is outlined in the lower panel. (c) Neutrophils passed each post to the left (L) or right (R) with statistically-equal frequencies. They also picked either one of the eight alternative paths around the three successive posts with equal chances. The pie-chart indicates the observed frequencies for each of the eight combinations of three consecutive left and right decisions, e.g. LRL = left at first post, right at second post, left at third post. (d) The length of the two extensions during the interaction between one neutrophil and three successive posts. The “winning” extensions (solid black line) had the same slope during the interaction with each post. The timing for the collapse of the “losing” leading edge (green dashed line) was different for each of the three posts. The “winning” and “losing” edges had similar extension dynamics before the collapse. In this particular example, during the interaction with the third post, the “winning” leading edge also collapsed for a brief time before switching again to extension behavior.

Neutrophils passed with statistically equal frequencies on the left (n = 82 events) vs. the right side of posts (n = 64) (p > 0.05) (Fig. 2c). These results demonstrate that splitting of the leading edge after interaction with the posts is symmetrical with respect to the axis of migration, and the choice of the collapsing leading edge is random. Given the eight possible routes past the three posts, the neutrophils showed no significant bias for any particular route (p > 0.05). Moreover, successive choices were not correlated, so that a decision to choose a particular direction at one post did not result in a preference for subsequently moving in the same direction. This indicates that neutrophils make independent decisions at each post and suggests that the persistence of any directional memory mechanism may be relatively short-lived, since neutrophils travel between each post in approximately 2.5 min. These results also suggest a symmetrical neutrophil rather than one with chirality, which has been previously proposed for neutrophil-like HL60 cell line, where new pseudopods form to the left of the centrosome-nucleus axis.¹⁴

For the majority of neutrophils, the overall pattern of edge splitting, extension, and collapse events was relatively consistent across the three posts (Fig. 2d). The leading edge split to follow both paths in 97.5% of the observed interactions between cells and posts. In less than 2% of the observed neutrophils, both leading edges collapsed at the same time, however, one quickly recovered to become the leading edge (Fig. 2d, third post).

Stochasticity during the migration of human neutrophils in bifurcating channels

The timescales for leading edge extension at asymmetric bifurcations and symmetrical posts were, on average, comparable (Fig. 3a). This process of leading edge extension was always slower than the leading edge collapse. For example, the two leading edges co-existed for an average of 66.7 s (average 67.6, 68.9, and 63.6 s for each of the three posts, respectively), and the average time of edge collapse was 48.6 s (average 43.5, 49.4 and 53.0 s, respectively, N = 80) (Fig. 3a). The collapse of the extended leading edge was also faster when passing the asymmetric or symmetric bifurcations, than after interaction with the posts (p < 0.05).

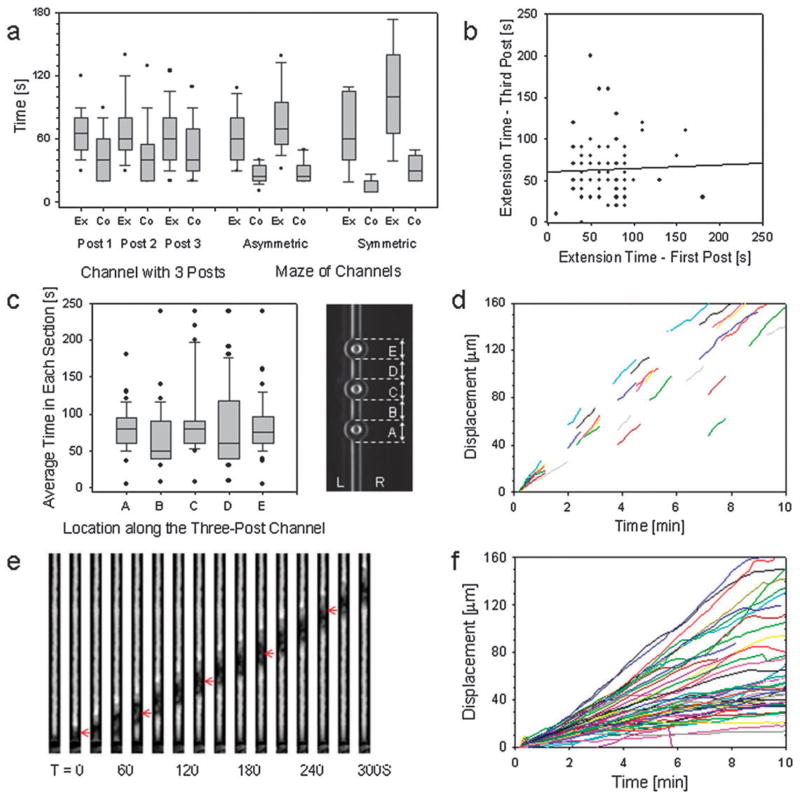
Fig. 3. Quantitative analysis of neutrophil migration through bifurcating channels.

(a) Average time for the extension (Ex) and collapse (Co) of the leading edges at bifurcations. During interactions with each of the three successive posts in a channel, the time for leading edge collapse was always shorter than the time for leading edge extension. When passing the asymmetric or symmetric bifurcations, however, the collapse of the extended leading edge was faster than after interaction with the posts (p < 0.05). The two sets of data for these conditions represent the splitting and merging of the channels, respectively. The horizontal lines indicate the median, 50% of the values are confined to the box, 90% of the values fall between the whiskers, and the outliers are indicated by dots. (b) For individual neutrophils, there is no correlation between the extension time for the leading edges during interaction with the first and third post. A straight line fit to the data shows the lack of correlation. Each dot represents one neutrophil. (c) We divided the length of the channel in five sections of approximately equal length (20 μm) that include sections with posts and straight sections, alternatively. The average time for passing through each of the five sections of equal length was similar regardless of the presence of post (86.5, 72.0, 96.3, 90.9, 86.0 s in sections from A to E, N=46). The box plot indicates the median, 50% of the values are confined to the box, 90% of the values fall between the whiskers, and the outliers are indicated by dots. (d) For most neutrophils, the velocity in the straight sections between posts was constant throughout the channel for individual neutrophils. In some of the observed neutrophils, the advance of the leading edge temporarily slowed down as the neutrophils passed by the posts, and the constant velocity was resumed in the straight sections of the channel. (e) Time sequence of images showing one human neutrophil migrating through a small channel 3 × 6 μm, toward a source of fMLP 100 nM. Individual frames at 50 s intervals are grouped in a montage. (f) Upon entering the straight channels, more than 90% of all cells observed (N= 70 human neutrophils, from 5 healthy donors) moved through persistently, without any pause. Median velocities ranged from 1 to 18 μm/min for all neutrophils, with 67% of cells having a median velocity from 3 to 10 μm/min. For every neutrophil, the velocity was relatively constant for the entire time inside the channels.

Surprisingly, the extension and collapse times for the leading edges interacting with each of the three posts was largely uncorrelated (p > 0.05). A comparison between the extension times for the first and third posts is shown in Fig. 3b, demonstrating the highly stochastic nature of leading edge expansion times. Even more surprisingly, this variability occurs while many other characteristics of neutrophil migration were uniform during the period of observation. Neutrophils moved with the same average velocity before and after encountering a post, and the timing for traveling through the different sections of the channels with posts was relatively uniform (Fig. 3c,d). This behavior is comparable to migration through straight channels when individual neutrophils travel at constant speed for extended periods of time (Fig. 3e,f). Together, these observations suggest that the mechanisms for directional decision making have an important stochastic component, while those regulating the migration velocity of confined neutrophils are robust and independent of the presence of small obstacles in front of the cells.

Proposed model for directional decision-making in neutrophils moving through bifurcating channels

The stochastic, symmetry-breaking phenomena exhibited by neutrophils at the cylindrical posts has not (to our knowledge) been previously observed, due to the unique experimental conditions used here. That is, when a neutrophil confined in a microchannel encounters a bifurcation presenting identical chemotactic gradients, it actually extends two leading edges, one along each path. After some time has elapsed, one leading edge will collapse, while the other one continues extending and subsequently leads the neutrophil on the latter path. Since this “tug-of-war” occurs over a wide distribution of timescales (Fig. 3a,c), it is difficult to reconcile this behavior with classical models of chemokine gradient sensing.^15–19 If leading edge extension and collapse were controlled by diffusive signaling throughout the entire cell, the distribution of timescales would be narrowly distributed and Gaussian. Moreover, a purely biochemical model cannot account for the mechanical interactions with the posts and the enclosing channel.

To better explain the directional decision making in human neutrophils observed in our assay, we postulate the presence of a chemoattractant sensing and amplification mechanism which is localized at the leading edge, and propose a chemomechanical model for controlling the balance between extension and collapse at the leading edge that involves microtubules. In this model, dynamically unstable microtubules participate in the signaling pathways triggered by chemoattractant²⁰ and control the polymerization of actin at the leading edge of the neutrophil in response to mechanical constrains. These pathways continue to work in each of the two sections after the leading edge is split following the contact with the post. During the subsequent “tug-of-war”, the stochastic behavior of the two leading edges is governed by microtubule dynamics under load.

A numerical model was implemented where the dynamic instability of microtubules is represented using Poisson statistics. For Poisson processes, the probability of a rare event over time t is given by equation P(t) = 1 − e^−t/τ, where τ is the mean time between events. This probability was evaluated at each time-step and compared with a randomly generated number selected from a uniform distribution [0, 1).

If the random number was larger than the probability at that particular time, the microtubule is unaffected and continues polymerization. However, if the random number was less than this probability, the microtubule undergoes catastrophic depolymerization. This is assumed to be instantaneous, so the microtubule length is set to zero and polymerization begins anew.

Following the work of Dogterom and coworkers, the polymerization rate of microtubules was assumed to be load-dependent:

$$\frac{\text{d}N}{\text{d}t}=k_{\text{on}}{Ce}^{-F\delta /k_{\text{B}}T}-k_{\text{off}}$$

where dN/dt is the polymerization rate, k_on and k_off are association and dissociation rate constants, respectively; C is the monomer concentration, F is a force and δ is a monomer size.²¹ Previous in vitro experiments showed that when a load is applied, the increasing force will decrease the polymerization rate until a steady-state length is reached. Surprisingly, this slowdown is not observed during our experiments in the trajectories of the neutrophil leading edges. This indicates that the microtubules do not experience a length-dependent load. Physically, this may occur if the extension of the leading edge is driven primarily by actin polymerization rather than microtubules. In this scenario, the microtubules experience a constant load, corresponding to a constant growth velocity.

One consequence of a constant load is that it can amplify the dynamic instability of individual microtubules, so that a bundle of microtubules can undergo catastrophic depolymerization and failure.²² In this scenario, the load may arise from the continuous expansion of the two leading edges at the front of a neutrophil as well as the interaction with a post. This load is conveyed to the microtubules, causing the collapse of some microtubules and redistributing the load among the remaining ones. If there are a small number of microtubules, this can result in a considerably enhanced load. This further accelerates the collapse of the rest of the microtubules in the same leading edges, ultimately leading to the retraction of that leading edge and allowing the remaining leading edge to drive the neutrophil forward around the post. For example, the individual load increases by 20% for a decrease from six to five microtubules, and by a total of 50% for a decrease from six to four. The total collapse of all microtubules in one section of the leading edge triggers its retraction at constant velocity (Fig. 4a), and subsequent reduction of the load at the remaining leading edge. Since the other leading edge has remaining microtubules, it continues forward at constant velocity, which is consistent with experimental observations.

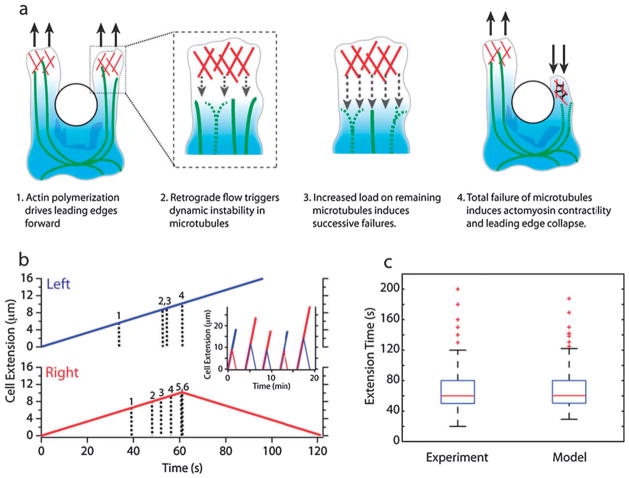
Fig. 4. Proposed model for local directional decision making in human neutrophils interacting with posts.

(a) Dynamics of the cytoskeleton during the interaction with the posts. (b) Simulated trajectory of successful (blue) and failing (red) leading edges containing six dynamic microtubules with a characteristic Poisson timescale of 40 s. During the time shown, the successful leading edge (blue) remains intact since it undergoes random microtubule collapses at well separated times of t = 33 s, 53 s and 61 s, respectively. In contrast, the failing leading edge (red) undergoes random microtubule collapses at closely spaced time intervals, starting at t = 39 s, with subsequent failures every 4 s or less. This causes sudden and large increases in load on the remaining microtubules that trigger their subsequent collapse. At t=61 s, the total catastrophic failure of all microtubules causes the leading edge to begin retracting. In the inset, five simulated trajectories are shown that were generated using these same parameters. (c) A comparison between simulated and observed extension time of the two leading edges, during the interaction between neutrophils and posts, shows good qualitative and quantitative agreement between the two. The stochastic behavior and the highly asymmetric distribution are relatively insensitive to the choice of parameters. Parameters were selected to match the experiments, particularly the median timescale of 60 s.

A representative simulated trajectory is shown in Fig. 4b for a leading edge containing six microtubules. These trajectories exhibit varying extension timescales and length scales that are qualitatively consistent with the experimental data (Fig. 4c). The experimentally observed symmetry breaking is also reproduced, with the leading edge collapsing on the left side for 50.6% of the time and on the right for 49.4% for N = 236 trajectories. A slower depolymerization rate will not affect the results of this model, since there is usually insufficient time for the microtubule to catch up to the leading edge.

The proposed model of cooperative microtubule dynamic instability is also consistent with the migration of neutrophils in straight channels. The wider leading edge will be associated with a larger number of microtubules (> 10). In this limit of large numbers, the failure of an individual microtubule corresponds to a considerably smaller increase in load, which may not make an appreciable difference. Thus, the total failure is expected to occur over much longer timescales, since the increase in load for the first few failures is comparatively small and more microtubules must fail for total collapse to occur. This is again consistent with our experiments, where the leading edge in straight channels (with twice the number of microtubules) undergoes sustained, unidirectional motion.

Discussion

The combination of “mazes” of microfluidic channels and chemoattractant gradients demonstrated here enables unique insights into the mechanisms of chemotaxis. By using this microfluidic assay, the migration of neutrophils was confined along one axis during the persistent migration towards the source of chemoattractant, reducing the number of micro-environmental variables. Furthermore, by integrating the bifurcating channels in the assay, the neutrophils were limited to two directional options, further focusing the analysis on the chemical and mechanical determinants of directional decision making in moving neutrophils.

These behaviors are difficult to resolve using any other chemotaxis assay. Neutrophil migration in the classical and more recent 2D planar chemotaxis assays^5–8,23,24 is characterized by inefficient, “biased random walk” with frequent stops across a flat surface towards the source of chemoattractant.^5,25,26 While the persistent migration of cells inside small channels has been previously reported (e.g. differentiated, neutrophil-like HL60 cell line,¹² or mouse dendritic cells),²⁷ or in-between glass and gel plates (e.g. human neutrophils²⁸ and mouse dendritic cells),²⁹ these systems are not sensitive to the directional choices of migrating cells. The use of 3D polymer matrix models is more advantageous since in vivo directional migration can also be recapitulated. However, the local microstructure can be highly heterogeneous and vary depending on preparation technique.¹¹ At different locations in this matrix, cells may encounter considerably different structural architectures, which will influence their mechanical interactions with the surrounding polymer “mesh”. This can complicate the investigation of mechanisms such as contact guidance, where the cell is oriented along a polymer bundle,¹³ particularly once the cell reaches a junction formed by the random intersection of other polymers. Using well-defined junction geometries comprised of microfluidic channels, the experiments described here establish that these contact guidance effects play a secondary role to (strong) chemoattractant gradients in neutrophil navigation.

These observations of neutrophils migrating through the asymmetrically bifurcating channels support the hypothesis that the chemical gradient sensing mechanisms are localized at the leading edge of the cells. In the presence of asymmetric bifurcations, neutrophils extended two leading edges, and the ensuing “tug-of-war” is consistently “won” by the leading edge at the most direct route towards the source of chemoattractant. A divergent signaling, allowing rapid switching between “frontness” and “backness”, may be at play in the leading edge, following the model previously proposed by Xu et al.³⁰ Localized signaling pathways that bias the probability of local lamellipod extension towards the direction of higher local chemoattractant concentration have been proposed as a mechanism to guide the directional migration in dendritic cells and fibroblasts.³¹ Other experimental observations and recent models have suggested that the leading pseudopod can spontaneously split into two, and only one of the new pseudopods is preferentially stabilized, steering the moving cell in the direction of the gradient.^32,33 This particular behavior of the pseudopod has been described in detail for the migration of slime mold Dictyostelium discoideum in shallow gradients^33,34 but its relevance to human neutrophils remains unclear. In this assay, human neutrophils maintained a unitary leading edge at all times and the only splitting was observed following the mechanical interaction with posts and bifurcations. The question of how the expansion and collapse of the leading edges is coordinated is only partially addressed in the presence of asymmetric bifurcations.

This mechanism is further elucidated in the scenario using symmetric bifurcations (posts), since the neutrophil cannot rely on either chemoattractant gradient or contact guidance for navigation. The resulting stochastic, symmetry-breaking decision behavior is difficult to reconcile with current biochemical models for cell polarization and chemotaxis that postulate the existence of a global inhibitor that diffuses between the front and the back of the cells.^15–19 If such an inhibitor was present, diffusing uniformly either from the back,¹⁵ or from the stimulated regions¹⁹ of the moving cells, the timescale to reach the leading edge would not vary considerably, contradicting our experimental observations. Moreover, these models do not include the chemomechanical couplings that may arise in these assay conditions. Instead, these behaviors likely arise from a discrete, cooperative process involving a small number of molecules that participate in positive feedback loops at the leading edge.³⁵

The proposed model for directional decision-making arises from the experimental observations of neutrophil behavior at symmetrical and asymmetrical bifurcations and yields several critical insights into the mechanisms of neutrophil chemotaxis. Based on the stochastic behavior of neutrophils at bifurcations, microtubules may play a central role in navigation and motility. Since microtubules are present in small numbers, a few random events may be sufficient to bias motility towards the source of chemoattractant. Such a role for the microtubules in integrating chemical signaling from the cell periphery during polarization has been previously proposed in neutrophils and other cells.^20,36,37 Finally, microtubules exhibit unique features that may be advantageous for signaling processing during chemotaxis, including dynamic instability for spontaneous, rapid depolymerization,²² as well as coupling with different pathways that modulate these dynamic processes in response to asymmetric stimulation.²⁰

The novelty of the proposed model is the role of microtubules for integrating the mechanical constraints of migration with the chemical stimuli. Following the interaction with the posts and the splitting of the leading edge, microtubules zfunction as mechanical sensors and help balance the mechanical load between the two leading edges. Indeed, single-molecule experiments have demonstrated that the dynamic instablity of microtubules can be biased when microtubules polymerize against a force. Moreover, the effect of load on bundles of several microtubules is additive and linear.³⁸ When multiple microtubules are polymerized in parallel, the spontaneous failure of one can cooperatively induce additional failures, since the load is redistributed among the remainder, with a higher force per microtubule.³⁹ This is analogous to a positive feedback mechanism that amplifies instability.

This combined chemical and mechanical system is very effective in facilitating the navigation of neutrophils through the bifurcating channels. The stabilization of microtubules by chemical stimulation at the leading edge could be temporarily overcome by the destabilization following the mechanical interaction with the cylindrical post, when the cell simultaneously extends two leading edges. The system becomes considerably more sensitive to noise, so that the destabilization of a few microtubules could lead to catastrophic collapse of one leading edge. This, in turn, removes the strain hindering the other leading edge, which wins the “tug of war” and is able to continue its constant movement forward.

In summary, we demonstrate a novel, high-throughput assay where cell navigation and motility can be independently interrogated in bifurcating microfluidic channels. The range of directional decisions was constrained to the binary choice between branches at asymmetric and symmetric bifurcations, allowing a comparison of the dynamics of stochastic and biased directional decisions. This precise control of migration conditions and quantitative outcome of experiments enabled us to hypothesize a role for microtubules in directional migration and propose a new chemotaxis model in which cytoskeleton dynamics play critical roles in the directional migration of human neutrophils. In the future, this model could be expanded to the study of cell motility mechanisms involved in cancer metastasis, human immune response, wound healing, or embryonic development, and could have a broader impact in health and disease conditions where cell motility plays key roles.

Insight, innovation, integration.

To study the directional decision making processes in neutrophils during migration in response to chemoattractant gradients, we designed a series of microfluidic devices that limit the directional choices that cells can make at any time. We observed that when migrating through microfluidic channels with posts, neutrophils split their leading edge into two sections and a “tug of war” ensues between the two sections. This competition is ultimately resolved by stochastic, symmetry-breaking behavior that is suggestive of directional decision-making localized at the leading edge, as well as a signaling role played by the cellular cytoskeleton.