Abstract
Stray neutrons generated in passively scattered proton therapy are of concern because they increase the risk that a patient will develop a second cancer. Several investigations characterized stray neutrons in proton therapy using experimental measurements and Monte Carlo simulations, but capabilities of analytical methods to predict neutron exposures are less well developed. The goal of this study was to develop a new analytical model to calculate neutron ambient dose equivalent in air and equivalent dose in phantom based on Monte Carlo modeling of a passively scattered proton therapy unit. The accuracy of the new analytical model is superior to a previous analytical model and comparable to the accuracy of typical Monte Carlo simulations and measurements. Predictions from the new analytical model agreed reasonably well with corresponding values predicted by a Monte Carlo code using an anthropomorphic phantom.
1. Introduction
The physical characteristics of proton beams make it possible to deliver a large and uniform dose to the target while sparing normal tissue, which may reduce the risk of radiation-induced secondary cancer relative to that of photon therapy (Miralbell et al 2002, Newhauser et al 2009, Fontenot et al 2009). The most common delivery method of proton beams is passively scattered proton therapy (PSPT). In the process of shaping the beam to the target during PSPT delivery, neutrons are produced in the treatment unit and in the patient (Zheng et al 2007, 2008), resulting in the patient being exposed to a whole body neutron dose about several hundred mSv (Newhauser et al 2009, Taddei et al 2009). The relative biological effectiveness of these neutrons for carcinogenesis is not well known (Hall 2006). In order to estimate a patient’s risk of developing radiogenic secondary cancer from the PSPT treatment, it is necessary to take into account the risk associated with the stray neutron exposures throughout the patient.
Many investigators have studied the stray neutrons in proton therapy using experimental measurements and Monte Carlo simulations (Binns and Hough 1997, Agosteo et al 1998, Yan et al 2002, Schneider et al 2004, Roy and Sandison 2004, Polf and Newhauser 2005, Mesoloras et al 2006, Tayama et al 2006, Wroe et al 2007, Zytkovicz et al 2007, Zacharatou Jarlskog et al 2008, Yonai et al 2008, Moyers et al 2008, Athar and Paganetti 2009, Shin et al 2009, Zheng et al 2007, 2008, 2009, Newhauser et al 2009, Taddei et al 2009, Pérez-Andújar et al 2009). Marked variations of neutron dose equivalent per therapeutic-absorbed dose (H/D) were found among studies, mainly because the stray neutron dose depends heavily on the design of the treatment apparatus, measurement or calculation method and the treatment technique.
Because of the complexity, cost and time required for both measurements and Monte Carlo simulations, it would be desirable to have analytical models that could be used to predict the H/D values in proton therapy or be used as an independent crosscheck of measured or simulated results. Zheng et al (2007) described an analytical model capable of predicting H/D values during PSPT. However, their model has only been tested against H/D values calculated in air. It was not known how well an analytical model could predict H/D values in a phantom.
The objective of this work was to develop an accurate analytical model to predict H/D values both in air and in a simple water phantom from a PSPT treatment. Monte Carlo methods were used to model the PSPT treatment unit and generate H/D values both in air and in a phantom.
2. Methods and materials
2.1. Monte Carlo simulations
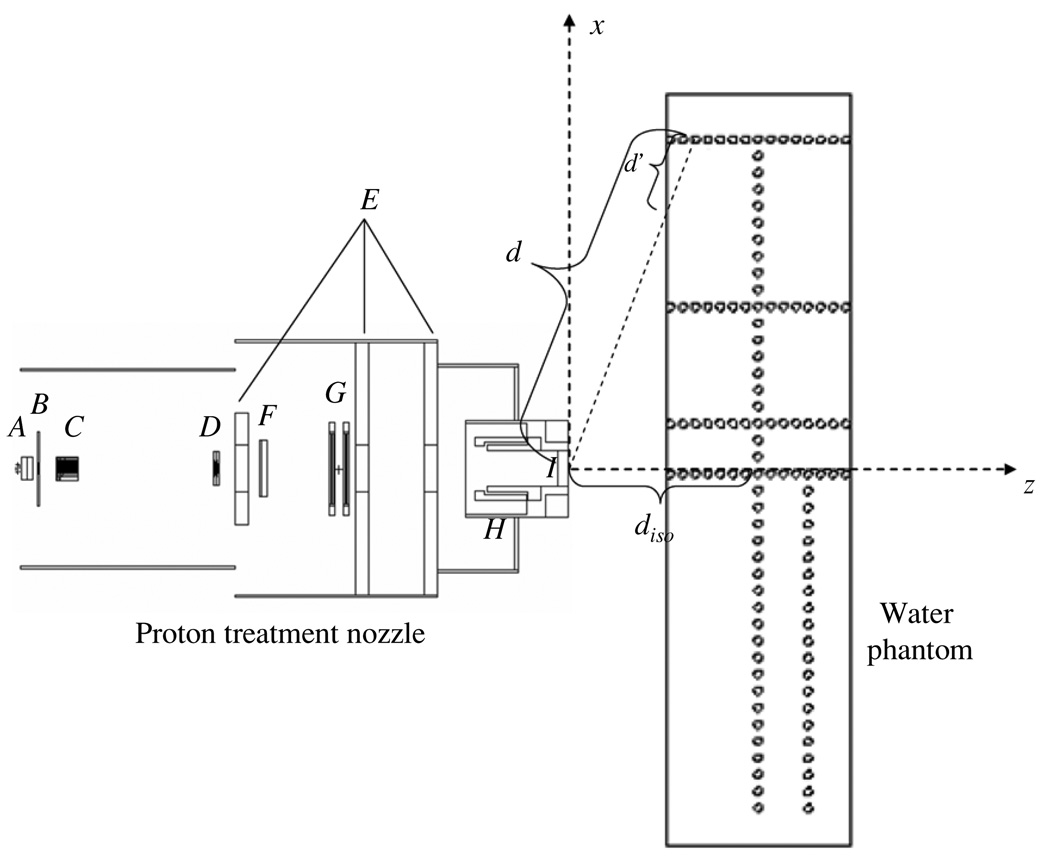
The Monte Carlo N-particle eXtended radiation transport code (MCNPX version 2.6, Pelowiz 2005) was used to model the proton beam delivery system and simulate neutron exposures. Nuclear interaction cross-section libraries were used for protons with energies below150 MeV, while physics models were used at energies above 150 MeV. Figure 1 shows a schematic of the PSPT treatment unit and the layout of the neutron receptors. The proton beam delivery system includes a vacuum window, a beam profile monitor, a range modulator wheel, a second scatter, shielding plates, a range shifter assembly, backup and primary monitors, the snout and the final aperture. The materials for each component can be found in Newhauser et al (2007) and Zheng et al (2007). The simulation geometry utilized a specifically defined condition: an unmodulated (i.e. pristine) 250 MeV proton beam incident upon a medium size (18 × 18 cm2) closed aperture (to conservatively estimate H/D values). The neutron absorbed dose was simulated in air in 2 cm diameter spherical receptors oriented in both the z and x directions. We also simulated neutron dose in a 30 × 180 × 44 cm3 water phantom (to mimic a patient) introduced at the end of the beam line and centered at the isocenter. The positions of spherical receptors were the same in simulations with and without the water phantom. The in-house Monte Carlo Proton Radiotherapy Treatment Planning (MCPRTP) code (Newhauser et al 2008) was used to generate all necessary input files; the simulations were run with parallel processing on 2.6 GHz, 64 bit processors. For more details of the geometric model of the PSPT treatment unit, the reader is referred to the previous works (Newhauser et al 2007, 2008).
Figure 1.
Schematic illustration of the PSPT treatment nozzle and the water phantom. The nozzle includes a vacuum window (A), a beam profile monitor (B), a range modulator wheel (C), a second scatter (D), shielding plates (E), a range shifter assembly (F), backup and primary monitors (G), the snout (H) and the final aperture (I). Neutron dose was calculated in 2 cm diameter spherical receptors (open circles) in both axial (z) and lateral (x) directions. In the figure, d indicates the distance from the effective neutron source to the neutron receptor, d′ indicates the distance from the phantom surface to the neutron receptor along the path between the effective neutron source and the receptor, diso indicates the distance from the effective neutron source to the isocenter. The figure is not drawn to scale.
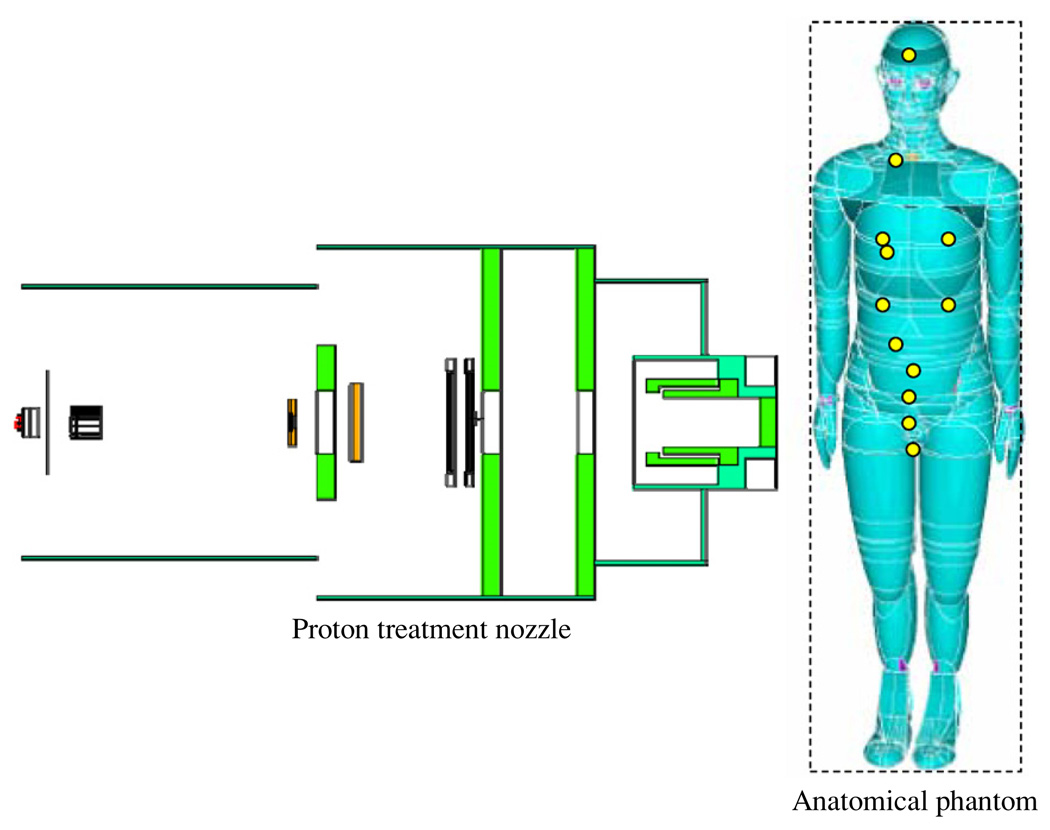
To verify predictions from the analytical model, we also used Monte Carlo simulations to predict H/D values in a prostate treatment of a computational anatomical male phantom (Billings and Yucker 1973). This phantom had been adapted for use in MCNPX and has been used in previous studies in our group (Fontenot et al 2008, Taddei et al 2008, Newhauser et al 2009). The phantom, shown in figure 2, was simulated with 2 cm diameter spherical receptors in the organs of interest (brain, lungs, breast, stomach, liver, colon, esophagus, thyroid, bladder, rectum, gonads and prostate).
Figure 2.
Schematic illustration of the PSPT treatment unit and the computational anatomical male phantom modeled using Monte Carlo simulations. The locations of the neutron dose receptors are shown as yellow circles on the phantom. The dash line box represents the imaginary box used to enclose the phantom for calculation convenience. The figure is not drawn to scale. (Rendering of anthropomorphic phantom was provided courtesy of Tom Jordan.)
2.2. Calculation of H/D
For simulations with the water phantom, the neutron absorbed dose per source particle, Dn/sp, was scored in each receptor, and the neutron equivalent dose per source particle was calculated using
| (1) |
where the mean radiation weighting factor for neutrons was calculated following methods previously reported by our group (Taddei et al 2008, Newhauser et al 2009).
For simulations in air, the neutron ambient dose equivalent was simulated instead of using the method of equation (1). This was done because the mean free path of neutrons in air is much longer than the diameter of receptors and the interaction probability of neutrons and their secondary particles inside receptors is very low. In contrast, scoring the neutron fluence is more effective because the track length of neutrons is scored directly instead of simulating neutron interactions and secondary particles tracks. Using the track-length estimate of neutron fluence, it was possible to obtain Monte Carlo tally convergence, which was essential for simulation results to be considered reliable, whereas convergence could not be obtained in air using the method of equation (1). Neutron spectral fluence per source particle, ΦE/sp, was simulated in each receptor (i.e. neutrons per cm2 per source proton) by the Monte Carlo code. Each ΦE/sp was then converted to ambient neutron dose equivalent per source proton (H/sp) values according to
| (2) |
where i is the index and n is the total number of neutron energy bins, and (H/Φ E)i and ΦEi/sp were, respectively, the ambient dose equivalent per fluence and the neutron fluence per source proton in the ith neutron energy bin. The conversion coefficients, (H/ΦE)i, were taken directly from ICRP (1996).
The therapeutic absorbed dose per source particle (D/sp) for a reference condition was calculated in separate simulations. The reference condition included a 10 × 10 cm2 collimated 250 MeV proton treatment field and the D/sp was determined on the central axis of the beam at the center of the pristine Bragg peak in a water phantom. H/D values were calculated by dividing H/sp by D/sp.
3. Analytical models of H/D
An analytical equation was used to model H/D as a function of receptor location following the method from Zheng et al (2007):
| (3) |
where d was the distance from the effective neutron source, which was found to be very close to the final collimating aperture (Zheng et al 2007), to the neutron receptor, (H/D)d was the H/D value at the neutron receptor, diso was a fitting parameter that indicated the distance from the effective neutron source to isocenter, and p was the parameter describing the shape of the dose falloff with distance. While their equation provided reasonable estimates of neutron dose equivalent in air, the presence of a water phantom has been shown to strongly influence neutron dose distributions from PSPT (Zheng et al 2008, 2009).
In this study, we generalized the model in equation (3) to predict H/D values both in air and in a water phantom. Specifically the model includes terms for an attenuation factor (AF) and an off-axis factor (OAF). The neutron dose decreases exponentially with depth in the phantom, or
| (4) |
where α is a fitting parameter which describes the attenuating property of the phantom material, and d′ is defined as the distance from the phantom surface to the neutron receptor along the path between the effective neutron source and the neutron receptor (see figure 1). In the lateral direction, the neutron dose distribution diverges and follows a Gaussian distribution, or
| (5) |
where x and y are the lateral distances from the dose receptor to the central axis and σ is the fitted Gaussian width parameter.
The neutron spectral fluence has been observed to contain two pronounced peaks: a low-energy evaporation peak ranging from 10 keV to around 10 MeV and a high-energy cascade peak ranging from around 10 MeV up to the incident proton energy (cf Zheng et al 2008, 2009). Based on that knowledge, we proposed the following equation to estimate the H/D value at position d in air:
| (6) |
where C1 is a fitted empirical parameter that apportions the relative dose contributions from high- and low-energy neutrons, p1 and p2 are the parameters governing dose falloff with distance for high- and low-energy neutrons, respectively. σ1 and σ2 are the corresponding Gaussian lateral width parameters, z is the axial coordinate for the neutron dose receptor and is used to scale the width parameters (see figure 1). The differences between equations (3) and (6) were that the neutrons were partitioned into two energy groups and the double Gaussian approach, with the separate Gaussian items characterizing the high-energy cascade neutrons and the low-energy evaporation neutrons.
Similarly, the H/D value in the water phantom was estimated using
| (7) |
where d′iso is the distance from the phantom surface to the isocenter, α1 and α2 characterize the attenuation properties for the high- and low-energy neutrons, respectively. This equation takes into account both divergence and attenuation of neutrons in the water phantom.
To facilitate calculation of d′ for the anthropomorphic phantom, we ‘enclosed’ the phantom in an imaginary box that is slightly larger than the phantom itself and calculated d′ as if the box were the phantom surface. Additionally, we approximated the tissue density within the anthropomorphic phantom as being identical to that of water when we predicted H/D values using analytical models. However, in the Monte Carlo simulations, the more realistic material and mass densities of the anthropomorphic phantom were used.
4. Results
Table 1 shows the values of the fit parameters from the previous analytical model (Zheng et al 2007) and the new analytical model from this work. The diso value was intentionally fixed at 33 cm, which is the distance from the final aperture to isocenter, because the majority of protons were stopped at the final closed aperture. Most of the p values were less than 2, which indicated that the neutron source was spatially distributed and not a point source. C1 values in the new model were less than 0.24, which indicated that more than two thirds of H/D values were associated with low-energy evaporation neutrons. The σ2 values were much larger than σ1 values, which indicated, as expected, that the low-energy evaporation neutrons were isotropically emitted whereas the high-energy neutrons were emitted in a forward cone centered about the central axis of the proton beam.
Table 1.
Fitting parameters for the analytical models (analytical model (new) is from this study, analytical model (old) is from Zheng et al (2007)) for the specific condition (an unmodulated 250 MeV proton beam incident upon a medium-sized closed aperture. The aperture was closed for both in-air and water phantom cases). Dashes indicate that parameters were not used in the given situation.
| Analytical model (old) | Analytical model (new) | |||
|---|---|---|---|---|
| Parameter | Air | Water phantom | Air | Water phantom |
| diso | 33 | 33 | 33 | 33 |
| p1 | 1.30 | 2.0 | 1.0 | 1.0 |
| p2 | – | – | 1.45 | 2.0 |
| C1 | – | – | 0.20 | 0.24 |
| α1 | – | – | – | 0.01 |
| α2 | – | – | – | 0.017 |
| σ1 | – | – | 15.85 | 9.18 |
| σ2 | – | – | 820.34 | 1011.07 |
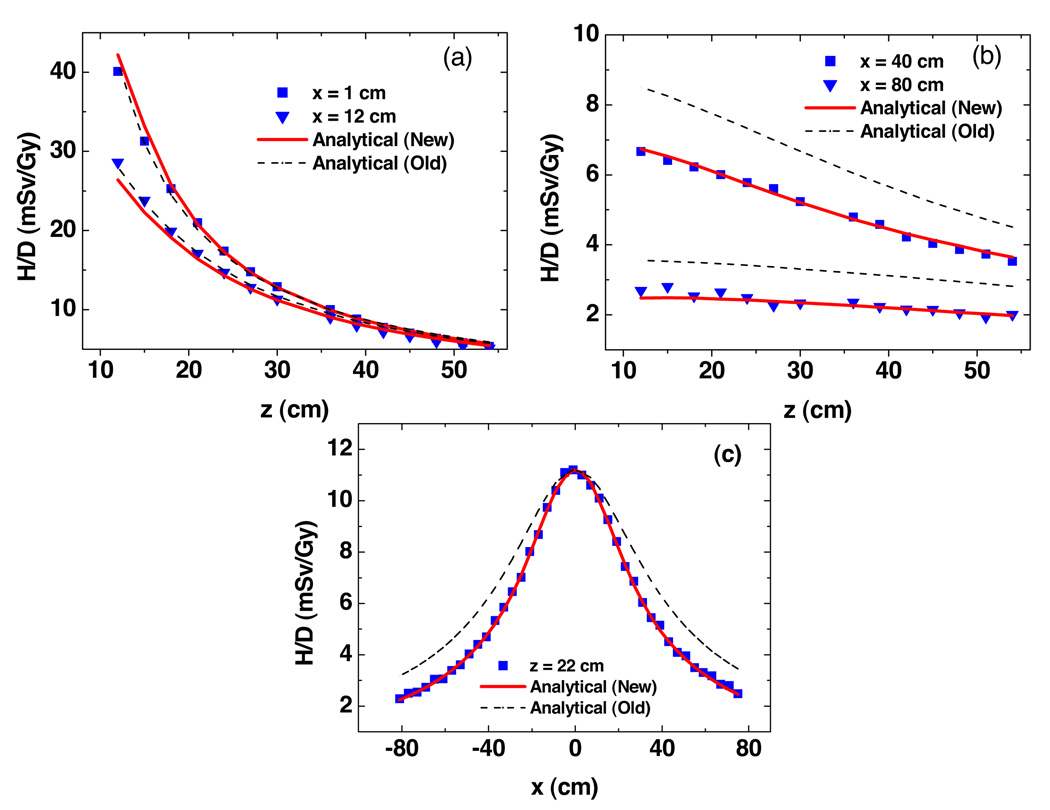
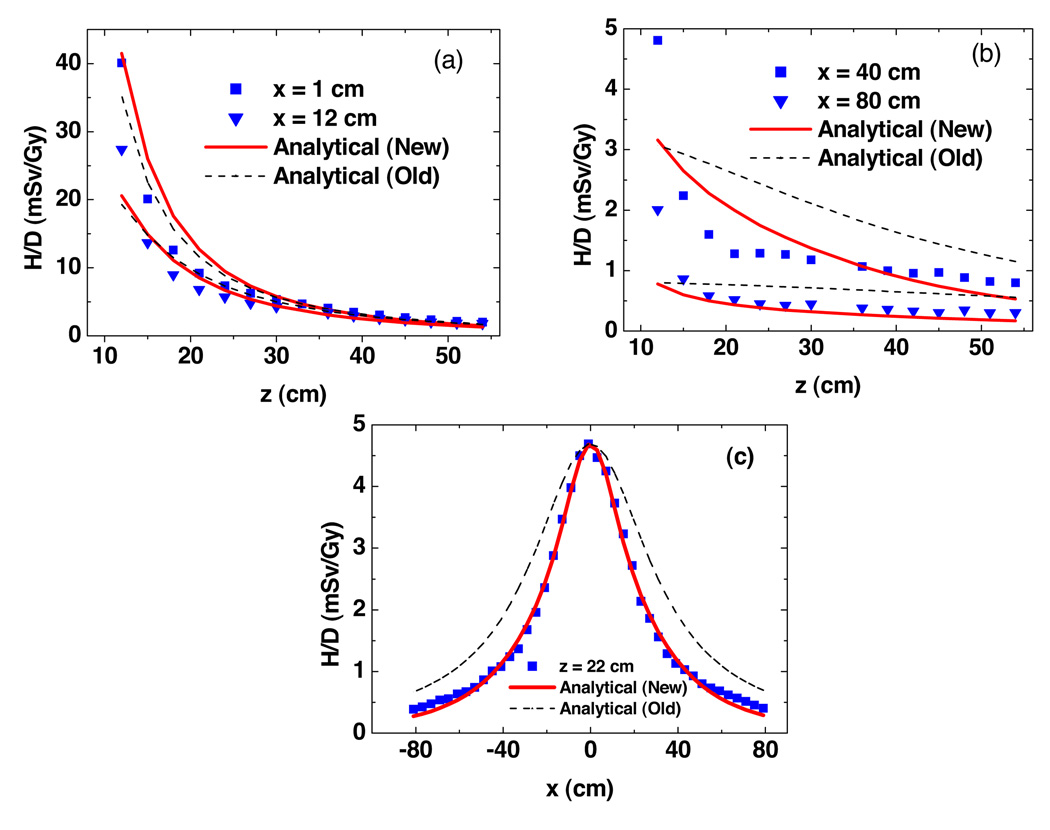
Figure 3 plots predicted H/D values from Monte Carlo simulations and analytical models as a function of vertical and lateral positions free in air. Near the central axis, both models fit the simulated data well. The new model provided better agreement than the old model farther away from the central axis. Figure 4 shows the predictions of H/D values from Monte Carlo simulations and analytical models as a function of vertical and lateral positions in the presence of a water phantom. The new analytical model showed better agreements at all locations. The uncertainties in wR and fluence-to-dose conversion factors were large and difficult to estimate, so they were taken as zero. The statistical uncertainties calculated by MCNPX were 1.8% (mean) and 5.4% (maximum) for fluence simulations in figure 3, and 2.9% (mean) and 10.4% (maximum) for dose simulations in figure 4.
Figure 3.
Results from Monte Carlo simulations and analytical models predictions of ambient neutron dose equivalent per therapeutic dose (H/D) free in air as a function of vertical distance (a) and (b) and lateral distance (c). These values were for a specific condition (an unmodulated 250 MeV proton beam incident upon a medium-sized closed aperture). Analytical model (new) is from this study, analytical model (old) is from Zheng et al (2007).
Figure 4.
Results from Monte Carlo simulations and analytical models predictions of neutron equivalent dose per therapeutic dose (H/D) in the water phantom as a function of vertical distance (a) and (b) and lateral distance (c). These values were for a specific condition (an unmodulated 250 MeV proton beam incident upon a medium-sized closed aperture). Analytical model (new) is from this study, analytical model (old) is from Zheng et al (2007).
In air, the discrepancies between predictions of H/D values from Monte Carlo simulations and analytical models were 2.56% (mean) and 12.6% (maximum) for the new analytical model, and 20.8% (mean) and 48.8% (maximum) for the old model. The maximum absolute discrepancy from Monte Carlo simulations was less than 5.1 mSv/Gy for both models. In the water phantom, the discrepancies between predictions of H/D values from Monte Carlo simulations and analytical models were 17.2% (mean) and 61.2% (maximum) for the new analytical model, and 44.2% (mean) and 103.4% (maximum) for the old model. The maximum absolute discrepancy from Monte Carlo simulations was less than 8.2 mSv/Gy for both models.
The H/D values in the anthropomorphic male phantom predicted using the Monte Carlo method (statistical uncertainties calculated by the MCNPX code were reported at the 68% confidence interval) and the analytical models are listed in table 2. These data revealed that predictions from both analytical models agreed reasonably well with simulated data. The discrepancy in H/D values was less than 55% for the new analytical model. The largest discrepancy was in the brain and this is possibly because the discrepancy between the real phantom surface and the imaginary box surface was the largest in the region of the head. This discrepancy would decrease to 22% if the d′ was reduced by half. The results were reasonably good, however, given the simplified treatment of the anatomical phantom surface and tissue densities in the calculation. Preliminary tests showed that the calculated results from the new analytical model were sensitive to the d′ parameter, which is related to differences in the shapes and locations of the water phantom and the anthropomorphic phantom surfaces.
Table 2.
H/D values in the anatomical male phantom from Monte Carlo simulations (H/DMC) with statistical uncertainties, analytical calculations (H/Dcal) and the absolute percentage differences between Monte Carlo and analytical predictions. These values were for a specific condition (an unmodulated 250 MeV proton beam incident upon a medium-sized closed aperture). Analytical model (new) is from this study, analytical model (old) is from Zheng et al (2007).
| Analytical model (new) |
Analytical model (old) |
||||||
|---|---|---|---|---|---|---|---|
| Organs |
d (cm) |
d′ (cm) |
H/DMC (mSv/Gy) |
H/Dcal (mSv/Gy) |
Diff (%) |
H/Dcal (mSv/Gy) |
Diff (%) |
| Brain | 85.62 | 64.86 | 0.76 ± 0.04 | 0.34 | 54.76 | 0.89 | 16.95 |
| Prostate | 33.02 | 25.01 | 5.99 ± 0.088 | 5.98 | 0.00 | 5.98 | 0.00 |
| Right lung | 49.74 | 33.82 | 1.78 ± 0.082 | 1.72 | 3.76 | 2.64 | 47.92 |
| Left lung | 59.41 | 47.82 | 1.15 ± 0.056 | 0.95 | 17.34 | 1.85 | 60.28 |
| Stomach | 50.61 | 40.49 | 1.78 ± 0.051 | 1.50 | 15.65 | 2.55 | 43.44 |
| Liver | 40.46 | 28.01 | 2.59 ± 0.066 | 2.86 | 10.52 | 3.99 | 54.02 |
| Colon | 33.81 | 23.60 | 4.69 ± 0.081 | 4.43 | 5.65 | 5.71 | 21.64 |
| Esophagus/thyroid | 59.26 | 43.97 | 1.31 ± 0.06 | 1.02 | 22.35 | 1.86 | 41.36 |
| Bladder | 33.43 | 25.32 | 6.36 ± 0.089 | 5.57 | 12.39 | 5.84 | 8.22 |
| Rectum | 33.47 | 25.35 | 5.75 ± 0.085 | 5.61 | 2.45 | 5.82 | 1.26 |
| Breast | 50.59 | 35.68 | 2.01 ± 0.066 | 1.61 | 20.06 | 2.55 | 26.72 |
| Gonads | 36.54 | 28.05 | 4.36 ± 0.074 | 4.14 | 4.99 | 4.89 | 12.14 |
5. Discussion
We developed a simple analytical model to predict H/D values in air and a water phantom for PSPT. The analytical model takes into account two distributed sources, neutron dose divergence, attenuation and scatter. The results of our study show that the accuracy of the new analytical model is comparable to the accuracy of typical neutron simulations or measurements.
In air, both the analytical model from Zheng et al (2007) and the new model developed in this work predicted H/D well near the central axis, while the new model provided better accuracy farther from the central beam axis. These findings revealed that an OAF correction should be taken into account. With the introduction of a water phantom, the new model gave overall better agreement than the old analytical model near the central axis regions and in distal regions. These results revealed that the AF and OAF correction are necessary. Overall, the result of this study suggest the potential for a simple analytical model to predict H/D values, in air or a water phantom, with sufficient accuracy for many practical research applications.
The analytical models provided reasonable accuracy in predicting H/D values in an anatomical male phantom with simplified phantom surface and uniform tissue density. We did not attempt to take into account the irregularity of real patient surface or variations in tissue density, as are routinely accomplished with ray tracing in commercial treatment planning systems. However, the simple model is applicable for estimation of H/D values in air or in box-shaped phantoms. Our study had several limitations. First, we only calculated H/D values based on a 250 MeV pristine proton beam, while most treatments utilize a spread-out Bragg peak (SOBP). However, previous studies showed that the effect of SOBP width is relatively small (Zheng et al 2008). Future studies are needed to extend the analytical model to take into account different treatment options such as beam energies, field size and spread-out Bragg peak width. Second, we only used a closed aperture in the simulations for simplicity, and it is also a conservative estimation of stray neutron dose (Zheng et al 2007, 2009). Third, our model is based on the PSPT unit at our institution; however, the modeling method reported here should be applicable with minor adaptation to other PSPT units.
Our method may find application in estimating out-of-field patient dose and in shielding requirements, especially in situations where measurements or Monte Carlo modeling are not feasible. Even when other dose estimation methods are feasible, the analytical model can also be used as an independent cross-check. Another potential application of our model is to extend the capability of current commercial treatment planning systems to calculate the out-of-field dose delivered to the patient during radiation treatment. The stray radiation exposures calculated by the analytical model may eventually be used in personalized patient risk assessments.
Although our study focused on PSPT, it might be possible to extend our model to spot scanning proton therapy. With the Monte Carlo method, it is possible to separate neutron dose into external neutrons and internal neutrons (Taddei et al 2009). However, the size and location of sources of internal neutrons (the predominant source in spot scanning beams) are highly variable and may pose considerable challenges to the model analytically.
Acknowledgments
The authors are grateful to Kathryn Carnes and John McCool for their assistance in preparing this manuscript and John Eley for helpful discussions. This work was supported in part by a Sowell-Huggins scholarship (RZ), by the National Cancer Institute (awards 1 R01 CA131463-01A1) and Northern Illinois University through a subcontract of a Department of Defense contract (award W81XWH-08-1-0205) (WDN) and by the Fogarty International Center (award K01TW008409) (PJT). The content in this paper is solely the responsibility of the authors and does not necessarily represent the official views of the sponsors.
References
- Agosteo S, Birattari C, Caravaggio M, Silari M, Tosi G. Secondary neutron and photon dose in proton therapy. Radiother. Oncol. 1998;48:293–305. doi: 10.1016/s0167-8140(98)00049-8. [DOI] [PubMed] [Google Scholar]
- Athar BS, Paganetti H. Neutron dose equivalents and associated lifetime cancer incidence risks for head and neck and spinal proton therapy. Phys. Med. Biol. 2009;54:4907–4926. doi: 10.1088/0031-9155/54/16/005. [DOI] [PubMed] [Google Scholar]
- Billings MP, Yucker WR. Summary final report: the computerized anatomical man (CAM) Huntington Beach, CA: McDonnell Douglas Corporation; Report MDC G4655. 1973
- Binns PJ, Hough JH. Secondary dose exposures during 200 MeV proton therapy. Radiat. Prot. Dosim. 1997;70:441–444. [Google Scholar]
- Fontenot J, Taddei P, Zheng Y, Mirkovic D, Jordan T, Newhauser W. Dose equivalent and effective dose from stray radiation during passively scattered proton radiotherapy for prostate cancer. Phys. Med. Biol. 2008;53:1677–1688. doi: 10.1088/0031-9155/53/6/012. [DOI] [PubMed] [Google Scholar]
- Fontenot JD, Lee AK, Newhauser WD. Risk of secondary malignant neoplasms from proton therapy and intensity-modulated x-ray therapy for early-stage prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2009;74:616–622. doi: 10.1016/j.ijrobp.2009.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall EJ. Intensity-modulated radiation therapy, protons, and the risk of second cancers. Int. J. Radiat. Oncol. Biol. Phys. 2006;65:1–7. doi: 10.1016/j.ijrobp.2006.01.027. [DOI] [PubMed] [Google Scholar]
- ICRP. Conversion coefficients for use in radiological protection against external radiation. ICRP Publication 74 Ann. ICRP. 1996;26:1–205. [PubMed] [Google Scholar]
- Mesoloras G, Sandison GA, Stewart RD, Farr JB, Hsi WC. Neutron scattered dose equivalent to a fetus from proton radiotherapy of the mother. Med. Phys. 2006;33:2479–2490. doi: 10.1118/1.2207147. [DOI] [PubMed] [Google Scholar]
- Miralbell R, Lomax A, Cella L, Schneider U. Potential reduction of the incidence of radiation-induced second cancers by using proton beams in the treatment of pediatric tumors. Int. J. Radiat. Oncol. Biol. Phys. 2002;54:824–829. doi: 10.1016/s0360-3016(02)02982-6. [DOI] [PubMed] [Google Scholar]
- Moyers M, Benton E, Ghebremedhin A, Coutrakon G. Leakage and scatter radiation from a double scattering based proton beamline. Med. Phys. 2008;35:128–144. doi: 10.1118/1.2805086. [DOI] [PubMed] [Google Scholar]
- Newhauser WD, et al. The risk of developing a second cancer after receiving craniospinal proton irradiation. Phys. Med. Biol. 2009;54:2277–2291. doi: 10.1088/0031-9155/54/8/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhauser WD, Fontenot J, Zheng Y, Polf J, Titt U, Koch N, Zhang X, Mohan R. Monte Carlo simulations for configuring and testing an analytical proton dose-calculation algorithm. Phys. Med. Biol. 2007;52:4569–4584. doi: 10.1088/0031-9155/52/15/014. [DOI] [PubMed] [Google Scholar]
- Newhauser WD, Zheng Y, Taddei P, Mirkovic D, Fontenot JD, Giebeler A, Zhang R, Titt U, Mohan R. Monte Carlo proton treatment planning calculations. Trans. Am. Nucl. Soc. 2008;99:63–64. [Google Scholar]
- Pelowiz DBE. MCNPX User’s Manual Version 2.50 LA-CP-05-0369. Los Alamos, NM: Los Alamos National Laboratory; 2005. [Google Scholar]
- Pérez-Andújar A, Newhauser WD, DeLuca PM., Jr Neutron production from beam-modifying devices in a modern double scattering proton therapy beam delivery system. Phys. Med. Biol. 2009;54:993–1008. doi: 10.1088/0031-9155/54/4/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polf JC, Newhauser WD. Calculations of neutron dose equivalent exposures from range-modulated proton therapy beams. Phys. Med. Biol. 2005;50:3859–3873. doi: 10.1088/0031-9155/50/16/014. [DOI] [PubMed] [Google Scholar]
- Roy SC, Sandison GA. Scattered neutron dose equivalent to a fetus from proton therapy of the mother. Radiat. Phys. Chem. 2004;71:997–998. [Google Scholar]
- Schneider U, Fiechtner A, Besserer J, Lomax A. Neutron dose from prostheses material during radiotherapy with protons and photons. Phys. Med. Biol. 2004;49:N119–N124. doi: 10.1088/0031-9155/49/9/n01. [DOI] [PubMed] [Google Scholar]
- Shin D, Yoon M, Kwark J, Shin J, Lee SB, Park SY, Par S, Kim DY, Cho KH. Secondary neutron doses for several beam configurations for proton therapy. Int. J. Radiat. Oncol. Biol. Phys. 2009;74:260–265. doi: 10.1016/j.ijrobp.2008.10.090. [DOI] [PubMed] [Google Scholar]
- Taddei P, Fontenot JD, Zheng Y, Mirkovic D, Lee AK, Titt U, Newhauser WD. Reducing stray radiation dose to patients receiving passively scattered proton radiotherapy for prostate cancer. Phys. Med. Biol. 2008;53:2131–2147. doi: 10.1088/0031-9155/53/8/009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei PJ, Mirkovic D, Fontenot JD, Giebeler A, Zheng Y, Kornguth D, Mohan R, Newhauser WD. Stray radiation dose and second cancer risk for a pediatric patient receiving craniospinal irradiation with proton beams. Phys. Med. Biol. 2009;54:2259–2275. doi: 10.1088/0031-9155/54/8/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tayama R, Fujita Y, Tadokoro M, Fujimaki H, Sakae T, Terunuma T. Measurement of neutron dose distribution for a passively-scattered nozzle at the Proton Medical Research Center (PMRC) Nucl. Instrum. Methods A. 2006;564:532–536. [Google Scholar]
- Wroe A, Rosenfeld A, Schulte R. Out-of-field dose equivalents delivered by proton therapy of prostate cancer. Med. Phys. 2007;34:3449–3456. doi: 10.1118/1.2759839. [DOI] [PubMed] [Google Scholar]
- Yan X, Titt U, Koehler AM, Newhauser WD. Measurement of neutron dose equivalent to proton therapy patients outside of the proton radiation field. Nucl. Instrum. Methods A. 2002;476:429–434. [Google Scholar]
- Yonai S, et al. Measurement of neutron ambient dose equivalent in passive carbon-ion and proton radiotherapies. Med. Phys. 2008;35:4782–4792. doi: 10.1118/1.2989019. [DOI] [PubMed] [Google Scholar]
- Zacharatou Jarlskog C, Lee C, Bolch WE, Xu XG, Paganetti H. Assessment of organ specific neutron doses in proton therapy using whole-body age-dependent voxel phantoms. Phys. Med. Biol. 2008;53:693–717. doi: 10.1088/0031-9155/53/3/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Fontenot J, Taddei P, Mirkovic D, Newhauser W. Monte Carlo simulations of neutron spectral fluence, radiation weighting factor and ambient dose equivalent for a passively scattered proton therapy unit. Phys. Med. Biol. 2008;53:187–201. doi: 10.1088/0031-9155/53/1/013. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Newhauser W, Fontenot J, Taddei P, Mohan R. Monte Carlo study of neutron dose equivalent during passively-scattered proton therapy. Phys. Med. Biol. 2007;52:4481–4496. doi: 10.1088/0031-9155/52/15/008. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Newhauser W, Klein E, Low D. Monte Carlo simulation of neutron spectral fluence and dose equivalent for use in shielding a proton therapy vault. Phys. Med. Biol. 2009;54:6943–6957. doi: 10.1088/0031-9155/54/22/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zytkovicz A, Daftari I, Phillips TL, Chuang CF, Verhey L, Petti PL. Peripheral dose in ocular treatments with CyberKnife and Gamma Knife radiosurgery compared to proton radiotherapy. Phys. Med. Biol. 2007;52:5957–5971. doi: 10.1088/0031-9155/52/19/016. [DOI] [PubMed] [Google Scholar]