Abstract
Multiple sclerosis (MS) affects both white matter and gray matter (GM). Measurement of GM volumes is a particularly useful method to estimate the total extent of GM tissue damage because it can be done with conventional magnetic resonance images (MRI). Many algorithms exist for segmentation of GM, but none were specifically designed to handle issues associated with MS, such as atrophy and the effects that MS lesions may have on the classification of GM. A new GM segmentation algorithm has been developed specifically for calculation of GM volumes in MS patients. The new algorithm uses a combination of intensity, anatomical, and morphological probability maps. Several validation tests were performed to evaluate the algorithm in terms of accuracy, reproducibility, and sensitivity to MS lesions. The accuracy tests resulted in error rates of 1.2% and 3.1% for comparisons to BrainWeb and manual tracings, respectively. Similarity indices indicated excellent agreement with the BrainWeb segmentation (0.858–0.975, for various levels of noise and rf inhomogeneity). The scan-rescan reproducibility test resulted in a mean coefficient of variation of 1.1% for GM fraction. Tests of the effects of varying the size of MS lesions revealed a moderate and consistent dependence of GM volumes on T2 lesion volume, which suggests that GM volumes should be corrected for T2 lesion volumes using a simple scale factor in order to eliminate this technical artifact. The new segmentation algorithm can be used for improved measurement of GM volumes in MS patients, and is particularly applicable to retrospective datasets.
Introduction
Determination of gray matter (GM) volume in brain magnetic resonance images (MRI) has become an important measurement tool for multiple sclerosis (MS) patient monitoring and research. Previously, MS was considered primarily a white matter (WM) disease, with prominent focal regions of demyelination visible by macroscopic examination of the tissue and on MRI. Histological studies of MS brain tissue have shown that MS lesions are also located in the gray matter and that these GM lesions make up a substantial proportion of overall tissue damage due to MS (Peterson 2001; Kutzelnig, 2005). While there are new MRI techniques that allow visualization of cortical lesions, such as fluid-attenuated inversion recovery (Bakshi 2001), double inversion recovery (Geurts 2005), averaged high resolution T1-weighted images (Bagnato 2006), and phase-sensitive inversion recovery (Nelson 2007), GM pathology is difficult to measure in vivo because most GM lesions are not visible on conventional MRI (Pirko 2007). Measurement of GM volume loss provides an alternative, indirect measure of GM pathology. Previous studies have shown that GM atrophy is detectable at all stages of MS (Chard 2004; Ge 2001; Sastre-Garriga 2004; Tiberio 2005) and is correlated with disability (Chen 2004; De Stefano 2003). These studies suggest that GM measurements are clinically relevant, provide important insights about disease progression, and may be useful in the evaluation the efficacy of new therapies.
To measure cross-sectional differences and changes over time in GM volumes, accurate segmentation methods must be used. A variety of different approaches to brain tissue segmentation have been described in the literature. Few algorithms rely solely on image intensity, (Schnack 2001) because these approaches are overly sensitive to image artifacts such as radiofrequency inhomogeneity, B0 inhomogeneity, and aliasing, and can not adequately account for overlapping intensity distributions across structures. Therefore, to improve segmentation accuracy, most tissue segmentation algorithms combine intensity information with other techniques, such as the use of a priori anatomic information (Chalana 2001; Van Leemput 1999) or edge information through deformable contours (Davatzikos 1995; Xu 1999; Zeng 1999). Intensity information is analyzed differently in each approach, including Gaussian mixture models (Ashburner 2005; Andersen 2002; Marroquin 2002; Zhang 2001), discriminant analysis (Amato 2003), k-nearest neighbor classification (Mohamed 1999), and fuzzy c-means clustering (Pham 1999; Suckling 1999; Ahmed 2002; Zhu 2003; Zhou 2007). The use of multiple images has significant advantages over a single image because the different contrasts can be enhanced between tissues. For example, fluid attenuated inversion recovery (FLAIR) images have desirable contrast between MS lesions and the normal-appearing brain tissue and can be combined with other images to obtain gray/white matter segmentation (Sajja 2006).
There are a few widely available and commonly used brain tissue segmentation methods that use both intensity and a priori anatomic information. These algorithms, such as the segmentation tool in SPM (Ashburner 2005) and FAST in FSL (Smith 2004), have been designed for general use, and therefore, are not necessarily optimized for specific pulse sequences or for application to images from patients with a specific disease. For example, the use of general-use programs to segment MR images of MS patients often results in misclassification of MS lesions as gray matter due to overlapping intensities, which then requires time-consuming manual editing and introduces operator variability into the measurements. These methods are also prone to classification errors due to partial volume effects between MS lesions and normal tissue. Furthermore, for retrospective image analysis, where image data may not have been acquired using optimal sequences for use with one of the widely available segmentation tools, a customized segmentation method may be required to obtain the most accurate results.
In this report, we present a new automated method to measure gray and white matter tissue volumes from MRIs using a probability-based tissue segmentation algorithm that incorporates intensity, anatomic, and morphologic information. The method has been designed specifically for application to retrospective analysis of images from multiple sclerosis patients. Results of tests to determine reliability and accuracy of the new method are also reported.
Materials and Methods
Algorithm Description
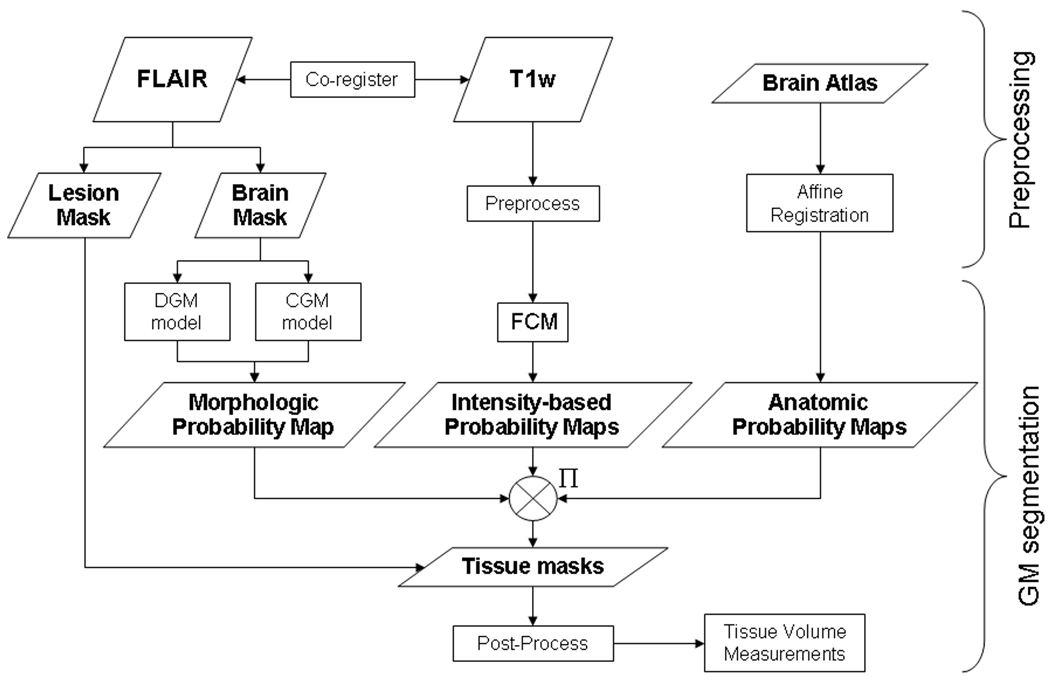
The overall flow chart, including pre-processing steps and gray matter segmentation steps, is shown in Figure 1. Prior to GM segmentation, the brain is isolated from non-brain tissues in fluid attenuated inversion recovery (FLAIR) images using a fully automated knowledge-based segmentation method, as previously described (Fisher 1997). The outer contour of the brain, a smoothed surface that includes the ventricles and other cerebrospinal fluid surrounding the brain, is also determined in this step, and the total brain parenchymal volume and volume within the outer contour are determined. In images of MS patients, T2 hyperintense white matter lesions are segmented in the FLAIR images using a modified version of the iterated conditional modes algorithm (Besag 1986).
Figure 1.
Overall segmentation process flow starting with the input FLAIR and T1-weighted images and the pre-labeled brain atlas, and ending with the segmented gray matter mask and volume. (DGM = deep gray matter, CGM = cortical gray matter, FCM = fuzzy c-means classification, GM = gray matter)
T1-weighted images, and/or any other images to be used in the tissue classification step, are pre-processed by anisotropic diffusion filtering (ADF) (Perona 1990), N3 intensity variation correction (Sled 1998), and inter-slice intensity correction programs. The inter-slice intensity correction algorithm estimates and reduces the loss of signal due to intensity drop-off in the superior and inferior slices. A single multiplication factor is estimated for each slice by measuring the mode of the pixel-by-pixel ratios between contiguous slices within the brain. FLAIR and T1-weighted images are co-registered using a normalized mutual information algorithm (Pluim 2003) with downhill simplex optimization (Press 1988). Patient motion between 2 interleaved sets is corrected using the same normalized mutual information registration algorithm by separating, registering, and re-combining the two interleaved image sets.
After preprocessing, voxels within the brain mask are classified into gray matter, white matter and cerebrospinal fluid. The classification algorithm uses a probability-based method where intensity, anatomic, and morphologic information are all incorporated to derive a final GM segmentation.
To calculate the intensity-based probability map, the grayscale values for all normal-appearing brain voxels (i.e. voxels included in the brain mask, but not included in the lesion mask) are analyzed with a modified fuzzy c-means (FCM) clustering method to generate probability maps for each tissue type. For this study, FCM was applied to the T1-weighted images. In addition to the standard FCM, our algorithm includes additional parameters to factor in local information, as shown:
| Eq. 1 |
where uik is the fuzzy membership of tissue i at voxel k, calculated from xk, which is the intensity at voxel k, and vi, which is the mean intensity for tissue i. The fuzzy membership with local information is u’ik, where uikn is the fuzzy membership for class i of voxel k’s local neighbor n. The additional parameters are w that weights one tissue over the other to account for various tissue intensity characteristics, and β, that determines the influence of the fuzzy memberships of local neighbors. Since cortical gray matter can be very thin, a 2D local region with 4 neighbors was used. The parameters β and w were determined based on the best results obtained as compared to manual tracing in terms of the similarity index (Zijdenbos 1994). Similarity index was calculated by Equation 2.
| Eq. 2 |
TP, FP, and FN are the number of true positive (correctly labeled as GM), false positives (incorrectly labeled as GM) and false negative (incorrectly not labeled as GM) voxels. The downhill simplex algorithm was used for optimization, where the cost function was the average similarity index between the automatically generated masks and the manually traced GM and WM masks. In this way, parameter β was set to 0.1, and w for GM and WM were calculated to be 0.85 and 0.10, respectively.
An individualized anatomy-based probability map is derived from the Harvard Brain Atlas (Kikinis 1996). The atlas was first converted to a general GM probability map by creating a mask image containing only GM structures and then applying morphologic operators and Gaussian filters with spherical 3D kernel of 2mm radius to smooth the result. The converted atlas-based GM probability map is individualized by aligning it with each patient’s MRI using a 12 degree-of-freedom affine transformation.
The third GM probability map, the individualized morphological probability map, is created from morphologic models of the cortical and deep GM. The cortical GM model represents the probability of cortical GM as a function of the distance from the approximated brain surface. This brain surface is determined by the mid-sagittal plane and the edges on initial brain segmentation excluding the lateral ventricle edges. The lateral ventricles are segmented by a series of morphologic operators (dilation, erosion, median filter, and seed fill) on the segmented brain mask. The mid-sagittal segmentation is achieved through minimization of left and right hemispheric intensity differences. The morphologic deep GM model consists of 3D ellipsoids with shapes and locations that are based on functions of the directions and lengths of the principal axes of the left and right lateral ventricles and the centroid positions of each cerebral hemisphere. The ellipsoids cover all the deep GM structures excluding the diencephalon, which can be captured by the cortical GM model because it borders the brain surface.
In the final step, a combined probability image is created as the product of all three GM probability maps. Then the binary GM mask is generated by setting a threshold of 0.5 on the combined probability map. The final GM tissue volume is calculated after a linear 3-class partial volume correction (Santago 1990). The normalized GM volume is calculated as: Gray matter fraction = [gray matter volume] / [outer contour volume].
Validation
Four different types of tests were performed to evaluate the performance of the new GM segmentation algorithm: (1) segmentation of simulated MRI datasets and comparison to correct results to determine accuracy; (2) segmentation of real MRI datasets and comparison to results from manual tracings as another way to evaluate accuracy; (3) segmentation of scan-rescan images to determine the reproducibility; and (4) segmentation of the same image with simulated MS lesions of various volumes to determine the effects of lesions.
(1) Accuracy Tests with Simulated MRIs
We used simulated MRI data (BrainWeb, http://www.bic.mni.mcgill.ca/brainweb/; Collins 1998) to evaluate the accuracy of segmentation in terms of volumetric errors and similarity indices by comparing our segmented tissue masks to the gold standard tissue masks. The segmentation algorithm was evaluated for the effects of rf inhomogeneities at 0%, 20%, and 40 using the similarity index (Equation 2).
(2) Accuracy Tests with Manually Traced Real MRIs
We used MRIs from 3 MS patients and 3 normal healthy controls to evaluate the segmentation accuracy in real MRIs that were acquired in 2000 as part of another study. The images were acquired on a 1.5T Siemens Vision scanner using a circularly polarized head coil, and included a FLAIR [30 contiguous axial slices, echo time (TE) = 105ms, repetition time (TR) = 6000ms, inversion time (TI) = 2000ms, 2 excitations (NEX), field of view (FOV) = 172mm×230mm, matrix size = 192×256, to yield an in-plane resolution = 0.9×0.9mm, and slice thickness 5.0mm] and a T1-weighted spin echo [30 contiguous axial slices, TE = 20ms, TR = 800ms, 1 NEX, FOV = 172mm×230mm, matrix size of 192×256, in-plane resolution 0.9×0.9mm, and slice thickness 5.0mm].
The images were processed through our automated GM segmentation algorithm and, separately, the GM was manually traced in each image. Volume errors and similarity indices were calculated using the manual segmentation as a gold standard. Pearson correlation coefficients were determined between volumes calculated from manual and automated segmentation. The leave-one-out approach was used to avoid testing and training on the same dataset. Because we originally optimized the segmentation parameters (w and β) using these same manually traced images, we could not use these optimized parameters for this part of the validation. Instead, for each of the six cases, we optimized the parameters separately using only the other five cases and excluding the test data.
(3) Reproducibility Tests with Repeated MRIs
For a separate study, MRIs were acquired from 9 MS patients who were imaged at 3 different time points within two weeks. Each image set was processed separately through the automated GM segmentation algorithm. The reproducibility of the algorithm was evaluated by calculating the coefficient of variation of GM volumes calculated from the repeated images for each patient.
(4) Tests for Effects of MS Lesions on Segmentation
Finally, the segmentation algorithm was tested for the effects of white matter lesions in the FLAIR images. Masks of segmented MS lesions were morphologically dilated with 3D spherical kernels of various sizes (1.2, 1.5, 1.9, 2.1, 2.6, 2.8, 2.9, 3.5, and 3.9 mm) in order to simulate different sized MS lesions within the same MRIs. The dilated lesion masks were masked by the brain tissue mask to ensure that “lesion” voxels did not extend into non-parenchymal space. The automated segmentation was then performed on the same MRI repeatedly using different lesion masks and GM volume was measured. This testing was repeated in 18 different MS patients to ensure that lesions of various starting sizes and locations were included. Linear regression was performed to evaluate the dependence of GM volumes on T2 lesion volumes.
Results
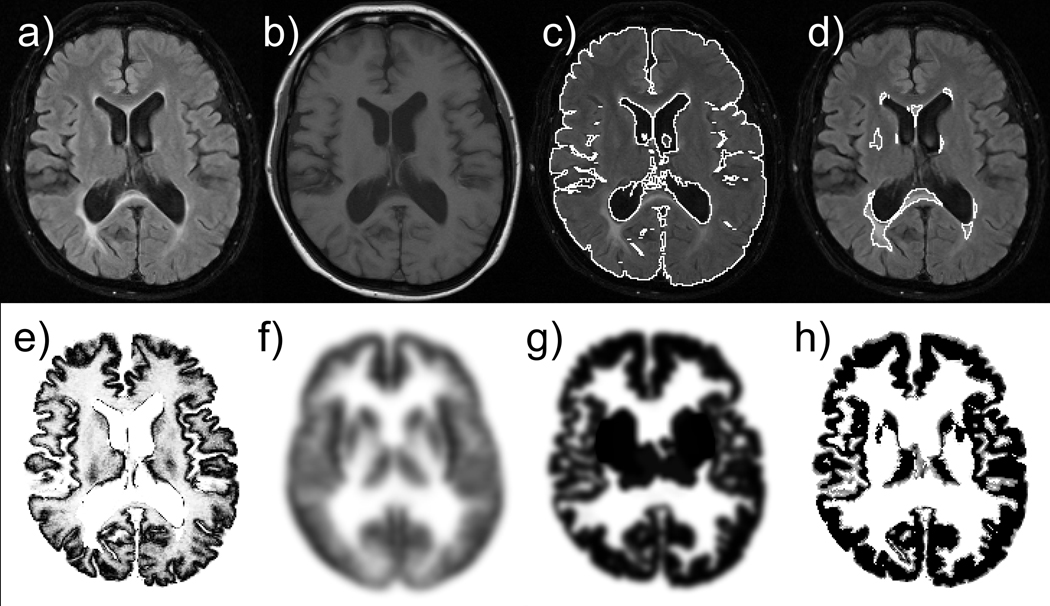
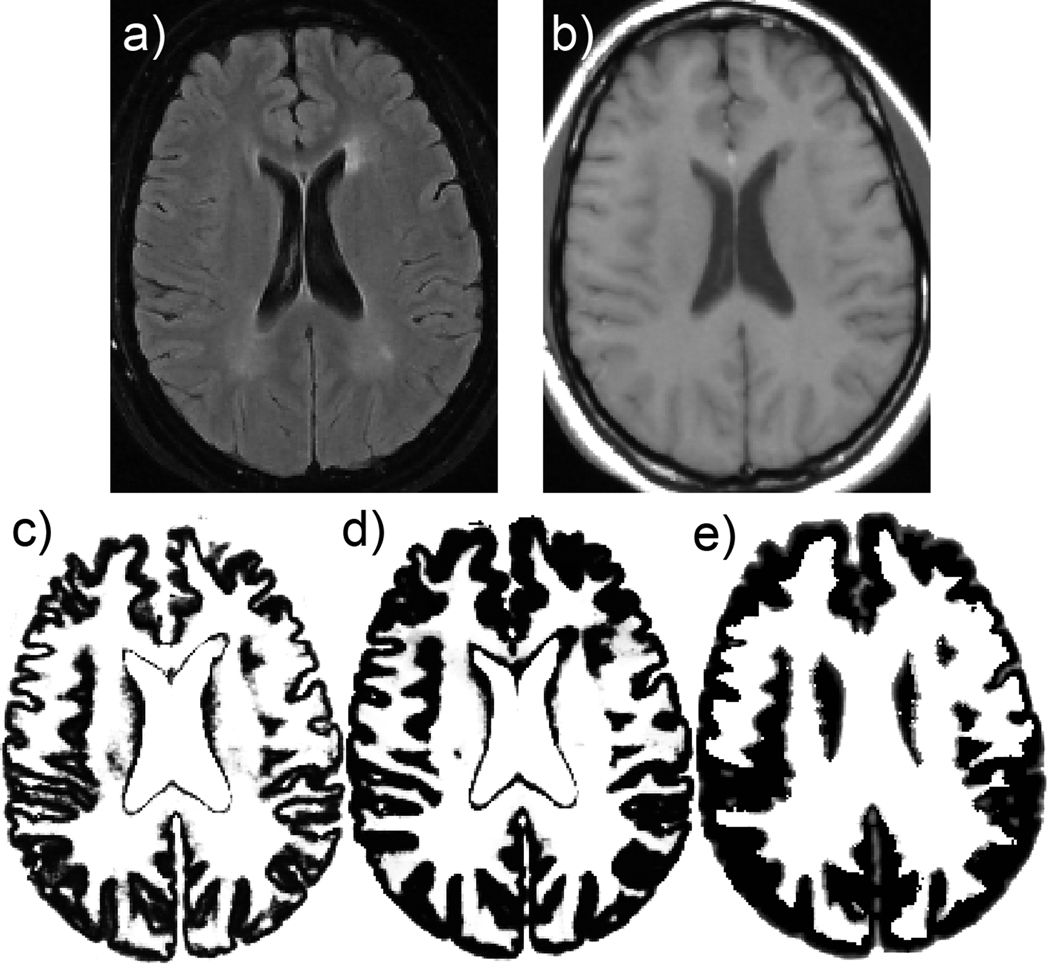
An example of a set of input (a–b), intermediate images (c–g), and final segmentation results (h) is shown in Figure 2. Figure 3 compares results obtained from our new method and two commonly available segmentation methods (FAST version 3.51 in FSL and SPM5). Note that our method successfully classified the periventricular MS lesion as WM whereas the other methods misclassified the lesion as GM or CSF.
Figure 2.
Example of input (a–b), intermediate (c–g) and final segmentation (h) images: a) input FLAIR image, b) input T1-weighted image, c) brain segmentation, d) lesion segmentation, e) intensity-based probability map, f) anatomy-based probability map, g) morphology-based probability map, and h) resulting GM mask.
Figure 3.
Comparison with commonly available segmentation methods: a) input FLAIR, b) input T1-weighted image, c) SPM5 GM, d) FSL GM, e) new method.
(1) Accuracy Results with Simulated MRIs
Using BrainWeb simulated MR images, the error was 1.20% for GM volume at 3% noise and 20% RF inhomogeneity level. The similarity index for GM mask images was 0.964. Similarity index of 0.7 or above is considered good agreement. The new segmentation program performed well in the presence of RF inhomogeneity and the various noise levels, as shown in Table 1.
Table 1.
GM similarity indices at various RF inhomogeneity and noise levels in accuracy test using BrainWeb simulation images.
| RF inhomogeneity levels | |||||
|---|---|---|---|---|---|
| 0% | 20% | 40% | Average | ||
| Noise levels | 0% | 0.974 | 0.975 | 0.967 | 0.972 |
| 1% | 0.971 | 0.974 | 0.966 | 0.970 | |
| 3% | 0.962 | 0.964 | 0.956 | 0.960 | |
| 5% | 0.945 | 0.949 | 0.941 | 0.945 | |
| 7% | 0.911 | 0.920 | 0.913 | 0.915 | |
| 9% | 0.866 | 0.873 | 0.858 | 0.866 | |
| Average | 0.938 | 0.943 | 0.933 | 0.938 | |
(2) Accuracy Tests with Manually Traced Real MRIs
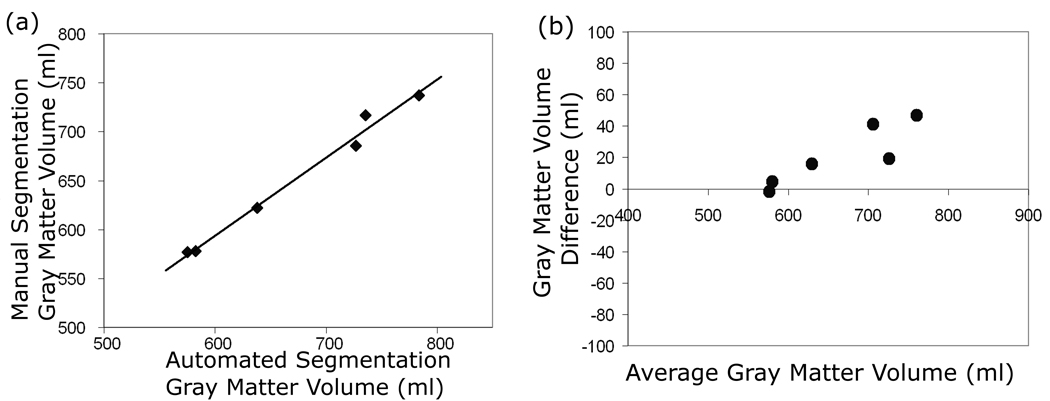
The comparison with manually traced segmentation showed good agreement. The mean absolute error (s.d.) for GM volume was 3.1% (2.6). The automated and manually derived tissue volumes for each image set were highly correlated (r=0.993), however, the Bland-Altman plot demonstrates that there is a bias toward higher differences in larger brains (Figure 4). The similarity indices of automated segmentation compared to manually tracing were good. In controls, the mean similarity index was 0.841, and in MS patients, the mean similarity index was 0.836.
Figure 4.
(a) Plot of GM volumes from manual versus automatic segmentation in 3 MS and 3 healthy normal control subjects. (b) Bland-Altman plot of the same subjects.
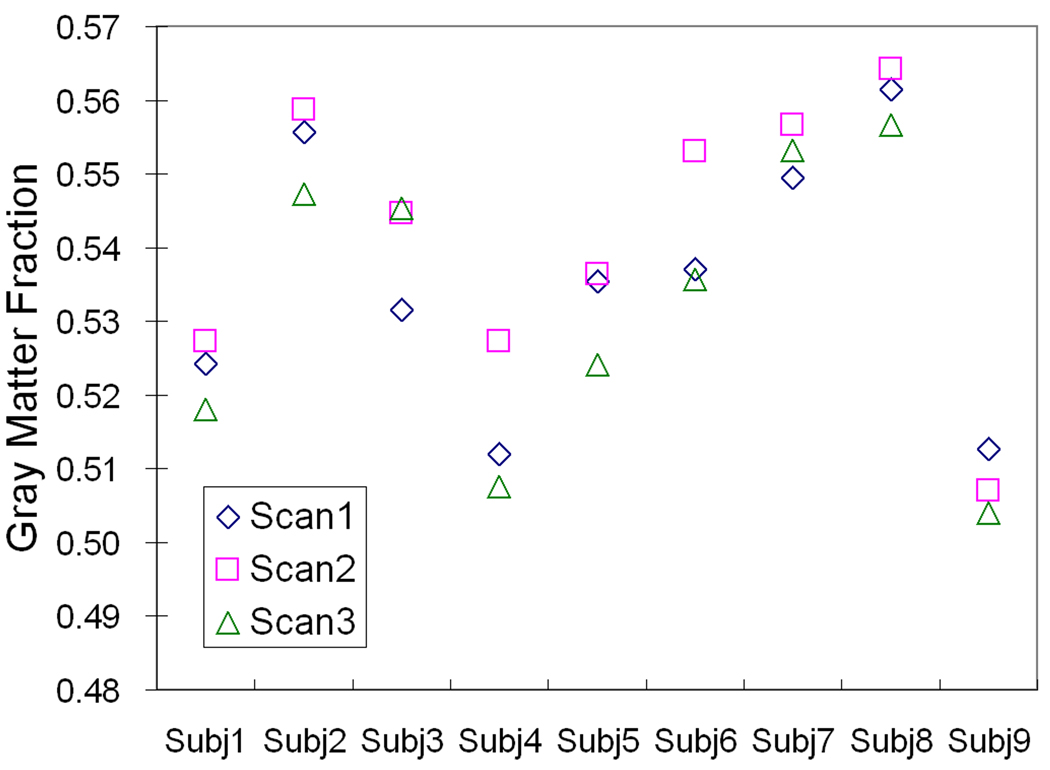
(3) Reproducibility Results with Repeated MRIs
The mean coefficient of variation for GM volumes obtained from 3 repeated MRIs was 1.0%. The coefficient of variation for gray matter fractions was 1.1%. The reproducibility data are shown in Figure 5.
Figure 5.
Gray matter fractions measured from scan-rescan images acquired on 9 MS patients. Each patient was scanned 3 times over a 2 week period.
(4) Effects of MS Lesions on Segmentation
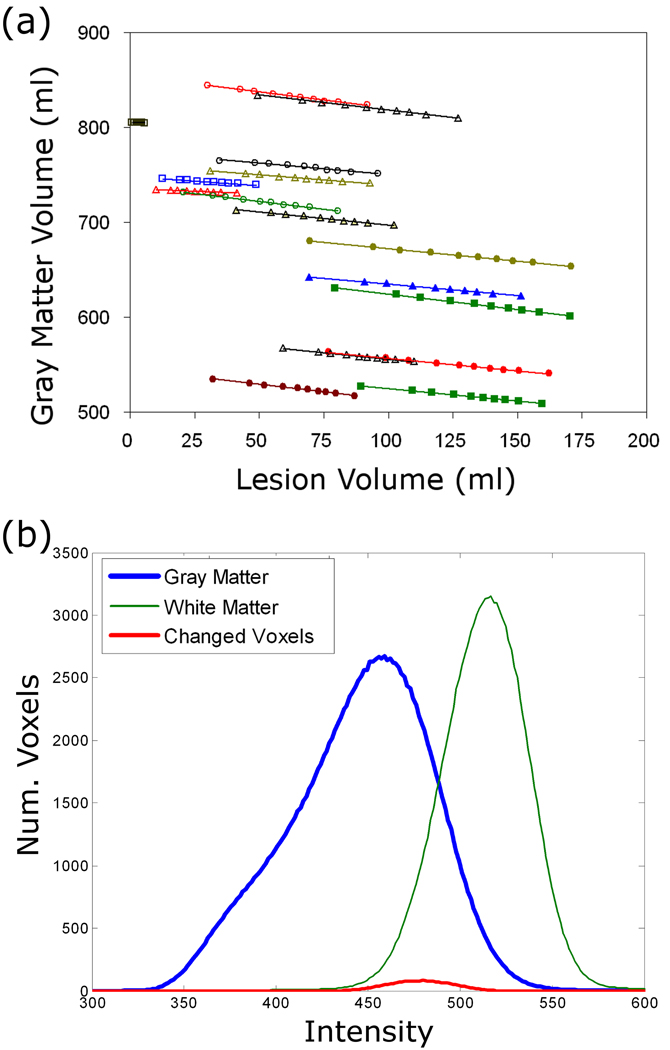
The effects of lesion size are shown in Figure 6 for all 18 MS patients. There is a clear and fairly consistent effect of total T2 lesion volume on the measured GM volume for each case. As the lesion size was systematically increased, the gray matter volume decreased. The lesion volume and the gray matter volume were inversely proportional with a mean (s.d.) slope of −0.26 (0.07). As shown in Figure 6b, this GM volume loss was caused by slight changes in fuzzy membership values for the voxels with intermediate intensities between GM and WM as the lesion sizes were increased.
Figure 6.
a) Effect of lesion size on automated gray matter volume measurements in 18 different MS patients where the average slope was −0.26. b) Histogram from GM, WM and the GM region that became WM when the lesion size increased during the simulation.
Discussion
This work describes a new, fully automated method for GM segmentation in brain MRIs that was specifically designed for MS patients. The major strength of the method is that it can be applied to analyze routine clinical MRIs and for retrospective analyses, as shown in the validation studies described here. Clinical quality MRIs commonly include conventional T1-weighted and FLAIR or proton-density/T2-weighted image sets, and the proposed method takes advantage of their different tissue contrasts. While there are accurate, sophisticated methods available to analyze high quality MRIs, (Ashburner 2005, Dale 1999) it may not always be feasible to acquire images of sufficient quality for such methods, as the acquisition times can be prohibitive when combined with other required scans. Furthermore, most of the newer techniques that require high contrast, high resolution images would not obtain reliable segmentation results with images acquired from previous MS clinical trials. There have been very few attempts to analyze routine clinical or previously acquired MRIs with suboptimal quality by today’s standards.
The new GM segmentation method combines probability maps derived from intensity statistics, anatomic information, and morphology. The use of both anatomic and morphologic probability maps is a unique aspect of our algorithm. These maps essentially provide patient-specific information about the locations of cortical GM and deep GM structures that is more precise than the use of either the anatomic or morphologic maps provide alone. This is a key step for correct tissue classification in MS brains since T1-hypointense lesions and lesion/WM partial volume voxels would otherwise be misclassified as GM. The misclassification of lesion voxels is a common problem with the application of general-use brain segmentation software, such as SPM, to segment GM in MS patients, and requires time-consuming manual editing to obtain an acceptable segmentation (Sanfilipo 2005). The misclassification of lesions as GM is a potential problem for both cross-sectional and longitudinal studies. In cross-sectional studies, comparison of SPM-derived GM volumes between different subjects without correcting misclassified GM voxels may lead to a result that is actually a composite of both GM and lesion volumes, which, in turn, may lead to misinterpretation of the results. As shown by the “staggering” of the data for each patient in Figure 6(a), initial GM volumes are not strongly correlated to lesion volume, but SPM-derived GM volumes may artificially appear to be correlated to lesion volume if the misclassification of T1 hypointense lesions is left uncorrected. In longitudinal studies, this presents an even bigger problem because MS lesions are highly dynamic, and the misclassified lesion volume change may be even greater than the true GM volume change. By performing the lesion segmentation step separately, masking out the lesions, and combining intensity, anatomic, and morphologic probability maps to segment GM, the misclassification of MS lesions can be avoided.
A related issue which can also adversely affect GM segmentation in MS brains is the misclassification of “dirty white matter”, that is, diffusely abnormal white matter, with intensity on T2-weighted MRI in between that of focal MS lesions and normal-appearing white matter. The T1-weighted spin echo images used here, which are very common in MS clinical trials and routine MRI exams, are not sensitive to dirty white matter, so this was not a problem for our algorithm. Extension of the algorithm for application to proton density / T2-weighted dual echo scans may require modifications to account for potential misclassification of dirty white matter. However, in general, the incorporation of the anatomic and morphologic probability maps also serves to minimize the misclassification of peri-lesional dirty WM.
The use of two different types of prior probability maps, anatomic and morphologic, is also important for segmentation of MS brains because many patients have a significant degree of atrophy, leading to enlargement of the lateral ventricles. For this reason, a simple affine transformation of an anatomic reference, such as a smoothed brain atlas or an average brain data set, would not provide a useful estimate of GM locations, particularly for deep gray matter structures. The morphologic probability map improves GM location estimates because it is derived directly from the patient image data and, therefore, takes into account the degree of brain atrophy for that individual. The use of the morphologic probability map is also much faster than the alternative approach of performing a full non-linear registration to map the atlas to each individual brain.
In order to illustrate one of the advantages of our approach for GM segmentation of MS brains, we included Figure 3, which compares results of our method to those of two widely-used and freely-available segmentation methods: FAST/FSL and SPM. This figure serves to demonstrate that our method successfully avoids the problem of lesion misclassification that plagues other techniques. However, the comparison is not fully justified, because our method utilizes more information as input, requiring both the T1-weighted image and the FLAIR lesion segmentation results. For this reason, we did not include a complete quantitative comparison of the different methods. During our testing, however, we did apply SPM and FAST/FSL to the same brain images that were manually traced. The average similarity indices (standard deviation) were 0.8381 (0.01), 0.7887 (0.04), and 0.7084 (0.08) for our method, SPM, and FSL, respectively. Previously published similarity indices of SPM and FSL with BrainWeb images were 0.934 and 0.90, respectively (Ashburner 2005, and Ferreira da Silva 2007), which are similar to the average SI of 0.94 reported here for our method applied to BrainWeb. Therefore, quantitatively, there is no appreciable difference between the accuracy of the different segmentation techniques. This makes sense given how small the lesion volume is in comparison to whole brain GM volume.
Various tests were performed to evaluate our new algorithm in terms of both numerical results (volumes) and segmented image results (GM masks). The accuracy and reproducibility of our new GM segmentation method were shown to be comparable to those of other published techniques (Chard 2002). It is difficult to directly compare validation results across segmentation techniques because of differences in evaluation methods, patient groups, and MRI acquisition parameters. The simulated MRIs available through BrainWeb offer one way to do direct comparisons. In comparison to other published results using BrainWeb images, our segmentation method performed comparably well (Ashburner 2005; Shattuck 2001; Zhu 2003). For GM segmentation, our method resulted in a similarity index of 0.938 as compared to 0.932 and 0.893 reported by Ashburner using SPM and by Shattuck using a partial volume model.
Another test performed was the comparison to manual tracings of gray matter in real MRIs. This was done because BrainWeb images are slightly unrealistic, with sharper edges between GM, WM, and CSF than what is observed in actual MRI data. While our algorithm clearly agreed well with manually segmented images, the numerical accuracy results were only moderately good, with a mean error rate of 3.1%. This is not surprising given that the “gold standard” for comparison is based on manual tracing, which is known to be error-prone and highly subjective. There was also an observed bias in the comparison between techniques -- the volume difference was greater in larger brains. This bias was found to be due to differences in the ability to distinguish the GM-CSF border in deep sulci in large and small brains. Brains with low gray matter volume typically have a significant degree of whole brain atrophy and vice versa. These brains with significant atrophy have very large sulci with clear GM-CSF edges, whereas those without significant atrophy have ambiguous GM-CSF edges due to partial volume effects in the tight sulcal spaces. The brains that were manually traced for the validation study had a very wide range in brain parenchymal fraction (0.74 to 0.87), and therefore a wide range in GM-CSF separation in the deep sulci, which made this bias evident.
Evaluation of the accuracy of segmentation algorithms is difficult due to the lack of a true gold standard. In this study, the accuracy tests were performed with widely used BrainWeb simulation images and with manually traced images, both of which result in fully quantitative evaluation of algorithm performance for detection of gray matter. To verify that this quantitative evaluation was representative of an expert qualitative review, a neuroradiologist was asked to perform a blinded review of the GM segmentation results for each of the 3 methods shown in Figure 3 as well as the manually traced GM results for 4 brains each. The results showed that our method resulted in acceptable GM segmentation in all cases while some results from other methods were unacceptable due to the misclassifications of lesions as GM and non-gray matter classified as gray matter. The mean subjective scores demonstrated consistency with the quantitative evaluation (manual tracing = 1.1, our method: 2.0, FSL: 2.5, and SPM: 2.5, where 1 = excellent segmentation and 3 = unacceptable results).
The scan-rescan test was performed in order to evaluate the applicability of our segmentation method for longitudinal studies of GM atrophy, wherein the extent of GM tissue loss can be estimated by the difference in GM fractions obtained at 2 different time points. Coefficients of variation of approximately 1% from repeated scans obtained within 2 weeks demonstrate that the algorithm is highly reproducible. The rate of GM atrophy in RRMS patients has been estimated to be about 0.86% per year (Chard 2004). Therefore, this method is most appropriate for application to longitudinal studies of duration 2 years, or longer. For shorter term studies, a more precise method for measurement of GM tissue loss is recommended.
We also performed a test to determine if the GM volume is affected by changes in total T2 lesion volume. We found that there was a systematic and linear relationship between GM volume and T2 lesion volume. Unlike the issue of misclassified lesion voxels discussed above, this effect stems from the fact that unsupervised clustering algorithms, such as fuzzy c-means or SPM, are sensitive to the distribution of the voxel intensities that are fed to it as input. The input intensity distributions determine the final cluster centers and class memberships of each voxel. Thus, even a relatively minor change in the input voxels can have an effect on the final clustering result, because voxels with intensities that fall in the overlap range between GM and WM may switch tissue types as the cluster centers change. In our algorithm, lesion voxels are masked out of the input before we run fuzzy c-means. Therefore, as the lesions grow or shrink, the actual voxels that are used as input in the intensity-based classification step will change, and this was shown by our simulations to have a clear effect on the resulting GM volumes (see Figure 6a). Figure 6b illustrates that the tissue type switching occurs in voxels with intensities between that of GM and WM. We were initially surprised by this observation, because we would expect the distribution of masked WM voxels to be unbiased. However, when the lesion size increases and the lesions are subsequently masked out, the distribution of WM tissue intensities actually shifts downward, closer to the GM cluster, presumably because the voxels that are surrounding the original lesions are not, in fact, a random sample of WM voxels, and their distribution is slightly biased toward brighter WM. With the slightly different distribution, the mean cluster intensities also change slightly, which causes some voxels to switch from GM to WM as the WM cluster shifts closer to GM. For example, some voxels that previously had a GM probability of 0.52, might end up with a GM probability of only 0.48 after the lesions are dilated. This effect occurs in any segmentation algorithms to some extent, and is significant because if left uncorrected in a longitudinal study of MS patients, some portion of the change in GM volume would appear to be correlated to T2 lesion volume and T2 lesion volume changes, just due to this technical issue. We performed a systematic test to calculate the extent and significance of this association, so that in future studies of GM volumes in MS patients, we can correct for the effects of T2 lesions using the calculated mean slope of the GM volume versus T2 lesion volume regression lines.
In summary, our results indicate that the new segmentation algorithm can be used for reliable measurement of GM volumes in normal healthy controls and MS patients even using MRIs of relatively poor quality from a retrospective study. Issues inherent to the analysis of MRIs of MS patients, such as the effects of lesions and whole brain atrophy, have been addressed directly in the design of the algorithm. We are currently using this method to measure GM atrophy in a large longitudinal study of MS patients to determine the kinetics of GM tissue loss. In general, quantitative measurement of gray matter is a valuable research tool due to its relevance in a wide variety of medical conditions in addition to MS, such as schizophrenia (Hulshoff Pol 2002), HIV dementia (Stout 1998), Alzheimer’s disease (Rusinek 1991). This algorithm is likely to be applicable and sensitive to GM tissue loss in a wide range of conditions.
Acknowledgements
This study was supported by the National Institutes of Health NINDS (P01-NS38667). The authors would like to thank Patricia Jagodnik for help with image data management and Smitha Thomas for evaluation of gray matter segmentation results.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahmed MN, Yamany SM, Mohamed N, Farag AA, Moriarty T. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imaging. 2002;21(3):193–199. doi: 10.1109/42.996338. [DOI] [PubMed] [Google Scholar]
- Amato U, Larobina M, Antoniadis A, Alfano B. Segmentation of magnetic resonance brain images through discriminant analysis. J. Neurosci. Methods. 2003;131:65–74. doi: 10.1016/s0165-0270(03)00237-1. [DOI] [PubMed] [Google Scholar]
- Andersen AH, Zhang Z, Avison MJ, Gash DM. Automated segmentation of multispectral brain MR images. J. Neurosci. Methods. 2002;122:13–23. doi: 10.1016/s0165-0270(02)00273-x. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Unified segmentation. NeuroImage. 2005;26(3):839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Bagnato F, Butman JA, Gupta S, Calabrese M, Pezawas L, Ohayon JM, Tovar-Moll F, Riva M, Cao MM, Talagala SL, McFarland HF. In vivo detection of cortical plaques by MR imaging in patients with multiple sclerosis. Am. J. Neuroradiol. 2006;27:2161–2167. [PMC free article] [PubMed] [Google Scholar]
- Bakshi R, Ariyaratana S, Benedict RHB, Jacobs L. Fluid-attenuated inversion recovery magnetic resonance imaging detects cortical and juxtacortical multiple sclerosis lesions. Arch. Neurol. 2001;58:742–748. doi: 10.1001/archneur.58.5.742. [DOI] [PubMed] [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures. J. R. Statist Soc. 1986;48(3):259–302. [Google Scholar]
- Chalana V, Ng L, Rystrom LR, Gee JC, Haynor DR. Validation of brain segmentation and tissue classification algorithm for T1-weighted MR images. Medical Imaging 2001: Image Processing. 2001;4322:1873–1882. [Google Scholar]
- Chard DT, Griffin CM, Rashid W, Davies GR, Altmann DR, Kapoor R, Barker GJ, Thompson AJ, Miller DH. Progressive grey matter atrophy in clinically early relapsing-remitting multiple sclerosis. Mult. Scler. 2004;10(4):387–391. doi: 10.1191/1352458504ms1050oa. [DOI] [PubMed] [Google Scholar]
- Chard DT, Parker GJM, Griffin CMB, Thompson AJ, Miller DH. The reproducibility and sensitivity of brain tissue volume measurements derived from an SPM-based segmentation methodology. J. Magn. Reson. Imag. 2002;15:259–267. doi: 10.1002/jmri.10064. [DOI] [PubMed] [Google Scholar]
- Chen JT, Narayanan S, Collins DL, Smith SM, Matthews PM, Arnold DL. Relating neocortical pathology to disability progression in multiple sclerosis using MRI. NeuroImage. 2004;23(3):1168–1175. doi: 10.1016/j.neuroimage.2004.07.046. [DOI] [PubMed] [Google Scholar]
- Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging. 1998;17(3):463–468. doi: 10.1109/42.712135. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Davatzikos CA, Prince JL. An active contour model for mapping the cortex. IEEE Trans. Med. Imaging. 1995;14(1):65–80. doi: 10.1109/42.370403. [DOI] [PubMed] [Google Scholar]
- De Stefano N, Matthews PM, Filippi M, Agosta F, De Luca M, Bartolozzi ML, Guidi L, Ghezzi A, Montanari E, Cifelli A, Federico A, Smith SM. Evidence of early cortical atrophy in MS: Relevance to white matter changes and disability. Neurology. 2003;60(7):1157–1162. doi: 10.1212/01.wnl.0000055926.69643.03. [DOI] [PubMed] [Google Scholar]
- Ferreira da Silva A Dirichlet process mixture model for brain MRI tissue classification. Medical Image Analysis. 2007;11:169–182. doi: 10.1016/j.media.2006.12.002. [DOI] [PubMed] [Google Scholar]
- Fisher E, Cothren RM, Tkach JA, Masaryk TJ, Cornhill JF. Knowledge-based 3D segmentation of the brain in MR images for quantitative multiple sclerosis lesion tracking. l SPIE Medical Imaging. 1997;3034:599–610. [Google Scholar]
- Ge Y, Grossman RI, Udupa JK, Babb JS, Nyul LG, Kolson DL. Brain atrophy in relapsing-remitting multiple sclerosis: Fractional volumetric analysis of gray matter and white matter. Radiology. 2001;220(3):606–610. doi: 10.1148/radiol.2203001776. [DOI] [PubMed] [Google Scholar]
- Geurts JJ, Pouwels PJ, Uitdehaag BM, Polman CH, Barkhof F, Castelijns JA. Intracortical lesions in multiple sclerosis: improved detection with 3D double inversion-recovery MR imaging. Radiology. 2005;236(1):254–260. doi: 10.1148/radiol.2361040450. [DOI] [PubMed] [Google Scholar]
- Hulshoff Pol HE, Schnack HG, Bertens MG, van Haren NE, van der Tweel I, Staal WG, Baare WF, Kahn RS. Volume changes in gray matter in patients with schizophrenia. Am. J. Psychiatry. 2002;159(2):244–250. doi: 10.1176/appi.ajp.159.2.244. [DOI] [PubMed] [Google Scholar]
- Kikinis R, Shenton ME, Iosifescu DV, McCarley RW, Saiviroonporn P, Hokama HH, Robatino A, Metcalf D, Wible CG, Portas CM, Donnino R, Jolesz FA. A digital brain atlas for surgical planning, model driven segmentation and teaching. IEEE Trans. Vis. Comput. Graph. 1996;2(3):232–241. [Google Scholar]
- Kutzelnigg A, Lassmann H. Cortical lesions and brain atrophy in MS. J. Neurol. Sci. 2005;233:55–59. doi: 10.1016/j.jns.2005.03.027. [DOI] [PubMed] [Google Scholar]
- Marroquin JL, Vemuri BC, Botello S, Calderon F, Fernandez-Bouzas A. An accurate and efficient bayesian method for automatic segmentation of brain MRI. IEEE Trans. Med. Imaging. 2002;21(8):934–945. doi: 10.1109/TMI.2002.803119. [DOI] [PubMed] [Google Scholar]
- Mohamed FB, Vinitski S, Faro SH, Gonzalez CF, Mack J, Iwanaga T. Optimization of tissue segmentation of brain MR images based on multispectral 3D feature maps. Magn. Reson. Imaging. 1999;17:403–409. doi: 10.1016/s0730-725x(98)00181-7. [DOI] [PubMed] [Google Scholar]
- Nelson F, Poonawalla AH, Hou P, Huan F, Wolinsky JS, Narayana PA. Improved identification of intracortical lesions in multiple sclerosis with phase-sensitive inversion recovery in combination with fast double inversion recovery MRI. Am. J. Neuroradiol. 2007;28(9):1645–1649. doi: 10.3174/ajnr.A0645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990;12(7):629–639. [Google Scholar]
- Peterson JW, Bo L, Mork S, et al. Transected neuritis, apoptotic neurons, and reduced inflammation in cortical multiple sclerosis lesions. Ann. Neurol. 2001;50:389–400. doi: 10.1002/ana.1123. [DOI] [PubMed] [Google Scholar]
- Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans. Med. Imaging. 1999;18(9):737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- Pirko I, Lucchinetti CF, Sriram S, Bakshi R. Gray matter involvement in multiple sclerosis. Neurology. 2007;68(9):634–642. doi: 10.1212/01.wnl.0000250267.85698.7a. [DOI] [PubMed] [Google Scholar]
- Pluim JP, Maintz JB, Viergever MA. Mutual-information-based registration of medical images: A survey. IEEE Trans. Med. Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C: The art of scientific computing. 2nd ed. Cambridge: Cambridge University Press; 2002. [Google Scholar]
- Rusinek H, de Leon MJ, George AE, Stylopoulos LA, Chandra R, Smith G, Rand T, Mourino M, Kowalski H. Alzheimer disease: Measuring loss of cerebral gray matter with MR imaging. Radiology. 1991;178(1):109–114. doi: 10.1148/radiology.178.1.1984287. [DOI] [PubMed] [Google Scholar]
- Sajja BR, Datta S, He R, Mehta M, Gupta RK, Wolinsky JS, Narayana PA. Unified approach for multiple sclerosis lesion segmentation on brain MRI. Ann. Biomed. Eng. 2006;34(1):142–151. doi: 10.1007/s10439-005-9009-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanfilipo MP, Benedict RH, Sharma J, Weinstock-Guttman B, Bakshi R. The relationship between whole brain volume and disability in multiple sclerosis: A comparison of normalized gray vs. white matter with misclassification correction. NeuroImage. 2005;26(4):1068–1077. doi: 10.1016/j.neuroimage.2005.03.008. [DOI] [PubMed] [Google Scholar]
- Santago P, Gage HD. Statistical models of partial volume effect. IEEE Trans. Med. Imaging. 1995;4(11):1531–1540. doi: 10.1109/83.469934. [DOI] [PubMed] [Google Scholar]
- Sastre-Garriga J, Ingle GT, Chard DT, Ramio-Torrenta L, Miller DH, Thompson AJ. Grey and white matter atrophy in early clinical stages of primary progressive multiple sclerosis. NeuroImage. 2004;22(1):353–359. doi: 10.1016/j.neuroimage.2004.02.008. [DOI] [PubMed] [Google Scholar]
- Schnack HG, Hulshoff Pol HE, Baaré WFC, Staal WG, Viergever MA, Kahn RS. Automated separation of gray and white matter from MR images of the human brain. NeuroImage. 2001;13:230–237. doi: 10.1006/nimg.2000.0669. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using a partial volume model. NeuroImage. 2001;13:856–876. doi: 10.1006/nimg.2000.0730. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imaging. 1998;18(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Stout JC, Ellis RJ, Jernigan TL, Archibald SL, Abramson I, Wolfson T, McCutchan JA, Wallace MR, Atkinson JH, Grant I. Progressive cerebral volume loss in human immunodeficiency virus infection: A longitudinal volumetric magnetic resonance imaging study. HIV neurobehavioral research center group. Arch. Neurol. 1998;55(2):161–168. doi: 10.1001/archneur.55.2.161. [DOI] [PubMed] [Google Scholar]
- Suckling J, Sigmundsson T, Greenwood K, Bullmore ET. A modified fuzzy clustering algorithm for operator independent brain tissue classification of dual echo MR images. Magn. Reson. Imag. 1999;17:1065–1076. doi: 10.1016/s0730-725x(99)00055-7. [DOI] [PubMed] [Google Scholar]
- Tiberio M, Chard DT, Altmann DR, Davies G, Griffin CM, Rashid W, Sastre-Garriga J, Thompson AJ, Miller DH. Gray and white matter volume changes in early RRMS: A 2-year longitudinal study. Neurology. 2005;64(6):1001–1007. doi: 10.1212/01.WNL.0000154526.22878.30. [DOI] [PubMed] [Google Scholar]
- van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE Trans. Med. Imaging. 1999;18(10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- Xu C, Pham DL, Rettmann ME, Yu DN, Prince JL. Reconstruction of the human cerebral cortex from magnetic resonance images. IEEE Trans. Med. Imaging. 1999;18(6):467–480. doi: 10.1109/42.781013. [DOI] [PubMed] [Google Scholar]
- Zeng X, Staib LH, Schultz RT, Duncan JS. Segmentation and measurement of the cortex from 3-D MR images using coupled-surfaces propagation. IEEE Trans. Med. Imaging. 1999;18(10):927–937. doi: 10.1109/42.811276. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. Morphometric analysis of white matter lesions in MR images: Method and validation. IEEE Trans. Med. Imag. 1994;13:716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]
- Zhou Y, Bai J. Atlas-based fuzzy connectedness segmentation and intensity nonuniformity correction applied to brain MRI. IEEE Trans. Biomed. Eng. 2007;54(1):122–129. doi: 10.1109/TBME.2006.884645. [DOI] [PubMed] [Google Scholar]
- Zhu C, Jiang T. Multicontext fuzzy clustering for separation of brain tissues in magnetic resonance images. NeuroImage. 2003;18(3):685–696. doi: 10.1016/s1053-8119(03)00006-5. [DOI] [PubMed] [Google Scholar]