The May threshold and life-history allometry

Abstract

One of Robert May's classic results was finding that population dynamics become chaotic when the average lifetime rate of reproduction exceeds a certain value. Populations whose reproductive rates exceed this May threshold probably become extinct. The May threshold in each case depends upon the shape of the density-dependence curve, which differs among models of population growth. However, species of different sizes and generation times that share a roughly similar density-dependence curve will also share a similar May threshold. Here, we argue that this fact predicts a striking allometric regularity among animal taxa: lifetime reproductive rate should be roughly independent of body size. Such independence has been observed in diverse taxa, but has usually been ascribed to a fortuitous combination of physiologically based life-history allometries. We suggest, instead, that the ecological elimination of unstable populations within groups that share a value of the May threshold is a likely cause of this allometry.

1. Introduction

Robert May's classic work demonstrated that unstable dynamics occur in some simple, discrete single-species population models when the average lifetime reproductive rate (R_max) exceeds a specific critical value (May 1974; May & Oster 1976). R_max is the net reproductive rate for a population in the absence of density-dependent feedbacks and thus represents a maximum potential generational growth rate for that population. May & Oster (1976) and others (Berryman & Millstein 1989; Thomas et al. 1980) suggested that the likelihood of population extinction is elevated when a population's R_max is high enough to lead to instability, and, in particular, chaos. Thus, there may be a practical upper limit to the rate at which populations can grow. However, it is unclear whether such an extinction process underlies other general patterns in biology. Here we argue that the existence of this critical value for R_max, which we call the May threshold, predicts a widely observed allometric invariance in life history.

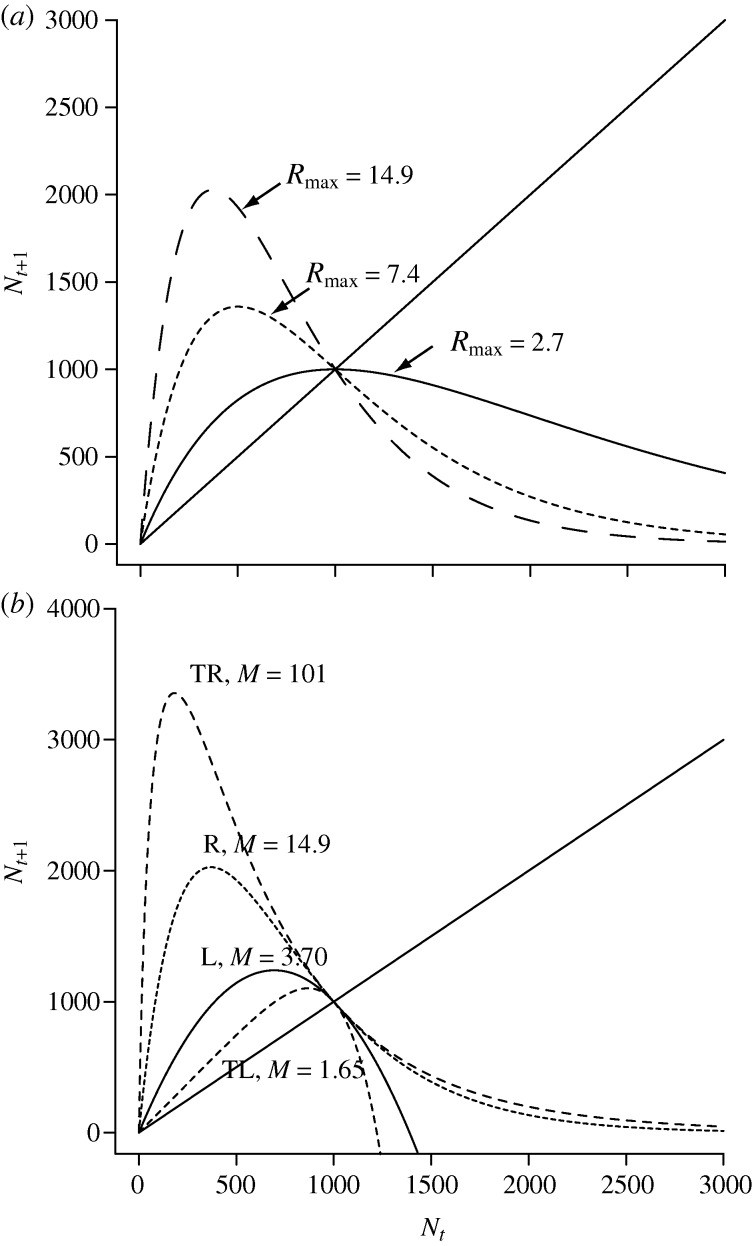
The specific value of the May threshold in single-species models depends on the density-dependence curve defined by the model, and how the shape of that curve changes with model parameters. Plotting N_t+1 versus N_t for a single model, and varying the parameter(s) determining population growth rates, illustrates the curve and its changing shape associated with different values of R_max (figure 1a). May showed that the tangent to this curve at the point where it intersects the 45° line (population equilibrium) determines the stability behaviour. When this tangent is shallower than −1.0, the population attains a stable equilibrium at carrying capacity; if steeper than −1.0, the population begins to cycle and, as steepness increases, chaotic behaviour ensues.

Figure 1.

Plots of N_t+1 versus N_t , illustrating the May threshold. (a) The May threshold is the value of R_max at the transition to unstable dynamics (see electronic supplementary material, appendix SA for details). (b). The May threshold (M) for several well-known one- and two-parameter models of density-dependent population growth, evaluated approximately at the point where chaotic behaviour begins (as observed in simulations using these equations, see electronic supplementary material, appendix SA for details); R=Ricker (May 1974; Ricker 1954); L=logistic May (1974); TR=θ-Ricker (Thomas et al. 1980), r=4.62, θ=0.585; TL=θ-logistic (Thomas et al. 1980; Gilpin & Ayala 1973), r=0.50, θ=5.50. The two-parameter examples in the figure represent pairs of parameters that result in marked asymmetry of the density-dependence curve, chosen to illustrate the wide range in variation in M that is possible even with these simple models.

Different models of density-dependent population growth generally have differently shaped curves, and reach the May threshold at different values of R_max (figure 1b) (Getz 1996). Unfortunately, the actual shape of density dependence is usually not precisely known in each population, and it is likely that it varies among species. If the shape of density dependence varies among taxa, the specific value of the May threshold varies as well (figure 1a,b). Abrams' (2009) generalization of the concept of density dependence accounts as well for the underlying dynamic properties of the population's resources, and leads to a variety of shapes far away from usual logistic-like curves. Our examples here are based on widely used, simpler models. Even within this narrow class, there is appreciable variation in shape and behaviour. Our assumption here is only that related species are likely to have generally similar curves, or at least that the curves' shapes do not vary consistently with body size (Fowler 1981, 1988; Sibly et al. 2005).

May's (1974) results were based on models with non-overlapping generations. This important element has been largely forgotten in favour of a discrete time formulation, which does not refer to any particular time unit. Returning to the original biologically meaningful generational time scale is critical for our argument. May's results have been generalized for the case of overlapping generations by Levin & Goodyear (1980) and more recently by Tuljapurkar et al. (1994). Instabilities have been shown to appear in these more complex models just as they do in the simpler ones. Recent fisheries data suggest that instability in populations under exploitation results from changes in demographic variables, consistent with modelling results (Anderson et al. 2008; Hsieh et al. 2006).

The exact range of values for instability, and whether the instability is periodic or chaotic, is not consequential for our argument. For our purposes, the more important aspect of May's discovery is simply the existence of an approximate critical value for R_max. Populations will generally have R_max values that are near or below the transition to unstable dynamics predicted by the value of the May threshold. Species that share similar density-dependence curves will share similar values of the May threshold.

These considerations immediately lead to the prediction of a general allometric regularity. R_max is measured in units of generation time and generation time scales positively with body size (e.g. Calder 1984). This means that organisms of different sizes (generation times) that have the same-shaped density-dependence curve have the same relationship between R_max and the stability criteria. They thus have the same May threshold. If R_max is limited to values near to but not exceeding the May threshold, then for any group of similar species, there should be no relationship between body size and R_max. Moreover, this size invariance would be observed within groups of similar organisms even if among such groups density-dependence curves differ such that the permitted range of R_max is different.

2. Empirical patterns

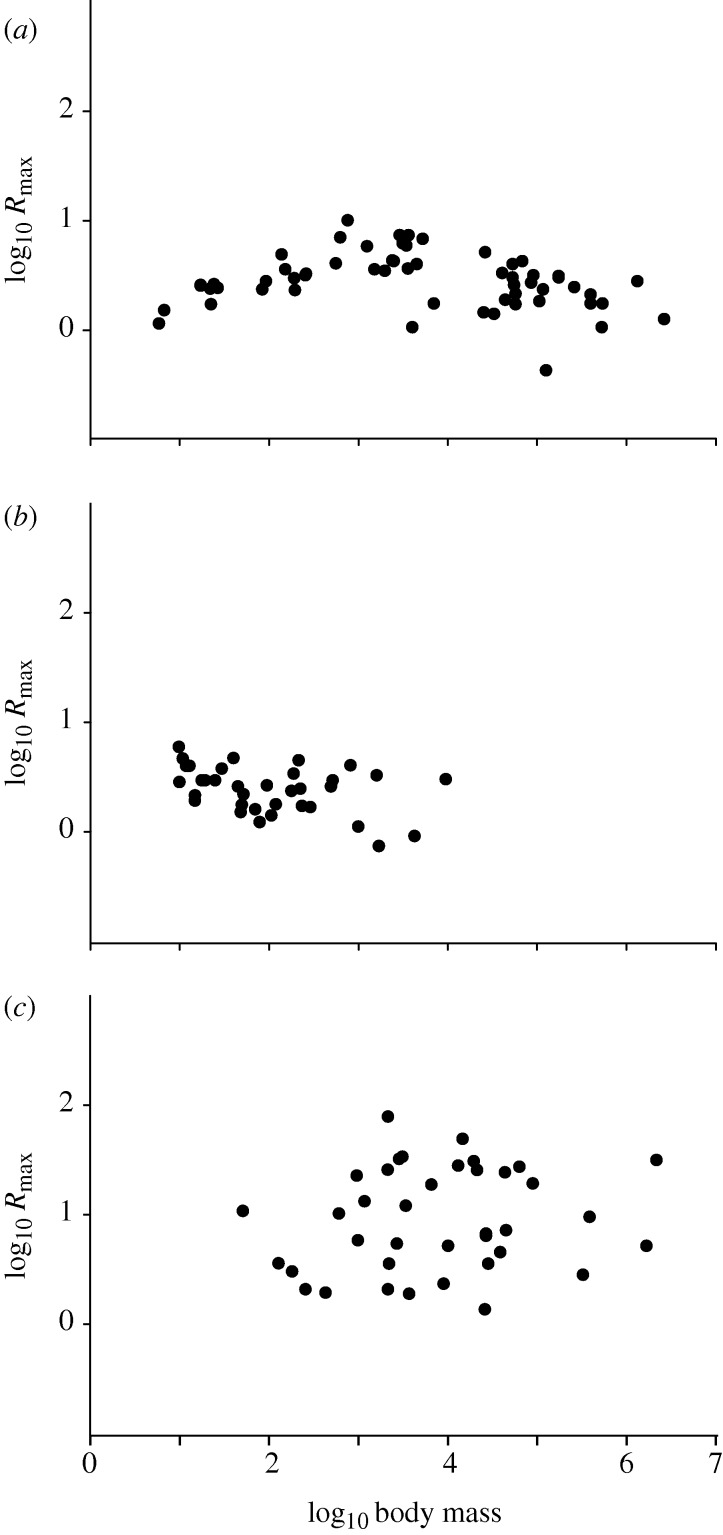
Plots of estimated R_max versus body mass for mammals, birds and fishes support both of these points (figure 2 and electronic supplementary material, appendix SB). Across many orders of magnitude in body mass there is little or no relationship with R_max within these taxa. However, the mean R_max values for mammals (3.2) and birds (2.7) are similar, but that for fishes is considerably higher (17.0), although among fishes there is still no trend with size. Substantial variation of R_max within groups presumably reflects variation in the population dynamics of different species, as well as the difficulty of estimating R_max accurately in natural populations. In addition, because species may differ in the frequency or degree to which they experience K versus r selection, species may vary in the degree to which they typically approach the May threshold for their group. However, in spite of the observed variation, the absence of any strong trend across such wide ranges of size is striking for the allometry of a life-history variable.

Figure 2.

Maximum generational growth rate (R_max) versus body mass (B, in g), for groups of vertebrates spanning a large range of sizes and for which species R_max values are available from the literature. Both variables are log₁₀-transformed, since our prediction is that the ordinary least-squares slope of such a relationship will not differ from 0. For three independent tests, a Bonferroni corrected p-value of ≤0.017 is required to indicate a significant departure from 0 at the 0.05 level (Rice 1989). (a) Mammals, log R_max=0.55−0.03(log B), p=0.17, n=58; R_max estimated as the product of annual birthrate and average female lifespan; adapted from Purvis & Harvey (1995). (b) Birds, log R_max=0.89−0.10(log B), p=0.023, n=36; R_max estimated as average lifetime production of female fledglings; see electronic supplementary material, appendix SC for data and sources. (c) Fishes, log R_max =0.68+0.068(log B), p=0.34, n=38; estimates of R_max based on empirical spawner-recruitment curves (number of reproducing females per generation; Myers et al. 1999); maximum reproductive rate is the slope at the origin for the fit of a Ricker-like model to the data.

3. Discussion

The size invariance of R_max has been noticed in mammals since at least the early 1980s (Calder 1984; Fowler 1988; Charnov et al. 2007). Students of allometry usually describe this invariance as the result of taking the product of a lifespan variable and another life-history variable that scales with body mass to the same power but of opposite sign (Calder 1984; Fowler 1988; Charnov 1993). For instance, Calder noticed that the number of births in a lifetime is the product of lifespan, a +1/4 power allometry of body size (B), and annual birthrate, a −1/4 power (i.e. B^+1/4×B^−1/4=B⁰). Fowler's observation was similar but based on the maximum intrinsic rate of increase, r_max (−1/4 power of mass) and generation length in years (+1/4 power of mass). In general, average lifetime reproduction rate has been thought of as a consequence of such independent matching allometric relationships, with lifespan or generation time expected to scale as +1/4, because the times associated with purely physiological processes usually scale that way. However, it is not obvious why physiological functioning per se should also determine the number of births across the lifespan, which has population and demographic implications that may not be wholly constrained by the physiological performance of an individual.

We believe that the size invariance of lifetime reproduction within taxa (and the variation in absolute values among them) is less likely to be a coincidental by-product of two independent allometries and more likely to be the result of the size independence of the May threshold among similar species. R_max cannot exceed the May threshold; species that cross this value go extinct owing to unstable dynamics (May & Oster 1976; Thomas et al. 1980). Today, we observe the set of species that persist under the ceiling imposed by their May threshold values. Ellner & Turchin (1995) investigated time-series data on population abundances to see whether the series were dominated by stable, oscillatory or chaotic behaviour. They found, consistent with our suggestion here, a concentration of data series with parameters close to but not over the threshold of chaos (see also Doebeli & Koella 1995).

Some additional considerations suggest directions for future research. Our argument applies only to species experiencing scramble competition (e.g. most vertebrates and insects). Species experiencing primarily contest competition, such as most plants and sessile animals, have population dynamics that are not subject to the instabilities discussed here. Thus, we predict that contest-competing taxa will not show size independence of average lifetime reproductive success. Also, carrying capacity (K) should affect the chance of extinction, independently of unstable dynamics. We thus expect that high-K species would be more resistant to extinction and be able to tolerate higher R_max values, other things being equal.

The selective process of elimination of unstable populations is one that operates on a level above individual organisms; ordinarily individual selection should favour fast growth rates and thus oppose it. In fact, one could consider the process to represent the differential mortality component of population or species selection. However, selective elimination alone does not fulfil the usual definitions of group selection (see Okasha 2006 for a recent review). In any case, we feel that the process implied by the existence of the May threshold should be uncontroversial and is of compelling generality. To avoid misunderstanding, we call this kind of selective process ecological elimination (cf. Ginzburg & Colyvan 2004, p.112), which is simply the elimination of ecologically unstable configurations.

If ecological elimination has shaped sets of extant species to contain only those that reproduce below the May Threshold for their group, we have a simple long-term evolutionary explanation of the size invariance of lifetime reproduction.