Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2010 Nov 11;44(24):9349–9356. doi: 10.1021/es101800k

Predicting Residential Air Exchange Rates from Questionnaires and Meteorology: Model Evaluation in Central North Carolina

Michael S Breen 1,*,†, Miyuki Breen 1,‡,§, Ronald W Williams 1,†, Bradley D Schultz 1,†
PMCID: PMC3001757  PMID: 21069949

Abstract

A critical aspect of air pollution exposure models is the estimation of the air exchange rate (AER) of individual homes, where people spend most of their time. The AER, which is the airflow into and out of a building, is a primary mechanism for entry of outdoor air pollutants and removal of indoor source emissions. The mechanistic Lawrence Berkeley Laboratory (LBL) AER model was linked to a leakage area model to predict AER from questionnaires and meteorology. The LBL model was also extended to include natural ventilation (LBLX). Using literature-reported parameter values, AER predictions from LBL and LBLX models were compared to data from 642 daily AER measurements across 31 detached homes in central North Carolina, with corresponding questionnaires and meteorological observations. Data was collected on seven consecutive days during each of four consecutive seasons. For the individual model-predicted and measured AER, the median absolute difference was 43% (0.17 h−1) and 40% (0.17 h−1) for the LBL and LBLX models, respectively. Additionally, a literature-reported empirical scale factor (SF) AER model was evaluated, which showed a median absolute difference of 50% (0.25 h−1). The capability of the LBL, LBLX, and SF models could help reduce the AER uncertainty in air pollution exposure models used to develop exposure metrics for health studies.

Short abstract

Evaluation of models to predict residential air exchange rates from questionnaires and meteorology is conducted.

Introduction

Numerous air pollution epidemiology studies have observed associations between ambient concentrations of particulate matter (PM) and increased rates of morbidity and mortality (1). These health studies often use air pollution measurements from central ambient monitoring sites as exposure surrogates. To better understand the linkages between ambient concentrations and exposures, we are developing an air pollution exposure model for individuals (EMI) in health studies (2−4). The EMI predicts personal exposures from ambient concentrations and questionnaire information such as building characteristics, occupant behavior related to building operation and indoor sources, and time-activity patterns. This study describes a critical aspect of the EMI: the evaluation of models that can predict the air exchange rate (AER) of individual homes based on questionnaire and meteorological data.

A residential AER model has several potential applications. First, the AER, which is the airflow into and out of a home, is an important mechanism for the entry of outdoor air pollutants and the removal of indoor source emissions. Since studies have shown that people in the United States and Canada spend approximately 66% of their time indoors at home, the residential AER is a critical parameter for air pollution exposure models (5,6). Field data collection costs and participant burden often limit the number of AER measurements, as well as in-home and personal air pollutant measurements. Therefore, a residential AER model integrated within an exposure model is a feasible method to determine exposure metrics for epidemiological analysis and risk assessments. Second, a mechanistic AER model has the potential ability to reduce the AER uncertainties that can exist in air pollution exposure models that often rely upon empirical AER models designed without a physical basis, or AER measurements in other homes. Third, an AER model can be applied for both individual and population air pollution exposure models in support of cohort and time-series health studies, and regulatory exposure assessments. The AER model inputs, which include housing characteristics and occupant behavior as related to building operation, can be obtained from questionnaires for individual-based models, and obtained from public databases such as censuses, property assessments, residential surveys (7), occupant window opening surveys (8) for population-based models. Finally, an AER model can be used for censored or missing measurements.

Mechanistic AER models, which account for the physical driving forces of the airflows (i.e., pressure differences across building envelope from wind and indoor−outdoor temperature differences, the stack effect), can be classified into two major categories: single-zone and multizone models (9,10). Single-zone models predict the AER for a whole building represented as a single, well-mixed compartment. Multizone models divide a building into a series of interconnected compartments with distinct pressures and temperatures. The input data required for the more complex multizone models (e.g., spatial configuration of windows, doors, and internal walls) are typically unavailable from questionnaires in health studies due to field data collection cost and participant burden. In this study, we consider single-zone models since these models are appropriate for buildings with no internal resistance to airflow, such as the single family homes included in the analysis (10).

Various single-zone AER models have been described in the literature (9,10). Two of the most widely used mechanistic models are the Lawrence Berkeley Laboratory (LBL) model (11) and the Alberta air infiltration (AIM-2) model (12). The AIM-2 model requires parameter values for the leakage coefficient and pressure exponent for individual homes that are derived from whole-building pressurization tests. The LBL model requires the effective leakage area for individual homes that can be derived from either whole-building pressurization tests (11) or leakage area models (13). Since pressurization tests for individual homes in cohort health studies are not feasible due to field data collection cost, we used the LBL model coupled to a leakage area model in this study. Another study that linked the LBL model with a leakage area model, population-level data from the U.S. Census Bureau and the Residential Energy Consumption Survey (7) were used to predict the average AER for each county in the US, and no model evaluation was performed (13). In this study, questionnaire data were used as inputs for the LBL model to predict AER for individual homes, which were then compared with corresponding AER measurements.

The LBL model predicts the AER due to airflow through small unintentional openings in the building envelope (i.e., air infiltration), but does not account for the airflow through large controllable openings (i.e., natural ventilation), such as open windows. In this study, we addressed this limitation by extending the LBL model (LBLX) using a previously developed model to predict the natural ventilation airflow through large controllable openings (10). We evaluated the LBLX model with window opening input data from questionnaires, and corresponding AER measurements.

In this study, we also evaluated an empirical scaling factor (SF) AER model that was reported in the literature (14). The SF model does not consider the driving forces from the wind (wind speed) and stack (indoor−outdoor temperature differences) effects. Instead, a scaling constant is used to relate leakage area to AER.

The AER has been measured in a few thousand homes in the U.S., but these measurements typically did not include sufficient details on housing characteristics and occupant behavior, which are needed for model inputs (15). The Research Triangle Park Particulate Matter Panel Study (RTP Panel Study), provides a unique data set to evaluate the residential AER models (16−19). The RTP Panel Study included daily residential AER measurements, meteorological data, and questionnaires on housing characteristics and occupant behavior related to building operation (i.e., window opening, indoor temperature) of 31 occupied detached homes for seven consecutive days in each of four consecutive seasons, thus representing various housing characteristics, occupant behavior, and weather conditions.

In this study, we used the questionnaires, meteorology, and AER measurements from the RTP Panel Study to evaluate the LBL, LBLX, and SF AER models (Table 1). Below, we first describe the RTP Panel Study, and then describe the AER models and the method for model evaluation.

Table 1. Comparison of Air Exchange Rate Models.

  models
features and inputs SF LBL LBLX
empirical or mechanistic modela empirical mechanistic mechanistic
airflows      
infiltration yes yes yes
natural ventilation no no yes
temporal resolution annualb hourlyc hourlyc
spatial resolution residential residential residential
building characteristics (inputs)      
floor area yes yes yes
house age yes yes yes
housing type (low income, conventional) yes yes yes
house height (number of stories) yes yes yes
local sheltering yes yes yes
occupant behavior/building operation (inputs)      
indoor temperature no yes yes
window opening area-duration no no yes
climatic region (input) yes no no
meteorology (inputs)      
outdoor temperature no yes yes
wind speed no yes yes
Open in a new tab
a

Empirical refers to regression-based model.

b

Annual resolution from house age that increases by one each year.

c

Limited by temporal resolution of meteorology (wind speed, temperature).

Materials and Methods

RTP Panel Study

The RTP Panel Study, conducted by the National Exposure Research Laboratory of the U.S. Environmental Protection Agency, represented a one year investigation of PM and related gaseous copollutants involving participants living across a 70 km distance in the vicinity of RTP in central North Carolina (NC) (16−19). The study included a low to moderate socioeconomic status cohort of 29 participants with controlled hypertension living in Raleigh, NC, and a moderate socioeconomic status cohort of eight participants with implanted cardiac defibrillators living in Chapel Hill, NC. Personal, residential indoor, residential outdoor and central-site ambient air monitoring was performed for seven consecutive days in each of four consecutive seasons (summer 2000 through spring 2001). All 24 h daily measurements were performed from 8 a.m. to 8 a.m. (±2 h) the following day. A maximum of six participants and their residences were monitored during each seven day period within each season. Monitoring during each season lasted approximately six weeks. Daily 24 h average AER were measured in each home using a perfluorocarbon tracer (PFT) method (20,21). The Brookhaven National Laboratory (BNL; Upton, NY) prepared the tracer sources and receptor tubes, and provided guidance on the types and number of tracer sources placed in each home. Sources were placed in the homes 24 h before the first day of measurement to allow for adequate distribution. The reported accuracy (based on known AER), precision (based on replicate measurements), and limits of the PFT-derived AER measurements for occupied homes is estimated to be 20−25%, 5−15%, and 0.2−5.0 h−1, respectively (10,21−23).

Data were also obtained on housing characteristics, occupant behavior, and meteorology (18,24). Daily questionnaires and time-activity diaries were collected for each subject. Participants recorded their location at 15 min intervals and time when certain activities related to housing operation were performed, including opening windows. For each open window, the opening height and duration was recorded. Indoor temperatures were measured continuously (1 min) at each home. Outdoor temperatures and wind speeds (2 m elevation) were measured hourly at a local State of NC air monitoring platform in Raleigh, NC.

The RTP Panel Study consisted of 37 participants living in 36 unique residences; two participants were family members living in the same house. The housing types of these residences consisted of 31 detached homes, three trailers, one duplex, and one apartment. In this paper, we evaluated the model for the 31 detached homes. The sample size for the other housing types was too small for sufficient analysis.

Air Exchange Rate Model Overview

The exchange of outdoor air with air inside a building can be divided into three categories: air infiltration, natural ventilation, and mechanical ventilation (10). Air infiltration is the airflow across building envelope from air leakage through small cracks around windows, doors, and other unintentional openings in the building envelope. Natural ventilation is the intentional airflow through open windows, doors, and other designed and controlled openings in the building envelope. Mechanical ventilation is the forced air movement by outdoor-vented intake and exhaust fans. In this study, all three AER models (LBL, LBLX, SF) include air infiltration, with natural ventilation included in the LBLX model (Table 1). Mechanical ventilation is not included in these residential AER models since detailed information on the specific type and operation of outdoor-vented fans was unavailable from the RTP Panel Study.

The driving mechanisms for AER are pressure differences across building envelope (10). The pressure differences for air infiltration and natural ventilation are induced by wind (wind effect) and indoor−outdoor temperature differences (stack effect). In this study, the two mechanistic models (LBL and LBLX) include the wind and stack effects from wind speed and temperature measurements, respectively (Table 1).

We developed computer simulations for the three models (LBL, LBLX, SF) to predict 24 h average AER, which are time-matched to the 24 h average AER measurements from the RTP Panel Study. Below, we first describe the AER models, and then the procedure for model evaluation. The complete method and subsequent analysis were implemented using MATLAB software (version R2009b, Mathworks, Natick, MA).

LBL Model

The LBL model assumes the building is a single, well-mixed compartment (11). The airflow rate is calculated as

graphic file with name es-2010-01800k_m001.jpg

where Qinf is the airflow rate, Ainf is the effective air leakage area, ks is the stack coefficient, kw is the wind coefficient, Tin and Tout are the average indoor and outdoor temperatures over time interval of calculation (24 h), respectively, and U is the average wind speed over time interval of calculation (24 h). The AER is calculated as Qinf divided by the building volume V.

The LBL model has two parameters (ks and kw) and five model inputs (Ainf,Tin,Tout,U, and V). Model inputs Ainf and V are from housing characteristics, Tin is from occupant behavior related to housing operation, and Tout and U are from meteorology, as described in Table 1. In this study, housing characteristics varied with home; occupant behavior varied with home and time (day); and meteorology varied with time. Parameters ks and kw were set to reported literature values based on house-specific information on house height and local sheltering (Supporting Information Tables S1−S3) (10).

To determine the model input Ainf, we used a literature-reported leakage area model and parameter values (14). This particular leakage area model, which was previously compared to an alternative model and shown to perform equally well (25), was used in this study since information on air leakage through floors is unavailable. The leakage area Ainf is calculated as

graphic file with name es-2010-01800k_m002.jpg

where NL is the normalized leakage and NF is the normalization factor. The NL is dimensionless, and was predicted from the year of construction Ybuilt and floor area Afloor as described by

graphic file with name es-2010-01800k_m003.jpg

where β0, β1, and β2 are the regression parameters. The NF is defined as

graphic file with name es-2010-01800k_m004.jpg

where H is the building height. For eq 4, H is in units of m, and is set to the number of stories multiplied by a story height of 2.5 m and adding a roof height of 0.5 m (14). As previously reported, this model was fit to a national database of leakage areas for 70 000 homes across 30 states in the Midwest (most-sampled region), West, South, and Northeast (least-sampled region) based on blower-door tests (14). These leakage areas were determined from a whole-building blower door method, which measures the airflow needed to pressurize a building to various indoor−outdoor pressure differences. The Afloor and Ybuilt for each home were obtained from the RTP Panel Study questionnaires.

The literature-reported parameters β0, β1, and β2 were estimated for low-income homes (β0 = 11.1, β1 = −5.37 × 10−3, and β2 = −4.18 × 10−3 m−2) and conventional homes (β0 = 20.7, β1 = −1.07 × 10−2, and β2 = −2.20 × 10−3 m−2) (14). The parameters for the low-income homes were estimated using measurements from the Ohio Weatherization Program, which included residences with household incomes below 125% of the poverty guideline (14). In the RTP Panel Study, the individual household incomes were not collected. From the 2000 U.S. Census, household income distributions are not available at the block level, but only at the block group level. Therefore, we examined the household income distributions at the block group for the 31 homes in the RTP Panel Study. Since each block group typically consisted of 1000 households, and the household incomes within each block group were not homogeneous in the study area, our ability to estimate the individual household incomes is limited. However, for the Raleigh cohort, a substantial percentage of households in each block group were below 125% of the 2000 poverty guideline. For the Chapel Hill cohort, a small percentage of households in each block group were below 125% of the poverty guideline. Therefore, the literature-reported parameter values for the low-income and conventional homes were used for the Raleigh and Chapel Hill cohorts, respectively.

To determine the model inputs Tin, Tout, U,  and V, we used data from the RTP Panel Study (Supporting Information Tables S5−S6). We calculated Tin from the 24 h average of continuous (1 min) measurements in each home. We calculated Tout and U from the 24 h average of hourly measurements at the State of NC monitoring platform in Raleigh, NC. To determine V, we multiplied Afloor by a ceiling height of 2.44 m (8 ft) (26).

LBLX Model

For the LBLX model, we extended the LBL model to include natural ventilation. We estimated the natural ventilation airflow through open windows using a literature-reported model and parameter values for large intentional openings (10). The natural ventilation airflow from the wind effect Qnat,wind is calculated as

graphic file with name es-2010-01800k_m005.jpg

where Cv is the effectiveness of the openings (dimensionless), and Anat is the area of inlet openings. Since Cv is typically between 0.25 and 0.35 for diagonal winds (10), we set Cv to 0.30. For Anat, we assumed that the inlet and outlet areas are equal, and set Anat to one-half total area of window openings. From the RTP Panel Study, we calculated the 24 h average total area of window openings from daily window opening data collected at each home (sum of opening height multiplied by duration across all open windows) multiplied by a window width of 0.6 m (Supporting Information Table S5).

The natural ventilation airflow from the stack effect Qnat,stack is calculated as

graphic file with name es-2010-01800k_m006.jpg

where CD is the discharge coefficient for the openings (dimensionless), g is gravitational acceleration (9.8 m/s2), ΔHNPL is the height from midpoint of lower window opening to the neutral pressure level (NPL) of the building, and max {Tin,Tout} is the maximum value between Tin and Tout. We set CD to the reported literature value of 0.65 (10). For ΔHNPL, we set the midpoint of lower window opening to 0.91 m (3 ft). Since the NPL (location with no indoor−outdoor pressure difference) varies between 0.3 and 0.7 times the building height (10), we set the NPL to one-half of the building height. The building height is set to the number of stories multiplied by a story height of 2.5 m and adding a roof height of 0.5 m (14).

Using a reported literature method to combine airflows from wind and stack effects (10), the airflow from natural ventilation Qnat was calculated as

graphic file with name es-2010-01800k_m007.jpg

Using a literature-reported method (10), the airflow from both infiltration and natural ventilation Qinf_nat was calculated as

graphic file with name es-2010-01800k_m008.jpg

where Qinf is the LBL model-predicted airflow from infiltration. The AER for the LBLX model is Qinf_nat divided by V.

SF Model

The empirical SF model predicts the AER using a scaling factor to relate the normalized leakage NL (eq 3) to the AER (14). The AER for the SF model is defined as

graphic file with name es-2010-01800k_m009.jpg

where F is the scaling factor and HC is the ceiling height. For eq 9, H and HC are in units of m. The building height H is set to the number of stories multiplied by a story height of 2.5 m and adding a roof height of 0.5 m (14). The ceiling height HC was set to 2.44 m (8 ft) (26). The normalized leakage NL describes only the tightness of a building. To account for the driving forces from the wind and stack effects, the SF model uses a scaling factor F unlike the LBL and LBLX models that use daily meteorological data (i.e., wind speed and temperature). The scaling factor F was set to the reported literature values that depend on climatic region, house height, and local sheltering (Supporting Information Figure S1, Table S4) (27).

Model Evaluation

For each model, we evaluated the differences between individual model-predicted and measured AER using two metrics: relative difference ε and absolute difference Δ. These metrics are calculated as

graphic file with name es-2010-01800k_m010.jpg

and

graphic file with name es-2010-01800k_m011.jpg

where AERmeas and AERpred are the measured and model-predicted AER, respectively. The relative difference ε typically indicates the amount of deviation better than the absolute difference Δ. However, for measured AER with extremely low values, a minor deviation could yield a large ε. In this case, Δ is more meaningful than ε for model evaluation. Therefore, both ε and Δ are used in this study. A positive value for ε and Δ indicates that the model overestimated the measured AER, while a negative value indicates underestimation.

The statistics ε and Δ and their absolute values |ε| and |Δ| are all calculated since they complement each other. The statistics |ε| and |Δ| evaluate the magnitude of deviation but do not indicate the bias (i.e., overestimation or underestimation). In contrast, the statistics ε and Δ indicate the bias.

Results

Summary statistics are provided for the number of detached homes, number of days windows opened, and daily measured AER in each season and cohort (Table 2). Homes during the spring and winter had the highest (50%) and lowest (22%) percentage of days with windows opened, respectively. Across all four seasons, the windows were opened on 39% of the days. Measured AER distributions had a positive skew (Supporting Information Figure S2) with values between 0.05 h−1 (minimum) and 4.87 h−1 (maximum), and 25th, 50th, and 75th percentiles of 0.32, 0.50, and 0.76 h−1, respectively.

Table 2. Number of Homes, Number of Days Windows Opened, And Summary Statistics for Measured 24 h Average Air Exchange Rates.

season:yeara or cohort number of detached homes number of days windows openedb air exchange rates (h−1)e
      sample size mean SD min p5 p10 p25 p50 p75 p90 p95 max
summer:2000 29 90 (44%) 203 0.50 0.58 0.05 0.16 0.21 0.26 0.36 0.50 0.70 1.53 4.83
fall:2000 27 63 (38%) 167 0.60 0.37 0.09 0.21 0.24 0.35 0.51 0.77 1.03 1.29 2.24
winter:2000−01 23 29 (22%) 129 1.11 0.88 0.23 0.34 0.40 0.56 0.81 1.25 2.53 3.34 4.87
spring:2001 23 71 (50%) 143 0.64 0.48 0.15 0.20 0.22 0.34 0.53 0.72 1.16 1.76 3.17
Raleigh cohortc 27 215 (39%) 555 0.70 0.66 0.05 0.21 0.24 0.32 0.51 0.77 1.29 2.00 4.87
Chapel Hill cohortd 4 38 (44%) 87 0.56 0.44 0.06 0.12 0.16 0.26 0.45 0.70 1.25 1.43 2.58
all 31 253 (39%) 642 0.68 0.63 0.05 0.20 0.23 0.32 0.50 0.76 1.27 1.85 4.87
Open in a new tab
a

Summer: June, July, and August; fall: September, October, and November; winter: December, January, and February; spring: March, April, and May.

b

Percentage of days windows opened relative to corresponding sample size are shown in parentheses.

c

Low to moderate socioeconomic status neighborhoods.

d

Moderate socioeconomic status neighborhoods.

e

SD corresponds to standard deviation, p5−p95 correspond to percentiles.

Summary statistics for the meteorological and questionnaire data are provided (Supporting Information Tables S5−S6). For indoor−outdoor temperature differences, the seasonal medians had large variations with a 6.9 fold change between the lowest (2.1 °C; summer) and highest (14.4 °C; winter) seasons. For wind speeds, the seasonal medians had relatively small variations with a 1.2 fold change between the lowest (4.5 km-h−1; fall) and highest (5.4 km-h−1; spring) seasons.

Summary statistics are provided for the distributions of the model-predicted and measured AER (Table 2, Supporting Information Table S7 and Figure S3). For the LBLX model, the model-predicted and measured AER had overall medians of 0.42, 0.50 h−1, 25th percentiles of 0.27, 0.32 h−1, and 75th percentiles of 0.60, 0.76 h−1, respectively. The overall quartiles for the LBL and SF models were slightly lower and higher than the LBLX model, respectively.

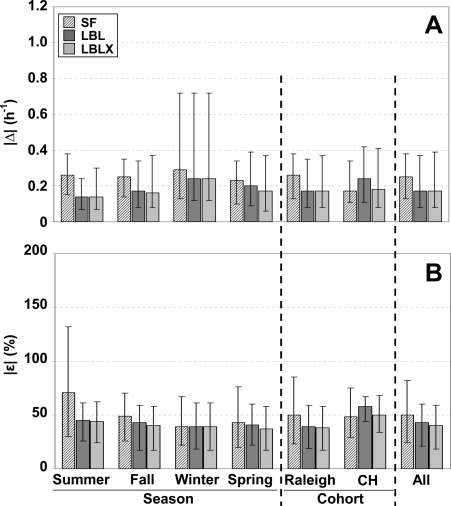
A comparison of the individual model-predicted and measured AER is shown for each season and cohort (Figure 1, Supporting Information Tables S8−S9 and Figures S4, S6). The LBL and LBLX models show similar results with overall |ε| medians of 43% and 40%, and |Δ| medians of 0.17 h−1 and 0.17 h−1, respectively (Figure 1, Supporting Information Table S8). The SF model had a slightly larger overall |ε| median of 50% and |Δ| median of 0.25 h−1. The overall |ε| medians for the LBL, LBLX, SF models are 18%, 15%, and 25% above the estimated PFT measurement uncertainty of 25%, respectively (22).

Figure 1.

Figure 1

Open in a new tab

Comparison of absolute differences for |Δ| (A) and |ε| (B) between individual model-predicted and measured AER for each model. Results are separated by season, cohort (Raleigh, CH-Chapel Hill), and across all days. Shown are medians with 25th and 75th percentiles.

The LBL and LBLX models show similar |ε| quartiles for each season and the Raleigh cohort with slightly larger |ε| quartiles for the Chapel Hill cohort (Figure 1, Supporting Information Table S8). The LBL model generally underestimates the AER with overall ε median of −29% and Δ median of −0.13 h−1 (Supporting Information Table S9, Figure S4). The LBLX model also tends to underestimate the AER, but with a smaller overall ε median of −18% and Δ median of −0.08 h−1.

As compared to the LBL and LBLX models, the SF model has larger |ε| quartiles for the summer and fall seasons and the Raleigh cohort, with similar |ε| quartiles for the winter and spring seasons and the Chapel Hill cohort (Figure 1, Supporting Information Table S8). The SF model tends to overestimate the AER with overall ε median of 20% and Δ median of 0.09 h−1 (Supporting Information Table S9, Figure S4).

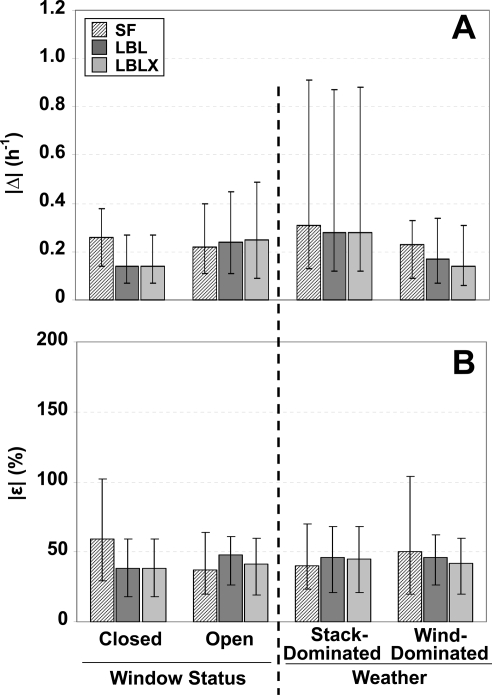
A comparison of the individual model-predicted and measured AER is shown for different window opening (Figure 2, Supporting Information Tables S10−S11 and Figure S5). The LBL and LBLX models are equivalent for days with windows closed, and therefore show identical results with |ε| medians of 38%, and ε medians of −18%. The SF model shows |ε| median of 59%, and tends to overestimate the AER with ε median of 33%. For days with windows opened, the LBLX model shows a lower |ε| median (41%) than the LBL model (48%), and the LBLX model tends to underestimate the AER less than the LBL model with ε medians of −46% and −20%, respectively. The SF model shows |ε| medians of 37%, and tends to overestimate the AER with ε median of −7%.

Figure 2.

Figure 2

Open in a new tab

Comparison of absolute differences for |Δ| (A) and |ε| (B) between individual model-predicted and measured AER for each model. Results are separated by window status and weather conditions. Shown are medians with 25th and 75th percentiles.

Since the AER driving forces are from the wind and stack effects, we evaluated the models at different weather conditions (Figure 2, Supporting Information Tables S10−S11 and Figure S5). A day was considered stack-dominated when the 24 h average wind speed U < 5.6 km-h−1 and indoor−outdoor temperature difference |Tin − Tout|>10 °C, and considered wind-dominated when U > 5.6 km-h−1 and indoor−outdoor temperature difference |Tin − Tout|<5 °C. This wind speed of 5.6 km-h−1 corresponds to a light breeze based on the Beaufort Wind Scale (28). This grouping yielded 110 stack-dominated days and 132 wind-dominated days. For stack-dominated and wind-dominated days, the LBL and LBLX models show similar |ε| quartiles and tend to underestimate the AER. These results are similar to the overall |ε| quartiles (Figure 1). The SF model shows a larger |ε| 75th percentile than the LBL and LBLX models for wind-dominated days, similar |ε| quartiles for stack-dominated days, and tends to overestimate the AER on wind-dominated days, and underestimate on stack-dominated days.

Discussion

Our goal was to evaluate three models (SF, LBL, and LBLX) that predict daily AER of detached homes from questionnaires and meteorology. Using literature-reported parameter values, the mechanistic LBL and LBLX models performed slightly better overall than the empirical SF model, and the individual model-predicted AER from these three models agreed reasonably well to the 642 daily AER measurements across 31 detached homes from the RTP Panel Study. These results suggest that it is possible to apply these models for individual-level air pollution exposure assessments that require house-specific predictions of daily AER. Since the summary statistics for the overall model-predicted and measured AER distributions also correspond reasonably well, these models potentially could be also applied for population-level exposure assessments. Furthermore, since the LBLX model can separately predict the AER for the air infiltration pathway and natural ventilation pathway, its integration with indoor air quality models could support the use of unique pathway-dependent penetration coefficients for certain air pollutants.

We can compare the AER models with those reported in the literature. For the SF model, one study qualitatively fit a model-predicted AER distribution to a national distribution of measured AER across the United States, and reported the spread of the distributions were in good agreement (14). Other studies have evaluated the LBL model using whole-building pressurization measurements to determine the leakage area. In one study, the LBL model had a mean |ε| of 25% across 16 detached homes (29). In another study, the LBL model had a mean |ε| of 26−46% (30). Our implementation of the LBL model, which uses a leakage area model, had a mean |ε| of 43%. Given the limitations of the leakage area model (14) and single-zone AER models (10), the measurement uncertainty of the PFT-derived AER data (accuracy of 20−25% and precision of 5−15% for occupied homes) (10,22,23), and the use of literature-reported parameter values in this study (i.e., no model fitting), our results for the LBL, LBLX, and SF models are reasonable. To the best of our knowledge, this study is the first time the LBL model has been extended to include natural ventilation (LBLX model) and evaluated with window-opening behavior data. Therefore, the LBLX model cannot be compared with similar models reported in the literature.

In this study, similar results were obtained for the mechanistic models that include both air infiltration and natural ventilation (LBLX) or only air infiltration (LBL). The LBL model may perform reasonably well since the effect from opening windows may only moderately increase the 24 h average AER. It is possible that windows are opened for only a few hours, whereas the air infiltration (i.e., unintentional openings) is constant. Also, windows may be opened more often on days with small indoor−outdoor temperature differences. Therefore, the driving force from the stack effect may be smaller on days with windows opened. Furthermore, the stack effect can be reduced after windows are opened from the thermal equilibrium created between indoor and outdoor temperatures (31). This provides a potential explanation for the median measured AER being highest in the winter (0.81 h−1) and lowest in the summer (0.36 h−1) even though the number of days with open windows was lowest in the winter (22%) and highest in the summer (44%), with the median indoor−outdoor temperature difference highest in the winter (14.4 °C) and lowest in the summer (2.1 °C), and similar median wind speeds in the winter (4.8 km hr−1) and summer (5.0 km hr−1). The median AER predicted with the LBL and LBLX models were also highest in the winter (0.63 h−1,0.64 h−1) and lowest in the summer (0.25 h−1, 0.27 h−1), respectively. Another study showed similar results with the median AER measured across 99 homes in Houston, Texas being highest in the winter (0.63 h−1) and lowest in the summer (0.37 h−1) (32). Since the LBL model does not require window opening data, this reduces participant burden and makes it more feasible to apply the model for health studies. The ability of the LBL and LBLX models to predict AER in other geographical areas with different seasonal window-opening behavior will be investigated with other exposure panel studies.

The selection of the preferable AER model(s) for a particular situation depends on the available data and the desired temporal resolution. The SF model is simpler since fewer input data are required, as compared to the LBL and LBLX models. However, the SF model has low temporal resolution (annual). The LBL and LBLX models have higher temporal resolution (e.g., hourly) but require more detailed input data than the SF model, which includes the indoor temperature, outdoor temperature, and wind speed. The SF and LBL models account for only air infiltration, whereas the LBLX model also includes natural ventilation. However, this requires additional input data (e.g., window opening height and duration) for the LBLX model.” Therefore, the SF model is preferable when limited data is available, whereas the LBL and LBLX models are preferable when high temporal resolution is desired and more detailed data is available.

The method to characterize the model uncertainty depends on the particular application. For estimating individual air pollutant exposures for specific people, such as those in cohort health studies with individual health outcomes, a comparison of the individual measured and model-predicted AER for each home would be appropriate. However, for estimating population distributions of air pollutant exposures for groups of people such as those in health studies with health outcomes at census tract to county level resolution, a comparison of the distributions of the measured and model-predicted AER across all homes would be appropriate. In this study, we performed both types of comparisons. The AER uncertainty determined from these comparisons could be used for uncertainty analysis (e.g., Monte Carlo simulations) of residential indoor air quality models.

Using mean values for certain parameters may increase the model uncertainty for individual-level AER estimates greater than the uncertainty for population-level AER estimates across a geographical region (e.g., zip code or city). This will likely be the case for mean population-level estimates, but not necessarily for estimates at the upper and lower percentiles (e.g., 95th and 5th percentiles). Also, this will depend on the distributions of these parameters and the errors across the region. In this study, using mean values for specific parameters could account for a substantial amount of the individual differences between measured and model-predicted AER, especially for the LBL and LBLX models that require more data.

Even though our model evaluation was based on AER of detached homes in central NC, we expect similar results for the LBL and LBLX models in detached homes with similar building characteristics, weather conditions, and occupant behavior. Since the LBL and LBLX models include the underlying physical mechanisms for the driving forces (i.e., wind and stack effects), these models in theory should perform similarly for different weather conditions. The ability of the LBL and LBLX models to predict AER in other geographical areas with different housing stock, weather, and occupant behavior needs to be investigated. To address this limitation of the study, we plan to perform additional model evaluation using other exposure panel studies such as the Detroit Exposure and Aerosol Research Study in Detroit, Michigan (22). In this study, we evaluated the models with data from the RTP Panel Study in central North Carolina since we are planning our initial model application for cohort health studies with participants living in the same geographical location.

Another limitation of this study is that mechanical ventilation could not be included in the AER models due to unavailable data. The modeling of AER was not a primary goal of the RTP Panel Study, and therefore detailed information on the specific type and operation of outdoor-vented fans was unavailable to accurately estimate their effect on the daily AER for individual homes. Typical bathroom fans, outdoor-vented kitchen range hoods, and clothes dryers have low-intermediate airflows and are used intermittently. Other types of outdoor-vented fans such as window fans, whole-house fans, and window/wall air conditioners operated with open outdoor vents can have a large effect on AER. These fans typically have intermediate (e.g., window/wall air conditioners) or high (e.g., window and whole-house fans) airflows. Whole-house fans are installed in few homes, and window/wall air conditioners can be operated with open or closed outdoor vents. The questionnaires did not distinguish between ceiling-mounted whole-house fans and roof-mounted attic fans. This distinction is important since whole-house fans ventilate the living space unlike attic fans that are designed to ventilate the attic. Whole-house fans move outdoor air into the living space through open windows by forcing air from the living space through the ceiling-mounted fan into the attic. Attic fans, which move outdoor air into the attic through the soffit or gable vents by forcing air from the attic through the roof-mounted fan to the outdoors, are expected to have a relatively small AER effect as compared to whole-house fans. Overall, we expect a small daily AER effect from bathroom fans and outdoor-vented kitchen range hoods, and a large AER effect from window/wall air conditioners (open outdoor vent), window fans, and whole-house fans. This will be investigated with other exposure panel studies that collected daily information on the use of mechanical ventilation (22).

We conclude that our study demonstrates the feasibility of using the LBL, LBLX, and SF models to predict daily AER for individual homes from questionnaires and meteorology. Results show that the model-predicted AER agree reasonably well to the daily AER measurements across detached homes from the RTP Panel Study. This capability could help to reduce AER uncertainty in air pollution exposure models used to predict exposure metrics for epidemiological analysis in health studies.

Acknowledgments

We thank Tom Long, Jennifer Richmond-Bryant, Lisa Baxter, Alexander Schneider, Haluk Ozkaynak, Alan Vette, Zhishi Guo, and Ronald Mosley for review comments and helpful suggestions. We acknowledge Charles Rodes and the staff of RTI International for their efforts in collecting the household survey data. The U.S. EPA through its Office of Research and Development designed, funded, and managed the RTP Panel Study described here under contract 68-D-99-012 to the RTI International and to Shaw University under collaborative agreement CR-828186. M.B. was supported by the U.S. Environmental Protection Agency Cooperative Training Program in Environmental Sciences Research with North Carolina State University, Training Agreement CT833235-01-0. Although the manuscript was reviewed by the U.S. Environmental Protection Agency and approved for publication, it may not necessarily reflect official Agency policy. Mention of trade names or commercial products does not constitute endorsement or recommendation for use.

Supporting Information Available

Six figures (Figures S1−S6), 11 tables (Tables S1−S11). This material is available free of charge via the Internet at http://pubs.acs.org.

Supplementary Material

es101800k_si_001.pdf (168.8KB, pdf)

References

  1. United States Environmental Protection Agency.Integrated Science Assessment for Particulate Matter (Final Report), EPA/600/R-08/139F; US EPA: Washington, DC, 2009. [Google Scholar]
  2. Breen M. S.; Breen M.; Williams R. W.; Rea A.. Air pollution exposure model for individuals in health studies: Parameter estimates for PM2.5 from Research Triangle Park PM panel study. In International Society for Environmental Epidemiology 20th Annual Conference, Epidemiology, 2008, 19, Supplement 6, S193.
  3. United States Environmental Protection Agency. Exposure Model for Individuals (EMI). Available at http://www.epa.gov/heasd/emi.
  4. Zartarian V. G.; Schultz B. D. The EPA’s human exposure research program for assessing cumulative risk in communities. J. Exposure Sci. Environ. Epidemiol. 2010, 20, 351–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Klepeis N. E.; Nelson W. C.; Ott W. R.; Robinson J. P.; Tsang A. M.; Switzer P.; Behar J. V.; Hern S. C.; Engelmann W. H. The National Human Activity Pattern Survey (NHAPS): A resource for assessing exposure to environmental pollutants. J. Exposure Anal. Environ. Epidemiol. 2001, 11, 231–252. [DOI] [PubMed] [Google Scholar]
  6. Leech J. A.; Nelson W. C.; Burnett R. T.; Aaron S.; Raizenne M. E. It’s about time: a comparison of Canadian and American time-activity patterns. J. Exposure Anal. Environ. Epidemiol. 2002, 12, 427–432. [DOI] [PubMed] [Google Scholar]
  7. Housing Characteristics: Residential Energy Consumption Survey; United States Department of Energy, Energy Information Administration: Washington, DC, 2001; http://www.eia.doe.gov/emeu/consumption. [Google Scholar]
  8. Price P. P.; Sherman M.; Lee R. H.; Piazza T.. Study of Ventilation Practices, And Household Characteristics in New California Homes, CEC-500-2007-033, Final Report, ARB Contract 03-326; California Energy Commission, PIER Program: Sacramento, 2007. [Google Scholar]
  9. Orme M.Applicable Models for Air Infiltration and Ventilation Calculations, Technical Note 51; International Energy Agency Air Infiltration and Ventilation Centre, Sint-Stevens-Woluwe: Belgium, 1999. [Google Scholar]
  10. The 2009 ASHRAE Handbook-Fundamentals; American Society of Heating, Refrigerating, and Air Conditioning Engineers: Atlanta, GA, 2009. [Google Scholar]
  11. Sherman M. H.; Grimsrud D. T. Infiltration-pressurization correlation: simplified physical modeling. ASHRAE Transactions 1980, 86, 778–807Lawrence Berkeley Laboratory Report, LBL-10163. [Google Scholar]
  12. Walker I. S.; Wilson D. J. Field validation of algebraic equations for stack and wind driven air infiltration calculations. ASHRAE HVAC&R Res. J. 1998, 4, 119–140. [Google Scholar]
  13. Sherman M.; McWilliams J.. Air leakage of U.S. Homes: Model Prediction, LBNL-62078; Lawrence Berkeley National Laboratory Report: Berkeley, CA, 2007. [Google Scholar]
  14. Chan W. R.; Nazaroff W. W.; Price P. N.; Sohn M. D.; Gadgil A. J. Analyzing a database of residential air leakage in the United States. Atmos. Environ. 2005, 39, 3445–3455. [Google Scholar]
  15. Murray D. M.; Burmaster D. E. Residential air exchange rates in the United States: empirical and estimated parametric distributions by season and climatic region. Risk Anal. 1995, 15, 459–465. [Google Scholar]
  16. Williams R.; Suggs J.; Rea A.; Leovic K.; Vette A.; Croghan C.; Sheldon L.; Rodes C.; Thornburg J.; Ejire A.; Herbst M.; Sanders W. The Research Triangle Park particulate matter panel study: PM mass concentration relationships. Atmos. Environ. 2003, 37, 5349–5363. [Google Scholar]
  17. Williams R.; Suggs J.; Rea A.; Sheldon L.; Rodes C.; Thornburg J. The Research Triangle Park particulate matter panel study: modeling ambient source contribution to personal and residential PM mass concentrations. Atmos. Environ. 2003, 37, 5365–5378. [Google Scholar]
  18. Wallace L.; Williams R.; Suggs J.; Jones P.. Estimating Contributions of Outdoor Fine Particles to Indoor Concentrations and Personal Exposures: Effects of Household Characteristics and Personal Activities, EPA/600/R-06/023; United States Environmental Protection Agency: Washington, DC, 2006. [Google Scholar]
  19. Wallace L.; Williams R. Use of personal-indoor-outdoor sulfur concentrations to estimate the infiltration factor and outdoor exposure factor for individual homes and persons. Environ. Sci. Technol. 2005, 39, 1707–1714. [DOI] [PubMed] [Google Scholar]
  20. Dietz R. N.; Goodrich R. W.; Cote E. A.; Wieser R. F.. Detailed Description and Performance of a Passive Perfluorocarbon Tracer System for Building Ventilation and Air Exchange Measurements, Measured Air Leakage of Buildings, ASTM STP 904; Trechsel H. R., Lagus P. L., Eds.; American Society for Testing and Materials: Philadelphia, PA, 1986; pp 203−264. [Google Scholar]
  21. Dietz R. N.; Cote E. A. Air infiltration measurements in a home using a convenient perfluorocarbon tracer technique. Environ. Int. 1982, 8, 419–433. [Google Scholar]
  22. Williams R.; Rea A.; Vette A.; Croghan C.; Whitaker D.; Stevens C.; McDow S.; Fortmann R.; Sheldon L.; Wilson H.; Thornburg J.; Phillips M.; Lawless P.; Rodes C.; Daughtrey H. The design and field implementation of the Detroit Exposure and Aerosol Research Study. J. Exposure Sci. Environ. Epidemiol. 2009, 19, 643–659. [DOI] [PubMed] [Google Scholar]
  23. Sherman M.; Wilson D. Relating actual and effective ventilation in determining indoor air quality. Build. Environ. 1986, 21, 135–144. [Google Scholar]
  24. Olson D. A.; Burke J. M. Distributions of PM2.5 source strengths for cooking from the Research Triangle Park Particulate Matter Panel Study. Environ. Sci. Technol. 2006, 40, 163–169. [DOI] [PubMed] [Google Scholar]
  25. McWilliams J.; Jung M.. Development of a Mathematical Air-Leakage Model from Measured Data, Report LBNL-59041; Lawrence Berkeley National Laboratory: Berkeley, CA, 2006. [Google Scholar]
  26. United States Environmental Protection Agency.Exposure Factors Handbook (Final Report), EPA/600/P-95/002F a−c; US EPA: Washington, DC, 1997. [Google Scholar]
  27. United States Environmental Protection Agency. Energy Star Home Sealing Specification, Version 1.0, October 16, 2001. Available at http://www.energystar.gov/ia/home_improvement/home_sealing/ES_HS_Spec_v1_0b.pdf.
  28. United States National Oceanic and Atmospheric Administration. Beaufort Wind Scale; US NOAA: Washington, DC, 2009. Available at http://www.crh.noaa.gov/greatlakes/safety/?s=bea. [Google Scholar]
  29. Wang W.; Beausoleil-Morrison I.; Reardon J. Evaluation of the Alberta air infiltration model using measurements and inter-model comparisons. Build. Environ. 2009, 44, 309–318. [Google Scholar]
  30. Palmiter L.; Francisco P. W.. Modeled and Measured Infiltration Phase III: A Detailed Case Study of Three Homes (Technical Report); Ecotope Inc.: Seattle, WA, 1996. [Google Scholar]
  31. Wallace L.; Emmerich S.; Howard-Reed C. Continuous measurements of air change rates in an occupied house for 1 year: The effect of temperature, wind, fans, and windows. J. Exposure Sci. Environ. Epidemiol. 2002, 12, 296–306. [DOI] [PubMed] [Google Scholar]
  32. Yamamoto N.; Shendell D. G.; Winer A. M.; Zhang J. Residential air exchange rates in three major US metropolitan areas: results from the Relationship Among Indoor, Outdoor, and Personal Air Study 1999−2001. Indoor Air 2010, 20, 85–90. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es101800k_si_001.pdf (168.8KB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES