Renal Function Equations before and after Living Kidney Donation: A Within-Individual Comparison of Performance at Different Levels of Renal Function

Abstract

Background and objectives: The Modification of Diet in Renal Disease (MDRD) study equation and the Cockcroft-Gault (CG) equation perform poorly in the (near-) normal range of GFR. Whether this is due to the level of GFR as such or to differences in individual characteristics between healthy individuals and patient with chronic kidney disease (CKD) is unknown.

Design, setting, participants, & measurements: We evaluated the performance of MDRD, CG per BSA (CG/_BSA) and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equations compared with measured GFR (mGFR; I-iothalamate) at 4 months before and 2 months after donation in 253 consecutive living kidney donors.

Results: mGFR declined from 103 ± 15 to 66 ± 11 ml/min per 1.73 m² after donation. All equations underestimated mGFR at both time points. Arithmetic performance analysis showed improved performance after donation of all equations, with significant reduction of bias after donation. Expressed as percentage difference, mGFR–estimated GFR (eGFR) bias was reduced after donation only for CG/_BSA. Finally, in 295 unselected individuals who were screened for donation, mGFR was below the cutoff for donation of 80 ml/min per 1.73 m² in 19 individual but in 166, 98, and 74 for MDRD, CDK-EPI, and CG/_BSA, respectively.

Conclusions: A higher level of GFR as such is associated with larger absolute underestimation of true GFR by eGFR. For donor screening purposes, eGFR should be interpreted with great caution; when in doubt, true GFR should be performed to prevent unjustified decline of prospective kidney donors.

Nowadays, many centers rely on estimating equations to provide an estimated GFR (eGFR) for renal function assessment. Many laboratories automatically report eGFR when serum creatinine (SCr) is requested. The limitations, however, are well established. In healthy individuals and patients with renal disease with (near-) normal renal function, performance is notoriously poor, with considerable systematic underestimation of true GFR and low accuracy (1–8).

The two most widely used equations, the Modification of Diet in Renal Disease (MDRD) and the Cockcroft-Gault (CG), both were derived from populations with reduced GFR (9–11). Recently, a new equation was reported by the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI), which was developed in a large data set in different populations, including renal patients as well as healthy individuals (12). It specifically pursues a better performance in the normal and higher ranges of GFR.

Poor performance of renal function equations for individuals without renal function impairment has been the subject of debate. Of note, the relationship between measured GFR (mGFR) and eGFR is different between healthy individuals and patients with chronic kidney disease (CKD) (2,5,7,13). Differences in body composition, in particular muscle mass, and creatinine handling between healthy people and patients with CKD were suggested to determine performance (2,14). Alternatively, level of mGFR as such was shown to influence performance of eGFR (7,13,15–17); however, these were cross-sectional observations, and level of mGFR may reflect between-individual differences in body composition. In longitudinal analysis of patients with CKD, Lee et al. (18) showed a strong negative association between bias of eGFR and mGFR, yet these studies cannot dissect the effects of CKD—with possible impact on body composition—from those of the differences in mGFR itself.

In healthy kidney donors, removal of one kidney leads to a subsequent reduction in GFR without disease-associated changes in body composition; therefore, our living kidney donor program could provide a unique opportunity to compare the pre- and early postdonation performance of eGFR in high and lower ranges of GFR in the same individuals within a limited time frame. In this study, we evaluated whether performance of eGFR in healthy individuals is dependent on the level of mGFR.

Materials and Methods

We evaluated 253 consecutive living kidney donors who donated kidneys between 1996 and 2007 in the University Medical Center Groningen. mGFR was measured as the urinary clearance of ¹²⁵I-iothalamate 4 months before and 2 months after kidney donation as part of the screening program and postdonation evaluation (19). eGFR was calculated from creatinine samples that were drawn on these same days. Procedures were conducted in accordance with the Declaration of Helsinki. For evaluation of practical consequences for screening for donation, data from 295 subsequent individuals who were screened for donation, without selection criteria other than referral for donation, were analyzed: The aforementioned 253 individuals, as well as 42 individuals who all completed the full screening program but did not donate for a variety of medical and nonmedical reasons.

GFR Measurement

mGFR was measured by constant low-dosage infusion of the radiolabeled tracer ¹²⁵I-iothalamate as described by Apperloo et al. (20). Simultaneously, effective renal plasma flow was measured as the clearance of ¹³¹I-hippurate. For the measurements, individuals were seated in a quiet room in a semisupine position. After drawing a blank blood sample, the priming solution containing 0.04 ml/kg body wt of the infusion solution (0.04 MBq of ¹²⁵I-iothalamate and 0.03 MBq of ¹³¹I-hippurate per ml of saline) plus an extra 0.6 MBq of ¹²⁵I-iothalamate was given, followed by constant infusion at 12 ml/h. For attainment of stable plasma concentrations of both tracers, a 2-hour stabilization period followed, after which the clearance periods started. Clearances were measured during the subsequent 2 hours and calculated as (U*V)/P and (I*V)/P, respectively. U*V represents the urinary excretion of the tracer, I*V represents the infusion rate of the tracer, and P represents the tracer value in plasma at the end of each clearance period. mGFR was calculated from UV/P of ¹²⁵I-iothalamate and corrected for voiding errors by multiplying the urinary clearance of ¹²⁵I-iothalamate with the ratio of the plasma and urinary clearance of ¹³¹I-hippurate. The day-to-day variability for mGFR is 2.5%. Creatinine was determined from blood samples that were drawn during the GFR measurement.

Calculations

The four-variable MDRD equation was used, which is standard for creatinine samples that are traceable to the isotope dilution mass spectrometry. eGFR by MDRD and CG equations was calculated as follows, with SCr and body weight in mg/dl and kg (9):

• MDRD = 175 * (SCr)^−1.154 * (age)^−0.203 * 0.742 (if female).

• Cockcroft-Gault = (140 − age) * body weight/(72 * SCr) * 0.85 (if female).

• CKD-EPI equation was calculated gender specific and stratified by creatinine levels. The following calculations were used (12):

• Female with SCr ≤0.7: GFR = 144 * (0.993)^age * (SCr/0.7)^−0.329

• Female with SCr >0.7: GFR = 144 * (0.993)^age * (SCr/0.7)^−1.209

• Male with SCr ≤0.9: GFR = 141 * (0.993)^age * (SCr/0.9)^−0.4111

• Male with SCr >0.9: GFR = 141 * (0.993)^age * (SCr/0.9)^−1.209

For both the MDRD and CKD-EPI equations, no correction for ethnicity was applied because none of the donors was black.

Body surface area (BSA) was calculated as according to DuBois and DuBois (21). mGFR and CG were normalized by dividing the raw sample by BSA and multiplying it by 1.73, giving mGFR/_BSA and CG/_BSA. Mean arterial pressure (MAP) was calculated as MAP = [(2 * diastolic pressure) + systolic pressure]/3.

Analysis of Predictive Performance

Performance of MDRD, CKD-EPI, and CG/_BSA against mGFR/_BSA was analyzed as proposed by Bostom et al. (22) and Stevens et al. (23), presenting bias, precision, and accuracy. Bias was calculated as median of the absolute difference (mGFR − eGFR) and of the percentage difference [(mGFR − eGFR)/mGFR * 100], giving a numeric or arithmetic value and a relative value. Precision represents the overall “fit” of the new model against the gold standard. It is represented by the interquartile range (IQR) of (mGFR − eGFR) and the R² of the linear regression of eGFR on mGFR. Accuracy reflects the proportion of individuals with eGFR values within ±30% of mGFR (P₃₀).

Calibration of Creatinine Samples

In our center, from blood samples that were drawn after March 1, 2006, SCr was measured by enzymatic assay on the Roche Modular. Before this date, samples had been measured by Jaffé alkaline picrate assay, on the MEGA (Merck KGaA, Darmstadt, Germany). Both methods were calibrated to the reference standard (Cleveland Clinic Laboratory measurements), as proposed by Coresh et al. (24). To this purpose, a total of 516 blood samples with a broad range of creatinine were sent to the Cleveland Laboratory, 177 of which were from before March 1, 2006. Samples for calibration purposes were stored at −80°C until measured on the Roche <P> module enzymatic assay with verified traceability to the reference standard isotope dilution mass spectrometry. Calibration equations were as follows: Calibrated SCr = [−0.300 + 1.217 * (University Medical Center Groningen Jaffé creatinine values in mg/dl)] for measurements before March 1, 2006, and [0.011 + 1.087 * (University Medical Center Groningen Roche creatinine values in mg/dl)] for measurements after March 1, 2006. MDRD, CKD-EPI, and CG were calculated from calibrated creatinine values.

Statistical Analysis

Analyses were performed using SPSS 16.0 and GraphPad Prism 5 for Windows. Data are given as means ± SD or medians (IQR). Paired-samples t test and Wilcoxon signed-ranks test were used to analyze differences between pre- and early postdonation values. For comparison of accuracy at both time points, χ² test was used. For all three equations, eGFR was plotted on true mGFR/_BSA, and linear regression was performed to display differences in the relationship from before to after donation. For limiting influence of extreme outliers, 95% of the data were used for regression analysis. Furthermore, pre- and postdonation biases were stratified according to tertiles of predonation mGFR/_BSA. Univariate and backward multivariate analyses were performed to evaluate determinants of pre- and postdonation bias.

To evaluate the value of eGFR for donor screening, Bayes theorem was applied to predict probability of an mGFR <80 given an eGFR <80 ml/min per 1.73 m². Calculations were as follows: Posterior change = (prior * likelihood)/evidence [i.e., p(A|B) = [p(A) * p(B|A)]/p(B)]. For the analysis, a break-up by gender, median age (50 years), and normal weight or overweight was made.

Results

Donor characteristics before and early after donation are given in Table 1. Estimates from MDRD, CKD-EPI, and CG/_BSA equations all significantly underestimated mGFR/_BSA at both time points (all P < 0.001). Over donation, BP (MAP) increased slightly but significantly (P < 0.001); body mass index (BMI) was unchanged. In a subset of 91 donors, paired measurements of 24-hour urinary creatinine excretion were available. Predonation 24-hour creatinine excretion was similar to postdonation values (1.60 ± 0.53 and 1.61 ± 0.67 g/d, respectively), consistent with stable muscle mass as a partial index of body composition at both time points.

Table 1.

Donor characteristics (n = 253)

Characteristic	Before Donation		After Donation		P
	Mean ± SD	Median (IQR)	Mean ± SD	Median (IQR)
% Female	57	—	57	—	—
Age (years)	49.5 ± 10.5	49.8 (43.0 to 56.0)	50.0 ± 10.5	50.5 (43.8 to 56.5)	By default
MAP (mmHg)	92 ± 9	92 (85 to 97)	93 ± 9	94 (86 to 100)	0.008/0.024
BMI (kg/m2)	26 ± 4	26 (23 to 28)	26 ± 4	26 (23 to 28)	NS
SCr (mg/dl)	0.88 ± 0.16	0.87 (0.76 to 0.99)	1.32 ± 0.26	1.30 (1.14 to 1.49)	<0.001
mGFR (ml/min)	115 ± 20	114 (101 to 128)	73 ± 13	72 (65 to 81)	<0.001
mGFR/BSA (ml/min per 1.73 m2)	103 ± 15	102 (92 to 113)	66 ± 11	66 (59 to 72)	<0.001
eGFR (ml/min per 1.73 m2)
MDRD equation	81 ± 15a	78 (71 to 89)a	51 ± 9b	50 (44 to 56)b	<0.001
CKD-EPI	89 ± 14a	88 (78 to 100)a	56 ± 11b	54 (47 to 62)b	<0.001
CG/BSA	95 ± 20a	94 (80 to 106)a	63 ± 13b	62 (55 to 71)b	<0.001

Donor characteristics before and shortly after donation. P values represent postdonation values compared with predonation values by paired-samples t test and Wilcoxon signed ranks test, respectively.

P < 0.001 compared with

^abefore donation and

^bafter donation mGFR/_BSA (paired samples t test and Wilcoxon signed-ranks test).

After donation, all donors had lower kidney function and higher SCr, reflecting loss of one kidney (Table 2). The absolute mGFR decline as well as the percentage decrease after donation was significantly underestimated by each of the tested equations (all P < 0.02), although the percentage decrease of MDRD and CKD-EPI were virtually constant to the change in mGFR.

Table 2.

Change in mGFR and eGFR before and after donation (n = 253)

Parameter	ml/min per 1.73 m2		% of Predonation (e)GFR
	Mean ± SD	Median (IQR)	Mean ± SD	Median (IQR)
Change in mGFR/BSA	37 ± 10	37 (31 to 43)	36 ± 7	36 (31 to 41)
Change in MDRD	31 ± 11a	29 (24 to 36)a	37 ± 9a	37 (32 to 43)
Change in CKD-EPI	33 ± 10a	33 (27 to 40)a	37 ± 9a	38 (33 to 43)a
Change in CG/BSA	32 ± 12a	31 (25 to 39)a	34 ± 8a	34 (29 to 39)a

^aP < 0.001 compared with change in mGFR/_BSA (paired-samples t test and Wilcoxon signed-ranks test).

Performance of Renal Function Equations

Performance of MDRD, CKD-EPI, and CG/_BSA equations before and after donation is given in Table 3. For the arithmetic values, performance was better after donation (P < 0.01). This is consistent with the higher R² of regression of eGFR on mGFR after donation. The relative difference, however, suggests similar performance of the MDRD equation and slightly worse performance after donation for the CKD-EPI equation with a larger median difference and IQR (P < 0.05). Overall accuracy, as estimated by the P₃₀, remained stable for MDRD and CKD-EPI equations, whereas it increased for CG/_BSA (P < 0.001 by χ²). The individual values of the change in bias over donation are given in Figure 1.

Table 3.

Overall performance of eGFR in kidney donors: Pre- and postdonation values for MDRD, CKD-EPI, and CG/_BSA in n = 253

Parameter	Difference between mGFR and eGFR (ml/min per 1.73 m2)		% Difference between mGFR and eGFR		R2	P30 (%)
	Median (95% CI)	IQR (95% CI)	Median (95% CI)	IQR (95% CI)
Before donation
MDRD	22 (20 to 25)	20 (14 to 26)	22 (20 to 24)	17 (12 to 21)	0.16	73 (68 to 79)
CKD-EPI	14 (11 to 16)	18 (14 to 22)	13 (11 to 16)	16 (13 to 21)	0.20	89 (85 to 93)
CG/BSA	10 (7 to 12)	21 (16 to 29)	10 (7 to 12)	21 (16 to 28)	0.14	90 (86 to 94)
After donation
MDRD	15 (14 to 16)a	12 (9 to 15)	23 (21 to 25)a	17 (12 to 21)	0.31	71 (65 to 76)
CKD-EPI	11 (9 to 11)a	12 (10 to 16)	16 (14 to 19)a	20 (15 to 23)	0.35	89 (85 to 93)
CG/BSA	4 (2 to 5)a	14 (11 to 18)	6 (3 to 9)a	22 (11 to 27)	0.31	93 (90 to 96)

Bias median mGFR − eGFR (ml/min per 1.73 m²; tested by paired Wilcoxon signed-ranks test). Precision: IQR of difference between mGFR and eGFR; R² from regressing eGFR on mGFR. Accuracy: Percentage of eGFR within 30% of mGFR (tested by χ²).

^aP < 0.05 before versus after donation.

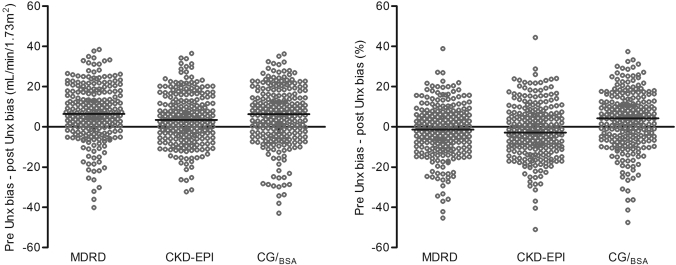
Figure 1.

Individual values of the change (Δ) in bias over donation (Unx). Δ was calculated as (predonation bias − postdonation bias) in ml/min per 1.73 m² for arithmetic values (left) and as a percentage difference for relative values (right). Error bars represent median bias. The arithmetic values show a positive median bias for all equations with a large variation between the individual donors. Relative values show a small negative median bias for MDRD and CKD-EPI study equations, again with large variation.

Correlation of Δ relative bias and the amount of decrease of mGFR over donation showed positive relations for all equations (i.e., a larger drop in mGFR correlates to a larger decrease of relative bias). R² values for the drop in mGFR in ml/min were 0.22, 0.30, and 0.31 and for the change in mGFR as percentage of predonation mGFR were 0.23, 0.25, and 0.33 for MDRD, CKD-EPI, and CG/_BSA, respectively (all P < 0.01).

Regression between mGFR/_BSA and eGFR

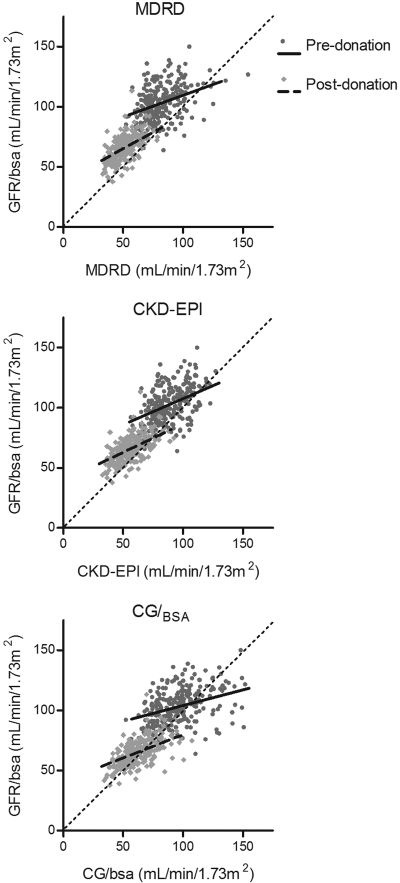
An overlay scatter plot for both time points was made for all three equations (Figure 2), showing the regression of GFR/_BSA and eGFR before and after donation in the same plot. It shows a steeper regression slope after donation for all three equations.

Figure 2.

Regression of eGFR on mGFR/_BSA for all three equations for predonation (dark dots; solid line) and postdonation (gray diamonds; dotted line) values. Pre- and postdonation slopes of the regression lines are, respectively, 0.36 ± 0.05 and 0.55 ± 0.05 for MDRD, 0.43 ± 0.06 and 0.47 ± 0.04 for CKD-EPI, and 0.26 ± 0.04 and 0.39 ± 0.04 for CG/_BSA.

Influence of Level of mGFR on eGFR Bias

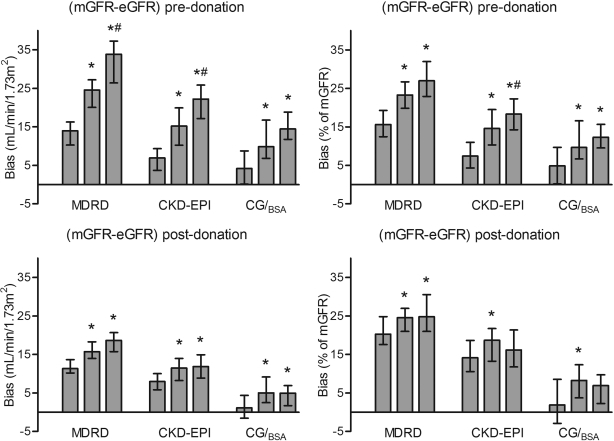
Pre- and postdonation biases were divided according to tertiles of predonation mGFR/_BSA. Figure 3 shows median bias for pre- and postdonation arithmetic and relative values for each equation. Pre- and postdonation arithmetic biases were higher in the higher tertiles of mGFR for all equations. For relative values, postdonation CKD-EPI and CG/_BSA showed stable bias over the tertiles.

Figure 3.

Pre- and postdonation bias as arithmetic (left) and relative values. Arithmetic bias was calculated as (mGFR − eGFR) and relative bias as [(mGFR − eGFR)/mGFR * 100]. Bias was divided according to tertiles of predonation mGFR/_BSA; therefore, pre- and postdonation tertiles contain the same donors. Tertile median (IQR) values of predonation mGFR/_BSA were 87 (82 to 92), 102 (99 to 106), and 118 (113 to 125), respectively. Corresponding values for postdonation mGFR/_BSA were 56 (53 to 62), 66 (61 to 71), and 73 (68 to 77) ml/min per 1.73 m². Bars represent medians with 95% confidence intervals. *P < 0.05 versus first tertile; #P < 0.05 versus second tertile.

Anthropometric Determinants of Bias before and after Donation

Univariate analysis of determinants of pre- and postdonation biases is listed in Table 4. Multiple significant factors on univariate analysis were combined in backward multivariate analysis. Bias in the MDRD equation after donation was best predicted by a model with age and BMI (R² = 0.03; P < 0.01). Pre- and postdonation biases of CG/_BSA were predicted by all tested factors: Age, BMI, and gender (R² = 0.28 and 0.26, respectively; both P < 0.001). Bias of CKD-EPI was not significantly influenced by these factors.

Table 4.

Univariate analysis of pre- and postdonation bias

Parameter	Age (R2; P)	BMI (R2; P)	Gender (R2; P)
Before donation
MDRD	0.012; 0.04	NS	NS
CKD-EPI	NS	NS	NS
CG/BSA	0.067; <0.001	0.183; <0.001	0.024; <0.01
After donation
MDRD	0.017; 0.02	0.011; 0.05	NS
CKD-EPI	NS	0.017; 0.02	NS
CG/BSA	0.102; <0.001	0.127; <0.001	0.026; <0.01

Practical Consequences for Donor Selection by a Bayesian Approach

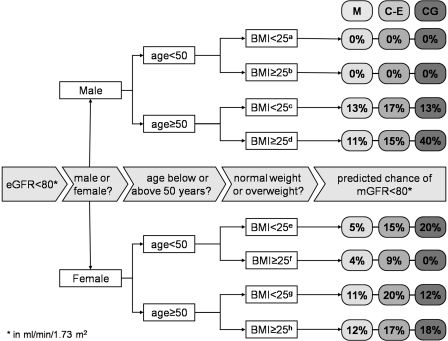
Finally, to address practical consequences for donor selection, we calculated the probability that a potential donor with an eGFR <80 ml/min per 1.73 m² indeed had an mGFR <80 ml/min per 1.73 m². Of the 295 potential donors analyzed (44% male; mean age 50 ± 11 years; BMI 27 ± 5 kg/m²), mean mGFR, MDRD, CKD-EPI, and CG/_BSA were 103 ± 16, 81 ± 15, 88 ± 14, and 95 ± 21 ml/min per 1.73 m², respectively. mGFR was <80 ml/min per 1.73 m² for 19 individuals; this was true for 166 individuals by MDRD, for 98 individuals by CKD-EPI, and for 74 individuals by CG/_BSA. The predicted probabilities of mGFR <80 when eGFR was <80 ml/min per 1.73 m² were 8, 14, and 18% for MDRD, CKD-EPI, and CG/_BSA equations, respectively. Analyses for subgroups defined by gender, age, and BMI are shown in Figure 4, showing that the prediction of true GFR <80 is slightly improved by taking into account these demographic parameters.

Figure 4.

Predicted probability of mGFR <80 when eGFR was <80 ml/min per 1.73 m² by Bayes theorem. Percentages represent probabilities calculated by Bayes theorem, for MDRD (M), CKD-EPI (C-E), and CG/_BSA (CG) equations in 295 subsequent individuals who were referred for donor screening without previous selection. Break-ups are made for gender, age, and BMI. The number of individual in each subgroup is as follows: ^an = 20, ^bn = 41, ^cn = 25, ^dn = 45, ^en = 39, ^fn = 43, ^gn = 34, and ^hn = 48.

Discussion

This article discusses the influence of level of mGFR on performance of eGFR in a situation of normal and lower mGFR in the same healthy individual. When expressed in ml/min, bias of eGFR is reduced at lower values of mGFR (i.e., after kidney donation). For bias expressed as percentage difference, this was true only for CG/_BSA. In the limited time frame, donor characteristics remained similar. The previously described determinants of bias—age, BMI, and gender—influenced bias, although only limited; therefore, these data support the assumption that mGFR is a determinant of performance of eGFR.

This study is the first to compare performance of eGFR in high and lower ranges of mGFR within the same individuals. Although we cannot exclude subtle changes in body composition, anthropometric parameters stayed virtually constant during this time frame, and age increased similarly for all individuals; therefore, our setting allows dissection of the effect of mGFR as such.

For arithmetic calculated bias (ml/min), all equations showed improved performance after donation. The relationship between eGFR and mGFR improved, although the difference for CKD-EPI was markedly lower than for MDRD and CG/_BSA (Figure 2). Influence of mGFR on arithmetic bias was confirmed (Figure 3).

For relative values (percentage difference), CG/_BSA performance significantly improved after donation, although influence of mGFR after donation was less. The MDRD study equation was stable in performance analysis, although mGFR influenced MDRD bias at both time points. CKD-EPI performed slightly worse for postdonation values, reflected by a loss of influence of mGFR on bias (Figure 3).

Although our data support an important role of the absolute level of GFR in the performance of eGFR, we cannot ascribe deviation from mGFR in these healthy individuals to mGFR alone. Healthy people may differ in body composition and physiology of creatinine handling from patients with CKD, leading to a more dominant effect of protein intake and muscle mass on SCr in healthy individuals, whereas in patients with CKD, true GFR may have a more dominant effect (2,14). Comparing performance in healthy individuals with lower mGFR to matched patients with CKD can give insight into this mechanism. Because both MDRD and CG equations were derived from populations with a reduced GFR (9,10), they may overstate the strength of the relationship between GFR and SCr in healthy individuals (14). The CKD-EPI equation was developed and validated in populations with a broader range of renal function and contains a spline function that enables it to capture differentially this relationship and therefore shows to be less influenced by mGFR in this study.

To account for variation in muscle mass as a variable in creatinine production, demographic and/or other anthropometric data were included in GFR estimating equations. The MDRD algorithm was shown to represent inadequately variance in muscle mass (23) and produces systematic errors in estimation of GFR. Performance of CG was found to deviate with age and BMI (16,26). Studies of renal transplant recipients confirmed age, gender, and BMI to be significant determinants of bias in MDRD and CG equations (15,17,26).

Variation among laboratories in reporting SCr has been proposed as an important cause of deviation of eGFR (11,24,27). We therefore used calibration equations to calibrate our serum samples to the Cleveland laboratory.

For MDRD and CG/_BSA, influence of level of mGFR could be explained by the approximately hyperbolic curve of the relation between mGFR and SCr, which translates to a stronger relationship between the equations and mGFR at lower levels of mGFR, here reflected by a steeper slope of regression of eGFR on mGFR after donation. The new CKD-EPI equation seems to be more stable in different conditions. mGFR had less influence on group performance of CKD-EPI compared with the other two equations. In individual analysis, however, CKD-EPI showed a similar variation as the other equations. Bias of CKD-EPI was not influenced by age, BMI, or gender.

All three equations significantly underestimated kidney function at both time points. This is in line with previous studies of the MDRD and CG equations; therefore, recently, the CKD-EPI equation was proposed (12). Predonation values of 43 donors included in this study were used in the external validation set of the CKD-EPI equation as well (12,19). For these 253 donors, CKD-EPI showed to be the most precise equation. Our analysis does support better performance of the CKD-EPI equation in healthy kidney donors when compared with MDRD, albeit not optimal. CKD-EPI does shows more stable performance than the other two equations, which is an important characteristic for clinical use.

For donor screening, underestimation by eGFR at normal or higher values of mGFR can have large consequences. It is known that generally <90% of eGFR results are even within ±30% of mGFR. Our Bayesian analysis, moreover, illustrates large impact of the GFR-dependent underestimation of mGFR by eGFR in a population of prospective donors, in which the previous probability of impaired renal function was low. For all three equations, the probability that an eGFR <80 ml/min per 1.73 m² indicated an mGFR <80 ml/min per 1.73 m² was low. Use of eGFR may declare a substantial proportion of potential donors unfit for donation on the basis of a flawed estimate. Another pitfall, however, may be acceptance of donors whose mGFR is far lower than estimated, with possible enhanced risks after donation. The influence of use of eGFR on donor screening needs more detailed evaluation, with special attention to long-term donor outcome.

Conclusions

Level of mGFR is an important modulator of performance of eGFR. Factors that contribute to differences in deviation of eGFR between individuals with higher and lower mGFR could be differences in creatinine handling and body composition between healthy people and patients with CKD and other factors related to the level of GFR as such. The unique nature of this study population is that body composition was removed as a contributing factor. This shows that mGFR as such is the main determinant of bias expressed in ml/min but also that bias expressed as a percentage difference is stable over the range of GFR investigated. Whereas for clinical use, use of eGFR has been discouraged at a value >60 (7), epidemiologic research tends to use eGFR above this level. We believe that application of eGFR in healthy individuals should be used with caution. All three equations discussed here are unreliable tools for evaluation of living kidney donors.

Disclosures

None.