Mathematical Modeling for the Pathogenesis of Alzheimer's Disease

Abstract

Despite extensive research, the pathogenesis of neurodegenerative Alzheimer's disease (AD) still eludes our comprehension. This is largely due to complex and dynamic cross-talks that occur among multiple cell types throughout the aging process. We present a mathematical model that helps define critical components of AD pathogenesis based on differential rate equations that represent the known cross-talks involving microglia, astroglia, neurons, and amyloid-β (Aβ). We demonstrate that the inflammatory activation of microglia serves as a key node for progressive neurodegeneration. Our analysis reveals that targeting microglia may hold potential promise in the prevention and treatment of AD.

Introduction

Alzheimer's disease (AD) is one of the most prevalent neurodegenerative disorders associated with aging, causing dementia and related severe public health concerns [1]. Despite extensive research effort and progress, the pathogenesis of AD remains incompletely understood, partly due to highly complex and intertwined intercellular cross-talks taking place throughout the aging process [2]. Consequently, despite limited treatment options to manage and slow the progression of AD, no effective cure is available.

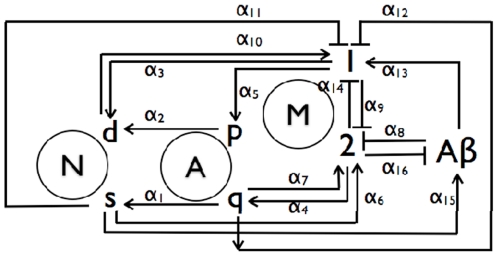
Although the deposition of amyloid-β (Aβ) peptides and formation of senile plaques in the brain is the cardinal morphological feature identifying the clinical phenotype of AD [3], [4], increasing clinical and basic studies suggest that inflammatory activation of microglia may play an equally important role during the initiation and progression of the disease [5]. Microglia are resident innate immune macrophages within brain tissues, capable of expressing pro-inflammatory mediators and reactive oxygen species when activated by inflammatory signals including amyloid-β (Aβ) [6]. In healthy brains, together with quiescent astroglia (Aq), resting microglia may adopt an anti-inflammatory state (M2) and in turn foster neuron survival (Ns) and prevent astroglia proliferation (Ap) [7], [8]. As inflammatory signals (e.g. Aβ) gradually build, microglia may adopt an activated pro-inflammatory state (M1), leading to A_p proliferation and neuron death (Nd) [9], [10], [11]. Neuronal debris, amyloid-β (Aβ), and/or proliferating astroglia (Ap) may in turn further exacerbate the inflammatory phenotype of M1 macroglia [12], [13]. The multiple positive and negative feedbacks among these cells are thus crucial for neurodegeneration that eventually alters the neuronal structure and function during the pathogenesis of AD (Figure 1).

Figure 1. Schematic of the AD mechanism that incorporates feedback influences from surviving and dead neurons, N_s and N_d, quiescent and proliferating astroglia A_q and A_p, reactive and normal microglia, M₁ and M₂, and Aβ.

The rates associated with the pathways are included in Table 1.

Due to its multi-cellular components and complex nature, conventional experimental approaches have failed to identify critical underlying causes for AD, contributing to the lack of an effective therapeutic treatment. Mathematical models can serve as powerful tools to understand the molecular and cellular processes that control complex diseases [14], [15]. Indeed, there have been several attempts to model the process of senile plaque formation [16], [17], [18], [19]. Specifically, these approaches focused on a nucleation step that is coupled with rates for the irreversible binding of Aβ monomers to the fibril ends, the lateral aggregation of filaments into fibrils, and fibril elongation through end-to-end association. Other modeling efforts examined the signaling cascade responsible for microglia migration and activation in response to an initial inflammation-provoking stimulus involving Aβ [16], [20].

However, no systematic modeling approaches have been reported to examine the network cross-talks among microglia, neuron, and astroglia, and the corresponding pathological consequence. Here, we evaluate the dynamic network involving multiple cross-talks among distinct states of microglia, astroglia, and neurons through a mathematical model. Our approach has led to an intriguing insight suggesting that microglia activation in addition to a threshold for Aβ may be the critical initiator for the pathogenesis of AD.

Methods

Mathematical Method

We propose a sixteen pathway AD mechanism involving seven species that is shown schematically in Fig. 1. The paths have rates α_i that implicitly represent the influences of intercellular signaling along them. The mechanism is based on an assumption of constant risk of neuronal death, i.e., a single event randomly initiates cell death independently of the state of any other neuron at any instant [21]. The spatiotemporal influence of diffusion is neglected since local cell events are assumed to occur on a slower timescale than signal dispersion through chemotaxis.

The seven rate equations for the cell populations and the number of Aβ molecules in an arbitrary local volume can be written through seven coupled rate equations, namely,

(1)

(2)

(3)

(4)

(5)

(6)

(7)

These relate the change in each cell population or the number of Aβ molecules at any instant to the values of all species at that time. For instance, Eq. (1) relates the rate of change in N_s to the A_q, A_p, and M₁ populations with the pathway weights α₁, α₂, and α₃, respectively. Whereas A_q increases the rate of change of N_s, A_p and M₁ decrease it. Equation (5) for the rate of change of the M₂ population is the most complex, since it involves nine pathway weights, and five cell populations and Aβ. The conversion of N_s into N_d is irreversible, whereas those of A_q and M₂ into A_p and M₁ are reversible.

The rates for each α_i are specified, as shown in presented in Table 1 for each pathway. Since the literature points to the path N_s → Aβ being dominant, we assume that it is also the fastest. Its rate is set at 1/year, i.e., each year every N_s cell stimulates the formation of a sustaining an Aβ molecule. Likewise, since neuronal survival decreases significantly once disease progresses, we assume that the overall path M₂ → A_q → N_s is slow so that the associated rates α₁ and α₄ are also relatively the smallest. The other rates are similarly specified in terms of their relative abilities to facilitate or inhibit the formation of a cell or Aβ molecule according to the particular pathway. Next, we specify the initial composition of the volume under consideration. These initial conditions for the seven species are presented in Table 2.

Table 1. Mathematical parameters describing the functional interactions among various cell types.

Rate	1/year	Pathway	S(Ns)	S(Nd)	S(M1)	S(M2)	Sensitivity
α1	10−5	Aq → Ns	50000	−50000	−6000	6000	Strong
α2	10−3	Ap → Nd	−500	500	−60	60	Weak
α3	10−2	M1 → Nd	−200	200	−35	35	Weak
α4	10−4	M2 → Aq	500	−500	150	−150	Weak
α5	10−2	M1 → Ap	−3	3	1	−1	Weak
α6	10−2	Ns → M2	500	−500	−6000	6000	Weak
α7	10−4	Aq → M2	5000	−5000	−50000	50000	Strong
α8	10−2	Aβ ⊥ M2	−400	400	5000	−5000	Moderate
α9	10−2	M1 ⊥ M2	−30	30	250	−250	Weak
α10	10−2	Nd → M1	−8	8	90	−90	Weak
α11	10−2	Ns ⊥ M1	500	−500	−6000	6000	Moderate
α12	10−4	Aq ⊥ M1	5000	−5000	−50000	50000	Strong
α13	10−2	Aβ → M1	−400	400	5000	−5000	Moderate
α14	10−4	M2 ⊥ M1	5000	−5000	−50000	50000	Strong
α15	1	Ns → Aβ	−10	10	100	−100	Weak
α16	10−2	M2 ⊥ Aβ	100	−100	−1000	1000	Weak
αr	1	M2 ⊥ Aβ	8	−8	−100	100	Weak

The rates α_i associated with the pathways of the AD mechanism, and the sensitivities of the N_s and N_d populations to variations in the values of α_i. The values for the sensitivity coefficients S(N_{j, j = s, d})  =  dN_j/dα_i are determined after 20 years for ±2.5% perturbations in each α_i value. A cell population is more sensitive to a change in a rate that produces a larger value of |S(N_j)|. Positive S(N_j) imply that a rate contributes to an increase in N_j while a negative value entails a corresponding population decrease.

Table 2. Sensitivities of the cell types to the initial conditions.

	Ns(0)	Nd(0)	Aq(0)	Ap(0)	M1(0)	M2(0)	Aβ (0)
Value	104	102	105	103	103	105	103
S(Ns)	1	≈0	≈0	≈0	−0.2	0	≈0
S(Nd)	≈0	1	≈0	≈0	0.2	≈0	≈0
S(Aq)	≈0	≈0	1	≈0	−0.2	≈0	≈0
S(Ap)	≈0	≈0	≈0	1	0.2	≈0	≈0
S(M1)	≈0	0.2	≈0	≈0	1.2	≈0	≈0
S(M2)	≈0	−0.2	≈0	≈0	−0.2	1	≈0
S(Aβ)	1	≈0	≈0	≈0	−0.2	≈0	≈0

Initial values X(0) of the initial cell populations and the number of molecules of Aβ in an arbitrary local volume and orders of magnitude for the sensitivity coefficients S(N_{j, j = s,d})  =  dN_j/d(X(0)) determined after 20 years for tenfold perturbations, i.e., 10× and 10⁻¹×, in these initial values.

Results

Our objective is to be able to describe neuropathogenesis during AD in terms of the N_s and N_d populations. Hence, we first determine the sensitivities of these cells to changes in the rates α_i, using the usual definition of the sensitivity coefficient,

(8)

The sensitivity coefficients for N_s, N_d, M₁ and M₂ cells, presented in Table 1, are determined after 20 years for ±2.5% perturbations in each α_i value. A cell population is more sensitive to a change in a rate that produces a larger value of |S(N_j)|. Positive values for S(N_j) imply that a rate contributes to an increase in N_j while a negative value implies that its influence leads to a corresponding population decrease. The sensitivity analysis shows that the N_s and N_d populations are most sensitive to the path A_q → N_s, which increases neuronal survival and decreases neuron death. Important paths that inhibit neuropathogenesis include A_q → M₂, A_q ⊥ M₁ and M₂ ⊥ M₁, while those that enhance disease involve M₁ → N_d, Aβ ⊥ M₂ and Aβ → M₁.

A similar analysis that perturbs the initial cell populations and the number of Aβ molecules tenfold is presented in Table 2. It shows that, in comparison to the other species, the M₁ population is most sensitive to these substantial perturbations in the initial amount of any species while N_d is only sensitive to the initial amounts of M₁ and M₂. This implies an important role for microglia during AD progression. The sensitivity coefficients S(M₁) and S(M₂), also presented in Table 1, show that, as for N_s and N_d, the dominant paths that inhibit neuropathogenesis by affirming M₂ and decreasing M₁ are also A_q → M₂, A_q ⊥ M₁ and M₂ ⊥ M₁. Once again, paths 7 and 14 involving Aβ, i.e., Aβ ⊥ M₂ and Aβ → M₁ promote AD progression. The model suggests that interventions aimed at decreasing α₈ and α₁₃, which involve M₁, M₂ and Aβ and contribute to AD progression, are the ones more likely to diminish neuropathogenesis. This intuitive result emphasizes that decreasing the number of reactive microglia and ensuring a sufficient population of quiescent astroglia is important in treating AD.

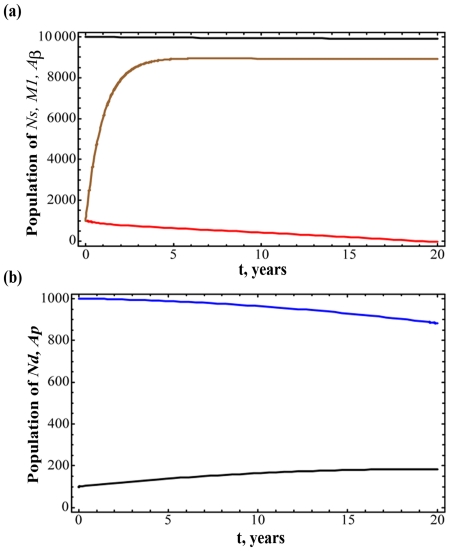
The temporal variation in various species for the rates in Table 1 is illustrated in Fig. 2. Figure 2(a) presents the N_s, M₁ and Aβ populations over 20 years, and Fig. 2(b) the corresponding values for N_d and A_p. Most notable is the influence of the removal rate α_r, which stabilizes the number of Aβ molecules after three years. Following that period, there is only a gradual increase in N_d that is coupled with a corresponding decline in N_s. Consequently, the microglia populations are also relatively stable. Therefore, the rates in Table 1 should be considered as being representative of a healthy population.

Figure 2. Dynamic simulation of various cell populations during the progression of Alzheimer's disease.

The (a) N_s (black), M₁ (red) and Aβ (blue), and (b) N_d (black) and A_p (blue) populations over 20 years for the rates reported in Table 1. The removal rate α_r stabilizes the net number of Aβ molecules after three years so that there is only a gradual increase in N_d and corresponding decline in N_s thereafter. The microglia populations are also consequently relatively stable.

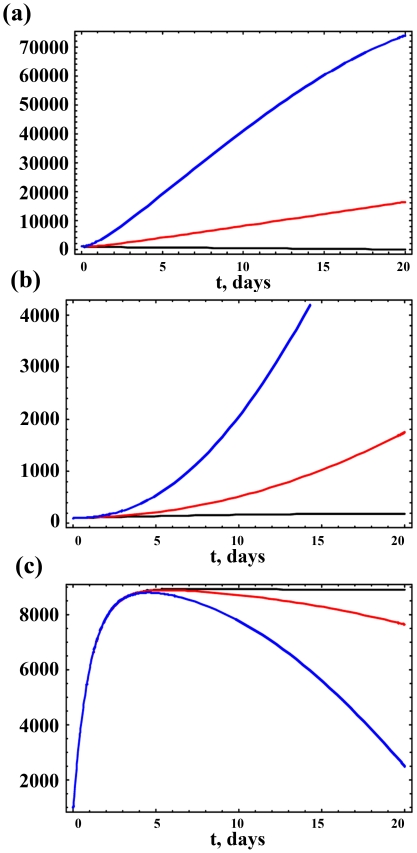
We examine the influence of varying α_r on neuropathogeneis in Fig. 3, which presents the M₁, A_p, Aβ and N_d populations over 20 years for three values of α_r. As α_r decreases, there is an increasing neuronal death. Thus, all four populations, which are associated with AD progression, increase. While microglia play an important role in AD, Fig. 3 shows how the local Aβ concentration plays a critical role in initiating and promoting AD.

Figure 3. Dynamic variations of cell populations given distinct Aβ removal rate.

Variations in the (a) M₁, (b) A_p, (c) Aβ, and (d) N_d populations over 20 years for three values of α_r  =  1× (black), 10⁻¹× (red), and 10⁻²× (blue) the value reported in Table 1 for the Aβ removal rate. As α_r decreases, there is an increase in neuropathogenesis so that all four populations increase.

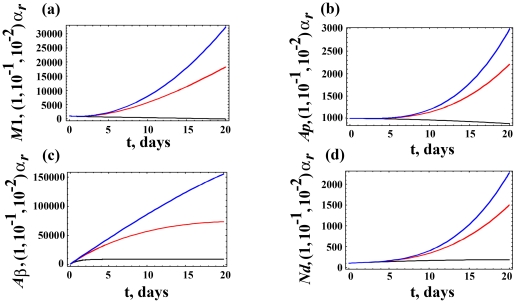
We investigate this further by varying α₈ and α₁₃. Figure 4 presents results for the M₁, N_d and Aβ populations over 20 years for three values of α₁₃. As α₁₃ increases, the M₁, A_p and N_d populations also increase, leading to an associated decrease in neuronal survival, as illustrated through Eqs. (1) and (2) of the mathematical model. A tenfold increase in α₁₃ leads to a near doubling in N_d after 20 years. As N_s decreases so does Aβ, but the smaller protein concentration is still sufficient to promote neuropathogenesis among the smaller N_s population. Identical results are obtained for similar variations in the rate α₈ for Aβ ⊥ M₂, since the sensitivity coefficients for each of M₁ and N_d towards paths 8 and 13 are identical.

Figure 4. Dynamic variations of cell populations given distinct impacts of Aβ on M1 macrophages (the value of α₁₃).

Variations in the (a) M₁, (b) N_d and (c) Aβ populations over 20 years for three values of α₁₃  =  1× (black), 10× (red), and 50× (blue) the value reported in Table 1 for the path Aβ → M₁. As α₁₃ increases, M₁ and N_d also increase and, consequently, there is an associated decrease in neuronal survival. This is also illustrated through Eqs. (1) and (2) of the mathematical model.

Discussion

We present a mathematical model for neuropathogenesis during AD that involves neurons, normal and reactive glial cells, and Aβ. It uses neuronal death as a surrogate for senile plaque formation. By monitoring neuronal health, we are able to identify intuitive strategies for interventions. In particular, the model suggests that the most effective intervention is one that improves the inhibition of reactive microglia and Aβ by normal microglia, and ensuring a sufficient population of quiescent astroglia. Overall, neuropathogenesis proceeds through the production of reactive microglia.

Our analysis is consistent with experimental data that indicate that inflammation may be an early initiator for AD, long before the apparent senile plaque formation [22], [23]. It further reinforces the notion that additional studies should be directed at examining earlier inflammatory signals and alterations involving microglia as a key node so as to better define AD initiation and understand mechanisms for effective prevention and treatment of the disease.

We realize that our mathematical analysis is an initial attempt to examine AD and may not fully account for the associate intertwined cellular communication pathways. Nevertheless, it serves as a hypothesis provoking and building process that should encourage integrated analyses of AD pathogenesis. Future experimental data examining the cross-talks among microglia, astroglia, and neurons will allow us to better refine our model and implement realistic parameters in the rate equations.