Abstract
Advances in high-throughput and mass-storage technologies have led to an information explosion in both biology and medicine, presenting novel challenges for analysis and modeling. With regards to multivariate analysis techniques such as clustering, classification, and regression, large datasets present unique and often misunderstood challenges. The authors' goal is to provide a discussion of the salient problems encountered in the analysis of large datasets as they relate to modeling and inference to inform a principled and generalizable analysis and highlight the interdisciplinary nature of these challenges. The authors present a detailed study of germane issues including high dimensionality, multiple testing, scientific significance, dependence, information measurement, and information management with a focus on appropriate methodologies available to address these concerns. A firm understanding of the challenges and statistical technology involved ultimately contributes to better science. The authors further suggest that the community consider facilitating discussion through interdisciplinary panels, invited papers and curriculum enhancement to establish guidelines for analysis and reporting.
Introduction
Advances in high-throughput and mass-storage technologies have led to an information explosion in both biology and medicine, improving and changing the face of health care, as well as presenting unique and complex challenges for analysis, modeling and inference. In the clinical arena, the twin objectives of identifying targets to minimize consumption of resources and improving quality of care drive the collection of large amounts of data. Similarly, in biology, describing the connection between genome, transcriptome, proteome, and phenome is fundamentally a problem of modeling biological information processes, involving both experimental and sequence information for an enormous number of factors. With regard to multivariate inferential techniques such as clustering, classification, and regression, many of these large datasets present unique and often misunderstood challenges. Salient issues discussed here are high dimensionality, multiple testing, dependence, scientific significance, information measurement, and information management.
Kettenring (2008) 1 reviewed several hundred papers in some detail as part of a comprehensive investigation into the practice of cluster analysis. Notably, he found that life sciences publications dominated this survey. But more importantly, he concluded that cluster analysis is among the most needed and widely used of the multivariate statistical methodologies and that it is perhaps the one with the most malpractice. He posited that, too often, a researcher's choice of analysis method is dictated and constrained by available software systems because of a lack of knowledge and/or understanding of the available tools and methodologies. These observations can be extended to analysis of large datasets in general. Literature on proper inference analysis and reporting in large datasets is limited, but anecdotally, many researchers concur that issues such as high dimensionality, multiple testing and dependence and their respective solutions, while known to varying degrees within the community, are often misused, misinterpreted, and misunderstood. In other words, there is a large gap between typical practice and best practice in the analysis of large datasets.
A principled analysis of any dataset, small or large, necessitates a firm understanding of the issues and statistical technology involved. Understanding the relevant factors in the analysis of large datasets is an important step in improving study design, structured analysis of data, and generalizability of results. Focus from the community for the development of guidelines for both analysis and the appropriate reporting of analyses performed will aid in this endeavor and ultimately contribute to better science. Here, we provide a discussion of specific problems encountered in the analysis of large datasets as they relate to modeling and inference. In an attempt to improve general understanding, we clearly define these issues, describe them, and present a brief summary of relevant research. This work does not cover general principles of data analysis, but rather those challenges specific to large datasets that affect inference. Some of the issues discussed are general, independent of the size of the data, but exacerbated in large datasets, and some are generated by the size of the data. Although we highlight methodological issues shared across informatics disciplines, we address these issues independently of their domain of application.
We recognize that the topics presented here are not exhaustive. ▶ puts these issues alongside other inference-related issues to give context. These include sample size, experimental design, data quality, and estimator appropriateness, among others. Again, this is not an exhaustive list, but rather a framework of relevant issues in inference to facilitate discussion and give context. The topics discussed in this article appear in boldface. We have chosen this set because they are especially salient in the era of large data and, more importantly, are often misunderstood. This paper is organized as follows: first, we discuss background and motivations; then we briefly review relevant methodological goals tackled in the inferential analysis of large datasets; next we present a set of salient methodological issues—high dimensionality, multiple testing, statistical significance versus scientific significance, dependence, information measurement and information management—and indicate, where possible, appropriate analytic solutions or further research problems; and finally, we offer conclusions derived from our exploration of the issues.
Table 1.
Table 1 A Framework of Issues in the Analysis of Data Sets. Bolded Rows Are Discussed Further in This Paper
| Issue | Brief Description | Present in Small Sets? | Present in Large Sets? |
|---|---|---|---|
| Sample size | issues related to the number of samples present in the data set. | X | |
| Data collection and design | issues related to methods for specifying data collection, sampling procedures, independent variables, dependent variables and how to control for external variables. | X | X |
| Data quality | issues such as noise, missing data, erroneous data and other factors which affect the quality of the data collected. | X | X |
| Dependence | issues related to samples and/or attributes of the data that are not independent or identically distributed. | X | X |
| Information Management | issues related to the identification of relevant and accurate information critical for analysis, including data quality management, integration, access control/privacy and performance. | X | X |
| Model/estimator appropriateness | issues related to model/estimator selection, quality and appropriateness with regard to the given dataset. | X | X |
| Multiple testing | issues related to the number of statistical tests on a given dataset which increases the likelihood of observing a significant result due to chance. | X | X |
| Computational Complexity | issues related to the ability to perform computations in an expedient manner | X | |
| Data integration/heterogeneity | issues related to the processing of data from different sources which may be represented differently and exhibit differing degrees of variability | X | |
| High dimensionality | issues that arise when there are a large number of attributes used to describe a given sample. | X | |
| Information measurement | issues related to the extraction and measurement of meaningful information from datasets complex in structure. | X | |
| Population drift | issues related to changes in the underlying population which may be subtle and difficult to detect. | X | |
| Secondary analyses | issues related to the secondary analysis of large population-based datasets where the database may not have been designed for the particular analysis performed. | X | |
| Statistical Sig. versus scientific Sig. | issues related to the observation of statistical significance in the case of a hypothesis that is not scientifically plausible. | X | |
| Visualization | issues related to the ability to depict the information in the data set | X |
Background and Motivations
The term “large dataset” was used academically as early as 1975, when the first conference on large datasets was held (http://portal.acm.org/toc.cfm?id=1282480) discussing database design and management. Some of the characteristics of large datasets, such as high dimensionality (see definition on page 762) and large sample size and their associated issues, were discussed in the statistics literature as early as 1958, 2,3 but the first formal definition of a large dataset was only reported in 1990 in the context of effectiveness research. Large datasets were defined as having the following characteristics: the size of the data is big (106 or greater); it is almost an unbiased representation of the real world, its information content may be unsatisfactory for what a particular researcher has in mind, and it has the ability to be linked with other datasets. 4 In 1995, the National Research Council Committee on Applied and Theoretical Statistics (CATS) gave an informal definition 5 : “a massive dataset is one for which the size, heterogeneity and general complexity cause serious pain for the analyst(s).” Both definitions are linked to potential methodological changes introduced by the nature of large datasets. The sentiment “pain” refers to a number of difficulties, including those formalized in ▶. Huber (1994, 1999), 6,7 motivated by the aforementioned changes in analytic methods, introduced this classification of size: 102—tiny, 104—small, 106—medium, 108—large, 1010—huge, 1012—monster. The size of the data impacts the storage mode which can vary from a piece of paper (tiny) to storage silos (monster) and the analytic methods used for information extraction. In many cases, changes in storage size have necessitated new methods for data analysis.
The possible definitions of a large dataset embody different perspectives, reflecting the philosophies of the different scientific fields that deal with these large datasets. The examples given here highlight issues such as size, integration, data heterogeneity, analysis complexity, and computational complexity for which appropriate analytic methods have been and are being developed. Furthermore, depending on the type of analysis and computations that will be performed, salient measures of data and computational complexity for a given dataset can be defined and used to guide decisions associated with the selection of appropriate algorithms for processing and extracting information. 8
In biomedicine, the number of databases has grown explosively over the last 10–20 years. In particular, medical practices and hospitals have implemented electronic systems to collect information on patients treated. In the molecular biology arena, the number of key databases of value to the biological community has grown exponentially from 300 to over 1,000 databases since 2000. 9
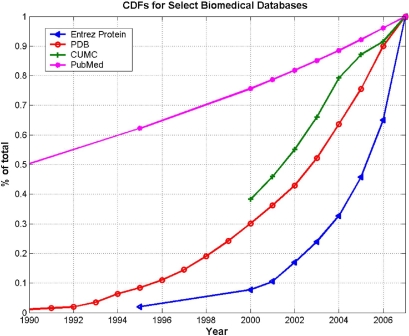
These databases themselves are growing at explosive rates. ▶ shows the cumulative distribution function (CDF) of the growth rate (as a percentage of total current entries) for several important databases in molecular biology and medicine: the Protein Data Bank (PDB), the Entrez Protein database, NCBI's PubMed, and clinical data maintained at Columbia University Medical Center. These examples highlight not only the explosive growth in this field but also the magnitude of complexity in terms of curation, integration, and analysis, making the understanding of large datasets and related methodological issues an important concern for informaticians today.
Figure 1.
Cumulative distribution functions (CDFs) for several important informatics resources. CDFs, showing growth rates of: the Entrez Protein database, compiled from a variety of sources including SwissProt, PIR, PRF and PDB; the Protein Data Bank (PDB), a repository for 3-D structural data of proteins and nucleic acids; PubMed, a service from the U.S. National Library of Medicine that provides citations to biomedical literature; and the Columbia University Medical Center (CUMC) clinical database, measured in number of rows.
Interdisciplinary Methodological Goals
Our guiding principle is that data are of interest if they can be used to answer important questions. Many analytic goals are common across informatics disciplines, and these goals frame the issues faced when analyzing large datasets. To facilitate discussion, we consider prediction, modeling, and inference as the main methodological goals of a given study. Among the common methods used to achieve these goals are classification, clustering, and regression, which we briefly overview here. 10
Classification, or supervised learning, aims to construct a rule to assign objects to one of a prespecified set of classes based solely on a vector of measurements taken on these objects. The construction of the rule is based on a training set of objects for which the true class is known. Classification can be thought of as predictive modeling, in which the output vector is categorical. Important techniques include logistic regression methods, naive Bayes methods, decision trees, neural networks, Bayesian networks, support vector machines, and hidden Markov models. Pattern recognition applications are often used to aid in image analysis. For example, features of objects in X-rays, such as intensity, perimeter, and area can be used for tumor identification. 11 Classification is also important for clinical decision support systems where symptoms, gene expression, and/or other factors are used as inputs for determination of diagnosis and therapy management. 12,13 More recently, classification techniques have been used for the development of biomarkers showing response to therapy and in building models based on gene expression for disease diagnosis/prognosis.
The purpose of clustering is to find natural groupings in the data through the use of distance metrics. There are many ways to do this, but the most common approach is hierarchical clustering, an unsupervised learning method. Other methods include K-means clustering, principle components based clustering, and self-organizing maps. Developing or reverse engineering networks also falls under the umbrella of clustering. Clustering is often used in latent semantic indexing to find similar documents or terms. 14 Other applications in biomedicine include measuring interpatient distances for improving diagnosis and determining appropriate treatment schedules, 15 in phylogeny, and in microarray data analysis for grouping functionally related genes.
Regression is a statistical analysis tool that quantifies the relationship between a dependent variable and one or more independent variables to depict trends in the data. There are well-known and widely used tools for regression modeling, including linear regression, logistic regression, radial basis function regression, and neural networks, among others. 16 Biomedical applications include decision support, longitudinal analysis of patient data, longitudinal analysis of gene expression, population comparison, and modeling of biological systems.
Interdisciplinary Methodological Issues
The above delineation of analytic tasks is meant to illustrate that, despite the overwhelming variety of phenomena that data can represent, there are some standard forms that data often take, some standard questions we can ask of data, and some standard issues we face. 14 This section offers a discussion of salient issues for inference in large datasets. We clearly define these topics and highlight the context in which the issue can be seen in biomedical data analysis. While we show the relevance of the issues across informatics disciplines, we describe them independently of their domain of application, drawing attention to analytic concerns and presenting a brief summary of relevant research. The issues presented here encompass active areas of research and, as such, a significant set of literature has already been published. Thus, the summaries given here are general. New methods are continually being developed and new challenges will present themselves. Whenever appropriate, we indicate where additional research is needed.
High Dimensionality
High dimensional data are data where each point/sample/element is described by many attributes. For example, a patient can be described by tens of thousands of genes, SNPs or clinical parameters such as x-rays, temperature or culture results. Other examples include data contained in spontaneous reporting systems (SRS), used for pharmacovigilance purposes and Medicare data, which map various medications or vaccines (rows) to possible adverse events (columns). R. Bellman coined the term, “the curse of dimensionality”, in the 1950s to describe the difficulty of optimization in high dimensional sets. High dimensional data are sparse; they show multicollinearity and exhibit model complexity, making model fitting computationally intensive and lending themselves to pitfalls such as model overfitting. For example, classification and clustering algorithms that generally work well in low dimensional situations perform poorly in high dimensions, because of the effect of dimensionality on the distance or similarity measure used by the algorithm. In particular, it is shown in 17 that for certain data distributions the relative difference of the distances of the closest and farthest data points of an independently selected point goes to 0 as the dimension increases. This occurs when all attributes are independent and identically distributed, and it is often said that “in high dimensional spaces, distances between points become relatively uniform”. In this case, the notion of the “nearest neighbor” point is meaningless.
The modeling difficulties introduced by high dimensionality are not insurmountable. We can define a dataset by (1) its size (number of independent entities, such as subjects in a clinical trial) and (2) its dimensionality (number of elements used to describe each subject, such as different clinical parameters measured). We denote the size of a set by n and its dimensionality by p. For example, in the case of microarray data, a cancer sample would count towards n, while the expression measurements for each gene would count towards p, the dimensionality. Then, the following representation of large datasets is useful as it indicates appropriate methodologies for analysis:
1 Large n, small p—Methodologically, this case conforms to the classical statistical paradigm, in which a sufficient number of independent data points provide measurements on a few dimensions. For very large samples, issues such as “statistical” versus “scientific” significance can arise.
2 Small n, large p—This is the paradigm met, for example, in microarray datasets. This case does not conform to the classical statistical paradigm in which n is much larger than p. Techniques employed to compensate for a large p generally fall under the area of feature selection/dimensionality reduction, or are methods specifically developed for this case. Methods include principle components analysis (PCA), compression methods and significance testing to select relevant features.18–22
3 Large n, large p—An example of data that conform to this paradigm is given by the Medicare and Medicaid databases. Depending on the type of research question, the toolkit of the analyst should include both classical statistical methods as well as more modern dimension reduction, classification and clustering methods such as K-nearest neighbors, random forests, CART (classification and regression trees), PCA and many more.
While the above classification is a simplification of what occurs in practice in terms of the type of data collected (image, free text, etc.), it is useful in terms of discussing the underlying principles of data analysis and the appropriate selection of methods. For example, in the “large n, small p” case, depending on the question of interest, appropriate classical statistical methods can be used. These methods provide for the generalizability of the results and aid inference. In the “small n, large p” case, a different set of tools is required. Spurred by the advent of high-throughput technology and data warehousing, these tools are an active area of research in a variety of fields (i.e., statistics, computer science, etc.). One such tool which allows for both inference and generalizability is dimension reduction, or feature selection. Feature selection is the process of selecting a subset of relevant features from high dimensional data in order to build a robust learning model. By removing irrelevant and redundant features, feature selection aids, for example, clustering and classifier performance by: 1) avoiding overfitting and overcoming the curse of dimensionality, 2) enabling the creation of faster models, and 3) providing insight into the underlying processes that generated the data. 23,24 There are three types of feature selection methods: filter methods, wrapper methods and embedded methods. 21,23 Other dimensionality reduction techniques include projection pursuit regression 25 and compression methods.
Less well-known are the blessings associated with high-dimensional data. For example, many “identical” dimensions allow us to “average” for more consistent results, 10,20 allowing the performance of dimension asymptotics that can be used to obtain distributions of functions of interest. Another blessing often encountered within high dimensional structures is the concentration of measure. It involves the tendency of functions to concentrate around their mean, and has been studied by several authors. 10,26 This principle relates to applications in combinatorial optimization, statistical learning, data analysis and data mining. For example, it has been used effectively to derive efficient sampling algorithms for inference in probabilistic graphical models. Many times high dimensional data are generated because the underlying processes measured are continuous in space and/or time. This “approach to continuum” is reflected by approximate finite dimensionality and hence an increasing simplicity of analysis.
Multiple Testing
Multiple testing is the process of subjecting the same dataset to many different statistical tests in the hopes of establishing significance of a hypothesis under study. A typical microarray study, designed to determine discriminant genes between 2 or more groups, requires ∼ 20–30,000 simultaneous tests to examine each gene. Here, the type I error rate (false positive risk) is fixed at some reasonable value but the null hypothesis is tested for many attributes. Thus, in a case of n = 10,000 genes and α = 0.05, there are 500 potential type I errors. As the number of tests increases so does the likelihood of observing a significant result due to chance, illustrating the multiple testing problem.
In contrast to single hypothesis testing which is run with the hope that a test is powerful enough to reject a null hypothesis, large-scale testing is often used to identify a subset of “interesting” cases that deserve further investigation. Therefore, standard methods such as the family-wise error rate (FWER) and even the more commonly used Benjamini-Hochberg false discovery rate (FDR) are often too stringent. The FDR is the expected proportion of erroneous rejections among all null hypothesis rejections and it is equivalent to the FWER when all hypotheses are true, but it is smaller otherwise, which makes the practical difference between them neither trivial nor small. 27 A variant of the expected proportion of falsely identified significant items, known as the local false discovery rate, is proposed in Efron 2004 28 for use in large-scale hypothesis testing. When concurrent tests on a given dataset are ordered by significance (p-value), multiple testing procedures simply limit the number of tests that are identified as significant. This can be helpful when considering scientific significance over statistical significance. While new FDR methods are being developed, popular methods include Benjamini-Hochberg, 27 empiric Bayes approaches 28–30 and others. 31,32 The selection of an FDR method should be based on knowledge about the underlying data structure such as distribution and dependence structure.
Statistical Significance versus Scientific Significance
When the number of points, for example the number of subjects in a study, is really large, it is possible, for a given hypothesis under study, to observe statistical significance even though the hypothesis may not be scientifically plausible. For example, when studying associations in a large dataset using simple methods such as χ2 statistics, it is possible to obtain statistically significant results that do not have scientific meaning. In a preliminary analysis, Cao, et al 33 found the pair (hypertension, suicide) to be statistically significant via standard methods. This is clearly not clinically plausible and prompted Cao et al to develop a method for the calibration of the critical value of the χ2 statistic to help the identification of an appropriate critical point beyond which significance can be declared. An alternative is to transform the testing problem into an estimation problem, by constructing, for example, appropriate confidence intervals. Another option is the use of biological enrichment, which enriches statistical results with domain information. For example, Gene Ontology (GO) enrichment is used to validate lists of statistically significant genes found by differential analysis with biological information encoded in the GO. It assesses the functional similarity of genes in the provided list with respect to the biological processes they comprise.
Dependence
Very large datasets are unlikely to arise in an independent, identically distributed manner. For example, although large clinical databases contain information on different patients, and these subjects are independent, they also contain measurements on the same patient over time and these measurements are dependent. Examples include daily glucose measurements or white blood cell count data taken over a specified period on individuals undergoing long-term dialysis for chronic renal failure. Measurements close in time tend to be correlated with one another. To obtain valid inferences for time-dependent data, a variety of methods have been developed in time series, longitudinal and functional data analysis areas of biostatistics.
Even information on different patients may exhibit correlation. For example, patients treated by the same clinical team are more likely to have similar outcomes. Because of this lack of independence, standard statistical methods used for sample estimation and analysis will underestimate values such as the required sample size. This is typically a factor in computer-based clinical decision support system studies. Chuang, et al 34 surveyed 24 such studies and found that none took into account this type of patient clustering in sample size calculations and only 14 (58%) took this factor into account at all. One solution is to multiply standard sample size estimates by a design effect term based on an intracluster correlation measurement. Another option is to use sample size formulas appropriate for correlated data. 35
High dimensional sets, especially, are subject to the existence of nontrivial, highly correlated data points or subspaces. 36 In the case of gene expression data, it is a reasonable assumption that genes or proteins that act together will exhibit strong correlation. For example, transcription factors can regulate key genes in multiple signal transduction pathways, creating a set of correlated factors. However, global correlation is also an important factor. Recent literature has indicated that underlying dependence structures in microarray data, as measured by pairwise gene expression correlation, show an average of correlation over 0.84, 37 suggesting that dependence between genes is a factor that we must consider in biological data analysis.
Specifically, dependent samples and/or dimensions will not reduce the variability of the data and thus will not improve analysis. This affects statistical modeling and the performance of the methods that assume independence, so methods that account for dependence need to be used. The study of dependence is an important and active area of research. Multivariate analysis methods to improve analysis of high-throughput and correlated genetic data have been proposed but are not widely known or used. 38,39 Similarly, multiple testing procedures, such as Benjamini-Hochberg, are rooted in the assumption that the variables are independent, and FDR methods that do not account for this could produce unreliable results. Methods that deal with this problem continue to appear in the literature. 40–42 Adjustments to existing FDR methods that can accommodate specific types of dependence structures have been proposed. 41,43–46 However, even these adjustments tend to be conservative. Again, method selection should be based on knowledge about the underlying dependence structure of the data.
Another consideration is the effect of data transformations on the dependence structure of the data. A typical goal in microarray studies is to use correlation information to reconstruct or reverse-engineer molecular pathways and networks. However, data transformations such as normalization methods have the potential to destroy or even create spurious correlation information, rendering flawed inferred networks. The practice of data transformation is not limited to the microarray analysis arena; the scaling of variables for clustering is a well-known headache. The most commonly used idea among practitioners is to standardize or autoscale individual variables. However, this is only effective in equalizing values if the variables themselves are independent. 1,47 In fact, the effect of transformation has not been well-studied and has only become a subject of research in the last 5 years. 48,49
Information Measurement
“Information” is a concept that spans many scientific fields including communication theory, biology, economics, law, and statistics. In its semantic context, the term information is used in an intuitive sense, but in its technical context, information is a well-defined function that quantifies the extent of uncertainty differentials. Large datasets provide a tremendous volume of data, but not necessarily a tremendous volume of information—the size of a dataset is not a guarantee that the data will contain information about the question of interest.
Large datasets are usually complex in structure and challenging in extracting meaningful information from them. One way of extracting information is through measures of computational and algorithmic complexity; another is through quantifying variability in these sets. Information measures can be used to guide decisions associated with the selection of appropriate algorithms for processing and extracting information, such that, for example, given a dataset with known characteristics, one can select an optimal classifier. However, it should be kept in mind that the choice of a particular algorithm biases the analysis towards solutions that play to the algorithm's strengths. The very practical problem of selecting a classification or clustering algorithm is not well addressed in the literature. 47
There are two types of information measures met in the literature, those that use probabilities and are thus stochastic information measures, and deterministic information measures. Examples of stochastic information measures include Fisher's information, Shannon's information, Kullback–Leibler information, and mutual information. Deterministic measures include various information functions and the algorithmic information content (AIC) measure. ▶ discusses each of these in more detail. 50–54 These information measures can be used to determine relationships between variables, similar to correlation metrics, and are thus useful in any kind of association study, or to quantify variability of features.
Table 2.
Table 2 A List of Important Information Metrics
| Metric | Brief Description | Formula | |
|---|---|---|---|
| Fisher information | Fisher 50,51 can be credited with developing the theory of statistical information, positing that the distribution of an event is altered by changes in the value(s) of parameters. This measure is useful in determining the dispersion of a feature of the data. |
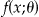 is the density of the event represented by X is the density of the event represented by X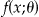
|
|
| Shannon information | Shannon's (1948) 52 definition of information measures variation in a distribution. This measure is the product of the amount of information provided by an event (which is inversely proportional to the probability of its occurrence) and the probability of the occurrence of the event. |
|
|
| Kullback–Leibler information | Kullback (1951, 1959) 53,54 presents a definition of information for discriminating between two distributions f,g that model 2 different populations. |
|
|
| Mutual information | mutual information is defined as the amount of uncertainty reduction in an event B when an event A is known. It can take the form of Kullback information, measuring the distance from independence by comparing the joint distribution with the product of the marginal distributions. |
|
|
|
| |||
| AIC | algorithmic information content (AIC) is a deterministic information criterion and equals the length of the most concise program that instructs a universal computer to produce the given dataset. | ||
The choice of information and complexity measure (stochastic or deterministic) must be closely aligned with the task performed. For instance, Sohn 8 derived a set of relevant data characteristics and used regression analysis to develop a statistical metamodel that compares the classification performances of several algorithms. Relevant data complexity measures that can be used for assessing computational complexity are discussed further in Sotoca, et al. 55
Information Management
Information management is necessary to ensure that relevant and accurate information critical for analysis is identified. To that end, we note data quality management, integration, access control/privacy, and performance as information management issues relevant to the analysis of large datasets.
Data quality problems include missing data points, outliers, data glitches, unreported changes in scale, format, or measurement, and many others. Too many missing or erroneous values can give an inaccurate view of the data and corrupt further data analysis. Because repeat experimentation is often expensive, a variety of methods have been developed to account for such data. Some of these issues can be addressed by using appropriate statistical methods, 56,57 while others require the implementation of specialized techniques for their identification, correction, and management. 58,59
Data integration is required to provide seamless access to diverse and voluminous data sources while maintaining and improving the integrity of data to elucidate normal and disease physiology; it is a valuable step in improving data analysis. 60,61 While the general area of integration presents many challenges, here we focus on analysis issues resulting from such integration. For example, because many microarray datasets are small and high-dimensional, dataset integration is often desirable as a leverage to increase sample size. However, this is complicated by systemic issues such as differences in technology, protocols, and experimental conditions across datasets. Systemic variability can overwhelm biological variability, creating a batch effect which confounds analysis. Literature is divided on the severity of systemic variability, 62 but experiment integration is an active area of research 63 with methods falling into two main categories: statistical meta-analysis 64–67 and heterogeneous data integration systems. 68–71
Conclusions
As shown by the exponential growth of key databases in this arena, large datasets are a growing part of regular practice in biomedicine. In the healthcare setting, thoughtful analysis can optimize the quality and cost of care. Similarly, genomic medicine provides sequence, transcriptomic, proteomic, and other information that can be further analyzed to tie developments in biology to the practice of medicine. To better understand the datasets we deal with, we have characterized analytic goals and presented a detailed discussion of germane issues for large datasets with a focus on appropriate methodologies available to address these concerns and areas of continued research. This lends itself to better study design, a structured analysis of data, as well as improved generalizability and inference. A firm understanding of the challenges and statistical technology involved ultimately contributes to better science.
Here, we further suggest that this motivates a focused effort by the community to address these issues in the forms of best practices guidelines, interdisciplinary panels, invited papers, curriculum enhancement and improved reporting practices. The large gap between “typical” and “best” practices for the analysis of large datasets can be narrowed. Available resources should match best practices, and/or researchers should have the tools to access or develop more appropriate platforms. Transparent reporting indicating how fundamental issues are addressed will increase trust in the reproducibility of the results. Thus, it is perhaps appropriate to consider the creation of guidelines not only for analysis, but also for the reporting of the analyses used. Guidance on this topic can be provided through expert panel formation and relevant publications such as Lang and Secic (2007). 72 However, we note that existing literature on the topic of reporting in medicine does not cover the specific issues found in the analysis of large datasets.
We believe that it is fundamentally important for researchers to have a basic understanding of the unique issues encountered in large dataset analysis to aid generalizability, inference, and reporting of generated results. These proposed forums serve the purpose of facilitating discussion on challenging issues and the feasibility for establishing firm guidelines in the art of analysis.
Acknowledgments
The authors thank Dr. Andrew Talal for his valuable contributions and insights in reviewing this paper.
Footnotes
Dr. Markatou's research was funded by NSF DMS-0504957 and OBE/CBER/FDA. Dr. Hripcsak is supported by NLM R01 LM06910 “Discovering and applying knowledge in clinical databases”. Anshu Sinha is supported by the NLM Informatics Research Training Program (T15 LM007079-17).
References
- 1.Kettenring JR. A Perspective on Cluster Analysis Stat Anal Data Min 2008;1:52-53. [Google Scholar]
- 2.Gilks WR. A rapid two-stage modeling technique for exploring large datasets Appl Stat 1986;352:183-194. [Google Scholar]
- 3.Dempster AP. A high dimensional two sample significance test Ann Math Stat 1958;294:995-1,010. [Google Scholar]
- 4.Heithoff KS, Lohr KN. Effectiveness and Outcomes in Health Care Proceedings of the Invitational Conference by the Institute of Med, Division of Health Care Sciences. Washington, DC, United States: National Academies Press; 1990. [PubMed]
- 5.Kettenring JR. Massive datasets Reflections on a Workshop. Telcordia Technologies, Inc; 2001.
- 6.Huber PJ. Huge datasetsIn: Dutter, Grossmann, editors. Compstat. Heidelberg: Verlag; 1994. pp. 7Proceedings. Physica.
- 7.Huber PJ. Massive datasets workshop: Four years after J Comput Graph Stat 1999;83:635-652. [Google Scholar]
- 8.Sohn SY. Meta analysis of classification algorithms for pattern recognition IEEE T Patterns Anal 1999;2111:1137-1144. [Google Scholar]
- 9.Galperin MY. The molecular biology database collection: 2007 Update Nucleic Acids Res 2007;35:D3-D4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Donoho DL. High-dimensional data analysis: The curses and blessings of dimensionality American Math. . Society Lecture—Match Challenges of the 21st Century. 2000.
- 11.In: Shortliffe EH, Cimino JJ, editors. Biomedical Informatics: Computer Applications in Health Care and BioMedicine. 3rd edn. New York: Springer-Verlag; 2006.
- 12.Shortliffe EH. Computer-based medical consultations: MYCINNorth Holland, N.Y: Elsevier; 1976.
- 13.Clancey WJ, Shortliffe EH. Readings in Medical Artificial Intelligence: The First DecadeBoston, MA, United States: Addison-Wesley, Longman Publishing, Co, Inc; 1984.
- 14.Murtaugh F, Starck JL, Berry MW. Overcoming the curse of dimensionality in clustering by means of the wavelet transform Comput J 2000;43:107-120. [Google Scholar]
- 15.Melton GB, Parsons S, Morrison FP, et al. Inter-patient distance metrics using SNOMED CT defining relationships J Biomed Inform 2006;396:697-705. [DOI] [PubMed] [Google Scholar]
- 16.Friedman J, Hastie T, Tibshirani R. Elements of Statistical Learning: Prediction, Inference and Data MiningNew York: Springer; 2001.
- 17.Beyer K, Goldstein J, Ramakrishnan R, Shaft W. When is the nearest-neighbor meaningful? Proceedings of the 7th International Conference on Database Theory. 1999. pp. 217-235.
- 18.Koller D, Sahami M. Toward optimal feature selection Proceedings of the Thirteenth International Conference on Machine Learning. 1996. pp. 284-292.
- 19.Kittler J. Pattern recognition and signal processingIn: Sijthoff, Noordhoff, editors. Feature Set Search. Alphen aan den Rijn, Netherlands: Algorithms; 1978. pp. 41-60.
- 20.Skalak D. Prototype and feature selection by sampling and random mutation hill climbing algorithms Proceedings of the Eleventh International Conference on Machine Learning. 1994. pp. 293-301.
- 21.Weston J, Muckerjee S, Chapelle O, et al. Feature selection for SVMs Proceedings of NIPS. 2000.
- 22.Jolliffe IT. Principal Component Analysis2nd edn. New York: Springer; 2002.
- 23.Saeys Y, Inza I, Larranaga P. A review of feature selection techniques in bioinformatics Bioinformatics 2007;2319:2507-2517. [DOI] [PubMed] [Google Scholar]
- 24.Guyon I, Elisseeff A. An introduction to variable and feature selection J Mach Learn Rev 2003; 3Mar;1:157-182. [Google Scholar]
- 25.Friedman JH, Stuetzle W. Projection pursuit regression J Am Stat Assoc 1981;76:817-823. [Google Scholar]
- 26.Pestov V. On the geometry of similarity search: Dimensionality curse and concentration of measure Info Process Lett 2000;73:41-51. [Google Scholar]
- 27.Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing J R Stat Soc B 1995;57:289-300. [Google Scholar]
- 28.Efron B. Large-Scale simultaneous hypothesis testing: The choice of a null hypothesis J Am Stat Assoc 2004;99(465):96-104. [Google Scholar]
- 29.Efron B, Tibshirani R, Storey JD, Tusher V. Empirical Bayes analysis of a microarray experiment J Am Stat Assoc 2001;96:1151-1160. [Google Scholar]
- 30.Efron B. Correlation and Large-Scale simultaneous significance testing J Am Stat Assoc 2007;102:93-103. [Google Scholar]
- 31.Storey JD. A direct approach to false discovery rates J R Stat Soc B 2002;64:479-498. [Google Scholar]
- 32.Genovese C, Wasserman L. Operating characteristics and extensions of the false discovery rate procedure J R Stat Soc B 2002;64:499-517. [Google Scholar]
- 33.Cao H, Hripcsak G, Markatou M. A statistical methodology for analyzing co-occurence data from a large sample J Biomed Inform 2007;403:343-352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chuang JH, Hripcsak G, Jenders RA. Considering clustering: A methodological review of clinical decision support system studies Proc AMIA Symp. 2000. pp. 146-150. [PMC free article] [PubMed]
- 35.Diggle PJ, Liang KY, Zeger SL. Analysis of Longitudinal DataOxford: Oxford, Science Press, Clarendon Press; 1994.
- 36.Clarke R, Ressom HW, Wang A, et al. The properties of high-dimensional data spaces: Implications for exploring gene and protein expression data Nat Rev Cancer 2008;81:37-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Klebanov L, Yakovlev A. Diverse correlation structures in gene expression data and their utility in improving statistical inference Ann Appl Stat 2007;12:538-559. [Google Scholar]
- 38.Xiao Y, Frisina R, Gordon A, Klebanov L, Yakovlev A. Multivariate search for differentially expressed gene combinations BMC Bioinform 2004;5:164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Szabo A, Boucher K, Jones D, et al. Multivariate exploratory tools for microarray data analysis Biostatistics 2003;4:555-567. [DOI] [PubMed] [Google Scholar]
- 40.Wright GW, Simon RM. A random variance model for detection of differential gene expression in small microarray experiments Bioinform 2003;19:2448-2455. [DOI] [PubMed] [Google Scholar]
- 41.Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency Ann Stat 2001;29:1165-1188. [Google Scholar]
- 42.Romano JP, Wolf M. Control of generalized error rates in multiple testing Ann Stat 2007;35:1378-1408. [Google Scholar]
- 43.Wu WB. On false discovery control under dependence Ann Stat 2008;361:364-380. [Google Scholar]
- 44.Yekultieli D, Benjamini Y. Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics J Stat Plan Infer 1999;82:171-196. [Google Scholar]
- 45.Storey JD. The positive false discovery rate: A Bayesian interpretation and the Q-value Ann Stat 2003;316:2013-2035. [Google Scholar]
- 46.Farcomeni A. Some results on the control of the false discovery rate under dependence Scand J Stat 2007;34:275-297. [Google Scholar]
- 47.Kettenring JR. The practice of cluster analysis J Classif 2006;23:3-30. [Google Scholar]
- 48.Qiu X, Brooks AI, Klebanov L, Yakovlev N. The effects of normalization on the correlation structure of microarray data BMC Bioinform 2005;6:120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Klebanov L, Chen L, Yakovlev A. Revisiting adverse effects of cross-hybridization in Affymetrix gene expression data: Do they matter for correlation analysis? Biol Direct 2007;2:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fisher RA. On the mathematical foundations of theoretical statistics Philos Trans Roy Soc London Ser A 1922;222:309-368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fisher RA. Theory of statistical estimation Proc Cambr Philos Soc 1925;22:700-725. [Google Scholar]
- 52.Shannon CE. A mathematical theory of communication Bell Syst Tech J 1948;27:379-423and 623–56. [Google Scholar]
- 53.Kullback S, Leibler RA. On information and sufficiency Math Stat A 1951;22:79-86. [Google Scholar]
- 54.Kullback S. Information Theory and StatisticsNew York: Wiley; 1959.
- 55.Sotoca JM, Sánchez JS, Mollineda RA. A review of data complexity measures and their applicability to pattern classification problems. Actas del III Taller Nacional de Mineria de Datos y Aprendizaje. TAMIDA 2005:77-83.
- 56.Little RJA, Rubin DB. Statistical Analysis with Missing DataNew York: Wiley; 1987.
- 57.Huber PJ. Robust StatisticsNew York: Wiley; 1981.
- 58.Dasu T, Johnson T. Hunting of the snark; finding data glitches using data mining methods MIT Workshop of Information Quality 1999:89-98.
- 59.Dasu T, Johnson T. Exploratory Data Mining and Data CleaningNew York: Wiley; 2003.
- 60.Louie B, Mork P, Martin-Sanchez F, Halevy A, Tarczy-Hornoch P. Data integration and genomic medicine J Biomed Inform 2007;401:5-16. [DOI] [PubMed] [Google Scholar]
- 61.Brazhnik O, Jones JF. Anatomy of data integration J Biomed Inform 2007;403:252-269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.MAQC Consortium The microarray quality control MAQC. Project shows inter- and intraplatform reproducibility of gene expression measurements. Nat Biotechnol 2006;249:1151-1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Huttenhower C, Hibbs M, Myers C, Troyanskaya OG. A scalable method for integration and functional analysis of multiple microarray datasets Bioinform 2006;22:2890-2897. [DOI] [PubMed] [Google Scholar]
- 64.Choi JK, Yu U, Kim S, Yoo OJ. Combining multiple microarray studies and modeling interstudy variation Bioinform 2003;19S:1i84–90. [DOI] [PubMed] [Google Scholar]
- 65.Rhodes DR, Yu J, Shanker K, et al. Large-scale meta-analysis of cancer microarray data identifies common transcriptional profiles of neoplastic transformation and progression Proc Natl Acad Sci USA 2004;101:9309-9314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hu P, Greenwood CMT, Beyene J. Integrative analysis of multiple gene expression profiles with quality-adjusted effect size models BMC Bioinform 2005;6:128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mulligan MK, Ponomarev I, Hitzmann, et al. Toward understanding the genetics of alcohol drinking through transcriptome meta-analysis Proc Natl Acad Sci USA 2006;10316:6368-6373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Troyanskaya OG, Dolinski K, Owen AB, Altman RB, Botstein D. A Bayesian framework for combining heterogeneous data sources for gene function prediction in Saccharomyces cerevisiae Proc Natl Acad Sci U S A 8July2003;100(14):8348-8353Epub 2003 Jun 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lee I, Date SV, Adai AT, Marcotte EM. A probabilistic functional network of yeast genes Science 2004;1:1555-1558. [DOI] [PubMed] [Google Scholar]
- 70.Pavlidis P, Weston J, Cai J, Noble WS. Learning gene functional classifications from multiple data types J Comput Biol 2002;92:401-411. [DOI] [PubMed] [Google Scholar]
- 71.Clare A, King RD. Predicting gene function in Saccharomyces cerevisiae Bioinform 2003;19S:2ii42–9. [DOI] [PubMed] [Google Scholar]
- 72.Lang TA, Secic M. How to Report Statistics in Medicine. 2nd edn. Philadelphia, PA: American College of Physicians; 2007.