Computational Reasoning across Multiple Models

Abstract

Computational support of clinical decisions frequently requires the integration of data in a variety of formats and from multiple sources and domains. Some impressive multiscale computational models of biological phenomena have been developed as part of the study of disease and healthcare systems. One can now contemplate harnessing these models arising from computational biology and using highly interconnected clinical data to support clinical decision-making. Indeed, understanding how to build computational systems able to reason across heterogeneous models and datasets is one of the major and perhaps foundational challenges of translational biomedical informatics. In this paper, the authors examine the use of multimodels (models composed of several daughter models) and explore three major research challenges to reasoning across multiple models: model selection, model composition, and computer aided model construction.

Introduction

Clinical decision-making often involves the integration of data from multiple sources, and harnesses knowledge from multiple domains. A clinician may need to integrate knowledge from genetic, pharmacological, physiological and organizational and social domains in working with patients to decide on the most effective treatment plan, or settle a difficult diagnostic question. This integration of knowledge “from cell to system” has been long anticipated, and in the 1980s Blois wrote of the nature of “vertical reasoning” that takes place in clinical decisions, from low-level biology through to clinical and organizational levels. ¹

The computational challenge in pragmatically bringing together the diverse knowledge bases that extend from systems biology through to clinical medicine into a single system is huge. Nonetheless, the last few years have seen some impressive and ambitious attempts at building detailed computational models in the biosciences, with projects such as the Physiome, ² e-cell, ³ the visible human project, ⁴ and indeed the ongoing program of annotation of genomes with functional interpretations in computable form. ⁵ McCulloch and Huber, ⁶ for example, report a computationally complex model consisting of nine daughter models across eight scales from the atomic level to the whole heart. In parallel, we are witnessing the beginning of an international phase of the large-scale “joining up” of biomedical databases, from tissue banks and electronic patient records, gene and protein databases like GenBank, ⁷ Kegg, ⁸ and the biomedical literature stored in repositories such as PubMed.

We thus seem to be at a period of historic opportunity in biomedical informatics, where we can contemplate harnessing models from computational biology and highly interconnected clinical data to help us model clinical knowledge domains, in support of model-based reasoning methods for clinical decision-making. We are moving from a period when decision-support systems (DSS) had access to a single homogenous database, to one in which a DSS may access a variety of knowledge and data services to complete its task, for example using the Web Services Description Language (WSDL; http://www.w3.org/TR/wsdl).

If we are to imagine such a systems informatics subdiscipline, which is all about integrating different biomedical, clinical and organizational systems, ⁹ then understanding how to build computational systems able to reason across heterogeneous models and datasets becomes one of the foundational challenges of translational biomedical informatics. In the remaining sections of this paper we will review the state of computational modeling in biomedicine, and explore three major challenges to reasoning across multiple models: Data Translation or exchange across models, ensuring compositional validity of model assemblies, and computer assisted model construction.

Modeling Biomedical Systems

The field of systems biology, the modeling of biological entities as sets of interacting systems, predates computational biology. ¹⁰ However, the application of computational methods in biology has redefined this field and there are now a wide variety of biological modeling methods. ¹¹

For example, Dokos, et al used differential equations to model the electrochemical activity in a single sinoatrial node cell; ¹² Fernandez, et al defined a set of finite-element models to describe the human skeleton-muscular system; ¹³ Schlessinger and Eddy used System Dynamics to model the physiology of diabetes before and after intervention; ¹⁴ Friedman, et al used Bayesian Networks and gene expression data to model metabolic pathways; ¹⁵ Regev, et al applied process algebra (also called π-calculus) originally developed to model computer processes to model biochemical pathway behavior; ¹⁶ Matsumo, et al used Petri-nets to model a genetic regulation mechanism; ¹⁷ Searls used formal languages to model DNA evolution; ¹⁸ King et al applied Inductive Logic Programming and first-order logic to model chemical properties of molecules; ¹⁹ and Hau and Coiera used qualitative differential equations to model the physiology of cardiac bypass patients. ²⁰

Life scientists well understand that models of individual biological systems such as gene networks or metabolic pathways do not reflect the true complexity and interconnectedness of whole organism biological systems and are hence always in some way incomplete or inaccurate. Thus, models of large biological systems have an inherent complexity, compounded by the fact that interrelated biological systems can operate at different temporal and spatial scales. ²¹

Multimodeling

An engineering approach to managing such complexity and diversity is to build many independent subsystem models and to then compose them as needed into higher-level models, and is called multimodeling. ²² The strength of the approach comes from a loose coupling of daughter models using a separate additional integration model. We can more formally define a multimodel as any two or more independently validated daughter models that interchange information to create a new, composite model.

Multimodeling allows each individual system to be modeled independently, using the most suitable computational environment. Candidate systems for multimodeling are ones in which two or more complex and interacting systems are to be modeled, especially if the interactions are themselves complex. Typically the daughter models will be of entities that are of different scales, use different data sources and/or use different computational representation or inference methods. Daughter models can have different physical properties such as scale (Example I) and/or computational properties, such as representation language or inference method (Example II). While multimodeling is still in its infancy, anecdotal evidence ^23,24 shows the approach has promise for biomedical informatics and work is underway to standardize mechanisms for model integration. ^25–27

The process of constructing a multimodel follows the same general steps used in any modeling process: a design and construction phase, a parameterization and configuration phase and validation. With multimodeling, design and construction consists of selecting daughter models and the methods to interchange data. Parameterization and configuration consists of implementation of the interchange, which may include translation between coordinate systems, units, file formats, databases and data. The behavioral validation of multimodels should be identical to other model validations, but specific challenges exist in ensuring the validity and legality of compositions. ²⁸

Example I: A Multimodel of Diabetes Management

The Archimedes system ²⁹ uses system dynamics to model multiple related biomedical systems at a wide range of scales, from tissue through to disease, patient and comorbidity, clinical tests, health system administration, and economic models. Archimedes allows a clinician to probabilistically evaluate the utility, risk, and ramifications of a given treatment.

Interaction between the daughter models in Archimedes is straightforward as all models share a common simulation method and environment. The daughter models can interchange information simply by passing variables. While this blurs the line between the multimodel and its daughters, this is a multimodel because each daughter model is developed, tested, and validated independently of the multimodel. ²⁹ The models run over mixed temporal scales with some operations taking longer than others and lag can be introduced between components. For example, a change in diet may take some time to affect a patient's LDL level.

The Archimedes model is implemented in the Smalltalk programming language. Daughter models are represented as Smalltalk objects and communicate through ad hoc interfaces. While Smalltalk is recognized as a standard language, its objects are not easily accessible from other languages. Therefore, while the multimodel is extensible through addition of more daughter models, such models have to be implemented in Smalltalk.

Example II: A Multimodel of Liver Cancer Treatment

New radiation and heat therapies for liver cancer are based on the injection and deposition of ultra-fine particles into the tumor and depend on accurate models of tumor location and size to determine the required dose. Multimodels have been explored as an approach to computing the optimal therapy plan for these complex clinical treatments. ³⁰

This treatment planning multimodel combines (1) a stochastic fractal model of tumor microvasculature, ³¹ (2) a probabilistic drug delivery and deposition model, and (3) a finite-element dose delivery model. While the models are all the same spatial scale, the temporal scales differ widely. Each stage in the simulation assumes that the previous stage is in steady state: angiogenesis is much slower than the drug delivery rate, so the delivery model can assume that the vasculature is static for the duration of the drug delivery simulation and, similarly, the treatment simulation assumes that the microparticle deposition is complete at the start of the treatment.

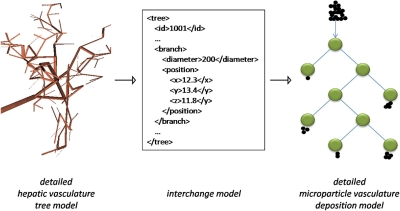
For the vasculature and deposition models to communicate, an interchange model is created to allow the values of shared parameters in the two models to be passed between them (▶). The interchange model is a simple tree representation of the full vasculature model. This interchange vasculature tree model describes structures starting from the arterioles that enter a tumor. Each branch of the arteriole is represented by a node element that records its radius and the branches immediately downstream from it. Thin capillaries are modeled as leaf nodes in the tree with their radius and their 3D position in the space of the tumor.

Figure 1.

Interchange between vascular and particle deposition models is mediated by a simpler interchange model that passes values for common parameters. In this example (see Example II), a simplified XML representation of the full vasculature model is used by the deposition model to obtain the values it needs to calculate microsphere concentrations and positions.

The deposition simulation takes the vascular geometry it obtains via the interchange model to calculate the probabilistic behavior of each microparticle as it reaches each branching of the tree, until it lodges in a vessel smaller than itself. The deposition model uses the radii of the vessels at each branch intersection that a particle passes through, to determine the proportion of microspheres that move further down a branch, until they lodge as a cluster in a capillary. Each cluster is used as a data point in a microsphere deposition field.

The resulting concentration of microparticles is subsequently shared across a further interchange model with the treatment model to calculate volumetric heat generation rates. ³⁰ The volumetric heat generation of each tetrahedral element in the finite element tumor heating model is calculated using the integral over the corresponding volume in the deposition model.

Challenges in Multimodeling Research

In the multimodelling setting, we are essentially creating a world where we have one or more libraries of models, each potentially created by different authors, using different representations and for different initial purposes. Our reasoning task begins with identifying which model or models are best suited to our current purpose, and then assembling a composite model and reasoning with that composite.

Such a multimodelling setting poses a number of challenges, both in constructing individual models, and then reasoning across multiple models. At the heart of the challenge is the need to capture information about each model in our library that describes what the model is about, and how it might be used. The idea that we need to capture such meta-level knowledge about models is nothing new, and indeed has been much explored from the early days of AI and expert systems. For example, in the 1970's the Teiresias system, part of the broader MYCIN research program, explicitly sought to define meta-level knowledge that would allow an expert system to “know what it knows” so that it could effectively manage different types of knowledge. ³²

Three kinds of meta-knowledge are needed to support multimodelling—knowledge that supports the choice of most appropriate model for a given task from a library of models; knowledge about how to compose individual models into multimodels, and knowledge about how to automate the process of model construction.

Reasoning about Model Choice

It is likely that many alternate models will be available to help with a given task, perhaps overlapping in the phenomena they model, just as there will be parts of the model space which are sparsely populated. Picking the right model from a model space for a particular reasoning task would require the library to store meta-knowledge about each model, describing attributes such as conformance with standards including controlled vocabularies, ontologies and knowledge representations, the purpose for which the model is constructed, and other classes of model with which it can be composed.

We can conceive of this meta-knowledge about a particular model as an abstraction layer or wrapper, that exposes the public properties of a model such as inputs and outputs (e.g. force tensors, neural network topology, disease symptoms) in a uniform manner so that users of the model don't require a detailed understanding of it's internal structure. The abstraction layer could be a simplified interface that is directly a part of the model, or it could be a separate model sitting in another part of the library. The abstraction layer should also accommodate formal specifications of a model's capabilities and the context for which it is designed, e.g. acceptable ranges for inputs and outputs, temporal or physical scale, or anatomic location (▶).

Table 1.

Table 1 Example of Abstraction Layer Elements for the Microsphere Deposition Model in Example II

Property Name	Value Type	Units	Range	Description
Parameter: Microspere diameter	scalar	μm		The diameter of each micro-particle to be deposited by the model. Allows the model to determine in which vessels the microspheres lodge.
Input: Vasculature tree	vessel diameter	μm	[1,∞]	Morphology of the blood vessels. The relative diameter of the branches of the same parent determines the proportion of microspheres travelling through each. The position of the branch determines the location of a microsphere cluster in that vessel if there is one.
Position (x,y,z)	3D point	mm	x:[−150,150], y:[−150,150], z:[−150,150]
Output:				The output of the model is the lodgement locations of clusters of microspheres in the space of the tumour. The field consists of the location of each cluster and the proportion of the microspheres in it.
Type - value	3D scalar field	Proportion	[0,1]
Type - domain	3D point	mm	x:[−150,150], y:[−150,150], z:[−150,150]

The abstraction layer specifies the constant values used in the model (parameters), the types of the variables that the model expects, the units assumed and acceptable range (input), and the form of the output that a simulation using the model calculates. The textual description of each element enables a human modeler to decide how the model can be used in a composition without understanding the internal representations and calculations made by the model.

Long-standing research challenges in navigating a model space remain unexplored. For example, a reasoning system might have a number of resource constraints, such as time or memory, which bound its operation for a particular task. Picking the model representation that best meets the needs of the reasoning task will require some mechanism to calculate the trade-offs when picking one model over another. ³³ In the situation where there is a family of similar models, each differing only in level of detail represented, we have proposed that the provision of intra-representational measures of the model space should allow a reasoner to draw conclusions about the level of model granularity that is most likely to produce an answer for a given query. Such metrics might be based upon internal attributes such as model completeness or complexity, or upon external measures such as behavioural adequacy. In the situation where there is a family of dissimilar models, each differing in representation (e.g., statistical vs. logical), then inter-representational measures are needed to allow a reasoner to draw conclusions about the likelihood that a specific model is best suited to the needs of a task. These might include estimates that a particular task is adequately represented in the model (are all the key concepts present?) as well as behavioural metrics (e.g., is a task computationally tractable using a particular representation?).

Model Interchange Methods

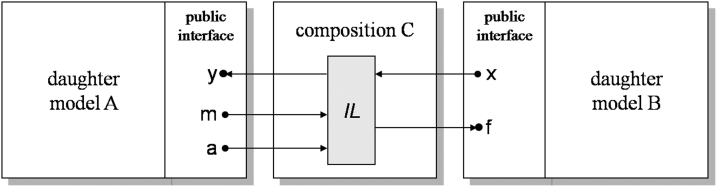
In order for two independently developed models to exchange information, an interchange model needs to be constructed which has the following requirements. For any two communicating daughter models A and B, the interchange of their inputs and outputs requires (▶):

• 1 An interchange language IL that is able to express the superset of variables and values that are communicated between A and B;

• 2 The generation of an interchange model C, which serves as a translator of the inputs and outputs between A and B;

• 3 A validation of the interchange model C.

Figure 2.

The composition of two daughter models is accomplished by the creation of a third interchange.

Interchange Languages

The public abstraction layer of a daughter model is represented using an interchange language. The U.S. National Library of Medicine's Unified Medical Language System (UMLS) provides a good example of ‘Rosetta Stone’ functionality by serving as an intermediary among different terminological systems. Several model interchange languages are currently under development or in use, for example, the Field Representation Language ²⁷ (FRL), System Biology Mark-up Language ²⁵ (SBML), and the Gene Feature Format v. 3 (GFF3; http://sequenceontology.org/gff3.shtml). Each is proposed as a standard for interchange with specific types of data or problem and thus can only interchange information between models of the same representation and type. For example, CellML ²⁶ uses public interfaces to facilitate interchange between CellML entities; FRL uses a special class of fields to represent field compositions.

Interchange languages need to be both portable and expressive. Portability implies that the interchange methods are independent of hardware, authoring tools and operating environment. Portability can be achieved by standardization of the language through international standards organizations or by relying on underlying portable language structures such as XML (http://www.w3.org/XML) and HDF5 (http://hdf.ncsa.uiuc.edu).

Expressiveness is a crucial issue, ³⁴ as it is unlikely that each daughter model in a multimodel composition will always be built using the same knowledge representation, and therefore the representations of the different daughter models may have different expressive powers. By definition then, when multiple representations are used, we will always be in a situation in which interchange is potentially a ‘lossy’ process of translation from one model to another, as concepts expressed in one daughter model are transformed into a less expressive concept for use by a second model.

Expressiveness thus captures the notion that any interchange language should be able to represent the superset of concepts needed to support the exchange of values between any two models. While this might seem to imply an extremely large language, interchange languages need only act as translators of data types and values, so that the output of one model can be input into another. There should be no need for such a language to model other internal aspects of a daughter model's structure or function. Consequently, interchange language expressiveness is a more bounded requirement than the much larger, perhaps intractable problem of expressing the superset of all concepts expressed across different model representations.

We can also impose bounds on the need for expressiveness in an interchange language by requiring daughter models to use standard representations, minimizing the diversity of representations needing accommodation. When model authors agree to adopt common standards, they trade off the expressive power of more locally appropriate model languages against broader utility of any models they build. In other words, we can build models to suit our local purposes very well, or build models that are slightly less well crafted, but can be more widely used by others. SBML, ²⁵ for example, is a fairly general language that can be used to describe and integrate any model expressible as a set of ordinary differential equations (ODEs). By contrast, the Model Description Language ³⁵ is specific to neural synapse modelling of a type solvable through Monte-Carlo simulations. Because the language is so specialized it is also very expressive with high-level constructs (e.g., “postsynaptic membrane”) relevant to its problem domain. In many ways this is the standard problem facing medical informatics in other domains e.g., exchange of clinical messages, or medical records. In the likely absence of a single universally standard model representation, interchange languages will always be needed.

The trade-off of expressive vs. reusable interchange language might need to be decided for each interchange within a multimodel. In the hyperthermia example (Example II), FRL was used to interchange data between the microsphere deposition model and heat transfer model because it conveys geometrical information in 3D space and provides a method to translate between coordinate systems. However, for the interchange of trees from the vasculature model to the microsphere deposition model a logical representation that includes connection between blood vessels was required and so an ad hoc XML tree representation was used.

Interchange Models

It is unlikely that a simple mapping exists between the public interfaces of any two models, and the act of translating values between them will require a third interchange model to be constructed. The interchange model maps variables that may have different names because of nomenclature and value differences in use by the builders of different models. Thus, the translation of numerical models will need to use rules about value types, unit conversion, and/or coordinate systems. For example, CellML ²⁶ allows the specification of units so that the software that reads the files can validate them and provide a conversion when possible. The Field Representation Language's mathematical library, the Abstract Field Layer ³⁶ verifies that the cardinality of composed fields' value types are the same across a composition or that an appropriate mapping is given.

An interchange model may also utilize knowledge about variable type, dimension, and mapping functions to translate a number of variables in one model to a smaller set of variables in another. For example, the physical variable force (f) can be mapped to the variables mass (m) and acceleration (a) using Newton's second law f = ma. Similarly, we might expect any temporal integration to conform to Allen's thirteen temporal relations. ³⁷

Validating Interchange Models

While an interchange model provides syntactic composition control, it is not sufficient to ensure that the overall composition is semantically valid. That two models can be assembled does not mean that the new assembly is meaningful. The challenge of ensuring composite entities represent legal concepts is not a new one to biomedical informatics. There is a long history of the use of compositional rules to ensure the combinations of terms from a terminological system represent meaningful clinical concepts, for example preventing syntactically correct but semantically invalid sentences such as “tibia treats penicillin”. ³⁸

Consequently, there is a need to develop methods that assist composition, preventing illegal compositions to occur, or identifying which portions of a composition are problematic. Such semantic composition controls use background knowledge about the type and purpose of models and model components, to ensure that syntactically well-formed assemblies are also meaningful. For example, we need to make sure that composite metabolic pathways obey the laws of chemistry and physics, that anatomical relationships are correct, or that models operate across compatible temporal scales.

Semantic constraints are often captured in an ontology. For example, an anatomical ontology may formally record the legal relationships between tissues at different developmental stages. ³⁹ While much work is devoted to developing ontologies in single domains, ⁴⁰ we would expect multimodelling to require a higher-level integrating-ontology to describe the relationships among genetic, transcriptional, proteomic, metabolic, and physiological systems. For example logical constraints can allow deductive systems to decide if a model is appropriate for a particular composition. Thus, a model of a mouse with a constraint “organism belongs to class Murine” would prevent an interaction with incompatible human models, whilst a more general constraint like “organism belongs to class Mammal” would permit such interactions.

Model compositions also have to satisfy criteria to ensure the functional validity of the multimodel ⁴¹ which require additional information to that available in the public interfaces of the daughter models. For example, the integration of two metabolic pathway models in the same cell model may be invalid because intermediate products of one pathway (hidden from the public interface) may actually interact with the other pathway. Similarly, when compositing two chemotherapy models for a patient with co-morbidity, drug-drug interactions must be checked to avoid adverse effects.

As a consequence, while we can strive for standardization of model and interchange languages, the act of model composition will often require additional background information to ensure that the composition is a valid one, and that knowledge may unfortunately be unique to the specific composition. Just how much of a problem this issue will become remains to be seen, as it is likely that for most compositions, a standard set of compositional validation rules will be more than sufficient. How we detect or manage the exceptions will remain an ongoing research question.

Automatically Generated Multimodels

We distinguish between multimodels composed by human modellers and ones composed automatically by computer. The former include systems in which computational support was available to the modeller, for example in the form of automatic model validation. The latter is restricted to multimodels in which the daughter models and their interactions were selected by automata.

Machine learning has been applied with some success to model building problems in system biology. ²³ These algorithms systematically examine a hypothesis space, and select models that are consistent with a training corpus (the maximised refutation principle), following a Popperian process ⁴² of conjecture and refutation. Working with multimodels generates several additional challenges to the machine learning task, when trying to develop models of complex systems, whether at the molecular, cellular or indeed human organisational levels.

Working with biological data sets at different temporal or spatial scales raises particular challenges. Firstly, some features or variables may demonstrate time varying behaviour at one scale and not at another. Consequently, relationships between variables may be present at a particular sampling rate, but disappear at slower or faster sampling rates. ²⁰ For example, models that include the skin-to-core temperature gradient, representing the level of vasoconstriction in the body generally appeared with slower time scales than the responses of other parameters like blood pressures.

Secondly, the effects of noise in a data set may mean that models learned at one scale are more or less affected by noise, and have different statistical validity. Typically, the finer the scale level, the lower we would expect to find the signal to noise ratio. Consequently we might be able to learn multiple models of the same system at different temporal abstractions, but will need to treat these models with different degrees of confidence. Variables present in a model at one scale may not appear in another, challenging the sharing of values across scales.

Learning time-varying behaviors is also challenging for a number of other pragmatic reasons. If a physiological system moves to a new state e.g., from normal to left ventricular failure, then the models that can be learnt also change. Trying to learn across a period of change will mean we are trying to induce a single explanatory model when more than one is needed. This class of problem becomes more likely, the finer the temporal scale being looked at. Understanding when to segment data in a way that recognises a new system state needs to be modelled is a substantial challenge, as yet unanswered.

Inductive Logic Programming (ILP) ⁴³ is a machine learning approach which may assist in this challenging learning environment. The ILP systems can integrate arbitrary background knowledge when learning models and this capability may make them suitable when knowledge is needed in order to recognise when different models are being learned, or assist in mapping between variables at different scales. The ILP systems are able to internalise syntactic composition rules, as well as semantic knowledge at an ontological level.

Model authorship remains a process that appears often to require innovation and creativity that can't currently be replicated by computational systems. However, by incrementally defining classes of compositions and the assumptions that need to be made by automatic model composition algorithms, we will make significant contributions to multimodelling and biomedical research, and our capabilities to automate these processes should also increase with time. Consequently for now it is likely that most multimodelling decisions will be made by humans assisted by the compositional metrics described here, and that the level of assistance provided by automated systems will increase as our understanding of the science of model composition grows.

Conclusions

The recent availability of high-throughput biological data, ontologies, and biomedical systems models has reinvigorated the idea of model-based reasoning. However, the complexity of the models requires novel approaches to organising and even generating new models.

Multimodelling is a promising approach for translational medicine because of its power to integrate data in arbitrary formats and from a variety of sources such as DNA sequence data, physiological first principles, and scientific literature. However, new approaches are needed to facilitate reasoning tasks over multimodels.