Abstract
Quantitative description of protein dynamics and interactions in vivo with temporal and spatial resolution is a key step in dissecting molecular mechanisms in cell biology. Fluorescence fluctuation spectroscopy (FFS) has recently emerged as a powerful in vivo tool for assessing molecular concentration and movement and formation of hetero- and homo-oligomeric complexes. This article discusses point FFS-based analysis methods that have proven useful to cell biologists, focusing on the kinds of information they provide, their pros and cons, and the basic instrumentation required. Along the way, we describe briefly a few recent examples where these analyses have helped address important biological questions.
INTRODUCTION
Molecular cell biologists rely on a variety of methods to decipher protein activities and interactions during dynamic cellular processes. These commonly include the traditional biochemical assays reconstituted with purified components or complex cellular fractions and the more modern live cell–based protein reporter assays. Although these approaches have provided amazing insights and vast amounts of information, understanding precise molecular dynamics and interactions in a cell's native environment remains challenging. Even coimmunoprecipitation, often interpreted as “in vivo interaction” in publications, really reflects proteins' ability to bind each other in a cell extract. Other methods of reporting protein interactions using live cells, such as two-hybrid (Fields and Song, 1989) or protein complementation assays (Remy and Michnick, 2004), report on the general ability of proteins to bind each other but do not provide spatial or temporal resolution in in vivo settings.
Early in the 1970s, Elliot Elson, Douglas Magde, and Watt Webb described how a statistical analysis of small fluctuations in fluorescence emission intensity as molecules diffuse through a focal volume could reveal detailed information about the dynamics of the diffusing fluorescent particles and their kinetic interactions (Elson and Magde, 1974; Magde et al., 1974). Nearly four decades later, technical improvements and commercially available systems have finally brought the power of fluorescence fluctuation spectroscopy (FFS) analysis to the door-front of cell and molecular biologists. At the same time, the continual improvement of autofluorescent proteins (AFPs) has allowed for these measurements to be implemented with minimal invasiveness to the cell, i.e., by using genetically coded fluorescent tags expressed at or near native levels. In this perspective, we review several basic FFS-based methods from a biologist's viewpoint. For more technical reviews, see recent method descriptions (Kim et al., 2007; Slaughter et al., 2010). Due to space limitation, we focus on three basic methods involving point FFS that have been successfully applied to live cells to generate useful biological insights.
THE PRINCIPLE OF FFS AND POINT FLUORESCENCE CORRELATION SPECTROSCOPY
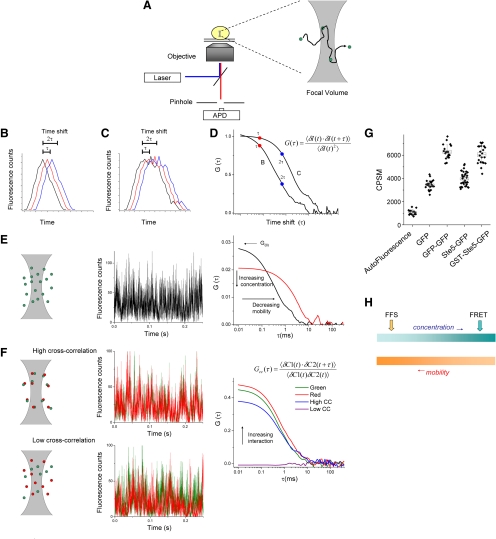
We are all familiar with laser scanning confocal microscopy, where a laser beam scans rapidly across a biological specimen and the fluorescence intensity of the emitted light is recorded and assembled into an image. The simplest type of FFS, point fluorescence correlation spectroscopy (FCS), is also performed using a confocal microscope but with important differences. In FCS, instead of scanning across the specimen, a laser beam is parked at the cellular location of interest for several seconds (Figure 1A). As fluorescent molecules diffuse in and out of the focal volume, the fluctuations of the emitted light due to changes in molecular number are recorded with single photon counters. Correlation analysis is one method to extract information from these recorded fluctuations (Figure 1, B–D). In the simplest case, imagine one molecule diffusing through the focal volume of a confocal microscope (Figure 1A). Fluorescence emission is collected and the correlation (likeness) of the emission profile is calculated by computationally shifting the data trace in time (with spacing τ, Figure 1, B–D). For a diffusing molecule, we expect that the larger the computation time shift τ of the data, the less overlap (similarity) there is with the initial trace. For rapidly diffusing particles, the likeness (correlation) of the data will decay rapidly with spacing τ, whereas for slowly diffusing particles it will persist for longer τ (Figure 1 B–D).
Figure 1.
Basis principles of single point FFS. (A) A high numerical aperture objective focuses a laser source to a diffraction limited focal volume. Fluorescence is collected through the same objective and passes through a pinhole before collection with an avalanche photodiode (APD). Inset depicts a single fluorescent molecule diffusing through the focal volume. (B and C) Theoretical fluorescence trace from a single molecule diffusing rapidly (B) or slowly (C). The data (black curve in each panel) is computationally shifted in time by spacing τ, 2τ (red and blue curves, respectively), and similarity, or correlation, is calculated (see the text for more detail). (D) Resultant correlation curves for traces in B and C, using the equation shown. G(τ) represents the amplitude of the correlation as a function of τ. The expected shift of the curve for the slow molecule toward the right compared with that for the fast molecule is shown. (E) Focal volume, a simulated fluorescence trace, and resultant correlation curve from single-color FCS measurement. The initial amplitude of the correlation curve (G0) is inversely proportional to concentration, and the decay of the curve with respect to τ is indicative of the average diffusion rate of the molecules. Two curves are shown, depicting different concentrations and different mobility. (F) Principle of cross-correlation spectroscopy. Two spectrally distinct probes are used. In addition to the autocorrelation analysis of the individual channels, the two channels are cross-correlated. The top row represents a strongly interacting pair, and is labeled high cross correlation. Note the similarity of the fluctuations in the two channels. The bottom row represents a noninteracting pair. The amplitude of the resultant cross-correlation curve is proportional to the strength of the interaction, as indicated by the arrow in the right panel. (G) In PCH, molecular brightness in counts per second per molecule (CPSM) are determined, and can be compared with controls, such as monomeric GFP and dimeric GFP (GFP–GFP) to determine the stoichiometry of the diffusing complex. Shown are examples of mostly monomeric Ste5-GFP and dimeric GST-Ste5-GFP (Slaughter et al., 2007). (H) FFS is ideally suited for mobile components present at low concentration, whereas FRET and other imaging methods are most successful at high concentration and low complex mobility.
This analysis works similarly with multiple molecules in the focal volume, as long as the number is small enough to be sensitive to fluctuations caused by molecules entering or leaving (see below; Figure 1E). The initial amplitude of the correlation curve (G0) is inversely related to the average number of fluorescent particles in the focal volume. Thus for an increased concentration, the amplitude of the correlation curve will decrease (Figure 1E, right panel). The shape of the curve reflects how fast the molecules move in and out of the focal volume (Figure 1E). One way to think of the correlation decay is a representation of the number of molecules that have a residence time of at least τ in the excitation volume. Most diffusing molecules are expected to have a residence time exceeding small values of τ, whereas few molecules are expected to have a residence time longer than large τ, and thus the correlation amplitude decreases with increasing τ. If particles diffuse rapidly (thus shorter residence time in the focal volume), the correlation would decay rapidly with increasing time lag τ, but if particles move slowly, correlation would hold high for longer periods (Figure 1E). For a more detailed description of the calculation and analysis of correlation curves, see Haustein and Schwille (2004).
The information generated with FCS, including both the concentration and diffusion coefficient (a measure of molecular size) of the molecule of interest, is already useful to cell biologists. Accurate assessment of these parameters first requires that we know the size of the focal volume. This can be accomplished by analysis of something of known diffusion coefficient (often fluorescein in 0.1 M NaOH) using an identical microscope configuration. For standard confocal microscopes with a high numerical aperture objective and a pinhole set at 1 airy unit to reject out of focus light, it is usually on the order of 0.3–0.5 femtoliters. To put this in perspective, this is ∼1/100 of the volume of a spherical cell with a radius of 2 μm. With this information, the amplitude of the correlation curve (G0) enables an estimate of the mobile concentration of the fluorescent particles at the site of the measurement.
To extract a diffusion coefficient, the shape of the autocorrelation curve can be analyzed using several established models, such as a three-dimensional free diffusion model. Given the viscosity of the environment (such as the cytosol), which can be estimated using a standard such as free green fluorescent protein (GFP; Slaughter et al., 2007), fitting with this model allows an estimate of average complex size. This must assume some sort of shape, for example, spherical. However, it is worth noting that for spherical shapes the diffusion coefficient scales with the inverse of the molecular volume to the one-third power, making it difficult to make precise size comparisons with this method. Information on protein mobility may help more rigorous assessment of the validity of qualitative models. For example, Fradin and coworkers used FCS and imaging in live Drosophila embryos to demonstrate that the diffusion of a protein involved in developmental pattern formation is rapid enough to account for a concentration gradient important for pattern formation along the anterior–posterior axis (Abu-Arish et al., 2010).
FLUORESCENCE CROSS-CORRELATION SPECTROSCOPY FOR ASSESSING HETERO-OLIGOMERIC INTERACTIONS IN VIVO
A very useful FFS method to molecular cell biologists is fluorescence cross-correlation spectroscopy (FCCS), which is based on the same principle: correlation analysis of fluorescence fluctuations. FCCS is designed to examine complex formation between two molecular species labeled with different colors (e.g., GFP and mCherry). Fluorescence fluctuations of each color are recorded independently but simultaneously using two detectors (Figure 1F). Complex formation between the proteins tagged with the two colors is reflected by their codiffusion, akin to molecules “riding the same car” as they enter or leave the focal volume (Figure 1F). Codiffusion can be measured through cross-correlation analysis of the fluctuations in the two channels as a function of time, with the amount of complexes proportional to the amplitude of the cross correlation (Bacia and Schwille, 2007). Most protein interactions in the cell are characterized by a dynamical equilibrium between bound and free species. Given the total mobile concentration of each of the binding partners determined by autocorrelation analysis of individual colors, and the concentration of the complex revealed from the relative amplitude of the cross correlation (Rigler et al., 1998), the equilibrium constants for the binding between the labeled proteins can be determined. We note that the cross-correlating species need not interact directly; they simply must be part of the same diffusing complex.
Two recent studies extensively used FCCS to characterize dynamic interactions among components of the mitogen-activated protein kinase (MAPK) cascade in yeast (Maeder et al., 2007; Slaughter et al., 2007). The dissociation constants for more than 10 pairs of proteins at their native concentrations in the yeast cytosol were reported using FCCS analysis. Interestingly, while a variety of conventional methods had previously reported the interaction between Fus3, a MAPK, and Ste5, a scaffold protein mediating the kinase cascade, FCCS revealed that this complex was surprisingly scarce in the yeast cytosol, compared with other well-documented interactions. Instead, the interaction was prominent on the cell cortex, as observed using fluorescence resonance energy transfer (Slaughter et al., 2007; fluorescent resonance energy transfer [FRET]; see below comparing FCCS and FRET). This highlights the usefulness of FCCS for detailing protein interactions quantitatively and with spatial resolution in vivo.
PHOTON COUNTING HISTOGRAMS FOR QUANTITATIVE OBSERVATION OF PROTEIN HOMO-OLIGOMERIZATION IN VIVO
The function of many regulatory and structural proteins depends on formation of homo-oligomeric complexes. Homotypic interactions leading to protein aggregate formation have also been implicated in many diseases (Aguzzi and O'Connor, 2010). To this point, detection of homo-oligomeric complexes and determination of protein stoichiometry within homo or hetero-oligomeric complexes are challenging for traditional approaches, especially at low expression levels and with cellular spatial resolution. The photon counting histogram (PCH), a different analysis method that takes advantage of the same fluorescence fluctuation data as FCS, is a powerful method for assessing protein homo-oligomeric complex formation and stoichiometry in vivo. In PCH, the distribution of photon events per time bin is analyzed using statistical methods to determine the average counts per second per molecule (CPSM) emitted by diffusing molecules as they traverse the focal volume. This is accomplished through a convolution of all the possible positions of the molecules within a focal volume with the expected photon yield of a molecule with a given molecular brightness at each point of the focal volume (Chen et al., 1999). In actuality, the shape of the photon distribution per time bin is fitted to determine what concentration and what molecular brightness is most likely to account for it, taking into consideration the contribution of Poisson counting noise. An accurate understanding of the excitation profile (the point spread function) is therefore required.
As the CPSM depends completely on, for example, the laser power used and detection efficiency, it is by nature a comparison technique. However, knowing a priori how particle brightness scales with the stoichiometry of the fluorescent probe allows us to relate CPSM to the stoichiometry of the tagged protein within the protein complex. For example, once a linear relationship in fluorescence brightness is established between GFP standards (1×, 2×, …) under a given set of experimental conditions, the brightness of the particles containing a GFP-labeled protein can be compared with the standards to report the stoichiometry of the protein per particle/complex (Chen et al., 2003; Slaughter et al., 2007, 2008; Figure 1G). In the study of MAPK signaling, for example, PCH revealed that dimerization of Ste5 may be a key requirement for its interaction with Fus3 (Slaughter et al., 2007). Digman et al. (2008a) used PCH and other methods to detail the diffusion and homo-oligomerization of the focal adhesion protein paxillin in CHO cells. It is worth noting that PCH simply reports the stoichiometry of a given protein within a diffusing complex, regardless of whether or not the proteins present in multiple copies interact directly.
A more complex scenario is when proteins that self-oligomerize also simultaneously participate in hetero-oligomeric interactions in an oligomerization state–dependent manner, with homo- and hetero-oligomeric complexes coexisting in a dynamic equilibrium. An extension of PCH in two dimensions (2dPCH) with spectrally distinct fluorophores has the unique ability to elucidate such complex situations (Hillesheim et al., 2006; Slaughter et al., 2008).
WHEN TO USE FFS AND ITS PROS AND CONS
With no exception, FFS methods must be applied to dynamical systems where components are mobile. Without fluctuation, i.e., if molecules are completely immobile, FFS will fail entirely (Figure 1H). However, FFS can work in cases where motion of molecules in and out of the focal volume is relatively slow, but this necessitates scanning techniques that limit exposure and photobleaching, at the expense of time resolution. For example, Schwille and coworkers implemented a scanning derivative of FCS to limit photobleaching while examining the rates of slow membrane diffusion in live yeast cells (Ries and Schwille, 2006). Along the same line, concentration is an important consideration in FFS. Jamming the focal volume full with hundreds of molecules will diminish the ability to tell if one or two enters or leaves. Thus, although imaging welcomes high protein concentrations for bright signals, FFS methods thrive at low concentrations (up to ∼400 nM). The use of low-expression vectors or homologous recombination to knock in the fluorescent tag is necessary for successful implementation in any cellular system. Although the native expression levels for many cytosolic yeast proteins examined to date (10–200 nM) are well within the preferred range for FFS, high concentration presents more of an obstacle for FFS in mammalian systems, where fluorescent fusion proteins are often overexpressed. However, the challenge of expression level in cell culture is not insurmountable. For example, Cleveland and colleagues successfully applied FCS and PCH in PTK2 cells to examine the cell cycle dependence of the molecular complexes and stoichiometry of Cdc20, a key activator of the anaphase promoting complex (Wang et al., 2006). Rigler and coworkers recently implemented a controllable expression system to mimic native expression in Drosophila salivary glands to examine transcription factor–DNA interactions, leading to a dynamic model of target site finding through multiple association and dissociation events (Vukojevic et al., 2010).
Among its many advantages, FCCS is particular useful for examining protein interactions that require the native environment and for quantitative comparisons of the strength of protein interactions at certain cellular locations or physiological stages. It is also wonderful to those researchers dreading long hours in the cold room. However, in addition to the general limitations that apply to all FFS methods described above, a present challenge for FCCS is the spectral bleed-through between the two fluorophores, which will generate false positives or background cross-correlation. For example, use of GFP and mCherry, which has been one of the most successful AFP pairs used in FCCS to date, results in a 3–5% bleed-through from the green into the red channel due to spectral overlap (using common filters that maximize detection of the GFP and mCherry). This produces a background cross correlation that considerably reduces the sensitivity for detecting relatively weak protein interactions. A cross correlation of 5% is expected for proteins present at ∼50 nM concentration and interacting with a Kd of 1 μM, but this level of interaction may be obscured by the background due to spectral bleed-through. Because of the possibility of fluorophore cross-talk, measurement of background cross correlation of a negative control, such as cells expressing the two fluorophores in unbound forms (e.g., unlinked GFP and mCherry), is required before data can be interpreted. Better yet, conclusions made from FCCS data of weak interactions can be reinforced if a biologically relevant mutation that specifically limits interaction of the two proteins also reduces the cross-correlation amplitude. Cross-talk is especially problematic when green and red fluorophores are present at different concentration ranges. If possible, the more highly expressed protein should be tagged with the red AFP, because red-to-green cross-talk is much less problematic than green-to-red cross-talk. It should be noted that possibly due to mCherry's sensitivity to photobleaching and/or poor folding, cross correlation is much less than 100% in live yeast even for a covalently linked GFP-mCherry dimer. The above problems strongly limit the dynamic range for FCCS to detect protein interactions. Fortunately, these are not insurmountable problems. For example, spectral bleed through can be eliminated by laser switching methods (Muller et al., 2005).
Finally, we compare FCCS with FRET, a popular method for assessing protein interactions in live cells. FRET reports protein interactions by detecting energy transfer from one probe, the donor, to a second probe, the acceptor, based on the proximity of two tagged proteins to the one-sixth power (Cheung, 1991). Also a very powerful technique, FRET does not require mobile particles, nor does it require low molecular concentration. In fact, because low molecular concentration can present a difficulty for FRET measurements, FRET is best applied to proteins that are concentrated in particular cellular locations (Figure 1H). Because many factors, such as the distance between or the relative orientation of the donor and acceptor probe, may lead to lack of a FRET even in the case of interacting proteins, a negative result with FRET may not be interpretable. FCCS, on the other hand, is not affected by probe distance or orientations and is more appropriate at low molecular concentrations. Furthermore, FCCS is more amenable to quantification of the extent of protein interactions. For example, an average FRET efficiency of 5% may reflect 5% of FRET between 100% of the pairs, or equally likely may reflect 10% FRET between 50% of the pairs. Such ambiguity does not exist for FCCS. For FRET data, more advanced analysis is required to attempt to differentiate between these two scenarios (Wallrabe and Periasamy, 2005; Digman et al., 2008b). Finally, an important difference to keep in mind is that a positive signal in FRET usually implies a direct interaction between the two examined proteins, whereas positive cross-correlation indicates simply that the two proteins are components of a same mobile complex. Thus, whether to use FRET or FCCS depends on what is known about the properties of the molecules and the type of information being sought after. We note that FRET between components of a diffusing complex may occur and will affect FCCS measurements. FRET to a red AFP will lower the molecular brightness of the green AFP and must be taken into account, especially if the researchers are attempting to examine stoichiometry of the species.
THE HARDWARE REQUIREMENTS FOR POINT FFS
Useful techniques must not require highly specialized equipment nor be difficult to establish. The basic system for point FFS is a confocal microscope with an adjustable pinhole that limits collection of out of focus light; however, a few special implementations are necessary for fruitful FFS applications. FFS works best on systems equipped with photon counting avalanche photodiodes. A high numerical aperture objective is generally required for studies in vivo, and for FCCS a color corrected objective is necessary so that the red and green focal volumes overlap well. Leading microscopy companies such as Carl Zeiss and Leica produce packaged systems or modules for FFS applications.
CONCLUSION
The applications of FFS in live cells have exploded in recent years. For a live cell system with mobile components, there simply is no substitute for FFS for discernment of interactions, concentration, and stoichiometry. In addition to the well-utilized model of yeast and cultured mammalian cells, these studies have moved into increasingly complex systems, such as Drosophila oocytes and zebrafish embryos, and have been used to investigate increasingly complex biological questions. Challenges that have restricted the field in the past (e.g., limited commercial instrumentation options or weak red autofluorescent proteins to pair with GFP) have either been completely remedied in the last 5 years or are steadily being resolved. The applications of FFS will continue to expand, driven by questions in cell and molecular biology—as in vivo applications stretch the original FFS algorithm in space and color (Kolin and Wiseman, 2007; Digman et al., 2009), leading to previously unimagined, powerful insights into dynamics of biological systems.
ACKNOWLEDGMENTS
We acknowledge Sue Jaspersen, Jay Unruh, and Swarna Mehrotra for critical reading of this manuscript and Doug Kellogg and Jagesh Shah for valuable comments. This work is supported by National Institutes of Health Grant GM057063 to R.L.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E10-05-0451) on October 27, 2010.
REFERENCES
- Abu-Arish A., Porcher A., Czerwonka A., Dostatni N., Fradin C. High mobility of bicoid captured by fluorescence correlation spectroscopy: implication for the rapid establishment of its gradient. Biophys. J. 2010;99:L33–L35. doi: 10.1016/j.bpj.2010.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguzzi A., O'Connor T. Protein aggregation diseases: pathogenicity and therapeutic perspectives. Nat. Rev. Drug Discov. 2010;9:237–248. doi: 10.1038/nrd3050. [DOI] [PubMed] [Google Scholar]
- Bacia K., Schwille P. Practical guidelines for dual-color fluorescence cross-correlation spectroscopy. Nat. Protoc. 2007;2:2842–2856. doi: 10.1038/nprot.2007.410. [DOI] [PubMed] [Google Scholar]
- Chen Y., Muller J. D., So P. T., Gratton E. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 1999;77:553–567. doi: 10.1016/S0006-3495(99)76912-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Wei L. N., Muller J. D. Probing protein oligomerization in living cells with fluorescence fluctuation spectroscopy. Proc. Natl. Acad. Sci. USA. 2003;100:15492–15497. doi: 10.1073/pnas.2533045100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung H. C. Resonance energy transfer. In: Lakowicz J. R., editor. Topics in Fluorescence Spectroscopy. vol. 2. New York: Plenum Press; 1991. pp. 128–176. [Google Scholar]
- Digman M. A., Brown C. M., Horwitz A. F., Mantulin W. W., Gratton E. Paxillin dynamics measured during adhesion assembly and disassembly by correlation spectroscopy. Biophys. J. 2008a;94:2819–2831. doi: 10.1529/biophysj.107.104984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Digman M. A., Caiolfa V. R., Zamai M., Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys. J. 2008b;94:L14–L16. doi: 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Digman M. A., Wiseman P. W., Horwitz A. R., Gratton E. Detecting protein complexes in living cells from laser scanning confocal image sequences by the cross correlation raster image spectroscopy method. Biophys. J. 2009;96:707–716. doi: 10.1016/j.bpj.2008.09.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elson E. L., Magde D. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- Fields S., Song O. A novel genetic system to detect protein-protein interactions. Nature. 1989;340:245–246. doi: 10.1038/340245a0. [DOI] [PubMed] [Google Scholar]
- Haustein E., Schwille P. Single-molecule spectroscopic methods. Curr. Opin. Struct. Biol. 2004;14:531–540. doi: 10.1016/j.sbi.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Hillesheim L. N., Chen Y., Muller J. D. Dual-color photon counting histogram analysis of mRFP1 and EGFP in living cells. Biophys. J. 2006;91:4273–4284. doi: 10.1529/biophysj.106.085845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. A., Heinze K. G., Schwille P. Fluorescence correlation spectroscopy in living cells. Nat. Methods. 2007;4:963–973. doi: 10.1038/nmeth1104. [DOI] [PubMed] [Google Scholar]
- Kolin D. L., Wiseman P. W. Advances in image correlation spectroscopy: measuring number densities, aggregation states, and dynamics of fluorescently labeled macromolecules in cells. Cell Biochem. Biophys. 2007;49:141–164. doi: 10.1007/s12013-007-9000-5. [DOI] [PubMed] [Google Scholar]
- Maeder C. I., Hink M. A., Kinkhabwala A., Mayr R., Bastiaens P. I., Knop M. Spatial regulation of Fus3 MAP kinase activity through a reaction-diffusion mechanism in yeast pheromone signalling. Nat. Cell Biol. 2007;9:1319–1326. doi: 10.1038/ncb1652. [DOI] [PubMed] [Google Scholar]
- Magde D., Elson E. L., Webb W. W. Fluorescence correlation spectroscopy. II. Experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- Muller B. K., Zaychikov E., Brauchle C., Lamb D. C. Pulsed interleaved excitation. Biophys. J. 2005;89:3508–3522. doi: 10.1529/biophysj.105.064766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remy I., Michnick S. W. Mapping biochemical networks with protein-fragment complementation assays. Methods Mol. Biol. 2004;261:411–426. doi: 10.1385/1-59259-762-9:411. [DOI] [PubMed] [Google Scholar]
- Ries J., Schwille P. Studying slow membrane dynamics with continuous wave scanning fluorescence correlation spectroscopy. Biophys. J. 2006;91:1915–1924. doi: 10.1529/biophysj.106.082297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigler R., Foldes-Papp Z., Meyer-Almes F. J., Sammet C., Volcker M., Schnetz A. Fluorescence cross-correlation: a new concept for polymerase chain reaction. J. Biotechnol. 1998;63:97–109. doi: 10.1016/s0168-1656(98)00079-0. [DOI] [PubMed] [Google Scholar]
- Slaughter B., D., Unruh J. R., Li R. Fluorescence fluctuation spectroscopy and imaging methods for examination of dynamic protein interactions in yeast. In: Walker J., editor. Methods in Molecular Biology: Yeast Systems Biology. New York: Humana (Springer); 2010. (in press) [DOI] [PubMed] [Google Scholar]
- Slaughter B. D., Huff J. M., Wiegraebe W., Schwartz J. W., Li R. SAM domain-based protein oligomerization observed by live-cell fluorescence fluctuation spectroscopy. PLoS ONE. 2008;3:e1931. doi: 10.1371/journal.pone.0001931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slaughter B. D., Schwartz J. W., Li R. Mapping dynamic protein interactions in MAP kinase signaling using live-cell fluorescence fluctuation spectroscopy and imaging. Proc. Natl. Acad. Sci. USA. 2007;104:20320–20325. doi: 10.1073/pnas.0710336105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vukojevic V., Papadopoulos D. K., Terenius L., Gehring W. J., Rigler R. Quantitative study of synthetic Hox transcription factor-DNA interactions in live cells. Proc. Natl. Acad. Sci. USA. 2010;107:4093–4098. doi: 10.1073/pnas.0914612107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallrabe H., Periasamy A. Imaging protein molecules using FRET and FLIM microscopy. Curr. Opin. Biotechnol. 2005;16:19–27. doi: 10.1016/j.copbio.2004.12.002. [DOI] [PubMed] [Google Scholar]
- Wang Z., Shah J. V., Berns M. W., Cleveland D. W. In vivo quantitative studies of dynamic intracellular processes using fluorescence correlation spectroscopy. Biophys. J. 2006;91:343–351. doi: 10.1529/biophysj.105.077891. [DOI] [PMC free article] [PubMed] [Google Scholar]