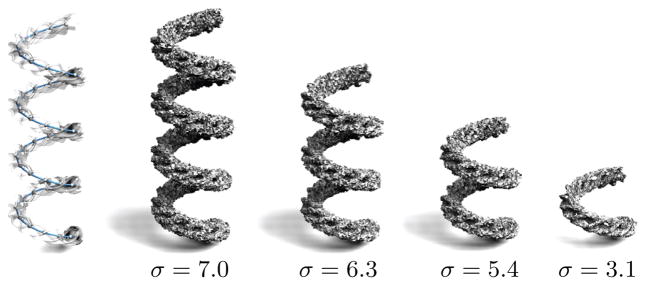Discovering Structural Regularity in 3D Geometry

Abstract

We introduce a computational framework for discovering regular or repeated geometric structures in 3D shapes. We describe and classify possible regular structures and present an effective algorithm for detecting such repeated geometric patterns in point- or mesh-based models. Our method assumes no prior knowledge of the geometry or spatial location of the individual elements that define the pattern. Structure discovery is made possible by a careful analysis of pairwise similarity transformations that reveals prominent lattice structures in a suitable model of transformation space. We introduce an optimization method for detecting such uniform grids specifically designed to deal with outliers and missing elements. This yields a robust algorithm that successfully discovers complex regular structures amidst clutter, noise, and missing geometry. The accuracy of the extracted generating transformations is further improved using a novel simultaneous registration method in the spatial domain. We demonstrate the effectiveness of our algorithm on a variety of examples and show applications to compression, model repair, and geometry synthesis.

1 Introduction

Regular geometric structures are ubiquitous in both natural and man-made objects. They play an important role in fields as diverse as biology, physics, engineering, architecture, and art. The detection of repeated structures is also an important mechanism in how we recognize and understand the world around us—for many objects are characterized by the presence of such patterns.

Repetition is prevalent in the structure of biological organisms, from the spinal column in mammals to the phyllotaxis of plant leaves. The study of symmetries, patterns, and repetitions is the central topic of the book On Growth and Form by D’Arcy Thompson [1992], which has remained a popular biology classic since its publication in 1917. Geometric regularity is often the result of a specific developmental growth process [Mandelbrot 1982]. Finding such repeated substructures can thus help to understand biological growth and analyze abnormalities due to, for example, external conditions such as temperature or water supplies.

Structural regularity also abounds in man-made objects, often as a result of economical, manufacturing, functional, or aesthetic considerations. One of the most prominent examples is architecture, where repetitive elements are fundamental in almost all design styles. In fact, we often recognize certain styles exactly because of the presence of such elements, such as the colonnade in the portico of a Greek temple. Repeating structures and motifs are also an essential component in decorative art, fashion, and interior design.

Discovering such regular structures in geometric models is a challenging task, since we typically have no prior knowledge of the size, shape, or location of the individual elements that define the pattern. Structures can be incomplete or corrupted by noise, and hidden amongst large components of the geometry that are not part of the pattern and therefore function as clutter or outliers. We present an algorithm addressing these challenges by simultaneously estimating the repetition pattern and detecting the repeating geometric element. We propose a mathematical framework that captures a wide variety of regular structures as shown in Figure 1.

Figure 1.

Regular structures discovered by our algorithm involve combinations of rotation, translation, and scaling of the repetitive elements.

We believe that our proposed approach captures a novel kind of meso-level structure in 3D geometry data that is different from both macro-scale global symmetries and the micro-regularity of a bump map texture. Our method finds a compact generative model that explains repetitive elements within an object thus giving access to important semantic information about the shape. The retrieved regularity patterns reveal the inherent geometric redundancy of a shape and can be utilized to form high-level models of the object for recognition, to improve the performance of lower-level compression and simplification algorithms, or to allow certain kinds of global editing operations that would be hard to achieve by other techniques. Our method is robust with respect to missing elements and partial regularity. This enables applications that reconstruct missing elements using the retrieved pattern as a prior for shape completion and non-local noise removal.

Contributions

The central objective of this paper is the detection of regular structures in geometric models and their use in advanced geometry processing operations. To achieve this goal, we make the following contributions:

• We present a computational framework for structure discovery that allows a unified and mathematically rigorous treatment of a variety of important 3D structures, including translational, rotational, and cylindrical grids, as well as helices and spirals. We show that these patterns can be represented as regular samplings of the commutative one- and two-parameter subgroups of the group of similarity transformations.

• We define a mapping function for transformations from matrix space to an auxiliary space in which generative models occur as uniform grids. We present a global optimization method for discovering and fitting such grids that robustly handles missing grid elements and outliers.

• We introduce an aggregation procedure that extracts large-scale repetitive elements and at the same time optimizes the generating transformations. This is achieved with a novel ICP-inspired quadratic objective function in the space of similarity transformations.

Repetitive patterns are generated by combining and applying a small number of generative transformations to geometry building blocks. Typically, these patterns are surrounded by other geometry which does not conform to the pattern. Our method simultaneously estimates a generative model that explains the repetitions present, as well as the geometry element being repeated. This is an interesting joint optimization, coupling continuous geometry registration in 3D with discrete pattern fitting in a suitable transform space.

Overview

We formalize the notion of structural regularity in Section 2 using the concept of discrete groups of transformations. Based on this mathematical framework, we introduce an algorithm for extracting regular structures that is composed of three main stages (see Figure 2). We first decompose the input shape into small local surface patches and estimate similarity transformations between these patches. A suitable mapping from the space of similarity transformations to an auxiliary 2D space, followed by clustering of transformations, yields characteristic lattice patterns for shapes containing regular structures. The second stage estimates the parameters of the generative model that gives rise to these patterns – this is done by a global optimization procedure in transformation space. The outcome of this second stage is a set of regular structures at the scale of the initial local surface patches. In the final stage, we aggregate spatially adjacent patches to build larger repetitive elements using a novel simultaneous registration method that optimizes the generating transformations in the spatial domain.

Figure 2.

Processing pipeline for automatic structure discovery. Transform analysis yields characteristic patterns in transformation space, model estimation determines the generating transformations, aggregation extracts the corresponding regular structures in the spatial domain.

Sections 3 to 5 discuss the three stages of our processing pipeline in more detail. In Section 6 we present results, analyze the scalability and robustness of our technique, and discuss a number of applications to model repair and geometry synthesis. We conclude with limitations and some directions for future research.

Related Work

The theory of discrete groups of transformations is a fundamental tool in the study of periodic patterns. Liu and colleagues [2004] present a computational model that detects peaks in the autocorrelation function of images to determine the periodicity of texture patterns. They propose a classification method to categorize 1D and 2D periodic patterns according to the 7 frieze groups or 17 wallpaper groups, respectively. Beyond applications in image analysis, they demonstrate the effectiveness of their method for applications in indexing, compression, and gait analysis.

Related approaches rely on the Fourier transform or other spectral methods to discover periodic patterns in signals [Hsu et al. 2001]. A good example is the constant Q transform [Brown 1991], widely used in detecting repeating patterns in acoustic signals such as music. Fourier methods have also been suggested in cognitive science as a tool the brain uses to extract structure from images [Blakemore and Campbell 1969]. For spatial data, autocorrelation and Fourier-based methods are most effective in recovering patterns composed of translations, reflections, and glide-reflections. Our approach extends the range of transformations to also include scaling and rotations and is thus capable of recovering non-translational structures such as rings, spirals, and helices (Figure 1).

Other approaches in image analysis are also related to our work. Leung and Malik [1996] detect interesting candidate regions in an image based on intensity variation. Matching elements are extracted using local search and grouped in a graph structure that encodes the repetitive pattern. Similarly, Schaffalitzky and Zissermann [1999] use edge detection to find interesting elements and successively grow patterns in a greedy fashion. They propose a grouping strategy for translational grids based on maximum likelihood estimation. Tuytelaars and colleagues [2003] employ invariant-based hashing and Hough transforms for finding regular patterns in images that can be characterized by a planar homology. Recently, Müller and co-workers [2007] proposed an algorithm for structure detection in building facades from images. Their approach exploits the strong geometric and orientation priors of common facade structures in a statistical model to detect translational symmetries and repetitive window structures. Korah and Rasmussen [2007] assume that the image is rectified and that regular lattice structures are composed of axis-aligned rectangles with a limited range of aspect ratios. We follow a different approach in that we make no prior assumptions on shape, size, or orientation of the repetitive elements. Instead, we infer these properties automatically during the optimization, once structural regularity has been detected in transformation space.

Our approach bears some loose relation to fractal image compression [Jacquin 1992]. In this class of algorithms the goal is to realize a given image as the fixed point of a contractive mapping in the space of images. The data for this mapping is extracted from ‘similarities’ between small rectangles in the image. Impressive compression rates have been demonstrated for images containing repetitive structures.

Structure discovery has also be addressed in computer aided design (CAD). Shikhare and co-workers [2001] proposed a compression scheme that exploits geometric patterns in CAD models. This method is most effective for procedurally designed models where the repetitive elements appear as separate connected components. Langbein and Martin [2006] introduced regularity feature trees that provide a concise description of symmetry features in order to capture important aspects of the geometric design intent. The method is specifically designed for shapes that are bounded by planar, spherical, cylindrical, conical, and toroidal surfaces and exploits the simple geometry of these typical CAD building blocks.

Liu and colleagues [2007] present a technique for segmenting periodic reliefs on triangle meshes that relies on the user to identify the repetitive elements. We avoid the need for such user assistance and employ a comprehensive analysis in transformation space to automatically extract a set of candidate elements.

Our method is also related to previous methods in symmetry detection. Podolak and colleagues [2006] propose a symmetry transform that captures a continuous measure of the reflective symmetries of a shape with respect to all possible planes. Rustamov [2007] extends this approach to include information on the spatial distribution of asymmetries. Mitra and co-workers [2006] detect partial and approximate symmetries using a sampling approach to accumulate local evidence of pairwise symmetries in a transformation space. The method of Martinet and colleagues [2006] is based on generalized moments and finds global symmetries in 3D shapes by comparing spherical harmonic coefficients. Various geometry processing applications make use of extracted symmetries, e.g., for symmetrization and symmetry-aware meshing [Golovinskiy et al. 2007; Mitra et al. 2007] or mesh segmentation [Simari et al. 2006].

The above symmetry detection methods are very successful for models with a few large-scale symmetries. They are less effective when the size of the symmetric elements becomes smaller and the number of repetitions increases. In our setting the signal is in the regularity of the repetitions and thus we rely on a sufficient number of repetitions for robust structure detection. In this sense our method can be considered complementary to existing work on symmetry detection – both address different aspects of structural regularity.

2 Transformations and Regularity

We consider the space of orientation-preserving similarity transformations, i.e., the subspace of the space of affine transformations whose elements are composed of uniform scaling, rotation, and translation. A similarity transformation T can be represented in homogeneous coordinates using a matrix H

$$\mathbf{H}=\left(\begin{array}{cc}s·\mathbf{R}& \mathbf{t}\\ \mathbf{0}& 1\end{array}\right),$$

where s is the uniform scaling factor, R is a rotation matrix, and t is a translation vector.

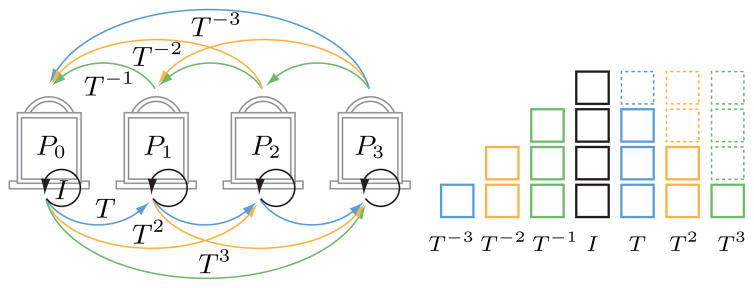
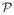We understand regularity as the repeated application of a similarity transformation (see Figure 3). More formally, we define a regular structure of size n as a tuple (, 𝒢), where the set = {P₀, …, P_n−1} is a collection of n patches P_k ⊂ 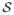of a given surface 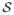, and 𝒢 is a transformation group acting on 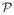. In the simplest setting, 𝒢 is a 1-parameter group with generating similarity transformation T. The elements of 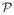can be represented as P_k = T^kP₀ for k = 0, …, n−1. Any element P_i ∈ 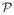of a regular structure can be transformed into any other element P_j ∈ 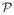by the similarity transformation T_ij = T^j−i. As illustrated in Figure 4, transformation T^l occurs n − |l| times, where −n < l < n.

Figure 3.

Schematic illustration of regular structures. The helix and spiral are generated by transformations that combine rotation with translation and scaling, respectively. The images on the right show the three types of commutative 2-parameter groups: rotation and translation along the rotation axis, two independent translations, rotation and scaling with center of scaling on the rotation axis.

Figure 4.

A 1D regular structure of size n gives rise to n² pairwise transformations that form a characteristic accumulative pattern.

Commutative 2-parameter groups

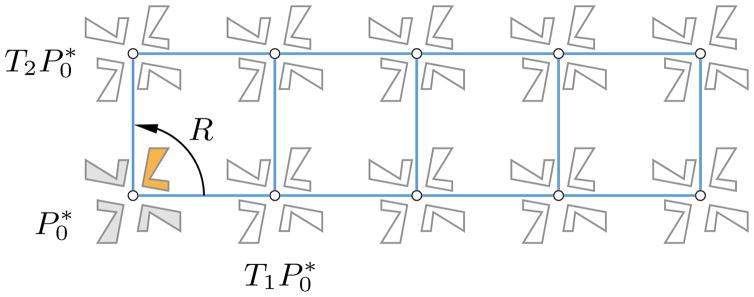
More complex regular structures can be generated by combining 1-parameter groups. The great variety of repetitive structures common in art, nature, or engineering is reflected in a rather involved mathematical classification. For instance, there are 17 distinct planar crystallographic groups of Euclidean transformations. The following properties of such a crystallographic group 𝒢 can be found in [Grünbaum and Shephard 1987]. The group 𝒢 is generated by rotations, reflections, and translations; furthermore, the translations contained in 𝒢 form a subgroup ℋ of finite index. This means that the pattern generated by the group 𝒢 and any patch P₀ equals the pattern generated by the subgroup ℋ and a bigger patch $P_0^{\ast }$ which is a finite union of copies of P₀ (Figure 5).

Figure 5.

The crystallographic group generated by translations T₁, T₂, and the rotation R creates a repetitive pattern when acting on the patch P₀ (orange). The same structure is created by the group of translations { $T_1^j{T}_2^k$} acting on the bigger patch $P_0^{\ast }=P_0\cup {RP}_0\cup R^2{P}_0\cup R^3{P}_0$ (gray). $P_0^{\ast }$ has 4-fold rotational symmetry.

It follows that the detection of general patterns (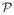, 𝒢) can be broken into two steps: First detect a pattern where the generative group consists of translations, then detect rotational and reflective symmetries of the basic patch of the first pattern. If we can deal with the first problem, the second one can be addressed by the method of [Mitra et al. 2006]. The spatial crystallographic groups have analogous properties. It turns out that there is an elegant way to handle not only groups of translations, but generally uniformly sampled commutative 1- and 2-parameter groups that involve rotation and scaling as well. We show in the appendix that the commutative 2-parameter groups fall into one of exactly three classes (Figure 3, right). Commutative k-parameter groups for k ≥ 3 cannot contain any rotation or scaling components, i.e., are composed of k independent translations. Our method naturally extends to this case.

The geometry of a k-parameter regular structure (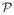, 𝒢) can be compactly represented by a single patch P₀ ∈ 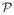, the group generator(s) T₁, …, T_k, and the integer dimension(s) n₁, …, n_k with n₁ · … · n_k = n = |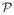|. We call P₀ the representative element and the tuple (P₀, {T_i}, {n_i}) the generative model of the regular structure.

Structure Detection

The objective of our algorithm can be formulated as follows: Given a shape 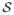, find a generative model (P₀, {T_i}, {n_i}) such that the union P₀ ∪ ··· ∪ P_n−1 covers as much of the surface 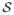as possible, while maximizing the number of repetitions n. In other words, we want to explain as much as possible of the given input shape with a generative model that is as simple and compact as possible.

The challenge in finding a regular structure lies in the fact that both 𝒢 and 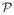are unknown. Size and shape of the geometric elements P_k are defined by the degree of regularity that they exhibit, hence we cannot decouple the estimation of 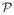and 𝒢. However, we can make use of the following observation: If P₀ is the representative element of (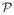, 𝒢), then any subset of P₀ will also generate a regular structure with transformation group 𝒢. Our approach for structure detection makes use of this observation by first estimating structural regularity at the level of small local surface elements. Collections of these surface elements that have a compatible transformation group are then aggregated to form large-scale structures.

3 Transformation Analysis

The first stage of our algorithm estimates and analyzes transformations between compatible local surface elements. We show how a suitable representation of these transformations leads to a characteristic lattice of transformation clusters for shapes containing regular structures.

Similarity Sets

Following the sampling approach proposed in [Podolak et al. 2006] and [Mitra et al. 2006], we first compute a uniform random sampling of the input model 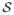with average sample spacing h. The user parameter h determines the smallest scale at which we wish to discover regular structures. Each sample point represents a small local patch of 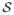. Our goal is to find evidence for a regular structure by analyzing the similarity transformations that map pairs of these patches onto each other. For this purpose patches are grouped into similarity sets Ω_l using a local shape descriptor that is invariant under similarity transformations. Only sample points with similar descriptor value are potential candidates for a regular structure, hence we can significantly reduce the number of relevant sample pairs and avoid the quadratic complexity of considering all pairwise matches. Subsequent processing will then be performed on each similarity set Ω_l independently.

We use a robust descriptor based on polynomial fitting of osculating jets as proposed by Cazals and Pouget [2003]. For each sample point we estimate the mean and Gaussian curvatures H and K respectively. Samples are grouped according to the value H²/K, which is invariant under uniform scaling, rotation, and translation. If no scaling is involved, we can further split the similarity sets based on the values of (H,K). Similar to [Mitra et al. 2006], we do not consider umbilical points, since the transformation between two such samples is not unique. Similarity sets Ω_l are processed in descending order of number of elements, since large collections of similar patches are more likely to contain a regular structure of significant size. Let Ω be the currently largest similarity set. We want to detect whether elements of Ω form a regular structure and, if so, estimate the parameters of the underlying transformation group from the collection 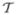= {T_ij |p_i, p_j ∈ Ω} of all pairwise transformations.

Local Alignment

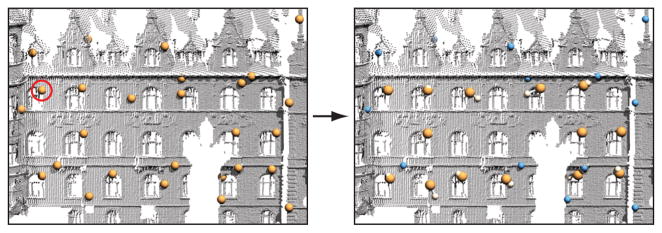
The estimated differential properties provide us with a means to approximate the similarity transformation T_ij that maps sample p_i ∈ Ω to sample p_j ∈ Ω. Translation and rotation can be derived by aligning the local frames computed from the surface normal and principal curvature directions. The uniform scaling factor can be calculated from the ratio of corresponding mean curvatures H_i/H_j. To improve the accuracy of the estimated similarity transformation and prune out incorrect matches, we refine this initial transformation using geometric registration. We employ local non-rigid ICP using instantaneous velocities as described by [Pottmann et al. 2006]. If the registration does not produce a good alignment of the local surface patches, the sample pair is discarded (see Figure 6). This improves the robustness of the following analysis of transformations and reduces the dependence on the specific choice of local shape descriptor, which only serves as tool to prune unnecessary sample pairs.

Figure 6.

Local alignment. The orange spheres on the left indicate the sample positions of the biggest similarity set. ICP alignment to the sample marked by the red circle yields the final positions shown on the right. Blue spheres indicate samples that have been discarded due to high alignment error.

Characteristic Patterns

Computing the group generators from the set 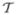of all pairwise transformations is a challenging task, since in general 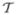contains many more elements than just the group transformations, and even these are often too numerous for an exhaustive computation. For example, an n × n regular grid gives rise to n⁴ pairwise transformations. To make this problem computationally tractable, we make use of the following important observation: The spatial coherence of regular structures leads to strong accumulative patterns in the corresponding transformation space.

Figure 4 illustrates this effect schematically for a simple 1- parameter translational structure. In Figure 7 we show the distribution of the pairwise transformations for a more complex 3D model. Even though the data is noisy and contains substantial holes due to occlusion during scanning, characteristic patterns in transformation space are noticeable. These patterns have two essential properties:

Figure 7.

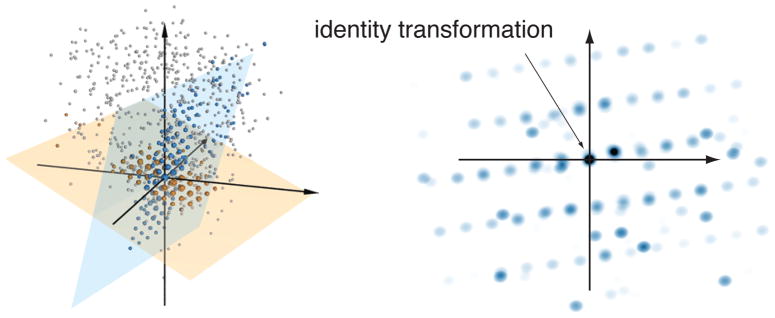
Characteristic patterns in transformation space. The plot on the left shows the distribution of translation vectors for the compatible pairs of the top three similarity sets of the building scan of Figure 1. We detect the two highlighted planes through the origin that correspond to the two dominant regular structures present in the model. Transformations close to these planes are shown in the corresponding color. The density plot on the right for the blue plane exhibits the typical grid pattern.

• All transformations of the underlying transformation group lie on a 2D plane through the origin in the space of affine transformations.

• The transformations accumulate in clusters that form a uniformly spaced grid.

This observation has important consequences for our algorithm: First, we only need to search for a linear sub-space of transformations that passes through the origin. Secondly, we can avoid exhaustive computation by randomized selection, since clusters remain dominant even for a sparse sub-sample of the set of all pairwise transformations. We thus select a small random subset Ω′ ⊂ Ω with |Ω′| ≪ |Ω| and only compute transformations for pairs (p_i, p_j) with p_i ∈ Ω′ and p_j ∈ Ω. For all our examples, Ω′ was at most 5% of the full similarity set Ω. Finally, we can exploit the uniform grid spacing of clusters to implement a robust global optimization for estimating the group generators as described in Section 4.

Transformation Mapping

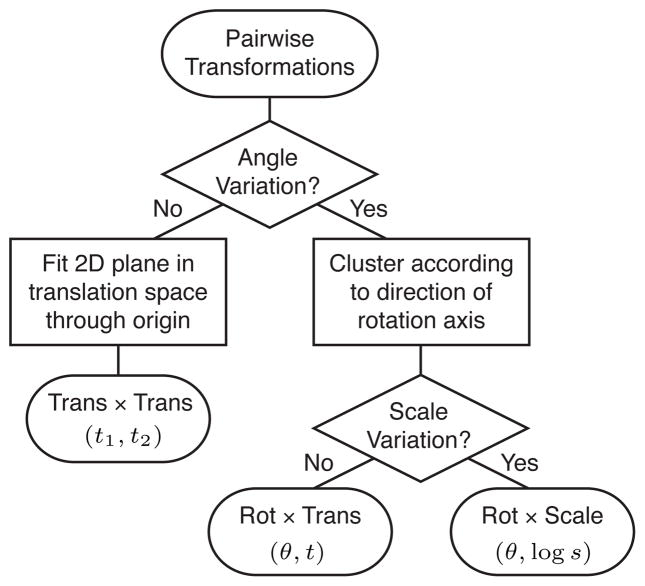
Similarity transformations that involve scaling and/or rotation do not immediately reveal a uniform grid structure on a linear subspace of the space of affine transformations: In general, transformations cluster at points on a curved manifold, which is significantly more difficult to detect. To address this issue, we introduce a suitable mapping function that exposes a similar uniform lattice structure for non-translational structures. In the definition of such a mapping it is crucial to avoid a dependence on the choice of origin, since the translation component depends on the center of scaling and the axis of rotation. Therefore, we only consider properties of the transformation that are invariant under a change of origin, such as the scaling factor s, the rotation angle θ, and the direction of the axis of rotation that we extract from the estimated transformation matrix H_ij of a sample pair (p_i, p_j).

Below we describe how we determine which of the three classes of 2-parameter structures shown on the right in Figure 3 can possibly be present in a given collection of similarity transformations and propose a suitable mapping function for each class. A flowchart of this procedure is shown in Figure 8.

Figure 8.

Algorithm for analyzing transformations.

We first determine if a rotational structure could be present by checking whether a significant fraction of the transformations have non-zero rotation angle. If no such evidence is found, the model can only contain regular structures of type Trans × Trans, and we search for suitable 2D planes through the origin in the space of 3D translation vectors (Figure 7) using a RANSAC method [Fischler and Bolles 1981]. All transformations are projected onto the retrieved planes, i.e. we apply a mapping of the form T ↦ (t₁, t₂) ∈ IR², where t₁, and t₂ are the coordinates of the projected translation vectors in the 2D sub-space.

In case we do find a significant number of rotations, we separate all transformations into sets with similar direction of rotation axis, since group transformations of a rotational structure need to have coinciding axis directions. For each such set we check if there is a significant variation in scaling factors. If so, the model potentially contains regular structures of type Rot × Scale and we apply the mapping T ↦ (θ, log s) to expose the uniform grid.

If no variation in scaling is detected, the model might still contain regular structures of type Rot × Trans. Since only translations parallel to the axis of rotation are possible in a commutative 2-parameter group, we apply the mapping T ↦ (θ, t), where the scalar t = t · a is computed as the projection of the translation vector t onto the unit direction vector a of the rotation axis.

Each of the mappings T ↦ (t₁, t₂), T ↦ (θ, log s), and T ↦ (θ, t) has the crucial property that composition of similarities corresponds to the sum of vectors in transformation space. If a second transformation T′ ∈ 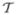is mapped to ( $t_1^{\prime },t_2^{\prime }$), or (θ′, t′), or (θ′, log s′), respectively, then the product TT′ is mapped according to

$$\begin{array}{ll}\text{case}\mathit{Trans}\times \mathit{Trans}:\hfill & T{T}^{\prime }\mapsto (t_1+t_1^{\prime },t_2+t_2^{\prime });\hfill \\ \text{case}\mathit{Rot}\times \mathit{Trans}:\hfill & T{T}^{\prime }\mapsto (\theta +{\theta }^{\prime },t+t^{\prime });\hfill \\ \text{case}\mathit{Rot}\times \mathit{Scale}:\hfill & T{T}^{\prime }\mapsto (\theta +{\theta }^{\prime },logs+log{s}^{\prime }).\hfill \end{array}$$

Here angles have to be understood modulo 2π. The identity transformation I = T⁰ is always mapped to the origin (0, 0), while the inverse transformation T⁻¹ is mapped to (−t₁, −t₂), or (−θ, −t), or (−θ, −log s), respectively. It follows that the group of transformations {T^kT^′j}, where j, k run in the integers, is mapped to a regular 2D lattice of vectors in transformation space.

4 Model Estimation

The goal of the model estimation stage is to obtain an estimate of the parameters of the generative model of a regular structure. Given the analysis of transformations described above, this amounts to finding regular lattices of clusters in a 2D distribution of points. Figure 7 illustrates two issues that make this task difficult:

• A number of spurious clusters are present that are not part of the regular structure. Since the similarity set Ω potentially contains more elements than those of the underlying regular structure, additional transformations appear in the set 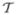that can obscure the grid pattern.

• Clusters that should be present are missing or too weak. The reason for this is twofold: There is a statistical variation in the distribution of the estimated transformations due to noise in the model and local variations of sample positions, which leads to inaccuracies in the estimation of pairwise transformations and thus less pronounced clusters. Cluster height is also reduced by missing transformations due to holes in the input data and the random sub-sampling of transformations.

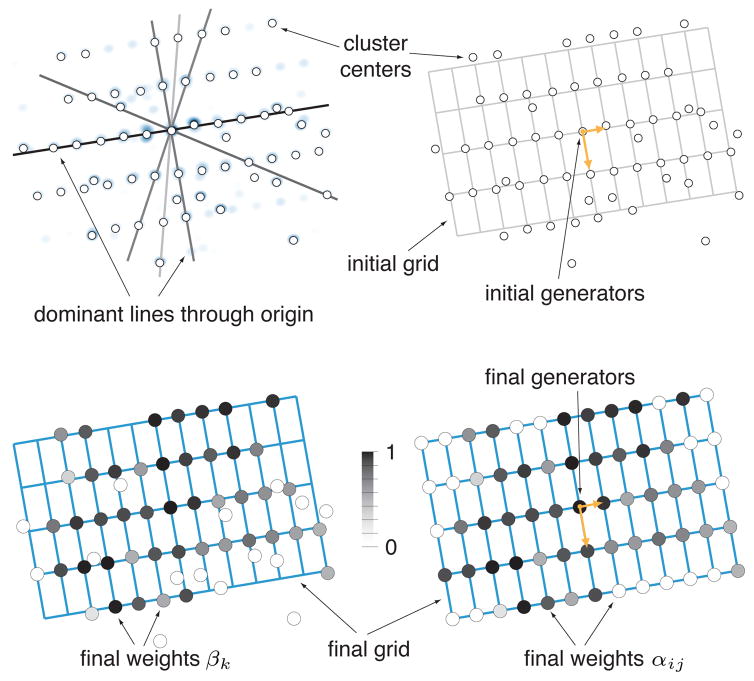
To reliably detect regular structures we therefore need a grid fitting approach that is robust to outliers and holes. We propose a global optimization method specifically designed for this task. This method operates on a set of cluster centers C = {c_k} that we extract from the set of transformations mapped to 2D space. We use mean-shift clustering for this purpose [Comaniciu and Meer 2002], but other methods can also be applied.

We describe our approach for an n₁ × n₂ regular grid of a 2- parameter group. 1-parameter groups can be considered a special case with n₂ = 1. Since the identity transformation is always part of a transformation group, the grid must pass through the origin and thus has only four degrees of freedom. This significantly reduces the search space and is a main reason for the robustness of the optimization. Grid locations X = {x_ij} can be represented with two vectors g₁, g₂ ∈ IR² such that x_ij = ig₁ + jg₂ with integers i, j subject to −n₁ < i < n₁ and −n₂ < j < n₂ (see also Figure 4 for a 1D example).

Energy Minimization

To find the unknown grid generators g₁ and g₂ we apply an optimization that combines different energy terms. We minimize the sum of squared distances of the grid locations to the cluster centers using the energy

$$E_{X\to C}={\sum }_i{\sum }_j{\alpha }_{ij}^2{\left|\right|{\mathbf{x}}_{ij}-\mathbf{c}(i,j)\left|\right|}^2,$$

where c(i, j) ∈ C is the cluster center closest to grid location x_ij. Similarly, we measure the distances of cluster centers to the grid as

$$E_{C\to X}={\sum }_{k=1}^{\mid C\mid }{\beta }_k^2{\left|\right|{\mathbf{c}}_k-\mathbf{x}(k)\left|\right|}^2,$$

where x(k) ∈ X is the grid location closest to cluster center c_k. The continuous variables α_ij and β_k are correspondence weights that measure how reliably a grid location can be mapped to a cluster center and vice versa. They are additional unknowns in the optimization that account for holes and outliers in the distribution of cluster centers. Values of α_ij and β_k close to zero indicate a hole or an outlier, respectively, while values close to one indicate a reliable match between transformation cluster and grid location. Two additional energies aim at maximizing the number of valid correspondences between grid locations and cluster centers:

$$E_{\alpha }={\sum }_i{\sum }_j{(1-{\alpha }_{ij}^2)}^2{E}_{\beta }={\sum }_k{(1-{\beta }_k^2)}^2.$$

Combining the different energy terms yields the objective function

$$E=\gamma (E_{X\to C}+E_{C\to X})+(1-\gamma )(E_{\alpha }+E_{\beta }),$$

where γ is a parameter that balances the fitting and correspondence terms. The grid generators are found as the minimizer of this energy

$${\mathbf{g}}_1,{\mathbf{g}}_2,\{{\alpha }_{ij}\},\{{\beta }_k\}=\underset{{\mathbf{g}}_1,{\mathbf{g}}_2,\{{\alpha }_{ij}\},\{{\beta }_k\}}{\text{argmin}}E.$$

We use an iterative Gauss-Newton solver to minimize the above objective function. The correspondence weights α_ij and β_k are initialized to one, since we do not assume any prior knowledge on holes or outliers. The initial values of the grid generators g₁ and g₂ are determined as clusters with ||g_i|| minimal on the most dominant lines through the origin (extracted using RANSAC). The grid dimensions are conservatively estimated from the furthest cluster on the lines. Closest cluster centers and grid locations in the fitting energies are re-assigned after each iteration.

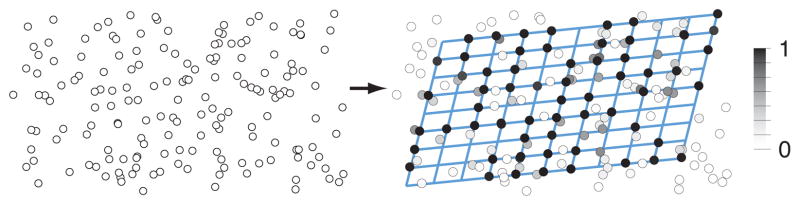
Figure 9 shows the results of our optimization method for the 7×3 regular structure of windows of Figure 6 that gives rise to a 13 ×5 grid in transformation space. A standard least-squares fit would not yield the desired result for such a distribution due to the strong influence of outliers and holes. In contrast, our approach automatically classifies holes and outliers and leads to a robust grid estimate. Figure 10 illustrates this feature for a more complex point set. Even though a pattern in the point set on the left is barely noticeable for the human eye, our method reliably detects the hidden lattice.

Figure 9.

Grid fitting. Cluster centers are extracted from the density distribution of mapped transformations (top left) and the grid is initialized according to the dominant lines through the origin (top right). The optimization simultaneously solves for the grid generators and the correspondence weights α_ij and β_k. After convergence, the latter accurately account for holes in the grid and outliers in the set of cluster centers, respectively (bottom row).

Figure 10.

Finding a grid amidst clutter. The correspondence weights β_k on the right show the reliable classification of outliers.

5 Aggregation

The model estimation stage operates in transformation space and provides us with a set of regular structures at the scale of the initial surface patches. The objective of the final stage is to extract large-scale repetitive elements and optimize the generating transformations using simultaneous registration of the extracted surface elements. This alignment in the spatial domain is essential, since transformations estimated from the small-scale surface patches can be inaccurate, which leads to accumulative errors that corrupt the quality of the extracted regular structures (see Figure 11).

Figure 11.

Simultaneous Registration. The colored points show the sample points that are closest to the bottom left element transformed using the estimated group transformations. Aggregation without registration leads to successively stronger misalignments (top row). Our coupled optimization with simultaneous registration significantly improves the accuracy of the generating transformations and allows extracting larger elements (bottom row).

We propose an interleaved optimization that alternates between local region growing and coupled registration. The goal of the former is to aggregate spatially adjacent patches of regular structures with compatible group structure. To determine which neighboring samples should be added to the patch, samples are prioritized with respect to the alignment error of the registration. We use a heap data structure to store all samples of the current patch boundary and incrementally add adjacent samples, similar to the region growing method of [Pauly et al. 2005].

Simultaneous Registration

We first discuss the case of a one-parameter regular structure. During registration we apply small changes to the generating transformation T of the group 𝒢 with elements T^k. We use a linearization and thus relate the matrices H₊, H of modified and original transformation T₊, T via

$${\mathbf{H}}_{+}\approx \mathbf{H}+\epsilon \mathbf{D}·\mathbf{H},$$

where ε is small and the matrix D has the form

$$\mathbf{D}=\left(\begin{array}{cccc}\delta & -d_3& d_2& {\overline{d}}_1\\ d_3& \delta & -d_1& {\overline{d}}_2\\ -d_2& d_1& \delta & {\overline{d}}_3\\ 0& 0& 0& 0\end{array}\right)$$ (1)

(cf. [Hofer et al. 2005]). This is equivalent to estimating the image point T₊(x) as

$$T_{+}(\mathbf{x})\approx T(\mathbf{x})+\epsilon (\mathbf{d}\times T(\mathbf{x})+\delta T(\mathbf{x})+\overline{\mathbf{d}}),$$ (2)

with d = (d₁, d₂, d₃) and d̄ = (d̄₁, d̄₂, d̄₃). When working with congruence transformations we let δ = 0. Iterated transformations are linearized by omitting terms of order ≥ 2 in the expression $T_{+}^k\approx {(\mathbf{H}+\epsilon \mathbf{D}·\mathbf{H})}^k$. We obtain

$$\begin{array}{c}{\mathbf{H}}_{+}^k\approx {\mathbf{H}}^k+\epsilon f_k(\mathbf{H},\mathbf{D})+{\epsilon }^2(\dots ),\text{with}\\ f_k(\mathbf{H},\mathbf{D})=\mathbf{D}·{\mathbf{H}}^k+\mathbf{H}·\mathbf{D}·{\mathbf{H}}^{k-1}+\cdots +{\mathbf{H}}^{k-1}·\mathbf{D}·\mathbf{H}.\end{array}$$

To set up the simultaneous registration procedure, assume that the model estimation procedure has related patch P_i to patch P_j by the transformation T^k. This knowledge contributes a term Q_ij to the objective function as follows: Let P_i be represented by sample points x_l and let y_l be that point in P_j that is closest to T^k(x_l). Moreover, let n_l be the unit normal vector of P_j at y_l. Then we form a combined point-plane and point-point distance term via

$$Q_{ij}:={\sum }_l\left({[(T_{+}^k({\mathbf{x}}_l)-{\mathbf{y}}_l)·{\mathbf{n}}_l]}^2+\mu {[T_{+}^k({\mathbf{x}}_l)-{\mathbf{y}}_l]}^2\right).$$

The point-point distance is used here for its regularizing effect; we use μ = 0.1 for all our examples. Inserting the first order estimate for $T_{+}^k$, the term Q_ij becomes a quadratic function Q_ij(εD) in the unknown elements of εD. Summing up over all patch pairs (P_i, P_j) that model estimation has related by a transformation T^k yields the final quadratic objective function

$$F(\epsilon \mathbf{D})={\sum }_{i,j}{Q}_{ij}.$$

Similar to the random selection of transformation pairs (Section 2), we can restrict the sum to a random subset of patch pairs. For structures with a large number of repetitions such as the amphitheater of Figure 1, less than 5% of all pairs is sufficient.

After solving the resulting linear system we have to update the group generator T by a true similarity or true congruence. For this projection onto the similarity group we use the method of Horn [1987] to best approximate the matrixH + εD·H by the matrixH₊ of a similarity transformation or congruence transformation. The registration algorithm iterates between step estimation “F → min” and projection.

So far we have considered one-parameter structures. A two-parameter structure generated by the original T plus an additional translation T₂ (with translation vector t₂) is as simple as the one-parameter case, since any group element is linear in t₂. For a two-parameter structure spanned by rotation R and scaling S, we linearize R and S and omit terms of order ≥ 2 in the products R^lS^k.

6 Results

The implementation of our structure detection algorithm follows the pipeline depicted in Figure 2. The user provides a point cloud or surface mesh as input and specifies the initial sample spacing h. Additional parameters include thresholds for cluster detection, grid fitting, and registration, for which we use the same default settings in all examples. The computation requires no additional user assistance and returns as output the detected set of regular structures, i.e., the representative elements, the number of repetitions, and the transformation group generators.

Scalability

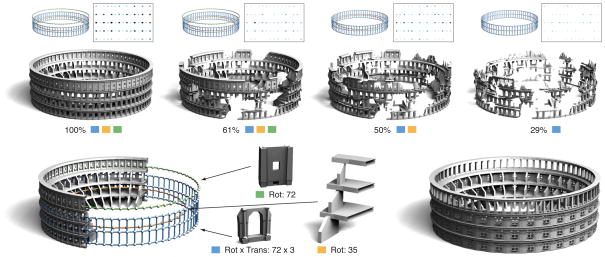
Figure 12 shows the results of our structure discovery algorithm on a complex architectural data set. The model exhibits a dominant 2-parameter structure composed of the arched window elements with a rotational component of 72 repetitions and a vertical translation of 3 repetitions. The top row of elements is detected as a separate 1-parameter ring structure. In the interior the algorithm finds a 1-parameter rotational structure of supporting columns with 35 repetitions. This example highlights an important feature of our algorithm. Due to the accumulation of similarity transformations in transformation space, structure detection is robust even for a sparse set of sample pairs. For example, the transformation group of the 2-parameter structure contains (72×3)² = 46,656 pairwise similarity transformations. However, dominant clusters sufficient for our global optimization method to extract the entire structure already appear when about 1,600 of these transformations are present.

Figure 12.

Structure discovery and procedural design on a 3D model of an amphitheater. The top row indicates which of the three regular structures can be reconstructed in their entirety when successively removing geometry. The density plots show a section of the distribution of transformations of the structure depicted in blue. The recovered structures are used to procedurally design a new model in the bottom right.

Robustness

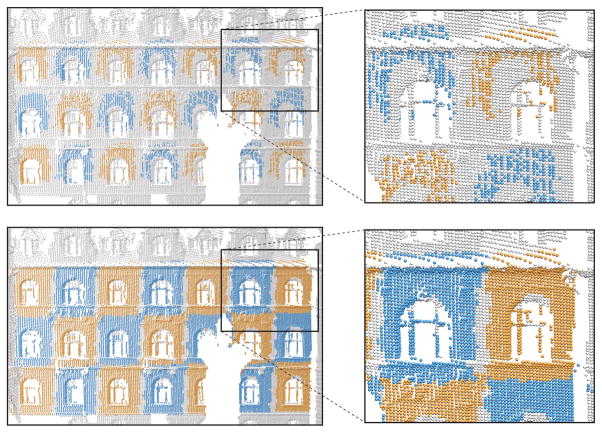
The characteristic accumulation of transformations also explains why our method is very robust with respect to missing geometry. We run the algorithm with the same parameter settings after successively removing random pieces of the amphitheater. As Figure 12 illustrates, the dominant structures are reliably detected even in the presence of substantial holes. Figure 13 shows that also regular structures with a relatively small number of repetitions can be detected in complex models with substantial clutter. This example also highlights the difference to top-down symmetry detection methods (cf. Figure 7 of [Mitra et al. 2006]). The latter extracts mostly pairwise symmetries, such as the global reflective symmetry or the rigid motions mapping the towers or chimneys onto each other. In contrast, our method detects translational and rotational grids of windows and other structural elements, but ignores the chimneys, since their spatial arrangement does not match any of the repetitive patterns defined in our framework. On the other hand, our method is capable of discovering and compactly representing structures composed of very small elements such as the balustrade, given a sufficiently dense sampling. Figure 14 shows the stability of our method with respect to noise in the input shape. Noise leads to errors in the pairwise transformations estimated for the initial surface patches. This results in overlapping transformation clusters that cannot be separated correctly by the clustering method. As the figure illustrates, our method tolerates high noise levels that can increase with the number of repetitions of the regular structure.

Figure 13.

Our method detects multiple 1- and 2-parameter structures. The blue regions denote the representative elements. All structures were detected with 30k samples distributed uniformly across the model, except for the balustrade, for which the rate was increased to 100k.

Figure 14.

Structure detection on procedural geometry with noise uniformly distributed in the interval [−σ, σ] in units of average local sample spacing. The images show the maximum noise level under which we still recover the helical structure. These models were generated with Carlo Séquin’s sculpture generator.

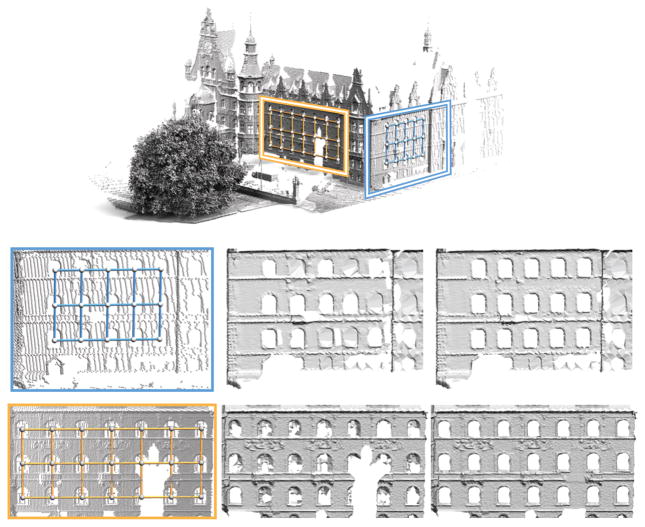
Model Repair

Figures 15 and 16 show structure detection and model repair on noisy and incomplete surface scans. Two 2- parameter translational structures have been discovered in the outdoor laser scan of Figure 15, even though they account for only roughly 35k of the 250k sample points of the whole model. Reconstructing a continuous surface from this point set is a challenging task, since the sampling is highly non-uniform and gradually decreases in density due to the perspective distortion of the single-viewpoint scanner. In addition, occlusion leads to substantial holes in the data. Traditional surface reconstruction methods that are oblivious to global structural information infer vertex connectivity using local smoothness priors only. As Figure 15 illustrates, this leads to inferior results in regions of low sampling density and holes. However, while local reconstruction fails, our robust global optimization still reliably detects the regular translational grid. This enables non-local reconstruction that exploits structural regularity to fill holes and increase the sampling rate in regions of low point density. We illustrate this functionality by replicating the representative element using the group transformations. In the future, we plan to investigate more sophisticated methods that achieve super-resolution reconstruction by combining the information of all elements of the extracted regular structure. This would be akin to the use of non-local means in image restoration [Buades et al. 2008].

Figure 15.

Structure detection and model repair on a complex outdoor scan. Our algorithm fully automatically discovers two translational grids within the acquired point cloud. Standard surface reconstruction yields an incomplete and inconsistent triangulation shown in the middle. The models on the right have been created by augmenting the point set using replicated samples from the representative elements prior to reconstruction.

Figure 16.

Model repair and geometry synthesis for a scan of a chambered nautilus shell. From left to right: photograph of original model, input data consisting of 72 registered laser scans, repaired model with additional synthesized elements indicated in orange.

The chambered nautilus shell of Figure 16 exhibits a characteristic spiral pattern of the chambers. The model is composed of 72 individual scans that have been aligned and merged. Even though substantial effort has been invested in the acquisition process, fine-scale detail is not adequately captured, and noise and holes corrupt the model. Our algorithm robustly detects the 1-parameter spiral structure with a generating transformation composed of rotation and scaling. Replication of the representative element using the generating transformation fills in missing regions and leads to a high quality reconstruction. This example highlights the high degree of precision of our simultaneous registration method, avoiding error accumulation common in iterative alignment schemes.

Geometry Synthesis

Structure detection facilitates advanced geometry synthesis operations as illustrated in Figures 12 and 16. The amphitheater has been edited by replacing the representative elements and changing the number of repetitions. The nautilus shell has been altered by extrapolating the regular structure to add additional repetitive elements. This type of high-level geometry editing, though intuitive, would be difficult to achieve manually or without a precise knowledge of the generating transformations. These examples illustrate the potential of automatic structure discovery for reverse engineering and CAD applications.

Performance

Table 1 lists statistics for the examples shown in this paper. Timings for transformation analysis include the sampling of the input model, computation of similarity sets using curvature descriptors, the ICP refinement to estimate the sample-pair transformations, and the classification and transformation mapping of regular structures. Since no prior information on the location, type, or scale of regular structures is assumed, transformation analysis operates on a uniform sampling of both the model and the set of pairwise transformations. Consequently, this stage is computationally the most involved of our pipeline. Model estimation and aggregation only process the set of detected small-scale regular structures and thus account for less than 5% of the total computation time.

Table 1.

Statistics for our algorithm. Timings are in seconds, mea­sured on a 3.4GHz Pentium with 2GB RAM.

	Theater	Castle	Helix	Outdoor	Nautilus
# Vertices	100,000	172,606	161,263	249,532	53,722
# Samples	26,013	29,815	15,844	49,742	88,505
# Pair Transforms	49,670	82,524	44,517	99,484	142,406
Transform Analysis	104.13	209.6	15.35	174.9	56.2
Model Estimation	0.23	3.64	0.55	1.79	0.66
Aggregation	4.41	6.92	0.16	0.31	1.29

Limitations

Currently our method cannot handle ‘warped’ sequential repetitive patterns of patches P₁, P₂, P₃, … where the transformation T_i,i+1 that maps P_i to P_i+1 is changing with the index i. For example, the colosseum of Rome has an elliptic base and therefore does not exhibit rotational symmetry. Our method cannot find a suitable generative model for such objects. We do not include patterns generated by non-commutative crystallographic groups directly, but offer only a two-stage process for detection: Applying the methods of this paper first, and detect symmetries of building blocks afterwards. At present it seems that the commutative case is at the limit of what can be done with our method of mapping to transformation space. In particular, iterative systems of transformations which generate fractals (in general non-commutative) are not considered in our framework.

7 Conclusions & Future Work

We have shown how to recognize and extract repetitive structures in 3D data without prior knowledge of the size, shape, and location of the individual elements that define the structure. An appropriate representation of similarity transformations reduces this problem to grid fitting in 2D. We introduced an optimization algorithm for detecting such grids which has proven very robust to outliers and missing data, thus facilitating structure discovery in complex geometries with substantial clutter. Simultaneous registration achieves a high degree of accuracy of the extracted generating transformations. Our method handles a wide variety of regular structures in a single unified framework, requires no user interaction, and is applicable for large, complex geometric models that can be noisy and highly incomplete. We have shown applications in compression, model repair, and large-scale geometry synthesis.

The method presented in this paper is not restricted to 2D groups and 3D geometry, which opens up new applications in the analysis of volumetric and general higher-dimensional scientific data. We would also like to point to a very general issue connected with this paper: The Kolmogorov complexity of an entity means the size of the shortest possible description of that entity, once language and syntax are formalized. Certainly repetitiveness in 3D shapes is an essential ingredient in their concise description. We leave further exploration of this relation between transformation groups and description complexity as a topic of future research.

Appendix

We describe how to classify the 1- and commutative 2-parameter subgroups of the group of similarities which represent a basic mathematical entity in our investigation of repetitive structures. Consider a similarity transformation T(τ) which is smoothly dependent on a time parameter τ and which at time τ = 0 starts with the identity transformation. Equation (2) shows that for the time value τ = 0 we have the linearization T(ε)(x) = x+ε(d×x+δx+d̄), and therefore

$${\frac{d}{d\tau }T(\tau )(\mathbf{x})|}_{\tau =0}=\mathbf{d}\times \mathbf{x}+\delta \mathbf{x}+\overline{\mathbf{d}}.$$ (3)

According to the general theory of matrix groups [Hall 2003], for every choice of d, d̄, δ there is a unique one-parameter subgroup T(τ) = exp(τ·D) such that (3) is valid. The type of one-parameter groups can be read off from properties of the velocity data d, d̄, δ[Hofer et al. 2005]:

case:	Trans	Scale	Rot	Rot + Trans	Rot + Scale
d	o	o	≠ o	≠ o	≠ o
d · d̄			0	≠ 0
δ	0	≠ 0	0	0	≠ 0

We can encode velocity data d, d̄, δ in a matrix D as in Equation (1), so there is a 1-1 correspondence between matrices D and oneparameter groups.

We now wish to find the commutative connected two-parameter subgroups of the similarity group. Note that all possible D’s form a vector space, denoted by 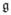, of dimension 7. According to the general theory [Hall 2003], any commutative 2-parameter subgroup H is the union of one-parameter groups whose velocity data constitute a 2-dimensional subspace 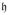of 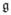such that

$$\mathbf{D},{\mathbf{D}}^{\prime }\in \mathfrak{h}\Rightarrow [\mathbf{D},{\mathbf{D}}^{\prime }]=\mathbf{O},\text{where}[\mathbf{D},{\mathbf{D}}^{\prime }]:=\mathbf{D}{\mathbf{D}}^{\prime }-{\mathbf{D}}^{\prime }\mathbf{D}.$$

An easy computation shows that the bracket operation applied to velocity data d, d̄, δ and d′, d̄′, δ′ results in

$${\mathbf{d}}^{″}=\mathbf{d}\times {\mathbf{d}}^{\prime },{\overline{\mathbf{d}}}^{″}=\delta {\overline{\mathbf{d}}}^{\prime }-{\delta }^{\prime }\overline{\mathbf{d}}+\mathbf{d}\times {\overline{\mathbf{d}}}^{\prime }-{\mathbf{d}}^{\prime }\times \overline{\mathbf{d}},{\delta }^{″}=0.$$

It is now a matter of linear algebra to find out which subspaces 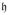fulfill these condition. It turns out that there are only the following possibilities:

• Case Trans × Trans: 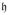is spanned by (o, d̄, 0) and (o, d̄′, 0), and so every 1-parameter group in H is a translation.

• Case Rot × Trans: After translating the coordinate system, 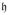is spanned by velocity data (d, o, 0) and (o, d, 0) which correspond to rotation about the axis d and translation parallel to this axis, respectively.

• Case Rot × Scale: After translating the coordinate system, 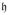is spanned by velocity data (o, o, 1) and (d, o, 0) which correspond to uniform scaling whose center is the origin, and a rotation about an axis through the origin, respectively.