Encapsulation of Capacitive Micromachined Ultrasonic Transducers Using Viscoelastic Polymer

Abstract

The packaging of a medical imaging or therapeutic ultrasound transducer should provide protective insulation while maintaining high performance. For a capacitive micromachined ultrasonic transducer (CMUT), an ideal encapsulation coating would therefore require a limited and predictable change on the static operation point and the dynamic performance, while insulating the high dc and dc actuation voltages from the environment. To fulfill these requirements, viscoelastic materials, such as polydimethylsiloxane (PDMS), were investigated for an encapsulation material. In addition, PDMS, with a glass-transition temperature below room temperature, provides a low Young's modulus that preserves the static behavior; at higher frequencies for ultrasonic operation, this material becomes stiffer and acoustically matches to water. In this paper, we demonstrate the modeling and implementation of the viscoelastic polymer as the encapsulation material. We introduce a finite element model (FEM) that addresses viscoelasticity. This enables us to correctly calculate both the static operation point and the dynamic behavior of the CMUT. CMUTs designed for medical imaging and therapeutic ultrasound were fabricated and encapsulated. Static and dynamic measurements were used to verify the FEM and show excellent agreement. This paper will help in the design process for optimizing the static and the dynamic behavior of viscoelastic-polymer-coated CMUTs.

I. Introduction

THE PACKAGING of a micromachined ultrasonic transducer is crucial for medical applications. This packaging material should electrically insulate the device from the environment, protect the device against humidity and other corrosive substances, and also be biocompatible. At the same time, this encapsulation should maintain transducer performance, especially the transfer of energy to and from the medium. While other microelectromechanical system (MEMS) devices, such as accelerometers and gyroscopes, are typically protected from the environment by hermetic sealing, capacitive micromachined ultrasonic transducers (CMUTs) require mechanical interaction to a fluid, which makes fulfilling the previous criteria very challenging. In this paper, we will discuss the requirements on such a coating material for a CMUT used in immersion applications. We will then present a model of polydimethylsiloxane (PDMS), a viscoelastic material, and verify the model using experiments.

A. Requirements for a CMUT Packaging Material

CMUTs have demonstrated promising performance, ease and flexibility of fabrication, and ease of electronics integration, which makes them advantageous over conventional piezoelectronic transducers [1], [2]. The encapsulation material of CMUTs should provide the matching acoustic impedance to the medium (1.5 MRayl for water or 1.63 MRayl for average human soft tissue [3]) to enable maximum transmission of energy into the medium. Based on the transmission line theory (1), the incident wave transmission efficiency is strongly related to the acoustic impedance matching condition [4]

$$T_{\text{energy}}=1-{\left(\frac{Z_m-Z_c}{Z_m+Z_c}\right)}^2$$ (1)

where T_energy, Z_c, and Z_m are the energy transmission ratio and the acoustic impedance of the coating material and the medium, respectively. The matching acoustic impedance can be further related to the Young's modulus based on the elasticity theory [4]

$$E=Z^2\cdot \frac{(1+\upsilon )(1-2\upsilon )}{\rho \cdot (1-\upsilon )}$$ (2)

where E, ν, Z, ρ represent the Young's modulus, the Poisson's ratio, the acoustic impedance, and the density, respectively. To match the acoustic impedance of 1.5 MRayl, a Young's modulus on the order of gigapascals (with a Poisson's ratio of 0.40 and a density of 1000 kg/m³) is needed (2).

Operation of a CMUT requires both a dc and ac voltage. The dc voltage sets the operation point of the device that determines the transmission and reception sensitivities [5] and the electromechanical coupling efficiency [6]. Since this point determines the performance of the device, it is important to predict and limit the impact of the encapsulation material on the pull-in voltage variation. In addition, a practical thickness of the coating should be on the order of hundreds of micrometers to protect the device against the regular contact ablation force and the electrical breakdown. Considering these factors and the Young's modulus of the CMUT plate material, a Young's modulus for the coating material on the order of megapascals is essential to limit the pull-in voltage variation.

Fulfilling the ac and dc requirements of this encapsulation material is challenging unless the coating materials are used that exhibit viscoelasticity. This paper presents the first modeling and verification of the viscoelasticity of polymers for CMUT immersion imaging applications.

B. Viscoelasticity

Many polymers used for MEMS applications exhibit viscoelastic behavior [7]–[9]. The Young's modulus and the Poisson's ratio change as functions of loading frequency. This occurs because a relaxation time is needed under a corresponding strain rate. As the loading frequency increases, the behavior of the polymer changes from rubbery to glassy [7], resulting in a change in the Young's modulus and the Poisson's ratio from the slow limit values (E_s, ν_s) to the fast limit ones (E_f, ν_f). The Young's modulus can differ up to several orders of magnitude, with the modulus being stiffer at higher frequencies [8]. Poisson's ratio decreases from close to 0.5 down to 0.35 ~ 0.4 [10], leading the (1 − ν)/(1 + ν)(1 − 2ν) factor to reduce by one order of magnitude. Due to these changes, the acoustic impedance increases from hundreds of kilorayls up to the megarayl range as the loading frequency is increased.

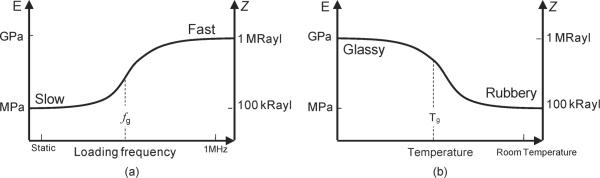
For CMUTs that operate in the megahertz range, a preferred rubber to glass transition frequency should be smaller than 1 MHz [Fig. 1(a)]. At low frequencies, the Young's modulus is in the megapascal range; as the loading frequency is increased to the ultrasonic region, the Young's modulus [Fig. 1(a)] approaches gigapascals, which translates to a good matching acoustic impedance. In terms of temperature, a material should be chosen so that it is in the rubbery state at room temperature for static loading and a glass transition temperature that is lower than room temperature [Fig. 1(b)] [7], [8].

Fig. 1.

Viscoelastic curves of PDMS in terms of the Young's modulus and acoustic impedance over (a) loading frequency or (b) temperature based on the theory of time-temperature superposition [7], [8]. T_g and f_g represent the glass-transition temperature under static loading and the glass-transition loading frequency at room temperature, respectively.

Among the polymers listed in Table I [9], PDMS fulfills the needed requirements because its glass transition temperature (T_g) is much lower than the room temperature. This characteristic provides the low static Young's modulus for preserving the CMUT's pull-in voltage; at the same time, it offers the matching acoustic impedance needed for efficient acoustic transmission. Finally, PDMS is a biocompatible substance which provides protection against biofouling, thermal instability, and dielectric breakdown [9]. However, since it is not photopatternable and plasma-etchable, a mold casting technique will be utilized to fabricate these encapsulation layers.

TABLE I.

Properties of Various Polymer Materials Commonly Used for MEMS Applications [9], [32]. PDMS, Different From Other Polymers, Has the Glass-Transition Temperature Much Lower Than the Room Temperature. PDMS Has the Modulus Three Orders Less Than That of Other Polymers as Listed, While the Densities Are All Among the Same Order

	Glass transition temperature (°C)	Modulus (GPa)	Density (g/cm3)
PDMS	−125	~0.001	1.00~1.64
Polyimide	390	~3.3	1.42~1.53
EPON SU-8	194	~4.5	1.2
PMMA	105	~2.5	0.9
Parylene	160	~2.5	1.1~1.4

PDMS has been routinely used as a lens material for piezo-electric ultrasound transducers [11]; processing techniques and material properties of PDMS are well understood. Previously, polymer coatings including PDMS were used to electrically insulate CMUTs in immersion applications [12]–[15] to create flexible arrays [16], [17] and to improve acoustic crosstalk suppression [18]–[21]. However, the study of using polymer coatings on a CMUT has been based on a “go and redesign” base such that a fundamental and systematic study providing a design rule has been absent. In addition, while analytical and finite element model (FEM) modeling of CMUTs with different shapes, gap heights, plate topologies, and plate stresses have been used to optimize bandwidth, output pressure, and sensitivity [22]–[24], none of these studies have considered the effects of the viscoelasticity of coating material layers on the CMUT's performance. To successfully perform a CMUT design that accounts for the effects of PDMS coating layers, we introduce a FEM that considers viscoelasticity and can be used to analyze the pull-in voltage and frequency response of CMUT for immersion.

In this paper, we model, fabricate, and measure the response of CMUTs with PDMS encapsulation. This enabled us to verify the viscoelastic model. First, the methodology and details of the FEM are described in detail in Section II, then, simulation and measurement results for two different CMUT designs are compared and discussed in Section III.

II. Methods And Materials

A. Fabrication Methods

The bandwidth and transmission efficiency of CMUTs can be optimized for diagnostic and therapeutic ultrasound, e.g., high-intensity focused ultrasound (HIFU), by changing the cell size, gap height, and plate thickness. A PDMS coating on different geometry CMUT cells has different effects. To demonstrate the implementation of PDMS encapsulation on CMUTs designed for different applications, both imaging and HIFU CMUTs were modeled, designed, and fabricated.

An imaging CMUT should be designed to provide high center frequency with wide bandwidth. A relatively thinner plate thickness and gap height with a smaller cell size were used. HIFU CMUTs are required to operate at single frequency but generate high output pressure, so a thicker plate and larger gap height were used (Table III) [25].

TABLE III.

Parameters of the CMUTs for Imaging and HIFU

Device	Imaging	HIFU
Configuration	1D linear array	Single element
Radius of CMUT cell	21.5 μm	50/ 70 μm
Thickness of Si plate	2.0 μm	6.0 μm
Gap height	0.15 μm	0.40 μm
Thickness of SiO2 insulator	0.30 μm	0.60 μm

Among the two developed CMUT fabrication technologies available, wafer bonding and sacrificial release techniques [26], [27], the fusion-bonding approach was chosen since the membrane thickness was 6 μm. In the sacrificial release process, forming such a thick membrane using chemical vapor deposition is not possible due to residual stress and deposition time for cells of those lateral dimensions. Fig. 2 shows the process used for fabricating the CMUT arrays based on a wafer bonding technique. First, the highly conductive Si wafers (0.01–0.025 ohm-cm) are selected. Then 400- and 150-nm-high cavities are formed by a two-step thermal oxidation-and-etch, a buffered oxide etch (BOE), and then a dry plasma etch. The second step etching is to remove the bird beak formed by the second oxidation step. Next, two kinds of silicon-on-insulator (SOI) wafers are selected, with the device layer thicknesses of 6 and 2 μm, respectively. The SOI wafers are then bonded on top of the etched wafers using fusion bonding. The handle wafers are then removed using wafer grinding (Silicon Quest International, Inc., Santa Clara, CA) and then wet etching in a hot tetramethylammonium hydroxide solution. The buried oxide layer is then removed by BOE, leaving the 6- and 2-μm plate covering the cavities. For the imaging CMUT, elements within an array are defined by separating the silicon plates with a dry plasma etch step. Then aluminum is deposited, and hot and ground electrodes are defined on the plate and the silicon substrate, respectively. Fig. 3 shows various views of the finished devices.

Fig. 2.

CMUT device fabrication using wafer bonding technique for (a) imaging CMUTs and (b) HIFU CMUTs. The process flow includes (1) first oxidation and BOE oxide etch, (2) second oxidation and dry etching, (3) wafer bonding, (4) handle wafer and buried-oxide (BOX) removal and etch back for substrate access, (5) top electrode deposition and patterning, and (6) PDMS coating.

Fig. 3.

Imaging CMUT pictures of the (a) SEM cross-sectional view of a cell, (b) six elements of one array with wire bonding, and (c) CMUT cells with plate deflection under dc bias of 80% of pull-in voltage measured by a white light interferometer. Similarly, HIFU CMUT pictures are shown in (d)–(f).

After fabrication, the devices were diced and then wired bonded to a custom-designed printed circuit board (PCB). Before application of the encapsulation material, we performed an oxygen plasma cleaning step on the CMUT surface and applied a primer (GE SS4120) on the PCB to increase the interface adhesion. Then, a 150-μm-thick layer of GE RTV 615 PDMS was mold casted by pressing a polystyrene plate on the CMUTs with a spacer. This was followed by a vacuum chamber degassing step, a curing cycle at 50 °C for 12 h, and a mold-releasing step. Finally, the exposed wires for interconnections were encapsulated by epoxy for water-immersion tests. We also prepared CMUTs for imaging without PDMS coating layers for comparison.

The pull-in voltage can be measured by sweeping the electrical impedance frequency for resonance, observing the membrane deflection under white light interferometry or the capacitance change [28]. The capacitance-bias voltage measurement was selected because the PDMS layer damps the resonance and blocks the optical access. To measure the capacitance as a function of dc bias voltage, we used an impedance analyzer (Model 4294A, Agilent Company, Palo Alto, CA). The pull-in of the plate causes a discontinuity in the capacitance-bias voltage curve (Fig. 5). The pull-in voltage measurement results were compared with the results from the FEM models with and without the coating layer.

Fig. 5.

Static behavior verification: capacitance versus dc bias voltage for the imaging CMUTs: (a) The experimental and the (b) modeling data. The measured capacitance larger than the modeling is due to the parasitics from the electrical interconnections of the experimental setup.

The frequency response was measured in vegetable oil that is electrically insulating for devices without coating and in water for devices with coating. The CMUTs are biased at a ratio of the pull-in voltage (80% for imaging CMUTs and 60% for HIFU CMUTs) and excited by a unipolar 10-V_pp 50-ns square pulse, generated by a function generator (Model HP 8116, Hewlett Packard Corporation, Palo Alto, CA). Next, the pressure was measured using a calibrated hydrophone (Model HNP-0400, Onda Corporation, Synnyvale, CA 94089) in the far field (2.25 mm for the imaging CMUTs and 10 mm for HIFU CMUTs). A fast fourier transform (FFT) was then performed on the Gaussian-windowed pressure signal. The pressure at the CMUT surface was calculated by compensating for attenuation and diffraction [6]. The time-domain pressure waveform and the frequency spectra were compared to the modeling results.

B. Simulation Methods

To properly account for the viscoelastic property of the PDMS on the CMUT plates, we developed a FEM (ANSYS 11.0, ANSYS Inc., Canonsburg, PA). Previously, Lohfink et al. demonstrated an axial symmetric model of a single circular CMUT plate with a waveguide liquid column [23]. However, they did not consider the PDMS coating. We extended this modeling approach by adding a PDMS layer on top of the CMUT plate. We accounted for the viscoelastic effects by creating two variations of FEMs.

The first FEM (nonviscoelastic FEM) considers the CMUT with the coating material without viscoelasticity. We used PLANE 42 elements [29] for both the plate and the PDMS layer [Fig. 4(a)], using either E_s or E_f as an appropriate material property for static or frequency response simulation, respectively.

Fig. 4.

Schematic of (a) the nonviscoelastic and (b) the viscoelastic FEM. FLUID 29, PLANE 42, PLANE 182, and TRANS 126 represent the element types used in the ANSYS model. The plots also show the roller boundary conditions (constrained to x-direction) and the anchor boundary conditions (constrained to both x-and y-directions). (c) The Prony series expansion used for PLANE 182 element in the viscoelastic FEM can be represented by a spring in parallel with a series set of a spring and a dashpot.

In a second FEM (viscoelastic FEM), which considers the viscoelasticity, we used the element type PLANE 182 [29]. PLANE 182 is a 2-D four-node structural solid element as PLANE 42 but has a special feature to address viscoelasticity.

PLANE 182 can feature a linear viscoelastic model based on the generalized Maxwell elements, a viscous damper, and a purely elastic spring connected in series. Bergstrom et al. [30] introduced a micromechanism about this model by illustrating the relaxation of the free chains within the polymer network. This model adequately describes the constitutive model of many amorphous polymers by decomposing the mechanical behavior into two parts, namely: an equilibrium network under long-time stress relaxation and a second network capturing the rate-dependent deviation from the equilibrium state. The Prony series expansion was used in ANSYS to express this model mathematically. The series constants were implemented in ANSYS code by using the “TB, PRONY” command to determine the viscoelastic moduli as functions of time, E(t) and ν(t) [29], [31], as follows:

$$E\left(t\right)=E_s+(E_f-E_s)\cdot \text{exp}\left(-\frac{t}{T_0}\right);$$ (2a)

$$\upsilon \left(t\right)={\upsilon }_s+({\upsilon }_f-{\upsilon }_s)\cdot \text{exp}\left(-\frac{t}{T_0}\right);$$ (2b)

and

$$E_f=\frac{(1+{\upsilon }_f)(1-2{\upsilon }_f)}{(1-{\upsilon }_f)}\cdot C_{11}$$ (2c)

where E_s = 6.4 MPa [32]; ν_s = 0.48; ν_f = 0.40 [10]; $C_{11}=\rho \cdot V_l^2$; V_l is the longitudinal wave velocity; and T₀ = 1 e–4 s, the relaxation time constant selected based on the glass-transition loading frequency at room temperature [8]. The equivalent mechanical model of the Prony series expansion used in our model comprises a spring in parallel with a series set of a spring and a dashpot [Fig. 4(c)].

Depending on the loading condition (dc or ac superimposed on dc) of the CMUT plate, a static analysis and transient response analysis was developed. From the static analysis, the pull-in voltage was obtained, which then was compared to the measured pull-in voltages of the fabricated devices with and without PDMS coating. The transient response analysis was used to calculate both the time-history and frequency response. A transient analysis rather than a harmonic analysis was chosen to analyze the effect of the echoes from the PDMS-water interface due to the acoustic impedance mismatch. Voltage loading was applied in two steps. First, a voltage step with a ratio of the calculated pull-in voltage (80% for the imaging CMUTs and 60% for the HIFU CMUTs) was used. Then, after waiting for one second, a unipolar 10-V_pp 50-ns square pulse was superimposed. The ambient pressure of 101 325 Pa was applied before the voltage load to consider the fact that the CMUTs feature an evacuated gap. The displacements from the plate and the PDMS surface were retrieved. The time derivative of the average displacement of the CMUT plate was calculated and then multiplied by the medium acoustic impedance to calculate the average surface pressure response. An FFT was performed on the Gaussian-windowed pressure pulse to calculate the frequency response. The attenuation from the PDMS layer was then compensated based on the loss [33], as follows:

$$\text{Loss in dB}=\alpha \cdot f^{\beta }\cdot r$$ (3)

where α = 0.4 dB/MHz/cm for GE RTV 615; β = 1.4; f is the frequency in megahertz; and r is the PDMS thickness in centimeters.

First, evaluating the differences between the reflected echoes from the PDMS-water interface of a 75- and a 200-μm-thick coating tested the transient model. Then, the effect of the acoustic impedance mismatch from different types of PDMS (GE RTV 615 and Sylgard 160, Table II) was analyzed. Next, the simulation results were compared to measurement results obtained from fabricated devices with different designs (Table III). To demonstrate how the coating material without viscoelasticity fails to preserve the CMUT operation point and performance, we processed the same calculations with the FEM that considers the coating without viscoelasticity.

TABLE II.

Acoustic Properties of PDMS

Type	V1 (m/s)	ρ (kg/m3)	Z (MRayls)
GE® RTV-615	1080	1020	1.1
Sylgard® 160	950	1580	1.5

III. Results And Discussion

A. Static Analysis: Comparison Between Model and Measurements

We first measured the capacitance with and without the 150-μm PDMS coating to verify the prediction of static operating point. The pull-in voltage of the device without PDMS was 142 V [Fig. 5(a)]. With PDMS, we also found a pull-in voltage of 142 V [Fig. 5(a)], which demonstrates that the PDMS coating is significantly less stiff than the plate at dc and does not affect the pull-in voltage. For nonviscoelastic FEM, only the model with E_s can fit the measurement, while E_f provides overestimated stiffness and results in a higher pull-in voltage [Fig. 5(b)]. The viscoelastic static modeling result [Fig. 5(b)] is consistent with the measurements by showing the same pull-in voltage of 142 V. This confirms that the model can simulate the PDMS modulus as the slow limit under a static loading and correctly predicts that a 150-μm PDMS coating does not alter the pull-in voltage.

B. Dynamic Analysis: Model Parameter Studies

We first verified the speed of sound and the effects from mismatched acoustic impedance in our transient model. This model uses the design parameters from the CMUT for imaging as an example.

1) Effects From Different PDMS Coating Thicknesses

The arrival times of the first impulse response wavelets (main signals) [Fig. 6(a) and (b)] are 185 and 69 ns for the 200- and 75-μm coatings, respectively. For both cases, we calculate 1080 m/s of the speed of sound of PDMS by using the travel time and the distance from the CMUT surface (plate-PDMS interface) to the PDMS-water interface, i.e., coating thickness. This speed matches with the input parameter, the longitudinal wave velocity of GE RTV 615 PDMS. The speed also confirms that the excited wave is traveling as the longitudinal wave instead of the higher-order extensional wave.

Fig. 6.

Viscoelastic FEM results showing the effect of different PDMS coating thicknesses: (a) 200- and (b) 75-μm of GE RTV 615 PDMS coating. t = 0 s corresponds to the beginning of the 50-ns pulse. The data were retrieved from the PDMS-water interface.

Because of the acoustic impedance mismatch between the GE RTV 615 PDMS (1.1 MRayl) and water (1.5 MRayl), echoes from the PDMS-water interface are present after the main signals [Fig. 6(a) and (b)]. The arrival time of the echo is exactly three times of the one-way traveling time through the PDMS layer. Except for the presence of the echoes, the main signals from both cases are identical to each other, indicating that the thickness of the coating does not change the CMUT plate characteristics and it does not alter the main signal.

From the comparison between these two different coating thicknesses [Fig. 6(a) and (b)], the main effect on the impulse response is the relative location of the secondary echo signal. For the 200-μm coating, a time window can be applied to filter away the echo safely. For the 75-μm coating, the echo overlaps with the main signal and filtering is impossible. Consequently, the presence of the echo alters the frequency spectrum [Fig. 6(b)]. For many ultrasound applications, such as imaging, the application of the time window is not practical. This is because the echo from the PDMS-water interface may arrive at the same time as the real signal, similar to the case of Fig. 6(b). Therefore, to design a good encapsulation, it is preferred to use a PDMS material that has good acoustic impedance matching to the medium. This point will be illustrated further in the following section.

2) Effects From Different Types of PDMS

We also demonstrate that the model could accurately reflect the influence of different types of PDMS (Fig. 7). Because Sylgard 160 is better matched to water than GE RTV 615, the return echo from the PDMS-water interface disappears [Fig. 7(b)].

Fig. 7.

Viscoelastic FEM results showing the effect from different types of PDMS: (a) 150 μm of GE RTV 615 and (b) 150 μm of Sylgard 160 on the CMUT for imaging. The average displacement from the plate-PDMS and the PDMS-water interfaces were both shown with a 1-nm offset apart in the y-scale for clearer visualization. The main signals (a-1, b-1) arrive at time zero, and then the excitations propagate upward into the PDMS-water interfaces. The transmission parts were shown at the PDMS-water interfaces at the arrival time of 139 ns (a-2) and 158 ns (b-2) individually. The reflection part (a-3) travels back to the plate-PDMS interface and arrives at the time of 278 ns, while there is no reflection for the Sylgard 160 case (b-3).

The transmission and reflection coefficient of GE RTV 615 PDMS (1.1 MRayl) to water (1.5 MRayl) is 84.6% and 15.4%, respectively. The peak amplitude of the main signal [Fig. 7(a)-1] is 2.79 nm. The measured transmitted [Fig. 7(a)-2] and reflected waves [Fig. 7(a)-3] are 2.33 and 0.37 nm, respectively. This matches with the calculated transmitted and reflected wave, which had amplitudes of 2.36 and 0.43 nm, respectively. The minor difference comes from the fact that we compare only the peak amplitude of the signal instead of the full energy.

Similarly, in the case using Sylgard 160 PDMS whose acoustic impedance closely matches that of water, the reflection coefficient is zero, which means that there is no reflected wave [Fig. 7(b)-3 and (b)-4]. Therefore, the transmitted wave [Fig. 7(b)-2] has the same amplitude (2.3 nm) as the main signal from the CMUT surface [Fig. 7(b)-1].

We also compare the peak amplitude of the main signals and the transmitted waves between both types of PDMS. Due to the heavier mass loading of Sylgard 160 (1580 kg/m³) compared to GE RTV 615 (1020 kg/m³, Table II), the main signal of the Sylgard 160 coated device is smaller {2.48 nm of peak amplitude [Fig. 7(b)-1]} than the GE RTV 615 coated device {2.79 nm [Fig. 7(a)-1]}. However, because of matched acoustic impedances, the transmitted wave from the Sylgard 160 case has a higher peak amplitude {2.48 nm [Fig. 7(b)-2]} compared to the GE RTV 615 case {2.33 nm [Fig. 7(a)-2]}. Therefore, to design a coating without compromising the amplitude, the acoustic impedance matching is important to maximize the transmitted energy; moreover, it has to be optimized by considering the tradeoff from the effect of the increased PDMS density.

C. Dynamic Analysis: Comparison Between Model and Measurements

1) CMUTs for Imaging

To address the coating effect, the measurement with 150-μm GE RTV 615 PDMS coating was compared to the one without coating (Fig. 8). Because of acoustic impedance mismatch between the PDMS-water interface, the additional echo was observed comparing the coating case to the noncoating one [Fig. 8(b)]. For the same reason, the signal amplitude was decreased due to the reflection loss. The measurements show that the coating increases the center frequency by 5%, and our viscoelastic FEM demonstrates an increase of 6% [Fig. 8(a), and Table IV]. The fractional bandwidth (FBW) was decreased by 21% after the coating based on the measurement [Fig. 8(a), and Table IV] and was 14% based on the modeling.

Fig. 8.

Comparison between the measurements (with and without the 150 μm of GE RTV 615 coating) and the viscoelastic FEM (with the 150 μmofGERTV 615 coating) results for imaging CMUTs: (a) the frequency domain and (b) and (c) the time domain. The data were retrieved from the PDMS-water interface.

TABLE IV.

Coating Effect of the CMUTs for Imaging

	No coating	150-μm coating	Coating effect
	Experiment	Experiment Modeling
fcenter	8.9 MHz	9.3 MHz	5%
		9.4 MHz	6%
FBW	81%	64%	−21%
		70%	−14%

The viscoelastic FEM results of the 150-μm coated devices were compared to the measurement (Fig. 8). The comparison shows that the center frequencies of measured and simulated devices differ by only 1% (Table V). In addition, the FBW is only overestimated by 9% in the model. The agreement can be further improved by using a real 3-D model that includes the element-to-element crosstalk and the effect of the finite element size of the CMUT.

TABLE V.

CMUTs for Imaging

	Modeling	Experiment	Error
flower-3dB	6.1 MHz	6.3 MHz	3%
fupper-3dB	12.7 MHz	12.3 MHz	3%
fcenter	9.4 MHz	9.3 MHz	1%
FBW	70%	64%	9%

For further comparison, the transmission impulse response from the nonviscoelastic FEM was also performed. The E_s was selected to preserve the static operation point (Fig. 9). Compared with the viscoelastic results, the response is underdamped which results in a smaller FBW in the frequency domain. This occurs because E_s leads to the smaller acoustic impedance of PDMS (2) and lower speed of sound (V_l = Z/ρ). The lower speed of sound also translates into the longer echo time, so we cannot see the slow echo in the figure.

Fig. 9.

Results from the nonviscoelastic FEM with E_s for imaging CMUTs with 150 μm of GE RTV 615 coating. The data were retrieved from the plate-PDMS interface. E_s leads to the slower speed of sound, so there was no data from PDMS-water interface before 1.2 μs.

2) CMUTs for HIFU

For the HIFU CMUTs comparison between the measurement and the modeling results, we evaluated the low-frequency design (radius = 70 μm) (Fig. 10) and the high-frequency design (radius = 50 μm) (Fig. 11). For the design with a 70-μm radius, the characteristic of the impulse response in the time domain was simulated well. A 50-ns pulse makes the discontinuity of the waveform from measurement [Fig. 10(a)] that we also found in the modeling result [Fig. 10(b)]. For the design with a 50-μm radius, the 50-ns pulse does not result in any discontinuity as the case in low-frequency design in both the measurement and modeling results [Fig. 11(a) and (b)]. The characteristics of the impulse response from measurement and modeling, including the ringing, are comparable.

Fig. 10.

Comparison between the (a) measurements and the (b) results from the viscoelastic model in the time domain and (c) those in the frequency domain for the HIFU device with a CMUT cell radius of 70 μm with 150 μm of GE RTV 615 coating. The data was retrieved from the plate-PDMS interface.

Fig. 11.

Comparison between the (a) measurements and the (b) results from the viscoelastic model in the time domain, and (c) those in the frequency domain for the HIFU device with a CMUT cell radius of 50 μm with 150 μm of GE RTV 615 coating. The data was retrieved from the plate-PDMS interface.

The simulated results agree with the measurements in the frequency domains, as well as in the time domain. The center frequency was measured at 3.4 MHz compared to the modeling at 3.7 MHz, which is only 8% of difference for the low-frequency design (Table VI). Similarly, the measured center frequency shows 6.2 versus 6.9 MHz from the modeling, reflecting only 11% of difference for the high-frequency design [Fig. 11(c), and Table VI]. In addition to the center frequency, the modeled frequency spectrum pattern matches the measurement very well. The only minor discrepancy is the frequency offset. Possible causes for this discrepancy include the following: the imperfect boundary constrain of the HIFU CMUT plate edge due to the thicker plate thickness; and the excitation pulse in the experiment might not be exactly the same as simulation. Nevertheless, the HIFU device was always tuned to operate at a single frequency and the off-resonance spectrum is much less important than that for imaging CMUTs.

TABLE VI.

CMUTs for HIFU (Radii of 70 and 50 μm)

Radius		Modeling	Experiment	Error
70 μm	flower-3dB	2.2 MHz	2.2 MHz	0%
	fupper-3dB	5.3 MHz	4.7 MHz	13%
	fcenter	3.7 MHz	3.4 MHz	8%
50 μm	flower-3dB	5.4 MHz	4.7 MHz	15%
	fupper-3dB	8.5 MHz	7.7 MHz	10%
	fcenter	6.9 MHz	6.2 MHz	11%

IV. Conclusion

PDMS exhibits viscoelasticity with a glass-transition temperature lower than room temperature that makes it an ideal coating material for CMUT operation. PDMS coatings preserve the static operation point due to the low Young's modulus at dc. The low modulus value comes from the rubbery state under static loading at room temperature. At the same time, it fulfills the acoustic matching requirement in the ultrasonic operating frequency region. The matching helps to secure the transmission efficiency and prevent from echo reverberations.

We have developed a viscoelastic FEM which can predict both the dc and ac behavior of a PDMS-coated CMUT. The viscoelastic FEM has been demonstrated to have good agreement with the measurement results. The model can correctly simulate the static operation point, frequency-dependent stiffness, mass loading, and results in the correct acoustic impedance. Based upon the correct static and dynamic parameters, the hydrodynamic and acoustic behavior can be simulated. We showed that the model and measurements of static results match perfectly. The comparisons of the center frequency and FBW match within 1% and 9% for imaging CMUTs and 8 ~ 11% for HIFU CMUTs. The discrepancy occurred because of the difference of the CMUT plate boundary constraint condition and the excitation pulse between the model and experiments.

We have also demonstrated additive effects on performance due to the presence of this encapsulation. Our measurements show that a 150-μm coating of GE RTV 615 PDMS preserves the pull-in voltage of CMUTs at 142 V and offset the center frequency by only 5%. The FBW was decreased by 21% and is due to the echo from the acoustic mismatch at the PDMS-water interface. A coating material with a better matching to water and limited attenuation can be used to reduce the effect on FBW.

With the experimental demonstration and the correct modeling, this paper provides the encapsulation strategy of CMUTs and will help in the design process for optimizing the static and the dynamic behavior of viscoelastic-polymer-coated CMUTs.

Biographies

Der-Song (Elvis) Lin (S'08) received the B.S. and M.S. degrees in civil engineering from National Taiwan University, Taipei, Taiwan, in 1995 and 1997, respectively. He received the M.S. degree in electrical engineering from Stanford University, Stanford, CA, in 2008. He is currently working toward the Ph.D. degree in mechanical engineering, with a Ph.D. minor in electrical engineering, at Stanford University.

He has been a Research Assistant in the E. L. Ginzton Laboratory, Stanford University, since 2004. His research interests include micromachined sensors and actuators. His current research focuses on large-scale packaging for 2-D transducer arrays and polymer encapsulation technology for micromachined ultrasonic device.

Mr. Lin won the NTU Presidential Award (1993) and was a Taiwan Ministry of Education Fellow (2004).

Xuefeng (Steve) Zhuang (M'08) received the B.S. degree in electrical engineering from Louisiana State University, Baton Rouge, in 2002, and the M.S. and Ph.D. degrees in electrical engineering from Stanford University, Stanford, CA, in 2004 and 2008, respectively.

He is currently with Kolo Technologies Inc., where he is responsible for new technology development. His research interests include micromachined sensors and actuators for medical and industrial applications.

Dr. Zhuang was a Stanford Graduate Fellow. He won the LSU University Medal and the McLaughlin Dean's Medal (2002).

Serena H. Wong (M'08) received the B.S., M.S., and Ph.D. degrees in electrical engineering from Stanford University, Stanford, CA, in 2002, 2003, and 2008, respectively. During her graduate studies, she worked on high-intensity focused ultrasound (HIFU) as a minimally invasive therapeutic tool for the treatment of cancer. In particular, she developed capacitive micromachined ultrasonic transducers for HIFU applications, such as the treatment of lower abdominal cancers.

After graduating, she worked as a Postdoctoral Researcher with Palo Alto Research Center on ultrasound imaging panels. She currently works with Hansen Medical on fiber optic sensors for robotic applications.

Dr. Wong is a 2002 National Science Foundation Fellow, a 2002 Stanford Graduate Fellow, and a member of Tau Beta Pi.

Mario Kupnik (SM'09) received the Ph.D. degree from the University of Leoben, Leoben, Austria, in 2004, and the Diplom Ingenieur degree from Graz University of Technology, Graz, Austria, in 2000.

He is currently a Senior Research Scientist in electrical engineering at the Edward L. Ginzton Laboratory, Stanford University, Stanford, CA. From summer 1999 to October 2000, he worked as an Analog Design Engineer at Infineon Technologies AG, Graz, on the design of ferroelectric memories and contactless smart card systems. His present research interests include the design, modeling, fabrication, and application of micromachined sensors and actuators, with a main focus on capacitive micromachined ultrasonic transducers mainly for air-coupled applications, including high gas temperatures. Examples are transit-time gas flowmeters for hot and pulsating gases, ultrasonic nondestructive evaluation using noncontact ultrasound, nonlinear acoustics, and bio/chemical gas sensing applications (electronic nose).

Dr. Kupnik serves on the Technical Program Committee of the IEEE Ultrasonics Symposium.

Butrus (Pierre) Thomas Khuri-Yakub (F'95) received the B.S. degree from the American University of Beirut, Beirut, Lebanon, the M.S. degree from Dartmouth College, Hanover, NH, and the Ph.D. degree from Stanford University, Stanford, CA, all in electrical engineering.

He is a Professor of electrical engineering at Stanford University. His current research interests include medical ultrasound imaging and therapy, chemical/biological sensors, micromachined ultrasonic transducers, and ultrasonic fluid ejectors. He has authored over 500 publications and has been principal inventor or coinventor of 88 U.S. and international-issued patents.

Dr. Khuri-Yakub was awarded the Medal of the City of Bordeaux in 1983 for his contributions to nondestructive evaluation, the Distinguished Advisor Award of the School of Engineering of Stanford University in 1987, the Distinguished Lecturer Award of the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society in 1999, a Stanford University Outstanding Inventor Award in 2004, and a Distinguished Alumnus Award of the School of Engineering of the American University of Beirut in 2005.