Rapid efficient coding of correlated complex acoustic properties

Abstract

Natural sounds are complex, typically changing along multiple acoustic dimensions that covary in accord with physical laws governing sound-producing sources. We report that, after passive exposure to novel complex sounds, highly correlated features initially collapse onto a single perceptual dimension, capturing covariance at the expense of unitary stimulus dimensions. Discriminability of sounds respecting the correlation is maintained, but is temporarily lost for sounds orthogonal or oblique to experienced covariation. Following extended experience, perception of variance not captured by the correlation is restored, but weighted only in proportion to total experienced covariance. A Hebbian neural network model captures some aspects of listener performance; an anti-Hebbian model captures none; but, a principal components analysis model captures the full pattern of results. Predictions from the principal components analysis model also match evolving listener performance in two discrimination tasks absent passive listening. These demonstrations of adaptation to correlated attributes provide direct behavioral evidence for efficient coding.

Much of the stimulation available to perceivers is redundant because some sensory attributes can be predicted from other attributes concurrently, successively, or as a consequence of experience with a structured environment (1–3). It has long been proposed that the role of early sensory processing is to detect, extract, and exploit redundancy and regularity in the input (1, 2). Capitalizing on such regularity would have a host of benefits: uncertainty is reduced, neural coding becomes more efficient, sensitivity to stimulus associations is heightened, and interactions with the environment become informed through learning.

Although these claims enjoy a long history, empirical evidence has not been plentiful. For example, the Efficient Coding Hypothesis, that early visual processing serves to produce an economical (nonredundant) representation of optical information (4), remains a hypothesis. There is some physiological evidence that responses of neurons at successive stages of processing become increasingly independent from one another, and such demonstrations have been clearest in the auditory system (5). Reduction of redundancy has been inferred from perceptual findings, such as the McCollough Effect (6) and other instances of adaptation to visual patterns (7–9).

Natural sounds typically include redundant attributes. For sounds created by real structures, including musical instruments and vocal tracts, changes in different acoustic dimensions cohere in accordance with physical laws governing sound-producing sources. For example, articulatory maneuvers that produce consonant and vowel sounds give rise to multiple acoustic attributes. Redundancy across attributes contributes to robust speech perception despite substantial signal degradation (10–12). Categorical perception, a well-known phenomenon for speech as well as complex sounds and images, is shaped by multiple attributes (13) and is largely defined by relative inability to discriminate physically distinct stimuli (14). To the extent that experience with speech sounds presents listeners with rich covariance among acoustic attributes, the present research may lend insights into how categorical perception should be explained by experience with naturally covarying acoustic attributes.

To investigate how listeners detect and exploit redundancy between stimulus attributes, we designed novel highly-controlled complex stimuli that varied across two physically independent acoustic attributes: attack/decay (AD) (Fig. 1A) and spectral shape (SS) (Fig. 1B). AD was defined as the temporal envelope in which amplitude increases linearly from zero to peak amplitude (attack) before decreasing linearly to zero at offset (decay) without any steady state. SS, defined as relative levels of energy across frequencies, was varied via summation of two instrument endpoints (French horn, tenor saxophone) in different proportions (see Methods for details). Human speech and musical instruments naturally vary in AD and SS. In principle, these attributes are relatively independent, both perceptually and in early neural encoding (15). In detail, each complex dimension is a correlation in as much as attack duration is negatively correlated with decay, and amplitudes of individual harmonics increase or decrease in concert across changes in SS. These physically complex attributes were chosen with the expectation that more complex attributes should be more plastic relative to elemental properties, such as frequency, which serves as a primitive dimension in the tonotopically organized auditory system.

Fig. 1.

Examples of temporal (AD) (A) and spectral envelopes (SS) (B) presented in the experiments. Stimuli 1, 10, and 18 in each 18-step series are illustrated. The frequency axis in B is magnified to show differences in spectral envelopes across stimuli. (C) Stimuli presented in Experiment 1. Listeners heard sounds with either a positive correlation between AD and SS (r_AD,SS = 0.97, Left; n = 20) or the counterbalanced negative correlation (r_AD,SS = −0.97, Right; n = 20). Blue shapes represent stimuli in the Consistent condition; red shapes represent the Orthogonal condition; green shapes represent Single-cue stimuli. Circles denote sounds presented during exposure; triangles depict sounds presented only at test. Filled shapes denote sounds presented at test; adjacent filled shapes of the same color were presented together in AXB trials.

We hypothesized that the auditory system will adapt to represent covariance among attributes in a manner consistent with efficient coding, so that listeners will exhibit differential discriminability of sounds, depending on whether they obey or violate this covariance. We provide direct evidence that correlation across complex stimulus attributes is rapidly, efficiently, and automatically exploited by the auditory system. Initially, encoding of correlation is so robust that previously discriminable differences that do not respect the correlation are perceptually lost. Only after continued experience does perception evolve to discover variance not accounted for by the correlation.

Results

Experiment 1.

A stimulus matrix was generated by crossing AD and SS series for which sounds separated by a fixed distance were approximately equally discriminable (Methods). Two stimulus subsets were selected from this matrix, each capturing a near-perfect correlation between acoustic cues but in orthogonal directions (circles in Fig. 1C: r_AD,SS = ±0.97). After 7.5 min of passive exposure to one subset of highly correlated stimuli, listeners discriminated sound pairs (three stimulus steps apart) of three types: (i) Consistent with the correlation experienced during passive listening; (ii) Orthogonal to experienced correlation; and (iii) differing in equal magnitude along only one stimulus dimension (Single-cue). Test sounds, presented in two-alternative forced-choice (AXB) trials, were drawn from a distribution with much lower correlation between cues (filled shapes in Fig. 1C: r_AD,SS = ±0.54). Two-thirds of sounds adhering to the correlation were removed, and two more sounds orthogonal to the correlation were added. This attenuated correlation allowed investigation of whether and how listeners recalibrate to new statistics, as the original correlation accounts for far less covariance in the test set. Complete details regarding testing protocols and statistical analyses are available in SI Methods.

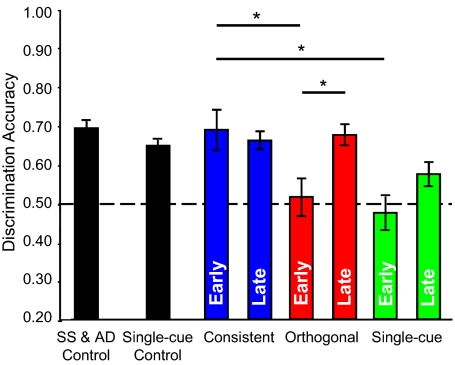
Relative to control performance absent passive exposure, listeners retained their ability to discriminate Consistent stimulus pairs but were at chance levels discriminating Orthogonal and Single-cue stimulus pairs immediately after exposure (Fig. 2). Passive listening caused listeners to treat two separate but highly correlated stimulus attributes as a single perceptual dimension that captured covariance. Subsequent active discrimination of sounds with less-correlated attributes facilitated listeners’ discovery of additional variance in test stimuli and performance improved. Listeners maintained performance levels on Consistent trials, marginally improved on Single-cue trials, and improved significantly on Orthogonal trials. Final performance did not significantly differ from baseline (control).

Fig. 2.

Listener performance in control and experimental sessions. Discrimination accuracy of sound pairs in AXB tasks is plotted on the ordinate. Black bars denote performance by separate listener groups in control experiments (absent passive exposure). Colored bars denote Experiment 1 performance (Consistent: blue; Orthogonal: red; Single-cue: green) immediately following passive exposure (left bar in each pair, labeled “Early”) and after further active discrimination (right bar in each pair, labeled “Late”). The dashed line at 50% accuracy indicates chance performance. Error bars denote SEM. Asterisks indicate significant contrasts of interest assessed by paired-sample t tests following Bonferroni correction for multiple comparisons (P < 0.0167).

Three simple unsupervised learning models, adopting similar architectures but reflecting different hypotheses about how perceptual systems exploit covariance, were contrasted to assess how each accounts for listener data (Fig. 3A). All models accept two inputs that encode, respectively, the AD and SS of a given stimulus. Via weighted connections, inputs generate output states computed over two units representing the perceptual state generated by a given sound. Assuming that discriminability of two stimuli increases with the dissimilarity of the states they produce, Euclidean distance between states generated by pairs of stimuli provides a model analog of perceptual discriminability.

Fig. 3.

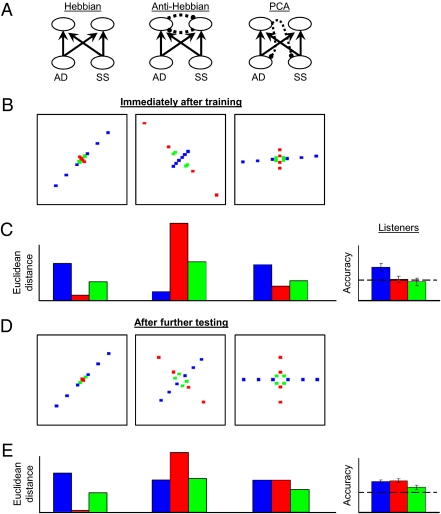
Neural network and listener performance in Experiment 1. For ease of understanding, all models employ localist representations of SS and AD, although in reality, distributed representations are assumed. (A) Network architecture for the Hebbian (Left), anti-Hebbian (Center), and PCA (Right) networks. Solid lines with arrows indicate directions of excitatory connections (identical across all networks); dashed lines with circles indicate directions of inhibitory connections. (B) Model representations of test stimuli when queried immediately after training. Representations are plotted in first-output-unit by second-output-unit space. Consistent: blue; Orthogonal: red; Single-cue: green. (C) Model representations expressed equivalently as Euclidean distances between neighboring stimuli in B. For B and C (Center), model representation and histogram are downscaled two times to accommodate substantial expansion of orthogonal dimension by the anti-Hebbian model. At far right, mean discrimination for the first two trials in each stimulus condition following exposure. The dashed line at 50% accuracy indicates chance performance. Error bars depict SEM. (D) Model representations after further testing with less-correlated test stimuli. (E) Model representations in Euclidean distances for stimuli plotted in D. At far right, mean listener performance in the second half of testing, using the same labeling as in C.

The models differ in how the weights change with experience. First is a Hebbian model (16, 17), in which connection weights adjust in proportion to the correlation between input and output node activations (Fig 3A, Left). Second, an anti-Hebbian (decorrelation) model (7, 18) (Fig. 3A, Center) orthogonalizes output dimensions by adjusting symmetric inhibition among output nodes proportional to the correlation between them. This model also maximizes the available dynamic range for each dimension. Finally, principal components analysis (PCA) was implemented in a third model (19) (Fig. 3A, Right). Connections to output units adjust in a Hebbian manner; however, the first output inhibits inputs to the second, effectively removing the principal component from the input pattern and leaving the second unit to capture residual covariance. This model captures correlation across inputs (like the Hebbian model) and orthogonalizes outputs (like the anti-Hebbian model).

All three models were trained until weight changes approached zero (Methods). For Hebbian and anti-Hebbian models, this occurred at convergence of the algorithm; for the PCA model, weight changes approached zero and training ceased shortly after the model had learned the first component of the input space. Euclidean distances between states generated by pairs of stimuli were computed for Consistent, Orthogonal, and Single-cue test pairs. Immediately after initial exposure (Fig. 3 B and C), both Hebbian and PCA networks maintained these distances for Consistent stimuli, but assimilated Orthogonal and Single-cue stimuli to the correlation by significantly reducing distances between the states they generated. In contrast, distances between Consistent pairs decreased in the anti-Hebbian model, and distances between Orthogonal and Single-cue pairs greatly increased, consistent with maximizing dynamic range and contrary to observed behavioral results.

Fig. 3 D and E show distances following model training with less-correlated test items. In the Hebbian model, distances between Orthogonal and Single-cue pairs did not recover to preexposure levels. Each output unit independently adjusted connections in proportion to correlation with input units. Because both outputs were equally correlated with input patterns in both training and test sets, they always acquired similar connection weights and produced similar activation states. The anti-Hebbian network adjusted distances somewhat toward preexposure levels following training with the test set. The Orthogonal dimension became less expanded and the Consistent dimension was less compressed. The PCA network adjusted distances in all conditions to preexposure levels following training with the test set. In this set, the orthogonal dimension captures additional stimulus variance, and the network's representation of variation along this dimension grows accordingly.

As a consequence of 7.5 min of passive exposure to correlation among complex stimulus attributes, discrimination of Orthogonal and Single-cue pairs was severely compromised. After further experience with the less-correlated test set, discriminability of the Orthogonal and Single-cue pairs returned to preexposure levels. Of the three models assessed, only the PCA network model qualitatively captured both of these effects. Data are consistent with a temporary reduction of dimensionality of the perceptual space, in this case similar to that provided by a principal components analysis.

This hypothesis remains tentative, however, because the PCA model was assessed at an intermediate point when learning from the training set had slowed to near zero. With extensive further training, the PCA model eventually acquired sensitivity to the Orthogonal component of the training patterns, so at convergence, it can faithfully reconstruct all stimuli (as also occurs for the closed-form linear algebraic solution). This finding suggests that listeners should eventually regain the ability to discriminate Orthogonal pairs with sufficient exposure to the same highly correlated stimulus set presented during passive exposure. Experiment 1 did not permit testing this prediction because test stimuli exhibited a far weaker degree of correlation than passive-exposure stimuli did. Thus, it was not clear whether the recovery to preexposure levels of performance occurred because the structure of the stimuli changed, or because the observed perceptual adaptation effects, like the PCA model, can eventually recover the lost dimension of variation with sufficient exposure. Experiment 2 was designed to further test the PCA model by measuring changes to the discriminability of Orthogonal pairs over time when the highly correlated structure of the stimulus set remains constant.

Experiment 2.

Experiment 2 employed only the stimuli presented during passive exposure in Experiment 1. Instead of a passive listening phase followed by an active discrimination phase, listeners performed the AXB task throughout the entire session. This process permits assessment of discriminability of Orthogonal pairs after differing amounts of exposure to the same stimulus set (Fig. 4A).

Fig. 4.

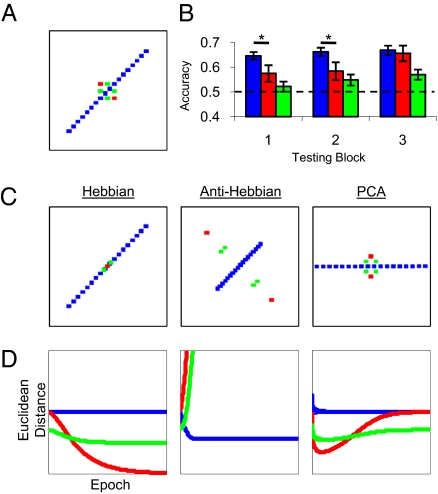
Neural network and listener performance in Experiment 2. (A) Listeners discriminated sounds with either a positive correlation between AD and SS (r_AD,SS = 0.97, n = 20) or the counterbalanced negative correlation (r_AD,SS = −0.97, n = 20). Consistent: blue; Orthogonal: red; Single-cue: green. (B) Listener performance in Experiment 2. The dashed line at 50% accuracy indicates chance performance. Error bars denote SEM. Asterisks indicate significant contrasts of interest assessed by paired-sample t tests following Bonferroni correction for multiple comparisons (P < 0.025). (C) (Left) Model representations of stimuli at the end of simulation. Simulations of the Hebbian network; (Center) anti-Hebbian network; (Right) PCA network. Representations are plotted in first-output-unit by second-output-unit space. (D) Measures of Euclidean distance between test points throughout the simulation for each model.

A comparable pattern of performance was found: discrimination of Consistent pairs remained relatively high throughout the experiment, but performance on Orthogonal trials was significantly inferior early in testing (Fig. 4B). Similar to performance in Experiment 1, perception quickly became attuned to the correlation among stimulus attributes, and discrimination of sounds that did not share this covariance was impaired. Following further discrimination testing, performance on Orthogonal pairs improved to levels consistent with those measured in control conditions with uncorrelated attributes.

The three network models were also tested with this stimulus set. Euclidean distances between the states generated by relevant pairs were computed following each pass through the stimulus set, and were compared against successive measures of listeners’ discrimination performance. The Hebbian model again assimilated Orthogonal and Single-cue stimuli to the correlation (Fig. 4 C and D, Left). Thus, this model predicts that performance on Orthogonal pairs should collapse and never recover. In the anti-Hebbian model, symmetric inhibition between outputs grew until activity of output units was uncorrelated. As a result, the Consistent dimension was strongly compressed, and the Orthogonal dimension strongly expanded (Fig. 4 C and D, Center). Thus, this model predicts that Orthogonal pairs should grow increasingly discriminable over time. The PCA model quickly discovered the principal component (the Consistent dimension) so that distances between Orthogonal pairs initially decreased (Fig. 4 C and D, Right). With further exposure to the same stimuli, the PCA model gradually captured the modest variance not explained by the first component, progressively increasing distances between Orthogonal pairs until reaching original relative values. Listener performance violated predictions of the Hebbian and anti-Hebbian models, but provided a good qualitative match to the PCA model, with discriminability initially decreasing, then increasing again, for Orthogonal pairs, and with no change to Consistent pairs.

Both experiments revealed how listeners maintain the ability to discriminate Consistent pairs but very rapidly lose the ability to discriminate Orthogonal pairs. Experiment 2 further suggests that additional variance is discovered only after the principal dimension is reified. In the PCA network model, these effects occur because a very high proportion of total variance (r² = 0.95) is captured by the correlation between stimulus attributes encountered during passive exposure (Experiment 1) or throughout discrimination testing (Experiment 2). For stimuli with a lesser degree of correlation, the PCA model will more rapidly become sensitive to variation along the Orthogonal dimension. If this model accurately captures perceptual adaptation effects observed thus far, this finding suggests that such effects should be attenuated or even eliminated with exposure to less strongly correlated stimuli. A third experiment was conducted to assess how discrimination of Consistent and Orthogonal pairs changes over time when participants continuously discriminate items from the less-correlated stimulus set used in the test phase of the Experiment 1 (Fig. 5A).

Fig. 5.

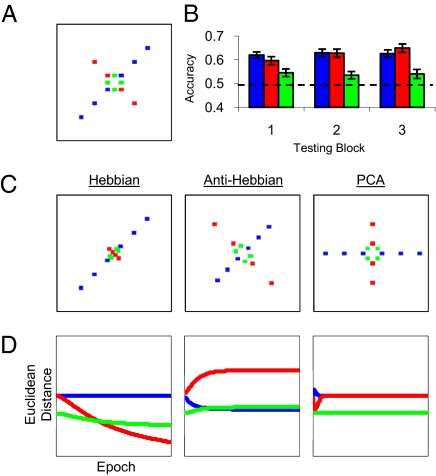
Neural network and listener performance in Experiment 3. (A) Listeners discriminated sounds with either a positive correlation between AD and SS (r_AD,SS = 0.54, n = 20) or the counterbalanced negative correlation (r_AD,SS = −0.54, n = 20). Consistent: blue; Orthogonal: red; Single-cue: green. (B) Listener performance. The dashed line at 50% accuracy indicates chance performance. Error bars denote SEM. No planned contrasts (paired t tests) revealed significant differences between Consistent and Orthogonal discrimination performance. (C) Model representations of stimuli at the end of simulation. (Left) Simulations of the Hebbian network; (Center) anti-Hebbian network; (Right) PCA network. Representations are plotted in first-output-unit by second-output-unit space. (D) Measures of Euclidean distance between test points throughout the simulation for each model.

Experiment 3.

A third listener group participated in an experiment identical to Experiment 2, with the only change being that test pairs depicted in Fig. 5A (and Fig. 1C) were used. In this experiment, listeners’ discrimination of Orthogonal pairs remained equivalent to that of Consistent pairs all throughout testing (Fig. 5B). This result suggests that strength of correlation must be fairly high, capturing a substantial proportion of total variance (at least greater than 0.29, or 0.54²), to elicit significant decline in discriminability of Orthogonal pairs.

Experiment 3 was also simulated with the same network models using analogs of less-correlated stimuli. The Hebbian model exhibited the same performance as in previous experiments (Fig. 5 C and D, Left), although it took longer to converge because of weaker correlation in the stimulus set. The anti-Hebbian network also performed similarly to prior results, although it required less inhibition to decorrelate dimensions and showed less compression of the Consistent and less expansion of Orthogonal dimensions relative to Experiment 2 (Fig. 5 C and D, Center). The PCA network showed a much smaller early effect of the correlation, producing an initial decrease in distances between Orthogonal stimuli (Fig. 5 C and D, Right) that was far shallower and more short-lived than in the previous simulation (Fig. 4D, Right). Furthermore, expansion of distances between Orthogonal pairs back to baseline distances occurred much more rapidly. As a result, the PCA network showed largely equal discriminability for Consistent and Orthogonal pairs across almost all of training, again mirroring behavioral data.

Discussion

Only the PCA network qualitatively matched listener performance at all stages across passive listening and active discrimination experiments. Data support the hypothesis that the auditory system rapidly and efficiently captures covariance (redundancy) across the set of complex stimuli. Like the PCA model, listener performance appears to initially capture the principal component of variation in the 2D stimulus space at the expense of the orthogonal component, and only gradually comes to encode remaining variance. Both the principal and second components become weighted proportional to the amount of variance accounted for by each dimension. Listeners’ performance cannot be explained by independent weighting of individual acoustic cues (AD, SS).

The particular PCA model investigated here (19) is certainly oversimplified and is unlikely to exactly reflect neural learning mechanisms. Psychophysical dimensions of AD and SS are almost certainly encoded across a large number of neurons. An important goal for future work will be to investigate learning mechanisms that capture the PCA-like adaptation phenomena as a consequence of learning over distributed representations.

A second challenge is to identify neurally realistic mechanisms for instantiating PCA-like performance. Conceivably, circuitry of auditory cortex may provide the required connectivities. Precortical processes might also be implicated, given that PCA has proven practical for depicting correlations across neurons in the vibrissal sensory area of rat thalamus (20). Subcortical auditory processes are at least plausible, given that fact that, relative to the visual system, much more processing (more synapses) occurs within the brainstem before cortex (21). Finally, corticothalamic and thalamocortical connections may be implicated. Identification of neural substrates should assist understanding of mechanisms that instantiate PCA-like perceptual effects and facilitate development of more authentic computational models.

It bears note that, because stimuli were normed to equivalent perceptual distances (just noticeable differences, JNDs), the perceptual space was linearized in a way that is amenable to a linear model such as PCA. The close correspondence between listener and model performance does suggest, however, that sensorineural processes adapt to reflect experienced covariance so that dimensions of the perceptual space are weighted in a statistically sensible fashion. Brief experience with highly-correlated items provides evidence that stimuli align along a single dimension, so discriminability of differences along an orthogonal component is reduced. Further experience with the same stimuli provides additional evidence that off-component items are not simply random noise and variation along the orthogonal component is recaptured.

Perceptual sensitivity to statistical structure is well-documented. Observers are known to adjust rapidly to changes in first-order (probability density) statistics in studies using optic (22) as well as optic and haptic (23) presentations. Individual neurons in the auditory cortex have been shown to be sensitive to relative probability of tone frequencies (24). Classic behavioral studies have shown visual aftereffects to contingencies among stimulus features (6). Especially for high-level vision, there is broad appreciation for the importance of higher-order statistical relationships among stimulus attributes (25–28). Within and across sensory modalities, perceivers are sensitive to redundancies across attributes that, although correlated in experience, are independent in principle (22, 27). Far less attention has been paid to higher-order statistics in audition (10, 11). However, there is good evidence that auditory cortical representations decreasingly correspond with physical stimulus dimensions (21, 29, 30), and this may be similar to the loss of acoustic dimensions (AD, SS) seen here, as more efficient dimensions better capture perceptual performance.

Studies concerning covariance among visual attributes have typically concentrated on analysis of natural scenes for which a lifetime of experience may be assumed (25) or require extensive training with novel complex stimuli (26). Here, listeners efficiently coded correlated stimulus attributes without explicit instruction or feedback over the course of a few minutes.

Brief experience with correlation between two acoustic attributes may illuminate how extended experience with natural covariance among many attributes contributes to categorical perception. Studies of categorical perception use highly familiar complex stimuli that vary continuously along multiple dimensions. One criterion of categorical perception—poor within-category discrimination—may arise from efficient coding of covariance structure in a high-dimensional feature space. To the extent that correlations between stimulus attributes are quite strong and there is reduction in dimensionality, one would predict that discrimination of stimulus differences that do not respect those correlations should be relatively poor.

Although the potential for second-order effects reported here may have been anticipated by Barlow (28), no empirical precedents exist for such rapid perceptual changes in response to correlated attributes in any modality. Additionally, present results are qualitatively consistent with only one of three common models for exploiting perceptual structure, and may help to inform theories about sensorineural mechanisms of perceptual adaptation and learning.

Because the world is lawful, input to sensory systems has structure (3, 31, 32). Efficient perceptual processing should match response properties of sensory neurons to statistical regularities of the stimuli to which they are exposed (1–3, 33, 34). Here, rapid unsupervised extraction of covariation across novel complex acoustic stimuli has been uniquely demonstrated. Listeners adapt quickly and efficiently to statistical contingencies in a fashion that suggests efficient coding of correlated complex stimulus attributes.

Methods

Stimuli.

One waveform period (3.78 ms duration = 264 Hz fundamental frequency) was selected from samples of a French horn and a tenor saxophone in the McGill University Music Database (35). Periods were iterated to 500-ms duration and matched in RMS energy. AD and SS, consistently among the primary attributes used in musical instrument classification tasks (36–38), were chosen as primary attributes here. AD was defined as the linear amplitude increase from zero at onset to peak amplitude (attack) before linear decrease to zero at offset (decay) without any steady state. Attacks in AD were varied in eight steps from 20 to 100 ms, modeled after discrimination-threshold data (39), and from 100 to 390 ms in nine equal logarithmic steps. Decays were calculated as the difference between 500 ms (total duration) and attack duration. SS, defined as relative levels of energy across frequencies, varied via 18 summations of the two instrument endpoints in different proportions, ranging from 0.2 to 0.8 and summing to 1 across instruments. Proportions were derived by varying 33-point, equivalent rectangular bandwidth-scaled (40) spectra processed by a simulated auditory filter bank (41) in equal-Euclidean-distance steps. All stimulus processing was conducted in MATLAB.

Testing.

After providing informed consent, six groups of University of Wisconsin undergraduates with normal hearing participated in two-alternative forced-choice (AXB; 250-ms interstimulus interval) discrimination tasks with stimulus pairs three steps apart. Participants indicated which stimulus sounded different by pushing labeled buttons without any feedback. Testing in Experiment 1 followed random presentation of 600 sounds over 7.5 min (circles in Fig. 1C). Complete information regarding experimental designs and statistical analyses can be found in SI Methods.

Models.

Three simple unsupervised network models were used. All models shared the same basic architecture: two input units (one corresponding to AD, the other to SS) that were fully connected in a feed-forward manner to two output units with no hidden layer and no bias. In the Hebbian (16, 17) model, these were the only connections, and weights were updated using standard Hebbian learning with normalization so that the sum of the weights received by each output unit always totaled 1. The anti-Hebbian model (7, 18) included reciprocal inhibitory connections between output units. Feed-forward weight values were fixed in this model, and inhibitory connections were adjusted in proportion to the correlation between output units. The PCA model (19) included inhibitory connections projecting from the first output back to input units at a fixed value of 1. Output activations and subsequent effects on input states were implemented serially: the first output unit was activated; its activation was “subtracted out” of the input values; then, the second unit was activated. Feed-forward weights were trained using standard Hebbian learning, resulting in the first output unit learning the principal component of the inputs and the second output learning the first component of the residuals. Each model was initialized with weights (2 × 2 identity matrix) that ensured output patterns initially mirrored input patterns.

Experiment 1.

Models were first trained with a stimulus set analogous to exposure sounds (coded as stimulus number 1 through 18; circles in Fig. 1C), changing weights according to the model's learning rule until weight-change magnitudes fell below a threshold of 0.001. This decrease occurred at convergence of Hebbian and anti-Hebbian algorithms, but occurred shortly after the PCA model had learned the first component of the input space. Models were then tested by comparing Euclidean distances (i.e., discriminability) among output patterns corresponding to experimental discrimination stimuli (filled shapes in Fig. 1C; Fig. 3 B and C). Next, models were further trained with test stimuli, simulating learning following further exposure to the less-correlated test items. Test pairs were presented until weights changes again fell below a threshold of 0.001, at which point Euclidean distances between output patterns were measured (Fig. 3 D and E).

Experiments 2 and 3.

Network simulations for Experiments 2 and 3 consisted of one continuous phase that served as both training and testing. Models were trained with the analog of either the highly correlated (Experiment 2) (Figs. 1C and 4A) or less-correlated stimulus set (Experiment 3) (Figs. 1C and 5A). Euclidean distances among output patterns were measured after each epoch (Figs. 4D and 5D). All simulations were conducted in MATLAB (code is available in SI Appendix).