How the brain integrates costs and benefits during decision making

Abstract

When we make decisions, the benefits of an option often need to be weighed against accompanying costs. Little is known, however, about the neural systems underlying such cost–benefit computations. Using functional magnetic resonance imaging and choice modeling, we show that decision making based on cost–benefit comparison can be explained as a stochastic accumulation of cost–benefit difference. Model-driven functional MRI shows that ventromedial and left dorsolateral prefrontal cortex compare costs and benefits by computing the difference between neural signatures of anticipated benefits and costs from the ventral striatum and amygdala, respectively. Moreover, changes in blood oxygen level dependent (BOLD) signal in the bilateral middle intraparietal sulcus reflect the accumulation of the difference signal from ventromedial prefrontal cortex. In sum, we show that a neurophysiological mechanism previously established for perceptual decision making, that is, the difference-based accumulation of evidence, is fundamental also in value-based decisions. The brain, thus, weighs costs against benefits by combining neural benefit and cost signals into a single, difference-based neural representation of net value, which is accumulated over time until the individual decides to accept or reject an option.

When we make decisions, the benefits of a decision option often need to be weighed against accompanying costs. Cost–benefit integration, thus, is an important aspect of decision making. However, value-based decision making is typically investigated in the context of decision uncertainty (1–3), so little is known about the neural mechanisms underlying the integration of costs and benefits as such.

Cost–benefit-based decision making involves the binary decision to either accept or reject a choice option based on two competing attributes—the option's expected rewards and losses. Such binary accept-versus-reject decisions bear a strong resemblance to two-alternative choices in perceptual decision making (4, 5). For example, when monkeys performed a direction-of-motion discrimination task in which they had to decide whether a noisy field of dots was moving in one direction or its opposite direction (e.g., leftward or rightward) and indicated their choice with a quick eye movement to the target on the respective side, motion-sensitive neurons in middle temporal visual area MT either respond to leftward motion or to rightward motion. Prefrontal and parietal neurons, in contrast, form a decision by accumulating the difference in the activities of populations of neurons in area MT that code for opposite directions of motion. The monkey's saccade response is faster when more dots are moving in one direction, and this effect is predicted by the strength of the accumulated neuronal difference signal (6). A difference-based decision mechanism has also been identified in the human dorsolateral prefrontal cortex (DLPFC) during perceptual face-house decisions (4, 7). Thus, we hypothesized that cost–benefit decisions involve an analogous decision mechanism, that is, the computation of a decision variable that is based on the difference of neural reward and loss anticipation signals (cf. ref. 8 for a similar proposal in the context of neurophysiological data).

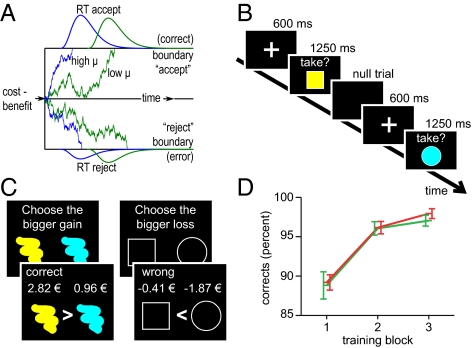
In perceptual decision making, both monkeys’ behavior and neural activity were accounted for by sequential sampling models of decision making. Specifically, monkeys’ behavior shows a speed–accuracy tradeoff, and neurons in the lateral intraparietal cortex (area LIP) accumulate evidence in favor of a particular decision alternative until a decision boundary is reached (9, 10). Evidence accumulation toward a decision boundary is also the key feature of sequential sampling models. Diffusion models, a popular type of sequential sampling models, assume a single directed drift process Σ that accumulates noisy information over time and moves with a rate μ toward one of two decision boundaries (Fig. 1A; cf. ref. 11). Importantly, sequential sampling models not only describe accuracy and response time in perceptual and memory tasks but can also describe value-based decisions (12, 13).

Fig. 1.

Diffusion model, behavioral paradigm, and training. (A) Schematic display of the diffusion model. The drift process has a neutral starting point between the two decision boundaries. Traces exemplify decision processes with high (blue) and low (green) drift rates, in which the difference of benefits minus costs drifts toward either an accept response (upper boundary) or a rejection (lower boundary). In this example, rejection decisions are interpreted as errors, because benefits outweigh costs. Response-time distributions show that lower drift rates are associated with slower accumulation processes (as the blue distribution is shifted nearer to the starting point than the green one) and higher error rates (as the green distribution has a larger mass in the rejections/errors). (B) Task paradigm with color/shape stimuli that are associated with different ranges of monetary benefits and losses. For example, a yellow square might be associated with a reward between 2 and 2.4 € and a loss between 0.4 and 0.8 € (see Fig. S1 for more details). Successful cost–benefit integration would lead participants to accept this stimulus. Null trials are variable intertrial intervals. (C) Training (SI Methods) involved three blocks each for colors (Left) and shapes (Right), each of which comprised 56 stimulus pairs. Participants first compared the presented pairs and then received feedback as shown, thus implicitly learning the value ranges associated with colors and shapes. The last two blocks were terminated when a criterion (95% correct) was reached, but never before 25 trials were completed. (D) Accuracy for the training session, displayed according to training block (x axis) and reward (green) versus loss (red) condition. Error bars represent SEM.

We hypothesized that weighing costs against benefits involves the accumulation of the difference between stimulus-associated benefits and costs over time. The benefits and costs related to the decision are, according to this hypothesis, associated with competing behavioral tendencies, that is, to either approach or avoid the stimulus. The cognitive process of cost–benefit integration, thus, is modeled as a drift toward either an upper (accept) or lower (reject) decision boundary. At the brain level, we hypothesized that the decision process involves separate representations of expected reward and loss, in the ventral striatum (1) and amygdala (14, 15), respectively, from which a comparison signal is computed. A neural representation of the resulting cost–benefit difference signal, in turn, should be accumulated in parietal or prefrontal cortex (cf. refs. 8, 16).

Diffusion models do not predict whether the cost–benefit difference is computed before or during the accumulation process, and neurophysiological data from perceptual decision making so far provide only indirect evidence as to the brain regions implementing this comparison process. However, a number of functional magnetic resonance imaging (fMRI) studies suggest that ventromedial prefrontal cortex (VMPFC) represents a global valuation signal (2, 17, 18), and lesion studies highlight VMPFC as a necessary basis for value-based decision making (19, 20). We thus hypothesized that VMPFC functions as a comparator region computing the difference between neural reward and loss signals, akin to the computation of perceptual difference signals in DLPFC (6, 7). According to the diffusion model, blood oxygen level dependent (BOLD) signals in comparator regions should be driven by the neural cost–benefit difference signal, and this effect should be greater for participants who are more efficient in cost–benefit integration (Fig. 1A). To test this hypothesis, we examined which brain regions are functionally coupled to the difference of neural reward and loss signal.

We furthermore hypothesized that brain regions that accumulate the cost–benefit difference over time (accumulator regions) should be functionally distinct from comparator regions. Comparator regions should show greatest and weakest activity for large positive and negative differences, respectively. In contrast, accumulator regions should show greater activity for harder than for easier decisions (16). The last prediction derives directly from the comparison of high versus low drift rates in Fig. 1A and from the fact that accumulation-related activity is a function of the area under the accumulation, ∫Σ (16) (see also below): In response-time paradigms (where participants respond as soon as they know the answer), more difficult trials have a lower drift rate μ and a prolonged accumulation process Σ, which results in an increase in the area under the accumulation process ∫Σ for harder trials. Given that we hypothesized that comparator regions feed their output into accumulator regions, and given that we further assumed that decision making depends on the efficiency of the connection between comparator regions and accumulator regions (21), we predicted (i) that accumulator regions are negatively correlated with the unsigned and normalized comparator region activity, such that accumulators are more strongly activated for hard trials independent of whether they have a net positive or net negative cost–benefit difference, (ii) that this effect depends on the individual efficiency of cost–benefit comparison, and (iii) that accumulator regions additionally show greater activation for harder trials.

To test these hypotheses, we measured functional brain activations while 19 participants decided to either accept or reject a series of single visual stimuli, each characterized by two visual attributes: color and shape (Fig. 1B; Fig. S1). In a preceding training session (Fig. 1C), participants had learned that different colors were associated with different monetary costs and different shapes with different monetary benefits, or vice versa (balanced across participants). Deciding whether or not to collect a stimulus thus required that subjects compared stimulus-associated costs against stimulus-associated benefits. Net outcomes of accepted stimuli were added over the course of the experiment and paid out afterward. We modeled behavioral data with a power-rate diffusion model (22), with the aim of quantitatively relating the drift parameter μ of the decision process to neural mechanisms measured with fMRI.

Results

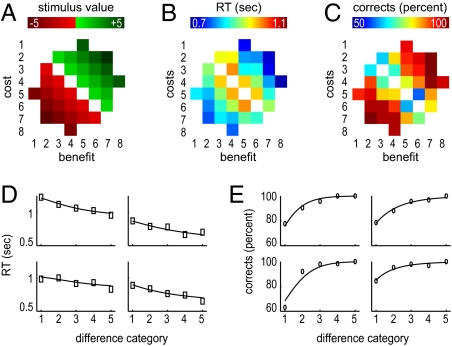
Participants successfully learned stimulus-reward associations (see details in SI Methods). Average performance-dependent earnings in the experiment were 22.27 Euro (€) and, as expected, participants were faster in trials with larger cost–benefit differences (Fig. 2 A–C; SI Results).

Fig. 2.

Behavioral results and model fit. (A) Categorical cost–benefit differences (ranging from −5 to +5) associated with stimuli from each cost–benefit difference category. Axes denote the eight categories of monetary benefits (x axis) and costs (y axis) from which the stimuli were generated. A more detailed version is found in Fig. S1. (B and C) Response times (RT; in seconds) and accuracy in percent correct, respectively, per category. (D and E) Fitted chronometric (D) and psychometric functions (E) together with observed data, for four exemplary participants. The x axis in these plots represents the five cost–benefit difference categories (A; Fig. S1) independent of the sign of the cost–benefit difference. The boxes (RT) and circles (accuracy) represent the observed data points, and lines represent the fitted functions. Model fits for all subjects are shown in Fig. S2.

The Diffusion Model Accounts for Cost–Benefit Decisions.

We used the power-rate diffusion model (22) to estimate participants’ drift rates. Fig. 2 C and D shows examples of fitted chronometric and psychometric functions for four representative subjects, and illustrates that the model describes behavior well (see Fig. S2 for all individual plots). To test the validity of fitting the power-rate diffusion model, we applied two different response-time criteria to different participants (1,700 ms vs. 1,250 ms; Methods). As expected, varying the response-time criterion modulated the decision boundary a [t(18) = 3.2, P = 0.005, JZS-BF = 0.11] but not the drift rate μ [t(18) = −0.82, P = 0.426, JZS-BF = 2.4]. JZS-BF is a Bayes factor and estimates how much more likely the null hypothesis is than the alternative hypothesis (23).

Given that we intended to test the hypothesis that the brain implements cost–benefit integration as described in diffusion models of decision making, we predicted that brain processes implementing cost–benefit comparison and evidence accumulation should be modulated by participants’ individual drift rates. We therefore calculated, for each participant separately, the median drift rate across all experimental conditions as an index of decision-making efficiency (see Table S1 for individual data). Median drift rates varied considerably (minimum = 0.56; maximum = 2.42; median = 0.89; mean = 0.97; SD = 0.45) and were subsequently entered as a predictor into individual-difference group analyses of fMRI data.

Neural Representations of Reward and Loss Expectation Signals.

We first identified brain regions representing anticipated costs and benefits, because we hypothesized that these function as input to the subsequent cost–benefit comparison in VMPFC. Importantly, benefits (i.e., monetary reward) and costs (i.e., monetary loss) associated with each stimulus were independent of each other (r = −0.22; P > 0.2) and of the absolute value of the cost–benefit difference (both r = 0). Thus, “pure” cost and benefit signals were identified by modeling brain activation, across all trials, with separate parametric predictors reflecting the amount of reward and the amount of loss coded in each stimulus.

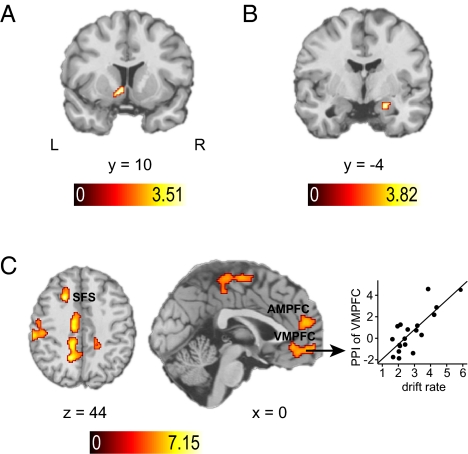
A neural signature of anticipated monetary reward was identified in several regions (Table S2), including the hypothesized left ventral striatum. Given that the ventral striatum was consistently associated with reward anticipation in previous literature (1), we extracted the time course t_vStr of this region (MNI coordinates x = −10, y = 10, z = −6; P < 0.005; k = 30 voxels; Fig. 3A) for the subsequent analysis of a cost–benefit difference signal. Also consistent with earlier reports (14, 15), we found a correlation of monetary loss with right amygdala (18,−2,−20; P < 0.005; k = 38; Fig. 3B) and extracted time course t_Amyg from this region. Note that the neural representations of expected benefits and costs were not significantly correlated with participants’ drift rates (ventral striatum: T_max = 0.285, r = 0.07, JZS-BF = 5.5; amygdala: T_max = 0.124, r = 0.03, JZS-BF = 5.7).

Fig. 3.

Brain activation results for cost–benefit comparison. (A) Localization of the ventral striatal (vStr) ROI, whose average time course was used to derive the neural difference signal D_neural = t_vStr – t_Amyg. (B) Localization of the amygdala ROI, whose average time course was used to derive the neural difference signal D_neural = t_vStr – t_Amyg. Activation results in A and B are shown at P < 0.005 (uncorrected). (C) Brain regions whose BOLD signals are coupled to the neural difference signal D_neural (identified using PPI analysis) and additionally modulated by the individual median drift rate (Inset), displayed at whole-brain corrected P < 0.05 (Methods). SFS, superior frontal sulcus.

Prefrontal Comparator Regions Compute Cost–Benefit Difference.

We conducted a psychophysiological interaction analysis (PPI) (24) to identify comparator regions computing the cost–benefit difference (CBD) based on the identified neural reward and loss signals. The physiological predictor was the difference D_neural of the standardized time series extracted from above-defined amygdalar and striatal regions of interest (i.e., D_neural = t_vStr – t_Amyg). The psychological predictor P coded whenever a stimulus was presented. Therefore, the expected correlation between the neural cost–benefit signal and BOLD signals from comparator regions was restricted to decision-related activity. The critical component of this analysis was the psychophysiological interaction term PPI_CBD = D_neural × P. Due to its physiological regressor D_neural, PPI_CBD identifies brain regions computing net values of the stimuli by subtracting stimulus-associated neural cost signals from neural signatures of expected monetary benefit. To ensure that we identified brain regions implementing the cognitive process as modeled with the diffusion model, we additionally required that comparator regions correlating with PPI_CBD do so to a greater extent for the more efficient decision makers with higher average participant-specific drift rates μ.

Prefrontal comparator regions defined in this way were found in VMPFC (−4,60,−6; cluster size k = 417, T_max = 6.12), anteromedial prefrontal cortex (AMPFC; 12,50,8; k = 586, T_max = 6.72), and in the posterior part of the dorsolateral prefrontal cortex (left posterior superior frontal sulcus; −22,18,44; k = 106, T_max = 7.15 ; Fig. 3C). Table S3 lists results outside prefrontal cortex. Fig. 3C visualizes those brain regions that show a modulation of the PPI_CBD effect by drift rate and illustrates that the dependency of the VMPFC signal on the neural cost–benefit difference signal was larger for participants with higher drift rates. Thus, as predicted, VMPFC is driven by the neural cost–benefit signal, and this effect is stronger in more efficient cost–benefit decision makers.

Accumulation of the Cost–Benefit Difference.

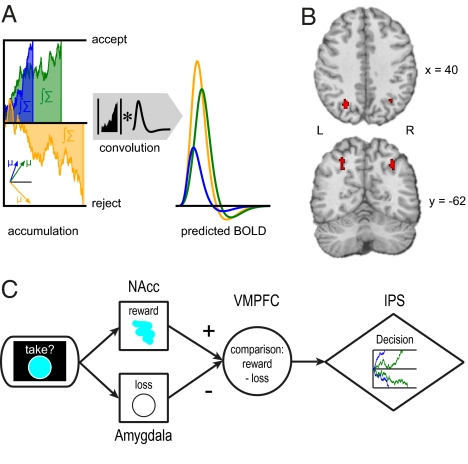
We had further hypothesized that the amount of accumulated information ∫Σ should be greater the longer the integration process takes, independent of the net result of the integration process (Fig. 4A). Accumulator regions were accordingly defined by three criteria. First, BOLD signals in accumulator regions, t_accumulator, should be negatively correlated with the normalized, absolute activation strength of comparison region VMPFC (i.e., t_accumulator ≈ −| t_VMPFC |), as accumulation should produce greater ∫Σ in conditions characterized by a small cost–benefit difference. Second, this inverse coupling of comparator and accumulator regions should be greater for subjects with higher median drift rate μ. This assumes that less efficient decision making is partially caused by a noisier connection between comparator regions and accumulator regions (21). A PPI analysis (Methods) was implemented to jointly test these two criteria and revealed three clusters in the middle intraparietal sulcus (mIPS; left: −40,−40,42, k = 59, T_max = 4.59 and −28,−66,38, k = 111, T_max = 4.69; right: 32,−52,40; k = 69; T_max = 4.5). Third, BOLD signal in accumulator regions should also be greater for harder trials, as defined by the absolute difference of the true stimulus-associated costs and benefits (16). We tested for this additional criterion by creating a conjunction map showing where the first two criteria are fulfilled and where, at the same time, the BOLD signal was greater for harder than for easier trials (Methods). This analysis identified the left (78 voxels) and right (38 voxels) mIPS as plausible neural accumulator regions (Fig. 4B).

Fig. 4.

Brain activation results for accumulation of the cost–benefit difference. (A) The diffusion model predicts greater BOLD signal in accumulator regions for harder decisions. (Left) Drift processes with a high (blue), medium (green), or low (yellow) drift rate μ. Lower drift rates signify harder decisions (within participants) or less efficient decision making (between participants). Because low-drift-rate decisions last longer, the area under the drift process (∫Σ) will also be greater for lower drift rates. Therefore, convolving the drift process with a hemodynamic response function leads to greater predicted BOLD signals for harder trials (Right). Note that accumulator regions should reflect the absolute value of the area under the drift process, as they are indifferent to the sign of the cost–benefit difference. (B) Accumulator regions are functionally coupled to the comparator region (VMPFC), modulated by individual drift rates, and are more strongly activated for more difficult trials as described in A. Accumulator regions in mid-intraparietal sulcus were identified by a conjunction analysis (see Methods for details). (C) Proposed brain mechanism for cost-benefit decision making: Cost and benefit signals from amygdala and nucleus accumbens (NAcc), respectively, are compared in VMPFC. The resulting difference signal is accumulated in intraparietal sulcus (IPS) until a decision threshold is reached.

Discussion

Decision making often involves weighing the benefits of an option against the costs of an option. Little is known, however, about the neural systems underlying such cost–benefit computations. Using fMRI and choice modeling, we tested the hypothesis that cost–benefit comparisons can be described by an accumulation process as postulated in sequential sampling models of decision making (9–13, 22). More specifically, we hypothesized a neural decision mechanism that accumulates information from a neural representation of the cost–benefit difference of a choice option until a decision boundary for accepting or rejecting the options is reached and the choice is executed. Consistent with theoretical proposals and behavioral modeling results (3, 4, 8, 12, 13), we hypothesized that the same basic brain mechanisms that were successfully used to explain perceptual decision making can also explain value-based decision making. Consistent with this hypothesis, our fMRI results indicate that this decision is implemented by a comparison of cost and benefit signals from amygdala and ventral striatum, respectively, in (among other regions) the ventromedial prefrontal cortex. Our results further suggest that the result of this difference-based computation is accumulated toward a decision threshold in parietal cortex (Fig. 4C).

Model-Driven Functional MRI Analysis.

The present results demonstrate the power of model-driven fMRI analysis, as the application of models such as the diffusion model allows quantifying well-defined decision mechanisms and stringently identifying their neural bases (25). Whereas the application of sequential sampling models to electrophysiological data can exploit the high temporal resolution of single-cell data (e.g., 10), our model-based approach exploits individual differences in an important decision parameter, that is, the efficiency of information accumulation (26). In the present study, this approach supports the hypothesis that analogous computational mechanisms are involved in perceptual and reward-based decision making. Tying neural activation data to model parameters may also help to clarify questions concerning the nature of neural effects observed. Brain activation effects suggestive of accumulator regions may, at least partly, also be due to postdecision processes such as confidence in the decision. However, our identification of decision-making regions from model-based PPI analyses links them closely to the hypothesized decision processes, making it unlikely that they represent postdecision processes.

Our results also shed light on the neurobiological causes for individual differences in reward-based decision making. The drift rate as a measure of participants’ decision-making efficiency correlated with how well people compared the neural signatures of monetary costs and benefits, and with how well the cost–benefit difference is read out into the accumulations process. In contrast, the drift rate did not correlate with the neural representations of costs and benefits as such, suggesting that less efficient decision makers had cost and benefit signals of the same quality but that they were worse at integrating this information. Hence, the paradigm we used here could be a useful tool to investigate decision-making deficiencies in clinical populations in the brain on a process level (19, 27).

Neural Mechanisms Underlying Cost–Benefit Comparisons.

Our results suggest the VMPFC, as well as AMPFC and left DLPFC, as candidate regions for cost–benefit comparison. Critically, changes in fMRI signals in these neural comparison regions were not due to decision difficulty. Rather, the task-related correlation with the difference of ventral striatal benefit signal and amygdalar cost signal implies that prefrontal comparison regions represent the value of the cost–benefit difference. We suggest that the positive correlation with the neural difference signal identifies plausible comparator regions that compute expected reward by trading off costs and benefits. This conclusion is considerably strengthened by our finding that the correlation between the neural cost–benefit difference signal and activity in prefrontal comparison regions such as VMPFC is modulated by participants’ drift rate. This correlation provides a crucial link between decision variables estimated from behavioral and neuronal data.

The VMPFC is a highly plausible candidate region for a neural mechanism of cost–benefit integration. For example, patients with VMPFC lesions have problems in determining the relative values of decision alternatives (20) and provide inconsistent judgments of subjective preferences in simple pairwise comparisons (28). Moreover, a number of fMRI studies have implicated VMPFC in representing expected rewards (e.g., 17, 18, 29), although the precise mechanisms of this value computation are still unclear (2). Given the converging evidence of earlier fMRI and lesion studies and our present study showing that VMPFC compares amygdalar and striatal reward signals, we conclude that the VMPFC is critical for the comparison of costs and benefits.

Neural Accumulation of Cost–Benefit Difference Information.

According to our criteria outlined above, activation in parietal accumulator regions should (i) be negatively correlated with the unsigned difference signal of the comparator region (VMPFC; Fig. 4A), (ii) depend on individual decision-making efficiency, and (iii) be greater for harder than for easier decisions. Note that the identified accumulator regions do not map onto neural systems associated with decision conflict (in anterior cingulate cortex or DLPFC) (30) or processing difficulty in general (31, 32). Rather, our finding of neural accumulators in parietal cortex is highly consistent with nonhuman and human data from perceptual decision making, as neurons accumulating perceptual evidence based on noisy stimuli were identified in parietal cortex (8, 16).

Conclusion

Our results suggest a neural implementation of a cost–benefit comparison mechanism. Neural signals coding decision-related reward and loss expectations are compared in VMPFC, and the resulting cost–benefit difference is accumulated in parietal cortex (Fig. 4C). We propose that value-based cost–benefit decisions rely on the same general neural mechanism that was shown to implement perceptual decision making. Both mechanisms compute a difference-based decision variable, by either comparing perceptual evidence or reward information, and accumulating the difference in parietal cortex. In sum, the functional neuroimaging data reported here provide strong support for the hypothesis that the process of cost–benefit integration is best explained as a stochastic information accumulation process.

Methods

Participants.

Nineteen healthy volunteers (5 males, mean age: 24.3 y) participated in a training session and an fMRI experiment. All were right-handed, had normal or corrected-to-normal vision, no history of psychiatric or neurological diseases, and no structural brain abnormalities. Informed consent was obtained according to a protocol approved by the local ethics committee.

Experimental Design.

Stimuli were combinations of eight colors and eight shapes (Fig. 1B; Fig. S1), that is, colored shapes center-presented on a dark background. In the training session, colors and shapes were presented separately, whereas 34 combined stimuli were selected for the fMRI experiment (Fig. S1). During training (0.5 h), ranges of monetary values (e.g., 2.00–2.40 €; Fig. S1) associated with colors and shapes were learned based on feedback in paired comparisons (Fig. 1C). Monetary values of colors/shapes varied from trial to trial and were randomly drawn from the value ranges shown in Fig. S1. Feedback concerned response correctness and monetary value of the items. Details on the training procedure are given in SI Methods.

In the fMRI experiment, target stimuli (i.e., colored shapes; Fig. 1B) appeared together with the cue “take?,” and subjects indicated (using response buttons) whether or not they accepted the stimulus offered. Presentation duration was varied between 1,250 ms (9 subjects) and 1,700 ms (10 subjects), to test the validity of the diffusion model (see below), and stimuli were followed by an inter stimulus interval of 3.7–20 s. Within each of four runs, all 34 stimuli were presented twice in pseudorandomized order (68 trials per run). Net values of accepted stimuli were added up during the experiment and one-fifth of the sum was paid out after the experiment. Stimuli missed by the participant were recorded to his/her disadvantage (i.e., gains were skipped, losses were counted). Feedback concerning the current account balance was given at the end of each run. A power-rate diffusion model of decision making (22) was fitted to the behavioral data to obtain a median drift rate μ for each participant (SI Methods), which was then used for model-driven fMRI analyses.

Data Acquisition and Analysis.

Functional data were acquired on a Siemens Trio 3T scanner using a standard echo planar imaging sequence with 37 oblique axial slices of 3 mm (field of view 192 mm, 3 × 3 mm in-plane, repetition time 2 s, echo time 30 ms, flip angle 70°). Four runs of 360 volumes were acquired, as well as a T1-weighted high-resolution MP-Rage scan. Preprocessing involved discarding the first six images, slice-time and motion correction, normalization to MNI152 space, and spatial smoothing (8 mm FWHM). Statistical analyses were performed using the general linear model with SPM5 (The Wellcome Trust Centre for Neuroimaging, London, U.K.). The four functional runs were modeled as separate sessions. General linear models were based on a canonical hemodynamic response function and its temporal derivative, and included regressors for incorrectly answered trials, motion parameters as covariates of no interest, and a temporal high-pass filter (128 s).

A first model localized regions of interest (ROIs) sensitive to the anticipation of monetary reward versus loss. This model included as regressors of interest the onsets of all correctly answered trials as well as continuous parameters that independently capture the variance in the amount of reward, the amount of loss, as well as their difference. A priori predicted activations for reward expectation in ventral striatum (1) and loss anticipation in amygdala (14, 15) were tested at T > 2.88 (P < 0.005 uncorrected; df = 18). Time courses of these functionally defined ROIs were extracted as first eigenvariates, standardized, and subtracted (i.e., D_neural = t_vStr – t_Amyg). Subsequently, D_neural was used as a physiological regressor in a PPI analysis (24) that aimed at identifying cost–benefit comparison regions. The psychological regressor P specified the presence of cost–benefit integration trials, and the interaction term PPI_CBD was formed by D_neural × P. To identify brain regions where the correlation with D_neural was greater for individuals who are more efficient in cost–benefit comparison (i.e., who have larger drift rate μ), the group analysis examined the effect of μ on PPI_CBD. To protect against false positives, we applied a whole-brain family-wise error correction of P < 0.05 using a double thresholding procedure. PPI group results were thresholded at T > 3.65 (P < 0.001, df = 17, uncorrected). According to Monte Carlo simulations with 1,000 iterations (33), a cluster size threshold of k > 65 assured a corrected significance criterion of P < 0.05, corrected for all brain voxels entering the statistical analysis.

Accumulator regions were identified based on three criteria (Introduction). First, BOLD signals in accumulator regions should be negatively coupled to the absolute time course of comparator regions. That is, when comparator regions show weak responses in trials with a small cost–benefit difference, independent of the sign of the difference, accumulator regions should be more strongly activated, as they accumulate information over a longer time. Second, the coupling between comparator regions and accumulator regions should be greater for more efficient subjects. Third, accumulator regions should show generally stronger activation for more difficult trials (16). These criteria were applied using a conjunction approach. We first identified brain regions that were inversely coupled to the absolute z-normalized time course of comparator region VMPFC (i.e., PPI_accumulator = −|t_VMPFC| × P), and identified brain regions in which PPI_accumulator was dependent on drift rate (using −μ to predict greater negative coupling between comparator and accumulator regions for persons with higher drift rate). This analysis was restricted to voxels showing negative coupling with the comparator region VMPFC by inclusive masking with the effect of PPI_accumulator alone (at P < 0.05 whole-brain corrected; see above). Multiple comparison correction (P < 0.05) for the masked analysis was achieved by applying a cluster size criterion of 43 voxels [at T > 3.65, P < 0.001, df = 17, uncorrected; determined from Monte Carlo simulation (33)]. Finally, a conjunction of the resulting voxels (that show a drift-rate-modulated effect of PPI_accumulator) with those voxels showing significant (P < 0.05 whole-brain corrected; see above) univariate activation for harder relative to easier decisions was derived by a logical “AND” operation. No additional statistical criteria were applied to the result of the AND conjunction, as it is based on two corrected activation maps.