>400 kHz repetition rate wavelength-swept laser and application to high-speed optical frequency domain imaging

Abstract

We demonstrate a high-speed wavelength-swept laser with a tuning range of 104 nm (1228–1332 nm) and a repetition rate of 403 kHz. The design of the laser utilizes a high-finesse polygon-based wavelength-scanning filter and a short-length unidirectional ring resonator. Optical frequency domain imaging of the human skin in vivo is presented using this laser, and the system shows sensitivity of higher than 98 dB with single-side ranging depth of 1.7 mm over 4 dB sensitivity roll-off.

The recent realization of high-sensitivity detection in optical coherence tomography (OCT) with Fourier-domain ranging [1–4] was followed by extensive efforts to develop high-performance OCT systems. Optical frequency domain imaging (OFDI) [4], alternatively referred to as swept-source OCT, is one of the Fourier-domain approaches that uses a wavelength-swept light source and an interferometer with a single-element photodetector. Development of a high-speed wavelength-swept laser with a polygon scanning filter [5,6] has efficiently utilized the high-sensitivity advantage of OFDI to achieve more than 1 order of magnitude improvement in imaging speed relative to conventional OCT [7]. In addition to the investigation of transient dynamic events [8], high-speed imaging has proven to be most clinically relevant by allowing microscopic imaging over large fields of view. For example, the polygon-based laser design has successfully been deployed for comprehensive imaging of entire human coronary arteries in vivo [9] and the entire distal esophagus of patients undergoing endoscopy [10]. Although the frequency-domain approach has already greatly improved the clinical utility of OCT, further improvements in acquisition speed would reduce procedure times and improve image quality through denser spatial sampling. Because the laser power and instantaneous linewidth degrade with increasing repetition rate above approximately 100 kHz, however, the design must be modified to enable high-speed performance. The approach of Telle and Tang [11], wherein the resonator round-trip transit time is synchronous with the repetition of an intracavity filter, has been adapted to achieve high repetition rates in a ~km-length optical fiber ring resonator incorporating a resonant Fabry–Perot filter [12]. This technology has recently achieved repetition rates up to 370 kHz in the laboratory setting [13] and 100 kHz for small-animal imaging in vivo [14]. An alternative approach that can preserve performance under high-speed operation is to reduce the resonator transit time to maintain overlap between the spectrum of the circulating light with the passband of the filter. In this Letter, we present a wavelength-swept laser using a high-finesse polygon scanning filter and short resonator that provides continuous wavelength tuning over 104 nm (1228–1332 nm) at a repetition rate of 403 kHz. Incorporating this laser in an OFDI system, we demonstrate high-speed imaging and a detection sensitivity roll-off of only 4 dB over the ranging depth of 1.7 mm.

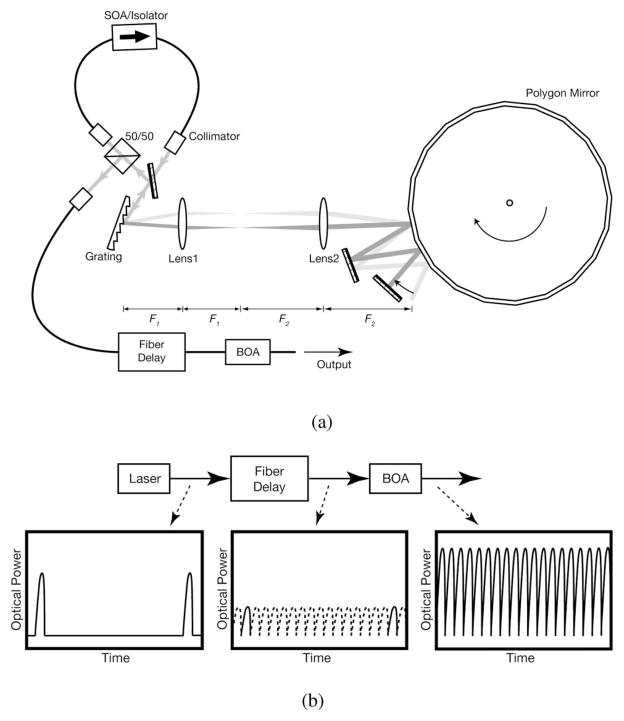
In the previous 115 kHz laser [6], a polygon scanning mirror with a large number of facets was used to increase the tuning repetition rate. Utilization of multiple reflections from the polygon mirror increased the sweep angle of the reflected light, thereby circumventing the reduction of free spectral range (FSR) of the filter that is proportional to the ratio of the sweep angle, θ, to the angle between different wavelengths converging to the polygon, φ: (FSR) ∝ θ/φ. However, increasing the number of polygon facets can limit performance. Consider, for example, the total wavelength sweep range per unit time and unit width of the filter passband, given by [(FSR)/δλ] · N · f_p = F · N · f_p, where δλ and F are bandwidth and finesse of the filter, respectively; N is the number of facet of the polygon; and f_p is the rotational rate of the polygon. As we increase N, the sweep angle, θ, which is proportional to the facet-to-facet angle of the polygon, is decreased correspondingly. Increasing N also reduces the width of each mirror facet requiring a reduction of the beam size to match to the reduced facet width by using a shorter focal length lens for lens 2, F₂, in Fig. 1(a). Because φ ∝ tan⁻¹ (1/F₂) ≈ 1/F₂ ∝ N with fixed filter bandwidth, the FSR turns out to be inversely proportional to N², (FSR) ∝ θ/φ ∝ 1/N², more accurately (FSR) = (2π²pD cos α/W)(1/N²), and so does the finesse of the filter, $F=(\text{FSR})/{(\delta \lambda )}_{3\text{dB}}=({\pi }^3/\sqrt{ln2})(D/\lambda N^2)$, where p is the grating pitch, D is the diameter of the polygon, α is the incident angle of the light on to the grating, and W is the 1/e² width of the Gaussian beam from the fiber-optic collimator. Therefore, the wavelength sweep rate becomes proportional to 1/N.

Fig. 1.

(a) Schematic of the wavelength-swept laser with a high-finesse polygon scanning filter. F₁ = 20 mm, F₂ = 30 mm. (b) An illustration representing the use of an optical delay line and booster amplifier to compensate for the reduced duty cycle of the laser.

Taking this relation into account, we reduced the number of facets of the polygon to N = 28 for high wavelength sweep rate in the new filter design. Similar to the previous polygon filter [6], the light was reflected four times (twice × round trip) from the polygon scanning mirror but without the folded telescope to reduce the path length of the filter, as shown in Fig. 1(a). While the previous laser had operated at 115 kHz tuning repetition rate over the FSR of 80 nm (9200 nm/ms) with N = 128, the FSR of the new filter was increased to 1672 nm with 25 kHz tuning repetition rate (41, 800 nm/ms). The gain level of the intracavity semiconductor optical amplifier (SOA) was adjusted to provide lasing over 104 nm, from 1228 to 1332 nm, yielding a 6.2% duty cycle as depicted in Fig. 1(b). The 15 laser scans are duplicated, sequentially delayed, and then interleaved by the fiber delay line, here a four-stage cascaded Mach–Zehnder interferometer [15], resulting in 16 wavelength sweeps during a single facet-to-facet rotation of the polygon. To support long photon intracavity lifetime by reducing the filter wavelength offset per round trip of the resonator, a set of short focal length lenses with a half-inch diameter was used for the telescope in the polygon filter. The length of the fiber pigtails of the SOA were also minimized to further reduce the resonator length. In this way, the round-trip time of the resonator was reduced to 2.5 ns, corresponding to an air-spaced ring resonator length of 0.76 m, and the filter wavelength shift per round trip was reduced to 52% of the 0.19 nm filter bandwidth. Unidirectional oscillation was achieved by using an isolator integrated inside the SOA butterfly package and by vertically displacing the input and output light of the filter. Before entering into the OFDI system, the 400 kHz (25 kHz × 16) sweep repetition rate output of the fiber delay line was amplified to 32 mW by a booster optical amplifier (BOA).

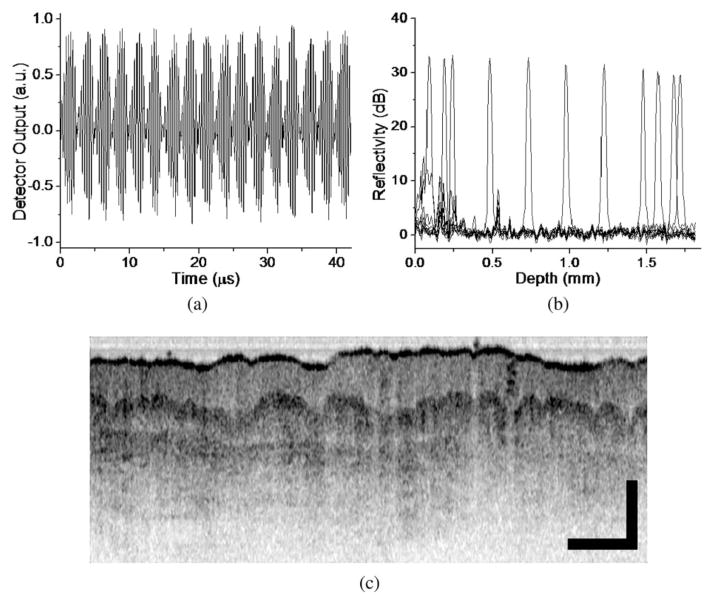
Figure 2(a) shows the output of a balanced receiver with a single reflection in the sample arm. A series of point-spread functions (PSFs) were measured with a partial reflector (−65 dB neutral-density filters and a gold-coated mirror) at various depth positions [Fig. 2(b)]. At the maximum speed of 403 kHz, the sensitivity of the system approximately 100 μm from the path-matched depth was measured to be 98 dB. The receiver output was digitized at a sampling rate of 180 MS/s (Signatec PDA16), limiting the axial imaging range to 1.8 mm at 403 kHz. The sensitivity of the OFDI system dropped by 4 dB at a path imbalance (free space) of 1.7 mm relative to that at the nearly path-matched delay. The relative intensity noise (RIN) of the laser was approximately −100 dB/Hz near zero frequency, and the dynamic range of the system was larger than 58 dB over a 1.7 mm imaging range. Figure 2(c) shows an exemplary OFDI image of human skin in vivo at the maximum A-line rate. The optical power on the sample was measured to be 18 mW, and the axial resolution was ~7.2 μm in the tissue.

Fig. 2.

(a) Balanced interference signal of an OFDI system using the high-speed laser. (b) Measured PSFs across depth. (c) OFDI image of human skin acquired in vivo at 403 kHz. Scale bar: 500 μm.

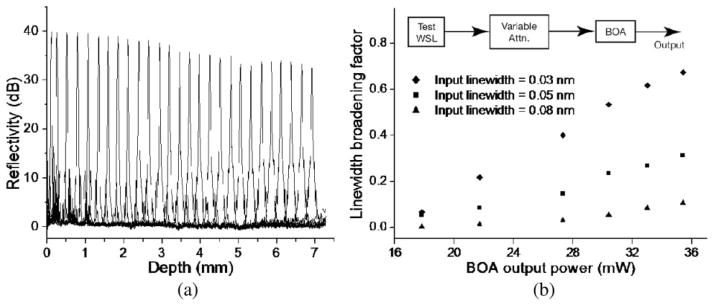
The high-finesse wavelength-scanning filter can also be configured to provide OFDI imaging with long ranging depth. With the same value of filter finesse, which is a function of polygon diameter and number of facets, we narrowed down the filter bandwidth to 0.055 nm and the FSR was reduced to 484 nm. Four wavelength sweeps with a tuning range of 120 nm were obtained in a single facet-to-facet rotation of the polygon, resulting in 101 kHz tuning repetition rate. Sensitivity of the system measured near the path-matched depth was 105 dB, and decreased to 99 dB at a path-imbalance of 6 mm, yielding 12 mm of ranging depth after removal of depth degeneracy, as shown in Fig. 3(a).

Fig. 3.

(a) Measured PSFs across depth with the laser configured for long-ranging depth operation. (b) Measured relative linewidth broadening, (δλ_out − δλ_in)/δλ_in, for three input line-widths, δλ_in. WSL, wavelength-swept laser.

The filter bandwidth can be further narrowed for ranging depth in excess of 12 mm at the expense of FSR. However, this narrow filter bandwidth is not efficiently translated to a narrow instantaneous laser linewidth owing to nonlinear linewidth broadening in the BOA [16]. To investigate this linewidth broadening effect, we built a separate wavelength-swept laser as an input light source to the BOA, as shown in Fig. 3(b). With a fixed instantaneous linewidth at the input, we measured the power and the instantaneous linewidth of the BOA output while changing the input power from 10 to 100 μW with a variable attenuator at the input port. This measurement was repeated across multiple input linewidths. Figure 3(b) shows the measured linewidth broadening of the BOA output relative to the input linewidth, (δλ_out − δλ_in)/δλ_in, as a function of output power and input linewidth. Input light with a 0.08 nm linewidth, which corresponds to 4.5 mm single-sided ranging depth defined by a system sensitivity drop of 6 dB, showed only slight broadening (10.7%) after amplification to 35 mW. However, a smaller input linewidth of 0.03 nm, corresponding to 12.0 mm single-sided ranging depth, was significantly broadened to 0.050 nm (67.2%) when it was amplified to 35 mW. This high relative broadening occurs when the input line-width is comparable to or less than the nonlinear line-width broadening, which is proportional to the light power in the BOA. Conversely, when the input linewidth is significantly larger than the nonlinear broadening of the BOA, the output linewidth is determined primarily by the input linewidth, i.e., the bandwidth of the wavelength-scanning filter. Thus, the nonlinear broadening in the BOA ultimately limits the achievable output line-width regardless of input linewidth. In practice, to obtain sufficient light power for the high-sensitivity OFDI imaging, the output of the wavelength-swept laser should be either amplified by a BOA or taken immediately after amplification in the intracavity SOA, indicating that the nonlinear linewidth broadening limits the achievable ranging depth in these OFDI systems.

In conclusion, we have demonstrated a high-speed wavelength-swept laser by counterintuitively decreasing rather than increasing the facet count on the polygon scanning filter and employing a delay-line stage. A wavelength sweep rate of 41, 800 nm/ms was achieved, and imaging of human skin at an A-line rate of 403 kHz was presented. Alternative implementations of the high-finesse wavelength-scanning filter for long ranging depth OFDI imaging were also demonstrated along with an analysis of the ultimate limitation in ranging depth due to nonlinear effects in the SOA.