Mutational analysis of kinetic partitioning in protein folding and protein–DNA binding

Abstract

Kinetic partitioning between competing routes is present in many biological processes. Here, we propose a methodology to characterize kinetic partitioning through site-directed mutagenesis and apply it to parallel routes for unfolding of the TI I27 protein and for recognition of its target DNA by the human papillomavirus E2 protein. The balance between the two competing reaction routes can be quantified by the partitioning constant K_p. K_p is easily modulated by point mutations, opening the way for the rational design of kinetic partitioning. Conserved wild-type residues strongly favor one of the two competing reactions, suggesting that in these systems there is an evolutionary pressure to shift partitioning towards a certain route. The mutations with the largest effects on partitioning cluster together in space, defining the protein regions most relevant for the modulation of partitioning. Such regions are neither fully coincident with nor strictly segregated from the regions that are important from each competing reaction. We dissected the mutational effects on partitioning into the contributions from each competing route using a new parameter called pi-value. The results suggest how the design of kinetic partitioning may be approached in each case.

Introduction

Kinetic partitioning takes place when a system of reacting molecules can take two or more competing routes (Hardy and Randall, 1991; Sinclair et al., 1994; Guo and Thirumalai, 1996; Frieden and Clark, 1997; Wildegger and Kiefhaber, 1997; Chiti et al., 2002; Thompson et al., 2002; Wright et al., 2003; Streaker and Beckett, 2006; Peng and Li, 2008). Kinetic partitioning may lead to different end products and biological outputs (Hardy and Randall, 1991; Streaker and Beckett, 2006), as in the competition between folding and misfolding (Sinclair et al., 1994; Chiti et al., 2002), in aminoacyl-tRNA synthesis (de Prat Gay et al., 1993) and in nucleotide incorporation during DNA replication (Fersht and Knill-Jones, 1981; Thompson et al., 2002).

Additionally, kinetic partitioning can take place between parallel fast and slow routes that eventually lead to the same end products, such as for parallel folding routes (Guo and Thirumalai, 1996; Frieden and Clark, 1997; Wildegger and Kiefhaber, 1997; Wright et al., 2003; Peng and Li, 2008) and parallel protein–DNA binding routes (Ferreiro and de Prat Gay, 2003). In these cases, the slower route may slow down the reaction below physiological requirements or lead to the accumulation of potentially deleterious intermediates (Guo and Thirumalai, 1996; Frieden and Clark, 1997).

The molecular basis of kinetic partitioning may be studied using site-directed mutagenesis. For example, the effect of mutations on folding and aggregation was recently studied for the protein AcP (Chiti et al., 2002). Remarkably, mutations in some regions of the domain change the speed of folding but not of aggregation, while mutations in other regions change the speed of aggregation but not of folding. Thus, a given mutation modulates partitioning by changing the speed of only one of the two competing reactions. However, this is not necessarily the case. In other systems, mutations may modulate kinetic partitioning by changing the speed of both reactions. Here, we propose a method to quantify and interpret such effects and apply it to two model protein folding and protein–DNA binding reactions.

Methods

Let us consider two competing kinetic routes A and B, with rate constants k_A and k_B.

(1)

We define the partitioning constant K_p and partitioning free energy ΔG_p:

(2)

ΔG_p takes negative values if route A is favored. The effect of a mutation on kinetic partitioning can be understood as the difference in ΔG_p between the wild type and mutant proteins:

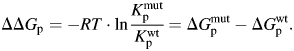(3)

ΔΔG_p takes negative values if the mutation favors route A.

Additionally, substitution of (2) in (3) shows that the effect of a mutation on kinetic partitioning can also be understood as the difference between the effects of the mutation on routes A and B:

(4)

Where ΔΔG_A is the effect of the mutation on route A and ΔΔG_B the effect of the same mutation on route B. In previous work, equation (4) was used to calculate ΔΔG_A from the values measured for ΔΔG_p and ΔΔG_B (Thompson et al., 2002).

Here, we make use of equation (4) to quantify how much a mutation influences partitioning by acting on route A or B. This analysis may be performed in two ways. On one hand, mutations with a large value of ΔΔG_p may be examined individually (de Prat Gay et al., 1993) as in phi-value analysis (Fersht et al., 1992). Additionally, groups of mutations that present a common slope in a plot of −ΔΔG_B versus ΔΔG_p may be interpreted together as in so-called Brønsted plots (Itzhaki et al., 1995). We would like to propose the name of π-value for the slope of such plot, where π stands for partition:

(5)

Results

Kinetic partitioning in protein folding

The 27th immunoglobulin domain of the human cardiac muscle titin (TI I27) unfolds via two parallel kinetic routes (Wright et al., 2003). Route L dominates at low denaturant concentrations, while route H dominates at high denaturant concentrations. The molecular mechanism of these two competing routes was studied using 22 point mutants and kinetic measurements at a wide range of denaturant concentrations (Fowler and Clarke, 2001; Wright et al., 2003). The two rate-limiting transition state ensembles for the two unfolding routes present different structures. The transition state ensemble for route L has a well-structured core formed by long-range interactions, while the transition state ensemble for route H involves more local contacts. It is not straightforward to predict how mutations can affect kinetic partitioning from the description of the two transition state ensembles.

Most of the 22 mutations have strong effects on kinetic partitioning in TI I27 unfolding (Table I). Nineteen mutations increase the partitioning constant at least 2-fold (corresponding to a free energy change of 0.41 kcal/mol) and favor unfolding route H. Mutation V13A changes K_p less than 2-fold and only two mutations, C63A and M67A, decrease K_p 2-fold or more and favor unfolding route L. Thus, wild-type residues strongly favor route L for TI I27 unfolding. Interestingly, mutations leading to the largest effects on partitioning, I23, G32, H56 and F73, cluster together in the TI I27 structure (Fig. 1A). For the remaining mutations, the effect on partitioning correlates with proximity to these four residues. Mutations of residues close to this quadruplet induce larger changes in K_p than mutations of residues far away from it. As summarized in Table III, the residues most important for kinetic partitioning are far apart from the folding nucleus for route H (Wright et al., 2003; Geierhaas et al., 2006), but show a considerable overlap with the folding nucleus for route L (Wright et al., 2003; Geierhaas et al., 2004).

Table I.

Mutational analysis of kinetic partitioning in TI I27 unfolding

TI I27 variant
I2A	−0.78	1.27	0.50
V4A	−1.64	2.92	1.27
L8A	−1.27	2.77	1.49
V13A	−1.89	1.70	−0.19
F21L	−0.75	2.24	1.50
I23A	0.59	1.35	1.94
L25A	−2.35	3.70	1.34
V30A	−0.45	1.40	0.94
G32A	0.07	2.03	2.09
L36A	−1.32	2.64	1.32
L41A	−1.40	2.16	0.76
C47A	−0.69	1.26	0.58
I49V	−0.26	0.69	0.44
H56A	−1.18	3.51	2.33
L58A	−0.39	1.10	0.71
L60A	−1.27	2.34	1.07
C63A	−0.99	0.43	−0.56
M67A	−1.87	1.32	−0.55
V71A	−0.94	2.16	1.22
F73L	−1.15	3.83	2.68
A75G	−0.15	1.33	1.18
A82G	−1.26	2.21	0.95

ΔΔG-values are in kcal/mol and were calculated as follows: , ,

. The rate constants used in the calculations are from (Wright et al., 2003) and (Fowler and Clarke 2001). The average error in the ΔΔG-values is 0.1 kcal/mol.

Fig. 1.

Effect of mutations on kinetic partitioning in TI I27 unfolding. The rate constants used are from (Fowler and Clarke 2001; Wright et al., 2003). (A) Structure representation of the TI I27 domain (Improta et al., 1996), prepared with Pymol (DeLano, W.L. The PyMOL Molecular Graphics System (2002) DeLano Scientific, Palo Alto, CA, USA). (B) Dissection of mutational effects on partitioning. The line is a linear fit to the data. A color version of this figure is available as Supplementary data at PEDS online.

Table III.

Comparison of protein regions important for kinetic partitioning, TI I27 unfolding and E2C–DNA association and dissociation

Kinetic partitioning in TI I27 unfolding: I23, G32, H56, F73 (this work)	Route L folding nucleus: F21, I23, W34, H56, L58, V71, F73 (Wright et al., 2003; Geierhaas et al., 2004)	Route H folding nucleus: L58, L60, C63, M67 (Wright et al., 2003; Geierhaas et al., 2006)
Kinetic partitioning in E2C–DNA association: K297, C298, Y301, R302, K349 (this work)	TSE for association along two-state route: K297, C298, Y301, R302 (Ferreiro et al., 2008)	TSE for association along multistate route: K297, K304, K325 (Sanchez et al., 2010)
Kinetic partitioning in E2C–DNA dissociation: T295, Y301, R302, K349 (this work)	TSE for dissociation along two-state route: K297, C298, Y301, R302 (Ferreiro et al., 2008)	TSE for dissociation along multistate route: T295, K305, K325, K327 (Sanchez et al., 2010)

TSE, transition state ensemble.

Table I shows that the 22 mutations have sizable effects on the speed of both unfolding routes. We have used a plot of versus ΔΔG_p to study the relative importance of both routes in the modulation of kinetic partitioning (Fig. 1B). The 22 variants are well described by a straight line (R-value 0.72, P-value 3 × 10⁻³), allowing us to analyze them as a group in addition to the mutant-by-mutant analysis. The slope, or π_H-value, is 0.86 ± 0.18, indicating that this set of mutations modulates partitioning mainly by speeding up unfolding along route H. It follows from equation (4) that the slope of the correlation between ΔΔG_p and is 0.14, indicating that the acceleration of unfolding along route L is only a minor determinant of kinetic partitioning between the two routes.

Kinetic partitioning in protein–DNA binding

The complex between the homodimeric C-terminal domain of the human papillomavirus type 16 E2 master regulator (E2C) and its target DNA is a well-characterized model for protein–DNA binding (de Prat Gay et al., 2008). The E2C:DNA complex associates and dissociates in vitro via a fast two-state route and a competing slower route with populated intermediates (Ferreiro and de Prat Gay, 2003), leading to kinetic partitioning. We previously studied the development of intermolecular interactions along both routes using 17 mutants (Ferreiro et al., 2008; Sanchez et al., 2010). Here, we will evaluate the effect of the same mutations on kinetic partitioning in E2C–DNA binding. Eight mutants in helix1 of E2C probe specific interactions with DNA bases; 9 mutants in helix1, the β2–β3 loop and the α2–β4 loop probe non-specific interactions with the DNA backbone.

We will first consider kinetic partitioning in E2C–DNA association. The transition state for association along the 2-state route is stabilized by native-like sequence-specific interactions between E2C and the DNA (Ferreiro et al., 2008), while the first transition state of the multistate route is stabilized only by a few non-native interactions (Sanchez et al., 2010). The effects of mutations on the stability of the two transition states relative to the unbound reagents are not correlated (Sanchez et al., 2010), making it difficult to understand a priori how mutations will modulate partitioning.

Figure 2A shows the effect of the 17 mutations on kinetic partitioning in E2C–DNA association. About half of the mutations have sizable effects on partitioning (Table II). Seven mutations increase the partitioning constant at least 2-fold (corresponding to a free energy change of 0.41 kcal/mol) and favor the multistate route. Seven mutations change K_p less than 2-fold and only three (Y301N, K325R and K304A) decrease K_p 2-fold or more and favor the two-state route. Thus, wild-type residues predominantly favor the two-state route for association of the E2C–DNA complex. Figure 2C displays the ΔΔG_p of conservative mutations on the surface of the DNA-bound conformation of the E2C homodimer (Cicero et al., 2006). Mutations to alanine are shown, except for K297R and R302M. Interestingly, mutations of residues K297, C298, Y301, R302 and K349 presenting the strongest effects on partitioning cluster together on the surface of the E2C domain. Other mutations lead to smaller changes in K_p. Table III shows that the set residues most important for kinetic partitioning in E2C–DNA association is similar to the group of residues stabilizing the transition state ensemble for association along the two-state route (Ferreiro et al., 2008), and has only K297 in common with the residues stabilizing the transition state ensemble for the initial association along the multistate route (Sanchez et al., 2010).

Fig. 2.

Effect of mutations on kinetic partitioning in E2C:DNA binding. Left panels: association kinetics. Right panels: dissociation kinetics. The rate constants used are from (Ferreiro et al., 2008; Sanchez et al., 2010). (A and B) Bar plot of all mutants, sorted by type of contact. (C and D) Surface of the DNA-bound conformation of the E2C homodimer (Cicero et al., 2006), prepared with Pymol (DeLano, W.L. The PyMOL Molecular Graphics System (2002) DeLano Scientific, Palo Alto, CA, USA). Residues contacting the DNA bases are underlined. Mutations to alanine are shown, except for K297R and R302M. Uncharacterized residues are in light gray. (E and F) Dissection of mutational effects on partitioning. Lines are linear fits to the data. A color version of this figure is available as Supplementary data at PEDS online.

Table II.

Mutational analysis of kinetic partitioning in E2C–DNA binding

E2C variant
Residues with specific contacts to bases
K297R	1.65	0.64	2.29	−1.66	1.93	0.27
C298A	1.09	−0.53	0.56	−0.08	a	A
C298G	0.90	0.01	0.91	−0.17	a	a
Y301F	−0.01	−0.09	−0.10	−0.24	0.07	−0.18
Y301A	0.85	−0.23	0.62	−0.25	0.84	0.59
Y301N	0.52	−1.04	−0.52	−1.82	−0.94	−2.76
R302M	0.85	−0.36	0.49	−0.46	1.66	1.20
R302Q	1.60	0.09	1.69	0.49	1.05	1.53
Residues with non-specific contacts to the DNA backbone only
T295A	0.01	−0.09	−0.08	1.10	0.73	1.83
K304A	0.42	−1.41	−0.99	−1.42	1.91	0.48
K305A	0.15	−0.27	−0.12	−0.48	0.08	−0.41
V324A	−0.03	0.01	−0.02	0.17	−0.28	−0.11
K325A	0.39	−0.36	0.03	−0.22	−0.12	−0.35
K325R	−0.24	−2.55	−2.79	0.31	−0.14	0.16
K327A	0.54	−0.29	0.25	−0.50	0.00	−0.50
K327R	0.03	0.26	0.29	0.10	0.13	0.22
K349A	0.77	0.26	1.03	−0.55	1.70	1.14

ΔΔG-values are in kcal/mol and were calculated as follows: , , , , , . The rate constants used in the calculations are from (Ferreiro et al., 2008) and (Sanchez et al., 2010). The average error in the determination of the rate constants is 10%, which propagates to an average error of 0.1 kcal/mol in the ΔΔG-values.

^aNot available.

We have used a plot of −ΔΔG_multistate versus ΔΔG_p to study the relative importance of the two-state and the multistate route in the modulation of kinetic partitioning in E2C–DNA association (Fig. 2E). The 17 E2C variants are well described by a straight line (R-value 0.88, P-value 3 × 10⁻³). The slope, or π_multistate-value, is 0.59 ± 0.08, indicating that about half of the increase in originates in an increase in the rate constant for association along the multistate route. It follows from equation (4) that the slope of the correlation between ΔΔG_p and ΔΔG_2state is 0.41, indicating that the same mutations increase to a similar extent by decreasing on average the rate constant for association along the two-state route. We conclude that, on average, our set of mutations favors the multistate route by concurrently speeding up association along the multistate route and slowing down association along the two-state route.

Next, we analyzed kinetic partitioning in dissociation of the E2C:DNA complex using the same set of mutants. The rate-limiting step for dissociation along the two-state route involves disruption of non-specific interactions between E2C and the DNA (Ferreiro et al., 2008), while the rate-limiting step for dissociation along the multistate route involves breaking specific interactions (Sanchez et al., 2010). The effects of mutations on the stability of the two transition states relative to the E2C:DNA complex are not correlated (Sanchez et al., 2010), effectively concealing how these mutations modulate partitioning.

There are data available for dissociation of 15 of the 17 E2C–DNA variant complexes (Table II). The mutational effects on kinetic partitioning in E2C–DNA dissociation are of similar size as the effects in E2C–DNA dissociation (Fig. 2B). Five of these 15 mutants increase the partitioning constant at least 2-fold (corresponding to a free energy change of 0.41 kcal/mol) and favor the multistate route. Five mutations change less than 2-fold and only three (Y301N, K304A and K327A) decrease 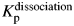2-fold or more and favor the two-state route. As observed for kinetic partitioning during association, wild-type residues predominantly favor the two-state route for dissociation of the E2C:DNA complex.

Figure 2C displays the effect of conservative mutations on the surface of the E2C homodimer (Cicero et al., 2006). Mutations to alanine are shown, except for K297R and R302M. Mutations of residues Y301, R302, K349 and T295 present the largest ΔΔG_p-values. Similar to what can be observed for E2C–DNA association, these four side chains are close to each other on the surface of the E2C domain. Mutations outside of this cluster lead to small changes in K_p. As displayed in Table III, the group of residues determining K_p for E2C–DNA dissociation partially overlaps with both groups of residues stabilizing the transition state ensembles for dissociation along the two-state route (Ferreiro et al., 2008) and the multistate route (Sanchez et al., 2010).

Figure 2F shows a plot of −ΔΔG_multistate versus ΔΔG_p and for dissociation of the E2C:DNA complex. The 16 E2C variants can be fitted to a straight line with a π_multistate value of 0.58 ± 0.16 (R-value 0.69, P-value 0.02). This shows that about half of the increase in by this set of mutants and the concomitant shift towards the multistate route originates in an acceleration of dissociation along the multistate route. According to equation (4), there is also a simultaneous deceleration of similar magnitude for dissociation along the two-state route.

Discussion

Kinetic partitioning between two competing reaction routes is relevant to many biological processes, such as aminoacyl-tRNA synthesis (de Prat Gay et al., 1993) and nucleic acid polymerization (Fersht and Knill-Jones, 1981; Thompson et al., 2002). In this work, we propose a method to characterize the molecular basis of kinetic partitioning using site-directed mutagenesis and free energy relationships. We applied the method to a protein unfolding reaction (Wright et al., 2003) and to association and dissociation of a protein–DNA complex (Ferreiro and de Prat Gay, 2003).

First, we used ΔΔG_p to quantify the effect of mutations on kinetic partitioning in TI I27 unfolding, E2C–DNA association and E2C–DNA dissociation. Most mutations are able to modulate partitioning and change K_p 2-fold or more (corresponding to a free energy change of 0.41 kcal/mol) (Tables I and II). Thus, kinetic partitioning in these systems may in principle be engineered by site-directed mutagenesis. Remarkably, most wild-type residues favor route L for TI I27 unfolding (Fig. 1A) and the two-state route for both association and dissociation of the E2C–DNA complex (Fig. 2A and 2B). This suggests that there is an evolutionary pressure to shift partitioning towards these routes. In support of this hypothesis, the residues with the largest ΔΔG_p-values show a high degree of conservation in both TI I27 (Wright et al., 2003) and E2C (Sanchez et al., 2008). It has been proposed that evolution may have favored route L for TI I27 unfolding in order to prevent misfolding of the domain (Wright et al., 2004). In the case of E2C–DNA recognition, we speculate that avoiding the multistate route for association and dissociation of the complex may prevent the population of non-native complexes (Sanchez et al., 2010) that could interfere with timely papillomavirus replication and early gene transcription (Sanchez et al., 2008).

Displaying the ΔΔG_p-values for conservative mutations on the structures of TI I27 and E2C reveals additional information. Interestingly, the mutations with the largest ΔΔG_p-values cluster together in space for TI I27 unfolding (Fig. 1A), E2C–DNA association (Fig. 2C) and E2C–DNA dissociation (Fig. 2D). Thus, we could detect the protein regions most relevant to partitioning in these three processes. We have also compared the protein regions most important for kinetic partitioning with those most important for the kinetics of protein folding or protein–DNA recognition (Table III). On the whole, we observe that the regions modulating kinetic partitioning are neither fully coincident with nor strictly segregated from the regions that are important from each competing reaction. We conclude that the location of the regions important for partitioning was not obvious from the description of the individual kinetic routes, and that our quantitative definition of kinetic partitioning provides useful information about the system.

Last, we have dissected ΔΔG_p into the contributions from the effect of the mutation on each competing kinetic route, ΔΔG_A and ΔΔG_B. In TI I27 unfolding, the π_H-value close to 1 indicates that most of the changes in partitioning originate in a change in the rate constant for unfolding along route H (Fig. 1B), with the changes in unfolding along route L contributing little to ΔΔG_p. Thus, if we wanted to modulate kinetic partitioning in TI I27 unfolding, it would be sufficient to design point mutations for faster or slower unfolding along route H. The scenario is different for kinetic partitioning in EC2–DNA association, where the changes in the rate constants for association along the two-state and multistate routes both contribute significantly to ΔΔG_p, leading to π_multistate-values close to 0.5 (Fig. 2E). This fact has interesting consequences from a design point of view. For example, we may wish to shift kinetic partitioning in E2C–DNA association towards the multistate route. We could achieve this goal by positive design, i.e. speeding up the preferred, multistate route (Hecht et al., 1990) or by negative design, i.e. slowing down the undesired, two-state route (Hecht et al., 1990). It follows from Fig. 2E and equation (4) that a mutation accelerating E2C–DNA association along the multistate route will also decelerate association along the two-state route. Thus, positive and negative design are intimately coupled in E2C–DNA association. Similar conclusions can be derived for kinetic partitioning in E2C–DNA dissociation from Fig. 2F and equation (4).

In summary, the application of our method for the mutational analysis of kinetic partitioning to two model systems has suggested that partitioning may play a role in evolution of these proteins, helped us identify the protein regions most important in modulating the balance between kinetic routes and suggested how partitioning may be engineered by protein design. We propose that our approach may be useful in other biological reactions where kinetic partitioning is present.

Supplementary data

Supplementary data are available at PEDS online.

Funding

This work was supported by Welcome Trust Grant [GR077355AYA to G.d.P.G.], Agencia Nacional de Promoción Científica y Tecnológica [PICT 2000 01-08959 to G.d.P.G.], Consejo Nacional de Investigaciones Científicas y Técnicas [postdoctoral fellowship to I.E.S.; D.U.F. and G.d.P.G. are Career Investigators].