Whole Muscle Length-Tension Relationships are Accurately Modeled as Scaled Sarcomeres in Rabbit Hindlimb Muscles

Abstract

An a priori model of the whole active muscle length-tension relationship was constructed utilizing only myofilament length and serial sarcomere number for rabbit tibialis anterior (TA), extensor digitorum longus (EDL), and extensor digitorum II (EDII) muscles. Passive tension was modeled with a two-element Hill-type model. Experimental length-tension relations were then measured for each of these muscles and compared to predictions. The model was able to accurately capture the active -tension characteristics of experimentally-measured data for all muscles (ICC=0.88±0.03). Despite their varied architecture, no differences in predicted versus experimental correlations were observed among muscles. In addition, the model demonstrated that excursion, quantified by full-width-at-half-maximum (FWHM) of the active length-tension relationship, scaled linearly (slope=0.68) with normalized muscle fiber length. Experimental and theoretical FWHM values agreed well with an intraclass correlation coefficient of 0.99 (p < 0.001). In contrast to active tension, the passive tension model deviated from experimentally-measured values and thus, was not an accurate predictor of passive tension (ICC=0.70±0.07). These data demonstrate that modeling muscle as a scaled sarcomere provides accurate active functional predictions for rabbit TA, EDL, and EDII muscles and call into question the need for more complex modeling assumptions often proposed.

1. Introduction

Modeling muscle force generation is necessary to understand both muscle function and human movement. Musculoskeletal models vary in their levels of complexity. Early models used simplistic representations of muscle to estimate function (Hill, 1938; Morgan et al., 1982; Kaufman et al., 1989). However, it has been suggested that these simple models are inadequate. Herzog and ter Keurs (1988) suggested that the width of the computationally-derived length-tension relationship of the human rectus femoris was much wider than estimated by a simple scaled sarcomere model. By introducing fiber length variability into their model, Ettema and Huijing (1994) improved and more closely matched modeled and experimentally-measured muscle length-tension relationships. Blemker and Delp (2006) further developed the idea of introducing complexities with a three-dimensional finite element model that incorporated tendon, aponeurosis, and constitutive muscle properties. The authors claim that it was critical to use this model over the lumped parameter model used in Delp et al. (1990) in order for their data to match knee extension moment arm-joint angle data from Buford et al. (1997).

Despite claims that simple models cannot appropriately capture muscle performance, they have been used extensively in the literature (Morgan et al., 1982; Delp et al., 1990; Herzog et al., 1990; Meijer et al., 1998). Huijing et al. (1989) modeled a muscle fiber as a scaled sarcomere and compared the results to experimentally-measured active length-tension data. The authors correctly predicted the characteristics of rat medial gastrocnemius, but were unable to accurately represent the semimembranosus. This discrepancy may stem from the vastly different architecture between the two muscles, but this idea has not been tested experimentally.

Current passive tension models typically rely on a generic curve (Zajac, 1989) that is scaled by a muscle's architectural parameters (Delp et al., 1990; Delp et al., 2007). These models do not incorporate any mechanism of passive load-bearing and do not consider potential load-bearing protein differences amongst muscles (Magid and Law, 1985; Prado et al., 2005).

Thus, most of the predictions of musculoskeletal models are not accompanied by explicit validations. As a result, it is often stated that a more complex model is “better” without providing objective criteria for such a statement. It is surprising that whole muscle isometric mechanical properties have not been validated against structurally-based predictions, given the popularity of the approach and the large number of architectural data sets in the literature. Therefore, the purposes of this study were: (1) to determine whether the experimentally-measured muscle length-tension relationship could be explained by modeling muscles based solely on their architecture and myofilament dimensions, and (2) to determine experimentally whether normalized fiber length scales linearly with muscle excursion as is often claimed.

2. Methods

Theoretical Model

To provide the a priori framework for the muscle length-tension relationship, three assumptions were made: (1) all muscle fibers are functionally in parallel; (2) all fibers and sarcomeres are identical; (3) muscle strain is uniformly distributed among sarcomeres and fibers. Therefore, any change in muscle length corresponds to an equivalent fiber length change. Actin filament length for rabbit striated muscle was based on the literature (1.16 μm, Ringkob et al., 2004) while myosin filament length was assumed to be 1.60 μm, the same length observed for all vertebrates (Walker and Schrodt, 1974). Sarcomere dimensions included Z-disk widths and length of the bare zone of the myosin filament (0.05 μm and 0.20 μm, respectively; Huxley, 1963). Using these assumptions, peak force was predicted at optimal sarcomere length (L_s0=2.50 μm). Relative tension developed at the point of interaction between the myosin filament and the Z-disks (1.70 μm) was determined by the number of cross-bridges that are formed in the zone of single overlap between actin and myosin filaments (67.59%; Stephenson et al., 1989). Reduction in length from this point was assumed to mimic experimental data (Gordon et al., 1966; Elmubarak and Ranatunga, 1984; Roots et al., 2007) and achieve zero force at 1.27 μm. Finally, the zero-force point of the descending limb (4.02 μm) was calculated as the sum of the myosin filament, actin filament, and Z-disk widths. Subsequently, the sarcomere length-tension relationship was scaled to the fiber length-tension relationship by multiplying all sarcomere length values by serial sarcomere number (calculated by dividing literature values for normalized fiber length by optimal sarcomere length). Based on the assumptions above, the width of the fiber length-tension relationship is equal to the width of the muscle length-tension relationship. This allows the fiber length-tension relationship (centered at optimal fiber length) to be aligned with optimal muscle length to yield the muscle length-tension relationship.

Passive tension was modeled using the two-element Hill-type model (Hill, 1938; Zajac, 1989) consisting of a contractile element in parallel with a passive elastic element. When not activated, the muscle is assumed to develop force in the passive element for muscle lengths greater than optimal length (L₀). The passive length-tension relationship is generated using the generic non-dimensional model popularized by Zajac (1989) and scaled by literature values for optimal muscle length for each muscle (Lieber and Blevins, 1989; Takahashi et al., 2007).

Experimental Validation of Theoretical Predictions

The tibialis anterior (TA; n=10), extensor digitorum longus (EDL; n=7), and extensor digitorum II (EDII; n=14) muscles of New Zealand White rabbits (mass=2.6±0.5 kg) were chosen due to their range of normalized fiber lengths (38.08 mm, 15.34 mm, and 10.71 mm, respectively; Lieber and Blevins, 1989; Takahashi et al., 2007). Animal preparation and measurement of isometric contractile properties were performed as previously described (Lieber and Fridén, 1993; Lieber et al., 1991). Briefly, rabbits were anesthetized with 5% isoflurane and a subcutaneous injection of a ketamine-xylazine cocktail (50 and 5 mg/kg body mass, respectively) and maintained on 2% isoflurane anesthesia. Heart rate and oxygen saturation were monitored (VetOx, Heska Co., Fort Collins, CO) throughout the test duration. A mid-line incision was made from the mid-thigh to the ankle. Steinmann pins (3.2 mm) were drilled at the lateral femoral condyle and proximal to the malleoli and secured to a custom-made jig to immobilize the leg. For the TA and EDL, the biceps femoris was split, exposing the peroneal nerve; for the EDII, the tibial nerve was exposed. A cuff electrode was placed around the nerve for direct stimulation (Pulsar 6Bp Stimulator; FHC, Bowdoinham, ME). Suture markers were placed at the distal and proximal muscle-tendon junctions to define muscle length and measure it at the neutral position (knee and ankle joints at 90°). The distal TA, EDL, or EDII tendon was transected, released from the extensor retinaculum (for TA and EDL), and clamped to a servomotor (Cambridge Model 310B; Aurora Scientific, Aurora, ON, Canada) at the muscle-tendon junction and aligned with the force-generating axis of the motor (Davis et al., 2003). Muscle temperature was maintained at 37°C with radiant heat, mineral oil, and a servo-temperature controller (Model 73A; YSI, Yellow Springs, OH).

The length-tension protocol consisted of a series of 100 Hz tetanic contractions (pulse width: 0.3 ms; amplitude: 10 V) over a 640 ms period. Two minute rest intervals were interposed between contractions to minimize fatigue. Measurements began at neutral muscle length (L_n) and ranged from -40%L_fn to 40%L_fn in increments of 5%L_fn (L_fn: normalized fiber length). Length and force were acquired for each contraction using a data acquisition board (610E series; National Instruments, Austin, TX) and a custom-written LabView program (National Instruments) at 4 kHz per channel. Passive tension at each muscle length was obtained by measuring the baseline (preactivation) force. Typical experimental muscle force traces for the TA, EDL, and EDII are shown in Fig. 1

Figure 1.

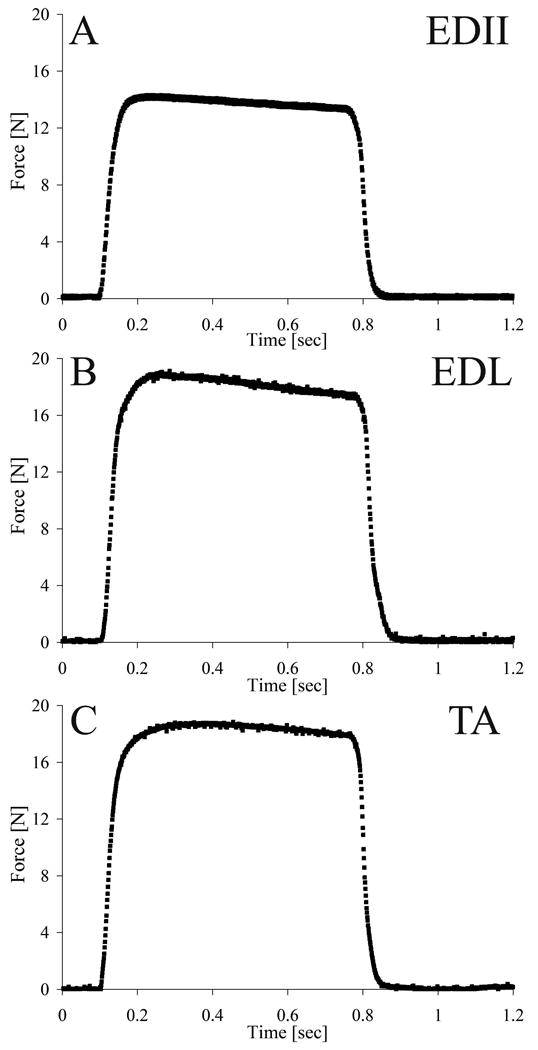
Sample record of muscle force (N) recordings from an isometric contraction at optimal length for (A) EDII, (B), EDL. (C) TA. Average force values on the plateau were used to construct the length-tension relationship.

Upon completion of testing, animals were euthanized with pentobarbital (Euthasol; Virbac AH, Fort Worth, TX), skinned, transected at the sacrum, and fixed for 3-5 days in 10% buffered formalin with hips, knees, and ankles held in 90 degrees of flexion and abduction (chosen arbitrarily) for architectural determination, according to the methods of Sacks and Roy (1982) as modified by Lieber and Blevins (1989). Mean sarcomere length (L_s), muscle length, and fiber length (for the purpose of this study, fiber length refers to the normalized length of the dissected muscle fascicles) were measured. Muscle length and fiber length were normalized to L_s0 to enable comparison among muscles by eliminating variability resulting from differences in joint fixation angle (Sacks and Roy, 1982). Active and passive force were converted to relative tension by normalizing to experimentally-measured peak active tension (P₀) to compare among muscles of different sizes. The relative muscle length-tension relationship was scaled by the experimentally-measured optimal muscle length obtained from architecture to compare experimental measurements with theoretical predictions.

Data Analysis

Piecewise linear regression and intraclass correlation coefficients (ICC) were used to characterize agreement between experimental and theoretical values of relative active and passive tension (SPSS, Chicago, IL). For active tension, ICC was used to quantify the level of experiment-model agreement for both the ascending (lengths less than or equal to L₀) and descending limbs (lengths greater than L₀) of the length-tension relationship. Paired t-tests were used to compare correlations between the two limbs. ANOVA was used to detect differences in correlations among muscles.

Due to assumptions listed for the theoretical model, the relative fiber length-tension relationships for all three muscles were expected to coincide. To test this idea, the relative muscle length-tension relationship was scaled to a fiber length-tension relationship by multiplying by the muscle length/fiber length ratio. Experimental measurements and theoretical predictions were then compared.

Full-width-at-half-maximum (FWHM) was chosen as a measure of excursion. However, data were not captured at exactly 50%P₀ for all trials, thus raw data were fit to a second order polynomial (r²=0.94±0.05) to permit calculation of FWHM. Linear regression was performed to investigate the relationship between FWHM and normalized fiber length. Subsequently, FWHM was normalized to optimal sarcomere length to facilitate comparisons among species as well as validate the regression findings of this study. Normalization was necessary as thin filament length varies among species and alters the width of the length-tension relationship (Walker and Schrodt, 1974). Studies were chosen that did not require extrapolation to the half-maximum point at long or short lengths: this resulted in data that included the rat soleus and medial gastrocnemius (Walmsley and Proske, 1981); cat soleus, extensor digitorum longus, and superficial vastus lateralis (Witzmann et al., 1982); and rabbit digastric (Muhl, 1982; Muhl and Newton, 1982) muscles. Using the methods above, a theoretically derived FWHM and normalized fiber length was predicted for each muscle. The results obtained from the different species were compared to predictions using ICC. Significance was set to p < 0.05 and data are presented as mean±SEM (standard error of the mean).

3. Results

The muscle length-tension relationship had the classic shape of an inverted parabola (Fig. 2). Literature values of normalized fiber length (TA: 38.08 mm, EDL: 15.34 mm, EDII: 10.71 mm; Lieber and Blevins, 1989; Takahashi et al., 2007) agreed well with measured lengths (TA: 38.47±2.94 mm, EDL: 15.34±1.06 mm, EDII: 10.47±1.01 mm) and predicted FWHM matched experimental FWHM (ICC=0.99).

Figure 2.

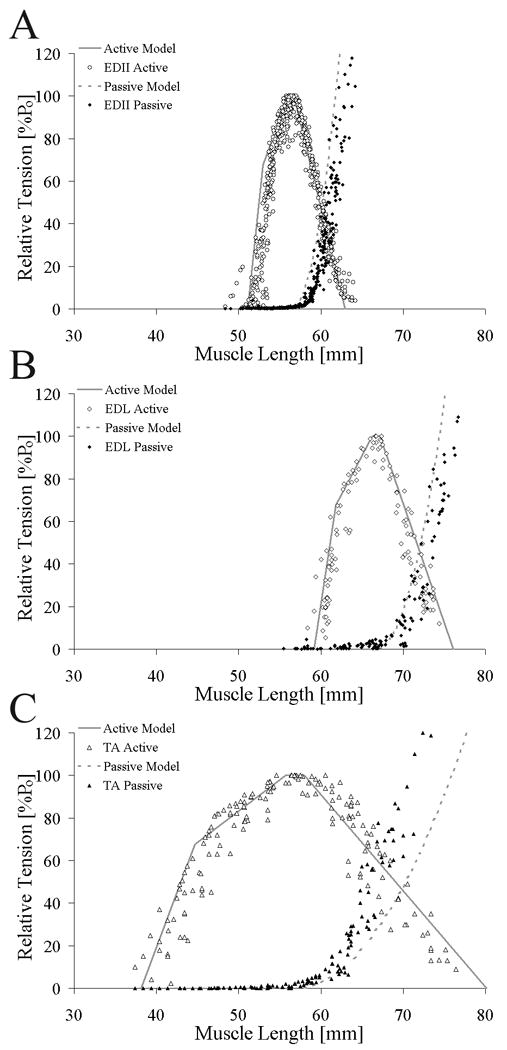
Relationship between active theoretical (solid gray line) and experimental (open symbols) whole muscle length-tension relationship and passive theoretical (dotted gray line) and experimental (filled symbols) whole muscle length-tension relationship for (A) EDII (○), (B) EDL (◊), and (C) TA (△). Theoretical and experimental data were highly correlated for all muscles (TA: r²=0.81, ICC=0.84; EDL: r²=0.90, ICC=0.86; EDII: r²=0.87, ICC=0.89). Relative tension (muscle tension normalized to maximum tension) was plotted on the ordinate to facilitate comparison between muscles.

Experimental isometric length-tension values obtained from TA, EDL, and EDII agreed well with theoretical predictions for active tension (average ICC = 0.88±0.03, p < 0.05, Fig. 2, Table 1) with 88% of the variability in the length-tension relationship explained by the model. Experimental data for the descending limb had consistently higher ICC values compared to the ascending limb (TA: p=0.034; EDL: p=0.033; EDII: p=0.001; Table 1). However, there were no significant differences in the correlation among the muscle's theoretical and experimental length-tension values (ICC: p=0.228; Table 1). When comparing relative fiber length-tension relationships, agreement between active experimental and theoretical values remained and the data sets were not different among muscles (Fig. 3). However, theoretical passive tension did not accurately predict the experimental data (dotted lines, Figs. 2 and 3; ICC=0.70±0.07, Table 1).

Table 1. Summary of active and passive model-experimental correlations.

Muscle	Portion of the Length-Tension Relationship	Intraclass Correlation Coefficient (ICC)
		Mean ± SEM
TAa	Active Ascending Limb	0.81 ± 0.05
	Active Descending Limb	0.92 ± 0.02
	Active Ascending + Descending	0.85 ± 0.04
	Passive Curve	0.60 ± 0.08
EDLb	Active Ascending Limb	0.81 ± 0.05
	Active Descending Limb	0.93 ± 0.03
	Active Ascending + Descending	0.86 ± 0.03
	Passive Curve	0.78 ± 0.10
EDIIc	Active Ascending Limb	0.81 ± 0.04
	Active Descending Limb	0.97 ± 0.01
	Active Ascending + Descending	0.90 ± 0.02
	Passive Curve	0.73 ± 0.03

Values represent mean ± standard error for ^an=10, ^bn=7, ^cn=14 animal subjects

Figure 3.

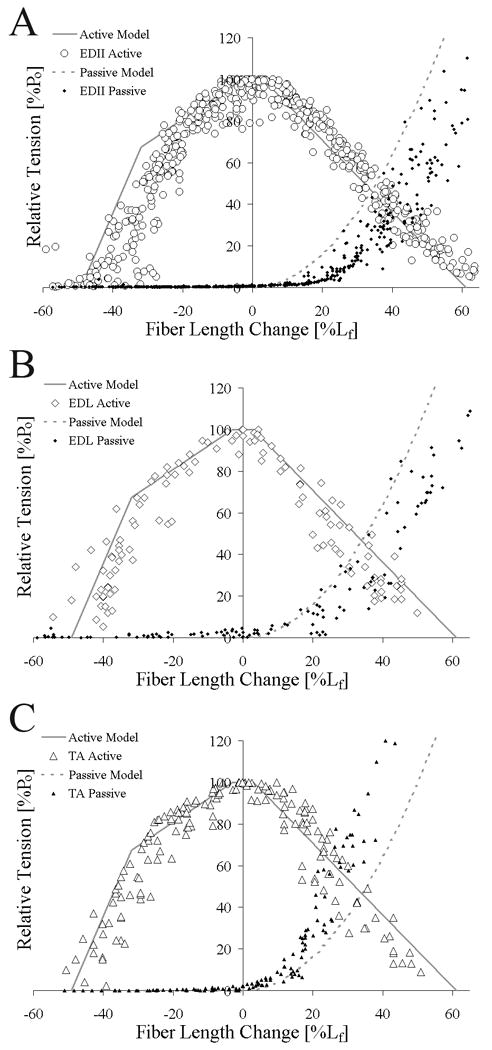
Relationship between active theoretical (solid gray line) and experimental (open symbols) relative fiber length-tension relationship and passive theoretical (dotted gray line) and experimental (filled symbols) relative fiber length-tension relationship for (A) EDII (○), (B) EDL (◊), (C) and TA (△). Theoretical and experimental data were highly correlated for all muscles and muscles were not significantly different from each other. Relative tension (muscle tension normalized to maximum tension) is plotted on the ordinate to facilitate comparison between muscles.

Because the model predicted almost 90% of the variability in the active tension data, it was extended to a linear regression of FWHM and normalized fiber length (Fig. 4A). Theoretical data yielded a slope of 0.68, with similar results for each individual muscle's raw data (TA: slope=0.73, r²=0.75; EDL: slope=0.71, r²=0.63; EDII: slope=0.74, r²=0.67). When normalized FWHM results were compared to literature values, the model explained 88% of the variance in the literature values for all species considered (Fig. 4B). The effect of normalizing FWHM to optimal sarcomere length allowed comparisons among different species (rat, cat, and rabbit) without altering the linear relationship of the original theoretical regression.

Figure 4.

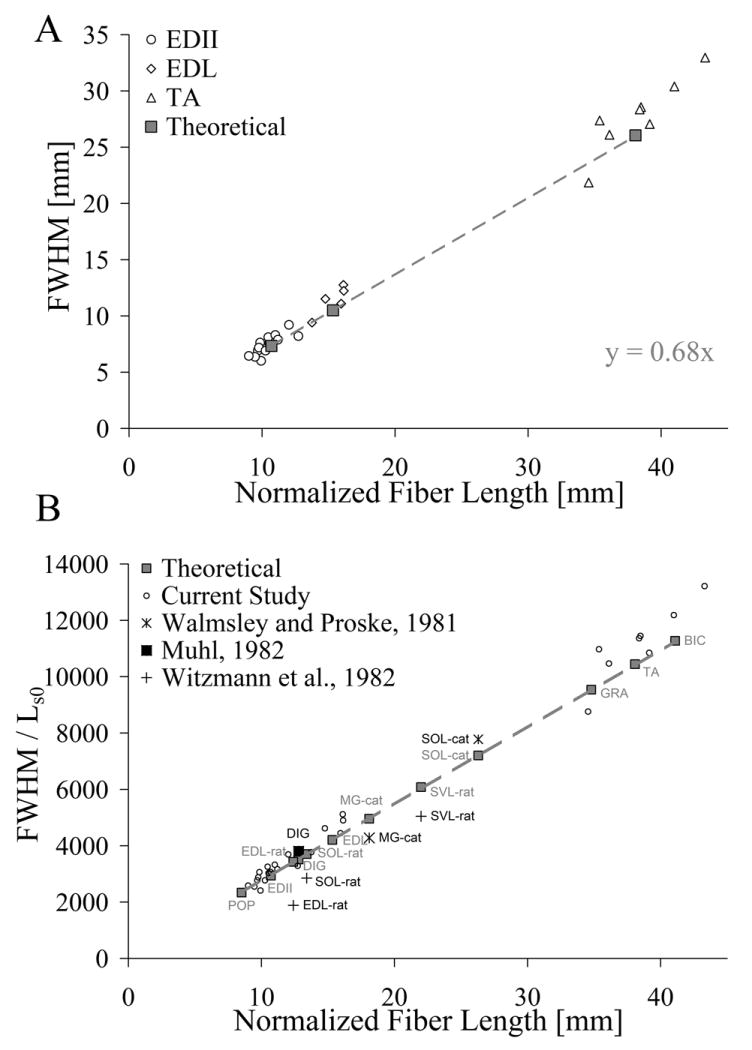
Linear regression of full-width-at-half-maximum (the width of the length-tension relationship at 50% of maximum tension—a measure of excursion) on normalized fiber length with experimental data overlaid. (A) Experimental data (open symbols: EDII (○), EDL (◊), and TA (△)) agree well with theoretical predictions (solid gray squares). The theoretical model predicted a linear relation (slope=0.68 mm/mm) between excursion and fiber length suggesting that a 1 mm increase in normalized fiber length extended FWHM by 0.68 mm. (B) Comparison of results with published literature across species. FWHM was normalized to the optimal sarcomere length of the species to facilitate comparisons among species. Data from Walmsley and Proske (+, Cat), Muhl (, rabbit), and Witzmann et al. (, rat) agreed well with the results of this study. Abbreviations: POP: Popliteus; EDII: Extensor Digitorum II; EDL: Extensor Digitorum Longus; DIG: Digastric; SOL: Soleus; MG: Medial Gastrocnemius; SVL: Superficial Vastus Lateralis; GRA: Gracilis; TA: Tibialis Anterior; BIC: Biceps Femoris.

4. Discussion

This study demonstrated that modeling rabbit whole muscle length-tension relationship as a scaled sarcomere explained 88% of the variation in experimentally-measured active tension data for TA, EDL, and EDII. The model succeeded in capturing functional characteristics of the given muscles while requiring only two variables: (1) myofilament length and (2) normalized fiber length (or serial sarcomere number). Previous studies have shown both filament-level (Gokhin et al., 2009) and fiber length (Walmsley and Proske, 1981; Williams and Goldspink, 1976; Bodine et al., 1982) changes are reflected in whole muscle function. Thus, our findings suggest that, to a first approximation, these muscles can be considered to act isometrically as a scaled sarcomere. These results could not be extended accurately to the modeling of passive tension using a simple two-element Hill-type model of skeletal muscle.

Morgan (1985) admits that “it is tempting to model a whole muscle simply as a scaled sarcomere,” but factors such as internal motion, tendon compliance, and sarcomere heterogeneity complicate the situation. Our study, however, suggests that additional complexities would do little to improve the experiment-model correlation since only 12% of the experimental variability is unexplained. This idea is further supported by the work of Sinclair (2001). By examining the effect of modeling fiber length distributions and comparing the results to those experimentally-measured by Huijing et al. (1989), Sinclair found that a homogeneous distribution of fiber lengths better predicted the length-tension properties of muscle at extreme lengths than more heterogeneous distributions. Yet, for the normal operating range of the rat semimembranosus (i.e. closer to optimum length), heterogeneous fiber and sarcomere length distributions provided little benefit beyond that of the scaled sarcomere model. Therefore, under normal conditions, the marginal benefits of added model complexities are low. This is applicable to most muscles since their operational range do not cover the entire length-tension relationship (Burkholder and Lieber, 2001), but more sophisticated models may be needed to examine muscles that operate over a wider range of sarcomere lengths (e.g. human biceps brachii muscle; Ismail and Ranatunga, 1978).

Delp et al. found success in employing the computationally-inexpensive cost of assumptions inherent in the scaled sarcomere (active) and adapted Hill-type (passive) models with the creation of the modeling software packages SIMM (Delp and Loan, 1995) and OpenSim (Delp et al., 2007). Despite optimistic results from both (Higginson et al., 2006; Xiao and Higginson, 2008), the overall accuracy of treating a muscle as a scaled sarcomere has been questioned. Herzog and ter Keurs (1988) found a large discrepancy between the length-tension relationship of the rectus femoris and that of the scaled sarcomere model. This difference may be explained by a lack of direct muscle force and length measurements in their experimental results, joint-dependent neural activation, overestimation of hip or knee moment arms, or underestimation of the series elastic component's stiffness. The theoretical basis of the scaled sarcomere model has been criticized as well (Allinger et al., 1996; Morgan, 1985), but again, in no case has the model been directly compared to experimental data.

The differences in muscle architecture (e.g. L_fn and pennation angle) between the three muscles did not change the level of agreement between experimental and modeled length-tension relationships. In contrast, Huijing et al. (1989) found experiment-model differences for a parallel-fibered muscle (rat semimembranosus; 2°), but not for a pennate muscle (rat medial gastrocnemius; 21°). These authors later concluded that for a parallel-fibered muscle, sarcomere length heterogeneity was, potentially, the main contributor to the width of the length-tension relationship (Willems and Huijing, 1994). This may help explain the experiment-model discrepancy exhibited by the rat semimembranosus. This idea may be further supported by the current study, in which a parallel-fibered muscle (TA: 2.54±0.47°) exhibited low L_s heterogeneity (coefficient of variation: 4.42±0.93%) and strong experiment-model agreement.

The sarcomere length-tension relationship defined by Gordon et al. (1966) was defined by experimentally controlling sarcomere length using a high-speed feedback controller. For a fixed-end contraction, as employed in the current study, the term “isometric” refers to fixed muscle (or fiber) length, not fixed sarcomere length. When single fiber experiments were performed without controlling sarcomere length, the plateau region of the length-tension relationship is often more broad, more curved in shape, and the descending limb extended to longer lengths (ter Keurs et al., 1978; Altringham and Bottinelli, 1985; Granzier and Pollack, 1990). However, these are not universal findings, as several studies of fixed-end contraction have matched the predicted sarcomere length-tension relationhip (Julian and Moss, 1980; Julian and Morgan, 1981).

The large difference in L_fn across muscles facilitated the extension of the active tension model to examine the relationship between excursion and L_fn. The results displayed a clear linear relationship between excursion and L_fn, demonstrating that a 1 mm change in L_fn corresponded to a 0.68 mm change in excursion. When extended to normalized excursion of rat and cat, the regression is not altered—validating the current relationship while suggesting that it may be extrapolated to other species without change. This general finding is reminiscent of the relationship between maximum tetanic tension and physiological cross sectional area that yielded specific tension for mammalian muscle (Powell et al., 1984).

The inability of the passive model to accurately reflect the experimental data stems from a divergence in both (1) the slope and (2) the position of the two curves. The slope of the theoretical model is fixed at a constant relative stiffness (dotted line, Fig. 3) and relies upon architectural properties for passive tension calculation. However, recent work has shown that a main determinant of passive tension is a muscle's protein composition, both myofibrillar and extramyofibrillar, and not muscle architecture (Magid and Law, 1985; Prado et al., 2005). The deviation in position results from the model's assumption that passive tension is first developed at L₀. This is not the case for all muscles. Thus, a more accurate model must incorporate a muscle-specific stiffness that depends on the muscle's protein composition and alters the position in which passive tension is developed.

The current study has several limitations. First, disruption of the myofascial compartment has been reported to result in a decrease in maximal force production and an increase in the length range between optimal muscle length and active slack length—thus lowering the slope of the ascending limb (Huijing and Baan, 2001; Smeulders et al., 2002). The patency of the anterior compartment may have widened the length-tension relationship at the extreme lengths, artificially improving the experiment-model correlations. Second, the data are explained in terms of relative force production, rather than absolute stress. This is consistent with other scaled sarcomere models (Herzog and ter Keurs, 1988; Herzog et al., 1990), in which a predicted model is compared to experimental results. This study does not attempt to correlate the modeled absolute stress with those measured in vivo. Third, real-time changes in sarcomere length were not measured during whole muscle contractions and thus, were not correlated with muscle length. These methods would be difficult to perform but have been executed by Llewellyn et al. (2008).

In addition to the limitations, several cautions regarding the data must be made. First, the muscles chosen in this study do not follow complex three-dimensional trajectories. Thus, the relationships presented in this study may not extend to modeling more architecturally complex muscles such as the rectus femoris or gluteus maximus. Second, maximal activation was used in the current study. It is known that submaximal activation distorts the length-tension relationship (Rack and Westbury, 1969). The purpose of the current study was to investigate a simple theoretical relationship and its ability to recreate a whole muscle's function. Thus, caution must be taken when extrapolating these data for physiological applications and other instances where sub-maximal activation might occur. In other words, the sarcomere length-tension relationship may not approximate the physiological length-tension relationship for everyday muscle function. Third, contraction-induced strain for the distal portion of the current system was less than 2% of muscle length, providing support that peak tension did occur at optimal length. This compliance would only underestimate the active tension by less than 8% across the length-tension relationship, if an offset did occur. Any proximal shortening may further contribute to this underestimation, but was not quantified. Therefore, for physiological muscle contractions, fiber shortening may be more substantial than experienced when clamped at the muscle-tendon junction (Fukunaga et al., 1997; Fukunaga et al., 2001; Maganaris et al., 2006). Finally, it is important to note that this study was performed under isometric conditions. Therefore, extrapolation to dynamic conditions must be made with caution.

In summary, these data demonstrate that, for the rabbit TA, EDL, and EDII muscles, modeling active muscle properties as a scaled sarcomere provide an accurate estimate of the whole muscle length-tension relationship, while a simple model of passive tension is unable to model experimental results. In addition, model and experimental active tension demonstrate that there is a linear relationship between muscle excursion and normalized fiber length and its scaling factor is 0.68 mm excursion per mm of fiber length.