Muscle Contributions to Whole-Body Sagittal Plane Angular Momentum during Walking

Abstract

Walking is a complex dynamic task that requires the regulation of whole-body angular momentum to maintain dynamic balance while performing walking subtasks such as propelling the body forward and accelerating the leg into swing. In human walking, the primary mechanism to regulate angular momentum is muscle force generation. Muscles accelerate body segments and generate ground reaction forces that alter angular momentum about the body’s center-of-mass to restore and maintain dynamic stability. In addition, gravity contributes to whole-body angular momentum through its contribution to the ground reaction forces. The purpose of this study was to generate a muscle-actuated forward dynamics simulation of normal walking to quantify how individual muscles and gravity contribute to whole-body angular momentum in the sagittal plane. In early stance, the uniarticular hip and knee extensors (GMAX, VAS), biarticular hamstrings (HAM) and ankle dorsiflexors (TA) generated backward angular momentum while the ankle plantar flexors (SOL, GAS) generated forward momentum. In late stance, SOL and GAS where the primary contributors and generated angular momentum in opposite directions. SOL generated primarily forward angular momentum while GAS generated backward angular momentum. The difference between muscles was due to their relative contributions to the horizontal and vertical ground reaction forces. Gravity contributed to the body’s angular momentum in early stance and to a lesser extent in late stance, which was counteracted primarily by the plantar flexors. These results may provide insight into balance and movement disorders and provide a basis for developing locomotor therapies that target specific muscle groups.

1. INTRODUCTION

Angular momentum is a physical quantity that governs multi-body dynamic movements. Walking is a complex dynamic task that requires the generation of whole-body angular momentum to maintain dynamic balance while performing a wide range of locomotor subtasks such as providing body support, forward propulsion and accelerating the leg into swing. During normal walking, angular momentum is generated about the body’s center-of-mass by movements of the body segments and the interaction of the feet with the ground that generates an external moment on the body. Previous studies have suggested that angular momentum is highly regulated by the central nervous system during walking (Herr and Popovic, 2008; Popovic et al., 2004a) and that control synergies or primitives may be used to provide this regulation (Popovic et al., 2004b; Robert et al., 2009). Others have suggested that controlling angular momentum may be important in maintaining dynamic balance and preventing falls during walking (Simoneau and Krebs, 2000), sit-to-stand tasks (Reisman et al., 2002; Riley et al., 1997), and recovering from a trip (Pijnappels et al., 2004). The importance of angular momentum in human locomotion has led to the development of momentum-based control algorithms for bipedal robots and humanoids to produce stable well-coordinated movements (e.g., Goswami and Kallem, 2004; Hofmann et al., 2009; Kajita et al., 2003).

In human walking, the primary mechanism to regulate angular momentum is muscle force generation. Muscles accelerate body segments and generate ground reaction forces that alter whole-body angular momentum to restore and maintain dynamic stability. However, no study has quantified which muscles are the primary contributors to whole-body angular momentum. Identifying those muscles responsible for regulating angular momentum has important implications for diagnosis and treatment of balance and movement disorders and the design of effective locomotor therapies that target specific muscle groups. In addition, previous studies have not addressed how gravity contributes to whole-body angular momentum. Although gravity acts through the body’s center-of-mass, gravity also contributes to the ground reaction forces which creates an external moment about the body’s center-of-mass, and therefore may have a significant contribution to the body’s angular momentum. The purpose of this study was to generate a muscle-actuated forward dynamics simulation of normal walking to quantify how individual muscles and gravity contribute to whole-body angular momentum about the medial-lateral axis in the sagittal plane.

2. METHODS

A previously described forward dynamics musculoskeletal model and simulation of sagittal plane walking (Neptune et al., 2009) was developed using SIMM (MusculoGraphics, Inc.) and consisted of rigid segments representing the mass and inertial characteristics of the HAT (head, arms and trunk) and two legs, with each leg consisting of a thigh, shank, patella, rear-foot, mid-foot and toes (Fig. 1). Foot-ground contact was modeled using 30 visco-elastic elements with coulomb friction distributed over the three foot segments. The dynamical equations-of-motion were generated using SD/FAST (PTC, Needham, MA). The model was driven by 25 Hill-type musculotendon actuators per leg that were combined into 13 functional groups based on anatomical classification. The muscle groups were defined as GMED (anterior and posterior portion of gluteus medius), IL (iliacus, psoas), RF (rectus femoris), VAS (3-component vastus), TA (tibialis anterior, peroneus tertius), PER (peroneus longus, peroneus brevis), FLXDG (flexor hallucis longus, flexor digitorum longus), EXTDG (extensor hallucis longus, extensor digitorum longus), SOL (soleus, tibialis posterior), GAS (medial and lateral gastrocnemius), BFsh (biceps femoris short head), HAM (medial hamstrings, biceps femoris long head) and GMAX (gluteus maximus, adductor magnus).

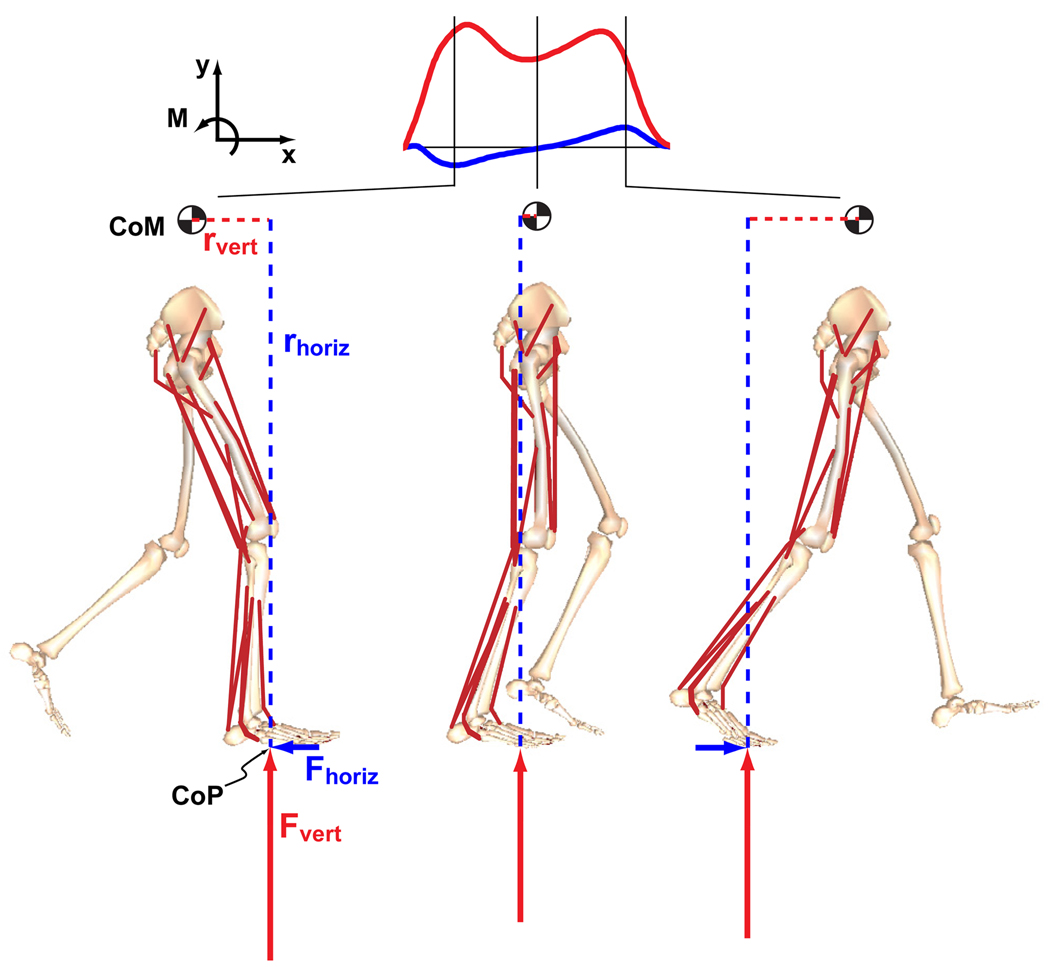
Figure 1.

The musculoskeletal model consisted of rigid segments representing the HAT (head, arms and trunk, represented by the pelvis segment) and two legs, with each leg consisting of a thigh, shank, patella, rear-foot, mid-foot and toes. Muscle and gravity contributions to the time rate of change of whole-body angular momentum in the sagittal plane was calculated from the external moment generated about the body’s center-of-mass by individual muscles and gravity. The horizontal and vertical components of the position vector from the center-of-pressure (CoP) to the center-of-mass (CoM) are defined by r_horiz and r_vert, respectively.

A walking simulation of a complete gait cycle was generated using dynamic optimization that fine-tuned the EMG-based excitation pattern of each muscle group such that the difference between the simulated and experimentally measured walking data (see Experimental Data below) was minimized (Neptune et al., 2009). The excitation magnitudes were allowed to vary between 0 and 1 while timing parameters from EMG data were used to constrain the excitation timing to assure the muscles were generating force at the appropriate time in the gait cycle. For those muscles where EMG data were not available (IL, GMED, BFsh, PER, FLXDG, and EXTDG), previously described EMG-based patterns (Neptune et al., 2009) or block excitation patterns were used.

2.1 Experimental Data

Kinematic, ground reaction force and muscle EMG data previously collected from 10 healthy adults (5 male, 5 female, mean age 27.7 ± 7.7 years) as they walked for 30 seconds at 1.3 m/s on a split-belt instrumented treadmill were used to generate the simulations. For complete details of the experimental procedures, see McGowan et al. (2008). Bipolar surface electrodes were used to record EMG data from the tibialis anterior, soleus, medial gastrocnemius, vastus medialis, rectus femoris, biceps femoris long head and gluteus maximus of the right leg using a telemetered EMG acquisition system (Noraxon, Scottsdale, AZ). Force and EMG data were collected at 2000 Hz using LabView (National Instruments, Austin, TX) software. High speed video (JC Labs, La Honda, CA) was collected at 200 Hz and digitized using Peak Motus software. EMG signals were high-pass filtered (40 Hz), demeaned, rectified and low-pass filtered (3 Hz).

2.2 Muscle and Gravity Contributions to Angular Momentum

To identify how individual muscles and gravity contribute to whole-body angular momentum in the sagittal plane, we quantified their contributions to the time rate of change of whole-body angular momentum over the gait cycle using the following relation:

$$\dot{H}=\overline{r}\times {\overline{F}}_{\mathit{\text{GRF}}}$$ (1)

where Ḣ is the time rate of change of sagittal plane whole body angular momentum, r̄ is the moment arm vector from each foot’s center-of-pressure (determined from the ground contact model) to the body’s center-of-mass (determined using SD/FAST), and F̄_GRF is the vector of each muscle and gravity’s contribution to the ground reaction forces. The r̄ × F̄_GRF term represents the external moment generated about the body’s center-of-mass by individual muscles and gravity (see Fig. 1). The time integral of this term (i.e., the angular impulse) leads to the instantaneous angular momentum of the body.

The contribution of each muscle to the ground reaction force was determined using a ground reaction force decomposition technique (Neptune et al., 2001), which involved a two-step process. First, the total ground reaction force was calculated at time step i from the ground contact elements based upon the current state of the system. Then, at time step i−1, all muscle forces were applied to the system except for the muscle of interest. The equations-of-motion were integrated over the time step from i−1 to i (dt=30 ms) and the ground reaction force was recomputed for the new state of the system. The muscle’s contribution to the ground reaction force was approximated by the difference in these quantities for the original and new system states. The process was repeated for each muscle and gravity.

To provide a comparison with previously published whole-body angular momentum data, Ḣ (i.e., the time rate of change of angular momentum, Eq. 1) was evaluated using the simulation net ground reaction forces and integrated with respect to time. To provide the initial conditions for the integration, the simulation whole-body angular momentum was determined at time t=0 as follows:

$$\overline{H}={\displaystyle \sum _{t=1}^n\left[\left({\overline{r}}_t^{\mathit{\text{COM}}}-{\overline{r}}_{\mathit{\text{body}}}^{\mathit{\text{COM}}}\right)\times m_i\left({\overline{v}}_t^{\mathit{\text{COM}}}-{\overline{v}}_{\mathit{\text{body}}}^{\mathit{\text{COM}}}\right)+I_i{\overline{w}}_i\right]}$$ (2)

where ${\overline{r}}_t^{\mathit{\text{COM}}},{\overline{v}}_t^{\mathit{\text{COM}}}$ and w̄_i are the position, velocity and angular velocity vectors of the i-th segment’s COM in the laboratory coordinate system, ${\overline{r}}_{\mathit{\text{body}}}^{\mathit{\text{COM}}}\text{and}{\overline{\nu }}_{\mathit{\text{body}}}^{\mathit{\text{COM}}}$ are the position and velocity vectors of the body COM in the laboratory coordinate system, m_i and I_i are the mass and moment of inertia of each body segment, and n is the number of body segments.

3. RESULTS

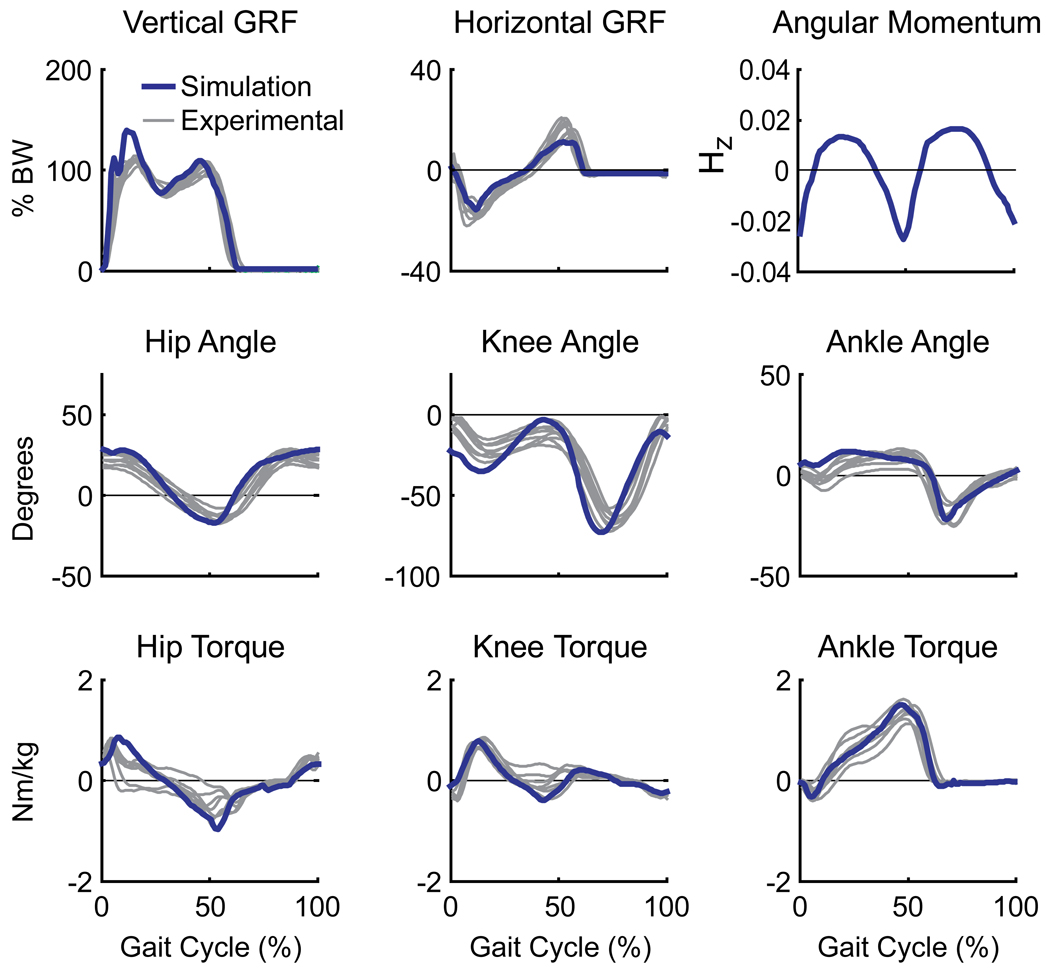
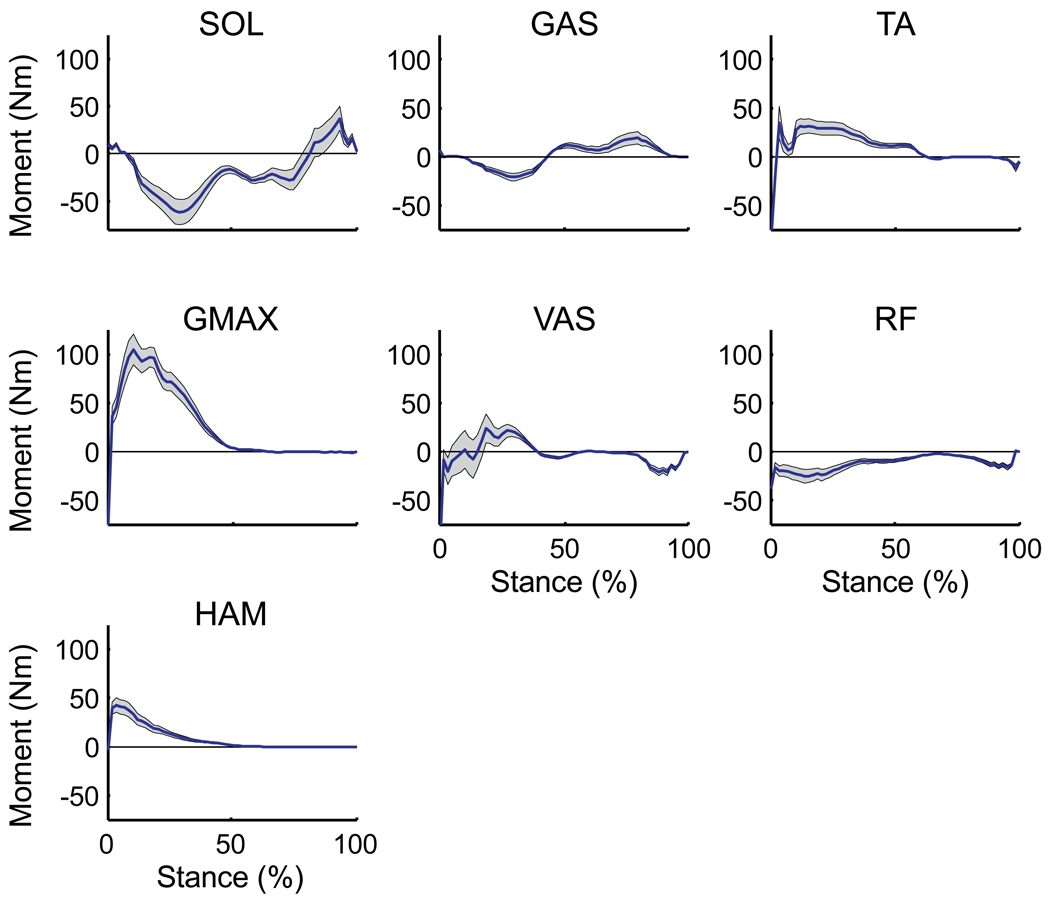
The walking simulation emulated well the group-averaged kinematic and ground reaction force data (Fig. 2). All joint angles and normalized ground reaction forces were nearly always within +/− 2 S.D. of the experimental data with an average error of 2.59 deg and 0.008 BW, respectively. The muscle excitation patterns also compared well with the experimental EMG data (Fig. 3). In addition, the simulation whole-body angular momentum trajectory (Fig. 2) was stereotypical and consistent with previous experimental measurements (e.g., Herr and Popovic, 2008). The close comparison of the kinetic, kinematic, EMG and angular momentum data confirmed the simulation was representative of normal walking mechanics.

Figure 2.

Comparison between the simulation (blue) and experimentally collected human subject (grey) data (McGowan et al., 2008). Grey lines represent individual averages for each subject’s ground reaction forces, joint angles, and intersegmental joint moments. Also shown is the simulation whole-body angular momentum about the medial-lateral axis (Hz) normalized by the product of body mass, height, and walking. Due to the marker set used to collect the experimental data, whole-body angular momentum from the subjects could not be computed.

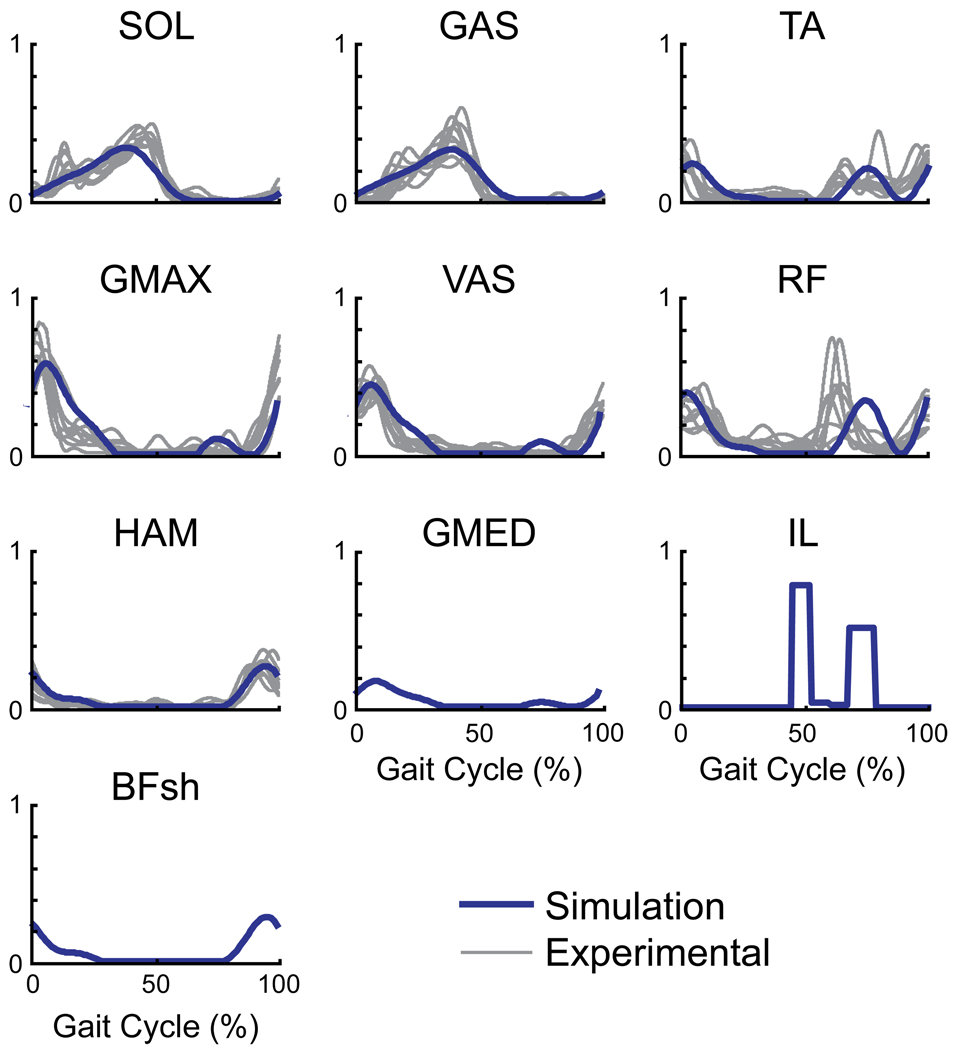
Figure 3.

Comparison of the simulation muscle excitation patterns (blue line) with experimentally collected EMG data (gray lines; McGowan et al., 2008) over the gait cycle. The EMG data represents the average pattern across trials for each subject (n=10). EMG data were not available for IL, GMED and BFsh. The small muscles controlling the foot (PER, FLXDG, and EXTDG) received individual block patterns and are not shown.

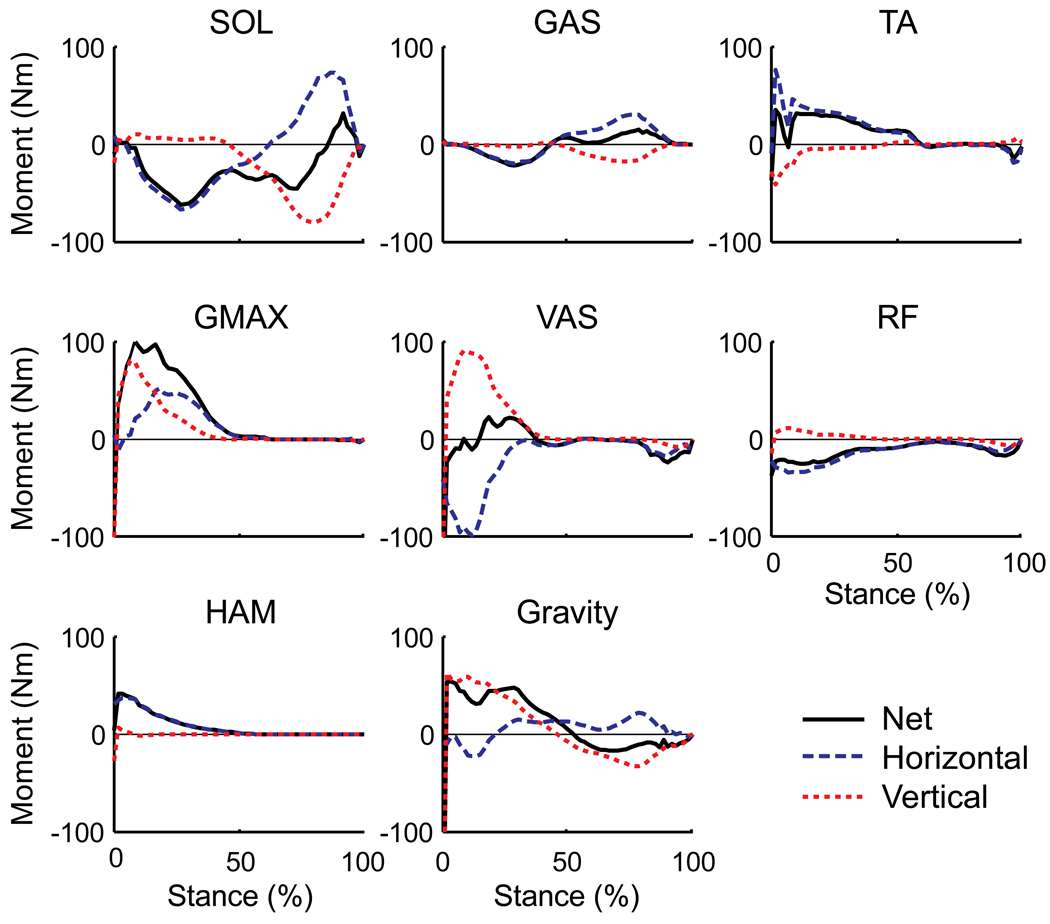
The uniarticular hip and knee extensors (VAS, GMAX), biarticular hamstrings (HAM) and ankle dorsiflexors (TA) in early stance and the ankle plantar flexors (SOL, GAS) in both early and late stance were the primary muscle groups contributing to whole-body angular momentum over the gait cycle (Fig. 4, see Net values). In early stance, VAS, GMAX, HAM and TA generated backward (positive) angular momentum while SOL and GAS generated forward (negative) momentum. In late stance, SOL and GAS generated angular momentum in opposite directions. SOL generated primarily forward angular momentum while GAS generated backward angular momentum (Fig. 4, compare Net values). The difference between muscles was due to their relative contributions to the horizontal and vertical ground reaction forces and the moment arms from the center-of-pressure to the body’s center-of-mass (Fig. 4, compare horizontal and vertical contributions). Gravity contributed primarily to backward angular momentum in early stance and forward angular momentum to a lesser extent in late stance (Fig. 4).

Figure 4.

External sagittal plane muscle moments generated by their contributions to the ground reaction forces over the stance phase. Since the muscle forces and kinematics are symmetrical, the muscle contributions to angular momentum are identical for both legs, and therefore the results from only one leg are shown. Positive values indicate the muscle is generating backward angular momentum, negative values indicate the muscle is generating forward angular momentum. Blue dashed lines are the contributions from the horizontal ground reaction force, red dotted lines are the contributions from the vertical ground reaction force. Solid black lines (Net) are the summed contribution from the horizontal and vertical components. All other muscle contributions were small and not shown.

4. DISCUSSION

In dynamic movement tasks, regulation of whole-body angular momentum is essential to restoring and maintaining dynamic balance and successfully executing locomotor maneuvers. Balance during walking is enhanced by minimizing changes in angular momentum through the generation of ground reaction forces that act through or near the body’s center of mass, thus minimizing the external moments acting on the body (i.e., zero moment control; Herr and Popovic, 2008; Popovic et al., 2004a). Further, acceleration of the body segments through active muscle force generation is an effective control strategy for generating needed angular momentum to enhance bipedal maneuverability and stability following perturbation (Herr and Popovic, 2008; Hofmann et al., 2009). However, no study has analyzed individual muscle contributions to whole-body angular momentum. The simulation results showed the majority of muscle contributions to angular momentum occurred in early stance, with the ankle plantar flexors also contributing in late stance. An interesting finding was that the ankle plantar flexors SOL and GAS had opposite effects on angular momentum in late stance, even though both contribute to the ankle joint moment. The uniarticular SOL generated forward angular momentum while GAS generated backward momentum. This is consistent with previous studies showing SOL and GAS having distinctly different biomechanical functions during walking; both muscles provide body support in late stance while SOL acts to accelerate the trunk forward and GAS acts to accelerate the leg into swing (Neptune et al., 2001).

The plantar flexors were also the primary muscles that counteracted the backward angular momentum generated by gravity. Even though gravity acts through the body’s center-of-mass, it generates angular momentum through its contribution to the ground reaction forces. Gravity generates backward angular momentum in early stance and some forward momentum in late stance (Fig. 4). Both SOL and GAS oppose the backward angular momentum generated by gravity in early stance, while GAS is the primary muscle group that opposes the forward angular momentum generated by gravity in late stance (Fig. 4). These results are consistent with previous studies showing the ankle muscles are used as the primary postural control mechanism in response to sagittal plane balance perturbations (e.g., Runge et al., 1999) and the first muscles activated during a reactive stepping task before the hip and knee muscles are utilized (Thelen et al., 2000). Given the plantar flexors' quick response time and ability to modulate angular momentum throughout stance, they appear to be an ideal mechanism for the nervous system to restore and maintain dynamic stability throughout the gait cycle.

The ankle dorsiflexors (TA) generated significant backward angular momentum in early stance. Despite being relatively weak muscles, they can generate large contributions to the ground reactions forces (Liu et al., 2006) that result in high angular momentum about the body’s center-of-mass. This is consistent with previous work showing older adults with poor balance and a history of falling have significant decreases in dorsiflexor strength and power (Skelton et al., 2002; Whipple et al., 1987). The ability of both TA and GAS to regulate whole-body angular momentum were consistent with the short latency responses of TA and GAS to sudden deceleration and acceleration impulses applied in early stance during treadmill walking (Berger et al., 1984) as well as other studies showing distal muscle weakness causes greater instability for pitch directed perturbations than proximal muscle weakness (Horlings et al., 2009).

With the exception of TA, the simulation results showed that whole-body angular momentum is generated by those muscles that act to extend the ankle (SOL, GAS), knee (VAS) and hip (HAM, GMAX) joints and suggest that dynamic stability may be compromised by muscle weakness or the inability to rapidly generate muscle forces in these groups. Previous studies have used angular momentum to investigate dynamic stability and distinguish between elderly fallers and non-fallers. Simoneau and Krebs (2000) showed that although whole-body angular momentum was similar between fallers and non-fallers, those with a history of falls had lower ankle and knee torque and power profiles during walking that may impair their ability to control angular momentum and lead to locomotor instability. Others have shown ankle and knee muscle strength and leg extension power to be lower in fallers (e.g., Perry et al., 2007) and that whole leg extension strength is the best indicator of the ability of older adults to prevent a fall following a gait perturbation (Pijnappels et al., 2008).

Perturbation studies have suggested that regulating whole-body angular momentum is an important mechanism to prevent a fall following a trip during walking. Pijnappels et al. (2004) showed that the support limb plays two important roles in balance recovery following a mid-swing trip by 1) generating adequate push-off force for body elevation that provides time and clearance for proper positioning of the recovery limb, and 2) restraining forward angular momentum of the body. Further analysis showed the support limb push-off force is achieved by rapid responses in muscle activity and corresponding joint moments from the ankle plantar flexors (SOL, GAS) and biarticular hamstring (HAM) muscles (Pijnappels et al., 2005a), with the response from the plantar flexors being especially high. A rapid response from SOL would be consistent with it providing the needed body elevation while GAS acts to restrain forward angular momentum (Fig. 4). Although HAM was not active beyond midstance in our simulation, a post-hoc sensitivity analysis showed that if HAM was active in late stance, it would act to restrain forward angular momentum. These results concur with the suggestions of others that trunk control is achieved by activity from the hamstring and/or gluteal muscles to create a hip extensor moment (Eng et al., 1994; Grabiner et al., 1996; Schillings et al., 2000). In a subsequent study, Pijnappels et al. (2005b) found that those older adults that fell following a trip had insufficient reductions in whole-body angular momentum due to a lower rate of change in the support limb hip extensor, knee flexor and plantar flexor moments and overall lower peak ankle moment compared to non-fallers. These results are in agreement with our simulation analysis showing GAS, HAM and GMAX are the primary muscle groups that generate backward momentum, which would act to restrain forward momentum following a trip. The recovery limb also plays an important role in responding to a trip by further restraining forward angular momentum as the foot is placed anteriorly to the body center-of-mass (Pijnappels et al., 2004; Pijnappels et al., 2006). Hip and knee extensor moments would be expected to further counteract the body’s forward angular momentum (Grabiner et al., 1993). The present simulation results suggest GMAX, HAM, VAS and TA activity in the recovery limb during subsequent ground contact would most likely be the primary mechanism to restrain forward angular momentum (Fig. 4).

A potential limitation of this study is that we did not include swinging arms in the musculoskeletal model. However, Herr and Popovic (2008) showed using principle component analysis that the arms contribute little to sagittal plane angular momentum. Similarly, others have shown swinging the arms contributes primarily to the body’s vertical angular momentum (e.g., Collins et al., 2009); therefore this model simplification should have a minimal influence on our results. Another potential limitation is that the individual muscle contributions to the time rate of change of angular momentum (Eq. 1) are dependent on the simulated center-of-mass and center-of-pressure positions and each muscle’s contribution to the ground reaction forces, which cannot be experimentally validated. In addition, the simulation emulated group average kinematic and kinetic data rather than subject-specific walking mechanics and at times deviated from the group average. Differences in walking mechanics may influence how muscles regulate angular momentum. For example, differences in body segment kinematics due to experimental or modeling errors may influence muscle contributions to the GRFs, and center-of-mass and center-of-pressure positions. Therefore, to address the influence of possible modeling or experimental errors on the results, we performed a sensitivity analysis on those quantities that contribute to the time rate of change of whole-body angular momentum (Eq. 1). At each point in the gait cycle, we systematically varied the individual components of r̄ and F̄_GRF one at a time ± 20% (for a total of 8 perturbations) and recomputed Ḣ. The sensitivity analysis showed that the results and our conclusions regarding how muscles regulate angular momentum are robust to such large variations in the r̄ × F̄_GRF terms (Fig. 5).

Figure 5.

Sensitivity analysis on those quantities that contribute to the time rate of change of whole-body angular momentum (Eq. 1). At each point in the gait cycle, the individual components of r̄ and F̄_GRF were varied one at a time ± 20% (for a total of 8 perturbations) and Ḣ was recomputed. The dark line is the nominal value and the shaded region indicates the range of values for the 8 perturbations.

The present study represents a first step towards understanding whole-body angular momentum regulation by muscles and gravity during normal walking and highlighted which muscles are the primary contributors to angular momentum over the gait cycle. However, angular momentum was only analyzed about the medial/lateral axis in the sagittal plane. Angular momentum about the anterior/posterior and vertical axes is also significant (e.g., Herr and Popovic, 2008), and therefore identifying which muscles regulate angular momentum about these axes remains an important area for future research. In addition, studies have hypothesized that whole-body angular momentum is highly regulated during normal walking, and therefore could serve as a control strategy for the nervous system and an effective mechanism to conserve metabolic energy (Herr and Popovic, 2008). Indeed, control algorithms have been developed for bipedal robots and humanoids that regulate whole-body angular momentum to produce a dynamically stable gait pattern (e.g., Goswami and Kallem, 2004; Hofmann et al., 2009; Kajita et al., 2003). Future work using muscle-actuated forward dynamics simulations could be used to test this hypothesis.

In summary, the simulation analysis showed that in early stance active muscles and gravity generate backward angular momentum, except the ankle plantar flexors which counteract these contributions and generate forward momentum to maintain dynamic equilibrium. In late stance, SOL and GAS where the primary contributors and generated angular momentum in opposite directions. SOL generated primarily forward angular momentum while GAS generated backward angular momentum, which counteracted the contribution from gravity. The plantar flexors are unique in that they are the only muscle groups that can regulate angular momentum throughout the gait cycle and appear essential to maintaining dynamic balance during walking. Thus, locomotor therapies that specifically target the plantar flexors to increase their muscle force and power output may prove effective in treating balance and movement disorders.