Optimality models in the age of experimental evolution and genomics

J J Bull; I-N Wang

doi:10.1111/j.1420-9101.2010.02054.x

. Author manuscript; available in PMC: 2011 Sep 1.

Published in final edited form as: J Evol Biol. 2010 Jul 14;23(9):1820–1838. doi: 10.1111/j.1420-9101.2010.02054.x

Optimality models in the age of experimental evolution and genomics

J J Bull ^*, I-N Wang ^†

PMCID: PMC3004014 NIHMSID: NIHMS217001 PMID: 20646132

Abstract

Optimality models have been used to predict evolution of many properties of organisms. They typically neglect genetic details, whether by necessity or design. This omission is a common source of criticism, and although this limitation of optimality is widely acknowledged, it has mostly been defended rather than evaluated for its impact. Experimental adaptation of model organisms provides a new arena for testing optimality models and for simultaneously integrating genetics. First, an experimental context with a well-researched organism allows dissection of the evolutionary process to identify causes of model failure – whether the model is wrong about genetics or selection. Second, optimality models provide a meaningful context for the process and mechanics of evolution, and thus may be used to elicit realistic genetic bases of adaptation – an especially useful augmentation to well-researched genetic systems. A few studies of microbes have begun to pioneer this new direction. Incompatibility between the assumed and actual genetics has been demonstrated to be the cause of model failure in some cases. More interestingly, evolution at the phenotypic level has sometimes matched prediction even though the adaptive mutations defy mechanisms established by decades of classic genetic studies. Integration of experimental evolutionary tests with genetics heralds a new wave for optimality models and their extensions that does not merely emphasize the forces driving evolution.

Keywords: experimental evolution, genomics, life history evolution, molecular evolution, theory

Introduction

Optimality models have long been a mainstay of predicting phenotypic evolution (Parker, 1978; Charnov, 1982; Stephens & Krebs, 1986; Parker & Maynard Smith, 1990; Krebs & Davies, 1997; Orzack & Sober, 2001; Perez-Escudero et al., 2009; West, 2009). Their premise is that natural selection of phenotypes ultimately drives the evolution of phenotypes towards states locally maximizing fitness. The main challenge to the naive use of optimality models is that evolutionary change is contingent on underlying genetics, and optimality models typically collapse all genetics into trade-off functions and standard modes of inheritance (e.g. Mendelism). This neglect of genetics has been defended on the grounds that genetic variation is virtually always observed no matter what trait is studied (Williams, 1966). The assumption that underlying genetics do not matter is known as the ‘phenotypic gambit’ (Grafen, 1984) or ‘phenotypic determinism’ (Oxman et al., 2008).

With several disagreements over the legitimacy of optimality models (Lewontin, 1989; Pierce & Ollasen, 1987; Orzack & Sober, 2001; Lewontin, 1978), there has been little consensus resolution (Gardner, 2009). In the spirit of scientific progress, many advocates of optimality argue that the approach should be evaluated based on the utility of its predictions. Failures can then inspire a search for the causes (Parker & Maynard Smith, 1990; West, 2009). Furthermore, some successes are impressive even in the absence of genetic details, and those successes alone might seem to justify use of optimality models. In particular, the theory of sex allocation (sex ratio) has proceeded largely free of genetic information (other than whether the genetic system is Mendelian, haplo-diploid, or sex-linked), and the predictions, based largely on ecological effects and population properties, have met with such remarkable success that the theory has been championed as the most powerful in all of evolutionary biology (Charnov, 1982; Orzack & Sober, 2001). It continues to exhibit deeper layers of success across many problems and systems (an amazing compilation and analysis is by West, 2009). The success of such a theory might justify abandoning or neglecting the pursuit of genetics, but because evolution rests on genetics, it seems that an understanding of genetics can only enhance an understanding and appreciation of optimality. Whether one regards optimality models in the strict sense that their utility and simplicity is lost by even attempting to include genetics, the question here is how much is to be gained by inclusion of genetic details. For example, sex ratio theory has gained interesting insights when genetic and behavioural constraints have been incorporated (Chs. 5.13.2, 11.3 West, 2009).

One of the main obstacles in incorporating genetics into optimality approaches is technical. Optimality offers the only hope of applying evolutionary principles to predict phenotypes in wild populations, and it is in precisely these settings that there is little hope of resolving the genetic bases of phenotypes, even in the age of molecular genomics. However, experimental evolution provides a new arena for optimality models, one that is often easily integrated with genetics. By manipulating the selective environment in which experimental populations are allowed to adapt, optimality models can be tested by direct observation of evolution. When the effort is combined with genomics tools – methods now feasibly applied to many model organisms – the genetic pathways of evolution can be identified. The models can thus become tools for integrating genetics and evolution, revealing the genetic details whose omission has so often been considered the fatal weakness of optimality approaches.

Our article makes no attempt to advocate or criticize optimality approaches. Instead, we describe the uses of and insights gained by experimental evolutionary tests of optimality models for some microbes. There are other issues with the utility of optimality models (e.g. Grafen, 2007), but our emphasis is on genetics: inclusion of genetics enhances the understanding attained with optimality models, and experimental tests of optimality can inform genetics. Our emphasis is further on microbes, especially bacteriophages (‘phages’) because of the accessibility of some phage phenotypes to optimality modeling, of the a priori knowledge of genetics underlying the phenotypes, and the ease of experimental adaptations and of identifying the genes involved in the evolution. The article is divided into three main sections. First, the nature of optimality models is reviewed, how they may fail and the contribution that experimental evolution combined with genomics may provide. Second, selected studies are reviewed. Third, related problems and future directions are proposed.

Characteristics of optimality models

Why optimality

Our interest in optimality models is three-fold. First, optimality models predict qualitative or quantitative outcomes – an endpoint of evolution – which enables easy testing. Second, they are simple models, confined to few phenotypes. Third, they provide ecologically relevant selective contexts for evolution of a trait, providing insight into evolution in nature. To be ecologically relevant, evolution of an optimum requires mutations that do not carry large, negative effects on traits outside the model. These properties of optimality-based evolution may be contrasted with evolution in response to strong, artificial selection, an approach that has a long history in plant and animal breeding: artificial selection may have little relevance to nature, the evolution may be accompanied by large negative effects on unselected traits, and there is no predicted phenotypic endpoint, except at boundaries. Merely asking whether a trait responds to selection seems to provide less evolutionary insight than allowing adaptation to occur in a natural context and observing whether phenotypes evolve as expected. There are likely no absolute distinctions separating optimality approaches from the alternatives, but the point of this article does not require a strict classification of optimality.

Basics

An optimality model is most simply a description of phenotype values that maximize an organism’s fitness in a specific environment (Parker & Maynard Smith, 1990). The environment may be static or dynamic, including the frequencies of different phenotypes (e.g. frequency-dependent selection). The model may also explicitly specify inheritance at some basic level, such as Mendelian diploid or haploid, haplo-diploid, or other, but often inheritance is implicit. Also, fundamental to many optimality models is a trade-off, a constraint that limits fitness maximization in several dimensions simultaneously. Next, we consider some key elements of optimality models.

Phenotype-fitness maps and genotype–phenotype maps

As is well appreciated, any model of evolution by natural selection requires (i) variation, (ii) inheritance of that variation, and (iii) differential reproductive success of the variants (Lewontin, 1970). Thus, to invoke an optimality model as a description of evolution requires all three pieces. Optimality models, and indeed most models of evolution by natural selection, interject another layer: phenotypes. Phenotypes are subsets of an organism, and a focus on phenotypes is an attempt to attribute specific causes of differential reproductive success. The chain of steps in the model thus becomes (i) phenotypic variation, (ii) inheritance of phenotypic variation, and (iii) differential reproductive success according to the phenotypic differences.

The essence of an optimality model is often the third step, attributing reproductive success to phenotypic differences (perhaps in a specific environment). Such a model is necessarily limited to explaining evolution of the phenotypes in question, with no reference to other phenotypes or even overall fitness of the organism. But it is the use of phenotypes that facilitates using a model of evolution with little emphasis on inheritance.

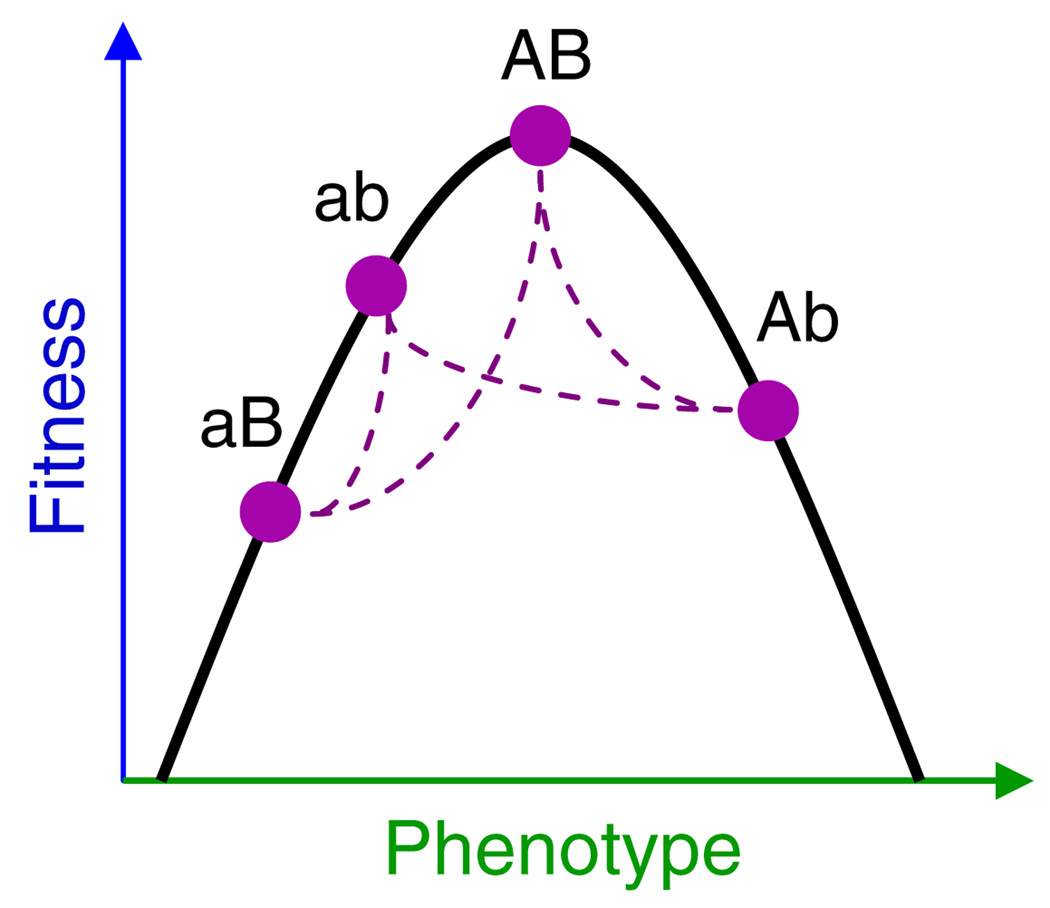
One of our goals is to consider the importance of step (ii), genetics, in affecting evolution of optimality. No one disputes that inheritance is needed, but the question is whether specific genetic details of each system impact the phenotypic outcome of evolution in a meaningful way, or instead whether arbitrary genetic variation is so ubiquitous that evolution will commonly obey natural selection of phenotypes (e.g. Williams, 1966). To facilitate the following presentation, we will refer to the relationship between fitness and phenotype in an optimality model as the phenotype-fitness map and to the relationship between genotype and phenotype as the genotype–phenotype map (Fig. 1). The partitioning of a model into these two components facilitates distinguishing the causes of model imperfection and thus the way to improve the model.

Fig. 1 — A visualization of the relationship between the genotype–phenotype map and phenotype-fitness map. The phenotype-fitness map is shown as a black parabola. The genotype–phenotype map is shown as four haploid genotypes situated at their respective positions in phenotype and fitness space. The dashed curves connect genotypes differing by a single mutational step, so evolution by single steps would have to follow those lines. A genetic constraint is evident in that a large population starting with genotype ab could not evolve to AB by single, adaptive mutational steps, even though AB has higher fitness than ab. Furthermore, if these were the only alleles available, the genotypes only sparsely cover the phenotype space. Figure developed and provided by Ben Kerr.

The phenotype-fitness map specifies how an individual’s fitness depends on its phenotypic values and represents step (iii) in the Lewontin model mentioned earlier. The ‘map’ is typically limited to few phenotypes – perhaps one – the simplest set needed to address the problem. The map is merely the fitness of an individual based on its values for each phenotype in the model. The neglect of other phenotypes does not imply that the phenotypes could exist outside the context of the organism, only that those phenotypes can evolve independently of others.

As noted earlier, a model of evolution by natural selection must also specify the inheritance of variation, step (ii), the genotype–phenotype map. The genotype–phenotype map describes what variation is allowed and how it is transmitted. In optimality models, many properties of the genotype–phenotype map are often implicit and lacking details, for example that every allowable phenotype is encoded by its own genotype and is transmitted asexually (Grafen, 1984; Parker & Maynard Smith, 1990). For other problems (e.g. sex ratio), the genotype–phenotype map includes biparental reproduction and modes of inheritance (Mendelian, sex-linked, etc.). Genetic details invariably omitted from optimality models are those likely to be idiosyncratic and specific within a species, such as pleiotropy, epistasis, mutation effect sizes and deviations from constraints, mutation rates and interaction with phenotypes outside the model. Inclusion of such detail may be considered to violate the very essence of optimality, but again, our purpose here is to ask what could be gained by including such detail, or conversely, what understanding of evolution is lost by excluding the detail.

Trade-offs and other constraints

Key to most optimality problems is that selection favours an intermediate phenotype that lies between the extremes that can be attained. Optimum intermediacy usually depends on a trade-off, a constraint in which increasing fitness through one dimension reduces fitness through another. High overall fitness is attained as a compromise between the conflicting gains and losses. Trade-offs are usually attributed to obvious or presumed functional constraints that absolutely prevent some phenotype combinations, such as those dictated by physical laws. For example, a species cannot achieve both a short generation time and large body size if growth takes time, or an offspring can only be male or female. Whether a trade-off is invoked in the genotype–phenotype map or the phenotype-fitness map depends on the model, as will be illustrated later.

Testing optimality models

How an optimality model may fail

Although optimality models have sometimes been used in an extreme manner to test whether organisms are maximally adapted (the ‘extreme’ adaptationism category of Gardner, 2009), they are now more commonly used to understand how traits may be influenced by natural selection (‘weak’ adaptationism, Gardner, 2009). Within this realm, there are two levels of optimality models, general and specific, and the goals – as well as the criteria for failure – differ between them (Parker & Maynard Smith, 1990). General models are intended to capture broad features of evolution, not to be parameterized with data nor fit quantitatively. Specific models are meant to predict quantitative outcomes. The most obvious approach in testing an optimality model is to compare predicted phenotypic values to the observed ones. Strong failure is indicated when the two differ qualitatively, and this is the only type of test that may be applied to general models. Quantitative differences represent failure of specific models.

However, an exception need be made for experimental evolutionary tests of specific models. Whereas natural populations can be expected to have attained quantitative optimality, experimental populations cannot. Experimental evolution is short term and often will not be conducted long enough to reach evolutionary equilibrium. As it is well appreciated that, even under ideal conditions, a population starting away from an optimum approaches the optimum in a series of steps – an adaptive walk (Fisher, 1930; Orr, 2005) – what can be evaluated is whether the initial trajectory moves in the predicted direction. A partial trajectory can be informative and can potentially refute evolution towards a predicted optimum, although a short-term trajectory can also be misleading (cf. Küummerlie et al., 2009). Furthermore, if multiple steps are observed, each of these can be evaluated independently of the others (e.g. for sex ratio Carvalho et al., 1998; Basolo, 1994).

The failure of an optimality prediction may have two general causes. Foremost, the phenotype-fitness map may be wrong. This failure means that the understanding of natural selection of phenotypes is wrong – that the fitness of an organism whose phenotype values are known does not match what the map indicates its fitness should be. Such misunderstanding may be obvious and trivial in some cases but subtle in others: the model may incorporate only some of a phenotype’s effects on fitness, or the model may omit some relevant phenotypes altogether. A case in point is the evolution of virulence caused to the host by infection of parasite. The phenotype-fitness map in optimal virulence models is often limited to a constant host death rate and constant parasite transmission rate as the only phenotypes (Bull, 1994; Ewald, 1994; Lipsitch & Nowak, 1995; Frank, 1996; Lipsitch & Moxon, 1997). The simple extension to allow those two rates to vary during the course of infection has obvious relevance to parasite fitness and especially to the evolution of virulence (e.g. Levin et al., 1996; Day, 2001; Ebert & Bull, 2003) quite aside from whether genetic constraints exist. Likewise, new sex ratio models have found significant improvements over old ones when incorporating limits on the information available to the individuals controlling sex ratio (Boomsma et al., 2003; Shuker & West, 2004).

Even when the phenotype-fitness map is largely correct, the genotype–phenotype map may be wrong. Genetic failures can be because of pleiotropy, a limited spectrum of mutations, or incorrect assignment of a trade-off (e.g. West & Buckling, 2003). A property of the genotype–phenotype map that may facilitate attainment of optimality is modularity – a gene contributes to one phenotype rather than to several phenotypes. Modularity should reduce pleiotropy and allow a finite set of mutations to more densely map onto the phenotype-fitness map.

Experimental evolution

In its most basic form, an experimental evolution protocol is the confinement of a reproducing population to a controlled environment, lasting potentially thousands of generations (Dykhuizen, 1983; Travisano & Lenski, 1996; Adams, 2004). It affords measurement of the organisms throughout the study, and when multiple treatments are used for replicate populations, the effect of the treatment variable can be observed directly. Selection in an evolution experiment is often intrinsic, merely allowing the fastest replicator to prevail under the conditions imposed. In the test of an optimality model, for example, organisms would be allowed to reproduce as they may, the experimenter not making decisions about who breeds. This latter protocol is intended to mimic natural selection. For some purposes, artificial selection protocols may also be included in the realm of experimental evolution. Trait values are artificially selected (sometimes referred to as screening), in which only those individuals whose characteristics meet a specific criterion are allowed to breed; this approach has often been applied in quantitative genetics when attempting to improve the marketability of a crop or livestock (Falconer, 1981).

Mutation introductions versus de novo evolution

Phenotypic progress in experimentally evolved populations requires genetic variation. The variation may be present initially, but if the population is started from an isolate, the relevant variation will be low in the founding population, and considerable time may be required for new mutations to arise and reach high enough frequencies for them to affect the population mean. A common short cut is to introduce known mutations and observe the short-term change. If the initial mutation frequency is as high as 0.1, the evolutionary progress will be greatly expedited, in contrast to a starting frequency of 10⁻⁵, for example (Crow & Kimura, 1970). Furthermore, if the frequency of the mutation can be monitored directly, the direction of selection can be observed even if change in the population mean phenotype is not measurable. Pairwise competition experiments (of alternative mutants) have often been used to detect selection of phenotypes because of the sensitivity they afford.

The main drawback of mutation-introduction experiments is that the introduced mutation(s) may not represent the type of variation that would be most strongly favoured in a pool of naturally arising mutations. Mutation-introduction experiments thus illustrate a possible direction of evolution – how evolution can happen – not one that will necessarily happen often or one that necessarily leads to highest fitness. Furthermore, a short-term experiment may not provide the full picture of selection, because the direction of selection may depend on the frequency of the mutant – the mutant may invade when rare but be selected against when common (frequency-dependent selection, Paquin & Adams, 1983; Kerr et al., 2002).

Tests of optimality are enhanced by experimental evolution and genomics

As anticipated earlier, a major benefit of using experimental evolution to test an optimality model is that it allows dissection of the evolutionary process. There are two main ramifications.

Experimental evolution facilitates identifying and partitioning the causes of model failure

The (partial) failure of an optimality prediction applied to a natural population will often pose a dilemma as to whether the cause is a bad phenotype-fitness map or a bad genotype–phenotype map. One benefit of many experimental population studies is that the fitness-phenotype map may be tested independently of the genotype–phenotype map. For example, if a model of a selfing plant assumes a particular fitness effect of leaf area or stem height, seed production (≈ fitness) can be measured for genotypes differing in leaf area (stem height) and compared to the fitness assumed by the map. With microbes in experimental environments, mutants with known phenotypic values can be grown to measure the short-term dynamics, from which fitness can be inferred. If the phenotype-fitness map is correct, population dynamics in the experimental conditions should be correctly predicted. Performing such a test requires that the values of the organism be known for all phenotypes of the phenotype-fitness map and requires some measure of fitness.

The separation of the two mappings means that, in failures of optimality predictions, experimental adaptations can directly expose the cause of failure. If the phenotype-fitness map has been verified, model failure must then lie in the genotype–phenotype map. Conversely, failure of the phenotype-fitness map identifies it as a source of model failure. Understanding the causes of model failure has obvious relevance to model improvement. If the failure lies in the phenotype-fitness map, model improvement may require a simple inclusion of another phenotype. A failure in the genotype–phenotype map of one species may reveal genetic mechanisms and principles that apply to other cases.

Experimental evolution allows integrating optimality tests with genetics

Tests of optimality models can be exploited to discover novel genetic bases of phenotypic variation and to test prior knowledge of the genetic evolution map; this point is one main emphasis of our review. The genetic bases of phenotype evolution can be studied after the adaptation, and the observed genetic changes and their phenotypic effects compared to any a priori knowledge of the genetics of the optimality phenotypes. Regardless of whether the model’s predicted phenotypic evolution succeeds or fails, the observed genotype–phenotype map may be compared with the predicted map to learn whether phenotypic variation selected in a natural context follows the genetic paths predicted from other genetics studies. The approaches of classical genetics often used experimental extremes to uncover effects (e.g. lethal rescue), so attempts to use that knowledge in predicting the genetic bases of evolution towards an optimum may fail because the relevant, small-effect mutations have been systematically missed by the usual methods of genetic dissection. In this review, it will become evident that experimental adaptations of model organisms with a solid basis for predicting the genetic basis of optimality evolution often fail profoundly in matching expectations at the genetic level.

Some model organisms are more amenable to genetic analysis than others. Whereas it is the case that genome sequences can now be obtained easily for many organisms, there are far fewer organisms with a good background for interpreting the genetic basis of phenotypic variation. Our review is limited to phages and bacteria, largely because they have a long history of genetic analysis and are easily manipulated in experimental evolution. We also note that incorporation of genetics into optimality models is not limited to experimental evolution. For example, a recent study measured the mutational input to sex ratio for comparison to levels of genetic variation in natural populations (Pannebakker et al., 2008).

Optimality studies using microbes

We describe three sets of studies in detail and two others briefly, partitioned according to organism – bacteriophages or bacteria – and problems addressed. The first two problems address the evolution of phage phenotypes, host range (adsorption rates), and lysis time. Both problems allow a clear separation of genotype–phenotype map and phenotype-fitness map, and both have simple, a priori genetic bases for the evolution. Thus, the bases of model failure are easily exposed. The third topic is optimal enzyme levels in a bacterium. It reveals that trade-off functions can be derived from physiological manipulations, how elements within a system of complex interactions can be studied in isolation (levels of a single enzyme in global metabolism) and that the genetic bases of evolution to a predicted optimum can defy well-established mechanisms of a classic genetic system.

Bacteriophages: the basic phenotype-fitness map has three phenotypes

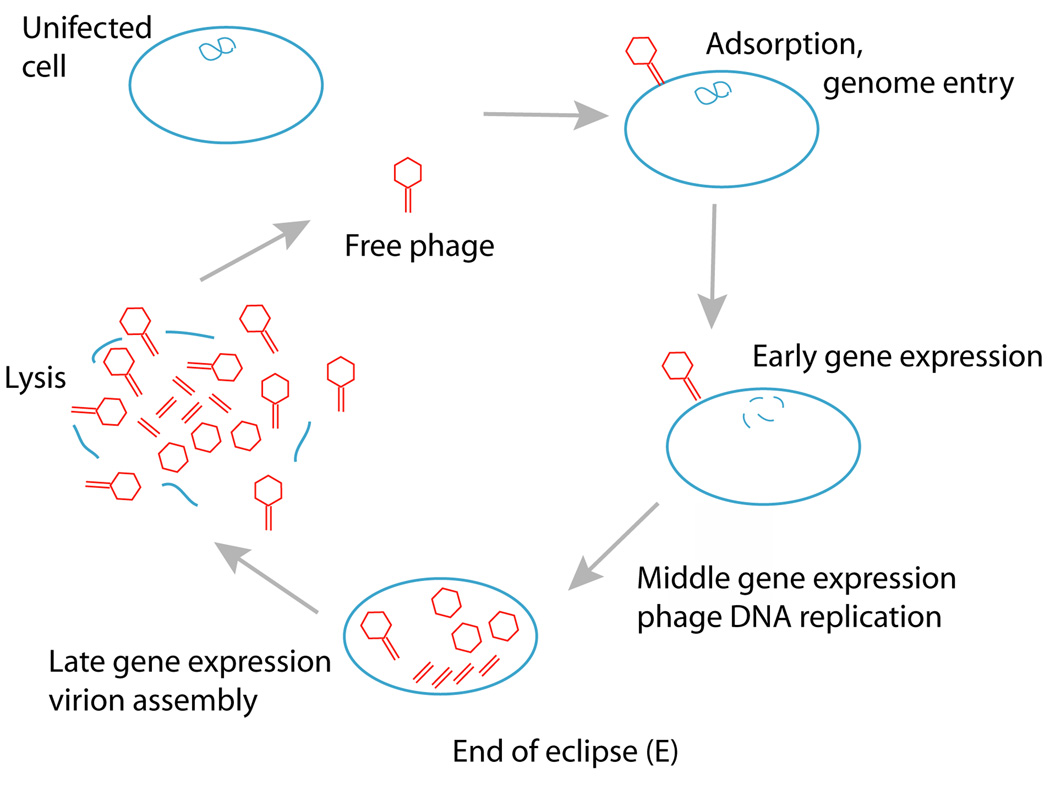
Bacteriophages (‘phages’) are viruses of bacteria. The phages we consider here are lytic and have a simple life cycle of (i) infection of a bacterial host, (ii) age of reproduction, the time from infection until the cell bursts open to release all progeny (referred to as lysis time or latent period), and (iii) fecundity or burst size (Fig. 2). Most phages have a narrow host range, infecting only a handful of strains within one bacterial species.

Fig. 2 — Phage life cycle, from free phage to infection, to eclipse, to lysis. Lysis typically occurs before all phage parts have been assembled, as drawn. The figure-8 inside the cell represents the bacterial genome, which is degraded by many phages.

The nature of selection, and hence the appropriate measure of fitness, depends fundamentally on how phage increase their numbers. For the two sets of studies reviewed here in detail, the environment allows continuous exponential growth of the phage population. Exponential growth is modelled as

N_{t} = N_{0} e^{rt},

(1)

where N denotes phage numbers, subscripted according to time t in minutes relative to the initial N₀. Population growth rate, r, is known as the ‘intrinsic rate of increase’ and is an exponential fitness measure: positive values indicate population expansion, negative values population contraction. How, then, do we calculate the value of r?

Phage populations grow faster than bacteria but because of their parasitic nature, phages need a constant supply of bacteria to keep growing. Continuous exponential growth of a phage population is thus achieved experimentally by periodic serial transfer and dilution of an aliquot from the current phage culture to fresh cells. With appropriate timing and dilution of transfers, phage never exhaust the supply of hosts. For a lytic phage in this environment, three parameters (plus cell density) completely specify fitness during exponential growth:

b (burst size, the number of phage progeny released when the cell bursts)
L (lysis time, minutes from infection to burst)
k (adsorption rate constant at which phage infect cells, units mL min⁻¹)

These parameters are the three phenotypes in the fitness model. Meanings of the first two parameters are intuitive, the third less so. Adsorption rate k accounts for both the ‘stickiness’ of the phage when it encounters a cell but also accounts for the encounter rate. The upper limit of k is thus near 10⁻⁸, depending somewhat on specifics of the system; this bound is because of the small size of phage and cell and the corresponding low chance of random encounter in a mL of liquid (Adams, 1959). When stickiness is so high that nearly all encounters result in infection, k nears this limit. Although it seems counter-intuitive, a 100-fold drop in adsorption rate (say from 5 × 10⁻⁹ to 5 × 10⁻¹¹) has a profound negative effect on the rate of phage growth when cells are common.

At any time, the change in density of free phage (Ṗ) comes from two sources: losses by adsorption to cells (rate −kCP) and gains from the burst of cells infected L minutes earlier (+bkCP_L), where P_L is phage density L minutes earlier, and C is cell density, assumed constant and always in substantial excess of P. Thus, Ṗ = −kCP + bkCP_L. With no between-cell variation in lysis time, once exponential growth of the phage population has been attained, fitness (r) obeys

r = kC (b e^{- Lr} - 1)

(2)

(Bull, 2006). This fitness equation is the phenotype-fitness map: given cell density (C) and phage phenotype values of (k, b, L), the growth rate of the phage is determined. Equation (1) has no closed solution. It may be solved numerically and is also amenable to some derivations, but for some conditions a simple approximation is more tractable and sufficiently accurate (Abedon et al., 2003; Wang, 2006; Guyader & Burch, 2008). This equation omits phage death and loss from the environment, both of which are easily incorporated but not needed here (Bull, 2006).

Fitness depends on three parameters and on cell density, all of which depend on the phage genotype and on the environment – the media can affect adsorption rate, for example, and the media affects cell growth, which in turn affects the phage burst size and lysis time. Fitness r is thus a combined genetic and ecological measure. Whereas it is obvious that phage fitness can be increased or decreased by changes in the parameters b, L, and k (e.g. by evolution), it is also the case that r can also be changed without any evolution, merely by changing the abundance or characteristics of cells. In the first two sets of studies discussed later, selection on phenotypes is achieved by modifying the cell characteristics to effect changes in r.

As a model of fitness, even under the assumed environmental conditions, eqn (1) has shortcomings. It assumes that the parameters are invariant; variation in burst size alone is not a problem (the mean suffices), but substantial variation in lysis time has a meaningful effect (Heineman & Bull, 2007). Furthermore, parameter values are necessarily estimated as averages in cultures with large numbers of phages whose life cycle is synchronized, and covariation between lysis time and burst size (which could arise because of physiological differences among infected cells) could lead to a difference between actual and realized fitness (cf. Springman et al., 2010).

Optimal diets: phage host range

Foraging was one of the earliest problems considered from an optimality perspective (Emlen, 1966; MacArthur & Pianka, 1966). The basic optimal foraging model predicts the diet for a consumer faced with a range of food types. The food items are small enough that the consumer is never sated, at least within the time frame of the foraging bout. Each food type is assigned three values: (i) an abundance in the environment, affecting the rate at which the consumer encounters the item, (ii) a value to the predator (e.g. caloric energy), and (iii) a cost to the consumer in the form of handling time. The phenotype is a multidimensional diet – the set of items chosen and the set of items avoided – and the phenotype-fitness map is the rate of energy consumption for a diet based on the prey abundances, values, and handling times.

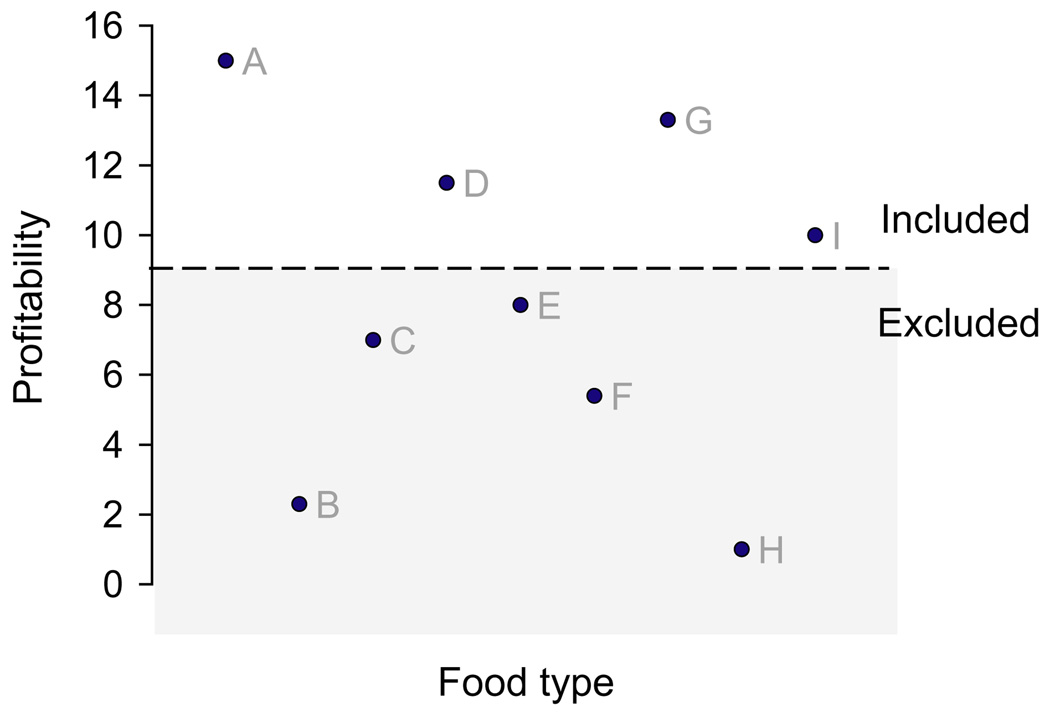
In the classic theory, an optimal diet maximizes the overall rate of energy intake. The optimal diet has the property that all food types whose value per cost – ‘profitability’ – exceeds a threshold should always be eaten, and all food types whose value/cost lies below the threshold should always be ignored (Fig. 3).

Fig. 3 — The qualitative nature of an optimal diet. Food types consist of A–I. All food types whose profitability lies above the threshold should be included (A, D, G, I), those below should be excluded (B, C, E, F, H, shaded in light grey). The threshold depends on abundances of the different (good) food types as well as on profitabilities. Drawn for arbitrary values.

The diet of a phage is the set of hosts it infects. Selection on diet is relevant when two or more potential host types exist for a phage, and the question is whether the phage benefits by infecting – attaching to – all host types or just some. Selection to avoid a host type may occur if infection of that host is less ‘productive’ than infection of others. In the extreme case that a host kills the infecting phage (known as an abortive infection), selection for avoidance is obvious. But what if the phage produces progeny from all hosts, just that fewer progeny result from some hosts than from others, or that lysis time is longer for some hosts? It might seem that infection of any host that produces progeny will benefit the phage, but selection depends on the overall growth rate of the phage population: the faster the growth of the phage population, the more the phage is selected to avoid all but the best hosts. Optimal foraging predicts which hosts should be infected.

The phenotype-fitness map for a phage infecting two cell types is given by a simple extension of (1):

r = k_{1} C_{1} (b_{1} e^{- L_{1} r} - 1) + k_{2} C_{2} (b_{2} e^{- L_{2} r} - 1),

(3)

where subscripts 1 and 2 refer to different host types and to the corresponding phage parameters for that host type (Bull, 2006). The modification to include additional host types is obvious.

From this equation, the phage optimal foraging result is easily derived. It is not intuitive, however: the profitability of host type i to phage fitness is given by ln(b_i)/L_i. The optimal phage diet has the same general form as for classical optimal foraging (MacArthur & Pianka, 1966; Emlen, 1966), including parasitoids (Charnov & Stephens, 1988): include all host types whose profitability exceeds a threshold and exclude all host types whose profitability is below the threshold (Bull, 2006; Guyader & Burch, 2008). The threshold depends on the profitability ratios and abundances of the different host types, both of which determine overall phage growth rate. An interesting property of the threshold is that it is affected only by the abundances of the types included in the diet, not by abundances of those excluded.

The genotype–phenotype map assumed here has three parts. (i) Only the adsorption rates evolve (k_i), not burst size or lysis time. (ii) Adsorption rates to different host types evolve independently of each other. (iii) Adsorption rates evolve to maximal levels for hosts included in the optimal diet and to minimal levels for excluded hosts.

The usual connotation of a host range is that of a binary, all-or-none phenotype: a host is or is not included in the diet. However, phages adsorb at a rate which is continuous. From a practical perspective, infection rates of 2–10 × 10⁻⁹ mL min⁻¹ are considered high, and rates 10-fold less or lower are considered low. For an outcome to strongly support the optimality model, initial infection of a host that is to be excluded should be accompanied by at least a 10-fold decline in the adsorption rate to that host without reducing adsorption rates to included hosts. Conversely, adsorption rates to included hosts should evolve to or be maintained in the 2–10 × 10⁻⁹ range without increasing rates to excluded hosts.

Genetic mechanisms

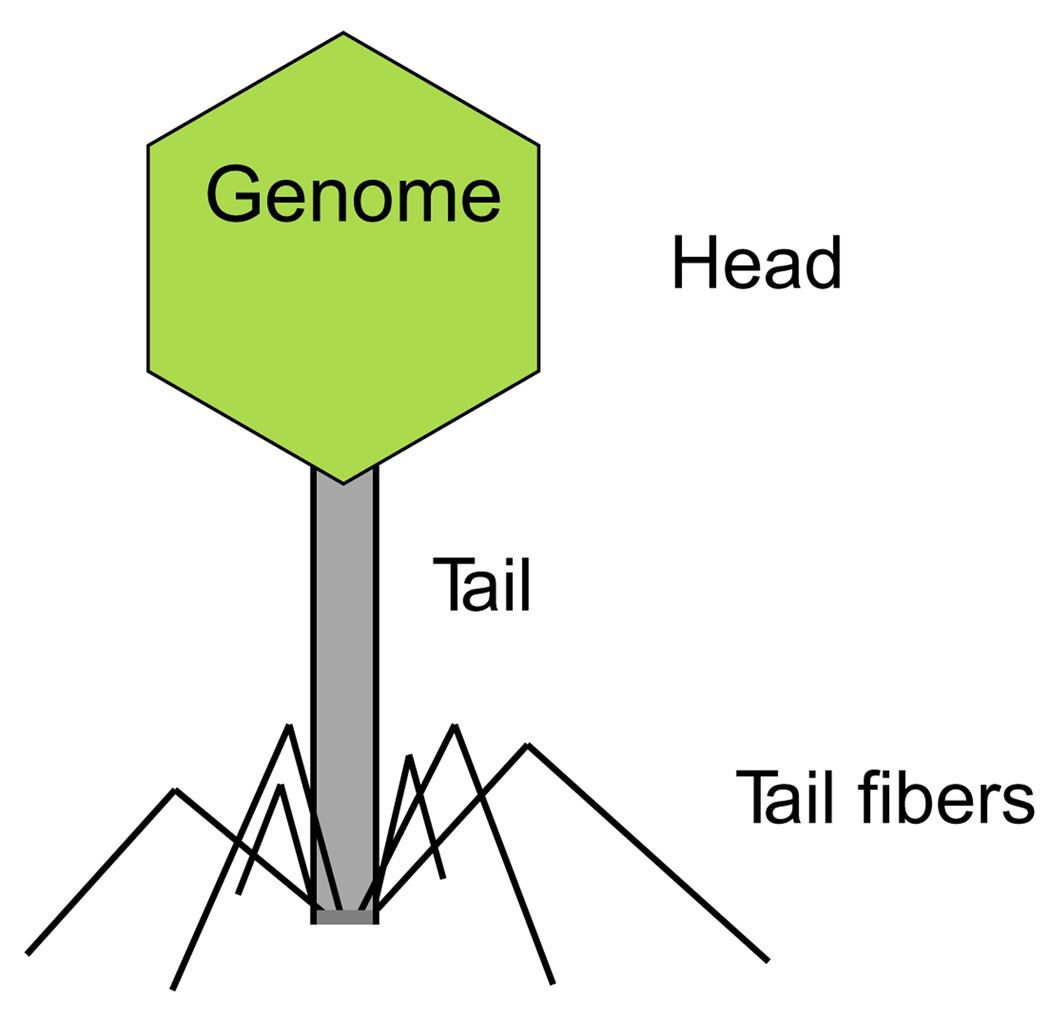
For a phage to infect a cell, the phage must bind receptors on the bacterial surface. Most phage particles carry their genomes in protein-coated balls (icosahedral heads), with one or more portals for the genome to exit the phage head into the cell. The ‘tailed’ phages have a single, long hollow rod attached to the icosahedral head, and the genome exits through this hollow rod (Fig. 4). Each tail has proteins at its distal end (referred to as tail fibres, side tail fibres, or tail spikes, depending on the morphology and phage), and these tail fibre and spike proteins determine which cell types get infected. Tail fibre and spike proteins are highly modular, with the only known phenotypes often being attachment and entry into the host (Riede et al., 1985; Hashemolhosseini et al., 1994a,b). Isometric phages are tailless. They have the icosahedral head, and each of the 12 vertices of the icosahedron has a spike, so the overall virion resembles a lumpy soccer ball. In isometric phages, host specificity is affected by capsid proteins, but the basis of host specificity is less clear than with the tailed phages (Crill et al., 2000).

Fig. 4 — A stereotypic tailed phage. The tail fibres often control adsorption. Some phages have tail spikes instead of tail fibres, which tend to clump at the base of the tail instead of radiating outward.

In the genotype–phenotype map of optimal diet models, burst sizes and lysis times are not affected by the evolution of adsorption rates. Does Nature agree? The modularity of tail fibre genes should be suited for an absence of pleiotropy on other phenotypes. Whether phages lacking tails can easily evolve to discriminate among arbitrary hosts is less clear; host range mutants of the tailless phage ϕ 6 typically affect other phage parameters (Ferris et al., 2007).

Two studies of optimal phage diet are available, one using a tailed phage and the other using a pair of tailless, isometric phages (Table 1). Some support for the model was observed in both cases, but failures of the genotype–phenotype map occurred in both studies and dominated the results with isometric phages. The tailed phage exhibited evolution largely consistent with an optimal diet because of a single mutation in its tail fibre gene, but one small discrepancy from optimality was observed. Importantly, the study of Guyader & Burch (2008) confirmed the phenotype-fitness map for specific combinations of host densities, thus demonstrating that the failure to evolve an optimal diet was in the genotype–phenotype map.

Table 1.

Optimal foraging by phages.

Phage

Results

ϕX174, G4 (tailless)¹

Each phage was evolved separately in environments with two hosts. Contrary to the model, G4 failed to evolve any change in host range or adsorption rate. ϕX174 showed a modest change in adsorption rate on one host, in the direction predicted by the model, but no significant change on the other host. The dominant outcome was limited evolution; the genetics of ϕX174 evolution were not investigated. An important dimension to this study was a verification of the phenotype-fitness map for the two phages in specific combinations of host densities

T7 (tailed)²

A wild-type phage that grew on two host types was selected strongly to discriminate – avoid one host, grow on the other. Discrimination evolved due to a mutation in the tail fibre gene. The tail fibre mutation was introduced into a wild-type background and tested against the wild-type phage. The phages competed in two-host environments in which host densities and relative host quality were varied from conditions that should favour discrimination to conditions that should favour infection of both hosts; selection in those environments was mild. Two optimal foraging predictions were supported. A third prediction failed quantitatively because the tail fibre mutation that caused avoidance of one host also caused slightly reduced adsorption to the other host, in violation of the model’s genotype–phenotype map

Open in a new tab

References:

(Guyader & Burch, 2008);

(Heineman et al., 2008).

In this example, the distinction of and interplay between the phenotype-fitness and genotype–phenotype maps is simple. An absence of host range evolution in one experiment and evolution of discrimination by a single tail fibre mutation in another are both easily integrated into the model to understand failure and success. Indeed, given that the phenotype-fitness map could be verified independently of evolution and could be trusted for any set of parameter values, the evolutionary test of optimality contributed relatively little beyond existing knowledge except that we might not have anticipated the genetic failure of one phage to expand host range.

The experimental conditions used in these studies may rarely occur in nature. Selection to avoid a productive host requires a continual high abundance of alternative hosts, and once the good hosts are exhausted, selection shifts to favour infection of the poor host. Natural contexts where the experimental conditions might occur include the leading edge of an epidemic wave of bacteriophage in a marine environment and possibly on biofilms grazed by phage, but our sense is that hosts are often limiting for phages. Furthermore, because a shift in the diet of a phage requires genetic evolution, not merely a change in behaviour or gene expression, phage diet will not change in environments that persist only in the short term. It may therefore be that evolution in nature primarily expands and contracts diet according to whether hosts are productive or not – in response to large fitness consequences – and that small differences in profitability have only momentary effects on selection and virtually no effect on evolution. These speculative conclusions necessarily rest on the genetic underpinnings of host range evolution; mechanisms that allowed plasticity of host range or some epigenetic form of inheritance might facilitate rapid response to conditions.

Does a limited application of the experimental conditions render the work unimportant? We suggest not. The fact that we can predict evolution of host range (in T7) for one set of conditions suggests that we can extrapolate to others. Furthermore, the failure of isometric phages to evolve changes in host range may mean that the fitness consequences of an optimal diet have ecological rather than evolutionary ramifications, affecting competition among distinct phage types rather than evolution within types (e.g. Guyader & Burch, 2008). The fact that the phenotype-fitness map was verified suggests that we indeed understand selection and that the lack of appropriate evolution has a genetic cause. Even when a phage does evolve an optimal diet under constant conditions, we can extrapolate from the experiment to decide how long conditions must be maintained in a wild population for selection to effect a change. The perspective provided by the optimality model also allows one to consider that selection to avoid host strains and to narrow a diet – a perspective rarely considered in prior work – may be as important as selection to expand or shift host range. The easy dissection of the phage system further encourages the experimental study of foraging behaviour in more complicated systems (Hillesland et al., 2009).

Phage lysis time

Phage lysis time is perhaps the most thoroughly studied, well-defined optimality problem for which genetic mechanisms are understood. There are several levels of prediction, and tests exist for three phages. The phenotype-fitness map is given by eqn (2).

Evolution of lysis time: the basic result

For a lytic phage, the time to lysis is its ‘age of reproduction.’ Faster lysis means a shorter generation time, beneficial in a growing population (r > 0). However, faster lysis leaves less time for progeny production, so burst size – fecundity – should ultimately suffer with earlier lysis, leading to a trade-off between the two parameters. Since a shorter generation time (earlier lysis) is increasingly selected in faster-growing populations, whereas the benefit of larger bursts is largely independent of population growth rate, earlier lysis should be favoured in faster-growing populations, accompanied by a decline in burst size. This Basic Result qualifies as a ‘general’ optimality model but not a ‘specific’ or quantitative one because it does not provide a quantitative outcome, nor does it even specify a functional form to the trade-off. Indeed, trade-offs forms could be imposed that do not favour an intermediate lysis time optimum.

The Basic Result follows from (1). Treating burst (b) as an increasing function of lysis time (L), which implies some form of trade-off, selection favours increased lysis time if

\frac{1}{b} \frac{\partial b}{\partial L} > r .

(4)

Increased lysis time is favoured if the proportional increase in burst size per increase in lysis time exceeds the intrinsic growth rate; conversely, decreased lysis time is favoured for the reverse inequality. If the population is barely growing (r ≈ 0), then virtually any increase in burst size is favoured. But as the population grows ever faster (r gets larger), proportionately larger increases in burst are required to offset any increase in lysis time.

The genotype–phenotype map underlying the Basic Result is minimal. The only requirement is qualitative – if lysis time evolves, burst size should change in the same direction. The (L, b) map may thus have few points (few functional mutations), the only requirement being that the boundary of best mutations increases in L as b increases.

A lysis time optimum

The Basic Result was first proposed by Abedon (1989), but it was the study of Wang et al. (1996) which developed lysis time as a quantitative optimality model and provided a general graphical solution for the optimum. The optimum has since been solved for a linear trade-off (justified below). The optimum lysis time (L̂) obeys

\hat{L} = E + \frac{1}{\hat{r}},

(5)

where E is ‘eclipse’ time, r is fitness, and a carat (^) indicates a value at the optimum (Bull, 2006). The fact that the optimum incorporates r̂ instead of r means that the optimum is not determined by the current (observed) growth rate unless the optimum has been attained. However, substitution of the current r in place of r̂ gives the direction of selection: if L exceeds $E + \frac{1}{r}$ selection favours a shorter lysis time, and vice versa.

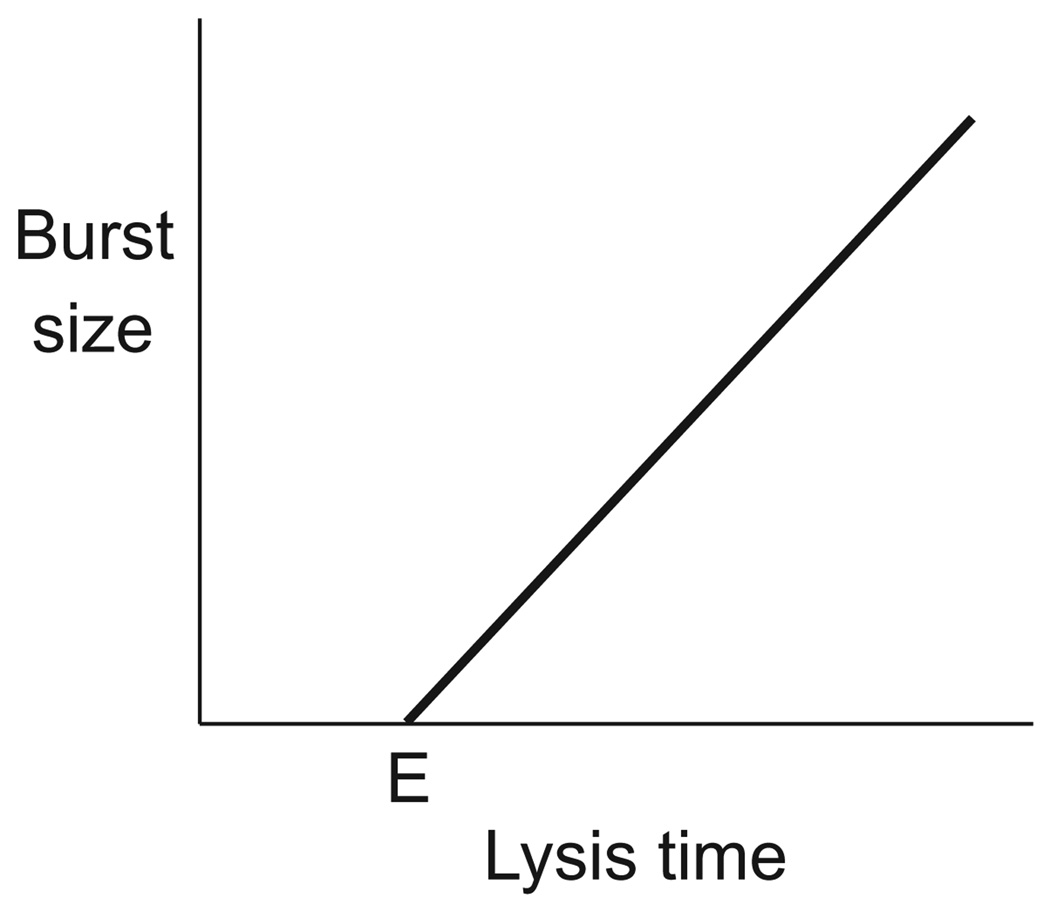
The key to this result is a trade-off in which burst size increases linearly with lysis time after eclipse (Fig. 5). Following phage infection, there is a period during which the genetic machinery of the cell is being co-opted by the phage, but no phage progeny have been assembled. Historically, this period is known as eclipse because all viable phage have temporarily ‘disappeared.’ At the end of the eclipse period (E), phage progeny start being formed. They normally remain inside the cell until lysis but can be detected earlier if the cell is ruptured artificially. Progeny numbers increase from E until lysis, and if the normal time of lysis is artificially suppressed, phage numbers increase beyond the normal burst size. Linearity of the lysis time/burst size relationship has been reported in several phages. Parallel optima are easily derived for simple curves emanating from E, and the optimum follows a similar form as in (5) except that the 1/r̂ term is scaled upward or downward according to whether the trade-off grows faster or slower than linear (not shown).

Selection on lysis time changes with the inverse of phage fitness, 1/r. How, then, does this result relate to the environment of the phage? Recall that r is a property of both the phage and cell density. By altering the abundance of cells, the population growth rate r can be changed experimentally, and the optimum is correspondingly shifted.

There are four interesting properties of this optimum. First, even though it is a ‘specific’ optimality model, it has considerable heuristic value. The optimum varies entirely as the inverse of the population growth rate (1/r̂), for a fixed eclipse time. Phage parameters and even the slope of the trade-off do not explicitly appear. The dependence on phage growth rate is easily translated into an importance of phage generation time to the optimum.

Second, because of the dependence on r̂, the optimum changes not only with changes in cell density and cell physiology (environment) but also with incidental adaptation. Given an adsorption rate, trade-off function, and cell density, there is a single lysis optimum. But that optimum changes if the trade-off or adsorption rate evolves. If the phage is poorly adapted to the environment for reasons other than lysis suboptimality, that adaptation will increase r (and r̂). A phage could thus shift from lysing earlier than the optimum to later than the optimum without any change in lysis time, as the phage adapts to the environment. A changing optimum may be difficult to attain.

Third, this optimum rests on a trade-off involving two of the three phenotypes in the phenotype-fitness map, burst size and lysis time. The trade-off itself is part of the genotype–phenotype map, because the trade-off is a restriction on what genetically determined phenotypes can arise and evolve. The phenotype-fitness map can accommodate any phenotype values, whether they obey a trade-off or not. The genotype–phenotype map also assumes that all phenotype combinations that obey the trade-off are attainable, but that no point above the trade-off can be attained. The involvement of two phenotypes in the genotype–phenotype map renders evolution of lysis time optimality a potentially more complicated feat than that for the diet problem, which involved only adsorption rates.

Last, although the phenotype-fitness map involves burst size but not eclipse time, the optimum includes eclipse time (E) instead of burst size. E appears because of its influence on burst for the trade-off assumed, but a different trade-off function might well cause E to be replaced by b in the optimum (recall that the Basic Result depends on b and L). As part of the trade-off function, E is fixed in the model, and evolution of a different value of E during the course of an experiment indicates that the trade-off function has evolved.

Physiology and genetics justify trade-off linearity

The assumption of a linear trade-off is not merely for convenience. Physiological manipulations of artificially expedited and delayed lysis in four unrelated phages exhibit remarkable linearity (Wang, 2006). By itself, physiological linearity does not imply genetic linearity – does not imply a linear trade-off – because physiological behaviour rests on the genetic state of the individual, and physiology changes when the genetic state changes. In this case, however, a linear trade-off seems justified because of the manner in which lysis is controlled. In most phages studied whose genomes are larger than 20 kb, lysis is controlled by a two-gene system (Wang et al., 2000). One gene encodes a lysin, an enzyme that rapidly degrades the cell wall, which in turn effects lysis. However, the lysin is blocked by the inner membrane from getting to the cell wall, and lysis cannot occur until the lysin gains access. The second lysis gene solves this problem. This second gene encodes a membrane protein known as a holin, and as the name suggests, this protein creates holes in the membrane, allowing the lysin access to the cell wall. Importantly, the holin acts in a yet-unknown saltatory manner, whereby the pores do not open gradually but rather open all at once. Cell lysis is thus sudden, not preceded by a gradual ‘bleeding’ of contents, and allowing phage production to continue unabated until the moment of rupture.

Holins appear to time lysis and seems as if they were evolved to fit the optimality model (Bull et al., 2004). Extensive work on the holin of phage λ has shown that most amino acid substitutions do not destroy function but merely alter the timing of lysis, and it is presumed that other holins behave similarly. Thus, the phage is equipped with a gene whose only apparent function is to modify lysis timing. Given the observed linear physiological association between lysis time and burst size plus the genetic modularity of lysis control, (i) the holin gene is the expected target of evolution in phage evolution of optimal lysis time and (ii) a linear trade-off seems justified. Indeed, Wang (2006) analyzed 11 mutants of the λ holin gene and observed approximate linearity. Thus, it seems as if the optimality model cannot fail in this case and that, again, any test will merely reaffirm prior knowledge (Bull et al., 2004).

Consequences of genetic imperfections around linearity

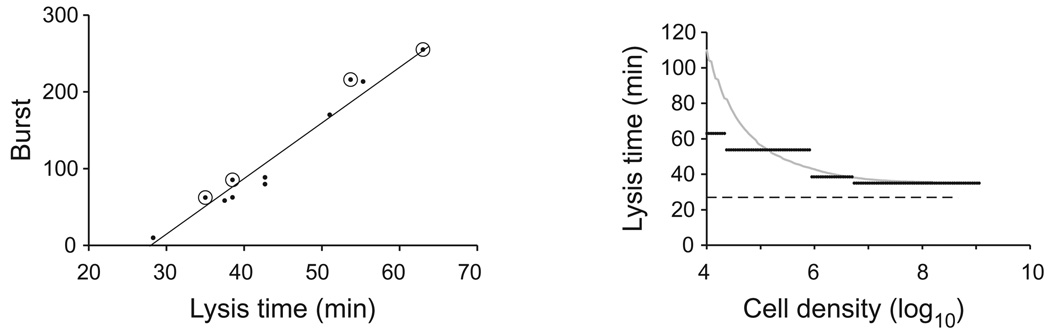
Even when a linear trade-off operates more or less, there will be differences between the assumed genotype–phenotype map and the realized genetics. Mutations in a single protein cannot cover the trade-off densely, and mutations in holin may cause at least slight deviations from linearity because of small interactions with other phenotypes. How, then, might these nuances affect quantitative optimality? For insight, we consider the 11 λ holin mutations characterized by Wang (2006). Parameterizing eqn (1) with the empirically determined mean lysis times, burst sizes and adsorption rate (neglecting measurement error), only four of the 11 mutations are expected to be favoured across the feasible range of experimental cell densities (Fig. 6). Although there is quantitative disagreement between the evolved lysis time (black lines) and the predicted lysis times (grey curve), the model is supported to first order. More serious failings because of genetic constraints are possible, as illustrated later by a study with phage T7.

Fig. 6 — Left: Lysis time and burst size of 11 characterized mutations in λ holin protein (Wang, 2006). The four symbols circled correspond to the only four mutations that selection would favour among these 11 across the range of cell densities of 10⁴–10¹⁰, as in the right panel. Right: Evolved lysis time from the set of mutations in left panel. Each horizontal line corresponds to a different mutation, and the horizontal span indicates the range of cell densities over which that mutation is superior to the others. Fitness was determined from (2), with an adsorption rate of 9.9 × 10⁻⁹. The grey curve corresponds to E+1/r, where r is calculated from (2) and E is set at 27, indicated by the horizontal, dashed line.

Experimental tests: the basic prediction is supported, optimality sometimes

Tests of the basic model have been conducted by three laboratories, each using different phages (Table 2). All work has supported the basic model, but only one study tested the optimality result (5), finding mixed support.

Table 2.

Experimental evolution of lysis time in phages.

Phage	Results
RB69¹	Basic Result supported, optimality model not tested. An early lysing holin mutation (with reduced burst size) introduced against wild-type prevailed at high cell density but not at low cell density
λ²	Basic Result and optimality model not tested. Eleven known holin mutations were separately introduced into a constant genomic background and characterized for lysis time and burst size. Fitnesses were measured in parallel under constant conditions. A mutant with intermediate lysis time had highest fitness, demonstrating existence of an intermediate optimum but not whether that optimum was quantitatively as predicted
λ³	Basic Result supported, optimality result not tested. Six known holin mutations were separately introduced into a common genomic background with side tail fibres (high adsorption rates) and tested in pairwise competitions with each other; the holin mutation lysing at 46 min had highest fitness. When the same holin mutations were tested in a genomic background without side tail fibres (low adsorption rates), the mutation lysing at 64 min was superior. The presence/absence of side tail fibres thus had the same qualitative effect as that predicted from high/low cell density
T7⁴	Basic Result supported, optimality result largely supported at high cell density, failed at low cell density. A T7 pre-adapted to growth at high cell density was further evolved at high density. The initial lysis time was 1.9 min too slow but evolved to within 1.3 min of the optimum; the final difference was statistically significant but too small to be considered biologically meaningful. The evolution was accompanied by a large deletion of nonessential genes and seven substitutions, one in the holin gene. The low cell density evolution was initiated with the phage evolved at high density, otherwise using the same environmental conditions. The low-density evolution exhibited a slight increase in lysis time (and larger burst size) but remained over 6 min too early. Eclipse time (E) also increased in violation of the model. Seven substitutions evolved, none in the holin, but one was just upstream of holin and could have been regulatory. Any role of other mutations in lysis time is unknown

Open in a new tab

References:

(Abedon et al., 2003);

(Wang, 2006);

(Shao & Wang, 2008);

⁴

(Heineman & Bull, 2007).

To summarize the experimental studies of lysis time evolution in phages, there is support for the Basic Result that evolution of earlier lysis is favoured in faster-growing populations and entails a reduction in burst size. No study has yet fully supported the optimality model based on (5), although mutants of λ approximate a linear trade-off and, if used in a mutation-introduction experiment, should approach the optimality prediction to first order. However, given the sensitivity of selection to small deviations from the linear trade-off (e.g. Fig. 6), de novo evolution of lysis time may well show larger deviations than expected even from the constructed holin mutants – any adaptation as a result of mutations outside of the holin may interact with the holin mutations.

The quantitative failure of the model for T7 at low density is remarkable (Table 2). The phage appears to have appropriate genetics for arbitrary evolution of lysis time (a confirmed holin) and exhibited a substantial number of molecular changes during and specific to the low-density adaptation. These anomalies have led to a more general investigation of lysis in T7, revealing other reasons to question the fit of T7 to the model assumptions (to the genotype–phenotype map). The first two concern the T7 holin gene. This gene is presumed to be a holin based on bioinformatic analyses, and it effected lysis in a phage λ expression system lacking the innate λ holin (Vukov et al., 2000). Nonetheless, the T7 holin gene is physically separated from the lysin gene by more than half the genome (25 000 bases), in contrast to the usual juxtaposition of both genes in other phage genomes. Furthermore, deletion of the holin gene results in only a minor delay in lysis (2 min) (consistent with prior work using amber mutations (Miyazaki et al., 1978; Heineman et al., 2009), in contrast to profound effects of holin knockouts in other phages (Wang et al., 2000). Third, genetic methods used to delay lysis that resulted in larger bursts in other phages have not yielded larger bursts in T7 (Heineman et al., 2009). It is as if phage production ceases at the normal time whether membrane permeabilization and lysis occurs or not. These last two observations are consistent with the failure of T7 to match a predicted late lysis but its success in matching early lysis (Heineman & Bull, 2007).

As with the example of host range, the question turns from the laboratory environment to nature. Is lysis time optimality relevant to phage natural history? It must again be appreciated that little is known of phage natural history outside the laboratory. If a phage in the wild experiences a range of permissive host strains at various densities and physiological states, there will be an optimal lysis time lasting as long as the host densities and states persist (Bull, 2006). However, as the phage exhausts hosts, invades new environments, and faces changes in its current environment, the optimum will change often and perhaps change greatly. Rapid changes in the optimum have the effect of weakening selection on specific lysis times and flattening the relationship between lysis time and fitness. Only if hosts are consistently uncommon and/or of poor physiological state would the optimum remain relatively constant – consistently for late lysis.

Holins seem so well suited for lysis time evolution that their existence can be construed to support a history of selection for lysis time changes (Bull et al., 2004). Yet, the failures of T7 to fit the optimality model and to fit the standard model of holin behaviour cause one to reconsider that interpretation. In addition to enabling genetic changes in lysis time, holins allow physiological changes in lysis time – plasticity – while allowing the dying cell to produce phage progeny unabated up to the final moment of lysis. Enabling a phage to physiologically achieve different abrupt lysis times under various host conditions may be as important or more important to fitness than allowing the phage to easily evolve different lysis times, when the optimum is only transitory anyway.

Virulence

From the perspective of a bacterial cell, phage lysis time is a simple model of parasite virulence, and in turn, the tests of optimality provide insight into efforts to predict virulence evolution of other parasites. For a lytic phage that will invariably kill its host, the concept of variation in virulence may seem irrelevant. Yet, when virulence evolution is considered from a general perspective, higher virulence in a phage is equated with a shorter lysis time. The results from phages support the most basic premises of virulence evolution models, that fitness can be captured by simple models and, especially, that higher virulence evolves at the expense of fecundity. It should be appreciated that the life cycle of a human parasite has far more dimensions than the life cycle of a phage in standardized laboratory conditions, and capturing the essence of parasite fitness is a substantial challenge. It is nonetheless encouraging that the phage work supports the foundations of some basic ideas about parasite fitness and evolution. It is further illuminating that genetic details preclude quantitative prediction, even in a system with few dimensions. Such insights may help guide the emphases in future modelling of parasite evolution.

Enzyme expression levels in bacteria

Enzymes perform valuable functions for a cell. They are also costly to produce. Whereas the metabolic cost to the cell may scale linearly (or more than linearly) with enzyme production, the benefit is saturating. For a single enzyme, the optimal expression level along this trade-off is intermediate, the value depending on how much substrate is available and how much the cell benefits by converting substrate. Generally, high levels of substrate are required to offset the cost of high levels of enzyme production, so the optimal enzyme level should follow substrate level monotonically.

A classic system of gene regulation is the lac operon, which controls the metabolism of the sugar lactose in the bacterium Escherichia coli. The operon consists of six elements – three genes and three regulatory elements – and is remarkably well studied. Dekel & Alon (2005) developed an optimality model for lactose metabolism in E. coli based on the expression levels of the protein that digests lactose, β-galactosidase, encoded by the lacZ gene. The phenotype-fitness map can be considered the model of bacterial growth rate with arbitrary cost and benefit parameters; the genotype–phenotype map is then the trade-off imposed by the integrated cost and benefit functions. The cost of expression was estimated empirically from reduced growth rates of E. coli induced to high levels of expression in the absence of lactose (physiological manipulations rather than genetic manipulations). Two different cost functions were fit to the data. The benefit function was based on standard parameters of sugar metabolism and on lactose concentration.

Several bacterial lines were each adapted for 500 generations in different concentrations of lactose as one of two carbon sources, so the cell benefited by metabolizing lactose but could grow without it. β-galactosidase activity evolved to higher levels in higher lactose concentrations. The 500-generation endpoints of six of the seven lines showed an excellent fit with optimality based on one of the two cost functions. Sequences were obtained for five of the lines over the expected sites of evolution (the lac operon and some associated genes). The line grown without lactose evolved a deletion of the promoter of lacZ, fully consistent with the uselessness of its expression in an environment without lactose. Two lines exhibited mutations in lacZ (a silent change only in one of the lines), whereas the other two lines had no mutations in any of the regions sequenced.

The optimum is based on a trade-off in which the fitness cost of the enzyme is because of its expression level. A reduced cellular enzyme activity could represent a reduction in enzyme amount or a reduction in the activity of individual molecules (Stoebel et al., 2008). Only the former is consistent with the model, because it specifically reduces the cellular burden. Enzyme activity per molecule was measured in these lines (except the line no longer producing enzyme) and found to have been maintained at wild-type levels, thus supporting the model. (Increased enzyme activity per molecule would also be compatible with the model but was not observed.)

The line grown at highest lactose concentration matched predictions at 400 generations but not at 500 generations: the cost function had changed in the last 100 generations and now differed from the ancestral wild-type function. (The other lines all maintained the wild-type cost function parameters.) Thus, it appeared that early evolution had obeyed the initial trade-off function but late evolution did not: evolution of a trade-off function resulted in model failure.

The lac system has some quirks that would normally have presented several challenges to such a simple study, but a priori knowledge of details enabled avoidance of the most serious ones. In a normal environment, lac expression is either turned on or off (no intermediate levels), so it would not obviously have been possible to parameterize the cost and benefit functions for intermediate lactose levels. Nor would it have been clear how to measure gene expression levels of individual cells, because cultures would be mixes of cells at maximal expression and cells at no expression. This difficulty was overcome by measuring parameters and conducting adaptations in media containing an inducer of the lac operon (IPTG), such that the operon was fully expressed at all times. A problem not explicitly dealt with was the fact that the adaptation was carried out by serial dilution, resulting in a daily varying lactose concentration. Dilution from media devoid of lactose into media with lactose can be lethal to normal cells (Dykhuizen & Hartl, 1978), and even without this complication, it is not clear what impact changing lactose concentrations have on evolution of a constant expression level. Despite these concerns, the study provides a major step in shedding light on enzyme expression levels.

Other examples

Three other examples are listed in Table 3. One pushes the ecological context of optimality to an extreme level of complexity, another addresses global optimality in a high dimensional system. They collectively illustrate the wealth of contexts for experimental evolution of optimality models.

Table 3.

Other experimental evolutions of optimality.

System	Results
λ induction¹	When infecting a cell, temperate phages have the ability to grow lytically or adopt a passive state in which they are cotransmitted indefinitely with the bacterial genome. A lysogen is a bacterium carrying the passive genome, and the genome can be induced to initiate the lytic cycle at any time. From the perspective of the phage, the optimal induction level varies with the opportunities for future survival of the lysogen and possibilities of phage infection of naive cells. Selection for changes in phage sensitivity to a known chemical trigger of induction led to a moderate evolutionary response, although optimality per se was not tested. The molecular basis of λ induction is well studied (Ptashne, 2004), and the candidate elements were sequenced. Only some lines carried mutations in candidate regions; mutations in the other lines were not identified
Global metabolism²	Flux theory can be used to predict optimization of entire metabolic networks. Attempts to predict network optimization have been confined to the highest level phenotypes, such as growth rate, oxygen consumption, and ATP production. The models ignore such fundamental details as variation in expression levels. Even so, results have been broadly supportive of the models. There is thus far little attempt to explore the genetics of optimality evolution or to explore individual components of the metabolic networks, but this area offers extraordinary opportunity for exploration
Group selection of phage growth rate³	Predators that extinguish their prey populations will go extinct. It may seem that selection opposes this outcome, but selection within a population invariably favours the selfish predator over the prudent predator, and the ensuing ‘Tragedy of the Commons’ does not prevent extinction. However, predators are favoured to avoid over-exploiting prey in structured populations, if local groups that go extinct are replaced by migrants from groups that persist. This process was simulated with phage T4 as predator against its Escherichia coli prey using two different migration structures in a global population consisting of 192 subpopulations. When migration was local, limited to neighboring subpopulations, the phage evolved a lower growth rate than when migration was global, and the difference in evolution traced to differences in adsorption rate, lysis time, and possibly burst size. The mutations underlying the lysis time differences resided in the phage antiholin (a type of holin). This experiment motivated a qualitative model for predicting the optimal phage growth rate in a ‘connected world’ (revealing that kin selection could also account for the evolution). The system thus illustrates the ecological complexity to which experimental evolution of optimality may aspire and that such experiments are even within the grasp of models incorporating the key experimental details

Open in a new tab

References:

(Refardt & Rainey, 2009);

(Ibarra et al., 2002; Schuetz et al., 2007; Snitkin & Segre, 2008, Perez 2009);

(Kerr et al., 2006; Eshelman et al., 2010; Wild et al., 2009).

A new direction for optimality: insights into the genetics of adaptation

Most of our detailed examples exhibited an unexpected phenotypic evolution or an unexpected genetic basis of phenotype evolution. These and similar studies provide an opportunity to explore novel genetic bases of evolution in an interesting context. So far, this opportunity has not been realized. In no study have the anomalies been explored in depth to yield new insights into the genetics of phenotype evolution, although the T7 lysis study is a reasonable start. Unexpected genetic outcomes may seem a nuisance to anyone interested in optimality per se, but they present an opportunity to develop a new understanding of the genetic basis of phenotypes, one highly relevant to adaptation. Incongruence between expected and observed genetic change is especially exciting for iconic model systems, such as the lac operon in E. coli and induction of λ lysogens, because those systems are thought to be fully understood. Experimental adaptations that led to the expected phenotypic changes by mutations outside the candidate regions may provide the means for reshaping our understanding of those classic genetic systems.

New sequencing technologies enable the easy identification of adaptive mutations, even in eukaryotes. Previously, sequencing has been a hurdle in exploring adaptations. For example, the above-mentioned studies of lac expression and λ induction were limited to sequences of candidate genetic elements; in some replicates of both studies, none of the adaptive mutations were in the candidate regions. Because sequencing was limited to the candidate regions, the ‘anomalous’ mutations were not discovered, despite the intrinsic interest they hold.

Identification of adaptive mutations is merely the first step in resolving the genetic basis of a phenotype, especially when unknown mechanisms are involved. It is commonplace that mutations identified in experimental studies, even of phages and bacteria, have no a priori basis for a phenotypic effect, and merely identifying them gives no special insight into evolution (Wichman et al., 2005; Fiegna et al., 2006; Bull & Molineux, 2008; Barrick et al., 2009). Experimental manipulations, assays involving biochemistry, site-directed mutagenesis, and genomics tools will typically be required to develop a thorough understanding of the genetic bases of phenotypes. The integration of optimality testing with these different levels of investigation may require collaboration across disciplines, but such collaborations are increasingly common.

Future directions

There are obviously many new optimality problems to pursue, and the efforts to integrate experimental evolution, genetics, and optimality are still few. Even so, we may contemplate the types of generalities and new questions that may arise out of future studies, as more examples of optimality success and failure accumulate.

Generalities in the causes of success and failure

Optimality models clearly succeed in some cases, sometimes spectacularly so. But there are many cases where optimality models have failed. If the phenotype-fitness map is correct, the basis of failure must lie within the genotype–phenotype map. A long-term goal of optimality modeling should be to understand general properties of the genotype–phenotype map that predispose the model to success versus failure. We suggest a few possibilities of this nature.

Number of pathways

Even the few studies reviewed here reveal a range of genetic outcomes. In some cases, optimality succeeded by any of several genetic mechanisms – termed ‘phenotypic determinism’ (Oxman et al., 2008) and supporting the ‘phenotypic gambit’ (Grafen, 1984). That is, multiple genetic pathways obeyed the same trade-off and allowed attainment of optimality, as observed in the gene expression study (Dekel & Alon, 2005). In other cases, the model succeeded but the pathway was limited to a single gene – termed ‘genetic determinism’ (Oxman et al., 2008) – illustrated by the T7 optimal foraging study and by holins as a mechanism to allow lysis time evolution. Success of optimality by genetic determinism may require special mechanisms, such as a modular genetic basis of the phenotype. As cases of phenotypic determinism come to be resolved, it will be interesting to search for generalities. Phenotypic determinism seems to underlie many arguments of adaptationism (Williams, 1966; Maynard Smith, 1982; Grafen, 1984), so the resolution of genetics underlying some cases will be most welcome.

Complexity of the genotype–phenotype map and trade-offs

The genotype–phenotype map is more complicated for some optimality problems than others. At one extreme, an optimality problem may be confined to a single parameter, as with optimal seed germination rates (Cohen, 1966), phage adsorption rate, induction of a lysogen, and expression of a single gene. Alternatively, an optimum may involve two or more fitness parameters, as with phage lysis time (affecting also burst size), metabolic networks, and phage growth rate. The genotype–phenotype map may be most suited for attaining the predicted optimum when the optimum involves changes in one parameter rather than several. For example, if evolution of the single parameter is as a result of a single gene and involves no trade-offs in the genotype–phenotype map, then evolution of the optimum is merely a matter of whether mutations in the gene can produce the intermediate value with minimal effects on other fitness traits. As the number of traits in the optimum increases, the potential for pleiotropy and other complications increases. Likewise, trade-offs that lie within the genotype–phenotype map and that involve multiple parameters may be more prone to optimality failure than constraints in the phenotype-fitness map or constraints on single parameters. The genetic and phenotypic simplicity of trade-offs may explain the widespread, often quantitative success of sex allocation models when used to predict sex ratios and sex change in which the alternatives are clear: male or female (West, 2009). Sex allocation has so far experienced considerably less (quantitative) success when predicting sex allocation in simultaneous hermaphrodites, perhaps because the appropriate trade-off between male versus female function is less clear than with male versus female individuals (West, 2009, p. 92).

Duration of adaptation, strength of selection

In an experimental evolution, there is likely a delicate balance between the strength of selection for an optimum and the duration of adaptation. Strong selection speeds evolution and facilitates overcoming drift and other impediments to adaptation. Thus, an optimum more strongly selected should be attained faster and perhaps more exactly than one weakly selected, all else equal (Perez-Escudero, 2009, West, 2009). The impact of strength of selection also depends on the duration of adaptation, and it would seem that attainment of a weakly selected optimum would merely require a longer period of adaptation. However, longer adaptations may be subject to evolution of parameters outside the model, such as a trade-off function. In quantitative genetics, genetic correlations dictate short-term, correlated evolution of phenotypes, but genetic correlations may decay under long-term selection (Falconer, 1981). Once the foundation of the optimality model changes, the optimum is likely to change, and the original model will fail. The actual loss of optimality was observed during the last period of adaptation in the gene expression study of Dekel & Alon (2005).

Evolution of genetic systems

One perspective in this review has been that the genetic system determines the evolutionary response to selection. This perspective may be reversed – the genetic system may evolve in response to selection, allowing the organism to better achieve optimality. The evolution of a new genetic system is a long-term process and will not be captured in most experimental adaptations, unless perhaps augmented by genetic engineering, but experimental tests of optimality (augmented with genetics) may nonetheless foster an understanding of the evolution of genetic systems. As one example from this article, phage lysis mechanisms typically involve a holin acting as a timer of lysis. Holins may have evolved to provide the phage with evolutionary flexibility in its evolution of lysis time (Bull et al., 2004); note that we provided an alternative view above. Likewise, the sex-determining mechanism of sexual species may evolve to enable sex ratio evolution (Charnov & Bull, 1977; Bull, 1983). There are no doubts many examples in which our understanding of the evolution of genetic systems will be enhanced by understanding underlying optimality principles.

Summary

A perspective on optimality models in evolutionary biology is presented. Optimality models have long been criticized for their omission of genetics as the underpinning of adaptation, and although they traditionally have neglected genetic details, there are some profound successes, most notably in sex allocation theory. Yet, the purpose of this review is not to defend or challenge the optimality approach but to show that there is a realm in which optimality models may both overcome this limitation and also be used to explore the genetics of adaptation in meaningful contexts. Experimental evolution of model organisms whose genetics are known enables the informed development of optimality models as well as discovery of the underlying genetics. Studies of bacteriophages and bacteria have begun forging this direction, but genetic analysis of the outcomes has yet to approach its full potential. Predictive models other than optimality models per se are also starting to be used in this fashion, especially to understand evolutionary trajectories of multidimensional phenotypes. The use of experimental evolution in testing predictive models appears to have a promising future, both for understanding evolution and for providing new ways to explore genetics.

Acknowledgments

We thank Stu West for encouragement and detailed comments on a first draft, Tom Caraco for perspective and advice, and Ben Kerr for comments from his laboratory group and for Fig. 1. Three reviewers (Andy Gardner, Tony Dean, and Kate Lessells) provided useful comments, and KL went to great effort to help us clarify our presentation of genotype–phenotype and phenotype-fitness maps. Long-term collaborations with I. J. Molineux and R. Heineman have helped JJB appreciate the value of understanding genetics in testing optimality models and other types of evolutionary predictions. Supported by NIH GM 57756 and the Miescher Regents Professorship (to JJB) and NIH GM 72815 (to INW).

References

Abedon ST. Selection for bacteriophage latent period length by bacterial density: a theoretical examination. Microb. Ecol. 1989;18:79–88. doi: 10.1007/BF02030117. [DOI] [PubMed] [Google Scholar]
Abedon ST, Hyman P, Thomas C. Experimental examination of bacteriophage latent-period evolution as a response to bacterial availability. Appl. Environ. Microbiol. 2003;69:7499–7506. doi: 10.1128/AEM.69.12.7499-7506.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Adams J. Microbial evolution in laboratory environments. Res. Microbiol. 2004;155:311–318. doi: 10.1016/j.resmic.2004.01.013. [DOI] [PubMed] [Google Scholar]
Adams MH. Bacteriophages. New York: Interscience Publishers; 1959. [Google Scholar]
Barrick JE, Yu DS, Yoon SH, Jeong H, Oh TK, Schneider D, Lenski RE, Kim JF. Genome evolution and adaptation in a long-term experiment with escherichia coli. Nature. 2009;461:1243–1247. doi: 10.1038/nature08480. [DOI] [PubMed] [Google Scholar]
Basolo A. The dynamics of fisherian sex-ratio evolution. Am. Nat. 1994;144:473–490. [Google Scholar]
Boomsma JJ, Nielsen J, Sundstrom L, Oldham NJ, Tentschert J, Petersen HC, Morgan ED. Informational constraints on optimal sex allocation in ants. Proc. Natl Acad. Sci. USA. 2003;100:8799–8804. doi: 10.1073/pnas.1430283100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bull JJ. Evolution of Sex Determining Mechanisms. Menlo Park, Calif.: Benjamin/Cummings Pub. Co., Advanced Book Program; 1983. [Google Scholar]
Bull JJ. Virulence. Evolution. 1994;48:1423–1437. doi: 10.1111/j.1558-5646.1994.tb02185.x. [DOI] [PubMed] [Google Scholar]
Bull JJ. Optimality models of phage life history and parallels in disease evolution. J. Theor. Biol. 2006;241:928–938. doi: 10.1016/j.jtbi.2006.01.027. [DOI] [PubMed] [Google Scholar]
Bull JJ, Millstein J, Orcutt J, Wichman HA. Evolutionary feedback mediated through population density, illustrated with viruses in chemostats. Am. Nat. 2006;167:E39–E51. doi: 10.1086/499374. [DOI] [PubMed] [Google Scholar]
Bull JJ, Molineux IJ. Predicting evolution from genomics: experimental evolution of bacteriophage t7. Heredity. 2008;100:453–463. doi: 10.1038/sj.hdy.6801087. [DOI] [PubMed] [Google Scholar]
Bull JJ, Pfennig DW, Wang IN. Genetic details, optimization and phage life histories. Trends Ecol. Evol. (Amst.) 2004;19:76–82. doi: 10.1016/j.tree.2003.10.008. [DOI] [PubMed] [Google Scholar]
Burt A, Trivers R. Genes in Conflict: The Biology of Selfish Genetic Elements. Cambridge, Mass: Belknap Press of Harvard University Press; 2006. [Google Scholar]
Carvalho AB, Sampaio MC, Varandas FR, Klaczko LB. An experimental demonstration of fisher’s principle: evolution of sexual proportion by natural selection. Genetics. 1998;148:719–731. doi: 10.1093/genetics/148.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
Charnov EL. Monographs in population biology. Princeton, NJ: Princeton University Press; 1982. The Theory of Sex Allocation. [PubMed] [Google Scholar]
Charnov EL, Bull J. When is sex environmentally determined? Nature. 1977;266:828–830. doi: 10.1038/266828a0. [DOI] [PubMed] [Google Scholar]
Charnov EL, Stephens DW. On the evolution of host selection in solitary parasitoids. Am. Nat. 1988;132:707–722. [Google Scholar]
Cohen D. Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 1966;12:119–129. doi: 10.1016/0022-5193(66)90188-3. [DOI] [PubMed] [Google Scholar]
Crill WD, Wichman HA, Bull JJ. Evolutionary reversals during viral adaptation to alternating hosts. Genetics. 2000;154:27–37. doi: 10.1093/genetics/154.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
Crow JF, Kimura M. An Introduction to Population Genetics Theory. New York: Harper & Row; 1970. [Google Scholar]
Day T. Parasite transmission modes and the evolution of virulence. Evolution. 2001;55:2389–23400. doi: 10.1111/j.0014-3820.2001.tb00754.x. [DOI] [PubMed] [Google Scholar]
Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]
Dykhuizen D, Hartl D. Transport by the lactose permease of escherichia coli as the basis of lactose killing. J. Bacteriol. 1978;135:876–882. doi: 10.1128/jb.135.3.876-882.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dykhuizen DE. Selection in chemostats. Microbiol. Rev. 1983;47:150–168. doi: 10.1128/mr.47.2.150-168.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dykhuizen DE, Dean AM, Hartl DL. Metabolic ux and fitness. Genetics. 1987;115:25–31. doi: 10.1093/genetics/115.1.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ebert D, Bull JJ. Challenging the trade-off model for the evolution of virulence: is virulence management feasible? Trends Microbiol. 2003;11:15–20. doi: 10.1016/s0966-842x(02)00003-3. [DOI] [PubMed] [Google Scholar]
Emlen JM. The role of time and energy in food preference. Am. Nat. 1966;100:611–617. [Google Scholar]
Eshelman C, Vouk R, Stewart JL, Halsne E, Lindsey HA, Schneider S, Gualu M, Dean AM, Kerr B. Unrestricted migration favours virulent pathogens in experimental metapopulations: Evolutionary genetics of a rapacious life history. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010 doi: 10.1098/rstb.2010.0066. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ewald PW. Evolution of Infectious Disease. Oxford [England]; New York: Oxford University Press; 1994. [Google Scholar]
Falconer DS. Introduction to Quantitative Genetics. 2nd edn. London; New York: Longman; 1981. [Google Scholar]
Ferris MT, Joyce P, Burch CL. High frequency of mutations that expand the host range of an RNA virus. Genetics. 2007;176:1013–1022. doi: 10.1534/genetics.106.064634. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fiegna F, Yu YT, Kadam SV, Velicer GJ. Evolution of an obligate social cheater to a superior cooperator. Nature. 2006;441:310–314. doi: 10.1038/nature04677. [DOI] [PubMed] [Google Scholar]
Fisher RA. The Genetical Theory of Natural Selection. Oxford: The Clarendon Press; 1930. [Google Scholar]
Frank SA. Models of parasite virulence. Q. Rev. Biol. 1996;71:37–78. doi: 10.1086/419267. [DOI] [PubMed] [Google Scholar]
Gardner A. Adaptation as organism design. Biol. Lett. 2009;5:861–864. doi: 10.1098/rsbl.2009.0674. [DOI] [PMC free article] [PubMed] [Google Scholar]
Grafen A. Natural selection, kin selection and group selection. In: Krebs JR, Davies NB, editors. Behavioural Ecology: An Evolutionary Approach. 2nd edn. Oxford, UK: Blackwell Scientific; 1984. pp. 62–84. [Google Scholar]
Grafen A. The formal darwinism project: a mid-term report. J. Evol. Biol. 2007;20:1243–1254. doi: 10.1111/j.1420-9101.2007.01321.x. [DOI] [PubMed] [Google Scholar]
Guyader S, Burch CL. Optimal foraging predicts the ecology but not the evolution of host specialization in bacteriophages. PLoS One. 2008;3:e1946. doi: 10.1371/journal.pone.0001946. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hashemolhosseini S, Holmes Z, Mutschler B, Henning U. Alterations of receptor specificities of coliphages of the t2 family. J. Mol. Biol. 1994a;240:105–110. doi: 10.1006/jmbi.1994.1424. [DOI] [PubMed] [Google Scholar]
Hashemolhosseini S, Montag D, Kramer L, Henning U. Determinants of receptor specificity of coliphages of the t4 family. a chaperone alters the host range. J. Mol. Biol. 1994b;241:524–533. doi: 10.1006/jmbi.1994.1529. [DOI] [PubMed] [Google Scholar]
Heineman RH, Bull JJ. Testing optimality with experimental evolution: lysis time in a bacteriophage. Evolution. 2007;61:1695–1709. doi: 10.1111/j.1558-5646.2007.00132.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heineman RH, Bull JJ, Molineux IJ. Layers of evolvability in a bacteriophage life history trait. Mol. Biol. Evol. 2009;26:1289–1298. doi: 10.1093/molbev/msp037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heineman RH, Springman R, Bull JJ. Optimal foraging by bacteriophages through host avoidance. Am. Nat. 2008;171:E149–E157. doi: 10.1086/528962. [DOI] [PubMed] [Google Scholar]
Hillesland KL, Velicer GJ, Lenski RE. Experimental evolution of a microbial predator’s ability to find prey. Proc. Biol. Sci. 2009;276:459–467. doi: 10.1098/rspb.2008.1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ibarra RU, Edwards JS, Palsson BO. Escherichia coli k-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 2002;420:186–189. doi: 10.1038/nature01149. [DOI] [PubMed] [Google Scholar]
Kerr B, Neuhauser C, Bohannan BJ, Dean AM. Local migration promotes competitive restraint in a host-pathogen ‘tragedy of the commons’. Nature. 2006;442:75–78. doi: 10.1038/nature04864. [DOI] [PubMed] [Google Scholar]
Kerr B, Riley MA, Feldman MW, Bohannan BJ. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418:171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
Krebs JR, Davies NB. Behavioural Ecology: An Evolutionary Approach. 4th edn. Cambridge, Mass: Blackwell Science; 1997. [Google Scholar]
Küummerlie R, Gardner A, West SA, Griffin AS. Limited dispersal, budding dispersal, and cooperation: an experimental study. Evolution. 2009;63:939–949. doi: 10.1111/j.1558-5646.2008.00548.x. [DOI] [PubMed] [Google Scholar]
Levin BR, Bull JJ, Stewart FM. The intrinsic rate of increase of HIV/AIDS: epidemiological and evolutionary implications. Math. Biosci. 1996;132:69–96. doi: 10.1016/0025-5564(95)00053-4. [DOI] [PubMed] [Google Scholar]
Lewontin R. The units of selection. Annu. Rev. Ecol. Syst. 1970;1:1–18. [Google Scholar]
Lewontin RC. Adaptation. Sci. Am. 1978;239:212–230. doi: 10.1038/scientificamerican0978-212. [DOI] [PubMed] [Google Scholar]
Lewontin RC. A natural selection. Nature. 1989;339:107. [Google Scholar]
Lipsitch M, Moxon ER. Virulence and transmissibility of pathogens: what is the relationship? Trends Microbiol. 1997;5:31–37. doi: 10.1016/S0966-842X(97)81772-6. [DOI] [PubMed] [Google Scholar]
Lipsitch M, Nowak MA. The evolution of virulence in sexually transmitted HIV/AIDS. J. Theor. Biol. 1995;174:427–440. doi: 10.1006/jtbi.1995.0109. [DOI] [PubMed] [Google Scholar]
MacArthur RH, Pianka ER. On optimal use of a patchy environment. Am. Nat. 1966;100:603–609. [Google Scholar]
Maynard Smith J. Evolution and the Theory of Games. Cambridge; New York: Cambridge University Press; 1982. [Google Scholar]
Miyazaki JI, Ryo Y, Fujisawa H, Minagawa T. Mutation in bacteriophage t3 affecting host cell lysis. Virology. 1978;89:327–329. doi: 10.1016/0042-6822(78)90067-3. [DOI] [PubMed] [Google Scholar]
Orr HA. The genetic theory of adaptation: a brief history. Nat. Rev. Genet. 2005;6:119–127. doi: 10.1038/nrg1523. [DOI] [PubMed] [Google Scholar]
Orzack S, Sober E. Adaptationism and Optimality. Cambridge Studies in Philosophy and Biology. Cambridge; New York: Cambridge University Press; 2001. [Google Scholar]
Oxman E, Alon U, Dekel E. Defined order of evolutionary adaptations: experimental evidence. Evolution. 2008;62:1547–1554. doi: 10.1111/j.1558-5646.2008.00397.x. [DOI] [PubMed] [Google Scholar]
Pannebakker BA, Halligan DL, Reynolds KT, Ballantyne GA, Shuker DM, Barton NH, West SA. Effects of spontaneous mutation accumulation on sex ratio traits in a parasitoid wasp. Evolution. 2008;62:1921–1935. doi: 10.1111/j.1558-5646.2008.00434.x. [DOI] [PubMed] [Google Scholar]
Paquin CE, Adams J. Relative fitness can decrease in evolving asexual populations of S. cerevisiae. Nature. 1983;306:368–370. doi: 10.1038/306368a0. [DOI] [PubMed] [Google Scholar]
Parker GA. Selfish genes, evolutionary games, and the adaptiveness of behaviour. Nature. 1978;274:849–855. doi: 10.1038/274849a0. [DOI] [PubMed] [Google Scholar]
Parker GA, Maynard Smith J. Optimality theory in evolutionary biology. Nature. 1990;348:27–33. [Google Scholar]
Perez-Escudero A, Rivera-Alba M, de Polavieja GG. Structure of deviations from optimality in biological systems. Proc. Natl Acad. Sci. USA. 2009;106:20544–20549. doi: 10.1073/pnas.0905336106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pierce GJ, Ollasen JG. Eight reasons why optimal foraging theory is a complete waste of time. Oikos. 1987;49:111–118. [Google Scholar]
Ptashne M. A Genetic Switch Phage Lambda Revisited. 3rd edn. Cold Spring Harbor, N.Y.: Cold Spring Harbor Laboratory Press; 2004. [Google Scholar]
Refardt D, Rainey PB. Tuning a genetic switch: experimental evolution and natural variation of prophage induction. Evolution. 2009;64:1086–1097. doi: 10.1111/j.1558-5646.2009.00882.x. [DOI] [PubMed] [Google Scholar]
Riede I, Degen M, Henning U. The receptor specificity of bacteriophages can be determined by a tail fibre modifying protein. Embo J. 1985;4:2343–2346. doi: 10.1002/j.1460-2075.1985.tb03936.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sachs JL, Bull JJ. Experimental evolution of conflict mediation between genomes. Proc. Natl Acad. Sci. USA. 2005;102:390–395. doi: 10.1073/pnas.0405738102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schuetz R, Kuepfer L, Sauer U. Systematic evaluation of objective functions for predicting intracellular fluxes in escherichia coli. Mol. Syst. Biol. 2007;3:119. doi: 10.1038/msb4100162. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shao Y, Wang IN. Bacteriophage adsorption rate and optimal lysis time. Genetics. 2008;180:471–482. doi: 10.1534/genetics.108.090100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shuker DM, West SA. Information constraints and the precision of adaptation: sex ratio manipulation in wasps. Proc. Natl Acad. Sci. USA. 2004;101:10363–10367. doi: 10.1073/pnas.0308034101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Snitkin ES, Segre D. Optimality criteria for the prediction of metabolic uxes in yeast mutants. Genome Inform. 2008;20:123–134. [PubMed] [Google Scholar]
Springman R, Keller T, Molineux IJ, Bull JJ. Evolution at a high imposed mutation rate: adaptation obscures the load in phage t7. Genetics. 2010;184:221–232. doi: 10.1534/genetics.109.108803. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stephens DW, Krebs JR. Foraging Theory. Monographs in Behaviour and Ecology. Princeton, NJ: Princeton University Press; 1986. [Google Scholar]
Stoebel DM, Dean AM, Dykhuizen DE. The cost of expression of escherichia coli lac operon proteins is in the process, not in the products. Genetics. 2008;178:1653–1660. doi: 10.1534/genetics.107.085399. [DOI] [PMC free article] [PubMed] [Google Scholar]
Travisano M, Lenski RE. Long-term experimental evolution in escherichia coli. iv. targets of selection and the specificity of adaptation. Genetics. 1996;143:15–26. doi: 10.1093/genetics/143.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
Vukov N, Scherer S, Hibbert E, Loessner MJ. Functional analysis of heterologous holin proteins in a lambda deltas genetic background. FEMS Microbiol. Lett. 2000;184:179–186. doi: 10.1111/j.1574-6968.2000.tb09011.x. [DOI] [PubMed] [Google Scholar]
Wang IN. Lysis timing and bacteriophage fitness. Genetics. 2006;172:17–26. doi: 10.1534/genetics.105.045922. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang IN, Dykhuizen DE, Slobodkin LB. The evolution of phage lysis timing. Evol. Ecol. 1996;10:545–558. [Google Scholar]
Wang IN, Smith DL, Young R. Holins: the protein clocks of bacteriophage infections. Annu. Rev. Microbiol. 2000;54:799–825. doi: 10.1146/annurev.micro.54.1.799. [DOI] [PubMed] [Google Scholar]
West SA. Sex Allocation. Princeton: Princeton University Press; 2009. [Google Scholar]
West SA, Buckling A. Cooperation, virulence and siderophore production in bacterial parasites. Proc. Biol. Sci. 2003;270:37–44. doi: 10.1098/rspb.2002.2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wichman HA, Millstein J, Bull JJ. Adaptive molecular evolution for 13,000 phage generations: a possible arms race. Genetics. 2005;170:19–31. doi: 10.1534/genetics.104.034488. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wild G, Gardner A, West SA. Adaptation and the evolution of parasite virulence in a connected world. Nature. 2009;459:983–986. doi: 10.1038/nature08071. [DOI] [PubMed] [Google Scholar]
Williams GC. Adaptation and Natural Selection. Princeton, NJ: Princeton University Press; 1966. [Google Scholar]

[R1] Abedon ST. Selection for bacteriophage latent period length by bacterial density: a theoretical examination. Microb. Ecol. 1989;18:79–88. doi: 10.1007/BF02030117. [DOI] [PubMed] [Google Scholar]

[R2] Abedon ST, Hyman P, Thomas C. Experimental examination of bacteriophage latent-period evolution as a response to bacterial availability. Appl. Environ. Microbiol. 2003;69:7499–7506. doi: 10.1128/AEM.69.12.7499-7506.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] Adams J. Microbial evolution in laboratory environments. Res. Microbiol. 2004;155:311–318. doi: 10.1016/j.resmic.2004.01.013. [DOI] [PubMed] [Google Scholar]

[R4] Adams MH. Bacteriophages. New York: Interscience Publishers; 1959. [Google Scholar]

[R5] Barrick JE, Yu DS, Yoon SH, Jeong H, Oh TK, Schneider D, Lenski RE, Kim JF. Genome evolution and adaptation in a long-term experiment with escherichia coli. Nature. 2009;461:1243–1247. doi: 10.1038/nature08480. [DOI] [PubMed] [Google Scholar]

[R6] Basolo A. The dynamics of fisherian sex-ratio evolution. Am. Nat. 1994;144:473–490. [Google Scholar]

[R7] Boomsma JJ, Nielsen J, Sundstrom L, Oldham NJ, Tentschert J, Petersen HC, Morgan ED. Informational constraints on optimal sex allocation in ants. Proc. Natl Acad. Sci. USA. 2003;100:8799–8804. doi: 10.1073/pnas.1430283100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Bull JJ. Evolution of Sex Determining Mechanisms. Menlo Park, Calif.: Benjamin/Cummings Pub. Co., Advanced Book Program; 1983. [Google Scholar]

[R9] Bull JJ. Virulence. Evolution. 1994;48:1423–1437. doi: 10.1111/j.1558-5646.1994.tb02185.x. [DOI] [PubMed] [Google Scholar]

[R10] Bull JJ. Optimality models of phage life history and parallels in disease evolution. J. Theor. Biol. 2006;241:928–938. doi: 10.1016/j.jtbi.2006.01.027. [DOI] [PubMed] [Google Scholar]

[R11] Bull JJ, Millstein J, Orcutt J, Wichman HA. Evolutionary feedback mediated through population density, illustrated with viruses in chemostats. Am. Nat. 2006;167:E39–E51. doi: 10.1086/499374. [DOI] [PubMed] [Google Scholar]

[R12] Bull JJ, Molineux IJ. Predicting evolution from genomics: experimental evolution of bacteriophage t7. Heredity. 2008;100:453–463. doi: 10.1038/sj.hdy.6801087. [DOI] [PubMed] [Google Scholar]

[R13] Bull JJ, Pfennig DW, Wang IN. Genetic details, optimization and phage life histories. Trends Ecol. Evol. (Amst.) 2004;19:76–82. doi: 10.1016/j.tree.2003.10.008. [DOI] [PubMed] [Google Scholar]

[R14] Burt A, Trivers R. Genes in Conflict: The Biology of Selfish Genetic Elements. Cambridge, Mass: Belknap Press of Harvard University Press; 2006. [Google Scholar]

[R15] Carvalho AB, Sampaio MC, Varandas FR, Klaczko LB. An experimental demonstration of fisher’s principle: evolution of sexual proportion by natural selection. Genetics. 1998;148:719–731. doi: 10.1093/genetics/148.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Charnov EL. Monographs in population biology. Princeton, NJ: Princeton University Press; 1982. The Theory of Sex Allocation. [PubMed] [Google Scholar]

[R17] Charnov EL, Bull J. When is sex environmentally determined? Nature. 1977;266:828–830. doi: 10.1038/266828a0. [DOI] [PubMed] [Google Scholar]

[R18] Charnov EL, Stephens DW. On the evolution of host selection in solitary parasitoids. Am. Nat. 1988;132:707–722. [Google Scholar]

[R19] Cohen D. Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 1966;12:119–129. doi: 10.1016/0022-5193(66)90188-3. [DOI] [PubMed] [Google Scholar]

[R20] Crill WD, Wichman HA, Bull JJ. Evolutionary reversals during viral adaptation to alternating hosts. Genetics. 2000;154:27–37. doi: 10.1093/genetics/154.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Crow JF, Kimura M. An Introduction to Population Genetics Theory. New York: Harper & Row; 1970. [Google Scholar]

[R22] Day T. Parasite transmission modes and the evolution of virulence. Evolution. 2001;55:2389–23400. doi: 10.1111/j.0014-3820.2001.tb00754.x. [DOI] [PubMed] [Google Scholar]

[R23] Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]

[R24] Dykhuizen D, Hartl D. Transport by the lactose permease of escherichia coli as the basis of lactose killing. J. Bacteriol. 1978;135:876–882. doi: 10.1128/jb.135.3.876-882.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Dykhuizen DE. Selection in chemostats. Microbiol. Rev. 1983;47:150–168. doi: 10.1128/mr.47.2.150-168.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Dykhuizen DE, Dean AM, Hartl DL. Metabolic ux and fitness. Genetics. 1987;115:25–31. doi: 10.1093/genetics/115.1.25. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Ebert D, Bull JJ. Challenging the trade-off model for the evolution of virulence: is virulence management feasible? Trends Microbiol. 2003;11:15–20. doi: 10.1016/s0966-842x(02)00003-3. [DOI] [PubMed] [Google Scholar]

[R28] Emlen JM. The role of time and energy in food preference. Am. Nat. 1966;100:611–617. [Google Scholar]

[R29] Eshelman C, Vouk R, Stewart JL, Halsne E, Lindsey HA, Schneider S, Gualu M, Dean AM, Kerr B. Unrestricted migration favours virulent pathogens in experimental metapopulations: Evolutionary genetics of a rapacious life history. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010 doi: 10.1098/rstb.2010.0066. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] Ewald PW. Evolution of Infectious Disease. Oxford [England]; New York: Oxford University Press; 1994. [Google Scholar]

[R31] Falconer DS. Introduction to Quantitative Genetics. 2nd edn. London; New York: Longman; 1981. [Google Scholar]

[R32] Ferris MT, Joyce P, Burch CL. High frequency of mutations that expand the host range of an RNA virus. Genetics. 2007;176:1013–1022. doi: 10.1534/genetics.106.064634. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Fiegna F, Yu YT, Kadam SV, Velicer GJ. Evolution of an obligate social cheater to a superior cooperator. Nature. 2006;441:310–314. doi: 10.1038/nature04677. [DOI] [PubMed] [Google Scholar]

[R34] Fisher RA. The Genetical Theory of Natural Selection. Oxford: The Clarendon Press; 1930. [Google Scholar]

[R35] Frank SA. Models of parasite virulence. Q. Rev. Biol. 1996;71:37–78. doi: 10.1086/419267. [DOI] [PubMed] [Google Scholar]

[R36] Gardner A. Adaptation as organism design. Biol. Lett. 2009;5:861–864. doi: 10.1098/rsbl.2009.0674. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] Grafen A. Natural selection, kin selection and group selection. In: Krebs JR, Davies NB, editors. Behavioural Ecology: An Evolutionary Approach. 2nd edn. Oxford, UK: Blackwell Scientific; 1984. pp. 62–84. [Google Scholar]

[R38] Grafen A. The formal darwinism project: a mid-term report. J. Evol. Biol. 2007;20:1243–1254. doi: 10.1111/j.1420-9101.2007.01321.x. [DOI] [PubMed] [Google Scholar]

[R39] Guyader S, Burch CL. Optimal foraging predicts the ecology but not the evolution of host specialization in bacteriophages. PLoS One. 2008;3:e1946. doi: 10.1371/journal.pone.0001946. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Hashemolhosseini S, Holmes Z, Mutschler B, Henning U. Alterations of receptor specificities of coliphages of the t2 family. J. Mol. Biol. 1994a;240:105–110. doi: 10.1006/jmbi.1994.1424. [DOI] [PubMed] [Google Scholar]

[R41] Hashemolhosseini S, Montag D, Kramer L, Henning U. Determinants of receptor specificity of coliphages of the t4 family. a chaperone alters the host range. J. Mol. Biol. 1994b;241:524–533. doi: 10.1006/jmbi.1994.1529. [DOI] [PubMed] [Google Scholar]

[R42] Heineman RH, Bull JJ. Testing optimality with experimental evolution: lysis time in a bacteriophage. Evolution. 2007;61:1695–1709. doi: 10.1111/j.1558-5646.2007.00132.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Heineman RH, Bull JJ, Molineux IJ. Layers of evolvability in a bacteriophage life history trait. Mol. Biol. Evol. 2009;26:1289–1298. doi: 10.1093/molbev/msp037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Heineman RH, Springman R, Bull JJ. Optimal foraging by bacteriophages through host avoidance. Am. Nat. 2008;171:E149–E157. doi: 10.1086/528962. [DOI] [PubMed] [Google Scholar]

[R45] Hillesland KL, Velicer GJ, Lenski RE. Experimental evolution of a microbial predator’s ability to find prey. Proc. Biol. Sci. 2009;276:459–467. doi: 10.1098/rspb.2008.1098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Ibarra RU, Edwards JS, Palsson BO. Escherichia coli k-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 2002;420:186–189. doi: 10.1038/nature01149. [DOI] [PubMed] [Google Scholar]

[R47] Kerr B, Neuhauser C, Bohannan BJ, Dean AM. Local migration promotes competitive restraint in a host-pathogen ‘tragedy of the commons’. Nature. 2006;442:75–78. doi: 10.1038/nature04864. [DOI] [PubMed] [Google Scholar]

[R48] Kerr B, Riley MA, Feldman MW, Bohannan BJ. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418:171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]

[R49] Krebs JR, Davies NB. Behavioural Ecology: An Evolutionary Approach. 4th edn. Cambridge, Mass: Blackwell Science; 1997. [Google Scholar]

[R50] Küummerlie R, Gardner A, West SA, Griffin AS. Limited dispersal, budding dispersal, and cooperation: an experimental study. Evolution. 2009;63:939–949. doi: 10.1111/j.1558-5646.2008.00548.x. [DOI] [PubMed] [Google Scholar]

[R51] Levin BR, Bull JJ, Stewart FM. The intrinsic rate of increase of HIV/AIDS: epidemiological and evolutionary implications. Math. Biosci. 1996;132:69–96. doi: 10.1016/0025-5564(95)00053-4. [DOI] [PubMed] [Google Scholar]

[R52] Lewontin R. The units of selection. Annu. Rev. Ecol. Syst. 1970;1:1–18. [Google Scholar]

[R53] Lewontin RC. Adaptation. Sci. Am. 1978;239:212–230. doi: 10.1038/scientificamerican0978-212. [DOI] [PubMed] [Google Scholar]

[R54] Lewontin RC. A natural selection. Nature. 1989;339:107. [Google Scholar]

[R55] Lipsitch M, Moxon ER. Virulence and transmissibility of pathogens: what is the relationship? Trends Microbiol. 1997;5:31–37. doi: 10.1016/S0966-842X(97)81772-6. [DOI] [PubMed] [Google Scholar]

[R56] Lipsitch M, Nowak MA. The evolution of virulence in sexually transmitted HIV/AIDS. J. Theor. Biol. 1995;174:427–440. doi: 10.1006/jtbi.1995.0109. [DOI] [PubMed] [Google Scholar]

[R57] MacArthur RH, Pianka ER. On optimal use of a patchy environment. Am. Nat. 1966;100:603–609. [Google Scholar]

[R58] Maynard Smith J. Evolution and the Theory of Games. Cambridge; New York: Cambridge University Press; 1982. [Google Scholar]

[R59] Miyazaki JI, Ryo Y, Fujisawa H, Minagawa T. Mutation in bacteriophage t3 affecting host cell lysis. Virology. 1978;89:327–329. doi: 10.1016/0042-6822(78)90067-3. [DOI] [PubMed] [Google Scholar]

[R60] Orr HA. The genetic theory of adaptation: a brief history. Nat. Rev. Genet. 2005;6:119–127. doi: 10.1038/nrg1523. [DOI] [PubMed] [Google Scholar]

[R61] Orzack S, Sober E. Adaptationism and Optimality. Cambridge Studies in Philosophy and Biology. Cambridge; New York: Cambridge University Press; 2001. [Google Scholar]

[R62] Oxman E, Alon U, Dekel E. Defined order of evolutionary adaptations: experimental evidence. Evolution. 2008;62:1547–1554. doi: 10.1111/j.1558-5646.2008.00397.x. [DOI] [PubMed] [Google Scholar]

[R63] Pannebakker BA, Halligan DL, Reynolds KT, Ballantyne GA, Shuker DM, Barton NH, West SA. Effects of spontaneous mutation accumulation on sex ratio traits in a parasitoid wasp. Evolution. 2008;62:1921–1935. doi: 10.1111/j.1558-5646.2008.00434.x. [DOI] [PubMed] [Google Scholar]

[R64] Paquin CE, Adams J. Relative fitness can decrease in evolving asexual populations of S. cerevisiae. Nature. 1983;306:368–370. doi: 10.1038/306368a0. [DOI] [PubMed] [Google Scholar]

[R65] Parker GA. Selfish genes, evolutionary games, and the adaptiveness of behaviour. Nature. 1978;274:849–855. doi: 10.1038/274849a0. [DOI] [PubMed] [Google Scholar]

[R66] Parker GA, Maynard Smith J. Optimality theory in evolutionary biology. Nature. 1990;348:27–33. [Google Scholar]

[R67] Perez-Escudero A, Rivera-Alba M, de Polavieja GG. Structure of deviations from optimality in biological systems. Proc. Natl Acad. Sci. USA. 2009;106:20544–20549. doi: 10.1073/pnas.0905336106. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Pierce GJ, Ollasen JG. Eight reasons why optimal foraging theory is a complete waste of time. Oikos. 1987;49:111–118. [Google Scholar]

[R69] Ptashne M. A Genetic Switch Phage Lambda Revisited. 3rd edn. Cold Spring Harbor, N.Y.: Cold Spring Harbor Laboratory Press; 2004. [Google Scholar]

[R70] Refardt D, Rainey PB. Tuning a genetic switch: experimental evolution and natural variation of prophage induction. Evolution. 2009;64:1086–1097. doi: 10.1111/j.1558-5646.2009.00882.x. [DOI] [PubMed] [Google Scholar]

[R71] Riede I, Degen M, Henning U. The receptor specificity of bacteriophages can be determined by a tail fibre modifying protein. Embo J. 1985;4:2343–2346. doi: 10.1002/j.1460-2075.1985.tb03936.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Sachs JL, Bull JJ. Experimental evolution of conflict mediation between genomes. Proc. Natl Acad. Sci. USA. 2005;102:390–395. doi: 10.1073/pnas.0405738102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Schuetz R, Kuepfer L, Sauer U. Systematic evaluation of objective functions for predicting intracellular fluxes in escherichia coli. Mol. Syst. Biol. 2007;3:119. doi: 10.1038/msb4100162. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Shao Y, Wang IN. Bacteriophage adsorption rate and optimal lysis time. Genetics. 2008;180:471–482. doi: 10.1534/genetics.108.090100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R75] Shuker DM, West SA. Information constraints and the precision of adaptation: sex ratio manipulation in wasps. Proc. Natl Acad. Sci. USA. 2004;101:10363–10367. doi: 10.1073/pnas.0308034101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Snitkin ES, Segre D. Optimality criteria for the prediction of metabolic uxes in yeast mutants. Genome Inform. 2008;20:123–134. [PubMed] [Google Scholar]

[R77] Springman R, Keller T, Molineux IJ, Bull JJ. Evolution at a high imposed mutation rate: adaptation obscures the load in phage t7. Genetics. 2010;184:221–232. doi: 10.1534/genetics.109.108803. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R78] Stephens DW, Krebs JR. Foraging Theory. Monographs in Behaviour and Ecology. Princeton, NJ: Princeton University Press; 1986. [Google Scholar]

[R79] Stoebel DM, Dean AM, Dykhuizen DE. The cost of expression of escherichia coli lac operon proteins is in the process, not in the products. Genetics. 2008;178:1653–1660. doi: 10.1534/genetics.107.085399. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Travisano M, Lenski RE. Long-term experimental evolution in escherichia coli. iv. targets of selection and the specificity of adaptation. Genetics. 1996;143:15–26. doi: 10.1093/genetics/143.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Vukov N, Scherer S, Hibbert E, Loessner MJ. Functional analysis of heterologous holin proteins in a lambda deltas genetic background. FEMS Microbiol. Lett. 2000;184:179–186. doi: 10.1111/j.1574-6968.2000.tb09011.x. [DOI] [PubMed] [Google Scholar]

[R82] Wang IN. Lysis timing and bacteriophage fitness. Genetics. 2006;172:17–26. doi: 10.1534/genetics.105.045922. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] Wang IN, Dykhuizen DE, Slobodkin LB. The evolution of phage lysis timing. Evol. Ecol. 1996;10:545–558. [Google Scholar]

[R84] Wang IN, Smith DL, Young R. Holins: the protein clocks of bacteriophage infections. Annu. Rev. Microbiol. 2000;54:799–825. doi: 10.1146/annurev.micro.54.1.799. [DOI] [PubMed] [Google Scholar]

[R85] West SA. Sex Allocation. Princeton: Princeton University Press; 2009. [Google Scholar]

[R86] West SA, Buckling A. Cooperation, virulence and siderophore production in bacterial parasites. Proc. Biol. Sci. 2003;270:37–44. doi: 10.1098/rspb.2002.2209. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R87] Wichman HA, Millstein J, Bull JJ. Adaptive molecular evolution for 13,000 phage generations: a possible arms race. Genetics. 2005;170:19–31. doi: 10.1534/genetics.104.034488. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R88] Wild G, Gardner A, West SA. Adaptation and the evolution of parasite virulence in a connected world. Nature. 2009;459:983–986. doi: 10.1038/nature08071. [DOI] [PubMed] [Google Scholar]

[R89] Williams GC. Adaptation and Natural Selection. Princeton, NJ: Princeton University Press; 1966. [Google Scholar]

System	Results
Lactose metabolism¹	Interacting phenotypes abound in metabolism because chemical modifications are ordered: the fitness impact of one step in a metabolic chain depends on the supply of substrate generated by upstream steps. A simple system of interaction was tested for lactose utilization by Escherichia coli. Entry of lactose into the cell must occur before metabolism offers any benefit, and the two steps are each effected by different proteins: permease for entry and β-galactosidase for metabolism. The selective effects of changes in levels of one enzyme depend on the levels of the other enzyme, and if permease levels are low but β-galactosidase levels are moderate or high in an environment with lactose, then early selection is for increases in permease. These interactions were measured and confirmed by partial mapping of the predicted fitness landscape. The study used a combination of natural mutants as well as physiological manipulations, without adaptations
Phage lysis versus adsorption²	A λ phage lacking side tail fibres is expected to evolve a relatively late lysis time because of its low adsorption rate. If lysis time and tail fibres are both allowed to evolve, one trait is often more strongly selected than the other: when adsorption rate is far from the optimum, its evolution is expected to take precedence over lysis time evolution unless lysis time is profoundly suboptimal. Competition studies among phages differing in both lysis time and side tail fibre status supported the predictions. The genetic variants were introduced in this study, so prediction was easy – high-adsorption mutants were already present – allowing the phage to achieve major fitness gains in a single step
Evolutionary feedback through population density³	When a population invades a new environment to which it is poorly adapted, equilibrium densities will often be low. Adaptation during this phase should be primarily to external conditions, because direct competitive interactions among conspecifics are uncommon. As adaptation progresses, density may increase, leading to an increase in interactions and selection on direct competition. In experimental adaptations of phage to chemostat environments, initial adaptation consistently resulted in higher density, whereas later adaptation varied in its effect on density, consistent with a shift in selection. Following the initial phase of evolution, one of four replicate populations even evolved a polymorphic state containing a defective genome whose existence absolutely required high population densities
Multiphase life histories⁴	The life history of E. coli subjected to serial transfer includes three phases: exponential growth, stationary phase at saturation, and lag phase when cells are diluted into new media, prior to initiation of exponential growth. Adaptation can improve any of these steps, but models suggested that, for a particular protocol, greater fitness improvement would result by first reducing the time in lag phase than from increasing exponential growth rate. Experimental adaptations exhibited the predicted evolutionary precedence; the genetic bases were not resolved at a molecular level, but two mutations were implicated in the lag phase improvement. The protocol was then modified so that greater benefit was predicted from enhancement of growth rate; experiments supported the reversed precedence

PERMALINK

Optimality models in the age of experimental evolution and genomics

J J Bull

I-N Wang

Abstract

Introduction

Characteristics of optimality models

Why optimality

Basics

Phenotype-fitness maps and genotype–phenotype maps

Fig. 1.

Trade-offs and other constraints

Testing optimality models

How an optimality model may fail

Experimental evolution

Mutation introductions versus de novo evolution

Tests of optimality are enhanced by experimental evolution and genomics

Experimental evolution facilitates identifying and partitioning the causes of model failure

Experimental evolution allows integrating optimality tests with genetics

Optimality studies using microbes

Bacteriophages: the basic phenotype-fitness map has three phenotypes

Fig. 2.

Optimal diets: phage host range

Fig. 3.

Genetic mechanisms

Fig. 4.

Table 1.

Phage lysis time

Evolution of lysis time: the basic result

A lysis time optimum

Fig. 5.

Physiology and genetics justify trade-off linearity

Consequences of genetic imperfections around linearity

Fig. 6.

Experimental tests: the basic prediction is supported, optimality sometimes

Table 2.

Virulence

Enzyme expression levels in bacteria

Other examples

Table 3.

A new direction for optimality: insights into the genetics of adaptation

Related problems

Evolutionary trajectories with multiple phenotypes

A common principle: differential selection

Table 4.

Conflict resolution

Future directions

Generalities in the causes of success and failure

Number of pathways

Complexity of the genotype–phenotype map and trade-offs

Duration of adaptation, strength of selection

Evolution of genetic systems

Summary

Acknowledgments

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases