Heuristic RNA pseudoknot prediction including intramolecular kissing hairpins

Abstract

Pseudoknots are an essential feature of RNA tertiary structures. Simple H-type pseudoknots have been studied extensively in terms of biological functions, computational prediction, and energy models. Intramolecular kissing hairpins are a more complex and biologically important type of pseudoknot in which two hairpin loops form base pairs. They are hard to predict using free energy minimization due to high computational requirements. Heuristic methods that allow arbitrary pseudoknots strongly depend on the quality of energy parameters, which are not yet available for complex pseudoknots. We present an extension of the heuristic pseudoknot prediction algorithm DotKnot, which covers H-type pseudoknots and intramolecular kissing hairpins. Our framework allows for easy integration of advanced H-type pseudoknot energy models. For a test set of RNA sequences containing kissing hairpins and other types of pseudoknot structures, DotKnot outperforms competing methods from the literature. DotKnot is available as a web server under http://dotknot.csse.uwa.edu.au.

INTRODUCTION

Pseudoknots are versatile structural elements that are abundant in both cellular and viral RNA. The first pseudoknots were experimentally identified in the early 1980s in tRNA-like structures in plant viruses (Rietveld et al. 1982, 1983). Subsequently, the pseudoknot folding principle was established (Pleij et al. 1985) and, over the years, many pseudoknots with an astonishing number of diverse functions have been discovered. Pseudoknots are known to participate in protein synthesis, genome and viral replication, and ribozyme structure and function (Staple and Butcher 2005; Brierley et al. 2007, 2008; Giedroc and Cornish 2009). H-type pseudoknots form when unpaired bases in a hairpin loop bond with unpaired bases outside the loop and have been found essential in the context of programmed -1 ribosomal frameshifting, telomerase RNA, and viral internal ribosome entry sites.

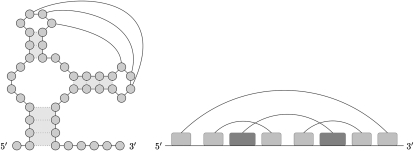
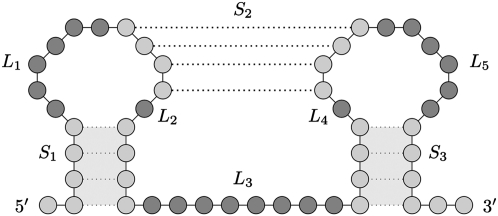
Simple H-type pseudoknots are the best-studied group of RNA pseudoknots and constitute the vast majority of entries in the pseudoknot database Pseudobase (van Batenburg et al. 2001). However, this should not lead to the conclusion that different types of pseudoknots are less frequent or less important in RNA three-dimensional folding and function. A more complex pseudoknot forms when unpaired bases in a hairpin loop bond with unpaired bases in another hairpin loop (Fig. 1). This type of pseudoknot is called an intramolecular kissing hairpin, H-H type pseudoknot, or loop-loop pseudoknot. The hairpin loops can also be located in different RNA molecules, which is referred to as an intermolecular kissing hairpin, RNA-RNA interaction, or a kissing complex (Brunel et al. 2002). Intramolecular kissing hairpins have been reported in different virus families as essential features for viral replication (Melchers et al. 1997; Verheije et al. 2002; Friebe et al. 2005). Kissing hairpins have also been found in some hammerhead ribozymes (Song et al. 1999; Gago et al. 2005), the Varkud satellite ribozyme (Rastogi et al. 1996), or as part of the signal recognition particle (Larsen and Zwieb 1991).

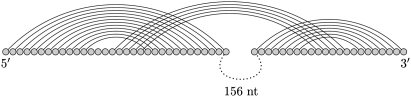
FIGURE 1.

Intramolecular kissing hairpin structure and its representation as crossing intervals on the line.

Due to the crossing of three stems, intramolecular kissing hairpin prediction is more complex than prediction of simple H-type pseudoknots. Most discoveries of kissing hairpins have been made in the laboratory with little aid of computational methods due to the lack of practical prediction algorithms. General kissing interactions are hard to predict as it leaves the field of secondary structure prediction, both in terms of the computational complexity and the energy model. Given an RNA sequence, the minimum free-energy (MFE) secondary structure without crossing base pairs can be calculated in O(n³) time and O(n²) space under an additive energy model using dynamic programming (Zuker and Stiegler 1981; Lyngsø et al. 1999). Free-energy minimization, including general pseudoknots, has been proven to be an NP-complete problem (Lyngsø and Pedersen 2000a). By restricting the types of pseudoknots that can be predicted, polynomial-time dynamic programming methods can be achieved. Rivas and Eddy (1999) introduced pknots for MFE structure prediction, including a broad class of pseudoknots such as chains of pseudoknots and kissing hairpins which take O(n⁶) time and O(n⁴) space. More practical algorithms run in O(n⁵) or O(n⁴) time, depending on the pseudoknot target class; however, kissing hairpins are not included in the recursion schemes (Akutsu 2000; Dirks and Pierce 2003; Reeder and Giegerich 2004). A tree-adjoining grammar algorithm by Uemura et al. (1999) using O(n⁵) time and O(n⁴) space allows pseudoknot chains of length three under a very simple energy model. Lyngsø and Pedersen (2000b) give a high-level description of a dynamic programming algorithm using O(n⁵) time and O(n³) space, which can predict kissing hairpins. A dynamic programming method requiring O(n⁵) time and O(n⁴) space for MFE structure prediction was presented by Chen et al. (2009) and includes kissing hairpins and chains of four overlapping stems. Apart from pknots, no implementations are readily available for MFE structure prediction, including intramolecular kissing hairpins.

Due to the computational complexity of dynamic programming for pseudoknot prediction, heuristic algorithms have been developed. A number of heuristic RNA structure prediction methods explicitly include kissing hairpins. FlexStem is a heuristic algorithm with the ability to fold overlapping pseudoknots, i.e., intramolecular kissing hairpins (Chen et al. 2008). HFold is based on the MFE folding for secondary structures and hierarchically calculates a joint structure using the available bases from a given secondary structure. The predicted structure may contain pseudoknots and (nested) kissing hairpins (Jabbari et al. 2008). A range of heuristic RNA structure prediction algorithms cover general types of pseudoknots and may, therefore, implicitly predict kissing hairpins. However, the pseudoknot target class remains elusive and there are no specific energy parameters for kissing hairpins. For example, simple kissing hairpins can be predicted by iterated stem adding procedures such as iterated loop matching (ILM) and HotKnots (Ruan et al. 2004; Ren et al. 2005; Andronescu et al. 2010). It must be noted that the underlying energy parameters may not be tuned for kissing hairpin prediction, and thus only very stable kissing hairpins are likely to be predicted.

Here, we present an extension of the heuristic pseudoknot search method DotKnot for prediction of H-type pseudoknots (Sperschneider and Datta 2010). DotKnot was initially designed as a specialized H-type pseudoknot folding method which returns only the detected pseudoknots for a given sequence. Our main contributions reported here are the following:

• Efficient prediction of a wider class of pseudoknots, namely intramolecular kissing hairpins.

• Prediction of a global structure to allow for performance evaluation with widely used algorithms for secondary structure prediction including pseudoknots.

• Prediction of a number of near-optimal pseudoknot and kissing hairpin candidates for further investigation by the user.

The main idea of the DotKnot method is to assemble pseudoknots in a constructive fashion from the secondary structure probability dot plot calculated by RNAfold (McCaskill 1990; Hofacker et al. 1994). Using a low-probability threshold, pseudoknotted stems can be seen in the dot plot. From the set of stem candidates found in the dot plot, DotKnot derives a candidate set of secondary structure elements, H-type pseudoknots, and kissing hairpins. The presence of the structure elements in the global structure is verified using maximum weight independent set calculations.

There are two main advantages of this heuristic approach. First, it is very efficient and therefore practical for longer RNA sequences. This is important as kissing loop interactions are known to stabilize the overall tertiary folding and are often long-range interactions. In contrast, kissing hairpin prediction using dynamic programming suffers from high computational requirements. For example, pknots is only able to run for sequences shorter than, say, 150 nt. Second, practical dynamic programming methods are fairly restricted with regards to the underlying additive energy model; however, nonadditive H-type pseudoknot energy models have been developed that are based on the important interference between opposite stems and loops (Gultyaev et al. 1995; Cao and Chen 2006, 2009). Heuristic methods such as DotKnot, which construct a number of pseudoknot candidates, allow for easy integration of such nonadditive H-type pseudoknot energy models, which can drastically improve prediction accuracy.

In the remainder of this paper, we evaluate the performance of DotKnot and several other methods from the literature and discuss the results for kissing hairpin prediction in detail. Afterward a description of the algorithmic framework of the DotKnot method is given and we show how DotKnot derives a global structure and near-optimal pseudoknots.

RESULTS

Kissing hairpin prediction can be handled by an extended version of DotKnot, pknots, and FlexStem. These methods are chosen for the evaluation because they employ specific energy parameters for kissing hairpins. The secondary structure prediction algorithm RNAfold is also included in the testing to compare results to a hierarchical folding approach where the kissing interaction is added by hand after obtaining the MFE structure. Note that only those algorithms that are freely available are compared. No implementation is available for a dynamic programming method for kissing hairpin prediction described in Lyngsø and Pedersen (2000b), Chen et al. (2009), and HFold (Jabbari et al. 2008).

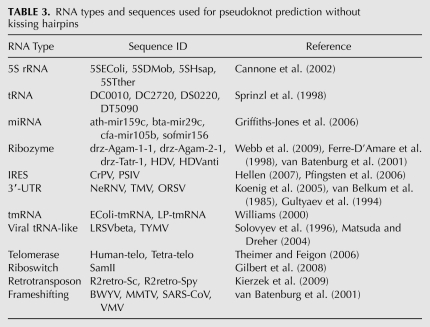
The test set for the kissing hairpin prediction evaluation is shown in Table 1. The number of kissing hairpins described and verified in the literature is fairly limited. For long RNA sequences including kissing hairpins, such as the signal recognition particle RNA (SRP RNA), structure prediction is also performed for the short sequence exactly harboring the kissing hairpin. This is done in order to compare prediction results to the computationally expensive pknots and to observe whether prediction accuracy improves for all methods if a short kissing hairpin sequence is given.

TABLE 1.

RNA types and sequences used for kissing hairpin prediction

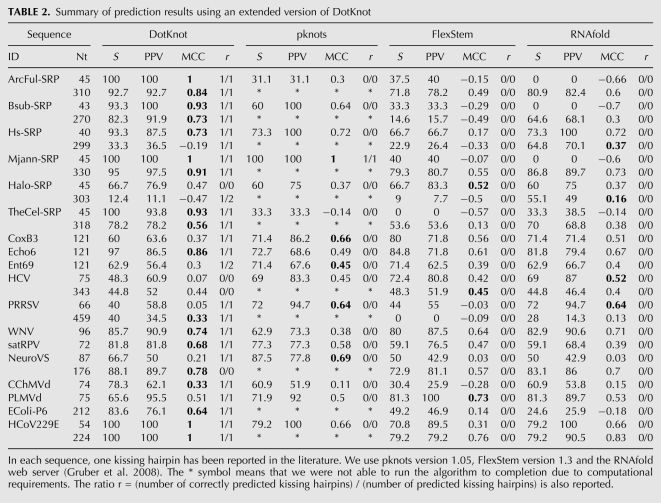
For each kissing hairpin reference structure in the test set, the predicted base pairs are analyzed and results are shown in Table 2. The number of correctly and incorrectly predicted base pairs in the global structure is counted (TP and FP). The number of base pairs in the reference structure that were not predicted is also reported (FN). Sensitivity S is defined as S = 100 × (TP/TP + FN), positive predictive value (PPV) as PPV = 100 × (TP/TP + FP), and Matthews correlation coefficient (MCC) as:

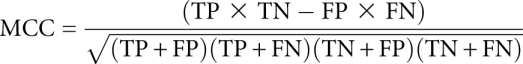The Matthews correlation coefficient is in the range from -1 to 1, where 1 corresponds to a perfect prediction and -1 to a prediction that is in total disagreement with the reference structure.

TABLE 2.

Summary of prediction results using an extended version of DotKnot

RESULTS

Structures with kissing hairpins

Signal recognition particle (SRP) RNA

The signal recognition particle (SRP) is a protein-RNA complex and participates in the translocation of proteins across membranes (Keenan et al. 2001). At the center is the SRP RNA, which typically consists of around 300 nt. A number of SRP RNA sequences with predicted secondary structures are available, for example for Archaeoglobus fulgidus, Bacillus subtilis, Homo sapiens, Methanococcus jannaschii, Halobacterium halobium, and Thermococcus celer (Zwieb and Samuelsson 2000). Tertiary kissing interactions have been established close to the 5′-end using phylogenetic analysis and molecular modeling (Larsen and Zwieb 1991; Zwieb and Müller 1997). The highly conserved kissing hairpin is a compact structure (Fig. 2). We evaluated the predictions for these six SRP RNA sequences and also for the corresponding six short sequences exactly harboring the kissing interaction. DotKnot predicts a kissing hairpin for all sequences except for the short Halobacterium halobium SRP RNA and shows the highest MCC for nine of the 12 sequences. Both DotKnot and pknots give perfect predictions (MCC = 1) for the Methanococcus jannaschii kissing hairpin and DotKnot also perfectly predicts the kissing hairpin in Archaeoglobus fulgidus. The prediction results for all four methods are poor for the long Halobacterium halobium SRP RNA. For the short sequence stretch, DotKnot returns a pseudoknot with lower free energy than the kissing hairpin. However, the desired kissing hairpin structure is found as the best near-optimal pseudoknot with lowest free energy (MCC = 1).

FIGURE 2.

Bacillus subtilis SRP RNA kissing hairpin structure as found in the Signal Recognition Particle Database (Zwieb and Müller 1997).

Viral replication

A kissing hairpin involving the poly(A)-tail is essential for synthesis of negative-strand RNA in the enteroviral 3′-UTR, e.g., in the Coxsackie B3 virus (Melchers et al. 1997). This tertiary structure element is highly conserved amongst members of the enteroviruses (Mirmomeni et al. 1997). The three sequences Coxsackie B3 virus, human echovirus 6, and human enterovirus 69 are chosen as a test set (Wang et al. 1999; Gardner et al. 2009). DotKnot predicts kissing hairpins in all of the three sequences and shows the best prediction for human echovirus 6 (MCC = 0.86). FlexStem and pknots predict no kissing hairpins and show a significantly lower MCC than DotKnot for the structure; however, pknots returns the best predictions for Coxsackie B3 virus and human enterovirus 69.

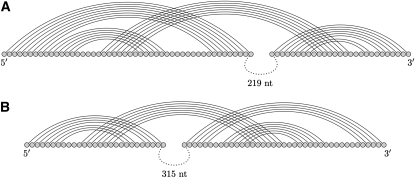
Initiation of negative-strand synthesis using a long-range kissing loop structure forming between coding and noncoding regions has been proposed for other virus families such as Flaviviridae and Nidovirales (Fig. 3). A kissing interaction has been established in the hepatitis C virus (HCV) involving the NS5B coding region and 3′-UTR (Friebe et al. 2005). In the porcine reproductive and respiratory syndrome virus (PRRSV), a hairpin loop in the ORF7 region bonds with another hairpin loop in the 3′-NCR (Verheije et al. 2002). The kissing hairpins in HCV and PRRSV are long-range interactions that span 219 nt and 315 nt, respectively.

FIGURE 3.

Long-range kissing hairpin interactions between coding and noncoding regions in the (A) hepatitis C virus (HCV) and (B) porcine reproductive and respiratory syndrome virus (PRRSV).

For the HCV long-range kissing hairpin, FlexStem and DotKnot predict nested structures with MCCs of 0.45 and 0.44, respectively. However, it is worth noting that the desired kissing hairpin structure is found as the best near-optimal pseudoknot with lowest free energy by DotKnot. For the PRRSV long-range interaction, DotKnot returns a short-range kissing hairpin structure involving one of the two hairpins and has the highest MCC of 0.33. Amongst the top three near-optimal pseudoknots with lowest free energy, DotKnot returns the reference long-range kissing hairpin involving both hairpins. To allow for a performance evaluation of pknots, results were also obtained for short sequences where the long loop between the coding and noncoding region is removed. For the short HCV sequence, RNAfold has the highest MCC as it correctly predicts most base pairs of the kissing hairpin stems S₁ and S₃. No kissing hairpin is predicted by DotKnot, pknots, and FlexStem. DotKnot predicts an H-type pseudoknot for the HCV sequence and has the lowest MCC amongst the kissing hairpin prediction algorithms. For the short PRRSV sequence, pknots and RNAfold correctly identify the noncrossing kissing hairpin stems S₁ and S₃, missing only one base pair. DotKnot is the only method which predicts a kissing hairpin for the PRRSV sequence; however, with lower MCC than the noncrossing predictions returned by pknots and RNAfold.

A compact kissing hairpin in the West Nile virus 3′-NCR is likely to be involved in viral replication (Shi et al. 1996). This structure element was suggested to be conserved in other flaviviruses, such as dengue virus (involving G-A base pairs) and yellow fever virus; however, further phylogenetic and structural investigation is needed. DotKnot returns a kissing hairpin structure and shows the highest MCC of 0.74 for all methods. A pseudoknotted MFE structure is returned by pknots and FlexStem predicts a noncrossing secondary structure with lower MCC than RNAfold.

Ribozymes

During genome replication, the hammerhead ribozyme in the satellite RNA of cereal yellow dwarf virus (satRPV) can alternatively form a compact kissing hairpin structure to inhibit self-cleavage (Song et al. 1999). DotKnot correctly identifies the kissing hairpin and has the highest MCC of 0.68. pknots has the second-highest MCC of 0.58 and predicts a H-type pseudoknot as the MFE structure. RNAfold shows the lowest MCC for all methods due to competing secondary structure elements.

Rastogi et al. (1996) report a kissing interaction in the Neurospora VS ribozyme. The pseudoknot is required for self-cleavage activity and forms in the presence of magnesium. In particular, the kissing interaction involves a hairpin loop within a multiloop structure. For the short Neurospora VS ribozyme sequence exactly harboring the kissing hairpin, DotKnot is the only method that predicts a kissing interaction (MCC = 0.21). A higher MCC of 0.69 is achieved by pknots for prediction of a noncrossing secondary structure. For the longer sequence, none of the algorithms predict a kissing hairpin. DotKnot returns a structure without any pseudoknots or kissing hairpins, yet it has the highest MCC of 0.78 for all methods. In particular, it perfectly predicts the multiloop structure using the MWIS calculations, whereas FlexStem and RNAfold have a lower MCC for their secondary structure predictions.

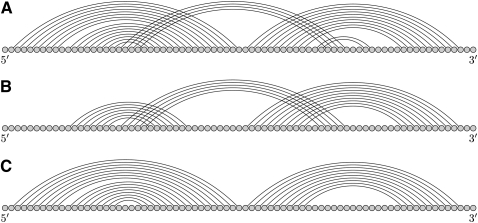
Viroids are 250–400-nt-long single-stranded RNAs that infect plants. Viroids are much smaller than viruses and contain no protective protein coat; therefore, the RNA secondary and tertiary structure of a viroid is critical for its life cycle and infection of the host cell. The group A peach latent mosaic viroid (PLMVd) and chrysanthemum chlorotic mottle viroid (CChMVd) can form hammerhead ribozymes and have been proposed to fold into a branched secondary structure containing a kissing loop interaction (Bussiere et al. 2000; Gago et al. 2005). DotKnot is the only method which predicts kissing hairpins for both sequences and has the highest MCC for the CChMVd structure. For the PLMVd kissing hairpin, FlexStem achieves the highest MCC by correctly predicting the noncrossing stems S₁ and S₃. In contrast, DotKnot correctly identifies the kissing interaction S₂, but does not predict parts of stem S₁ because it is interrupted by a bulge loop. A comparison of the prediction results is shown in Figure 4.

FIGURE 4.

(A) The peach latent mosaic viroid (PLMVd) P8 pseudoknot is a kissing interaction between the P6 and P7 stems. The proposed structure for the complete 338-nt-long PLMVd viroid is described in Bussiere et al. (2000). (B) DotKnot predicts the minimal kissing interaction, however misses parts of stem S1 due to a bulge loop (MCC = 0.51). (C) FlexStem predicts the noncrossing stems, but no kissing interaction (MCC = 0.73).

Ribonuclease P (RNase P) is a ribozyme which cleaves precursor tRNA molecules. Archaeal and bacterial RNase P RNA structure is highly conserved. The Escherichia coli RNase P RNA contains a kissing hairpin structure (P6) nested within a pseudoknot (P4) (Westhof and Altman 1994; Brown 1999; Harris et al. 2001). Only the minimal sequence stretch covering the kissing hairpin P6 is used in the test set, as pseudoknots with internal crossing structures are not considered in the DotKnot algorithm. DotKnot predicts the kissing hairpin interaction with the highest MCC of 0.64. In contrast, RNAfold has a low MCC of -0.18 for the predicted MFE secondary structure. FlexStem predicts two pseudoknots for the sequence (MCC = 0.14).

Programmed -1 ribosomal frameshifting

Programmed -1 ribosomal frameshifting in some group 1 coronaviruses is facilitated by a long-range kissing hairpin (Fig. 5). The kissing hairpin has been confirmed in human coronavirus 229E (HCoV-229E) (Herold and Siddell 1993) and has been suggested for other group 1 members, such as TGEV, HCoV-NL63, and PEDV using phylogenetic analysis (Eleouet et al. 1995; Baranov et al. 2005; Plant et al. 2005). One should note that the TGEV frameshifting site has the potential to fold into a three-stemmed pseudoknot, as observed in the SARS coronavirus (Plant et al. 2005). For both the long and short HCoV-229E sequences, DotKnot returns the kissing hairpin with MCC of 1. All other methods do not find the kissing hairpin and have significantly lower predictive accuracy.

FIGURE 5.

Human coronavirus 229E (HCoV-229E) long-range kissing hairpin.

Structures without kissing hairpins

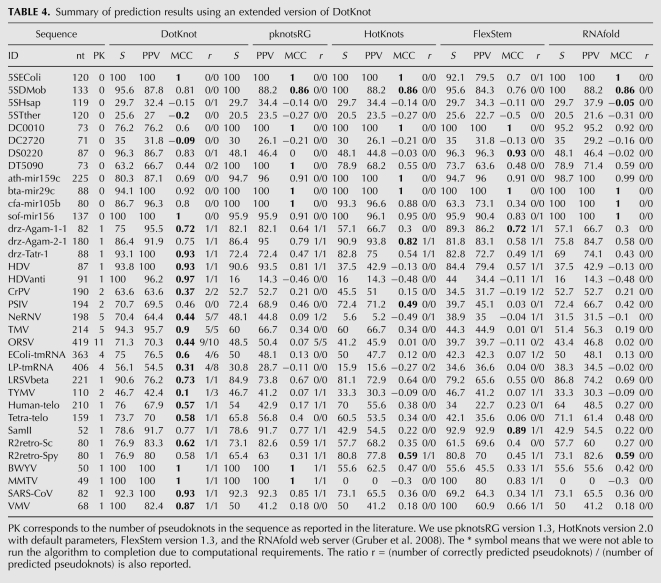
A test set for RNA structures without kissing hairpins is used to assess the prediction of false positive kissing hairpins by DotKnot and to evaluate the prediction results for a number of methods from the literature. The test set contains pseudoknot-free sequences (5S rRNA, tRNA, and miRNA) and sequences which contain one or more pseudoknots and are reported in the pseudoknot database Pseudobase (Table 3; van Batenburg et al. 2001). The sequence lengths range from 52 nt to 419 nt. Predictions are obtained from the practical dynamic programming algorithm pknotsRG (Reeder and Giegerich 2004), the heuristic methods HotKnots (Ren et al. 2005; Andronescu et al. 2010), and FlexStem (Chen et al. 2008), as well as the secondary structure prediction algorithm RNAfold (Hofacker et al. 1994). Results are shown in Table 4.

TABLE 3.

RNA types and sequences used for pseudoknot prediction without kissing hairpins

TABLE 4.

Summary of prediction results using an extended version of DotKnot

For our test set of pseudoknot-free structures, DotKnot predicts spurious H-type pseudoknots and kissing hairpins in three of the 12 sequences. For the nested structures, the dynamic programming methods pknotsRG and RNAfold show the highest average MCCs of 0.59 and 0.57, respectively. DotKnot and HotKnots both have an average MCC of 0.55, and FlexStem achieves 0.52.

For our test set of pseudoknotted structures, false positive kissing hairpins are predicted in one of the viral 3′-UTR structures (ORSV), in the Escherichia coli tmRNA, and the turnip yellow mosaic virus (TYMV) tRNA-like structure. No spurious hairpins are predicted for any of the remaining sequences in the test set. It should be noted that for the Escherichia coli tmRNA and TYMV sequences, prediction of false positive kissing hairpins leads to a higher MCC for the DotKnot predictions.

Our test set includes H-type pseudoknots as well as more complex pseudoknot foldings. For example, the ribozyme structures consist of double pseudoknots and nested pseudoknots feature in the cricket paralysis virus (CrPv) and Plautia stali intestine virus (PSIV) IRES elements. DotKnot is only able to fold H-type pseudoknots and kissing hairpins, whereas HotKnots and FlexStem cover general pseudoknot interactions; yet, DotKnot shows the highest MCC for five of the seven complex pseudoknot structures. Furthermore, DotKnot has the highest MCC for the 3′-UTR, tmRNA, viral tRNA-like, telomerase, and frameshifting structure predictions in our test set. For all pseudoknotted structures, DotKnot shows the highest average MCC of 0.68. Lower average MCCs are achieved by pknotsRG (0.41), FlexStem (0.28), RNAfold (0.2), and HotKnots (0.2).

DISCUSSION

The general pseudoknot prediction problem is intractable due to the vast structure search space. Dynamic programming methods for MFE structure prediction including pseudoknots need to achieve a reasonable balance between the complexity of allowed pseudoknots and computational requirements. A number of heuristic methods include a broad class of pseudoknots which may cover multiple crossing stems or nested pseudoknots. However, it might not be desirable to include arbitrarily complex pseudoknots in an RNA prediction algorithm due to the lack of thermodynamic parameters and knowledge about steric requirements. On the other hand, if a biologically relevant pseudoknot class such as kissing hairpins is known, it can easily be included as a predefined structure type in pseudoknot search programs such as DotKnot.

DotKnot outperforms pknots, FlexStem, and RNAfold for our test set of kissing hairpins. Except for three sequences, DotKnot returns a kissing hairpin structure as the result and has the highest average MCC of 0.56 for the test set. In contrast, the dynamic programming method pknots only detects a kissing hairpin for one of the sequences and has an average MCC of 0.46.

FlexStem predicts no kissing hairpins for any of the sequences and has the lowest average MCC of 0.18. FlexStem uses the same energy penalties as pknots for overlapping pseudoknots such as kissing hairpins. The energy parameters for pseudoknots estimated by pknots and adopted by FlexStem might be the reason for the poor kissing hairpin predictions. RNAfold has an average MCC of 0.31 for our test sequences. For three of the SRP RNA sequences in our test set, RNAfold does not predict any true positive base pairs for the noncrossing stems. This shows that a hierarchical folding approach where kissing interactions are searched for after obtaining a MFE structure might not always be successful. Thus, specialized pseudoknot folding methods which adopt specific energy parameters are needed for RNA structure prediction including pseudoknots.

DotKnot detects 23 out of 26 kissing hairpins for our test set. This might lead to the conclusion that introducing false positive kissing hairpins is inevitable due to the large number of candidates. However, we find that for our negative control set, DotKnot only predicts false positive kissing hairpins in three of the sequences and outperforms the competing algorithms for the set of pseudoknotted structures. It must be noted that for the pseudoknot-free sequences in our test set, the free energy minimization methods pknotsRG and RNAfold give the best results. DotKnot is a heuristic pseudoknot prediction method which does not aim to compete with free-energy minimization algorithms for secondary structure prediction. DotKnot does not guarantee to find the MFE structure given a sequence; however, we find that it reliably predicts stable secondary structure elements which may compete with pseudoknot formation. DotKnot shows the best average MCC for our test set of pseudoknotted sequences and is a practical pseudoknot prediction tool for finding pseudoknots in longer sequences. A comparison of running times is given in Supplemental Table 1.

We think that the underlying energy parameters for H-type pseudoknots (Cao and Chen 2006, 2009) and kissing hairpin parameters chosen by us are the main reasons for the high predictive accuracy. An RNA folding algorithm can only be as accurate as the quality of underlying energy parameters allows; therefore, laboratory investigations into RNA energy parameters such as long-range kissing hairpin interactions are highly desirable. To overcome the approximate nature of RNA energy parameters, one can gain confidence in predictions by using comparative information. Pseudoknots are known to be highly conserved and the DotKnot method will be extended in the future to take into account multiple alignment information using the probability dot plots.

MATERIALS AND METHODS

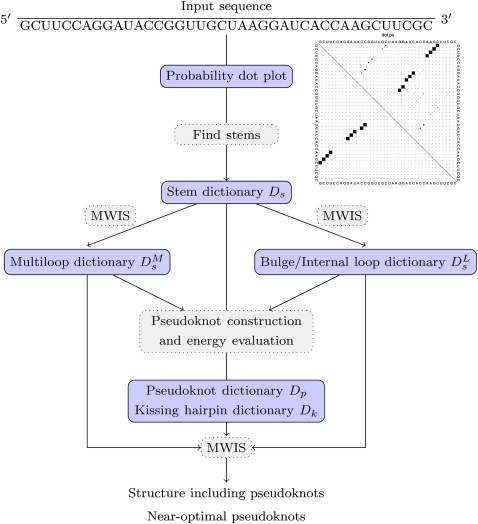
In this section, we describe the basics of the DotKnot algorithm and its extension to the prediction of a global structure, including H-type pseudoknots and intramolecular kissing hairpins (Fig. 6).

FIGURE 6.

Extending DotKnot for the prediction of kissing hairpins. The structure returned as an output may contain both H-type pseudoknots and kissing-hairpin–type pseudoknots. A number of near-optimal H-type pseudoknots and kissing hairpins may also be reported. MWIS stands for maximum weight independent set calculation.

The DotKnot algorithm

The basis of the DotKnot method is the secondary structure probability dot plot calculated by RNAfold (Hofacker et al. 1994). From the dot plot, a set of promising stems is extracted using the base pair probabilities and stored in the dictionary D_s. Note that by setting a low-probability threshold, potential pseudoknot stems can be discovered. Using the stem dictionary D_s, noncrossing secondary structure elements with low free energy are assembled using maximum weight independent set (MWIS) calculations. Stems interrupted by bulges or internal loops are stored in dictionary D_s^L and multiloops are stored in dictionary D_s^M. Stems and secondary structure elements are then used to construct recursive H-type pseudoknots. H-type pseudoknot energies are evaluated with the aid of advanced energy models (Cao and Chen 2006, 2009). The presence of the H-type pseudoknots is verified using a MWIS calculation on the set of all possible structure elements. Outer stems may include nested pseudoknots. In the first version of DotKnot, only pseudoknots were returned as a result. In the current version, the user can choose to additionally see the global structure derived by the final MWIS calculation. For algorithmic details of the first version of DotKnot for detecting H-type pseudoknots, see Sperschneider and Datta (2010).

Our first extension presented here is the ability to predict intramolecular kissing hairpins. The type of recursive kissing hairpin structure allowed in the extended DotKnot method is shown in Figure 7. The crossing of three stems results in five loops which can contain recursive secondary structure elements. Note that we restrict a kissing hairpin structure to be shorter than 400 nt to improve runtime. Furthermore, MFE folding is known to become inaccurate for longer sequences due to the underlying approximate energy parameters (Eddy 2004; Reeder et al. 2006). Long-range interactions are especially hard to predict using MFE folding, as tertiary interactions and forces are likely to further stabilize the structure.

FIGURE 7.

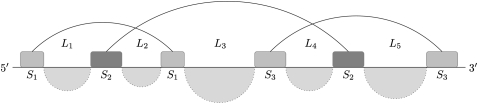
Kissing hairpin prediction class where recursive secondary structure elements are allowed in each of the five loops L₁, L₂, L₃, L₄, and L₅.

The second extension is that in addition to the best global folding, the best local H-type pseudoknots and kissing hairpins in terms of two criteria are returned. This can help to identify promising pseudoknot foldings and may compensate for the limitations of the energy parameters. DotKnot returns the best pseudoknots in terms of estimated free energy to length ratio (Reeder and Giegerich 2004). This helps to identify local pseudoknots and will favor pseudoknots with compact structure and low free energy. Additionally, DotKnot returns pseudoknots with lowest estimated free energy, regardless of their lengths. For each criterion, a user-set number of pseudoknots are returned.

Kissing hairpin prediction

Assembling kissing hairpin candidates

An intramolecular kissing hairpin is a planar pseudoknot that can be decomposed into two core H-type pseudoknots (Fig. 8). The main idea of the extended DotKnot algorithm is to create a list of H-type pseudoknots, which are subsequently combined into kissing hairpin candidates. Core H-type pseudoknots are assembled from stems which are extracted from the base pair probability dot plot calculated by RNAfold. Each stem s_i ∈ D_s has two energy weights w_stack (s_i) (simple stacking free energy) and w(s_i) (free energy). Only stems s_i are used for kissing hairpin construction where w_stack (s_i) < −5.0 kcal/mol and w(s_i) < 2.0 kcal/mol. During pseudoknot construction, a certain base pair overlap is allowed as crossing stems with a fixed length are combined (see Supplemental Material).

FIGURE 8.

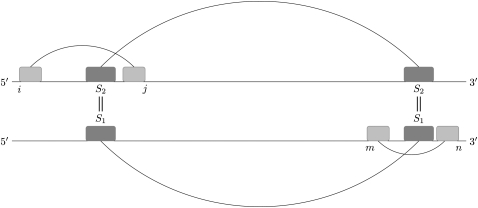
A kissing hairpin can be decomposed into two core H-type pseudoknots, where the second stem S₂ of the first pseudoknot equals the first stem S₁of the second pseudoknot. Note that for a kissing hairpin, j < m has to hold. Otherwise, a triple helix interaction is formed.

The H-type pseudoknots are stored in a specific manner in order to assemble kissing hairpins efficiently. There are two dictionaries, 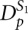and 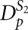. Dictionary 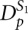has a stem as a key and as values the list of corresponding pseudoknots which contain this stem as a first pseudoknot stem S₁. Dictionary 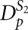has a stem as a key and as values the set of corresponding pseudoknots which contain this stem as a second pseudoknot stem S₂. For each stem in dictionary 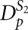, a key existence test is performed in dictionary 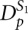. If the same stem is found in both dictionaries, the values for the stem entry in 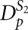are combined with the values for the stem entry in 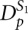to form a kissing hairpin (Fig. 8). An indication of the stem probability in the secondary structure folding ensemble is given by the confidence indicator which is defined as the average probability of participating base pairs in a stem. We demand that the three kissing hairpin stems have a confidence sum of >1 × E⁻³. Kissing hairpins consist partly of noncrossing stable secondary structure elements and base pairs below this threshold are unlikely to participate in secondary structure formation (Hofacker and Stadler 1999).

Recursive structure formation in the loops

A kissing hairpin candidate structure has three stems S₁, S₂, and S₃, and five loops L₁, L₂, L₃, L₄, and L₅ (Fig. 7). Given the set of kissing hairpin structures, the five loops are investigated for internal secondary structure elements. Note that internal pseudoknots in the loops are not allowed due to the lack of knowledge about three-dimensional folding. Only secondary structure elements from dictionaries D_s, D_s^L, and D_s^M can form in each of the five loops in a consecutive fashion. Recursive secondary structure elements are found using a MWIS calculation as described in Sperschneider and Datta (2010). Note that for three-dimensional folding reasons in a kissing hairpin structure the following is assumed: There must be at least one nucleotide in loops L₁ or L₂ (L₄ or L₅) that is left unpaired.

Energy evaluation for kissing hairpins

The critical point for kissing hairpin prediction is the underlying energy model. As it is a tertiary structure element, many different types of forces apart from canonical base-pairing are likely to play a role, for example noncanonical base-pairing, base triples, backbone interactions, or ion concentrations (Batey et al. 1999). No experimentally measured energy parameters for intramolecular kissing hairpins have been established to date and thus heuristic energy estimation has to be used. Here, the free energy for each kissing hairpin k₁,…,k_n in dictionary D_k is approximated by adding the stacking energies, including dangling ends for the three stems S₁, S₂, and S₃, plus a length-dependent value for the loop entropies (Fig. 9). An extended version of the parameterized pseudoknot energy model (Rivas and Eddy 1999; Dirks and Pierce 2003; Reeder and Giegerich 2004) is used:

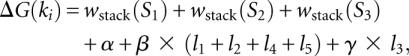where l_i is the number of unpaired nucleotides in the loop L_i (i = 1,…,5). In this model, loop L₃ attracts a penalty γ for each unpaired nucleotide, whereas the four other loops are penalized using the value β. Without the kissing interaction, loop L₃ would not contribute entropic terms according to the Turner model. A kissing interaction between two non-neighboring hairpin loops with a long loop L₃ is thus not unlikely and, therefore, γ is set to 0.0 kcal/mol. Here, the initiation penalty for forming a kissing hairpin is set to α = 9.0 kcal/mol and β to 0.5 kcal/mol. For kissing hairpins with recursive secondary structure elements in the five loops, the stabilizing free-energy weights of the internal elements are added to the overall free energy. The loop entropy for the recursive kissing hairpin is then re-estimated using the remaining number of unpaired nucleotides in the five loops.

FIGURE 9.

Energy estimation for a kissing hairpin: the three stems S₁, S₂, and S₃ contribute stabilizing stacking energies and each unpaired nucleotide in loops L₁, L₂, L₃, L₄, and L₅ is penalized.

Kissing hairpins with negative free energy are stored in the kissing hairpin candidate dictionary D_k. Despite the low number of stem candidates, the number of kissing hairpin candidates is relatively high due to the large structure space. The same length-normalized filtering step as in the first version of DotKnot is used. As an additional measure for kissing hairpin stability, the normalized kissing hairpin free energy must fulfill ΔG(k_i)/l_i ≤ ε where l_i denotes the length of the kissing hairpin candidate structure k_i. Kissing hairpins are assumed to contribute to the overall stability of an RNA structure. This filtering step helps to eliminate unlikely kissing hairpins with high free energy and improves runtime of the method.

Verification of kissing hairpins in the sequence

The presence of kissing hairpin candidates in an RNA sequence is verified using the MWIS calculation of the DotKnot algorithm (Sperschneider and Datta 2010). The structure elements from the three secondary structure dictionaries D_s, D_s^L, and D_s^M, as well as the recursive H-type pseudoknot candidates stored in D_p and the kissing hairpin candidates stored in D_k participate in the MWIS calculation using free-energy weights. Outer stems are allowed to contain nested structure elements, including pseudoknots and kissing hairpins. The output consists of the (possibly empty) set of detected crossing structures such as H-type pseudoknots and kissing hairpins (Fig. 6). Additionally, the global structure derived by the MWIS calculation, including secondary structure elements and near-optimal pseudoknots, if desired, is displayed.

SUPPLEMENTAL MATERIAL

Supplemental material can be found at http://www.rnajournal.org.