Bayesian spatial modeling of disease risk in relation to multivariate environmental risk fields

Abstract

The relationship between exposure to environmental chemicals during pregnancy and early childhood development is an important issue which has a spatial risk component. In this context, we have examined mental retardation and developmental delay (MRDD) outcome measures for children in a Medicaid population in South Carolina and sampled measures of soil chemistry (e.g. As, Hg, etc.) on a network of sites which are misaligned to the outcome residential addresses during pregnancy. The true chemical concentration at the residential addresses is not observed directly and must be interpolated from soil samples. In this study, we have developed a Bayesian joint model which interpolates soil chemical fields and estimates the associated MRDD risk simultaneously. Having multiple spatial fields to interpolate, we have considered a low-rank Kriging method for the interpolation which requires less computation than Bayesian Kriging. We performed a sensitivity analysis for a bivariate smoothing, changing the number of knots and the smoothing parameter. These analyses show that a low-rank Kriging method can be used as an alternative to a full-rank Kriging, reducing computational burden. However, the number of knots for the low-rank Kriging model need to be selected with caution as a bivariate surface estimation can be sensitive to the choice of the number of knots.

1. Introduction

Mental retardation and development delay (MRDD) in young children has enormous public health implication as they have relatively high prevalence rates of 2-4% or more in most populations. However, the causes of approximately 50% of MRDD cases still remain unknown [1]. One possible cause for MRDD is environmental chemical exposure. Exposure to lead and mercury have been reported to be associated with MRDD in several studies. Since the cerebral neuronal development occurs in utero and in the first 2 years of postnatal life, it is necessary to investigate the association between MRDD and prenatal environmental exposure to different chemicals. This association has not been examined well since it is difficult to detect the environmental exposure.

Since it is difficult to observe environmental exposure directly, it must be inferred or interpolated from observed samples. However, the errors involved in this interpolation have been largely ignored in other studies which can result in misleading risk estimates associated with the exposures [2-4]. To overcome this problem, we combine the interpolation of soil chemicals and the estimation of the associated risk simultaneously by employing a Bayesian approach. Our method addresses the same problem as that of Fuentes et al.[5] who examined the association between the predicted fine particles and mortality. However, they used the predicted particles as ‘plug-in’ estimates and this does not account for the interpolation error associated with each spatial predictor. They also used a special form of Poisson data model with full Bayesian Kriging. Here we use a joint model which interpolates and fits the risk model simultaneously. Our approach is similar to that of Smith et al. [6] in which residential radon levels are linked to leukemia risk, although we examine a more complex multivariate interpolation problem in this study. Employing a Bayesian approach and having multiple chemicals to interpolate means that computational intensity is an important factor for choosing an interpolation method in this study.

In this paper, we will present an analysis of the effects of multiple soil chemicals on MRDD risk. In general, in environmental risk assessment studies there could potentially be a large number of spatially-referenced predictors and so the computational burden of joint modeling is an issue. Since the purpose of our paper is to develop a statistical method which can be applied to this situation, we have chosen a spline method (low-rank Kriging) instead of Kriging [7] in our Bayesian approach. To compare the predictive performance of the spline method with Kriging, a simulation study is also presented here.

The remainder of this paper is organized as follows. The motivating MRDD data are described in Section 2. The development of a Bayesian logistic spatial model relating residential chemicals to MRDD outcome is detailed in Section 3. Low-rank Kriging methods for multiple spatial fields are considered in the model development. In Section 4, a simulation study is performed to verify the prediction performance of low-rank Kriging with different number of knots in comparison with full-rank Kriging. In Section 5, results from the proposed Bayesian logistic spatial model are summarized. Finally, a discussion of our analytic approach is provided in Section 6.

2. Materials

2.1. MRDD data from Medicaid in South Carolina

This work is motivated by a study of MRDD incident cases in Medicaid population in South Carolina between 1996 and 2001. Medicaid is a health insurance for individuals with low incomes in the United States, covering low-income parents, children, seniors, and people with disabilities. During each month of pregnancy, residential addresses for mothers are recorded. Other available mom and baby characteristics include: mother's age, mother's ethnicity, mother's alcohol consumption during pregnancy, parity, birth weight, baby sex and follow-up time. We term these covariates as ‘mom and baby’ or ‘individual’ covariates. Using spatial cluster analysis, MRDD clusters were identified first and then five clusters were selected for soil sampling. There were 6535 MRDD cases and controls from the five clusters. Details of cluster analysis were described previously [8]. Data from five further clusters would be added later in the study. This will possibly increase the data set to about 13000 cases and controls. In this study, a preliminary sample from this large dataset was randomly selected and used to develop a statistical model which will be applied to the original data at a later stage, once all the data become available. This dataset comprises 141 MRDD cases and controls from month 6 of pregnancy, year 1998 in the second cluster.

2.2. Soil Samples from MRDD clusters

In each chosen cluster, soil samples were collected from a network of sample sites which has a regular grid pattern covering the whole cluster area [9]. These soil sample sites are spatially misaligned to the residential addresses of pregnant women. Thus, interpolation of soil chemical fields is required to link MRDD cases to environmental exposure risk. In this study, we used nine soil chemicals from 119 soil samples collected from the second cluster to develop our statistical model. Thus we have nine spatial fields to interpolate here but the original dataset includes nine soil chemical measures for each of ten clusters. This means we have ninety spatial fields to interpolate. The implication of the need for interpolation of a large number of predictors to a large number of outcome sites clearly supports the need for computational efficiency. Nine chemicals measured in soil samples include arsenic (As), barium (Ba), beryllium (Be), chromium (Cr), copper (Cu), lead (Pb), manganese (Mn), nickel (Ni) and mercury (Hg). We denote these observed soil chemicals at sample sites as ‘environmental’ covariates.

3. Methods

3.1. Logistic Spatial Model

Assume first that we observe a realization of a spatial process where a binary mark is observed on a set of locations. Here we assume that residential addresses of MRDD cases are the locations with binary mark y_i =1 and controls as y_i = 0. The controls are the residential locations of pregnant women who had a normal child and the MRDD cases are the residential locations of pregnant women who subsequently had a child with a MRDD diagnosis. This latter group is a subset of the local birth population. Thus we use a logistic regression to model this spatially-referenced outcome. We observe covariates that relate to the individual outcome such as ‘individual’ covariates and ‘environmental’ covariates which were described in Section 2. We term this model ‘logistic spatial’.

Data are in the form (x_i, y_i), 1 ≤ i ≤ n, where the y_i is a binary outcome for x_i and x_i ∈ ℜ² represents geographical locations. y_i can be regarded as a Bernoulli random variable and we modeled the probability of having MRDD using a logit link function:

$$\begin{array}{l}{y}_i\sim \mathit{\text{Bernoulli}}(p_i)\\ \text{logit}(p_i\mid {\mathbf{\text{u}}}_i,{\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i))={\beta }_0+{\mathbf{\text{u}}}_i{\beta }_1+{\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i){\beta }_2+{\varepsilon }_i\end{array}$$ (1)

where u_i = (u_li,…,u_qi) is a vector of individual covariates with corresponding regression parameters ${\beta }_1^T=\left\{{\beta }_{11,\dots ,}{\beta }_{1q}\right\}$; ${\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i)=\{z_1^{\ast }({\mathbf{\text{x}}}_i),\dots ,z_p^{\ast }({\mathbf{\text{x}}}_i)\}$ is a vector of latent soil chemicals at x_i; ${\beta }_2^T=\left\{{\beta }_{21,\dots ,}{\beta }_{2p}\right\}$ is a vector of regression parameters of environmental covariates in the model; and ε_i represents a random effect term. Here, the star symbol (*) denotes the unobserved ‘true’ covariates. The inclusion of a random effect term is intended to make some allowance for confounding in the outcome and could take a variety of forms. A convolution model [10] is often assumed where an additive combination of an uncorrelated and spatially-correlated effect is employed. Often a conditional autoregressive (CAR) model is assumed for the latter effect. However, recently it has been found that CAR components can be confounded or collinear with spatially-referenced predictors (such as, in this case, soil chemicals) [11, 12] and so spatial predictor effects may be masked by this effect. We have performed a variogram analysis of residuals from a logistic model fit to non-spatial predictors (mom and baby covariates) and found negligible spatial correlation. Taking these two considerations into account, we have employed only an uncorrelated random effect term to accommodate confounding. Ma et al. [11] reported improved power in estimation of predictor effects when using such an effect with a zero mean Gaussian prior specification. We have assumed that specification here: ɛ_i ∼ N(0, σ_ɛ²).

In our study, environmental covariates, z*(x_i), are not observed at the outcome sites but they are observed at different geographical locations (soil sample sites). Let z(s_j) = {z₁(s_j),…, z_p(s_j)}, 1 ≤ j ≤ m denote a vector of observed soil chemicals at s_j where s_j ∈ ℜ² represent the soil samples sites. Then, our model must allow for both the prediction of z*(x_i) from z(s_j) and fitting the logistic spatial model reflecting the uncertainty in the predicted values. This can be achieved by fitting a joint model which will be developed in the following section.

3.2. Joint posterior distribution

Our logistic spatial model includes both mom and baby covariates and unobserved environmental covariates which must be predicted from the observed soil samples. For the prediction of the latent soil chemical concentrations, a low-rank Kriging [13, 14] is employed in this study. These two parts comprise our joint model and we have two likelihoods at two different sets of the locations.

The joint posterior distribution is proportional to the product of the likelihood function associated with the logistic spatial model (Equation (1) in Section 3.1.), the low-rank Kriging model (Section 3.3.2.), the predictive distribution of the latent spatial fields (Section 3.3.3.) and prior distributions for the model parameters:

$$\begin{array}{ll}\text{Pr}(\mathit{\text{θ}},\mathbf{\text{β}},{\mathbf{\text{z}}}^{\ast },\varepsilon \mid y,\mathbf{\text{z}})\propto & \left[\prod _i\mathit{\text{Bern}}(y_i;p_i({\mathbf{\text{u}}}_i,{\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i),{\beta }_0,{\beta }_1,{\beta }_2,\varepsilon ))\right]\\ & \times \left[\prod _{j}f(\mathbf{\text{z}}({\mathbf{\text{s}}}_j);\mathit{\text{θ}})\right]\\ & \times \left[\prod _{i}f({\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i);\mathbf{\text{z}}({\mathbf{\text{s}}}_j),\mathit{\text{θ}})\right]\\ & \times \text{Pr}({\beta }_0)\text{Pr}({\beta }_1)\text{Pr}({\beta }_2)\text{Pr}(\mathit{\theta })\text{Pr}(\varepsilon )\end{array}$$ (2)

where β₀, β₁ and β₂ represent regression parameters for the logistic spatial model and ε represents a random effect as defined in Section 3.1.; θ represents a vector of parameters for the low-rank Kriging model; the latent soil chemical concentrations, z*(x_i), are a function of θ. The models for soil chemical concentrations will be defined in the following section (Section 3.3).

We used Markov chain Monte Carlo (MCMC) methods to sample from the joint posterior distribution. It is difficult to use standard software routines, such as those found in WinBUGS to perform MCMC sampling in our case since our hierarchical model is very complex and several spatial fields need to be interpolated. Instead, we implemented a MCMC algorithm for our model within the C language. A Metropolis-Hasting algorithm [15] is used. The details of the Metropolis-Hasting algorithm used in this study are given in the Appendix.

3.3. Prediction of multiple environmental covariates

3.3.1. Kriging vs. Splines

In this study, Kriging could have been employed for the prediction of soil chemical concentrations assuming a stationary, multivariate Gaussian distribution which is often regarded as optimum interpolation in geostatistics. Quantifying spatial variability through the covariance function, Kriging can produce maps of optimal predictions from incomplete and noisy spatial data [7]. Kriging requires matrix decomposition whose complexity increases as O(n³) in the number of locations, n. If posterior sampling is employed for Kriging in a Bayesian approach, the matrix decomposition is required at every iteration of an MCMC algorithm and the computational burden increases. Note that if we assumed a prior cross-covariance structure for the spatial predictors then this would increase computation time and reduce parsimony in the model. We have not pursued that approach here. The details of Bayesian Kriging are provided by Banerjee et al. [16]. Having multiple soil chemical concentrations to interpolate, we considered an alternative spatial prediction method which is less computationally intense and decided to use a spline method: low-rank Kriging [13, 14, 17]. Low-rank Kriging requires a covariance matrix decomposition once a priori before running an MCMC algorithm fixing a spatial range parameter. This means that the computation can be reduced by 9 × O(119³) × total iteration of the MCMC algorithm for the preliminary sample dataset and by 90 × O(119³) × total iteration of the MCMC algorithm for our original dataset. Although Bayesian Kriging provides a more flexible modeling method which enables us to estimate a spatial range parameter, we chose to use a low-rank Kriging model due to this computational advantage. There is extensive literature available on spline models. A review of different spline models for univariate data is given by several authors [14, 18, 19]. For bivariate and higher-dimensional data, the details are presented by Denison et al. [20] and Ruppert et al. [14].

3.3.2. Low-rank Kriging model for multiple soil chemicals

In this section, a low-rank Kriging model for each soil chemical is developed. As a check for the assumption of prior independence of the fields we examined the empirical correlation between the observed measurements. When the sample correlations were calculated, most chemicals did not have high correlations (Table 1). This further supports our assumption for a univariate model for each soil chemical. For the p th chemical, let $z_{\mathit{\text{p}}}^T=\{z_p({\mathbf{\text{s}}}_1),\dots ,z_p({\mathbf{\text{s}}}_m)\}$ denotes a 1×m vector of the p th chemical concentration where 1≤ p ≤ P. Let {κ₁,…,κ_K} be a set of K < m distinct points which is a representative subset of {s_j}, 1 ≤ j ≤ m. This subset is often selected by a space filling algorithm and we have examined that approach here. These points are referred to as knots. Different strategies for the selection of knots are described by Ruppert et al. [14]. The number of knots was determined by K = max{20, min(m/4, 150)} following Ruppert et al. [14]'s recommendation. In this study, two knot location patterns were used: 1) knots were placed over the whole study area using a space filling algorithm, (this was performed by the R package, field), and 2) knots were placed close to the prediction locations generating random points based on a kernel smoothed intensity of the outcome sites. This was carried out by the R package ( spatstat).

Table 1. Correlations of different soil chemical concentrations (n=119).

	As	Ba	Be	Cr	Cu	Pb	Mn	Ni	Hg
As	1.000	0.143	0.080	0.038	0.031	0.363	0.281	-0.021	0.133
Ba		1.000	0.735	0.396	0.504	0.128	0.703	0.651	0.063
Be			1.000	0.635	0.657	0.101	0.642	0.723	0.001
Cr				1.000	0.628	0.178	0.493	0.733	0.009
Cu					1.000	0.317	0.347	0.671	0.174
Pb						1.000	0.274	0.211	0.329
Mn							1.000	0.501	0.098
Ni								1.000	-0.010
Hg									1.000

The low-rank Kriging model for the p th chemical can be represented as follows:

$$\begin{array}{l}{z}_p={\mathbf{\text{W}}}_p{\alpha }_p+{\stackrel{\sim }{\mathbf{\text{Z}}}}_p{\stackrel{\sim }{\text{v}}}_p+{\mathbf{\tau }}_p\\ {\mathbf{\text{W}}}_p={[\text{1}{\mathbf{\text{s}}}_j]}_{1\le j\le m},{\stackrel{\sim }{\mathbf{\text{Z}}}}_p={[C(\Vert {\mathbf{\text{s}}}_j-{\kappa }_k\Vert /{\rho }_p)]}_{1\le j\le m,1\le k\le K}\\ {\mathbf{\Omega }}_p={[C(\Vert {\kappa }_k-{\kappa }_{k^{\prime }}\Vert /{\rho }_p)]}_{1\le k,k^{\prime }\le K}\end{array}$$ (3)

where α_p is a fixed-effect parameter vector for W_p; ṽ_p is a random-effect parameter vector for Z̃_p; E(ṽ_p) = 0; $\text{cov}({\stackrel{\sim }{\text{v}}}_p)={\sigma }_{\text{v}p}^2{\Omega }_p^{-1}$; and ${\tau }_p\sim N(0,{\sigma }_{\tau p}^{2}I)$.

Here, the first-order trend is assumed and C(r) is an inter-point covariance function. In what follows, we have assumed a special case of Matérn family covariance model for C(r) fixing the Matérn smoothness parameter at ν =3/2:

$$C(r)=(1+\left|r\right|)e^{-\left|r\right|}$$ (4)

The spatial range parameter ρ_p controls the smoothness of the fitted surface and the larger ρ_p, the smoother the surface. Note that if we fix ρ_p a priori, we can fit the model using a generalized linear model framework. Equation (3) becomes a linear mixed model:

$$z_p={\mathbf{\text{W}}}_p{\alpha }_p+{\mathbf{\text{Z}}}_p{\text{v}}_p+{\tau }_p,\left[\begin{array}{c}{\text{v}}_p\\ {\tau }_p\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_{\text{v}p}^{2}I& 0\\ 0& {\sigma }_{\tau p}^{2}I\end{array}\right]\right)$$ (5)

where ${\mathbf{\text{Z}}}_p={\stackrel{\sim }{\mathbf{\text{Z}}}}_p{\Omega }_p^{-1/2}$; and ${\text{v}}_p={\Omega }_p^{1/2}{\stackrel{\sim }{\text{v}}}_p$.

Employing a Bayesian approach, both the spatial range parameter and the partial sill parameter can be estimated. In this study, the partial sill parameter $({\sigma }_{\text{v}p}^2)$ is estimated using the joint distribution described in Section 3.2 whereas the spatial range parameter for each chemical (ρ_p) is estimated a priori from a variogram analysis. This provides significant savings in computation albeit at the expense of some bias. After fixing ρ_p, we need to invert the 119×119 dimension covariance matrix, Ω_p, only once at the beginning but not at every MCMC iteration for each chemical. In several studies, the spatial range parameter has been fixed as it is difficult to obtain a reliable estimate due to its lack of identification with the partial sill, without resort to profile likelihood within 2 stage procedures (see Dietrich and Osborne [21]; Hoeting et al. [22])

After inspecting the contour plots of nine soil chemicals, a variogram analysis was performed for each chemical by the R package, geoR assuming a Matérn covariance function. The estimated spatial range parameter for each chemical is used to fix ρ_p a priori for the suggested logistic-spatial model. The rationale for fixing this parameter is two-fold: 1) the need to avoid estimation problems and 2) to reduce the computation time.

While French et al. [13] suggest an approach whereby ρ_p is fixed at 1) ${\widehat{\rho }}_p=\underset{1\le j,j^{\prime }\le m}{\text{max}}\Vert {\mathbf{\text{s}}}_j-{\mathbf{\text{s}}}_{j^{\prime }}\Vert$ and 2) ${\widehat{\rho }}_p=1/20\times \underset{1\le j,j^{\prime }\le m}{\text{max}}\Vert {\mathbf{\text{s}}}_j-{\mathbf{\text{s}}}_{j^{\prime }}\Vert$, using a much smaller value to assess the effect of extreme values, we have used variogram analysis which yields a different value for ρ̂_p for each chemical more closely matching the spatial structure of the predictor.

3.3.3. Prediction of multiple soil chemicals using Low-rank Kriging

As explained in Section 3.1., we measured soil chemical concentrations at the sample site but not at the outcome site. Thus, we treat the latent soil chemical concentrations as missing values. The details of fitting linear mixed-effect models with missing values are presented by Schafer and Yucel [23].

For the p th chemical, let z_p(obs) denote a vector of the observed chemical concentrations at the sample sites and z_p(mis) denote a vector of the latent chemical concentrations at the outcome sites. In our MCMC algorithm, let ${\mathit{\theta }}_p^{(t)}=({\alpha }_p^{(t)}{,\text{v}}_p^{(t)},{\tau }_p^{(t)},{\sigma }_{\text{v}p}^{2(t)},{\sigma }_{\tau p}^{2(t)})$ and z_p(mis)^(t) represent current versions of the unknown parameters and missing data respectively. Then, θ^(t) and $z_{p(\mathit{\text{mis}})}^{(t)}$ are updated as follows:

$$\mathbf{1}\mathbf{)}{\mathit{\theta }}^{(t+1)}\sim f({\mathit{\theta }}^{(t)};z_{p(\mathit{\text{obs}})},z_{p(\mathit{\text{mis}})}^{(t)})$$ (6)

$$\mathbf{2}\mathbf{)}{z}_{p(\mathit{\text{mis}})}^{(t+1)}\sim f(z_{p(\mathit{\text{mis}})}^{(t)};{\mathit{\theta }}^{(t+1)},z_{p(\mathit{\text{obs}})})$$ (7)

In our low-rank Kriging model, the posterior predictive distribution of z_p(mis) is as follows:

$$\begin{array}{l}{z}_{p(\mathit{\text{mis}})}\mid {\mathit{\theta }}_p\sim N({\text{W}}_{\text{x}p}{\alpha }_p+{\text{Z}}_{\text{x}p}{\text{v}}_p,{\tau }_p)\\ {\text{W}}_{\text{x}p}={[\text{1}{\mathbf{\text{x}}}_i^T]}_{1\le i\le n},{\text{Z}}_{\mathit{\text{xp}}}={[C(\Vert {\mathbf{\text{x}}}_i-{\kappa }_k\Vert /{\rho }_p)]}_{1\le i\le n,1\le k\le K}{\Omega }_p^{-1/2}\end{array}$$ (8)

where C(r), κ_K, and Ω_p are as defined in Equation (3).

At the t th iteration of the MCMC algorithm, both z_p(obs) and $z_{p(\mathit{\text{mis}})}^{(t)}$ are used as the complete data to update θ_p for the low-rank Kriging model described in Section 3.3.2. Then, we update $z_{p(\mathit{\text{mis}})}^{(t+1)}$ using the joint posterior distribution in Equation (2) which comprises the posterior predictive distribution above (Equation (8)) and the logistic spatial model likelihood. In this way, the risk estimate can reflect the uncertainty involved in the prediction procedure properly which cannot be achieved by using plug-in estimates. For the details of the Metropolis-Hasting algorithm for the prediction, please refer to the Appendix.

4. Simulation Study

Using the low-rank approximation helps to improve computational speed [24]. For one-dimensional data, it has been found that low-rank Kriging has a similar prediction mean square error compared to full-rank Kriging [25]. It has also been found that low-rank smoothing performs as well as full-rank smoothing in terms of mean square error for one-dimensional data [26]. For a penalized spline model, it has been shown that sensitivity to the knot locations in one dimension is quite low [26, 27]. However, for higher-dimensional data, the effects of the number of knots and their locations on low-rank Kriging have not been tested previously to our knowledge. Thus, as part of our analysis we performed a simulation study to evaluate the effect of the number of knots on the performance of low-rank Kriging for bivariate data prior to fitting the multiple field models.

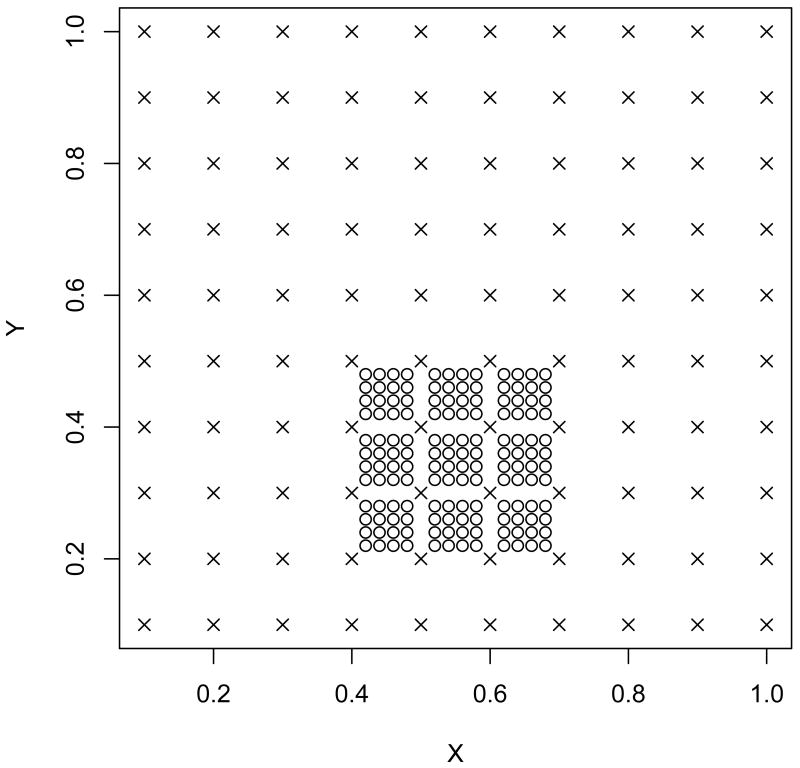
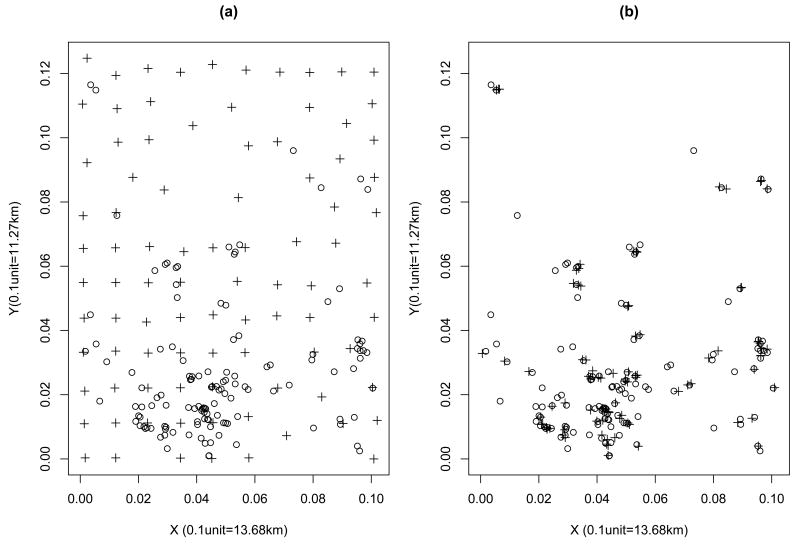
Firstly, a 10 by 10 regular grid was created within a unit square {0.1,…,1}×{0.1,…,1}. This first grid was assumed to be soil sample sites. Let s_j denote the first grid where s_j ∈ ℜ² and 1 ≤ j ≤ 100. Imitating our MRDD outcome which was observed on a fine grid, the second grid was created from all combination of x2 = {0.42, 0.44, 0.46, 0.48, 0.52, 0.54, 0.56, 0.58, 0.62, 0.64, 0.66, 0.68} and y2 = {0.22, 0.24, 0.26, 0.28, 0.32, 0.34, 0.36, 0.38, 0.42, 0.44, 0.46, 0.48}. Let x_i denote the second grid where x_i ∈ ℜ² and 1 ≤ i ≤ 144. The graphical representation of these two grids is shown in Figure 1.

Figure 1.

Two sets of grids for simulation. × represents the first grid and ○ represents the second grid.

We generated y^true(s_j) and y^true(x_i) from a stationary spatial Gaussian random field on both s_j and x_i This simulation was performed in R using the GaussRF package assuming zero mean and Matérn covariance function. Let W^T = {s_j x_i} be the grid which includes both the first grid (s_j) and the second grid (x_i), then the Gaussian random field can be represented as follows:

$$\begin{array}{l}{y}^{\mathit{\text{true}}}(\mathbf{\text{W}})\sim \mathit{\text{MVN}}(0,\sum )\\ \sum (\mathbf{\text{W}},{\mathbf{\text{W}}}^{\prime })={\sigma }^2(1+\Vert \mathbf{\text{W}}-W^{\prime }\Vert /\rho ){\text{e}}^{(-\Vert W-W^{\prime }\Vert /\rho )}\end{array}$$

We used y^true(x_i) as a prediction set and y^true(s_j) as a modeling set here. Bayesian Kriging was performed assuming the correct form of the model (zero mean, Matérn covariance function). This model was fitted using the SpBayes package in R. Low-rank Kriging models were fitted with different number of knots (K =5, 10, …,95) using the nlme package in R. For each K, knots were selected as a representative subset of x_i via a space-filling algorithm using the field package in R. We tested the performance of low-rank Kriging for each number of knots using a different set of values for σ² and ρ. All the combinations of (1, 0.5, 0.25) for each parameter were used.

The procedure for our simulation study is as follows:

1. Generate 500 samples of y^true(s_j) and y^true(x_i)

2. For each sample, leave out y^true(x_i) and use only y^true(s_j) to fit Bayesian Kriging and low-rank Kriging.

3. Predict ŷ_full(x_i) using the fitted Bayesian Kriging model

4. Predict ŷ_{low_K}(x_i) where K =5, 10, …,95 using the fitted low-rank Kriging model with K knots.

5. Calculated mean squared error of prediction (MSEP) for 500 samples as follows:

   $$\begin{array}{l}{\mathit{\text{MSEP}}}_{\mathit{\text{full}}}=\frac{1}{144}\sum _i{(y^{\mathit{\text{true}}}({\mathbf{\text{x}}}_i)-{\widehat{y}}_{\mathit{\text{full}}}({\mathbf{\text{x}}}_i))}^2\\ {\mathit{\text{MSEP}}}_{\mathit{\text{low}}―K}=\frac{1}{144}\sum _i{(y^{\mathit{\text{true}}}({\mathbf{\text{x}}}_i)-{\widehat{y}}_{\mathit{\text{low}}―K}({\mathbf{\text{x}}}_i))}^2\mathit{\text{where}}K=5,10,\dots ,95\end{array}$$

6. Find the 2.5^th and 97.5^th quantiles of MSEP_full. We call this ‘95% MSEP Range of Bayesian Kriging’. Then, count how many times MSEP_{low_K} falls in this range

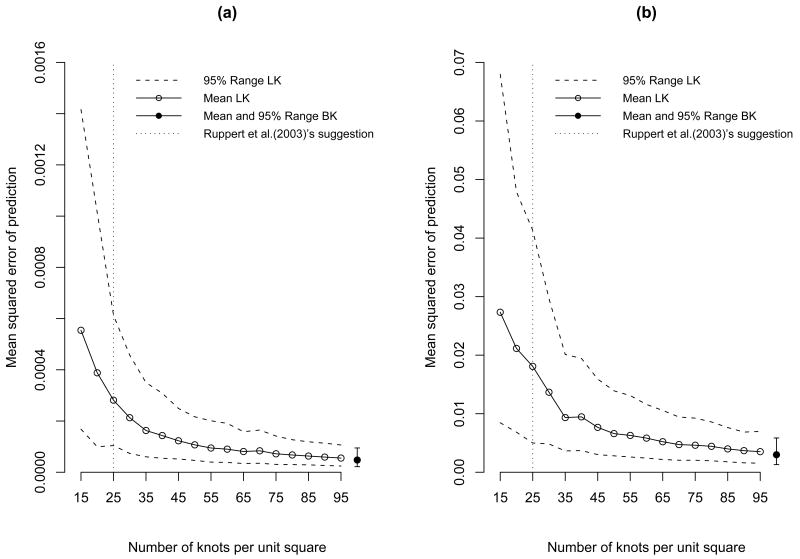
Figure 2 shows the mean squared error of prediction (MSEP) for the low-rank Kriging with each number of knots and the full-rank Bayesian Kriging with different σ² and ρ. The MSEP is the average squared difference between the estimate and the true value. The separate error-bar plot represents the mean and the 2.5th and 97.5th quantiles of MSEP of Bayesian Kriging estimates. These plots indicate that the MSEP is smaller in general when the spatial surface is smoother, i.e. ρ is larger. For both plots, the 95% MSEP range of Bayesian Kriging is narrow indicating that the model recovers the simulated data well. For both cases, as the number of knots increases, the MSEP decreases; it decreased rapidly at the beginning and then improvement became smaller. Ruppert et al. [14] recommend K=25 knots which is depicted by the vertical line. We can see that the 95% range of low-rank Kriging with 25 knots is much wider than that of Bayesian Kriging for both cases. When we used different sets of σ² and ρ, similar results were observed.

Figure 2.

Mean-squared error of prediction of low-rank Kriging (LK) and Bayesian Kriging (BK) with (a) σ²=1 and ρ=1 and (b) σ²=1 and ρ=0.25.

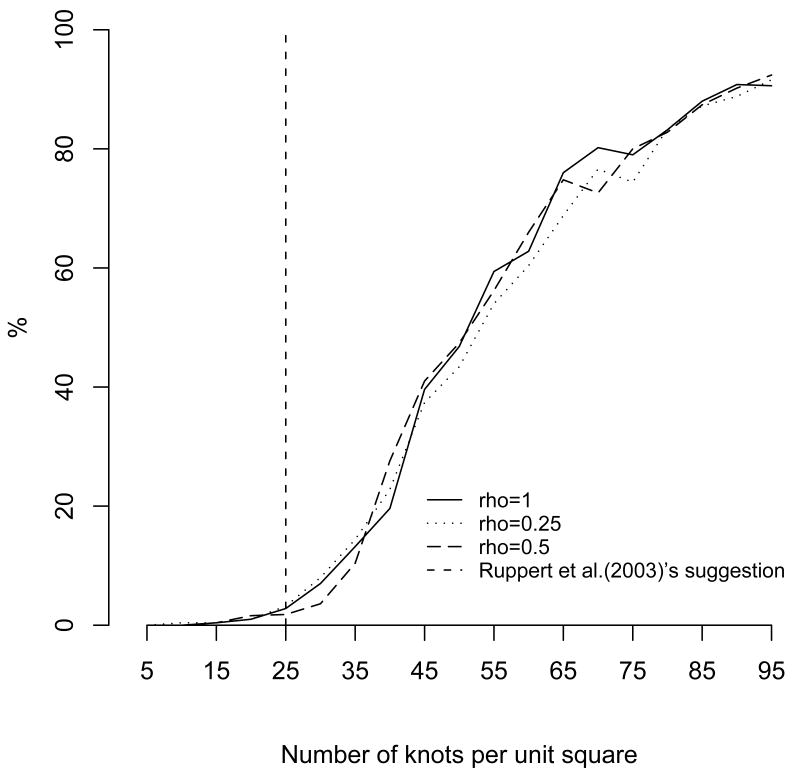
To compare the prediction performance of low-rank Kriging with different number of knots to Bayesian Kriging, the percentage of the MSEP of low-rank Kriging falling in the 95% MSEP range of Bayesian Kriging is calculated varying the smoothing parameter (Figure 3). We can see that if we followed Ruppert et al.'s suggestion, about 3% of the MSEP of low-rank Kriging fell in the 95% MSEP range of Bayesian Kriging. To achieve about 80%, at least 65 knots are required when the surface is smooth (ρ =1) and 80 knots when the surface is less smooth (ρ = 0.25). Of course, the above results suggest that Ruppert et al's suggestion is highly conservative. It should be noted that the results assume that Bayesian Kriging is the ‘gold-standard’ for comparison.

Figure 3.

Percentage of mean-squared error of prediction (MSEP) of low-rank Kriging falling in the 95% MSEP Range of Bayesian Kriging with σ²=1 different ρs.

5. Application: analysis of the MRDD outcome in a Medicaid population in South Carolina

In this section we use the MRDD data collected by Medicaid in South Carolina to fit our Bayesian joint model. The response variable is the diagnosis of MRDD (yes (y_i=1) or no (y_i=0)). During each month of pregnancy, residential addresses for mothers were recorded. In addition to the geographical location, mother's age, mother's ethnicity, mother's alcohol consumption during pregnancy, parity, birth weight, baby's sex and follow-up time were also available. After MRDD clusters were identified, five areas were selected for soil sampling. In this study, data from the second cluster in month 6 of pregnancy, year 1998 were randomly selected for our analysis (n=141). In the area, 119 soil samples were taken and 9 chemical concentrations were measured: arsenic (As), barium (Ba), beryllium (Be), chromium (Cr), copper (Cu), manganese (Mn), nickel (Ni), lead (Pb) and mercury (Hg). Table 1 shows the sample correlations between the nine soil chemicals. About 50% of chemical combinations had the correlation less than 0.3 and about 11% of chemical combinations had the correlation greater than 0.7. The lowest and highest correlation was observed between Be and Hg (r=0.001) and Ba and Be (r=0.735), respectively.

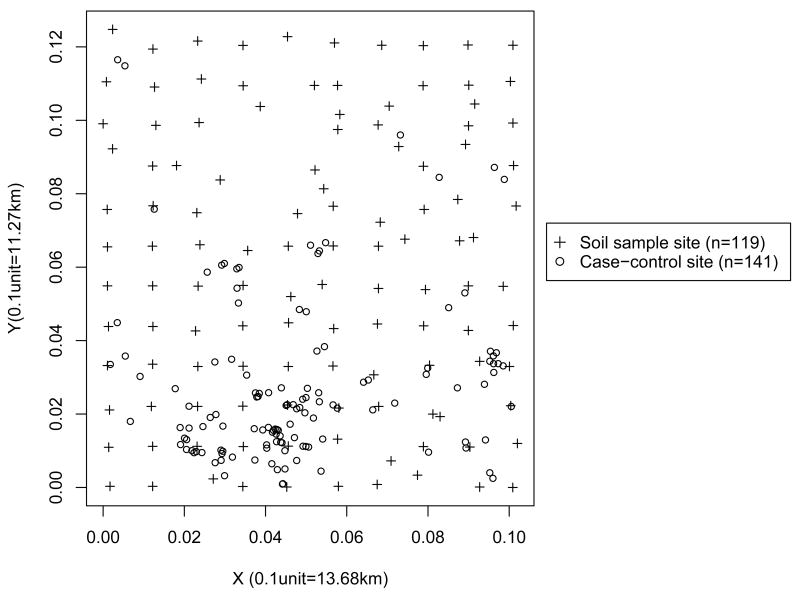
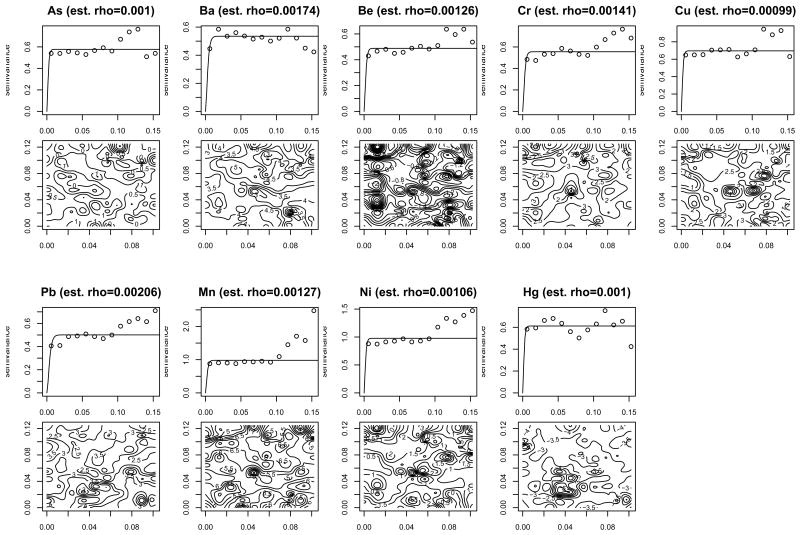
Figure 4 shows the MRDD outcome sites and the soil sample sites in the selected cluster. It shows that the soil sample sites are misaligned to the locations of pregnant women's residential addresses. It also illustrates the grid for the soil sample sites are coarser than that for the outcome sites. Figure 5 shows empirical semivariogram and contour plots of nine chemical concentrations from 119 soil samples. The empirical ssemivariogram and contour plots were drawn using the geoR and the MBA package in R, respectively. It also shows the estimated spatial range parameter. For all chemicals, we can see some peaks in certain regions and smooth variations in other regions. Spatially-varying chemical concentrations within the area suggest that potential hotspots exist. It appears that soil chemicals have different spatial patterns and thus a variogram analysis, was performed separately, for each chemical to estimate a spatial range parameter ρ_p. The estimated values found for ρ̂_p were 0.001, 0.0017, 0.0013, 0.0014, 0.001, 0.0021, 0.0013, 0.0011, 0.001 for As, Ba, Be, Cr, Cu, Pb, Mn, Ni and Hg, respectively.

Figure 4.

Plot of case-control sites and soil sample sites

Figure 5.

Empirical semivariogram (circle) with fitted variogram model (line) and associated contour plots of soil chemical measures (n=119).

5.1. Results of the logistic-spatial model

5.1.1 Plug-in Model vs. Joint Model

Using the estimated spatial range parameter from the variogram analysis, we fitted a Bayesian joint model with K=90 knots. These knots were selected from the soil sample sites using a space filling algorithm. Two chains with different initial values were run and thinning=10 was used to reduce autocorrelation. The details of the MCMC algorithm are provided in the Appendix. For comparison, a logistic spatial model was fitted in WinBUGS using the full-rank Bayesian Kriging estimates as plug-in which is a common modeling strategy. The Bayesian full-rank Kriging estimates were obtained using the R package SpBayes. For the plug-in model, it took about 2.8 hour to obtain Kriging estimates for soil chemicals and 5 minutes to run the logistic spatial model. For the joint model, it took about 15 hours. All models were run on a laptop with Intel Core 2 Duo T9500 processor and 3.5 GB RAM.

Table 2 shows the summary statistics for the two models. The logistic spatial model parameters are reported as a posterior mean and the 95% credible interval for both models. The first model is a logistic model with plug-in estimates of soil chemicals obtained from the full-rank Kriging (Model with FK plug-in). The second model is our suggested model, the joint model with a low-rank Kriging with 90 knots (Joint model with LK_90) developed in Equation (1). 90 Knots (75% of data points) were selected as our simulation study suggests the use of at least 65% of data points to achieve about 80% prediction performance comparable to the full-rank Kriging.

Table 2. Summary of a logistic spatial model with plug-in estimates from a full-rank Kriging (Model with FK plug-in) and a joint model with a low-rank Kriging with 90 knots placed on soil sample sites (Joint Model with LK_90).

	Model with FK plug-in			Joint Model with LK_90
	Mean	95% Cred. Int.		Mean	95% Cred. Int.
Intercept	2.036	-3.911	11.141	0.536	-9.557	12.356
Mother's age (year)		-0.549	-0.009		-1.051	0.041
Mother_Black (ref. Mother_non_Black)	-0.523	-3.221	1.871	-1.724	-7.706	3.046
Birth weight (Kg)	-0.129	-2.014	1.558	-0.849	-4.493	2.414
Female Baby (ref. Male Baby)		-5.392	0.093		-8.762	0.945
Mother's alcohol consumption (ref. No)	-1.725	-8.380	3.245	-1.435	-12.019	6.509
Parity (birth)	0.173	-0.820	1.274	0.396	-1.628	2.808
Follow-up time (year)	0.303	-0.087	0.799	0.634	-0.159	1.641
As (mg/Kg)	0.903	-0.671	2.941	5.987	-7.564	21.024
Ba (mg/Kg)		-0.321	-0.026		-0.794	-0.319
Be (mg/Kg)	-3.652	-15.455	4.356	-4.062	-19.612	7.684
Cr (mg/Kg)		0.016	0.507		-0.123	1.711
Cu (mg/Kg)	0.015	-0.219	0.239	-0.194	-0.997	0.261
Pb (mg/Kg)	-0.006	-0.061	0.045	0.066	-0.091	0.217
Mn (10 mg/Kg)		-0.001	0.011		0.025	0.050
Ni (mg/Kg)	0.052	-0.132	0.255	-1.317	-4.434	1.018
Hg (mg/Kg)	-0.062	-11.972	11.610	-0.373	-13.014	11.824

Significant at the 5% level

Close to significant

When the full-rank Bayesian Kriging estimates for soil chemicals were used as plug-in values, mother's age (mean [95% credible interval]: -0.259 [-0.549, -0.009]), Ba (-0.148 [-0.321, -0.026]) and Cr (0.257 [0.016, 0.507]) were significant at the 5% level. Baby sex (-2.521 [-5.392, 0.093]), follow-up time (0.303 [-0.087, 0.799]) and Mn (0.005 [-0.001, 0.011]) were relatively close to significant, having more than 90% of posterior samples of the risk estimates lying below/above zero. In our suggested model, Ba (-0.505 [-0.794, -0.319]) and Mn (0.035 [0.025, 0.050]) were significant at the 5% level and mother's age (-0.424 [-1.051, 0.041]), baby sex (-3.304 [-8.762, 0.945]), follow-up time (0.634 [-0.159, 1.641]) and Cr (0.703 [-0.123, 1.711]) were relatively close to significant compared to other covariates which were consistent with the model with plug-in values. In general, for the significant covariates, the joint model has a larger magnitude of the logistic regression parameter and a wider 95% credible interval than the model with the plug-in values.

Model comparisons are performed with respect to the deviance information criterion (DIC). DIC is defined as the posterior mean of the deviance (-2*log likelihood) plus pD, the estimated effective number of parameters in the posterior distribution. pD is defined as half the posterior variance of the deviance [28]. DIC for the model with plug-in estimates and our suggested model was 156.221 and 2440.391, respectively. However, these DIC values cannot be compared directly since the model with plug-in values has a logistic likelihood only whereas the joint model has two likelihoods (normal and logistic likelihoods). To compare these two models, DIC for the joint model was calculated using logistic likelihoods only. The deviance for the joint model was smaller than that of the model with plug-in values (53.543 vs. 28.111) in part because it contains chemical values that are estimated parameters. However, the joint model also has greater variability in the converged sampler and to account for this variability we calculated DIC as explained above. The calculated DIC for the joint model was DIC=69.566 which was less than the half of the DIC of the model with plug-in values (DIC=156.221).

5.1.2 Joint model with different knot locations and numbers of knots

To investigate whether placing knots close to the prediction locations can help the prediction of soil chemicals and thus the joint model, our suggested model was fitted again with 90 knots placed close to the outcome sites. As explained in 3.3.2, knots were generated based on a kernel smoothed intensity of the outcome site locations by the R package, spatstat. Figure 6 shows these two sets of knots selected based on soil sample sites and outcome sites. To determine whether similar results are obtained following Ruppert et al. [14]'s suggestion, a joint model with K=30 knots (25% of data point) was also fitted.

Figure 6.

Knots selected based on: (a) soil sample sites using a space filling algorithm and (b) outcome sites using a kernel-smoothed intensity of the outcome sites (+: knots, o: outcome sites).

Table 3 shows the comparison between three joint models. First model is the originally suggested joint model presented in Table 2 (90 knots placed on sample sites). Second model is the joint model with low-rank Kriging with 90 knots placed close to the outcome sites (90 knots placed on outcome sites). Third model is the joint model with low-rank Kriging with 30 knots placed on soil sample sites (30 knots place on samples sites). As all these models are joint models which have two likelihoods, we can compare DIC to find a better model. The first model has the smallest DIC of 2440.39 followed by the second model (DIC=2848.52) and the third model (DIC=2851.308). This result suggests that the low-rank Kriging can be affected by the knot location for two-dimensional data which is in contrast to one-dimensional data where the prediction result is rather insensitive to the knot location [14, 25]. As seen in the simulation study, using reduced number of knots affected the model fit, increasing DIC by 411 compared to the originally suggested model. DIC can also be calculated using the health model likelihood only. When we compared two joint models with different knot placements, the model with knots placed on the outcome sites had a smaller DIC (DIC=45.190) than the model with knots placed on sample sites (DIC=69.566).

Table 3. Comparison of three joint models with different knot locations (sample sites vs. outcome sites) and knot numbers (90 vs. 30).

	90 knots placed on sample sites			90 knots placed on outcome sites			30 knots placed on sample sites
	Mean	95% Cred. Int.		Mean	95% Cred. Int.		Mean	95% Cred. Int.
Intercept	0.536	-9.557	12.356	-1.342	-14.063	11.339	1.424	-11.344	19.738
Mother's age (year)		-1.051	0.041		-1.41	-0.004	-0.276	-1.041	0.311
Mother_Black (ref. Mother_non_Black)	-1.724	-7.706	3.046	-1.686	-8.694	3.643	-1.823	-9.185	3.912
Birth weight (Kg)	-0.849	-4.493	2.414	-2.449	-7.13	1.034	-0.555	-4.326	2.678
Female Baby (ref. Male Baby)		-8.762	0.945	-2.998	-9.816	2.294	-0.896	-7.674	4.909
Mother's alcohol consumption (ref. No)	-1.435	-12.019	6.509	0.312	-10.055	11.142	0.179	-9.972	10.189
Parity (birth)	0.396	-1.628	2.808	-0.334	-3.671	2.317	-1.571	-5.733	1.381
Follow-up time (year)		-0.159	1.641	0.512	-0.333	1.772	0.523	-0.402	1.887
As (mg/Kg)	5.987	-7.564	21.024	-1.323	-10.599	6.741	1.376	-6.579	10.227
Ba (mg/Kg)		-0.794	-0.319		-0.478	-0.029		0.121	0.601
Be (mg/Kg)	-4.062	-19.612	7.684	-1.059	-15.111	10.839	0.446	-12.817	13.146
Cr (mg/Kg)		-0.123	1.711	0.721	-0.505	1.642	-0.337	-1.619	1.034
Cu (mg/Kg)	-0.194	-0.997	0.261	-0.293	-3.861	2.117	-1.473	-4.677	0.583
Pb (mg/Kg)	0.066	-0.091	0.217	-0.033	-0.555	0.467		0.478	1.300
Mn (10 mg/Kg)		0.025	0.050		0.055	0.074		-0.144	-0.112
Ni (mg/Kg)	-1.317	-4.434	1.018	-1.37	-7.702	2.12	0.848	-1.442	5.603
Hg (mg/Kg)	-0.373	-13.014	11.824	0.137	-10.46	13.313	0.243	-10.818	11.541
	DIC=2440.391			DIC=2848.521			DIC=2851.308

Significant at the 5% level

Close to significant

When knots are placed close to the outcome sites, mother's age (-0.680 [-1.41, -0.004]), Ba (-0.255 [-0.478,-0.029]) and Mn (0.066 [0.055, 0.074]) were significant at the 5% level. This result is similar to the originally suggested joint model. When 30 knots placed on the sample sites were used, Ba (0.330 [0.121, 0.601]), Pb (0.768 [0.478, 1.300]) and Mn (-0.122[-0.144, -0.112]) were significant at the 5% level. This results are quite different from the suggested joint model and the model with plug-in estimates since the sign of the logistic regression parameter is opposite for Ba and Mn.

5.1.3 Joint model with different spatial range parameters

In the suggested model, we estimated the spatial range parameter ρ_p using a variogram analysis for each soil chemical. To assess the sensitivity of the results to the choice of the spatial range parameter, a sensitivity analysis was performed. Two joint models were fitted separately using 2*ρ̂_p and 1/2*ρ̂_p where ρ̂_p was obtained from a variogram analysis for each chemical. Table 4 shows the results of comparing the suggested model with these two modes with different ρ_p values. Compared to the suggested model, some different results were observed. When 2*ρ̂_p was used, Ba (0.021[0.021, 0.022]), Cr (-5.385[-6.245, -4.682]), Pb (5.701[4.185, 7.794]) and Hg (0.065[0.053, 0.077]) were significant at the 5% level. When 1/2*ρ̂_p was used, Ba (0.022[0.022, 0.024]), Cr(-6.628[-8.862, -4.296]) and Hg (0.271[0.236, 0.296]) were significant at the 5% level. No mom and baby covariates were significant at the 5% level. When we compared DIC, our suggested model has the smallest DIC suggesting the best model fit (DIC=2440.391 vs. 3003.621 vs. 2995.552).

Table 4. Comparison of joint models with different spatial range parameters (sensitivity analysis).

	Model with estimated rho			Model with 0.5*Estimated rho			Model with 2*Estimated rho
	Mean	95% Cred. Int.		Mean	95% Cred. Int.		Mean	95% Cred. Int.
Intercept	0.536	-9.557	12.356	-0.786	-16.257	11.748	-0.719	-14.916	11.518
Mother's age (year)		-1.051	0.041		-1.999	0.220	-0.650	-2.055	0.319
Mother_Black (ref. Mother_non_Black)	-1.724	-7.706	3.046	-5.021	-18.930	3.603		-22.718	2.116
Birth weight (Kg)	-0.849	-4.493	2.414	-1.204	-6.342	3.074	-0.770	-6.592	4.031
Female Baby (ref. Male Baby)		-8.762	0.945	2.429	-4.905	13.104	1.814	-4.522	10.144
Mother's alcohol consumption (ref. No)	-1.435	-12.019	6.509	0.038	-11.146	12.707	-0.435	-12.376	10.825
Parity (birth)	0.396	-1.628	2.808		-11.259	0.346		-10.698	0.739
Child's age last seen Medicaid (year)		-0.159	1.641	0.538	-0.450	2.128	0.523	-0.583	2.193
As (mg/Kg)	5.987	-7.564	21.024	-0.081	-12.565	13.386	-0.100	-11.33	10.075
Ba (mg/Kg)		-0.794	-0.319		0.022	0.024		0.021	0.022
Be (mg/Kg)	-4.062	-19.612	7.684	0.224	-10.444	9.911	-2.875	-15.025	5.746
Cr (mg/Kg)		-0.123	1.711		-8.862	-4.296		-6.245	-4.682
Cu (mg/Kg)	-0.194	-0.997	0.261	0.219	-12.452	14.042	-0.102	-12.627	12.573
Pb (mg/Kg)	0.066	-0.091	0.217	0.168	-2.233	2.775		4.185	7.794
Mn (10 mg/Kg)		0.025	0.050	-2.538	-10.777	2.637		-10.021	0.766
Ni (mg/Kg)	-1.317	-4.434	1.018	0.637	-0.299	1.312	0.073	-0.517	0.757
Hg (mg/Kg)	-0.373	-13.014	11.824		0.236	0.296		0.053	0.077
	DIC=2440.391			DIC=2995.552			DIC=3003.621

Significant at the 5% level

Close to significant

Although some similar results were obtained such as Ba which was significant at the 5% level for all three models, different results were also observed. The sign of the effect for Ba was different in the models with different ρ_p values, Cr was close to significant in the suggested model but became significant at the 5% in the models with different ρ_p values. Other chemicals such as Pb and Hg also became significant in the model with different ρ_p values.

5.2. Chemical prediction by low-rank Kriging with different spatial range parameters and numbers of knots in MRDD data

In this section, four different low-rank Kriging models were considered for chemical prediction using a different set of knot numbers K, and different spatial range parameters ρ_p to investigate how the number of knots and the spatial range parameter affects low-rank Kriging prediction. All the combinations of ρ̂_p = (0.16, 0.008) and K = (30, 90) were used. ρ̂_p =0.16 was chosen as the maximum distance between sample sites within the study area $\left({\widehat{\rho }}_p=\underset{1\le j,j^{\prime }\le m}{\text{max}}\Vert {\mathbf{\text{s}}}_j-{\mathbf{\text{s}}}_{j^{\prime }}\Vert \right)$ as recommended by French and Wand [13]. ρ̂_p=0.008 is selected as a much smaller value $\left({\widehat{\rho }}_p=1/20\underset{1\le j,j^{\prime }\le m}{\text{max}}\Vert {\mathbf{\text{s}}}_j-{\mathbf{\text{s}}}_{j^{\prime }}\Vert \right)$. K=30 (25% of data) was chosen following the suggestion of Ruppert et al. [14]. To compare the prediction performance of low-rank Kriging with different number of knots, K=90 (75% of data) was also selected since our simulation study found that about 65-80% of data points are needed to achieve similar prediction results to the full-rank Kriging. We also fitted a Bayesian full-rank Kriging model (FK) using the R package spBayes assuming a Matérn covariance function. We assume that Bayesian Kriging is the ‘gold-standard’ for comparison. The prediction performance of each low-rank Kriging was measured by the mean squared error of prediction (MSEP) which was calculated as follows:

$$\mathit{\text{MSEP}}=\frac{1}{141}\text{∑}_{i=1}^{141}{(\text{FK}\_\text{estimate‐LK}\_\text{estimate})}^2$$

Table 5 shows the prediction performance of different low-rank Kriging models measured by mean squared error of prediction (MSEP). When the smoothing parameter was fixed at ρ̂_p=0.16, the low-rank Kriging with 30 knots and that with 90 knots had similar MSEP for all chemicals. It was because the estimated bivariate surface was too smooth for both models. In contrast, when we used ρ̂_p=0.008, the low-rank Kriging with 90 knots had much smaller MSEP for all chemicals than the low-rank Kriging with 30 knots by a factor varying from 1.9 (Ba) to 14.7 (Pb). When 30 knots are used, MSEP for most chemicals are similar between ρ̂_p=0.16 and ρ̂_p=0.008 whereas when 90 knots are used, most chemicals have smaller MSEP when ρ̂_p=0.008 is used.

Table 5. Mean squared error of prediction (MSEP) of the low-rank Kriging with 30 knots (LK_30) and that with 90 knots (LK_90).

	rho=0.16		rho=0.008
	LK_30	LK_90	LK_30	LK_90
As	1.08	1.06	1.06	0.46
Ba	691.89	688.54	883.94	458.31
Be	0.020	0.020	0.025	0.0072
Cr	42.19	42.58	61.58	14.31
Cu	96.66	96.35	86.61	21.95
Pb	1402.84	1400.02	1138.83	77.28
Mn	75494.82	74572.78	74909.58	31379.03
Ni	16.90	16.53	17.03	2.25
Hg	0.0019	0.0019	0.0019	0.00083

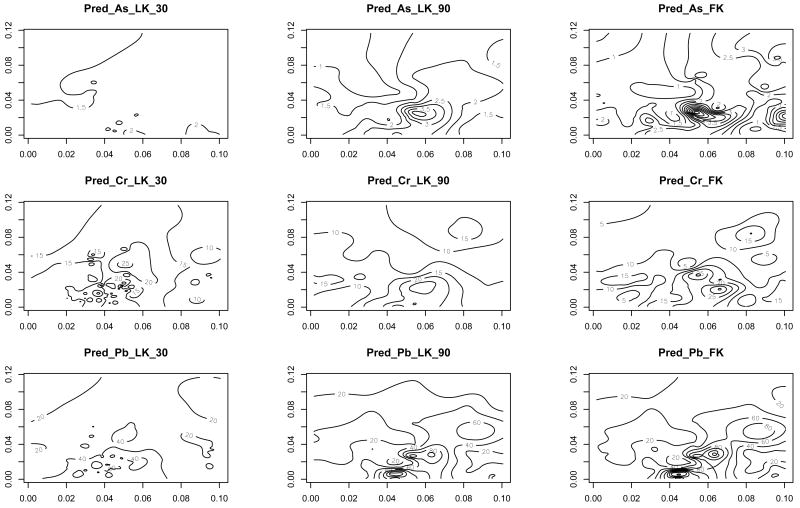
Figure 7 shows contour plots of predicted As, Cr and Pb at the outcome sites by the low-rank Kriging with 30 knots, the low-rank Kriging with 90 knots and full-rank Kriging. For both low-rank Kriging models, ρ̂_p = 0.008 was used. To make the contour plots comparable, contours are drawn at the same level in three plots for each chemical. The general patterns across the region seem similar between the full-rank Kriging and the low-rank Kriging with 90 knots whereas the chemical estimates from the low-rank Kriging with 30 knots are too smooth as compared to the full rank Kriging. Similar results were also observed for other chemicals (not shown here).

Figure 7.

Contour plots of predicted As, Cr and Pb at mothers' residential addresses by low-rank Kriging with 30 knots (LK_30), low-rank Kriging with 90 knots (LK_90) and full-rank Kriging (FK).

6. Discussion

We present a Bayesian joint model which interpolates several spatial fields and estimates the associated risk simultaneously for a binary outcome. Low-rank Kriging imposes less computational burden compared to a full-rank Kriging. Employing a Bayesian approach, low-rank Kriging can reduce computational complexity significantly since it does not invert the spatial covariance matrix at each MCMC iteration as the full-rank Kriging model does. This is achieved by fixing the spatial range parameter a priori which makes low-rank Kriging have a generalized linear model specification.

Different approaches are possible for choosing the spatial range parameter. French and Wand [13] suggested fixing the spatial range parameter at the maximum distance between two sites within the study area. Another way to choose the spatial range parameter is to use a variogram analysis as we adopted in this study. The spatial range need to be selected with caution as these affect low-rank Kriging prediction performance compared to the full rank Kriging. Our sensitivity analysis suggests that the results can be sensitive to the choice of the spatial range parameter. This implies that the interpretation for those soil chemicals can be different depending on what ρ_p values were used to fit the joint model. Thus, it seems necessary to estimate range parameters properly. Based on our findings, it appears that employing variogram analysis is a better approach than Ruppert et al.'s recommendation.

It was found that the knot specification has little effect on low-rank smoothing splines performance for one-dimensional data [26, 27]. However, the effect of knot specification on two-dimensional data has not been investigated in depth. We investigated the effect of different number of knots and knot locations for two-dimensional data in this study. Our simulation study and data example suggest that if a surface is smooth (large spatial range parameter), less knots are required but for less smooth surface (smaller spatial range parameter) more knots are required to achieve similar prediction with the full-rank Kriging. Although Ruppert et al. [14] provide a recommendation based on their experience, our simulation study shows that it is a bit conservative. With a reasonable number of knots and spatial range parameter, low-rank Kriging performs as well as full-rank Bayesian Kriging. It is obvious that there is tradeoff between computational speed and the performance of approximation. In our data example, it was found that knots covering the study area had a better model fit supported by smaller overall DIC. This area can be an interesting area where further research is required. As our joint model has both the health model likelihood and the exposure model likelihood, DIC was calculated using both likelihoods and compared between different joint models. It can be argued that only the health model likelihood need be considered for DIC as that is the main focus of the analysis. However, the prediction of the unobserved soil chemicals is affected by the exposure model fitting and thus it seems necessary to find the best exposure model to obtain accurate prediction of those soil chemicals. Thus, we decided to use overall DIC as our criteria which consider both exposure and health model likelihoods for the DIC calculation.

There are some issues which need to be addressed with regard to our modeling strategy. First, the choice of a spatial range parameter is important as it controls the smoothness of the bivariate surface. The spatial range parameter could have been estimated in our joint model but we did not use this approach for computational expediency. If this parameter were estimated, a spatial covariance matrix needs to be inverted at each MCMC iteration which requires a computation similar to Full-rank Kriging. Secondly, we used an unstructured random effect rather than spatial random effect for our binary outcome as it has been reported that using a conditionally autoregressive (CAR) model to spatially referenced data can mask spatial predictor effects [11, 12]. Thirdly, our joint model was fitted as a full model using all the available mom and baby covariates and soil chemical concentrations. DIC is a reliable measure to compare different Bayesian model fits. We used DIC to compare different joint models in this study. However, we did not perform variable selection to find the best submodel since we have sixteen covariates and the number of possible submodels is large (2¹⁶). A different variable selection approach is needed for our analysis and we will use a MCMC method for variable selection in the future work. Finally, in our joint model, each chemical concentration was modeled separately as a univariate model though we observed multiple chemical concentrations in the soil samples. A multivariate model which captures the possible correlations between chemical measures might provide an appropriate prediction although this was not investigated in this study. In the future, we will develop a method which introduces these possible correlations between chemical concentrations into a joint model.

Our joint model found significant association between MRDD outcome and Ba, Mn and possibly Cr concentrations which was consistent with the model with plug-in estimates. However, our joint model can find an association which is close to the unobserved truth reflecting the uncertainty involved in the chemical prediction which the model with plug-in estimates cannot. It should be also noted that the true association between MRDD and soil chemical concentrations could be more subtle as we did not perform variable selection.

In this paper, we showed that a low-rank Kriging can have similar prediction performance to the full-rank Kriging when the number of knots and the smoothing parameter are selected with caution. This enables us to employ a Bayesian approach and obtain the risk estimates of soil chemical concentrations reflecting the uncertainty involved in the spatial field prediction. Thus, it is recommended to use the joint model approach so that the risk associated with soil chemical concentrations can be properly assessed.

Appendix

The MCMC algorithm

Markov chain Monte Carlo (MCMC) sampling is an iterative numerical method which simulates complex and non-standard multivariate distribution [29]. It generates correlated draws from the joint posterior distribution of model parameters. For our MRDD data analysis, a Metropolis-Hastings algorithm [15, 29] was employed to sample for all the parameters. This Metropolis-Hasting algorithm can draw samples from any probability distribution and does not involve knowledge of the conditional posteriors to update the parameters.

General description for Metropolis-Hastings algorithm is as follows: let y denote the observed data and θ = (θ₁,…,θ_n) represent a vector of all the parameters. Values for θ are to be sampled sequentially at each iteration of the MCMC sampler.

Metropolis-Hastings Sampler

1. Assign starting values to θ⁽⁰⁾

2. Set t = 0

3. For 1 ≤ i ≤ n, draw ${\theta }_i^{\ast }$ from the proposal density $J_i({\theta }_i^{\ast };{\theta }_i^{(t)})$

4. Compute the ratio of the densities $r=\frac{p({\theta }_i^{\ast };y)J_i({\theta }_i^{(t)};{\theta }_i^{\ast })}{p({\theta }_i^{(t)};y)J_i({\theta }_i^{\ast };{\theta }_i^{(t)})}$ where p is the full conditional distribution of θ_i

5. Set ${\theta }_i^{(t+1)}=\{\begin{array}{ll}{\theta }_i^{\ast }& \text{with probability min}(r,1)\text{and}\\ {\theta }_i^{(t)}& \text{otherwise}\end{array}$

Any distribution from which samples are readily obtainable can be used as the proposal distribution.

Now we present the specific use of Metropolis-Hastings in our MCMC algorithm. From Equation (2), (5) and (8), our joint posterior distribution becomes:

$$\begin{array}{l}\prod _i\mathit{\text{Bern}}(y_i;p_i({\mathbf{\text{u}}}_i,{\mathbf{\text{z}}}^{\ast }({\mathbf{\text{x}}}_i),{\beta }_0,{\beta }_1,{\beta }_2,\varepsilon ))\\ \times \prod _p\prod _j\left[N(z_p({\mathbf{\text{s}}}_j);{\alpha }_p,{\mathbf{\text{W}}}_p,{\mathbf{\text{Z}}}_p{,\text{v}}_p,{\tau }_p)\right]\\ \times \prod _p\prod _i\left[N(z_p^{\ast }({\mathbf{\text{x}}}_i);z_p({\mathbf{\text{s}}}_j),{\alpha }_p,{\mathbf{\text{W}}}_{xp},{\mathbf{\text{Z}}}_{xp}{,\text{v}}_p,{\tau }_p)\right]\\ \times \prod _p\left[\prod _{k}N({\text{v}}_p;{\sigma }_{{\text{v}}_p})\prod _{i+j}N({\tau }_p;{\sigma }_{{\tau }_p})\right]\\ \times \text{Pr}({\beta }_0;{\sigma }_{{\beta }_0})\text{Pr}({\beta }_1;{\sigma }_{{\beta }_1})\text{Pr}({\beta }_2;{\sigma }_{{\beta }_2})\text{Pr}(\varepsilon ;{\sigma }_{\varepsilon })\text{Pr}({\sigma }_{{\beta }_0})\text{Pr}({\sigma }_{{\beta }_1})\text{Pr}({\sigma }_{{\beta }_2})\text{Pr}({\sigma }_{\varepsilon })\\ \times \prod _p\left[\text{Pr}({\alpha }_p;{\sigma }_{{\alpha }_p})\text{Pr}({\sigma }_{{\alpha }_p})\text{Pr}({\sigma }_{{\text{v}}_p})\text{Pr}({\sigma }_{{\tau }_p})\right]\end{array}$$ (9)

For priors, normal distributions priors are used for β₀,β₁,β₂,ε and α_p as follows:

$${\beta }_0\sim N(0,{\sigma }_{{\beta }_0}^2),{\beta }_1\sim N(0,{\sigma }_{{\beta }_1}^2),{\beta }_2\sim N(0,{\sigma }_{{\beta }_2}^2),\varepsilon \sim N(0,{\sigma }_{\varepsilon }^2),{\alpha }_p\sim N(0,{\sigma }_{{\alpha }_p}^2)$$

For hyperpriors, uniform distributions are assumed for standard deviation parameters [30]:

$$\begin{array}{l}{\sigma }_{{\beta }_0}\sim U(0,10),{\sigma }_{{\beta }_1}\sim U(0,10),{\sigma }_{{\beta }_2}\sim U(0,10),{\sigma }_{\varepsilon }\sim U(0,10)\\ {\sigma }_{{\alpha }_p}\sim U(0,10),{\sigma }_{\tau p}\sim U(0,10),{\sigma }_{\text{v}p}\sim U(0,10)\end{array}$$

At each iteration of our Metropolis-Hastings sampler, we

1. Update parameters of the low-rank Kriging model for each chemical concentrations using observed and unobserved measures

2. Use the low-rank Kriging parameters, predictive distribution and the logistic spatial model likelihood to update unobserved chemical concentrations at the outcome sites

3. Use the predicted soil chemical concentrations to update the regression parameters in the logistic spatial model

To run the Metropolis-Hastings sampler,

1. Select K knots as described in Section 3.3.2.

2. Initialize all the parameters

3. For the p th chemical, calculate ${\Omega }_{\mathit{\text{p}}}^{-1/2}$, Z_p and Z_xp fixing ρ̂_p using the estimated spatial range parameter from a univariate variogram analysis as described in Section 3.3.2 and 3.3.3.

4. At t iteration, update all the parameters for the low-rank Kriging for each p th chemical where 1 ≤ p ≤ P calculating the density ratio r using the joint distribution in (9)

5. At t iteration, update all the unobserved chemical concentrations for each p th chemical where 1 ≤ p ≤ P calculating the density ratio r using the joint distribution in (9)

6. At t iteration, update β = (β₀,β₁,β₂), ε, σ_β = (σ_β0, σ_β1, σ_β2), and σ_ε for the logistic spatial model calculating the density ratio r using the joint distribution in (9)

Two chains with different initial values were run for 100,000 times and the convergence was checked by Gelman-Rubin statistics and a visual inspection of trace plots of the deviance (-2 log likelihood). After convergence was checked, additional 50,000 samples were drawn for summary statistics and thinning=10 was used to reduce autocorrelation.