Effect of Volume-of-Interest Misregistration on Quantitative Planar Activity and Dose Estimation

Abstract

In targeted radionuclide therapy (TRT), dose estimation is essential for treatment planning and tumor dose response studies. Dose estimates are typically based on a time series of whole body conjugate view planar or SPECT scans of the patient acquired after administration of a planning dose. Quantifying the activity in the organs from these studies is an essential part of dose estimation.

The Quantitative Planar (QPlanar) processing method involves accurate compensation for image degrading factors and correction for organ and background overlap via the combination of computational models of the image formation process and 3D volumes of interest defining the organs to be quantified. When the organ VOIs are accurately defined, the method intrinsically compensates for attenuation, scatter, and partial volume effects, as well as overlap with other organs and the background. However, alignment between the 3D organ volume of interest (VOIs) used in QPlanar processing and the true organ projections in the planar images is required. The goal of this research was to study the effects of VOI misregistration on the accuracy and precision of organ activity estimates obtained using the QPlanar method.

In this work, we modeled the degree of residual misregistration that would be expected after an automated registration procedure by randomly misaligning 3D SPECT/CT images, from which the VOI information was derived, and planar images. Mutual information based image registration was used to align the realistic simulated 3D SPECT images with the 2D planar images. The residual image misregistration was used to simulate realistic levels of misregistration and allow investigation of the effects of misregistration on the accuracy and precision of the QPlanar method. We observed that accurate registration is especially important for small organs or ones with low activity concentrations compared to neighboring organs. In addition, residual misregistration gave rise to a loss of precision in the activity estimates that was on the order of the loss of precision due to Poisson noise in the projection data. These results serve as a lower bound on the effects of misregistration on the accuracy and precision of QPlanar activity estimate and demonstrate that misregistration errors must be taken into account when assessing the overall precision of organ dose estimates.

I. INTRODUCTION

Dose estimation is essential for treatment planning and studies of tumor response in targeted radionuclide therapy (TRT). Dose estimates are typically based on quantitative imaging techniques such as whole body conjugate view planar or SPECT imaging of the patient after administration of a planning dose. Quantifying the activity in the organs from these studies is an essential part of dose estimation.

The conventional method for quantifying activity from planar images is based on using the geometric mean of conjugate view scintillation camera whole-body scans (Thomas et al., 1976) and has been used in many clinical trials (e.g., O’Donnell et al., 1999; Matthay et al., 2001; Koral et al., 2003). However, this method for quantifying organ activities based on planar scans has several limitations that can result in limited accuracy (Wu and Siegel, 1984). The overlap of an organ’s projection with the projections of other organs or background regions is perhaps the major limitation for planar processing methods. Other limitations arise from the approximate nature of the methods used to compensate for attenuation, scatter, system resolution and partial volume effects (Thomas et al., 1988; Leichner et al., 1993; Siegel et al., 1999). These limitations can produce inaccurate and imprecise activity estimates. While it is possible to improve the estimates by improved background and overlap correction (Liu et al., 1996; Kojima et al., 2000; Sjogreen et al., 2002) and the addition of source thickness compensation to the geometric mean attenuation compensation, these methods require additional information that must be obtained from some 3D imaging modality such as SPECT or CT.

We have previously developed a processing method for quantifying organ activities from planar scans, the Quantitative Planar (QPlanar) method, which explicitly uses 3D organ volumes of interest (VOIs) to provide improved activity estimates in a way that is theoretically rigorous (He and Frey, 2006). The QPlanar method is based on maximum likelihood estimation (Carson, 1986) and an accurate computational model of the image formation process. While still using data from conjugate view planar scans, it provides both accurate and theoretically rigorous compensation for image degrading factors including attenuation, scatter, the collimator-detector response, partial volume effects, and background and organ overlap. We have shown that this method provides organ activity estimates with accuracy that approaches that of quantitative SPECT, but uses data from conventional planar wholebody scans and requires reduced processing times (He and Frey, 2006).

However, the QPlanar method requires definition of 3D organ VOIs that are aligned with the planar images. This means that the 3D VOIs must be well registered to the positions of the organs at the time that the planar images were acquired. These VOIs would typically be defined using a 3D imaging study, such as SPECT or x-ray CT. Since these 3D images would be acquired at a different time than the planar images, they would need to be registered to the planar projections. The goal of this research was to study the effects of VOI misregistration on the accuracy and precision of organ activity estimates obtained using the QPlanar method.

In previous work, we studied the effect of misregistration on the accuracy of QPlanar activity quantification by shifting the 3D VOIs in one of three orthogonal directions (two directions in the transaxial planes and one axially) (He and Frey, 2010). That study thus evaluated the sensitivity of accuracy to shifts of fixed distances. However, since it did not model variability in misregistration that would be seen with patients, it did not provide information about precision. In addition, the shifts studied were rather arbitrary and not based on the magnitude of shifts that would be present in patient data.

Studying the effects of VOI misregistration on accuracy and precision requires a realistic computational model of the degree and variability of misregistration that would be expected clinically. In this paper, we studied these effects using a computational model based on residual misregistration obtained between 3D SPECT and 2D planar images obtained after applying a registration method. In this model, we implicitly assumed that the 3D information was obtained from a SPECT/CT scan. The SPECT and CT images in the SPECT/CT scan were assumed to be perfectly registered. The CT image was used to provide high resolution anatomical information, and the SPECT image provided data that, in addition to defining the structures functionally, could be more easily registered to the data from the planar scans.

Given this assumption, we modeled the misregistration of the organ VOIs with the planar images by residual misregistration of SPECT and planar nuclear medicine images after applying a mutual information based image registration method to align realistic simulated 3D SPECT images with 2D planar images. The residual misregistration after this procedure was used as a computational model for the misregistration that would be observed clinically when registering SPECT and planar images using such an algorithm. It should be noted that the misregistrations and the registration algorithm modeled only rigid transformations of the planar and SPECT data.

II. METHODS

A. QPlanar Method

The QPlanar method uses conjugate view whole-body scans, an accurate computational model of the image formation process, and an iterative maximum likelihood algorithm to estimate the activities in a set of non-overlapping VOIs. In this context, non-overlapping means that the VOIs do not overlap in the 3D object space, but may (and in general will) at least partially overlap in projection space. The method assumes there are uniform (or at least known) activity distributions in each of the VOIs (including the background, though multiple background regions could be used), and that the planar scan is equal to the weighted sum of the projections of the VOIs, where the weights are the organ activity concentrations.

The VOI projections are estimated using a projector that accurately models the effects of attenuation, scatter, and the full collimator-detector response, and thus is a realistic computational model of the image formation process. The forward model is given by:

$$p_i=\sum _{r=0}^N{a}_r{C}_{\mathit{ir}}.$$ (1)

In equation (1), p_i is the counts in the projection bin i, a_r is the total activity in the rth VOI, C_ir is projection matrix describing the probability that a photon emitted in the rth VOI will be detected in projection bin i, and N is the number of VOIs (He and Frey, 2006).

A maximum likelihood-expectation maximization (ML-EM) algorithm is used to estimate the organ activities that result in the best fit between the estimated and measured equations (Carson, 1986). Due to the assumption of uniform organ activities, the method implicitly includes partial volume compensation similar to that performed using, e.g., the geometric transfer matrix method (Rousset et al., 1998; Du et al., 2005). The update equation for the QPlanar algorithm is:

$$a_r^{n+1}=\frac{a_r^n}{\sum _{i=0}^M{C}_{\mathit{ir}}}\sum _{i=0}^M\frac{C_{\mathit{ir}}{p}_i}{\sum _{j=0}^N{a}_j^n{C}_{\mathit{ij}}},$$ (2)

where p_i is the measured projection in bin i, a_rⁿ is the estimated activity concentration in region r after the n-th iteration, M, is the total number of projection bins in the anterior and posterior projection images, and the remainder of the symbols have the same meaning as in Equation 1. Equation 2 is applied iteratively until the activity estimates converge. Due to the relatively small number of VOIs, the matrix C can be precalculated and stored, allowing the computations in Equation 2 to be performed very rapidly. The calculation of C is performed by filling each VOI with a constant activity concentration having unit total activity and projecting it into the anterior and posterior projections. Since the numbers of projections and organs are small, the precalculation takes less time than a single iteration of a SPECT reconstruction.

It is evident that the QPlanar method requires knowledge of the 3D organ VOIs. In practice, these will often be determined by segmenting 3D SPECT or CT images. Since the planar and SPECT/CT images will not, in general, be registered, some post-acquisition registration will be required. Also, the planar images would often be acquired at different times than the SPECT images, and could thus represent very different underlying activity distributions.

B. Mutual Information Based Image Registration

In this work we used mutual information-based image registration methods to register the SPECT and planar images. These methods have been found to be useful in multi-modality image registration (Maes et al., 1996) which, as mentioned above, is useful in this application because of the difference in underlying activity distributions between the planar and SPECT images resulting from their different times of acquisition. Mutual information measures the amount of information two images contain about each other. When images are well-registered, they tend to have a maximum amount of common information, i.e., mutual information (Viola and Wells, 1995).

We implemented a 2D-to-3D mutual information-based registration algorithm. In the method, a rigid transformation specified by 5 parameters including 2 translations (x and z) and 3 rotations (yz, xz and xy) (see Figure 1 for details) was applied to a reconstructed SPECT image. The x-axis is in the transaxial plane along the left-right lateral direction, the y-axis is aligned with the anterior-posterior axis in the patient and the z-axis is along the axial direction, which is aligned with the inferior-superior axis of the patient. A simple projection of the image was taken along the axis of the transformed image that is perpendicular to the anterior and posterior projection image plane. As a result, it was not necessary to consider the translation in the direction of the y-axis since it does not affect the projections. The translation parameters x and z were the shifts parallel to the x- and z- axes, respectively; the rotation parameters yz, xz and xy represented rotations around x-, y- and z- axes, respectively.

Figure 1.

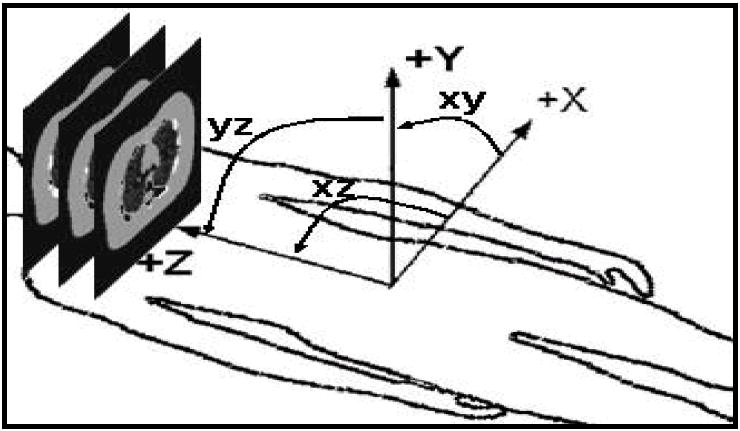
3D to 2D transformation parameters (x, z, yz, xz, xy). Because of the planar images were generated from projecting in y direction, parameter y is not considered in transformation parameters.

We computed the MI between the projection and geometric mean of the anterior and posterior planar projections. We used the residual error after this mutual information based registration procedure as a simulation model for misregistration of the VOIs and planar images that would be obtained following a registration procedure in a clinical study.

A MI-based registration method was implemented by searching for the transformation parameters that maximized the mutual information. The search was performed using Powell’s algorithm (Esteban and Morales, 1995), a nonlinear optimization algorithm well suited for image registration tasks. In this case, the function maximized was the mutual information of the planar and SPECT projections with respect to the five rigid transformation parameters (2 translations and 3 rotations).

C. Experimental Design

In a typical clinical study to estimate organ dose, a combination of planar and SPECT images would be acquired at various time points after administration of a planning dose of the imaging agent. In this work we modeled acquisition of a clinical dose estimation imaging procedure where planar images are acquired at 1, 5, 24, 72, and 144 hours after injection of a planning dose, and a SPECT/CT image is acquired just after the 24 hour planar image.

C.1 Data Generation

We used the 3D NCAT phantom (Segars et al., 2001) to provide a realistic numerical model of patient anatomy. Monte Carlo simulation methods, using a previously-validated MC simulation code (He et al., 2005; Song et al., 2005) that included modeling of the effects of septal penetration and scatter, were used to generate low-noise projections of 7 organs (Heart, Lungs, Liver, Kidneys, Spleen, Marrow and Blood Vessel) of interest and the whole body remainder. The activity distribution in all organs was uniform except in the heart and lungs. The lungs included a model for airways (Garrity et al., 2003) which resulted in 27% of the voxels in the lung containing air, and thus having no activity. In the heart, the blood-to-myocardium activity ratio was 107:130 for all time points.

During the simulation, both In-111 photopeaks (171 keV and 254 keV) were simulated using two 14% wide energy windows centered at each photopeak. The low-noise projections were generated into 128 transaxial and 170 axial projection bins with a 0.442 cm pixel size at 120 views over 360°. Scaling and summing of these projections was used to generate planar or SPECT projections with noise levels and activity distributions based on In-111 ibritumomab tiuxetan (Zevalin) patient scans. The activity distribution for the SPECT scan modeled that observed at 24 hours post injection. The acquisition time for patient SPECT/CT scans was 30 s per view for 120 views over 360° using a GE Millenium VH/Hawkeye system with MEGP collimator. The average over all slices of the total counts in a sinogram was 1.34×10⁵. Planar scans were generated with activity distributions appropriate for imaging at 1, 5, 24, 72, and 144 hours post injection (Figure 2). The count level in the planar images corresponded to a 20 min scan time. The total organ activity and organ volumes simulated in the heart, lungs, liver, kidneys, spleen, bone marrow, blood vessel and body remainder at the 5 time points are shown in Table 1. The total counts in the anterior and posterior planar images at each of the time points are shown in Table 2. Noise was simulated using a Poisson-distributed pseudo-random number generator. Since the organ activities and acquisition times were based on clinical scans, and the camera sensitivity modeled that of a real gamma camera system, the resulting noise levels were clinically realistic.

Figure 2.

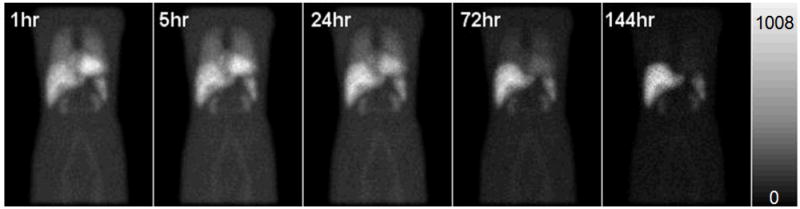
The anterior noisy In-111 planar images with activity distribution 1hr, 5hr, 24hr, 72hr and 144hr after administration simulated.

Table 1.

Organ volumes and activities in NCAT phantom.

Organs	Volume (c.c.)	Total Activity (MBq)
		1hr	5hr	24hr	72hr	144hr
Heart	656	16.7	14.9	9.70	3.29	0.65
Lungs	1333	12.0	10.9	7.59	3.02	0.76
Liver	1313	22.7	21.9	19.2	13.8	8.40
Kidneys	146	2.22	2.12	1.77	1.13	0.58
Spleen	122	3.34	3.12	2.71	1.80	0.97
Bone Marrow	572	2.78	2.61	2.06	1.14	0.47
Blood vessels	266	4.98	4.68	3.70	2.04	0.84
Body remainder	35975	108.4	101.6	79.7	43.1	17.1

Table 2.

Mean total counts in the anterior and planar images.

	1hr	5hr	24hr	72hr	144hr
anterior	3,066,212	2,867,432	2,236,318	1,217,779	516,817
posterior	3,066,674	2,875,688	2,249,690	1,237,523	530,703

The planar scans used during registration were scatter compensated using the Triple Energy Window (TEW) method (Ogawa et al., 1991) followed by taking the geometric mean of the conjugate views. The SPECT images used in the registration were reconstructed using the iterative ordered subsets-expectation maximization (OS-EM) algorithm (Hudson and Larkin, 1994) with compensation for attenuation, scatter, and the full collimator and detector response (He and Frey, 2006).

We investigated the accuracy of registration using SPECT reconstructed with iteration 5-30 iterations of OS-EM using 24 subsets per iteration. The number of subsets used was appropriate for the count level in the projections. To verify this, we also used 20 iterations using 6 subsets per iteration (comparable to 5 iterations of 24 subsets) and, as will be described below, found essentially no difference in the registration accuracy.

C.2 Image Registration

To study the effects of misregistration on quantitative accuracy, we registered the SPECT and planar images using 50 randomly selected starting values for the transformation parameters (x, z, xy, xz, yz). This is equivalent to having SPECT images with 50 different random orientations with respect to the planar images. The starting parameters were varied uniformly over ±5 pixels for the x and z translations and ±5° for rotations around the x, y and z axes. We selected these ranges as being reasonably representative of what could be achieved in clinical practice after moderately careful positioning of the patient and modest manual registration in the projection of planar and SPECT projections. We did not model non-rigid deformations in this work. While this limits the realism of the misregistration model, at present we have no data to provide a realistic computational model of the non-rigid misalignments and organ deformations that would arise due to differences in patient position for the different image acquisitions.

Using these images and starting values, we then performed a mutual information based registration procedure to register the SPECT and planar images. In each case, the SPECT image obtained from an activity distribution representing 24 hours post injection was individually registered to planar images obtained from activity distributions representing 1, 5, 24, 72, and 144 hours post injection. We used SPECT images resulting from 5, 10, 15, 20, 25 and 30 iterations (24 subsets per iteration) to study the effects of iteration number on the residual misregistration.

D. Accuracy of Registration Parameters

The accuracy of the activity estimates is ultimately the parameter of interest. However, it is instructive to first investigate the magnitude of the residual misregistration for the various registration parameters.

For all combinations of iteration numbers and planar image time points, small residual misregistration was generally obtained for all parameters except for yz (rotation around the x-axis) and xy (rotation around the z-axis). This is not surprising as the projections of the SPECT images are relatively insensitive to rotations about these two axes. Figure 3 shows the mean and standard deviation of the registration error for each of the registration parameters for 3 of the time points (1, 24, and 144 hr) and two of the iteration numbers (5 and 15). The accuracies of the estimated registration parameters were better than 0.1 ± 0.3 pixels for the x shift, 0.3 ± 0.6 pixels for the z shifts, and better than 0.2 ± 0.5 degrees for rotation around the y-axis. Similar accuracies were observed for other combinations of time points and iteration numbers. The precisions of the estimates for the 144 hr time point were worse than for the other time points, indicating a larger spread of residual error values. This is likely because the In-111 labeled tracer was almost completely absent from the blood by 144 hours post injection, and thus there was little activity in the lungs and heart, as seen in Figure 2. The lack of tracer in the blood provided fewer features for the algorithm to use in establishing the optimal registration. To study how far the registration results were from the truth, the mean of absolute errors for registration parameters with and without registration to SPECT images after 5 iterations were computed and are presented in Table 3. These values of the mean absolute error represent the average error, regardless of direction, for each of the registration parameters. The average absolute error values showed similar trends compared to the standard deviations of the error presented in Figure 3.

Figure 3.

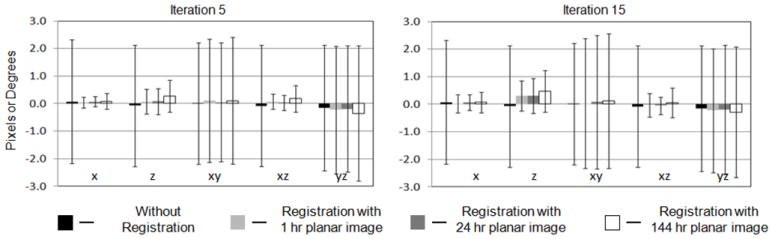
Mean and standard deviations of errors for x, z, xy, xz and yz parameters from registration of SPECT images obtained with 5 and 15 iterations with planar images from 1 hr, 24 hr and 144 hr time points.

Table 3.

Comparison of mean of absolute errors with and without registration to SPECT images after 5 iterations.

	Without registration	1hr	5hr	24hr	72hr	144hr
x (pixel)	2.46	0.21	0.18	0.20	0.23	0.27
z (pixel)	2.18	0.42	0.28	0.36	0.43	0.51
xy (degree)	2.49	2.54	2.47	2.51	2.53	2.55
xz (degree)	2.33	0.30	0.26	0.24	0.34	0.41
yz (degree)	2.59	2.49	2.51	2.54	2.55	2.57

We also investigated the effect of iteration number on registration errors. The means of the absolute value of the registration error for shifts in the x direction are shown in Figure 4. Similar trends were observed for the z and xz registration parameters. These data suggest that a smaller number of iterations is better in terms of achieving accurate registration. This is likely due to the presence of increased noise in images obtained using more than 5 iterations (about 120 updates), which served as a confounding factor in the registration process. For the xy and yz registration parameters we did not note any consistent trend as a function of iteration number. This is likely due to the general insensitivity of the projection to the values of these parameters. Based on these data, we evaluated the accuracy of activity estimates using the SPECT images obtained after 5 iterations (24 subsets per iteration).

Figure 4.

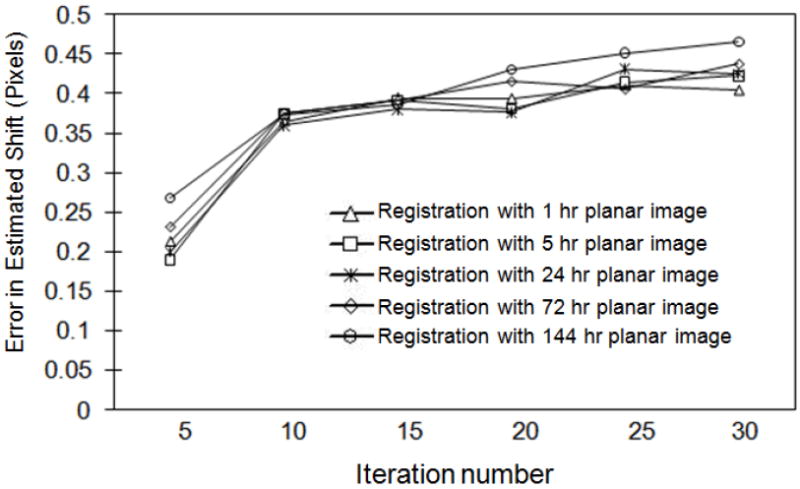
Mean of absolute value of error in shift in x direction as a function of iteration number for planar images at all five time points.

E. Effect of Residual Misregistration on Accuracy of Activity Estimates

Figure 5 shows the mean percent error and standard deviation of each organ’s activity estimated from planar images from the 5 hr time point using the QPlanar method and 3D VOIs transformed using the residual misregistration from SPECT images.

Figure 5.

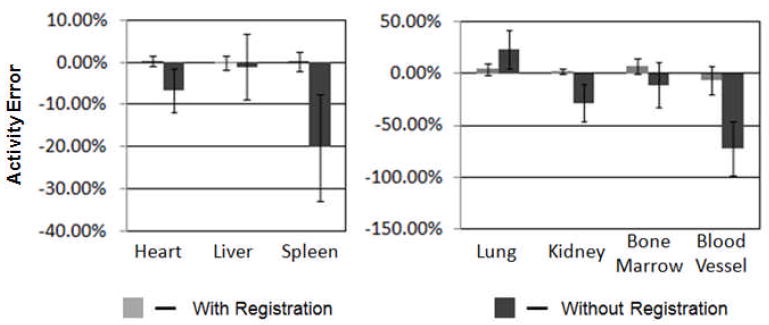
Comparison of the mean percent errors and standard deviation in organ activity estimates at the 5 hr time point with and without registration.

The largest mean errors and standard deviations were observed for small organs, i.e., the blood vessel (-6.72±13.54%) and bone marrow (6.80±7.19%). This demonstrates that minor misregistration can produce substantial error in activity estimates for small organs. For the other organs the accuracies were better than 5%, i.e., heart (0.35±1.26%), liver (-0.08±1.61%), spleen (2.17±2.35%) and kidney (0.21±2.41%), in spite of the relatively large residual misregistration for the xy and yz parameters. The percent standard deviations were small for most of the organs except for the lungs (5.63%), marrow (7.19%) and blood vessels (13.54%). Note that the larger variability for the lungs was likely because activity in pulmonary blood vessels was not included as part of the lungs. Thus, errors in accurately positioning the blood VOI would produce errors in the estimated lung activity, as some of the blood will be included in the lung VOI. Achieving improved registration accuracy may require further optimizing the SPECT images, for example by post-reconstruction filtering to control image noise.

Figure 5 also compares the mean and standard deviation of errors with and without registration. Although our focus was not on the magnitude of accuracy improvement with registration, the comparison provides information about the different effects of registration on different organs. For example, the accuracy of activity estimates for small organs, e.g., kidney, spleen, bone marrow and blood vessel, was improved substantially compared to no registration. This demonstrates that registration is more important in terms of improving accuracy for smaller organs, and suggests that good registration is essential for tumors. The improvement in accuracy for large hot organs was smaller than for small hot organs. For example, the accuracy was improved from -6.7% to 0.4% for heart and from -1.1% to -0.1% for liver. This demonstrates that misregistration plays a less important role in activity estimate accuracy for large and hot organs. However, large organs with low activity compared to their neighbors, such as the lungs, showed dramatic increases in accuracy after registration. The reasons for differences in behavior of small and large and cold and hot organs will be discussed in more detail below.

To provide additional insight into the nature of the errors, Table 4 also shows the range and the median of the percent error as well as the average percent absolute errors to illustrate how far the activity estimates were from the truth.

Table 4.

Errors in organ activity estimates at the 5 hr time point with and without registration.

%		Heart	Lung	Liver	Kidney	Spleen	Bone Marrow	Blood Vessel
Mean ± STD	W	0.4 ± 1.3	4.3 ± 5.6	-0.1 ± 1.6	2.2 ± 2.4	0.2 ± 2.4	6.8 ± 7.2	-6.7 ± 13.5
	W/O	-6.7 ± 5.2	22.9 ± 18.6	-1.1 ± 7.7	-28.2 ± 17.8	17.8 ± 12.7	-11.2 ± 21.7	-72.2 ± 25.7
Range	W	-3.1 - 3.1	-11.0 - 16.7	-4.0 - 4.9	-3.1 - 10.9	-4.6 - 8.0	-12.3 - 18.6	-33.4 - 22.8
	W/O	-20.0 - 2.1	-5.6 - 62.3	-18.3 - 12.9	-1.1 - 69.2	-31.2 - 20.2	-40.0 - 39.2	-95.4 - 35.9
Median	W	0.4	4.1	-0.2	1.6	-0.5	8.4	-8.0
	W/O	-5.8	23.0	-0.2	-23.7	-19.7	-4.6	-80.0
Mean of absolute	W	1.0	5.7	1.2	2.4	1.7	8.9	12.5
	W/O	6.9	23.2	6.2	28.2	20.2	17.5	72.2
p-value*		0.01	0.01	0.01	0.007	0.001	0.01	<10e-5

W: with registration, W/O: without registration.

^*p-value is for paired t-test comparing activity estimates w/ and w/o registration.

In light of the relatively small difference in accuracy and the large standard deviations, one might ask whether registration makes a statistically significant difference in the accuracy of the organ activity estimates. To assess this, we tested the statistical significance of the differences between organ activity estimates with and without registration. We computed the two tailed p-value for a paired t-test; the resulting p-values are shown in Table 4. In all cases the differences were significant with p-values of 0.01 or less. The p-values were small despite the large standard deviations due to correlations between the errors with and without registration for a given initial misregistration. These data indicate that mutual information misregistration is significantly better than manual registration having residual misregistration of +/- 5 pixels or degrees. However, the major focus of this work was not to demonstrate the necessity of registration, but to provide estimates of effect of residual misregistration on accuracy and precision.

For many antibodies, the liver is the dose limiting organ and is thus of particular clinical importance. Table 5 shows the mean, standard deviation and range of errors and mean of absolute errors in activity estimates for the liver resulting from the residual misregistration between SPECT images after 5 iterations and the planar images at each of the 5 time points. Despite the relatively poor registration accuracy for two of the registration parameters (xy and yz), activity estimates for the liver were quite good, with average absolute errors less than 1.56%; the largest errors were for the 144 hour time point.

Table 5.

Statistical errors in liver activity estimates at each time point with registration.

%	1hr	5hr	24hr	72hr	144hr
Mean ± STD	0.2 ± 1.7	-0.1 ± 1.6	0.4 ± 1.5	-0.2 ± 1.8	-0.4 ± 2.0
Range	-4.1 - 5.2	-4.0 - 4.9	-3.4 - 5.4	-5.2 - 4.8	-5.8 - 8.1
Mean of absolute	1.41	1.38	1.53	1.55	1.56

For dosimetry, the organ residence times are the parameter of ultimate interest. They are based on the activity estimates at all time points, and it is thus important to evaluate the effect of misregistration on them. We estimated the residence time by fitting the activity estimates at each time point with an exponential decay function, integrating the resulting curve and dividing this value by the total injected activity. Figure 6 shows the mean and standard deviation of the percent error in the residence times for each organ estimated from planar images with registration.

Figure 6.

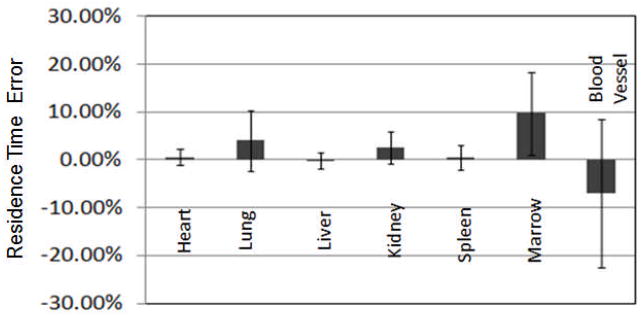
The percent errors and standard deviation in residence time estimates for each organ estimated from planar images with registration.

From these data, we observed that the accuracy and precision of errors in the residence times were very similar to the errors in the activity estimate at the 5 hr time point, and thus the low count levels in later time points, and resulting larger residual misregistrations, did not have an undue impact on the accuracy or precision of the residence time estimates.

III. DISCUSSION

In this experiment, SPECT images acquired 24 hr post injection and reconstructed using OS-EM algorithm with 24 subsets were registered with the planar images at time points ranging from 1 to 144 hours. We used 24 subsets per iteration since we have already found that optimal quantification requires a large number of updates (He et al., 2005). However, the effects of noise in the images reconstructed with a large number of subsets on the registration results may raise a concern. To investigate this, we also performed OS-EM reconstruction using 6 subsets and compared the registration results from images obtained with 20 iterations using 6 subsets and 5 iterations using 24 subsets. The observed differences in registration accuracy were very small. We used 10 random sets of initial misregistrations chosen from the 50 sets to perform the comparison. The maximum differences in estimated registration parameters were 0.07 and 0.12 pixels and 0.11 degrees for x, z and xz parameters, respectively. This demonstrates that the count level in the projection data (an average of 1.34×10⁵ counts per slice) at 24 hr after administration was high enough for 24 subsets to be appropriate for the registration task.

One important observation from this data is that the variations in organ activity estimates due to the registration errors were larger than variations resulting from statistical noise (He and Frey, 2006). For example, the standard deviation due to residual misregistration was 1.3% for the heart and 1.6% for the liver compared to standard deviations due to Poisson noise of 0.31% for the heart and 0.16% for the liver. The difference was even larger for small organs. For example, the standard deviations due to misregistration were 7.2% and 13.5%, but 0.52% and 0.81% due to statistical noise for the bone marrow and blood vessels, respectively. As a result, considering the effects of misregistration on accuracy and precision is important in evaluating image quantification methods and understanding the accuracy and precision of organ dose estimates.

Above we observed that large, hot organs tend to be less effected by misregistration errors than small ones. This can be understood in terms of the fractional error in the region of intersection between the projection of the true organ and the VOI. A fixed registration error will result in a larger fractional error in the overlapping regions for a small organ compared to a large one. For example, a 2 pixel shift in the transaxial (x-axis) position of the VOI will result in a 14% decrease in the overlap region for the heart (volume = 656 cc) compared to 28% for kidneys (volume = 146 cc).

Second, we observed larger errors in organ activity estimates for cold organs than for hot ones. For example, the lungs had an activity concentration of 9.0 Bq cm^-3 compared to 25.5 18.7, and 17.3 Bq cm^-3 in the heart, blood vessels and liver, respectively. Thus, misregistration errors for the lungs resulted in including portions of hotter organs in the projected VOI. Since the activity concentration in the lungs was small, even small shifts resulted in a large increase in the counts underlying the projection of the VOI. For example, a 2 pixel shift in the transaxial (x-axis) direction resulted in including 1.8% of the heart activity as part of the lungs. This will, however, represent about 5% of the activity in the right lung. As a result, the effect of this misregistration would be larger for the lungs than for the heart.

The combination of the two factors described above explains why misregistration plays a less important role in activity estimates for large and hot organs. However, despite the fact that the average effect is small, there were substantial variations in accuracy, resulting in imprecision in activity estimates, for large and hot organs. As mentioned above, this demonstrates that misregistration may be an important contributor to the imprecision of dose estimates and should be considered when assessing the overall reliability of dose estimates.

One limitation of this experiment is that the model used to simulate misregistration model used modeled only rigid misregistrations. In clinical studies, some degree of non-rigid deformation in organ shapes or relationships is likely. It would be difficult to achieve good registration in the presence of such non-rigid deformations. As a result, the errors in activity and residence time estimates due to organ misregistration should be considered lower limits on the clinically observable effects.

Another limitation of the experiment performed was we modeled a uniform activity distribution in all the organs except the lungs and heart. The QPlanar method used in this work assumes that the activity distribution in any VOI is uniform. Thus, nonuniform activity distribution in an organ may result in both reduced accuracy for the QPlanar method and have some impact on the accuracy of registration. It is interesting to consider how the results of this experiment might be different if the activity distribution inside an organ was nonuniform.

As noted, the activity distributions in the lungs and heart in this study had some modest nonuniformities. In the lungs, 27% of the voxels had uniform activity. These voxels were distributed throughout the lungs based on the lung airway model used. For the heart, the myocardium had approximately an activity concentration ~18% lower than the blood. The effects of misregistration on accuracy and precision were similar for the heart and liver, indicating that this level of nonuniformity is not a major factor on organ activity accuracy and precision. For the lungs, as pointed out above, the accuracy and precision was worse than for other organs. However, it seems much more likely that, as discussed above, the errors were due to the close proximity of other high activity organs such as the liver, heart, and blood. It is thus difficult to make conclusions about the effects of activity distribution nonuniformity based on the results for the lungs. Nevertheless, it seems reasonable, based on data for the heart and the fact that the registration is with respect to the organ projections, that modest nonuniformities that might be expected in normal organs would have little effect on the results of this study.

Another type of uniformity not addressed in this work is the case when tumors, which may have high uptake or necrotic regions with no uptake, are present in an organ. There are two effects to be considered: the effect on the QPlanar method and the effect on registration accuracy. While we have not performed systematic studies, we have performed some experiments indicating that a large tumor or necrotic region inside an organ with a substantial difference in activity concentration does degrade the accuracy of the QPlanar method. This is an area that requires further additional studies. However, it should be noted that, if the tumors were delineated in the SPECT or CT scan used to define the VOIs, they could be included as a separate VOIs in the QPlanar estimation procedure. This would potentially reduce the effect of the nonuniformity on the accuracy of the organ activity estimate. In terms of the registration accuracy, if the tumors move inside the organ in a way consistent with the motion model used in the registration (i.e., rigidly in this work), then they would be unlikely to degrade the registration accuracy. In fact, the tumors might provide another feature that could provide information about how well the images are registered, and thus improve registration accuracy. On the other hand, if the tumors move differently than the registration model used (i.e., they move nonrigidly inside the organ), then registration accuracy would be degraded. This would in turn lead to reduced accuracy and precision of the organ activity.

IV. CONCLUSION

In this work, we investigated the effect of misregistration on the accuracy and precision of organ activity and residence estimates from In-111 planar images using the QPlanar quantification method. This experiment modeled misregistration as the residual misregistration after a mutual information 2D-3D image registration procedure. Since the initial misregistrations and registration algorithm modeled only rigid misregistration, the results of this paper should be considered lower limits on the clinically achievable errors due to misregistration.

The results show that registration was important and resulted in statistically significant improvements in organ activity estimates. The improvement was larger for small or low-activity organs compared with large and hot organs, and that there was a larger contribution of residual misregistration to imprecision of activity or residence time estimates for small or low-activity organs than large and hot organs. This suggests that careful and accurate registration is essential for small organs and objects such as tumors. The data showed that the residual misregistrations were random in nature and thus degraded the precision of activity and residence time estimates; the standard deviations resulting from misregistration variations were larger than those due to statistical noise. This demonstrates that the imprecision due to residual misregistration plays an important role in the overall precision of activity and dose estimates using the QPlanar method. From this conclusion, it can be deduced that the effects of registration imprecision should be included in any estimate of the precision of dose estimates.