Bayesian Analysis of Genetic Interactions in Case-Control Studies, With Application to Adiponectin Genes and Colorectal Cancer Risk

Abstract

Complex diseases such as cancers are influenced by interacting networks of genetic and environmental factors. However, joint analysis of multiple genes and environmental factors is challenging, owing to potentially large numbers of correlated and complex variables. We describe Bayesian generalized linear models for simultaneously analyzing covariates, main effects of numerous loci, gene-gene and gene-environment interactions in population case-control studies. Our Bayesian models use Student-t prior distributions with different shrinkage parameters for different types of effects, allowing reliable estimates of main effects and interactions and hence increasing the power for detection of real signals. We implement a fast and stable algorithm for fitting models by extending available tools for classical generalized linear models to the Bayesian case. We propose a novel method to interpret and visualize models with multiple interactions by computing the average predictive probability. Simulations show that the method has the potential to dissect interacting networks of complex diseases. Application of the method to a large case-control study of adiponectin genes and colorectal cancer risk highlights the previous results and detects new epistatic interactions and sex-specific effects that warrant follow-up in independent studies.

Introduction

Genome-wide association studies have successfully identified many single nucleotide polymorphisms (SNPs) or candidate genes that are associated with complex diseases such as cancers. An important follow-up procedure is to characterize their effects on disease risk, including any interactions among them or with environmental exposures, and to identify undiscovered genes (Cordell 2009; Manolio et al. 2009; Thomas et al. 2009; Cantor et al. 2010). Since complex diseases are caused by a network of interacting factors, the ideal analysis is to simultaneously consider multiple loci, environmental factors, and their interactions. Such joint analyses would improve the power for detection of causal effects and hence potentially lead to increased understanding about the genetics of diseases.

There are considerable challenges, however, to perform joint analyses of multiple genetic and environmental variables. First, with multiple SNPs and environmental factors, there are many possible main effects and interactions, most of which are likely to be zero or at least negligible, leading to high-dimensional sparse models. In addition, there are many more possible interactions than main effects, requiring different modeling and parameterization for main effects and interactions. Second, genetic association studies usually genotype SNPs with strong linkage disequilibrium (LD), introducing highly correlated variables. Third, SNP data often include genotypes with low frequencies that create predictors with near-zero variation. Finally, separation, which arises when a predictor or a linear combination of predictors is completely aligned with the outcome, is a common phenomenon in logistic regression with discrete predictors (e.g., Gelman et al. 2008). Because SNP data are discrete, separation can be a serious problem in case-control association studies. These and other complications result in challenges in terms of modeling, computation and interpretation, and thus require sophisticated techniques.

One way to handle these problems is using a Bayesian or penalized likelihood approach that uses appropriate prior information on coefficients to obtain stable, regularized estimates. Various prior distributions or penalties have been suggested. Park and Hastie (2008) propose logistic regression with quadratic penalization (i.e., normal prior) to fit gene-gene (G×G) and gene-environment (G×E) interactions. They show that the penalized logistic regression overcomes the problems and outperforms other popular methods such as multifactor dimensionality reduction (MDR) (Ritche et al. 2001) and tree-structure learning method (FlexTree) (Huang et al. 2004). Malo et al. (2008) apply ridge regression to fit all SNPs in a single genomic region and show that such multiple-SNP analyses accommodate linkage disequilibrium among SNPs and have the potential to distinguish causative from noncausative variants. Several authors have made substantial progress in adapting alternative Bayesian or penalized high-dimensional models to genetic association studies (e.g., Tanck et al. 2006; Xu 2007; Hoggart et al. 2008; Yi and Banerjee 2009; Wu et al. 2009; Sun et al. 2010).

In this article we describe Bayesian generalized linear models for simultaneously analyzing environmental exposures, main effects of numerous loci, G×G and G×E interactions. Following Gelman et al. (2008), we use the Student-t family as prior distributions on the coefficients, with the innovation that different hyperparameters are assigned to different types of effects (i.e., main effects, G×G and G×E interactions). This prior specification allows us to reliably estimate both main effects and interactions and hence to increase the power for detection of real signals. We show that our approach includes many previous methods as special cases and thus inherently takes over advantages of the previous approaches. Similarly to Gelman et al. (2008), we fit our Bayesian generalized linear models by incorporating an expectation-maximization (EM) algorithm into the usual iteratively weighted least squares as implemented in the general statistical package R. This strategy leads to stable and flexible computational tools and allows us to apply any generalized linear models to genetic association studies. Our algorithm differs from that of Gelman et al. (2008) in treating variances rather than coefficients as missing data and hence avoids computationally intensive matrix calculation in the E-step. Another methodological contribution made in this article is a novel method to interpret and visualize models with multiple interactions by computing the average predictive probability. The proposed method has been incorporated into the freely available package R/qtlbim (Yandell et al. 2007).

We demonstrate the effectiveness of our method in an application to a large case-control study of adiponectin genes and colorectal cancer risk described in Kaklamani et al (2008). Current epidemiological evidence suggests an association between obesity, hyperinsulinemia, and colorectal cancer risk. Adiponectin is a hormone secreted by the adipose tissue, and its serum levels are inversely correlated with obesity and hyperinsulinemia. Kaklamani et al (2008) is the first report of an association between variants of the adiponectin pathway and risk of colorectal cancer. However, their analyses fitted separate logistic models for each SNP and did not consider interactions. Our reanalysis highlights the previous results and detects new epistatic interactions and sex-specific effects that warrant follow-up in independent studies. We evaluate our method using extensive simulations based on the real genotypic data. The simulations show that our method has the potential to dissect interacting networks of complex diseases.

Statistical Methods

Generalized Linear Models of Interacting Genes in Case-Control Studies

We consider genetic association analysis of population case-control studies in which unrelated individuals are typed at a number of SNPs. We describe our method for modeling interactions in targeted genetic studies with moderate numbers of SNPs (for example, 100 SNPs). For i = 1, 2, ⋯, n, let y_i denote the disease status of individual i, where y_i = 1 represents a disease case and y_i = 0 represents a control. For each individual, the SNP data consist of the genotypes at S loci. Let g_is ∈ {1,2,3,NA} denote a three-level factor indicating the genotype of individual i for SNP s, with g_is = 1 if homozygous for the more common allele, g_is = 2 if heterozygous, g_is = 3 if homozygous for the minor allele, and g_is = NA if the genotype is missing. Hereafter, for each SNP we denote common homozygote, heterozygote, and rare homozygote by c, h, and r, respectively. In addition to the SNP data, for each individual we have exposure variables, referred to as environmental factors, which are included in the model as covariates to adjust for confounding effects and/or to detect gene-environment interactions.

We use generalized linear models (GLMs) to relate disease status to SNP genotypes and environmental factors. We simultaneously fit environmental effects, main effects of markers, pairwise gene-gene (G×G or epistatic) and gene-environment (G×E) interactions. The generalized linear model is expressed as

$$h(\text{Pr}(y_i=1))={({\beta }_0+X_E{\beta }_E+X_G{\beta }_G+X_{GG}{\beta }_{GG}+X_{GE}{\beta }_{GE})}_i\triangleq X_i\beta$$ (1)

where h is a link function or transformation which relates the linear predictor X_iβ to the disease probability Pr(y_i = 1), β₀ is the intercept, β_E and β_G are the vectors of environmental effects and all possible main effects, respectively, β_GG and β_GE are the vectors of all possible G×G and G×E interactions, respectively, and X_E, X_G, X_GG, and X_GE are the corresponding design matrices of effect predictors.

Various link functions are provided in GLMs (McCullagh and Nelder 1989), all of which can be adapted in our Bayesian framework. The logit transformation defines h(p) = logit(p) = log(p/(1-p)), leading to a logistic regression which is commonly used in case-control studies. The probit transformation is h(p) = Φ⁻¹(p), where Φ is a cumulative standard normal distribution function. The probit link is obtained by postulating the existence of a latent normally distributed variable underlying the binary outcome. Another commonly used transformation is the complementary log-log (cloglog) link, h(p) = log[-log(1-p)]. Wray and Goddard (2010) recommend use logistic and probit models for multi-locus analysis of genetic risk of disease in case-control studies. Wray et al. (2010) provide a genetic interpretation of area under the ROC curve (AUC) in genomic profiling based on a probit model.

We code the main-effect predictors using the Cockerham genetic model, although other models, for example, the codominant model, also can be used. The Cockerham model defines two main effects for each SNP (i.e., additive and dominance effects). The additive predictor is coded as (g–2), leading to −1, 0, and 1 for genotypes c, h, and r, and the dominance predictor as (g−1)(3-g)–0.5, equaling −0.5 for c and r and 0.5 for h, respectively (Cordell 2002; Zeng et al. 2005; Yi et al. 2005). The epistatic predictors are constructed by multiplying two corresponding main-effect variables, introducing four G×G interactions for a pair of SNPs, i.e., additive-additive, additive-dominance, dominance-additive, and dominance-dominance interactions. Following Gelman and Hill (2007), we code each binary exposure input as 0 and 1, and standardize other exposures to have a mean of 0 and a standard deviation of 0.5. This scaling puts continuous variables on the same scale as symmetric binary variables. Finally, we construct G×E predictors by multiplying two corresponding main-effect and environmental variables.

Missing SNP data are a common phenomenon in association studies. Removing individuals with any missing SNP genotypes largely reduces sample size and thus results in the loss of valuable information. We use a simple, but reasonable, method to impute missing SNP data. For each SNP with missing genotypes, we compute the sample proportions of three genotypes, and then assign the missing additive and dominance predictors by the expected values, i.e., x_a = f_r - f_c and x_d = 0.5 (f_h – f_c - f_r), where x_a and x_d are the additive and dominance predictors, f_c, f_r and f_h are the sample proportions of genotypes c, r, and h, respectively. This computationally efficient method is widely used for gene mapping in both animal experimental crosses (e.g., Haley and Knott 1992) and human association studies (e.g., Park and Hastie 2008). The previous studies and the analyses in this work show that this imputation method yields a reasonable result (Haley and Knott 1992; Park and Hastie 2008).

Prior Distributions

Nonidentifiability is a common phenomenon in classical analysis of genetic case-control data, owing to the problems of high-dimensionality, collinearity and separation. We handle these problems by using a Bayesian approach that places appropriate prior distributions on coefficients to obtain stable estimates. We assume independent Student-t priors $t_{{\nu }_j}({\mu }_j,s_j^2)$ on coefficients β_j, with µ_j, ν_j and s_j predetermined. We are motivated to use the t distribution because it allows for flexible modeling, robust inference, and easy and stable computation (Gelman et al. 2003; Gelman et al. 2008; Yi and Banerjee 2009). The distribution $t_{{\nu }_j}({\mu }_j,s_j^2)$ can be expressed as a mixture of normal distributions with mean µ_j and variance distributed as scaled inverse-χ²:

$${\beta }_j|{\tau }_j^2~N({\mu }_j,{\tau }_j^2),{\tau }_j^2~\text{Inv}-{\chi }^2({\nu }_j,s_j^2),j=0,1,\cdots ,J,$$ (2)

where J is the number of the coefficients, and the hyperparameters µ_j, ν_j > 0 and s_j > 0 represent the center, the degrees of freedom and the scale of the distribution, respectively.

The coefficient-specific variances ${\tau }_j^2$ result in distinct shrinkage for different coefficients. These variances are not the parameters of interest, but they are useful intermediate quantities to allow easy and efficient computation. The hyperparameters ν_j and s_j control the global amount of shrinkage in the effect estimates; larger ν_j and smaller $s_j^2$ induce stronger shrinkage and force more effects to be near zero. Using cross-validation on a corpus of data sets, Gelman et al. (2008) showed that the Cauchy prior distribution with center 0 and scale 0.75 (i.e., µ_j = 0, ν = 1, s_j = 0.75) is a good consensus choice, but for any particular datasets, other hyperparameters can perform better. Following the usual principles of noninformative or weakly informative prior distributions, Gelman et al. (2008) recommends using, as a default prior, independent Cauchy distributions on all coefficients, each centered at 0 and with scale 10 for the intercept and 2.5 for all other coefficients. However, this default prior is not appropriate for our models of multiple interacting genes, because 1) as illustrated earlier, our models are high-dimensional and sparse, thus requiring priors that can shrink most coefficients near zero while allowing for occasional large coefficients, and 2) our models include many more interactions than main effects, thus requiring different priors for different types of effects.

We set all µ_j = 0 and propose the following way to choose ν_j and s_j. For β₀, β_E and β_G, we use the priors recommended by Gelman et al. (2008), i.e., (ν₀, s₀) = (1, 10) for β₀, and (ν_j, s_j) = (1, 2.5) for β_E and β_G. For G×E interactions β_GE, we set (ν_j, s_j) = (1, 2.5k_G/k_GE), where k_G and k_GE are the total numbers of main effects and G×E interactions, respectively. For G×G interactions β_GG, we set (ν_j, s_j) = 1, 2.5k_G/k_GG), where k_GG are the total number of G×G interactions. This prior applies more stringent restrictions on interactions. The prior chosen by this approach may not be optimal for some particular datasets, but it is easy to implement and performs well as shown later in this report. We developed our computational algorithm based on the general form of the Student-t prior (2), allowing users to choose appropriate priors for any particular datasets.

Relationship with Similar Methods

The Bayesian model with the Student-t priors includes previous methods in the literature as special cases:

1. At s_j = ∞, the t prior corresponds to a flat distribution. Placing flat priors on all β_j corresponds to a classical model, which usually fails in our problem as illustrated earlier. However, our framework has the flexibility of setting flat priors to some predictors (e.g., relevant covariates) that perform no shrinkage;

2. At ν_j = ∞, the t prior is equivalent to a normal distribution ${\beta }_j~N(0,s_j^2)$, which leads to a ridge regression when setting a common scale s_j ≡ s. Malo et al. (2008) applied ridge regression to multiple-SNP analysis for continuous traits. Park and Hastie (2007) proposed using ridge logistic regression to fit G×G and G×E interactions in case-control studies;

3. Setting ν_j = s_j = 0 corresponds to placing Jeffreys’ prior upon each variance, $p({\tau }_j^2)\propto 1/{\tau }_j$, which is equivalent to a flat prior on ${\tau }_j^2$, leading to improper priors p(β_j) ∝ |β_j|⁻¹. The normal-Jeffreys prior has been studied (Figueiredo 2003; Griffin and Brown 2007) and applied to genetic analysis (Xu 2003; Kiiveri 2003; Bae and Mallick 2004);

4. At ν_j = 1, the t prior is equivalent to the Cauchy distribution, which has been extensively studied by Gelman et al. (2008).

Our framework is closely related to some existing methods which use the double-exponential priors (Tibshirani 1996; Park and Casella 2008; Griffin and Brown 2007; Yi and Xu 2008; Wu et al. 2009; Sun et al. 2010). Because a double-exponential distribution can be expressed as a mixture of normal distributions with mean 0 and variance distributed as exponential, the algorithm described in the next section can be used with minor modification. Although the double-exponential priors have been widely applied, Gelman et al. (2008) show the Cauchy class of prior distributions to outperform existing implementations of the double-exponential priors using cross-validation on a corpus of data sets.

EM Algorithm for Model Fitting

Our Bayesian generalized linear model can be computed using Markov chain Monte Carlo (MCMC) algorithms that fully explore the joint posterior distribution of the parameters by alternatively sampling each parameter from its conditional posterior distribution. However, it is desirable to have a faster computation that provides a point estimate (i.e., the posterior mode) of coefficients and standard errors (and thus the p-values). Such an approximate calculation has been routinely applied in statistical analysis (Gelman et al. 2008).

We use the EM algorithm to fit the models with the Student-t priors by estimating the marginal posterior modes of the coefficients β_j’s (Yi and Banerjee 2009). The algorithm treats the unknown variances ${\tau }_j^2$’s as missing data and replaces the terms including these variances in the joint posterior of (β, τ²) by their conditional expectations at each step. Then, at each step of the algorithm, we update β by maximizing the expected value of the joint posterior density,

$$\begin{array}{l}\text{log}p(\beta ,{\tau }^2|y)\propto {\displaystyle \sum _{i=1}^n\text{log}p(y_i|X_i\beta )+{\displaystyle \sum _{j=0}^J\text{log}p({\beta }_j|{\tau }_j^2)+{\displaystyle \sum _{j=0}^J\text{log}p({\tau }_j^2|{\nu }_j,s_j^2)}}}\hfill \\ \propto {\displaystyle \sum _{i=1}^n\text{log}p(y_i|X_i\beta )-{\displaystyle \frac{1}{2}\sum _{j=0}^J\left(\text{log}{\tau }_j^2+\frac{{({\beta }_j-{\mu }_j)}^2}{{\tau }_j^2}\right)+{\displaystyle \sum _{j=0}^J\left(\frac{{\nu }_j}{2}\text{log}{s}_j^2-(\frac{{\nu }_j}{2}+1)\text{log}{\tau }_j^2-\frac{{\nu }_j{s}_j^2}{2{\tau }_j^2}\right)}}}\hfill \end{array}$$ (3)

where ${\tau }^2=({\tau }_0^2,\cdots ,{\tau }_J^2)$, and the likelihood p(y_i | X_iβ) is defined in Equation (1) and depend on the link function.

The E-step of the EM algorithm computes the expectation of (3), averaging over ${\tau }_j^2$’s and conditional on the current estimates, β̂_j’s, and the observed data y_i’s. We need evaluate only the expectation $\mathrm{E}(1/{\tau }_j^2)$, because other terms in (3) are not linked to β and will not affect the M-step. It can be easily shown that the conditional posterior of ${\tau }_j^2$ is $\text{Inv}-{\chi }^2\left(1+{\nu }_j,\frac{{\nu }_j{s}_j^2+{({\widehat{\beta }}_j-{\mu }_j)}^2}{1+{\nu }_j}\right)$ (e.g., Yi and Xu 2008), and thus the conditional expectations of $1/{\tau }_j^2$ equals ${\left(\frac{{\nu }_j{s}_j^2+{({\widehat{\beta }}_j-{\mu }_j)}^2}{1+{\nu }_j}\right)}^{-1}$. Therefore, the E-step of our EM algorithm is equivalent to replacing the variances by

$${\widehat{\tau }}_j^2=\frac{{\nu }_j{s}_j^2+{({\widehat{\beta }}_j-{\mu }_j)}^2}{1+{\nu }_j}$$ (4)

In the M-step, we use a modified iterative weighted least squares (IWLS) algorithm to update β by maximizing log p(β,τ̂² | y) (Gelman et al. 2008; Yi and Banerjee 2009). The standard IWLS algorithm approximates a generalized linear model by a normal likelihood and then updates parameters from the weighted normal linear regression (Gelman et al. 2003). The generalized linear model likelihood p(y_i | X_iβ) is approximated by the weighted normal likelihood

$$p(y_i|x_i\beta )\approx N(z_i|X_i\beta ,{\sigma }_i^2)$$ (5)

where the pseudo-data z_i and pseudo-variances ${\sigma }_i^2$ are determined by the likelihood p(y_i | X_iβ) and depend on the current estimates, β̂_j’s, and y_i’s (Gelman et al. 2003; Gelman et al. 2008; Yi and Banerjee 2009). Under the classical framework (i.e., with uniform prior), β can be easily updated from this normal linear regression if it is identified. For our Bayesian model, however, we update β from the model: $z_i~N(X_i\beta ,{\sigma }_i^2),{\beta }_j|{\widehat{\tau }}_j^2~N({\mu }_j,{\widehat{\tau }}_j^2)$, which is equivalent to the augmented weighted regression

$$z_{*}~N(X_{*}\beta ,{\sum }_{*}),$$ (6)

where $z_{*}={\left(\begin{array}{c}z\\ \mu \end{array}\right)}_{(n+J+1)\times 1}$ is the vector of all z_j and all (J + 1) prior means µ_j, $X_{*}={\left(\begin{array}{c}X\\ I_{J+1}\end{array}\right)}_{(n+J+1)\times (J+1)}$ is constructed by the design matrix X of the regression $z_i~N(X_i\beta ,{\sigma }_i^2)$ and the identity matrix I_(J+1), and Σ_* is the diagonal matrix of all pseudo-variances ${\sigma }_i^2$ and prior variances ${\widehat{\tau }}_j^2$. With the augmented X_*, this regression is identified even if the original data are high-dimensional and have collinearity or separation (Gelman et al. 2008). Thus, we can update β by performing this augmented weighed regression.

Following Gelman et al. (2008), we implement these computations by altering the glm function in R for fitting generalized linear models, inserting the steps for calculating the augmented data and updating the variances into the iterative procedure. However, our algorithm differs from Gelman et al. (2008) in treating the variances rather than the coefficients as missing data and thus avoids computationally intensive matrix calculation in the E-step. Therefore, our algorithm should be faster and converges more rapidly than Gelman et al. (2008) for large-scale models.

The EM algorithm is initialized by setting each τ_j to a small value (say τ_j = 0.1) and β to the starting value provided by the standard IWLS as implemented in the R function glm. We repeat the E-step and the M-step until convergence. At convergence of the algorithm, we obtain all outputs from the R function glm, including the estimate β̂, standard errors, p-values (for testing β_j = 0), and deviance and Akaike information criterion (AIC). The standard errors are calculated from the inverse second derivative matrix of the log-posterior density evaluated at β̂ (Gelman et al. 2008). The p-values are then determined by the estimate β̂ and standard errors as in the classical framework.

Interpreting the Fitted Models

Models involving multiple interactions are difficult to interpret because variables jointly affect the outcome and thus single coefficients are less informative. The warnings from linear models for normally distributed traits apply to generalized linear models of interacting genes with two important additions. First, the linear predictor is used to predict the link functions h(Pr(y_i = 1)), which are nonlinear on the case probability Pr(y_i = 1), and thus the coefficients cannot be interpreted on the scale of the data. Second, the predictors are coded as functions of the genotypes, rather than the genotypes themselves, leading to further difficulty in interpreting the coefficients.

We propose to interpret the fitted models by presenting the average predictive probability for each of the SNPs and each pair of SNPs (or a SNP and a covariate) that significantly interact each other. We compare these probabilities with those from the null model that includes only an intercept term. Thus, the average predictive probabilities clearly show which genotypes increase or are protective against the risk averaging over the data points and all other predictors. To calculate the average predictive probability for the genotype g_s = k of the s^th SNP, we construct new main-effect matrix X_Gs by replacing the additive and the dominance variables of the s^th SNP for all individuals by (k–2) and (k−1)(3-k)–0.5, respectively, and remaining other columns of X_G unchanged. We then construct interactions X_GGs and X_GEs from X_Gs and X_E. The average predictive probability for the genotype g_s = k of the s^th SNP is

$$\text{Pr}(y=1|g_s=k)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{Pr}(y_i=1|g_{is}=k)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{h}^{-1}(X_i^s\widehat{\beta })}}$$ (7)

where k = 1, 2, or 3 represent genotypes c, h, and r, respectively, n is the number of individuals, β̂ is the estimate of β, and $X_i^s$ is the i^th row of the new design matrix (1, X_E, X_Gs, X_GGs, X_GEs). Similarly, the average predictive probability for the two-locus genotype (g_s, g_s’) = (k, k’) is

$$\text{Pr}(y=1|g_s=k,g_{s\text{'}}=k\text{'})=\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{Pr}(y_i=1|g_{is}=k,g_{is\text{'}}=k\text{'})=\frac{1}{n}{\displaystyle \sum _{i=1}^n{h}^{-1}(X_i^{ss\text{'}}\widehat{\beta }),}}$$ (8)

which can be easily modified to a SNP and a discrete covariate by replacing the second SNP by the covariate. For a continuous covariate, we can extend this calculation by comparing a unit difference in the covariate (e.g., x = 0 with x = 1) (Gelman and Hill 2007).

Adiponectin Genes and Colorectal Cancer Risk

Case-Control Design, Selection of SNPs, and Genotypes

Epidemiological evidence suggests an association between obesity, hyperinsulinemia, and colorectal cancer risk. Adiponectin is a hormone secreted by the adipose tissue, and its serum levels are inversely correlated with obesity and hyperinsulinemia. Approximately one third of colorectal cancer are inherited (Lichtenstein et al. 2000) but colorectal cancer susceptibility genes discovered thus far only account for a small fraction of cases (Xu and Pasche 2007; Valle et al. 2008). A better understanding of the genetic causes of this disease is likely to lead to decreased morbidity and mortality from colorectal cancer. Kaklamani et al. (2008) investigated the association of variants of the adiponectin (ADIPOQ) and adiponectin receptor 1(ADIPOR1) genes with colorectal cancer risk in two case-control studies. We reanalyzed the main study by using the proposed method. The study participants, the haplotype-tagging SNPs of genes ADIPOQ and ADIPOR1 and genotyping are briefly summarized here.

The case-control study included a total of 441 patients with a diagnosis of colorectal cancer and 658 unrelated controls. All cases and controls were white and of Ashkenazi Jewish ancestry and from New York, New York. Information regarding sex, current age for controls, and age at colorectal cancer diagnosis for cases was recorded. The colorectal cancer risk was significantly associated with sex and age (see Table 1). Thus, our analyses included these two factors as covariates.

Table 1.

Baseline characteristics and genotype frequencies of colorectal cancer cases and controls. The p value for each SNP is for testing the deviation from Hardy-Weinberg equilibrium (HWE) among controls. The genotypes c, h, and r represent common homozygote, heterozygote, and rare homozygote, respectively.

			Cases N=443 n (%)	Controls N=658 n (%)	p-value
Age: median (range)			63.6 (31.3–94.8)	51.5 (25.5–86.0)	1.2×10−14
Sex	Male		256 (23.2)	211 (19.2)	2×10−16
	Female		187 (16.9)	447 (40.6)
ADIPOQ
	rs2232853	c	261 (60.7)	393 (60.4)	0.63
		h	149 (34.7)	231 (35.5)
		r	20 (4.7)	27 (4.1)
	rs12733285	c	147 (33.5)	200 (30.7)	0.08
		h	223 (50.8)	347 (53.2)
		r	69 (15.7)	105 (16.1)
	rs1342387	c	113 (25.9)	179 (27.7)	0.73
		h	224 (51.4)	313 (48.4)
		r	99 (22.7)	155 (23.9)
	rs7539542	c	181 (41.7)	306 (47.1)	0.99
		h	209 (48.2)	280 (43.1)
		r	44 (10.1)	63 (9.7)
	rs10920531	c	153 (35.3)	236 (36.6)	0.77
		h	216 (49.8)	301 (46.7)
		r	65 (14.9)	108 (16.7)
ADIPOR1
	rs266729	c	245 (56.2)	340 (51.7)	0.78
		h	164 (37.6)	271 (41.1)
		r	27 (6.2)	47 (7.1)
	rs822395	c	185 (42.7)	301 (46.0)	0.07
		h	203 (46.9)	265 (40.5)
		r	45 (10.4)	88 (13.5)
	rs822396	c	307 (70.7)	477 (73.4)	0.77
		h	114 (26.3)	157 (24.2)
		r	13 (2.9)	16 (2.5)
	rs2241766	c	279 (63.1)	389 (59.3)	0.41
		h	143 (32.4)	240 (36.6)
		r	20 (4.5)	27 (4.1)
	rs1501299	c	208 (47.8)	285 (44.8)	0.37
		h	181 (41.6)	293 (46.1)
		r	46 (10.6)	58 (9.1)

Five haplotype-tagging SNPs were selected to capture variations in the major blocks in each of genes ADIPOQ and ADIPOR1. The selected SNPs are functionally-relevant, show a minimum allele frequency of 10% in Caucasians, and either affect adiponectin levels or are associated with risk for insulin resistance, cardiovascular disease and diabetes. The genotypic frequencies of these ten SNPs are shown in Table 1. The frequencies of missing genotypes were low, from 0.3% to 3%. No significant deviation from Hardy-Weinberg equilibrium (HWE) was found for each SNP among controls.

Results

Using single-SNP analyses under codominant and dominant or recessive models, Kaklamani et al. (2008) found that three SNPs (rs266729, rs822395 and rs1342387) were associated with colorectal cancer risk. However, their analyses did not fit all variables simultaneously and did not consider interactions. We used the proposed method to reanalyze the data of Kaklamani et al. (2008) by fitting two models; the first model jointly fitted age, sex, all 20 main effects of the ten SNPs and 20 sex-gene interactions (Analysis I), and the second simultaneously fitted age, sex, all 20 main effects, 20 sex-gene interactions and 180 epistatic interactions (Analysis II). Three link functions, logit, probit and complementary log-log (cloglog), were used. We employed the Cockerham model to construct main-effect, sex-gene and epistatic variables, coded the variable sex as 0 or 1 for female or male, and standardized age by subtracting the mean and dividing by 2 standard deviation, and imputed the missing SNP genotypes using the method described earlier. We used the proposed prior distributions for the coefficients.

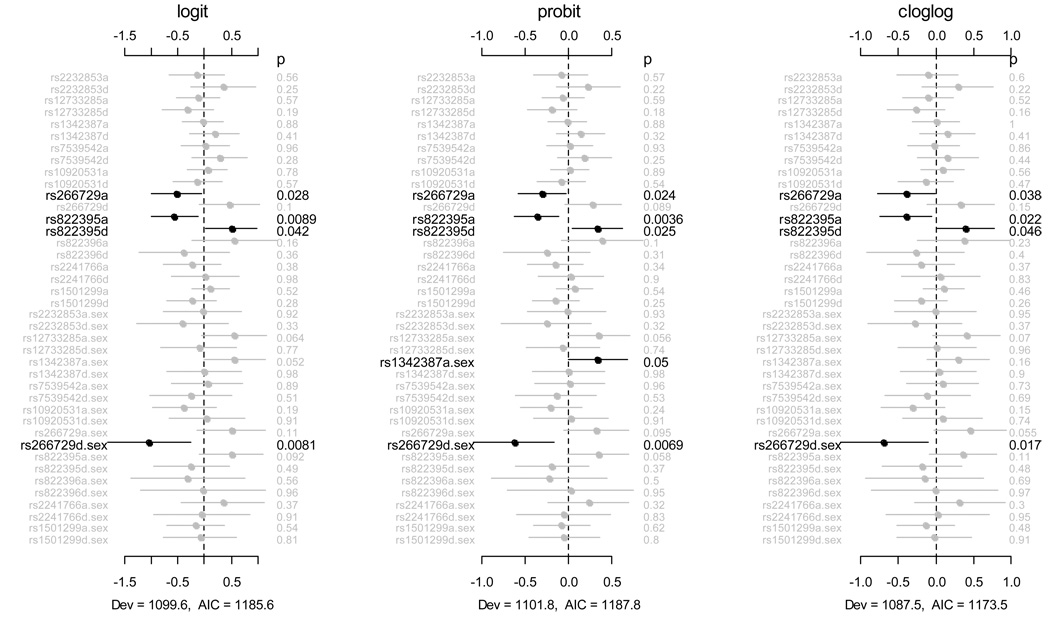
Figure 1 displays the coefficient estimates, standard errors, and p-values for all main effects and sex-gene interactions under Analysis I. The results from the three models with different link functions were qualitatively similar, detecting three significant main effects rs266729a, rs822395a and rs822395d, and one significant interaction rs266729d.sex under significance level of 0.05. There were additional interactions that were close to the significance level of 0.05. The main effect of rs1342387, which was found in the original analysis under the dominant model, was not significant in our Cockerham model, although it came up as a marginally significant gender interaction. The estimated coefficients of the covariates age and sex were very significant and positive in sign (not shown here), indicating that older and male subjects were associated with the increased risk of colorectal cancer.

Figure 1.

Analysis I: jointly fitting age, sex, all main effects of the ten SNPs and sex-gene interactions with three link functions, logit (left), probit (middle) and cloglog (right). The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂. Estimated effects of age and sex are not displayed. The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and p-values, respectively. The deviance (Dev) and Akaike information criterion (AIC) under each model are also shown.

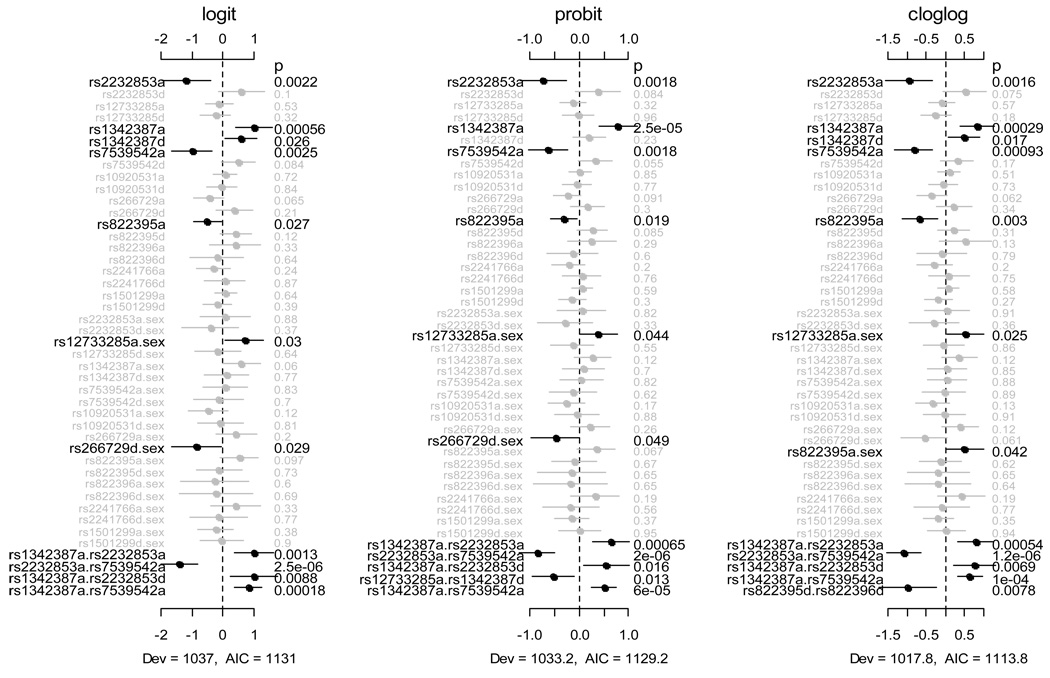
Figure 2 shows the coefficient estimates, standard errors, and p-values for all main effects, sex-gene interactions and significant epistatic interactions under Analysis II. The Bayesian logistic model identified four epistatic interactions involving three pairs of SNPs, which were also significant in the probit and cloglog models. The latter two models each detected one additional interaction. The estimated coefficients of age and sex were similar to those in Analysis I. Most of the significant main effects and sex-gene interactions detected in Analysis I remained or were close to significant, although uncertainties about some of them became slightly larger. Importantly, the epistatic models detected additional main effects, all of which were associated with the interacting SNPs. We used two summary measures, the deviance and the Akaike information criterion (AIC), to compare different models; lower deviance indicates better fit to data and lower AIC means better predictive power. The epistatic models had lower deviance and AIC than the non-epistatic models. This indicated that inclusion of epistatic interactions improved the fit of the model to data and reduced out-of-sample prediction error.

Figure 2.

Analysis II: jointly fitting age, sex, all main effects of the ten SNPs, sex-gene and epistatic interactions with three link functions, logit (left), probit (middle) and cloglog (right). The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂. Estimated effects of age and sex are not displayed. Only epistatic interactions with p-value smaller than 0.05 are displayed. The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and p-values, respectively. The deviance (Dev) and Akaike information criterion (AIC) under each model are also shown.

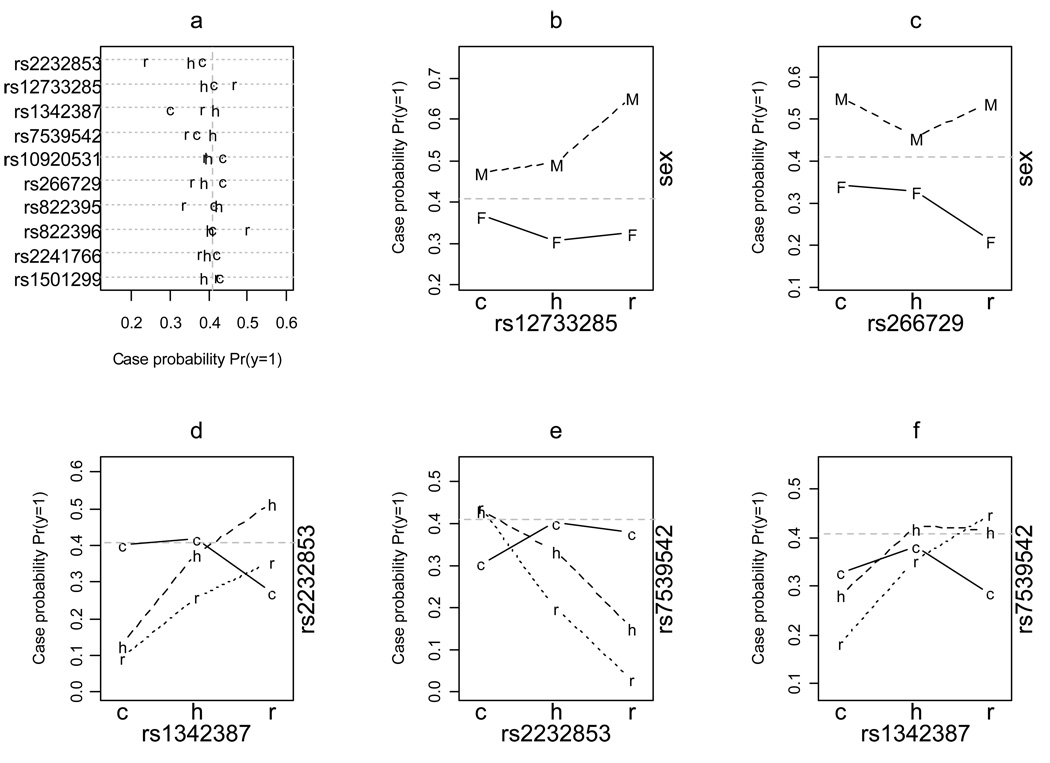
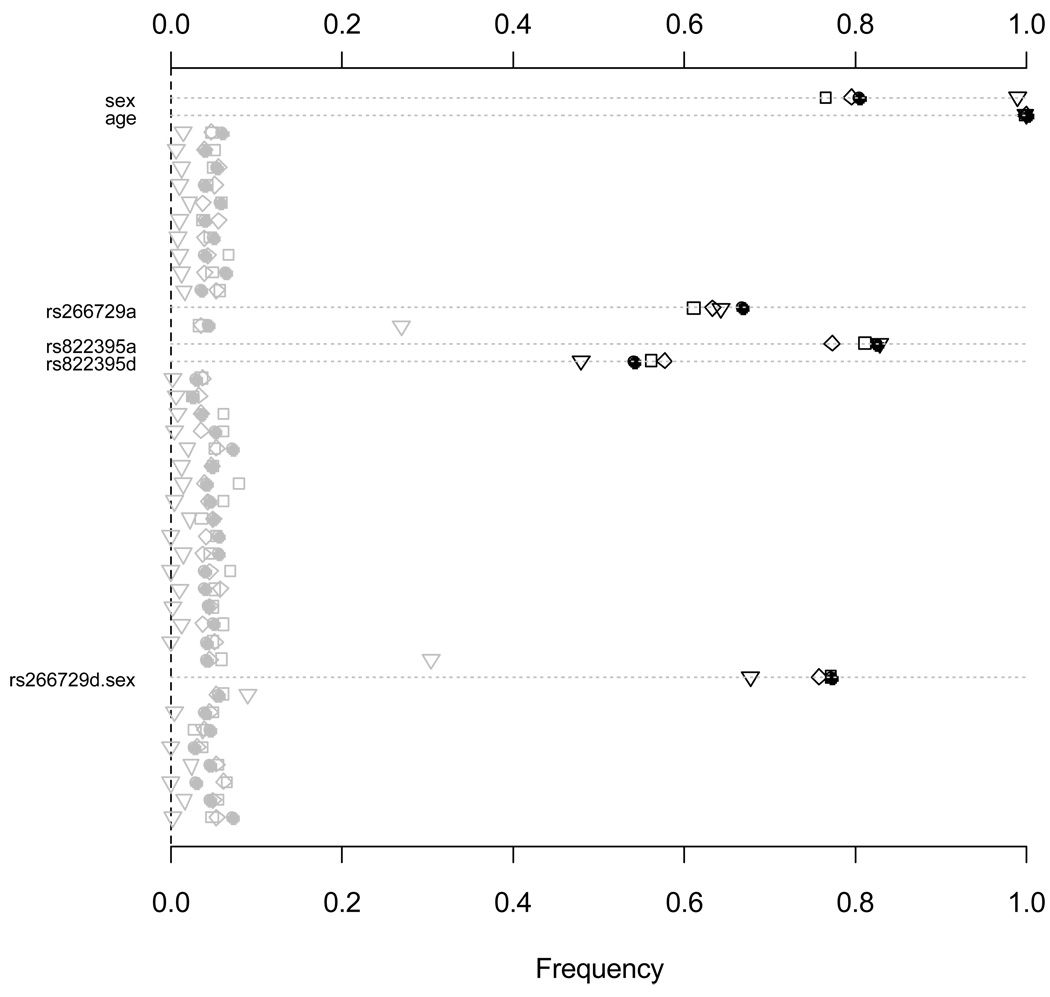
The fitted models included multiple effects and interactions and thus were difficult to understand. As described earlier, however, the average predictive probability provides a useful way to interpret the interaction models. We computed the average predictive probabilities based on the epistatic logistic models. The probit and cloglog models gave similar results. Figure 3a displays the average predictive probabilities of each SNP, clearly showing which genotypes were associated with increased or decreased risk. Figure 3b and Figure 3c plot the average predictive probabilities of rs12733285 and rs266729 separately for males and females. These two SNPs were estimated to have sex-specific effects. As illustrated in these figures, the interactions were larger for the rare homozygotes. Figure 3d–f displays the average predictive probabilities of three pairs of SNPs that significantly interacted. This graph shows that the average predictive probabilities of a SNP varied with the other SNP.

Figure 3.

Average predictive probability for a) each genotype, b–c) each combination of sex and genotypes of SNPs rs1273385 and rs266729, and d–f) each two-locus genotype at SNPs that show significant interactions. The genotypes c, h, and r represent common homozygote, heterozygote, and rare homozygote, and the notation M and F represent male and female, respectively. The vertical (a) and horizontal (b–f) dotted gray line represents the mean of probabilities.

Simulation Studies

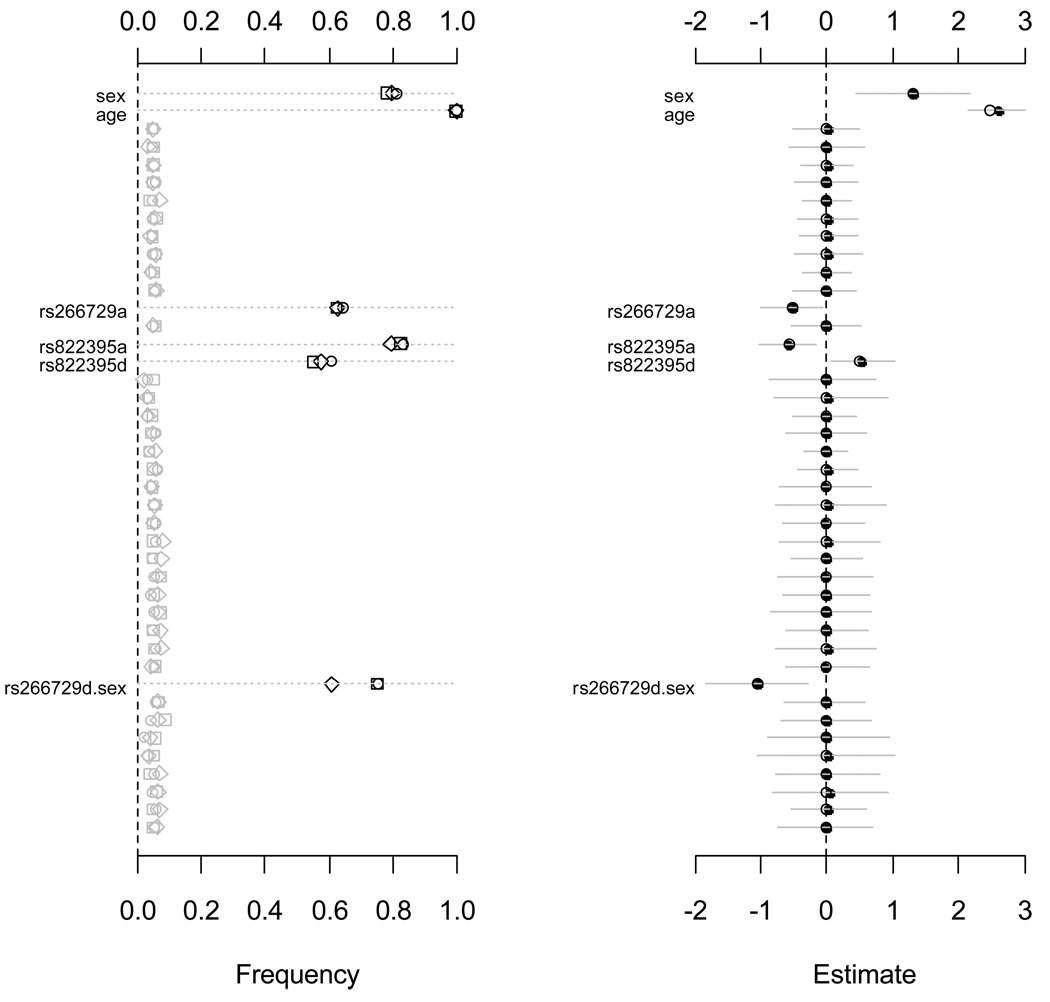
We used simulations to validate the proposed models and algorithm and to study the properties of the method. We compared the proposed method with several alternative models described earlier. Our simulation studies used the real genotype data of the 10 SNPs and the covariates sex and age in the above case-control study, and generated the case-control indicator y_i for each individual from the binomial distribution Bin(1, logit⁻¹(X_iβ^true)) conditional on the assumed ‘true’ coefficients β^true, where X_i was constructed as in the above real data analysis. Two sets of β^true were considered and corresponded to the two fitted logistic models illustrated above (see Figures 1 and 2), taking the estimated values for the significant effects and 0 for the others. Therefore, the first simulation (Simulation I) assumed six non-zero coefficients (two covariates, three main effects, and one sex-gene interaction), and the second (Simulation II) assumed 13 non-zero coefficients (two covariates, five main effects, two sex-gene and four gene-gene interactions). The assumed values β^true are displayed in the right panels of Figures 4 and 6. For each situation, 1000 replicated datasets were simulated. We calculated the frequency of each effect estimated as significant at the threshold level of 0.05 over 1000 replicates. These frequencies corresponded to the empirical power for the simulated non-zero effects and the type I error rate for other effects, respectively. We also examined the accuracy of estimated coefficients by calculating the mean and 95% interval estimates.

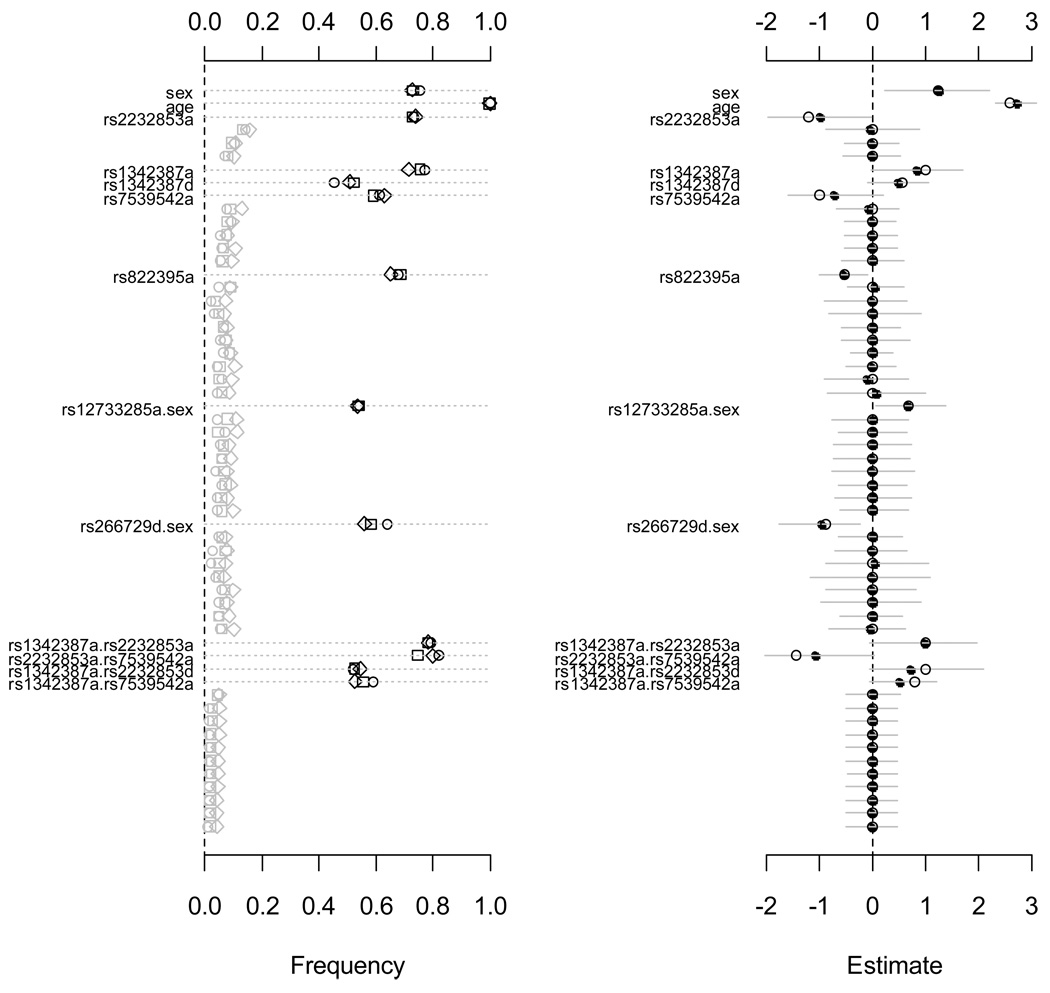
Figure 4.

Simulation I: jointly fitting age, sex, all main effects of the ten SNPs and sex-gene interactions using the proposed priors. The left panel shows the frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates with three link functions, logit (circle), probit (square) and cloglog (diamond). The right panel shows the assumed values (circle), the estimated means (point) and the 95% intervals (gray line) with the logit link function. Only effects with non-zero simulated value are labeled. The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂.

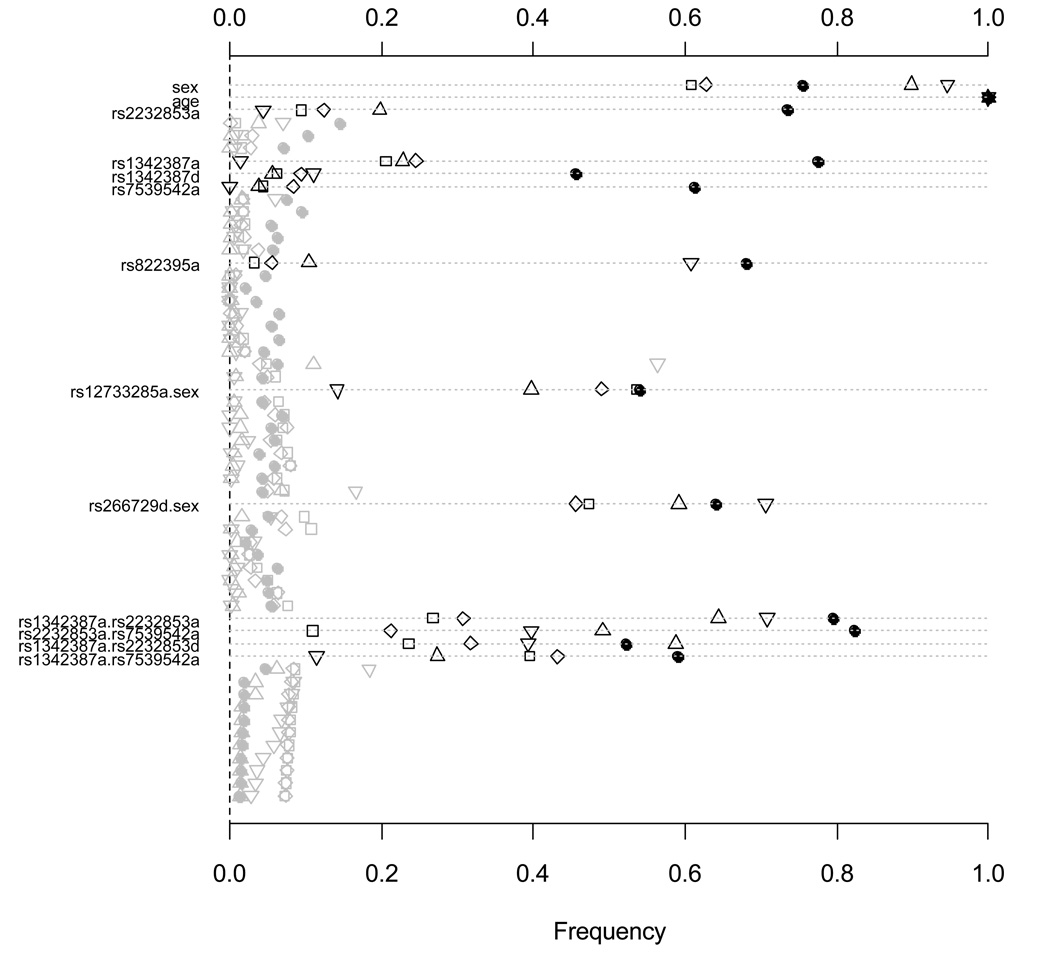
Figure 6.

Simulation II: jointly fitting age, sex, all main effects of the ten SNPs, sex-gene and epistatic interactions using the proposed priors. The left panel shows the frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates with three link functions, logit (circle), probit (square) and cloglog (diamond). The right panel shows the assumed values (circle), the estimated means (point) and the 95% intervals (gray line) with the logit link function. Only effects with non-zero simulated value are labeled. The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂. Only 15 epistatic interactions with the smallest p-values are displayed.

For each of 1000 simulated datasets in Simulation I, we jointly fitted age, sex, all 20 main effects of the ten SNPs and 20 sex-gene interactions. We first used the three link functions (logit, probit and cloglog) and the proposed priors as in our real data analysis (i.e., independent Student-t distributions on all coefficients with center 0, degrees of freedom 1, and scale 10 for the intercept and 2.5 for the covariates, main effects of SNP and sex-gene interactions). As shown in Figure 4, all the simulated non-zero effects were detected with reasonably high power, ranging from 58% to 100%, and the frequencies for other effects were close to zero. The estimates of all effects were accurate; the estimated means overlapped the simulated values.

We then analyzed the simulated datasets using logistic regressions with three alternative priors on all coefficients, i.e., uniform distribution, normal distribution N(0, 2.5²), and Jeffreys’ prior. These priors lead to the existing models described earlier. For this simulation with relatively small number of variables, the logistic models with flat and normal priors performed reasonably, detecting all the simulated effects, although the powers were slightly lower than the proposed model for most of the simulated effects (Figure 5). The model with Jeffrey’s prior also detected all the simulated effects, but generated a high type I error rate for two spurious effects.

Figure 5.

Comparison with existing models (I): jointly fitting age, sex, all main effects of the ten SNPs and sex-gene interactions using different priors. Frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates using 1) uniform prior (ν_j, s_j) = (∞, ∞) (□), 2) normal prior (ν_j, s_j) = (∞, 2.5) (◊), and 3) Jeffreys’ prior (ν_j, s_j) = (0, 0) (∇), for all effects. The points (•) represent the analysis using the proposed priors. Only effects with non-zero simulated value are labeled. The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂.

In Simulation II, we analyzed each of 1000 simulated datasets by jointly fitting age, sex, all 20 main effects of the ten SNPs, 20 sex-gene interactions, and 180 epistatic interactions. We first used the three link functions and the proposed priors as in our real data analysis, i.e., independent Student-t distributions on all coefficients with center 0, degrees of freedom 1, and scale 10 for the intercept, 2.5 for the covariates, main effects of SNP and sex-gene interactions, and 2.5*20/180 (= 0.27) for epistatic interactions. As shown in Figure 6, the analyses detected all the simulated non-zero effects with reasonably high power, ranging from 50% to 100%, and the frequencies for other effects were close to zero. The estimates of all effects were also accurate.

We then used logistic regressions with five alternative priors, i.e., uniform distribution, normal distribution N(0, 2.5²), Cauchy distribution with scale 2.5, Cauchy distribution with scale 0.27, and Jeffreys’ prior. All these priors put the same global shrinkage parameters for different effects. We found that for most of simulated datasets the logistic model with uniform priors on all coefficients (i.e., classical logistic model) was non-identifiable, yielding meaningless estimates that are a function of the iterations (not shown in Figure 7). The other four informative priors generated identified models, but provided much lower power for detection of the simulated effects (Figure 7).

Figure 7.

Comparison with existing models (II): jointly fitting age, sex, all main effects of the ten SNPs, sex-gene and epistatic interactions using different priors. Frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates using 1) normal prior (ν_j, s_j) = (∞, 2.5) (□), 2) t prior (ν_j, s_j) = (1, 2.5) (◊), 3) t prior (ν_j, s_j) = (1, 0.27) (Δ), and 4) Jeffreys’ prior (ν_j, s_j) = (0, 0) (∇), for all effects. The points (•) represent the analysis using the proposed priors. Only effects with non-zero simulated value are labeled. The notation for main effects, a and d, indicate additive and dominance effects, respectively. The term X₁.X₂ represents interaction between X₁ and X₂. Only 15 epistatic interactions with the smallest p-values are displayed.

Discussion

We have proposed Bayesian generalized linear models with Student-t prior distributions on the coefficients for jointly analyzing environmental exposures, numerous SNPs, and their interactions. We recommend a simple, but reasonable, method to specify the global shrinkage hyper-parameters for main effects and interactions. Real and simulated data analyses have shown good performance. Our method has remarkable features. First, our model includes existing methods as special cases that have been particularly designed to handle problems encountered in genetic association studies. Second, our method can deal with various types of continuous and discrete phenotypes and any generalized linear models, although the focus here is on binary disease traits. This flexibility allows us to conveniently analyze data using different models. Statistical interactions are defined relative to some particular models and thus affected by changes of models or scale (Berrington and Cox 2007; Cordell 2002; Cordell 2009). Our hierarchical generalized models would allow us to investigate whether an interaction can be removed by a transformation of the scale and to detect additional interactions that are only present in a particular model. Finally, we fit our Bayesian model using an adaption of the standard algorithm and software for classical generalized linear models, leading to a stable and easily used computational tool. Although a fully Bayesian computation that fully explores the posterior distribution of parameters provides more information, our mode-finding algorithm quickly produces all results as in routine statistical analysis, can be valuable for identifying significant variables, and is potentially applicable to large-scale genetic data. It would be appealing to treat the hyper-parameters as unknowns and estimate them from the data so that the model can shrink the coefficients as much as can be justified by the data. Yi and Xu (2008) developed MCMC algorithms to jointly estimate all hyper-parameters and model parameters. Future research will extend the proposed algorithm to estimate the hyper-parameters.

The current study attempts to reanalyze data from a previous case control study on the role of adiponectin polymorphisms in colon cancer risk. Using single-SNP analyses under codominant and dominant or recessive models, Kaklamani et al. (2008) found that three SNPs (rs266729, rs822395 and rs1342387) were associated with colorectal cancer risk. The previous analysis did not evaluate interactions between SNPs or any sex-specific effects. Our current analysis confirmed the significant association of rs266729, rs822395 and rs1342387 and colon cancer and detected several interactions between SNPs. More specifically we found that there were significant interactions between rs1342387 and rs2232853, rs2232853 and rs7539542, rs1342387 and rs7539542. Furthermore we found that two SNPs, rs12733285 and rs266729, had a sex-specific effect. Although there is a need for confirmatory studies the new findings from our current analysis highlight the importance of Bayesian analysis of genetic interactions.

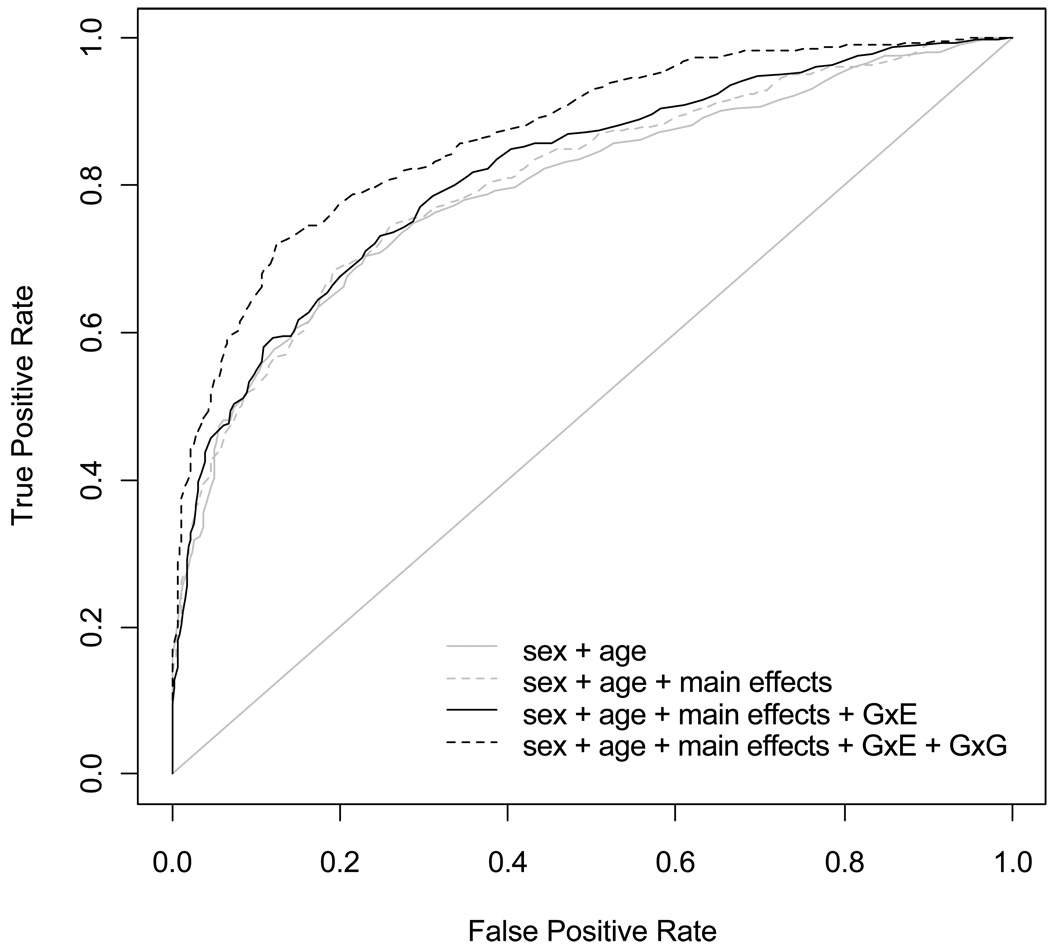
Jointly modeling genetic, environmental factors and their interactions has important implications for disease risk prediction and personalized medicine (Moore and Williams 2009). Studies using only a limited number of significant loci have typically failed to achieve satisfactory prediction performance (Jakobsdottir et al. 2009; Kraft et al. 2009). However, joint analysis of many markers may largely improve the accuracy of risk prediction (Lee et al. 2008; Wei et al. 2009), and interaction effects could be beneficial for risk prediction models (Wei et al. 2009; Moore and Williams 2009). Although interactions sometimes enhance the risk prediction only marginally based on the commonly used ROC curve, these models can identify combinations of multiple susceptibility loci that confer very high or low risk (Bjornvold et al. 2008; Clayton 2009). We have proposed to interpret the models using the average predictive probabilities for any factors, which clearly show which genotypes increase or are protective against risk. With respect to the adiponectin genes and colorectal cancer risk, the epistatic model increases the area under the ROC curves (AUC) slightly (0.87) compared to the nonepistatic model (0.82) (Figure 8). As shown in Figure 3, however, the epistatic model is highly predictive for some combinations of interacting loci, but frequencies of multi-locus genotypes are usually low and thus inclusion of interactions may not largely improve the overall prediction in the entire population.

Figure 8.

Receiver operating characteristic (ROC) curves for risk prediction with four models simultaneously fitting: 1) age and sex (gray solid), 2) age, sex, and main effects of SNPs (gray dotted), 3) age, sex, main effects of SNPs, and sex-gene (black solid), and 3) age, sex, main effects of SNPs, sex-gene and epistatic interactions (black dotted). The areas under the ROC curves (AUC) for these four models are 0.79, 0.81, 0.82, and 0.87, respectively.

We illustrate our method by jointly fitting 222 predictors. In principle our Bayesian method can effectively fit many more variables in a single model. We have experimented with up to thousands of main effects and interactions, as in a candidate gene study involving ~ 100 SNPs, or following an initial screen in a GWAS. If the data include potentially huge numbers of possible variables (as in GWAS or large-scale candidate gene studies), however, we recommend to perform a preliminary analysis to weed out unnecessary variables or use a variable selection procedure to build a parsimonious model that includes the most important predictors. Our Bayesian method can be incorporated into various variable selection procedures. Yi and Banerjee (2009) propose a model search strategy that provides a flexible way to deal with large-scale data. Their procedure differs from most variable selection methods by simultaneously adding or deleting many correlated variables.

Candidate gene studies usually consist of data at different levels, i.e., haplotype tagging SNPs within multiple candidate genes which may be functionally related or from different pathways. Most the statistical methods, including the method proposed here, consider only individual-level predictors (i.e., SNPs and covariates) and ignore gene-level information. There is a growing need for sophisticated approaches to modeling the multilevel variation simultaneously (Dunson et al. 2008; Thomas et al. 2009). One way to incorporate the gene-level information into our method is modeling the means µ_j in the prior distributions of coefficients β_j using gene-level predictors, µ_j = U_jγ. Thomas et al. (2009) discuss possibilities for what could be in the set of predictors U_j. Our future research will develop algorithms for estimating β and γ simultaneously and investigate the performance of the extended model. Another extension of our approach is to model interactions in a structured way, for example with larger variances for coefficients of interactions whose main effects are large. This is a hierarchical model version of the general advice for studying interactions (Gelman and Hill 2007; Kooperberg et al. 2009).