Abstract
The design and characterization of a time-resolved functional imager using a wide-field excitation scheme for small animal imaging is described. The optimal operation parameters are established based on phantom studies. The performance of the platform for functional imaging and the simultaneous 3D reconstruction of absorption and scattering coefficients is investigated in vitro.
OCIS codes: (170.6920) Time-resolved imaging, (170.3010) Image reconstruction techniques, (170.6960) Tomography
1. Introduction
Optical imaging is fast developing as an imaging modality of choice in preclinical settings owing to its high sensitivity, low cost of implementation and ease of adaptability to functional and molecular imaging applications [1]. The unique advantages of optical imaging combined with the recent advances of transgenic animal models and optical molecular markers underscore the potential of diffuse optical techniques in whole-body small animal imaging [2]. Several molecular imaging platforms localizing and quantitating the expression of bioluminescent reporters (Bioluminescence Tomography) and the concentration of fluorescent molecular markers (Fluorescence Molecular Tomography) in vivo have been developed in the recent years [3,4]. The quantitative accuracy of the molecular imaging platforms is however dependent on the a priori knowledge of in vivo distribution of optical properties [5–7]. These properties can be obtained by Functional Diffuse Optical Tomography (FDOT) which allows the reconstruction of the absolute concentrations of endogenous molecules in the tissue, like hemoglobin, deoxy-hemoglobin, water and lipids in vivo [8], thereby improving the accuracy of molecular imaging platforms.
Whole-body functional DOT of small animals however presents a particularly challenging problem due to the complex distribution of a wide-range of optical properties in the small volumes encountered in murine models [5,9]. Moreover, the ill-posed nature of the inverse problem in DOT due to the high scattering of photons even in the Near-Infrared (NIR) window hampers the quantitative accuracy and resolution of the reconstructed parameters [10]. Furthermore, as FDOT is a model based imaging technique, the accuracy of the reconstructed images is critically dependent on the accurate estimation of the average background optical properties [11].
In this paper, we present the development of an optical imaging platform for molecular and functional imaging, with a focus on its performance in FDOT applications. We consider three distinct approaches towards performing accurate FDOT of small animals. First, the datatype used for reconstruction plays a critical role in optical tomography performances and is related to the type of instrumentation employed. Current instrumentation for DOT may be classified into three domains based on the characteristics of the light source employed, namely, continuous wave (CW), intensity modulated (Frequency Domain - FD) and pulsed (Time Domain - TD). CW systems are the most commonly used systems owing to the ease of implementation and the relatively robust measurements. However, as these systems measure the change in the amplitude of photons exiting the tissue, they have limited information content and are unable to separate the effects of absorption and scattering [9]. Frequency domain systems employ intensity modulated sources and the changes in amplitude and phase of the photons transmitted through the tissue are used to reconstruct the functional parameters. However, FD platforms are limited in their application in small animal imaging due to the small volumes encountered in murine models which necessitates the modulation of the source in the GHz range for robust contrast in the phase function [12]. DOT systems employing a time domain approach record temporally resolved measurements of photon flux on the tissue surface referred to as the temporal point spread function (TPSF). The time-domain measurements provide a superior data set which can be processed to provide numerous datatypes in the time-domain (time-gates, mean time-of-flight, Laplace transform, Mellin transform) [13], in the frequency domain (datatypes equivalent to intensity modulation in the range of several hundred Mhz) [14] and continuous wave by integration of the TPSF [15]. The time-resolved data sets however are extremely sensitive to system noise and thus TD DOT platforms demand a careful calibration of the system parameters to obtain accurate reconstructions [16].
Second, the use of constraints derived from the known spectral behaviors of the chromophores in the NIR window is another approach used to overcome the non-uniqueness of the inverse problem in FDOT and have shown an improvement in quantitative accuracy when used with the CW and FD datatypes [17–19]. Multispectral FDOT platforms classically employ multiplexed laser diodes to probe the tissue at select wavelengths. The use of a tunable laser source allows the use of a wide range of wavelengths while improving the configurability of the system apropos the selection of optimal wavelengths.
Third, the resolution of the reconstruction of a complex 3D volume can be improved by increasing the number of point source-detector pairs acquired by the system [20]. The application of this strategy to whole-body FDOT however requires a prohibitively long acquisition time making it impractical for live animal imaging studies. The recent development of wide-field illumination strategies presents a novel tomographic approach where the point source excitation is replaced by structured excitation schemes [21,22]. The resolution of subsurface absorption contrasts by the modulation of spatial frequency of the excitation patterns has been experimentally validated in the CW and frequency domain in a reflectance scheme [22,23]. Moreover, the optical intensities dependent on the modulation frequencies can be used to estimate the absorption and scattering coefficients [24,25]. Recently, Bassi et al experimentally demonstrated the temporal propagation of spatial frequencies in a turbid media and its feasibility for the reconstruction of absorptive perturbation in the transmittance geometry [26]. The use of wide-field patterns reduces the number of source-detector pairs required for tomographic reconstruction drastically reducing the time of acquisition. However, the application of spatially modulated patterns becomes more complex when used with irregular boundaries, such as those encountered in murine models, and requires a correction based on the surface profile [27]. Alternatively, the reconstruction of absorptive inclusions using the CW and time-gate datatype using wide patterns having uniform intensity has been demonstrated [28,29]. It should be noted that the limited spatial frequency information present in the uniform intensity patterns limits their application in estimating the average optical properties; however, the ease of adaptability of such patterns to complex geometries combined with the fast acquisition time of fully time-resolved tomographic data sets makes it an ideal excitation scheme for whole-body FDOT of small animals.
In this paper, we describe the development and characterization of a novel small animal imaging platform for functional DOT. The system acquires multispectral measurements to allow functional tomography with spectral constraints. A wide-field excitation scheme is employed to allow dense spatial sampling within a short acquisition time and a gated CCD camera is used as the detector to acquire the optimal time-resolved data sets. In Section 2, we first provide a brief description of the theoretical approaches we employed to perform time-resolved spectroscopy and solve the inverse problem in functional tomography. Second, we provide a detailed description of the platform. In Section 3 we establish in vitro the operating parameters to be optimized for accurate estimation of optical properties in transmittance in a murine geometry. In Section 4 we present investigations validating the performance of the platform in functional imaging and tomographic reconstruction of absorption and scattering coefficients in vitro. In Section 5 the characteristics of the system are summarized and the future investigations towards further development of this platform are described.
2. Methods
2.1 Theory
In this section the theoretical framework used in conjunction with this platform is described. First, the model used for estimating the bulk optical properties using time-resolved spectroscopy is detailed. Second, a Monte Carlo based model of photon propagation using the time-gate datatype, is described.
2.1.1 Time resolved spectroscopy
Time-resolved spectroscopy (TRS) is the most accurate technique to estimate the optical properties of thick highly scattering tissue. TRS fits the experimentally acquired TPSF to the analytical expression describing the temporal propagation of photons through the medium [30]. As stated previously, a pattern excitation scheme may be used as the source in TRS; however, the analytical expression is prone to error in the case of a mouse model with irregular surface geometry. Therefore, to mitigate the associated source of inaccuracy, a point excitation scheme is employed to spectroscopically estimate the average optical properties of the medium by measuring the TPSF at finite points on the model. The analytical expression utilized for TRS in this paper is defined below.
For a homogeneous slab of thickness d and absorption coefficient μa and reduced scattering coefficient μs', the temporal point spread function measured at a distance ρ from the axis of excitation is given by Eq. (1).
| (1) |
where and are the positions of the image sources used to model the extrapolated boundary conditions [31], and c is the speed of light in the medium. The infinite series of source images are used to force the fluence rate to zero at the two boundaries. In our implementation only the first 4 pairs of image sources were considered. The analytical function from Eq. (1) is convolved by the instrument response function (IRF) representative of the impulse response of the system to obtain the theoretical TPSF for this system. The experimental TPSF (10% of the peak value on the rising edge to 1% of peak value on the falling edge) is fit to the above computed theoretical TPSF using a sequential quadratic programming method (fmincon, MATLAB).
2.1.2 Time-gated reconstruction using Perturbation Monte Carlo
The anatomical complexity of the imaged volume in pre-clinical DOT necessitates the use of a rigorous model of light propagation in tissues for quantitative accuracy, especially when considering time-resolved data types such as early gates [32]. In this work, a perturbation Monte Carlo (pMC) based forward model is used for modeling the photon propagation in murine models [33]. The flexibility of the pMC model allows the accurate modeling of complex boundary conditions and remains valid for the wide range of optical properties encountered in small animal models. We provide below a brief description of this model.
The Monte Carlo method for light propagation is a photon tracing method where the path of photon propagation from a point source to a point detector, referred to as the sd pair, through the model having background optical properties μa and μs' is simulated. The path length and the number of scattering events along the path of propagation are recorded. The final measurement of the photon packet at the detector, W referred to as the photon weight, can be then calculated. In the pMC framework, a perturbation in the average optical properties (δμa and δμs), results in a perturbed detector reading at the time gate t and is given by Eq. (2).
| (2) |
where, is the unperturbed detector reading, p(rj,t) is the number of collisions and L(rj,t) is the path length in voxel rj at time gate t and n is the total number of photons. and are the perturbed optical properties and . computed in Eq. (2) is extended to an arbitrary wide-field excitation scheme by assigning a uniform probability of photon injection across the area of excitation with initial photon weights on source plane simulating the intensity profile of the pattern. The unperturbed detector reading is used to compute the Jacobian matrix for a specific gate and can be linearized using the Born formulation and is expressed as,
| (3) |
where, is the difference in the finals weights for the ith source-detector pair at time gate t and and are the Jacobians at the jth voxel given by,
| (4) |
It may be noted that Eq. (3) can be extended to multiple gates. The average optical properties obtained by TRS are used to compute the unperturbed detector measurements W(t) and in turn the Jacobian matrix J. The experimental measurements obtained at time-gate t and the Jacobian J is used to solve the inverse problem in Eq. (3) to simultaneously compute the perturbation in μa and μs' in the 3D volume.
In this work, a set of simple binary patterns spanning half of the space along the x and y axis are employed as the wide-field illumination scheme [29]. This set was selected for the ease of experimental implementation. Moreover, the use of uniform wide patterns ensures the injection of significant number of photons into the medium allowing the acquisition of measurements with high signal to noise ratio. It should be noted that the optimal illumination scheme may be dependent on the surface geometry and the distribution of optical properties in the model [34] and they have not been investigated in this work.
2.2 Instrumentation
Figure 1 shows a schematic of the platform presented in this paper. The system employs a tunable Ti-Sapphire laser (Mai Tai HP, Spectra-Physics, CA, USA) which generates 100fs pulses at 80MHz in the NIR spectral band (690nm-1020nm) as the source. The average laser power has dynamic range of 760mW-3W over its tuning range. A computer-controlled power controller (Application Note 30, Newport, CA, USA) is used in conjunction with the laser to maintain the incident laser power at a constant value with an accuracy of 100 μW when tuning the laser during the imaging session. The source is injected into a 400µm multi-mode fiber with 0.22 numerical aperture which guides the pulses to a 97/3 non-polarizing beam-splitter (Ozoptics, ON, Canada). The 3% channel is connected to a variable attenuator (Ocean Optics, FL, USA) and is focused directly on a diffusing paper on the imaging stage through a 400 µm multi-mode fiber. This channel is used as a temporal reference measured simultaneously during acquisition. The variable attenuator is used to adjust the signal level on the reference channel while tuning to correct for the change the spectral sensitivity of the detector. This allows for an in-experiment calibration of the incident power and t0 of the IRF reducing the estimation errors due to uncertainties in the time of injection [35]. The 97% channel is injected into 15x beam expander (BE15M-B, Thorlabs). The expanded beam is incident on digital micro-mirror device based light processing (DLP) board (Discovery 1100, Texas Instruments). The DLP comprises of 1024 x 768 micro-mirrors which are independently controlled by pulse-width modulation to generate a maximum of 256 grayscale levels. The pixelated nature of the micro-mirrors however results in 2D diffraction patterns in the reflected beam where the higher order diffraction beams appear as ghost images [36]. In this system, the higher-orders are re-imaged on the imaging chamber using a bi-convex lens (75mm focal length) to provide an area of excitation spanning 40mm x 25mm. It may be noted that the position of the lens used can be modified to optimize the area of illumination on the imaging chamber. Moreover, as the tip of the fiber is directly imaged on the chamber, the intensity profile of the excitation pattern is non-uniform which necessitates the calibration of the excitation pattern within each experiment protocol. Furthermore, the pattern thus obtained can be supplied directly to the MC model allowing an accurate modeling of the experimental settings.
Fig. 1.
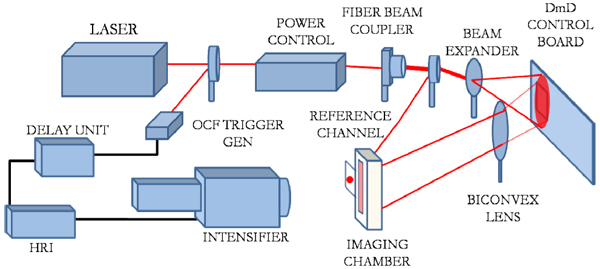
System Schematic
The time-gated detection system is implemented using an ultrafast gated intensified CCD camera (Picostar HR, LaVision GmbH, Germany) as the detector. The synchronization of the laser pulses with the intensifier shutter is achieved using an optical trigger (OCF-401, Becker & Hickl GmbH, Germany). The pulse train is conditioned using the HRI-delay unit (Kentech Instruments, UK) to potentially achieve 1ps resolution in the temporal measurements over a 50ns scan range. The output from the delay unit is connected to the High-Rate Imager (HRI) which controls the intensifier gating and gain modulation. Intensifier gating refers to the operation of the shutter where the photons are integrated at each time bin over a specified duration, referred to as the gate-width. The gate-width can be set to a preset value ranging from 200ps to 1000ps, (COMB modes) or can be controlled through external signals (RF or logical triggering). In this implementation the HRI is operated in the COMB mode where the gate is shifted over the measurement window at specific intervals to measure the TPSF. The total number of photons measured at each time-bin is referred to as the time-gate data type. The measured signals are further amplified by changing the gain voltage across the micro-channel plate (MCP) in the intensifier before impinging on a P43 phosphor screen. The images formed on the screen are imaged by the 12-bit CCD at a resolution of 1376 x 1040. The ICCD camera can detect a maximum of 4096 photons at each gate and the recorded images are binned over 8 x 8 pixels post-acquisition to create 1mm2 detector measurements.
3. System Characterization
In this section we investigate and identify system control parameters which can impact the stability and noise characteristics of the platform. The set of optimal operating parameters necessary for quantitatively accurate performance of the system are defined based on their impact on the accuracy in the estimation of optical coefficients by time-resolved spectroscopy.
3.1 Temporal Characteristics
System stability in time-resolved instrumentation is characterized by the stability of the IRF characteristics during the system operation. Three characterization experiments were conducted to determine the effect of individual system components on the IRF characteristics. In each experiment the IRF was measured by focusing the source at a single point on a white paper on the imaging stage.
First, the stability of the overall system was characterized by measuring the IRF at 700nm with the ICCD employing 200ps gates at 5ps temporal resolution over a 2hr period at 90s intervals. A temporal drift of 5ps was observed after a 1.5hr stabilization/warm-up period. The power control has negligible effect on the IRF with less than 5ps change in the IRF FWHM and less than 10ps variation in t0 with the change in power from 7mW to 150mW. Second, the effect of tuning the laser on the IRF was characterized by measuring the IRF at seven wavelengths, 700nm-740nm-770nm-805nm-825nm-860nm-880nm, with the ICCD employing 300ps gates at 20ps intervals. Figure 2(a) shows a t0 drift of 500ps across this range which can be attributed to the pulse generation mechanism of the laser source. An increase in the FWHM was also observed with the width increasing from 150ps at 700nm to 220ps at 880nm. The shift in the position of t0 and the broadening of the pulse due to the tuning operation requires the measurement of the IRF at each wavelength during the imaging session.
Fig. 2.
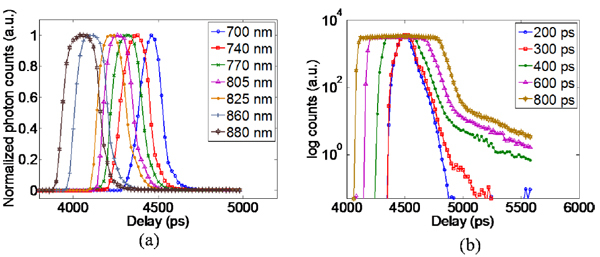
(a) IRF of the system across the NIR window for gatewidth of 300ps (b) IRF measured for varying gatewidth settings on the ICCD.
Third, the ICCD control parameters for the MCP voltage and the gatewidth were tested for their effects on the temporal characteristics of the system. The MCP voltage was found to have minimal effect on the IRF with less than 5ps variation in the t0 and FWHM for a change in MCP voltage from 400V to 800V. However, as expected, the gatewidth had a pronounced effect on the FWHM with the width of the IRF approximating the size of the gate especially for the larger gates (Fig. 2(b)).
3.2 Noise Characteristics
The signal-to-noise ratio of the measurements becomes an important system characteristic when using the ICCD camera in the NIR spectral window due to the relatively low sensitivity of the photocathode. In this implementation a TPSF with ~4000 photons measured at the maximum gate is defined as the optimal signal level and the SNR for the measurements on this platform is defined as the ratio of integrated counts to the standard deviation of the counts at each detector. The CCD counts (signal) in each experiment maybe amplified by increasing the gain voltage applied to the MCP or by increasing the power of the incident excitation field. However, the SNR for a given number of CCD counts decreases with the increase in gain voltage due to the amplification of the native dark noise of the detectors [37]. The system has a dark noise of ~40 counts after warm-up and is removed by background subtraction of dark images averaged over 16 frames. It may be noted that the dark noise level is dependent on the ambient temperature and the room temperature must be carefully controlled to avoid fluctuations in the dark noise level during the imaging session.
In this experiment we investigated the impact of the deterioration of SNR due to increase in gain voltage on the accuracy of estimated optical properties. TPSF were recorded in transmittance through a 3.44 cm thick resin phantom having homogeneous optical properties (µa = 0.06cm−1 and µs' = 11.3cm−1) at multiple MCP voltages (400V-800V) with the ICCD employing 200ps gates at 20ps intervals. The incident power of the source was kept constant through the experiment at 30mW. The optical properties in a 1.2cm radius area around the axis of excitation (~450 detectors) were estimated by TRS. The coefficient of variation (cv) given by the ratio of the standard deviation of the estimated optical properties to the mean value of the estimated optical properties was used as the figure of merit used to evaluate the impact of SNR. Figure 3 shows that the estimated absorption coefficient is more sensitive than the scattering coefficient to the reduced SNR with the cv of both coefficients increasing by more than 50% for MCP gain voltages above 600V. Therefore the ICCD camera should be operated below 600V for accurate estimation of optical properties. In experimental scenarios where higher CCD counts are required (e.g. highly absorbing media) the signal can be amplified by increasing the incident power.
Fig. 3.
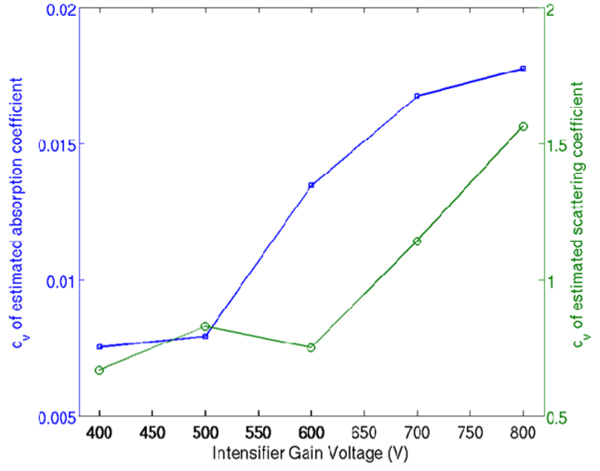
Variation of the estimated optical properties with increasing MCP voltage.
3.3 Impact of gate-width selection on quantitative accuracy
The gate-width defined as the time of integration of photons at each gate, has a pronounced effect on the temporal and noise characteristics of the system. The total number of photons detected at each gate can be increased by using longer gates, thereby improving the SNR of the measurements. Conversely, as the FWHM of the IRF is comparable to the gate –width, increasing the gate-width (Fig. 2(b)) limits the range of optical properties that can be accurately estimated on this platform as the width of the IRF becomes comparable to the width of the TPSF measured for tissues having high absorption coefficient and/or low scattering coefficient. The broad range of optical properties encountered in small animals therefore makes the selection of gate-width a critical factor affecting the accuracy of the estimated optical properties.
The effect of gate-width on estimation of physiologically relevant optical properties by time-resolved spectroscopy was investigated by using a 2cm thick liquid phantom. The liquid phantom was constructed by a mixture of Intralipid-20% (Sigma Aldrich, MO, USA) as the scattering agent and Black India ink (Higgins-Sanford) as the absorber diluted in water. TPSF were measured at a resolution of 20ps using different gate-width settings (200ps, 300ps, 400ps, 600ps and 800ps) for an MCP gain voltage of 400V and integration time of 100ms. Two separate experiments were conducted to estimate the absolute optical properties for the above detector settings; first, with increasing absorption coefficient (0.05cm−1 to 0.37cm−1) and constant scattering coefficient (8cm−1) by increasing the volume of India ink and second, with increasing scattering coefficient (6cm−1 to 16cm−1) for a constant absorption coefficient (0.07cm−1) by increasing the volume of Intralipid-20%. Figure 4(a)-(b) shows the estimated absorption and scattering coefficients obtained for various values of absorption coefficient. It may be noted that the broadening of the IRF for gatewidths has minimal effect on the estimation of absorption coefficient below 600ps. However, gatewidths less than 300ps must be used for the accurate estimation of the scattering coefficient with an estimation error less than 10%. Figure 4(c)-(d) show the estimated absorption and scattering coefficients with increasing scattering coefficient. The gatewidth has a less pronounced effect on the estimation of scattering coefficient. It is expected as the FWHM of the TPSF increases with increasing scattering coefficient and is not significantly biased by the broadening of the IRF. In this case, the maximum error of estimation ~8% was obtained when using 800ps gates for the lower values of scattering. Nevertheless, the broadening of the IRF affects the estimation of absorption coefficient, with estimation error greater than 20% when using 800ps gates. The increase in the estimated absorption coefficient with the volume of Intralipid may be attributed to the cross talk between absorption and scattering coefficients [38]. It is therefore determined that gatewidths shorter than 300ps must be used for the accurate estimation of optical properties in small animal imaging for estimation errors less than 10%.
Fig. 4.
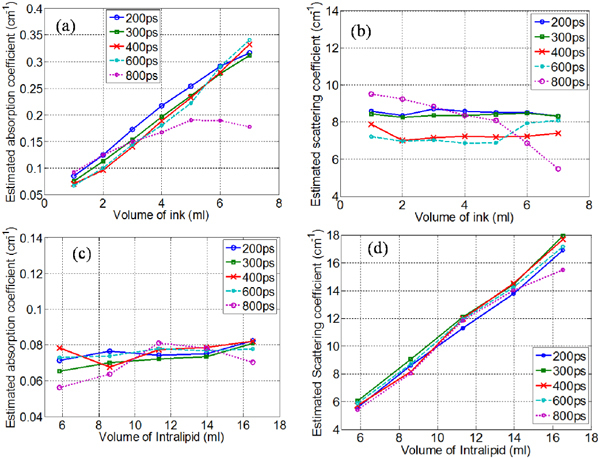
(a)-(b) Estimated absorption and scattering coefficient with increasing volume of ink. (c) - (d) Estimated absorption and scattering coefficient with increasing volume of Intralipid-20%.
4. System Validation
4.1 Multispectral time-resolved spectroscopy
In this experiment, performance of the platform in the estimation of the concentration of multiple chromophores in a homogenous mixture is investigated. The accurate estimation of the mixture composition is dependent on the accuracy of estimated optical properties at multiple wavelengths in the NIR window. India ink and Bovine Hemoglobin (Sigma Aldrich, MO, US) were selected as the two chromophores for this experiment. The absorption spectra of the two chromophores were calibrated before the experiment using a spectrophotometer (USB2000, Ocean Optics, FL) (Fig. 5(a) ). A 2cm thick liquid phantom was constructed using a polycarbonate tank carrying a mixture of, 5.7% hemoglobin and 0.1% ink and water to provide μa of 0.18cm−1 and μs' of 7cm−1 at 740nm. Wavelengths of 740-770-840-860-880 nm were selected for this experiment based on the spectral behavior of the chromophores (Fig. 5(a)). TPSF were measured using 300ps gates at 20ps interval over a 1.8ns time window for a single source-detector pair. The linear relationship between the absorption coefficient and the concentration of each chromophore weighted by its extinction coefficient at each wavelength is used to estimate the composition of the mixture [33].
Fig. 5.
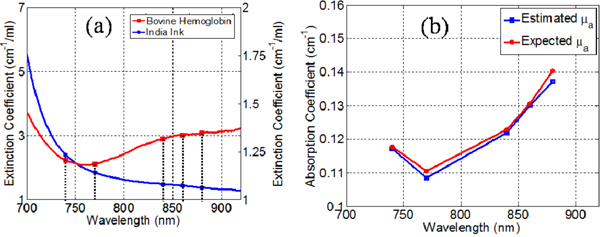
(a) Comparison of the absorption spectra of India ink and Bovine hemoglobin, (b) Comparison the estimated and expected absorption coefficients.
The error in the estimated concentration of ink and blood was 6% and 4.5% respectively (Fig. 5(b)). The scattering coefficient was estimated within 10% error. These results validate the quantitative accuracy of the platform when using multi-spectral time-gated data sets.
4.2 Simultaneous reconstruction of absorption and scattering coefficients
In this experiment we investigated the performance of this system for tomographic reconstruction of absorption and scattering coefficients using the time-gate datatype on a murine model phantom. The phantom (Fig. 7(a) ) consisted of a 2cm thick polycarbonate tank carrying a mixture of Intralipid-20% and India ink in (μa = 0.05cm−1; μs' = 9cm−1). Two tubes with 10mm inner diameter were suspended in the tank with India ink and Intralipid-20% solutions added to tubes 1 and 2 to simulate localized contrast in absorption (μa = 0.4cm−1; μs' = 9cm−1) and scattering (μa = 0.05cm−1; μs' = 18cm−1) respectively. The inclusions were selected to simulate perturbations comparable to the size of large organs (e.g. liver, lungs) in murine models.
Fig. 7.
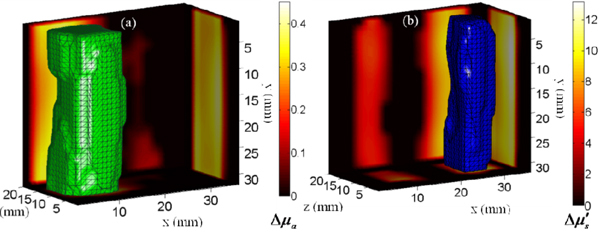
(Media 1 (3.3MB, AVI) ) (a)-(b) show the 50% isovolumes of the reconstructed differential absorption and scattering coefficients respectively. (Boundary maps) The reconstructed slices along y = 15mm, z = 11mm and x = 13mm and 29mm for (a) and (b) respectively.
A set of basic bar shaped patterns spanning half of the excited surface (40mm x 25mm) are employed as the wide-field illumination scheme for tomographic reconstruction (Fig. 6(a) ). The experiment protocol employed 36 'bar' patterns (18 patterns along the x-axis and 18 patterns along the y-axis) as the source. The intensifier was operated with a gatewidth of 300ps at 20ps intervals spanning a 2.2ns time window and two sets of measurements were acquired; first, with the tube containing the background mixture (homogeneous) and second, with the added India ink and Intralipid solutions (heterogeneous). The optimum signal was obtained using 560V across the MCP and an integration time of 50ms per gate on the CCD. The entire acquisition protocol was completed in 9 minutes. The acquired images were post-processed to generate 1mm x 1mm detectors. 88 point detectors at a separation of 3mm along the x-axis and 5mm along the y-axis were selected for the reconstruction. Figure 6(b) shows the comparison of the homogenous and heterogeneous TPSFs at two point detectors located over the absorption and scattering perturbation. It may be noted that the absorptive perturbation produces higher contrast for later gates while the scattering perturbation has predominant contrast in the early gates with minimal contrast observed in later gates. The normalized born contrast function at three time gates (TG1 – 20% of peak intensity on the rising edge, TG2 – peak intensity and TG3 – 50% of peak intensity on the falling edge) across the excited volume shows a distinct separation of the contrast due to the two perturbations with predominant contrast due to the scattering object during the early gate while the scattering perturbation showed minimal contrast during the late gates (Fig. 6(c)).
Fig. 6.
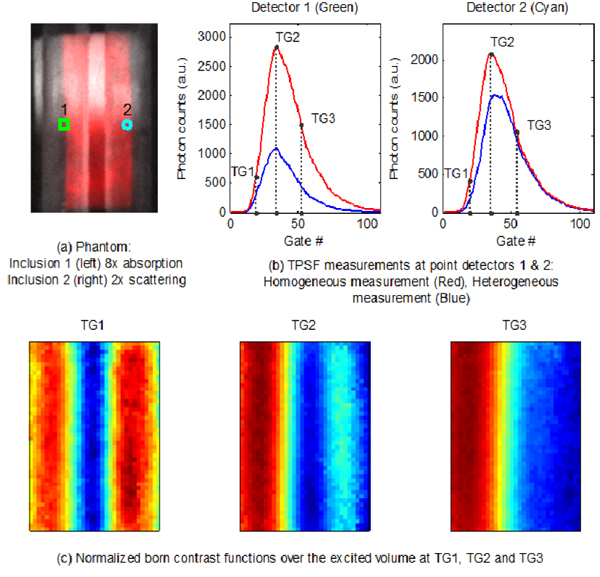
Time-gated measurements and contrast functions using wide-field patterns. (Media 1)
To solve the inverse problem, the measurement vector was constructed by heuristically selecting 6 time gates for each detector (8%, 12% and 17% of the peak on the rising edge; peak; 80% and 60% of the peak on the falling edge). It should be noted that the time-gates were selected based on the homogenous measurement. The phantom volume was modeled as a slab discretized into 2mm x 2mm x 2mm voxels and the Jacobians for perturbations in the scattering and absorption coefficients were computed using the average optical properties. The MC simulations using 2x1010 photons were launched on a supercomputer BlueGene (CCNI at RPI). The Jacobians calculated were scaled by their mean-column value to reduce the inter-parameter cross talk [39]. A spatially varying regularization was applied while solving the inverse problem [40]. The regularization parameter was empirically determined to have a value of 103 on the source detector layers and 5x102 on the penultimate layers. The problem was solved using a least-squares algorithm (lsqr, MATLAB). The 3D visualization of the reconstructed optical properties is shown in Fig. 7. The mean value of the 50% isovolume for both parameters was found to have an error less than 5% (Absorption coefficient, inclusion 1: Expected value = 0.35 cm−1, Reconstructed mean value = 0.33 cm−1; Scattering coefficient, inclusion 2: Expected value = 9.0 cm−1, Reconstructed mean value = 8.92 cm−1).
5. Conclusion
In this work, the design and characterization of a time-domain imaging platform for 3D reconstruction of functional parameters in preclinical imaging is described. The system integrates a tunable laser spanning the NIR window and a gated intensified CCD camera to provide spatially and temporally dense time-gated multispectral data sets. A digital light processor is used to generate structured illumination schemes which allow an unprecedented reduction in the acquisition time of said data sets while retaining high quantitative accuracy.
The instrument response function of the system was characterized and the tuning of the laser and the gate-width of the gated CCD were found to have significant impact on the temporal characteristics of the system. The accurate estimation of optical properties of homogenous phantoms by time-resolved spectroscopy was used as the metric for determining the optimal system parameters for pre-clinical studies. Gatewidths shorter than 300ps were found to be optimal for estimating optical properties in small animal models with estimation errors less than 10% obtained when using 300ps gates which is typical for time-resolved spectroscopy. The use of gain voltages higher than 600V across the MCP for signal amplification resulted in the deterioration of the signal to noise ratio increasing the variability of estimated optical properties by more than 50%.
The estimation of functional parameters was investigated by multispectral time-resolved spectroscopy and the composition of the mixture was estimated accurately with an error less than 6% demonstrating the quantitative accuracy of this platform for functional imaging studies. Further studies will investigate the quantitative and spatial performance of this system in 3D functional tomography studies in vivo and future work will also focus on multimodal studies using anatomical information provided by Magnetic Resonance Imaging (MRI) acquired in a non-concurrent setting to further reduce the ill-posedness of the problem [41]. It may be noted that in the case of an animal model, the background measurements cannot be experimentally acquired. In this case, we propose the use of the average optical properties determined by TRS to be used to numerically generate the background measurements using the MC model, which can then be used for inversion in the perturbative framework.
Finally, the time-gated data sets acquired using simple wide-field patterns were able to successfully separate the two targets exhibiting absorptive and scattering contrasts and quantitatively reconstruct the mean optical properties within 5% error. The reconstructed absorption coefficient demonstrated minimal inter-parameter crosstalk. The results presented were obtained by empirically selected time-gate data. In silico and in vitro studies will be undertaken to determine the optimal time-gates for minimizing the cross talk observed in the scattering coefficients and also determine the dependence of the optimal gates on the contrast levels and baseline optical properties.
In conclusion, the system described in this paper presents a novel approach towards performing whole-body functional imaging of small animals with increased resolution and quantitative accuracy. The reduction in the acquisition time of dense data sets using wide-field excitation schemes allows the whole-body 3D reconstruction of functional parameters. Thanks to the flexibility of the system design, this platform can be easily adapted for applications in small animal time-resolved fluorescence molecular imaging studies. Moreover, the concurrent acquisition of functional parameters will improve the accuracy of molecular imaging techniques.
Acknowledgements
The authors gratefully acknowledge the support of the Computational Center for Nanotechnology Innovations (CCNI) at RPI.
References and links
- 1.Hielscher A. H., “Optical tomographic imaging of small animals,” Curr. Opin. Biotechnol. 16(1), 79–88 (2005). 10.1016/j.copbio.2005.01.002 [DOI] [PubMed] [Google Scholar]
- 2.Achilefu S., Dorshow R. B., Bugaj J. E., Rajagopalan R., “Novel receptor-targeted fluorescent contrast agents for in vivo tumor imaging,” Invest. Radiol. 35(8), 479–485 (2000). 10.1097/00004424-200008000-00004 [DOI] [PubMed] [Google Scholar]
- 3.Contag C. H., Bachmann M. H., “Advances in in vivo bioluminescence imaging of gene expression,” Annu. Rev. Biomed. Eng. 4(1), 235–260 (2002). 10.1146/annurev.bioeng.4.111901.093336 [DOI] [PubMed] [Google Scholar]
- 4.Weissleder R., Ntziachristos V., “Shedding light onto live molecular targets,” Nat. Med. 9(1), 123–128 (2003). 10.1038/nm0103-123 [DOI] [PubMed] [Google Scholar]
- 5.Alexandrakis G., Rannou F. R., Chatziioannou A. F., “Effect of optical property estimation accuracy on tomographic bioluminescence imaging: simulation of a combined optical-PET (OPET) system,” Phys. Med. Biol. 51(8), 2045–2053 (2006). 10.1088/0031-9155/51/8/006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang X., Badea C. T., Johnson G. A., “Three-dimensional reconstruction in free-space whole-body fluorescence tomography of mice using optically reconstructed surface and atlas anatomy,” J. Biomed. Opt. 14(6), 064010 (2009). 10.1117/1.3258836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lin Y., Yan H., Nalcioglu O., Gulsen G., “Quantitative fluorescence tomography with functional and structural a priori information,” Appl. Opt. 48(7), 1328–1336 (2009). 10.1364/AO.48.001328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Intes X., Chance B., “Non-PET functional imaging techniques: optical,” Radiol. Clin. North Am. 43(1), 221–234, xii (2005). 10.1016/j.rcl.2004.07.002 [DOI] [PubMed] [Google Scholar]
- 9.Cheong W. F., Prahl S. A., Welch A. J., “A review of the optical properties of biological tissues,” IEEE J. Quantum Electron. 26(12), 2166–2185 (1990). 10.1109/3.64354 [DOI] [Google Scholar]
- 10.Arridge S. R., Lionheart W. R., “Nonuniqueness in diffusion-based optical tomography,” Opt. Lett. 23(11), 882–884 (1998). 10.1364/OL.23.000882 [DOI] [PubMed] [Google Scholar]
- 11.Cheng X. F., Boas D. A., “Systematic diffuse optical image errors resulting from uncertainty in the background optical properties,” Opt. Express 4(8), 299–307 (1999). 10.1364/OE.4.000299 [DOI] [PubMed] [Google Scholar]
- 12.Netz U. J., Beuthan J., Hielscher A. H., “Multipixel system for gigahertz frequency-domain optical imaging of finger joints,” Rev. Sci. Instrum. 79(3), 034301 (2008). 10.1063/1.2840344 [DOI] [PubMed] [Google Scholar]
- 13.Hillman E. M. C., Hebden J. C., Schmidt F. E. W., Arridge S., Schweiger M., Dehghani H., Delpy D. T., “Calibration techniques and datatype extraction for time-resolved optical tomography,” Rev. Sci. Instrum. 71(9), 3415 (2000). 10.1063/1.1287748 [DOI] [Google Scholar]
- 14.Patwardhan S. V., Culver J. P., “Quantitative diffuse optical tomography for small animals using an ultrafast gated image intensifier,” J. Biomed. Opt. 13(1), 011009 (2008). 10.1117/1.2830656 [DOI] [PubMed] [Google Scholar]
- 15.Kumar A. T. N., Raymond S. B., Dunn A. K., Bacskai B. J., Boas D. A., “A time domain fluorescence tomography system for small animal imaging,” IEEE Trans. Med. Imaging 27(8), 1152–1163 (2008). 10.1109/TMI.2008.918341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liebert A., Wabnitz H., Grosenick D., Macdonald R., “Fiber dispersion in time domain measurements compromising the accuracy of determination of optical properties of strongly scattering media,” J. Biomed. Opt. 8(3), 512–516 (2003). 10.1117/1.1578088 [DOI] [PubMed] [Google Scholar]
- 17.Corlu A., Choe R., Durduran T., Lee K., Schweiger M., Arridge S. R., Hillman E. M. C., Yodh A. G., “Diffuse optical tomography with spectral constraints and wavelength optimization,” Appl. Opt. 44(11), 2082–2093 (2005). 10.1364/AO.44.002082 [DOI] [PubMed] [Google Scholar]
- 18.Gulsen G., Xiong B., Birgul O., Nalcioglu O., “Design and implementation of a multifrequency near-infrared diffuse optical tomography system,” J. Biomed. Opt. 11(1), 014020 (2006). 10.1117/1.2161199 [DOI] [PubMed] [Google Scholar]
- 19.Srinivasan S., Pogue B. W., Jiang S., Dehghani H., Paulsen K. D., “Spectrally constrained chromophore and scattering near-infrared tomography provides quantitative and robust reconstruction,” Appl. Opt. 44(10), 1858–1869 (2005). 10.1364/AO.44.001858 [DOI] [PubMed] [Google Scholar]
- 20.Konecky S. D., Panasyuk G. Y., Lee K., Markel V., Yodh A. G., Schotland J. C., “Imaging complex structures with diffuse light,” Opt. Express 16(7), 5048–5060 (2008). 10.1364/OE.16.005048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thompson A. B., Hawrysz D. J., Sevick-Muraca E. M., “Near-infrared fluorescence contrast-enhanced imaging with area illumination and area detection: the forward imaging problem,” Appl. Opt. 42(19), 4125–4136 (2003). 10.1364/AO.42.004125 [DOI] [PubMed] [Google Scholar]
- 22.Lukic V., Markel V. A., Schotland J. C., “Optical tomography with structured illumination,” Opt. Lett. 34(7), 983–985 (2009). 10.1364/OL.34.000983 [DOI] [PubMed] [Google Scholar]
- 23.Konecky S. D., Mazhar A., Cuccia D. J., Durkin A. J., Schotland J. C., Tromberg B. J., “Quantitative optical tomography of sub-surface heterogeneities using spatially modulated structured light,” Opt. Express 17(17), 14780–14790 (2009). 10.1364/OE.17.014780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cuccia D. J., Bevilacqua F., Durkin A. J., Ayers F. R., Tromberg B. J., “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Saager R. B., Cuccia D. J., Durkin A. J., “Determination of optical properties of turbid media spanning visible and near-infrared regimes via spatially modulated quantitative spectroscopy,” J. Biomed. Opt. 15(1), 017012 (2010). 10.1117/1.3299322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bassi A., D’Andrea C., Valentini G., Cubeddu R., Arridge S., “Detection of inhomogeneities in diffusive media using spatially modulated light,” Opt. Lett. 34(14), 2156–2158 (2009). 10.1364/OL.34.002156 [DOI] [PubMed] [Google Scholar]
- 27.Gioux S., Mazhar A., Cuccia D. J., Durkin A. J., Tromberg B. J., Frangioni J. V., “Three-dimensional surface profile intensity correction for spatially modulated imaging,” J. Biomed. Opt. 14(3), 034045 (2009). 10.1117/1.3156840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bélanger S., Abran M., Intes X., Casanova C., Lesage F., “Real-time diffuse optical tomography based on structured illumination,” J. Biomed. Opt. 15(1), 016006 (2010). 10.1117/1.3290818 [DOI] [PubMed] [Google Scholar]
- 29.Chen J., Venugopal V., Lesage F., Intes X., “Time-resolved diffuse optical tomography with patterned-light illumination and detection,” Opt. Lett. 35(13), 2121–2123 (2010). 10.1364/OL.35.002121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Patterson M. S., Chance B., Wilson B. C., “Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties,” Appl. Opt. 28(12), 2331–2336 (1989). 10.1364/AO.28.002331 [DOI] [PubMed] [Google Scholar]
- 31.Haskell R. C., Svaasand L. O., Tsay T. T., Feng T. C., McAdams M. S., Tromberg B. J., “Boundary conditions for the diffusion equation in radiative transfer,” J. Opt. Soc. Am. A 11(10), 2727–2741 (1994). 10.1364/JOSAA.11.002727 [DOI] [PubMed] [Google Scholar]
- 32.Niedre M. J., Ntziachristos V., “Comparison of fluorescence tomographic imaging in mice with early-arriving and quasi-continuous-wave photons,” Opt. Lett. 35(3), 369–371 (2010). 10.1364/OL.35.000369 [DOI] [PubMed] [Google Scholar]
- 33.Chen J., Intes X., “Time-gated perturbation Monte Carlo for whole body functional imaging in small animals,” Opt. Express 17(22), 19566–19579 (2009). 10.1364/OE.17.019566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dutta J., Ahn S., Joshi A. A., Leahy R. M., “Illumination pattern optimization for fluorescence tomography: theory and simulation studies,” Phys. Med. Biol. 55(10), 2961–2982 (2010). 10.1088/0031-9155/55/10/011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ntziachristos V., Chance B., “Accuracy limits in the determination of absolute optical properties using time-resolved NIR spectroscopy,” Med. Phys. 28(6), 1115–1124 (2001). 10.1118/1.1373674 [DOI] [PubMed] [Google Scholar]
- 36.Using Lasers with DLP® DMD technology, http://focus.ti.com/pdfs/dlpdmd/Using_Lasers_with_DLP(r)_Technology.pdf
- 37.Selb J., Stott J. J., Franceschini M. A., Sorensen A. G., Boas D. A., “Improved sensitivity to cerebral hemodynamics during brain activation with a time-gated optical system: analytical model and experimental validation,” J. Biomed. Opt. 10(1), 011013 (2005). 10.1117/1.1852553 [DOI] [PubMed] [Google Scholar]
- 38.D'Andrea C., Comelli D., Pifferi A., Torricelli A., Valentini G., Cubeddu R., “Time-resolved optical imaging through turbid media using a fast data acquisition system based on a gated CCD camera,” J. Phys. D Appl. Phys. 36(14), 1675–1681 (2003). 10.1088/0022-3727/36/14/304 [DOI] [Google Scholar]
- 39.Intes X., Chance B., “Multi-frequency diffuse optical tomography,” J. Mod. Opt. 52(15), 2139–2159 (2005). 10.1080/09500340500217290 [DOI] [Google Scholar]
- 40.Pogue B. W., McBride T. O., Prewitt J., Österberg U. L., Paulsen K. D., “Spatially variant regularization improves diffuse optical tomography,” Appl. Opt. 38(13), 2950–2961 (1999). 10.1364/AO.38.002950 [DOI] [PubMed] [Google Scholar]
- 41.Intes X., Maloux C., Guven M., Yazici B., Chance B., “Diffuse optical tomography with physiological and spatial a priori constraints,” Phys. Med. Biol. 49(12), N155–N163 (2004). 10.1088/0031-9155/49/12/N01 [DOI] [PubMed] [Google Scholar]


