Abstract
With the use of adaptive optics (AO), high-resolution microscopic imaging of living human retina in the single cell level has been achieved. In an adaptive optics confocal scanning laser ophthalmoscope (AOSLO) system, with a small field size (about 1 degree, 280 μm), the motion of the eye severely affects the stabilization of the real-time video images and results in significant distortions of the retina images. In this paper, Scale-Invariant Feature Transform (SIFT) is used to abstract stable point features from the retina images. Kanade-Lucas-Tomasi(KLT) algorithm is applied to track the features. With the tracked features, the image distortion in each frame is removed by the second-order polynomial transformation, and 10 successive frames are co-added to enhance the image quality. Features of special interest in an image can also be selected manually and tracked by KLT. A point on a cone is selected manually, and the cone is tracked from frame to frame.
OCIS codes: (010.1080) Adaptive optics, (180.1790) Confocal microscopy
1. Introduction
Fundus imaging is the fundamental basis for clinical research and patient care in ophthalmology. Normally, the image resolution is restricted by ocular aberrations. The adaptive optics (AO) technique can compensate for the ocular aberrations to get nearly diffraction-limited resolution. Microscopic imaging of the living human retina at the single cell level has been achieved with AO [1–3]. AO has also been combined with optical coherence tomography (AO-OCT) [4–6] and confocal scanning laser ophthalmoscope (AOSLO) [7–9] to improve their lateral resolution for imaging of human retina.
However, the high resolution of the AO retinal imaging systems has been compromised by the eye motion. This eye motion includes components of various frequencies from low to a relatively high frequency (50-100Hz) [10]. When the observed object appears to be fixed in the field of view, the motion sweep any projected point of the object across many cone diameters. With a small field size (about 1 deg field, 280), the motion affects quality severely.
There were several methods to estimate and eliminate the effect of retinal motion. A patch-based cross-correlation was used to remove translational motion [11]. Vogel et al. applied a map-seeking circuit (MSC) algorithm to compute eye motion vectors and then compensate the motion. This algorithm allows one to account for more general motions [12]. Arathorn et al. projected a stimulus directly onto the retina with MSC algorithm. With good fixation stability, stimulus location accuracy of averaged 1.3 microns has been achieved [10].
In this paper a computational technique known as Kanade-Lucas-Tomasi (KLT) [13] is applied to track the features in the retinal image. KLT is a tracking algorithm with low computational complexity and high accuracy. The tracked features can be provided by Scale-Invariant Feature Transform (SIFT) [14] which automatically abstracts stable point features with subpixel resolution. With the tracked features, the influence of the motion is removed by the second-order polynomial transformation and images of the same area are co-added to improve the image resolution and quality. On the other hand, cones, vessels or other structures can also be tracked by selecting features of these structures.
2. Method
2.1 KLT algorithm [13]
KLT is a well-known tracking algorithm for tracking features from frame to frame. The algorithm is done by iteration, and its computational complexity is low. KLT algorithm has high accuracy of subpixel level.
In retina images, there may be complex motion between two frames. The motion can be approximated by affine motion in a small window around a selected feature in the image. The affine motion can be represented by
| (1) |
where
| (2) |
is a deformation matrix, and d is the translation of the feature window’s center. The image coordinates x are measured with respect to the window’s center. The point x is in the first image I and is the correspond point in the second image J. Given the two images I and J and a window in image I, KLT can find the D and d that minimize the dissimilarityε:
| (3) |
where W is the given feature window and is a weighting function. could be a Gaussian-like function to emphasize the central area of the window. To minimize this equation, we differentiated it with respect to D and d and set the result to zero. This yields the following two equations:
| (4) |
| (5) |
where
| (6) |
is the spatial gradient of the image intensity and the superscript T denotes transposition. could be approximated by its Taylor series expansion truncated to the linear term:
| (7) |
where . This equation, combined with Eq. (4) and Eq. (5), would yield the following equations:
| (8) |
| (9) |
Equation (8) and Eq. (9) can be solved iteratively with a initial value. After several iterations, if ε is smaller than a threshold, D and d are determined. By Eq. (1), in the second image can also be determined and a point pair are matched.
2.2 Abstracting tracked features
SIFT is an image registration algorithm [14]. This algorithm can automatically abstract point features which are blob-like structures with subpixel resolution from two images. Then the point features can be represented by descriptors and matched by minimum Euclidean distance for the descriptor vector. The matching algorithm in SIFT is complex. And when noise is added, some points are incorrectly matched by SIFT. But the point features abstracted by SIFT can be easily tracked. Therefore, the features detector algorithm in SIFT can be used to provide stable point features. There are three basic steps in the features detector algorithm of SIFT: First, Gaussian function is used to generate scale space of an image; Second, extrema are detected in the scale-space; Third, edge responses of the extrema are eliminated. After these steps, point features are detected. KLT algorithm can track the point features. KLT algorithm occasionally loses features, because these features may go out of bounds or vary from frame to frame, or because the computation fails. If it is desired to always maintain a certain number of features, the features can be abstracted repeatedly by SIFT.
Both the SIFT and KLT algorithms are completely automatic. However, the features can be not only abstracted by SIFT but also be selected manually. If you are interested in s special structure and unfortunately there are no features abstracted by SIFT on the structure, you can use a mouse to select a feature. This feature can also be tracked by KLT.
2.3 Removing distortion
With the tracked points, the second-order polynomial transformation can be used to remove distortions of the retina image [15]. And if more complex transformation such as three-order polynomial transformation is used, more general distortions can also be removed. The second-order polynomial transformation of a distorted image point to the corrected image point can be written in the following form:
| (10) |
where the distortion is represented by a and b parameters. The second-order polynomial transformation allows mappings of all lines to curves. Given a set of matched points, the parameters can be determined as follows. Assume k points match in the reference and distorted images. A matrix R is defined which contains the coordinates of the k matched points in the reference image:
| (11) |
The D matrix contains the corresponding points in the distorted image:
| (12) |
An A matrix is defined contains the transformation parameters:
| (13) |
The linear regression estimate for A is given by:
| (14) |
To implement the second-order polynomial transformation at least six corresponding point pairs are needed.
3. Experimental results
An AOSLO system for real-time (30Hz) retina imaging was set up in our laboratory [9]. Figure 1 shows a schematic diagram of the setup. A beam of light emitted from a 635nm laser diode is collimated, and then is focused to a small spot on retina by eye. Two scanning mirrors (horizontal scanner: 16 KHz resonant scanner, vertical scanner: 30Hz galvometric scanner) are used to control the focused spot to scan the retina. Light scattered back from retina is split into two parts. One part enters photomultiplier tubes (PMT) for signal detection. By synchronizing the PMT signal and two scanning mirrors, the image of retina can be consecutively recorded. And the other part is captured by a Shack-Hartmann wavefront sensor with 97 effect subapertures in 11 × 11 arrays. The slope data of the wavefront are acquired by a computer and transferred to control signals for a 37-channel deformable mirror(DM). After 20-30 iterations, the error of the corrected wavefront approaches the minimum and the system becomes stable.
Fig. 1.
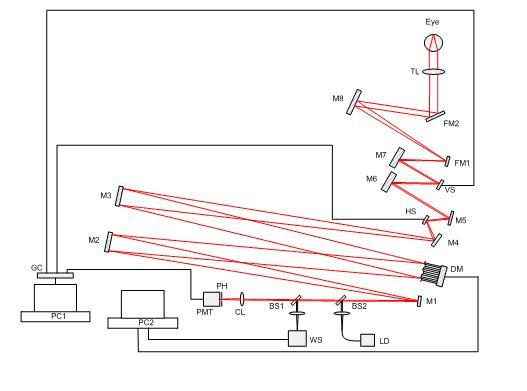
The schematic of AOSLO system. HS, horizontal scanner; VS, vertical scanner; WS, wavefront sensor; DM, deformable mirror; PMT, photomultiplier tubes; BS1, BS2, beam splitter; CL, collecting lens; FM1, FM2, folding mirrors; LD, laser diode; M1~M8, spherical mirrors; PH, pinhole; TL, trial lens; GC, grabbing card.
The device was tested with vivid eyes of volunteers. Video clips of the retina were recorded by the device. The frame size was 512 × 480 pixels, and the field of view was 1 degree (about 280). SIFT was used to abstract point features and then the point features were tracked by KLT. The accuracy of the KLT algorithm was subpixel, that was less than 0.55 microns. Due to some point features go out of bounds or varying from frame to frame, or due to computation failure, some of them could not be tracked. Point features were abstracted repeatedly by SIFT when the loss of point features was significant. The tracked point features in 100 frames are shown in the video clips Tracked_Points.MOV, and the first frame is shown in Fig. 2 . Black frames in the video are due to blinking, and the number of point features in these frames is nearly zero. The total numbers of the tracked point features in the 100 frames are shown in Fig. 3 and abstracting features repeatedly by SIFT is shown by the sharp spikes. At least six corresponding point pairs are needed to implement the second-order polynomial transformation, and more point pairs can improve the transformation’s accuracy. Thus, in order to improve the accuracy, all of the tracked features were used.
Fig. 2.
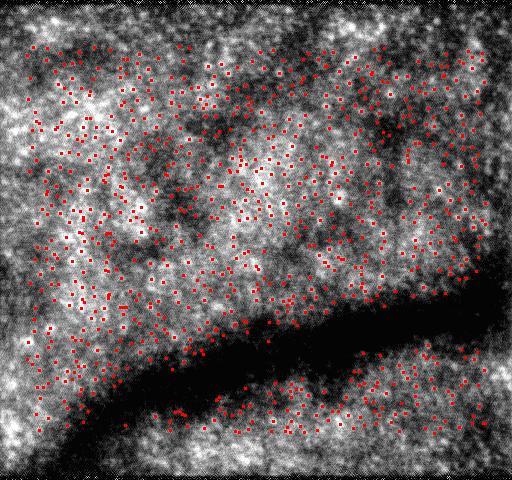
(Media 1 (1.8MB, MOV) ) The first frame of Tracked_Points.MOV.
Fig. 3.
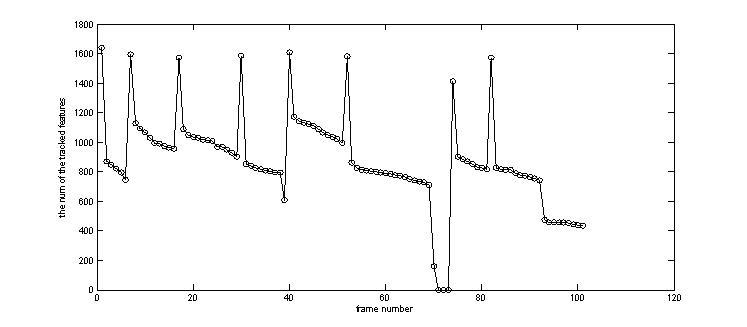
The number of the tracked features from frame to frame.
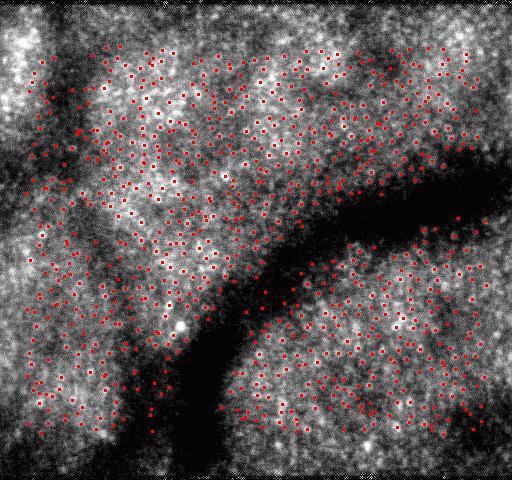
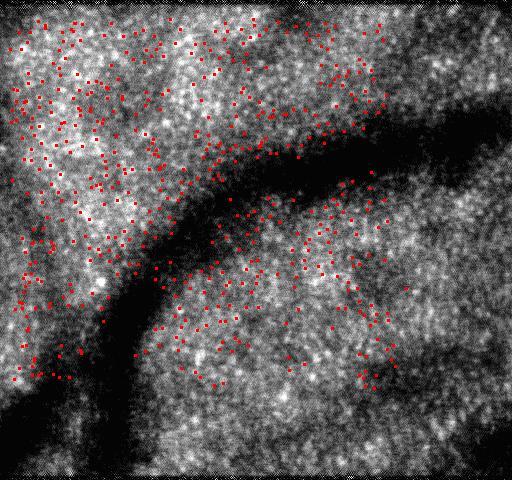
With all of the tracked points, the second-order polynomial transformation described in section 2.3 was used to remove distortions of the images. The second-order polynomial transformation allows one to consider more general motions such as scale and rotation about the optical axis of the eye, but only simple translational motion can be considered by usually used patch-based cross-correlation algorithm [13]. The point features abstracted by SIFT in the reference image are shown in Fig. 4(a) , and the points matched by KLT in an image are shown in Fig. 4(b). The image with distortions removed by the second-order polynomial transformation is shown in Fig. 4(c).
Fig. 4.

Removing distortions by the second-order polynomial transformation. (a) shows the point features abstracted by SIFT in the reference image. (b) shows the points matched by KLT in a distorted image. (c) shows the corrected image with distortions removed by the second-order polynomial transformation.
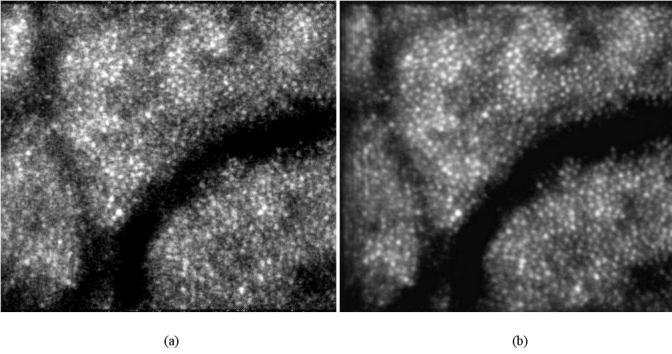
Ten successive frames with distortions removed are co-added, and the result is shown in Fig. 5(b) . The reference frame is shown in Fig. 5(a). If more frames are selected, the superposition is small and the image quality isn’t improved evidently. The power spectra of Figs. 5(a) and 5(b) are compared in Fig. 6 . It can be seen that at the high frequencies which probably correspond to noise, the power spectrum of Fig. 5(b) is decreased. It indicates that the noises are effectively suppressed and the image quality is improved.
Fig. 5.
co-added 10 successive frames. (a) the reference frame. (b) the average image without distortions.
Fig. 6.
Average power spectra of Figs. 5(a) and 5(b).
Both the SIFT and KLT algorithms are completely automatic and none of human intervention is required. The features can be not only abstracted by SIFT but also be selected manually. As an example, a point on one cone was selected manually, and the cone was tracked by KLT algorithm in 20 frames of the video. The point selection was done by mouse click on the image. The result is shown in the video clips Tracked_Cone.MOV, and the first image is shown in Fig. 7 . The horizontal position and vertical position of the tracked cone are shown in Fig. 8 .
Fig. 7.
First frame of Tracked_Cone.MOV.
Fig. 8.
Horizontal position and vertical position of the tracked cone.
4. Discussion and conclusions
Features of the AOSLO retinal image have been abstracted by SIFT algorithm and tracked by KLT algorithm. The tracking accuracy is subpixel level which is less than 0.55 microns with 1 degree field and 512 × 480 pixel image size. With the tracked points, the second-order polynomial transformation has been used to remove complex distortions of the frames and 10 corrected frames have been co-added to enhance the image quality. Our algorithms allow one to consider more general retinal motions such as scale and rotation about the optical axis of the eye, but only simple translational motion can be considered by usually used patch-based cross-correlation algorithm.
The retinal motions within 100 successive frames were estimated, and the transformation parameters in Eq. (13) were calculated. The expectations (E) and standard deviations (STD) of the transformation parameters are shown in Table 1 . Because the transformation parameters are signed, the expectations are small. Standard deviations of parameters and are greater than others. However, the other parameters can improve the transformation’s accuracy.
Table 1. The expectations(E) and standard deviations(STD) of the transformation parameters.
| E | 3.35 | 0.98 | −0.0047 | 0. 00020 | −0. 0013 | −0. 00054 | 0. 56 | 0. 0039 | 0. 99 | 0. 00034 | −0. 00065 | 0. 000031 |
| STD | 11.05 | 0.060 | 0.022 | 0.0027 | 0.013 | 0.0061 | 8.30 | 0.042 | 0.084 | 0.0024 | 0.0065 | 0.0019 |
Both the SIFT and KLT algorithms are completely automatic. However, the features can be not only abstracted by SIFT but also be selected manually. As an example, a point on a cone has been selected by mouse click on the image, and the cone has been tracked from frame to frame.
When AOSLO retinal image size is 512 × 480 pixels, the average computation time of the SIFT algorithm on our computer(CPU is intel Q9300) is 719ms. The average computation time of one feature converging in KLT is 1.09ms. If the frequency of the video is 30HZ, 30 features can be tracked in real-time by KLT algorithm. We will complement the SIFT and KLT algorithms on GPU, and more features will be able to be tracked in real-time.
Acknowledgments
This research was supported by the Knowledge Innovation Program of the Chinese Academy of Sciences, Grant No.KGCX2-Y11-920.
References and links
- 1.Liang J., Williams D. R., Miller D. T., “Supernormal vision and high-resolution retinal imaging through adaptive optics,” J. Opt. Soc. Am. A 14(11), 2884–2892 (1997). 10.1364/JOSAA.14.002884 [DOI] [PubMed] [Google Scholar]
- 2.Roorda A., Williams D. R., “The arrangement of the three cone classes in the living human eye,” Nature 397(6719), 520–522 (1999). 10.1038/17383 [DOI] [PubMed] [Google Scholar]
- 3.Ling N., Zhang Y., Rao X., Li X., Wang C., Hu Y., Jiang W., “Small table-top adaptive optical systems for human retinal imaging,” Proc. SPIE 4825, 99–105 (2002). [Google Scholar]
- 4.Hermann B., Fernández E. J., Unterhuber A., Sattmann H., Fercher A. F., Drexler W., Prieto P. M., Artal P., “Adaptive-optics ultrahigh-resolution optical coherence tomography,” Opt. Lett. 29(18), 2142–2144 (2004). 10.1364/OL.29.002142 [DOI] [PubMed] [Google Scholar]
- 5.Zhang Y., Rha J., Jonnal R., Miller D., “Adaptive optics parallel spectral domain optical coherence tomography for imaging the living retina,” Opt. Express 13(12), 4792–4811 (2005), http://www.opticsinfobase.org/abstract.cfm?URI=oe-13-12-4792 10.1364/OPEX.13.004792 [DOI] [PubMed] [Google Scholar]
- 6.Zawadzki R. J., Jones S. M., Olivier S. S., Zhao M., Bower B. A., Izatt J. A., Choi S., Laut S., Werner J. S., “Adaptive-optics optical coherence tomography for high-resolution and high-speed 3D retinal in vivo imaging,” Opt. Express 13(21), 8532–8546 (2005), http://www.opticsinfobase.org/abstract.cfm?URI=oe-13-21-8532 10.1364/OPEX.13.008532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Roorda A., Romero-Borja F., Donnelly Iii W., Queener H., Hebert T., Campbell M., “Adaptive optics scanning laser ophthalmoscopy,” Opt. Express 10(9), 405–412 (2002), http://www.opticsinfobase.org/abstract.cfm?URI=oe-10-9-405 [DOI] [PubMed] [Google Scholar]
- 8.Burns S. A., Marcos S., Elsner A. E., Bara S., “Contrast improvement of confocal retinal imaging by use of phase-correcting plates,” Opt. Lett. 27(6), 400–402 (2002), http://www.opticsinfobase.org/ol/abstract.cfm?URI=ol-27-6-400 10.1364/OL.27.000400 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jing L. U., Hao L. I., Ling W. E. I., Guohua S. H. I., Yudong Z. H. A. N. G., “Retina imaging in vivo with the adaptive optics confocal scanning laser ophthalmoscope,” Proc. SPIE 7519, 75191I (2009). [Google Scholar]
- 10.Arathorn D. W., Yang Q., Vogel C. R., Zhang Y., Tiruveedhula P., Roorda A., “Retinally stabilized cone-targeted stimulus delivery,” Opt. Express 15(21), 13731–13744 (2007), http://www.opticsinfobase.org/abstract.cfm?URI=oe-15-21-13731 10.1364/OE.15.013731 [DOI] [PubMed] [Google Scholar]
- 11.J. B. Mulligan, “Recovery of motion parameters from distortions in scanned images,” Proceedings of the NASAImage Registration Workshop (IRW97), NASA Goddard Space Flight Center, MD (1997). [Google Scholar]
- 12.Vogel C. R., Arathorn D. W., Roorda A., Parker A., “Retinal motion estimation in adaptive optics scanning laser ophthalmoscopy,” Opt. Express 14(2), 487–497 (2006). 10.1364/OPEX.14.000487 [DOI] [PubMed] [Google Scholar]
- 13.J. Shi and C. Tomasi, “Good Features to Track,” IEEE Conference on Computer Vision and Pattern Recognition, 593–600 (1994). [Google Scholar]
- 14.Lowe D. G., “Distinctive Image Features from Scale-Invariant Keypoints,” Int. J. Comput. Vis. 60(2), 91–110 (2004). 10.1023/B:VISI.0000029664.99615.94 [DOI] [Google Scholar]
- 15.Ryan N., Heheghan C., de Chazal P., “Registration of digital retinal images using landmark correspondence by expectation maximization,” Image Vis. Comput. 22(11), 883–898 (2004). 10.1016/j.imavis.2004.04.004 [DOI] [Google Scholar]


