Quantitative Photoacoustic Image Reconstruction using Fluence Dependent Chromophores

Abstract

In biomedical photoacoustic imaging the images are proportional to the absorbed optical energy density, and not the optical absorption, which makes it difficult to obtain a quantitatively accurate image showing the concentration of a particular absorbing chromophore from photoacoustic measurements alone. Here it is shown that the spatially varying concentration of a chromophore whose absorption becomes zero above a threshold light fluence can be estimated from photoacoustic images obtained at increasing illumination strengths. This technique provides an alternative to model-based multiwavelength approaches to quantitative photoacoustic imaging, and a new approach to photoacoustic molecular and functional imaging.

1. Introduction

Photoacoustic tomography (PAT) can provide images related to the distribution of optical absorption within highly scattering media such as biological tissue. Its many applications to date include, among other things, preclinical studies of tumor growth, breast imaging, imaging of the microvasculature and small animal imaging [1, 2, 3, 4, 5]. Photoacoustic images, while useful, and while closely related to the distribution of optical absorption, do not give quantitative measures of absorption as they are weighted by the unknown, non-uniform, light fluence in the tissue. Rather, the image amplitude for any given point is proportional to the absorbed optical energy density there, h = μ_aϕ, where ϕ is the local light fluence and μ_a the optical absorption coefficient. A serious implication is that multiwavelength spectroscopic methods cannot be applied directly to PAT images, which significantly restricts its use to only a qualitative imaging modality for many applications. If this dependence on the light fluence could be removed then PAT would quickly become a very powerful tool for molecular and functional imaging, particularly for preclinical studies.

Attempts to estimate the absorption coefficient distribution, or the concentration distribution of a chromophore, have so far mostly been model-based, ie. the optical coefficients in a model of diffuse light transport were iteratively adjusted until the modelled image matched that measured. [6, 7, 8, 9, 10] One complication of the model-based approach is the non-uniqueness introduced if the optical scattering is also unknown and spatially-varying, although this may be overcome either by using multiple illumination patterns, [11], or prior knowledge of the spatial geometry of the absorbers [10, 12], by assuming knowledge of the wavelength dependence of the scattering and the specific absorption spectra of the chromophores. [8, 9]

Another potential drawback to model-based methods is the size of the inverse problem due to the large image size/spatial resolution ratio available in PAT, particularly a problem when using Hessian-based inversion methods. [13] A different approach, using complex geometrical optics, has also been proposed, [11] but this shares a requirement of the model-based methods that μ_a > 0 everywhere (and that in practice the image amplitude is above the noise everywhere). This is necessary for these methods because otherwise the images (the data) is not carrying sufficient information about the fluence.

It would be much simpler, and would avoid all these problems, if it were possible to measure the fluence within the tissue directly. Unfortunately there are currently no modalities that can do this with the same depth and resolution as PAT. However, it may be possible indirectly to measure the fluence at the points of interest (ie. where the PAT image is non-zero). Here we suggest the use of a contrast agent whose absorption falls quickly to zero above some known fluence. In this case it may be possible to determine the fluence inside the tissue with the same resolution as a PAT image. We show how this may allow the spatially varying concentration distribution of the chromophore to be recovered.

2. Fluence Dependent Chromophores

The specific absorption coefficient of many absorbers varies, often irreversibly, with the light fluence, α = α(ϕ). For example, many organic dyes show fluence-dependent changes in their absorption due to optical saturation [14], transient formation of isomers [15], or even permanent photobleaching [16]. Gold nanorods undergo shape changes above a certain fluence level, which result in significant changes to the absorption spectrum in the near-infrared. [17, 18] Indeed, at a given wavelength, the absorption of a gold nanorod can decrease abruptly as soon as the fluence reaches a threshold related to its melting point.

The question of interest here is: are there any types of fluence dependence (any functions α(ϕ)) which would allow the concentration of the chromophore with this dependence to be recovered from photoacoustic images? The idea would be to obtain images at multiple illumination strengths and from these, and knowledge of α(ϕ), to recover the chromophore’s concentration at every point. This could be considered analogous to estimating concentration using images at multiple wavelengths due to the wavelength dependence of absorption α = α(λ), except that - as was mentioned above - such spectroscopy is not possible with PAT images without knowledge of the fluence. So what is different here? The difference is that the absorption of a fluence dependent chromophore could, indirectly, give information about the values of the fluence inside the tissue. This extra information cannot be accessed by varying the wavelength and would be sufficient to allow the concentration to be estimated.

3. Estimating Spatially Varying Chromophore Concentrations

Here, one type of fluence dependence is considered: a chromophore whose specific absorption coefficient falls rapidly to zero above some threshold fluence. The specific absorption coefficient for this ‘switching-off type of absorber can be idealized as α(x) = α₀U(ϕ_th - ϕ(x)) where U(y) is the unit step function (0 for y < 0, 1 for y ≥ 0) and α₀ is the specific absorption coefficient at fluences below the known threshold fluence ϕ_th. (Gold nanorods that undergo a rapid shape change above a certain fluence, as mentioned above, are potential candidates.) Consider an example consisting of a distribution of a chromophore with this switching property in a turbid medium with background absorption μ_a0. (It is not necessary to assume that this is spatially uniform.) Here it is shown that the chromophore concentration distribution, C(x), can be estimated using a series of PAT images generated with gradually increasing illumination strengths. (The incident light intensity is increased, in small steps, for each subsequent image.) In general, the total absorption at a point x in the tissue may be written as the combination μ_a(x) = μ_a0(x)+C(x)α(ϕ(x)) where the second term is a contribution from the fluence dependent chromophore, and C(x) is its concentration. Substituting the expression for α from above gives the absorption coefficient as

$${\mu }_a\left(x\right)={\mu }_{a0}\left(x\right)+C\left(x\right){\alpha }_{0}U\left({\varphi }_{th}-\varphi \left(x\right)\right).$$

When the fluence everywhere is below the threshold ϕ_th, the magnitude of the PAT image h(x) will increase linearly with the illumination intensity. Just before the threshold fluence is reached somewhere, the image amplitude at a point x can be written as

$$h_0\left(x\right)=\left({\mu }_{a0}\left(x\right)+C\left(x\right){\alpha }_0\right){\varphi }_0\left(x\right).$$

(Here we will assume that the absorbed energy images can be reconstructed exactly. In practice, artefacts and uncertainties will, of course, affect the accuracy with which the chromophore concentrations can be estimated.) If the illumination intensity is increased by a small factor k so that the fluence reaches the threshold in some places, then in those regions the chromophore will become non-absorbing (will ‘switch-off’).

It is helpful at this stage to divide the domain into three non-overlapping regions, A_n, B_n, and C_n, which change with each increase in fluence, such that on step n: A_n contains the points where the fluence is below the threshold and always has been, A_n = {x : ϕ_m(x) < ϕ_th for all m ≤ n} (chromophore still absorbing); B_n contains the points where the fluence exceeded the threshold for the first time on this step, B_n = {x : ϕ_m(x) < ϕ_th for all m < n - 1 and ϕ_n(x) ≥ ϕ_th} (chromophore just switched off); C_n contains the points where the fluence exceeded the threshold on some previous step, irrespective of its current value, C_n = {x : ϕ_m(x) ≥ ϕ_th for at least one m ≤ n} (chromophore switched off on a previous step). In practice there may be a delay of one step between reaching the threshold and the chromophore not absorbing, but this does not affect the argument significantly.

The image at an arbitrary step, n (the fluence has been increased n times) can now be written as

$$h_n\left(x\right)=\{\begin{array}{c}\begin{array}{cc}\left({\mu }_{a0}\left(x\right)+C\left(x\right){\alpha }_0\right){\varphi }_n\left(x\right)& \mathrm{for}x\in A_n,\end{array}\\ \begin{array}{cc}({\mu }_{a0}\left(x\right){\varphi }_n\left(x\right)& \mathrm{for}x\in B_n\mathrm{or}{C}_n.\end{array}\end{array}$$ (1)

When Cα₀, the absorption change in B_n, is small enough that the fluence at regions outside B_n will not be changed significantly by the chromophore switching off, the fluence can be approximated by

$${\varphi }_n\left(x\right)\approx \{\begin{array}{c}\begin{array}{cc}k{\varphi }_{n-1}\left(x\right)+\delta \varphi & \text{for}x\in B_n,\end{array}\\ \begin{array}{cc}k{\varphi }_{n-1}\left(x\right)& \text{elsewhere}.\end{array}\end{array}$$ (2)

In other words, within the regions A_n and C_n the fluence distribution, ϕ_n, can be approximated by scaling the previous fluence ϕ_n-1, but in region B_n, where the absorption has changed, there will also be a perturbation to the fluence. The difference between an image h_n and a scaled version of the previous image kh_n-1 can now be written as

$$k{h}_{n-1}\left(x\right)-h_n\left(x\right)\approx \{\begin{array}{c}C\begin{array}{cc}\left(x\right){\alpha }_{0}k{\varphi }_{n-1}\left(x\right)& \text{for}x\in B_n,\end{array}\\ 0\begin{array}{cc}& \text{elsewhere}.\end{array}\end{array}$$ (3)

The term μ_a0δϕ_n was disregarded because δϕ_n is small, by design, as the illumination strength is only increased slightly. (μ_a0 may also be small.) By making the approximation kϕ_n-1(x) ≈ ϕ_th, x ∈ B_n, an expression for the concentration of the chromophore in the region B_n can be obtained:

$$C\left(x\right)\approx \{\begin{array}{c}\left(k{h}_{n-1}\left(x\right)-h_n\left(x\right)\right)/\left({\alpha }_0{\varphi }_{th}\right)\begin{array}{cc}& \text{for}x\in B_n,\end{array}\\ 0\begin{array}{cc}& \text{elsewhere}.\end{array}\end{array}$$

Initially, any point x is contained in region A₀, so B₀ = C₀ = {}. As the incident illumination is increased (and assuming the optical properties take physiologically realistic values), x will go from being in A_n to B_n and eventually to C_n. In other words, region A_n will shrink, A_n = A_n-1 - B_n, and region C_n will grow, C_n = C_n-1 + B_n-1 until all x lie in C_n for some sufficiently large n. Because of this, the set B₁ ∪ B₂ ∪… will eventually contain every point in the domain once. This, and the fact that the concentration estimate above is zero outside B_n allows the chromophore concentration to be obtained everywhere by summing the estimates obtained at each step:

$$C\left(x\right)\approx \sum _n\left(k{h}_{n-1}\left(x\right)-h_n\left(x\right)\right)/\left({\alpha }_0{\varphi }_{th}\right)$$ (4)

4. Numerical Simulation

In order to investigate this method of recovering chromophore concentration, a finite element model of the diffusion approximation to the light transport equation was used to simulate the above proposal. [19] A point source was located centrally at 0.1 mm depth in a 15mm × 15mm domain (represented by a 100×100 pixel mesh), and the background scattering was set by defining the optical diffusion constant to be D = 1.5 mm. A boundary condition was imposed to ensure there was no incoming photon flux from outside the domain. The anisotropy factor was set to g = 0.9. Gaussian random noise was added to the image of absorbed energy density at 5% of the mean value. At each step the source strength was increased by 10% (k = 1.1). The amplitude of the fluence was set initially so that it was everywhere below the value of the threshold fluence ϕ_th. The background absorption coefficient was μ_a0 = 0.02 mm^-1. The nonlinear absorbers were restricted to three regions: two squares, in which the absorption coefficient (before switching off) was μ_a,sq = Cα₀ = 0.04 mm^-1, and a circle where μ_a,circ = Cα₀ = 0.02 mm^-1. In fact, for convenience and without loss of generality, α₀ was set to 0.04 (squares) and 0.02 (circle) so that the concentration distribution C(x) took values from 0 to 1 (see Fig. 2A). (Deliberately, no specific units of concentration have been indicated, to avoid the erroneous idea that these numbers somehow indicate a minimum detectable concentration. The minimum concentration that could be recovered in practice will depend on both the molar absorption coefficient of the actual contrast agent used, and the SNR, which itself will be a factor of the instrumentation.)

Fig. 2.

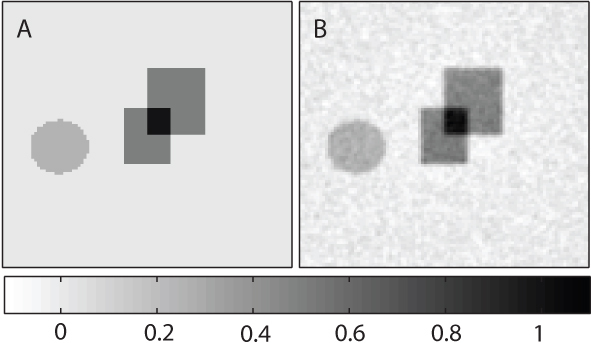
A: The true values of the concentration of the nonlinear chromophore (arranged so that they lie between 0 and 1). The image size is 15 mm × 15 mm. B: The estimate of the concentration obtained using Eq. (4).

Figure 1 shows the PAT image amplitude at points (3.75mm,3.75mm), dashed line, and (7.5 mm,7.5mm), solid line. In the former case the absorption coefficient remains the same throughout the experiment, so the image amplitude just increases by 10% at each step as k = 1.1. At the latter point - located at the centre of the domain - the nonlinear chromophore is present, and at step 22 the fluence there has reached the threshold fluence, ϕ_th, thus rendering the chromophore non-absorbing from then on. The abrupt jump in the photoacoustic image amplitude that results can be seen clearly in the solid curve of Fig. 1. As the threshold fluence is known (it is a property of the chromophore) it is features of this sort that give an indication of the fluence within the tissue.

Fig. 1.

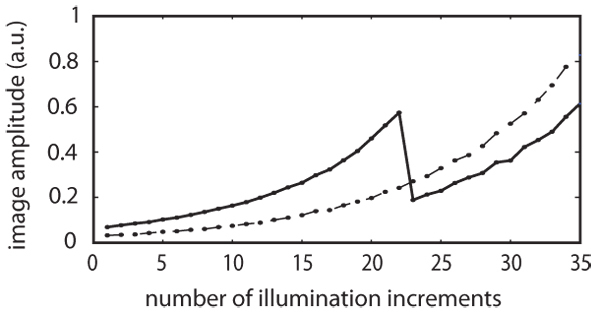
The photoacoustic image amplitude at the central point (7.5mm,7.5mm), shown by the solid line, and at the point (3.75mm,3.75mm), shown by the dotted line. In the former case, the nonlinear chromophore is present and image amplitude falls abruptly after step 22 at which the local fluence reaches the threshold value ϕ_th. At the latter point the only absorption present is due to (linear) background absorbers, so the image amplitude increases in proportion to the incident light intensity.

Figure 2A shows the true concentration of the nonlinear chromophore, and Fig. 2B is the estimate obtained using Eq. (4). Figure 3 shows a profile through both Figs. 2A (dashed line) and 2B (solid line). There is clearly good agreement between the estimated concentration and the true values. This will improve further with increases in the signal-to-noise ratio, but decrease near the edges of objects with a large value of Cα₀, as Eq. (2) becomes increasingly approximate.

Fig. 3.

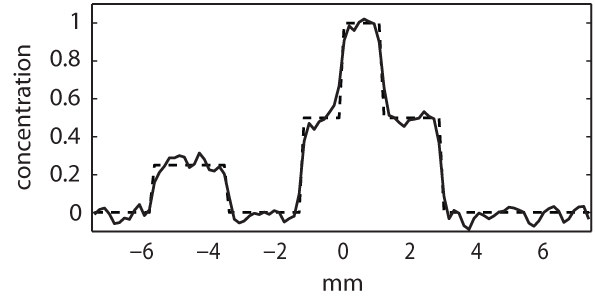
Profiles through Figs. 2A and 2B showing the true concentration (dashed line) and its estimate using Eq. (4) (solid line), showing that the concentration of a chromophore whose absorption switches off at some known fluence threshold may be estimated from multiple photoacoustic images obtained at increasing illumination strengths.

5. Discussion

5.1. Residual absorption.

The model of the contrast agent used here - one in which the absorption falls abruptly to zero at a threshold fluence - is clearly an idealisation. In practice there is likely to be a remaining residual absorption, due in part to the probabilistic nature of molecular changes. The details concerning this residual absorption, and its dependence on parameters such as the illumination duration, will depend on the mechanism by which absorption changes occur; if the absorption change is due to some kind of photochemical effect then the situation is likely to be different from when the absorption change is due to a thermal mechanism. If the residual molar absorption coefficient, α_res (which could be determined experimentally beforehand for a given pulse energy and duration) is not affected by subsequent illuminations, then it can be incorporated straightforwardly into the scheme of Section 3 by redefining the background absorption to include it: μ_a0^′(x) = μ_a0(x) + C(x)α_res and α₀ in Eq. (3) is replaced by α₀ - α_res. It is more likely, though that the residual absorption will decrease due to the light from subsequent steps, which would complicate the concentration estimation, and it would be pragmatic to look for measures to minimise the residual absorption should be taken. One way to do this might be to optimise the combination of pulse energy and illumination pulse duration.

Consider the case of a heat-induced shape change in a gold nanorod. (a) Fixed pulse energy: for any illuminating pulse whose duration is short enough that thermal diffusion is negligible then, for a fixed pulse energy, the same degree of heating will occur in the nanorods leading to the same absorption change. However, the thermal diffusion time will depend on a number of factors (the tissue type, the density of the gold nanorods within the tissue [20], whether they are clumped, any coating they are carrying [21], etc) and for a single nanorod may well be less than the laser pulse duration, in which case thermal diffusion may become important and shorter pulse durations could lead to larger absorption changes for a given pulse energy. (b) Fixed peak power: if the fluence rate is high enough to deliver enough energy to overcome thermal diffusion and cause sufficient temperature rise to cause the require shape changes, then increasing the pulse duration while keeping the peak power constant could reduce the residual absorption simply by virtue of supplying more energy. One potential drawback of a longer pulse duration is that it might result in a longer scan, and therefore an increased chance that the background absorption will change during the measurements.

5.2. Fluence dependence in real contrast agents.

In general, the molar absorption coefficient α of a contrast agent is likely to depend on the fluence in a more complicated way than has been assumed here. As a simple example: if the nanorod population had a range of sizes then there may be a transitional range of fluences from ϕ_L to ϕ_H, over which α decreases as the fluence increases, rather than the abrupt change assumed above. If the molar absorption as a function of fluence does not contain clear features (abrupt changes or changes of gradient, for instance) associated with known fluences - in the way that the cut-off was associated with the threshold fluence ϕ_th - then recovering the chromophore concentration using a variant of the approach described here becomes more difficult. Where such features are present though, it may be possible to devise a means by which to estimate the concentrations.

5.3. Fluence increment and SNR.

There is a trade-off at the heart of the method, related to the size of the fluence increment. A larger increment could result in a greater signal-to-noise ratio (SNR) in the difference image but may violate the assumption that δ_ϕ is small. Also, when the fluence level is low, in the initial steps, the SNR is likely to be worse than at later steps where the fluence is greater. The optimal increment may therefore change with the fluence level, and it may be advantageous to make larger increases in fluence at the low levels than at the higher levels later on. The multiplicative increase factor k could be adjusted at each step, and these k_n taken into account when estimating the fluence.

6. Summary

This paper has introduced the idea of using the fluence dependence of the specific absorption coefficient of a chromophore to estimate its concentration. It has been shown that the concentration of a chromophore may be recovered from photoacoustic images obtained at increasing illumination strengths if the chromophore stops absorbing above a critical fluence threshold. It is also known that an equivalent result holds for a chromophore that switches on at a fluence threshold. [22] The following general questions remain open: what characteristics must the fluence dependent specific absorption coefficient α(ϕ) have if it is to enable chromophore concentration estimation? Is it possible to recover the concentrations of two or more chromophores with different fluence dependences? These results could lead to the design of new contrast agents that would facilitate single wavelength quantitative (and thus molecular) photoacoustic imaging.