Early Afterdepolarizations and Cardiac Arrhythmias

Abstract

Early afterdepolarizations (EADs) are an important cause of lethal ventricular arrhythmias in long QT syndromes and heart failure, but the mechanisms by which EADs at the cellular scale cause arrhythmias such as polymorphic ventricular tachycardia (PVT) and Torsades de Pointes (TdP) at the tissue scale are not well-understood. Here we summarize recent progress in this area, discussing i) the ionic basis of EADs, ii) evidence that deterministic chaos underlies the irregular behavior of EADs, iii) mechanisms by which chaotic EADs synchronize in large numbers of coupled cells in tissue to overcome the source-sink mismatches, v) how this synchronization process allows EADs to initiate triggers and generate mixed focal-reentrant ventricular arrhythmias underlying PVT and TdP, and vi) therapeutic implications.

Introduction

Dramatic improvements have been made in the clinical treatment of cardiac arrhythmias over the past several decades. However, the advances have primarily involved application of engineering strategies, including devices such as implantable cardioverter defibrillators (ICDs) and catheter ablation techniques. Antiarrhythmic drug therapy has been a disappointment, following upon the sobering results of clinical trials such as CAST ¹ and SWORD ². However, only 20% of the 300,000 patients who will die suddenly each year have clinical indications for ICD implantation ³, and catheter ablation, although curative for many supraventricular arrhythmias, is not yet reliable for preventing sudden cardiac death. Thus, the need to understand cardiac arrhythmia mechanisms is greater than ever, if we are to make progress towards biologically-based therapies. A successful effort will require a multiscale approach to relate events at the protein scale, which constitute the major biological targets for drugs and genetic interventions, to the properties emerging at the cell, tissue and organism scales which cause the actual arrhythmias that kill people. Fortunately, the experimental and computational tools needed to meet this challenge are being developed rapidly.

This article summarizes recent progress along these lines for one important class of arrhythmogenic mechanisms, namely early afterdepolarizations (EADs). EADs in intact cardiac tissue were described nearly a half century ago as a form of triggered activity ⁴. Subsequently, EADs were implicated as the primary mechanism promoting arrhythmias in acquired and congenital long QT syndromes (LQTS), including Torsades des Pointes (TdP), polymorphic ventricular tachycardia (PVT) and ventricular fibrillation (VF). The strong association leaves little doubt that EADs at the myocyte level cause these arrhythmias at the myocardial tissue level. However, the mechanistic understanding remains incomplete. Five critical questions are: 1) What are the key dynamical mechanisms that cause EADs to form when repolarization reserve is reduced? 2) Since myocytes in intact tissue are well-coupled to their neighbors, how does the tendency of an individual myocyte to develop an EAD overcome the repolarizing influence of adjacent myocytes without EADs? - or, phrased differently, how do EADs develop synchronously in a critically large enough mass of coupled myocytes to overcome the local source-sink mismatch, so that an overt EAD can trigger a premature ventricular complex (PVC)? 3) If EADs are focal, what is the basis of the shifting QRS electrical axis during PVT and TdP, which implies that the foci must continuously shift their location? 4) Why have mapping experiments provided evidence suggesting with both focal and reentrant mechanisms of PVT and TdP? 5) If EADs preferentially occur during bradycardia, how do they cause triggered activity at fast heart rates?

In this article, we review recent progress towards answering these critical questions. The first two sections briefly summarize the current understanding of the ionic mechanisms of EADs and their dynamical origins, including recent evidence that the commonly observed beat-to-beat irregularity of EADs is not random, but deterministic chaos. The third section describes how the source-sink mismatch in well-coupled cardiac tissue requires a critical mass of literally thousands of myocytes to develop an EAD synchronously on the same beat, in order for an overt EAD to trigger a premature ventricular complex (PVC). The fourth section describes how the chaotic EAD behavior combined with the smoothing effect of electrotonic gap junction coupling permits normally irregular EADs to synchronize regionally, producing macroscopic “EAD islands” next to areas without EADs. The fifth section demonstrates how this synchronization mechanism produces shifting focal activations, mixed with reentry, which arise suddenly from normal or bradycardic heart rates and produce characteristic features of PVT and TdP. The sixth section compares this predicted behavior to experimental observations. The final section discusses clinical and therapeutic implications.

Ionic mechanisms of EADs

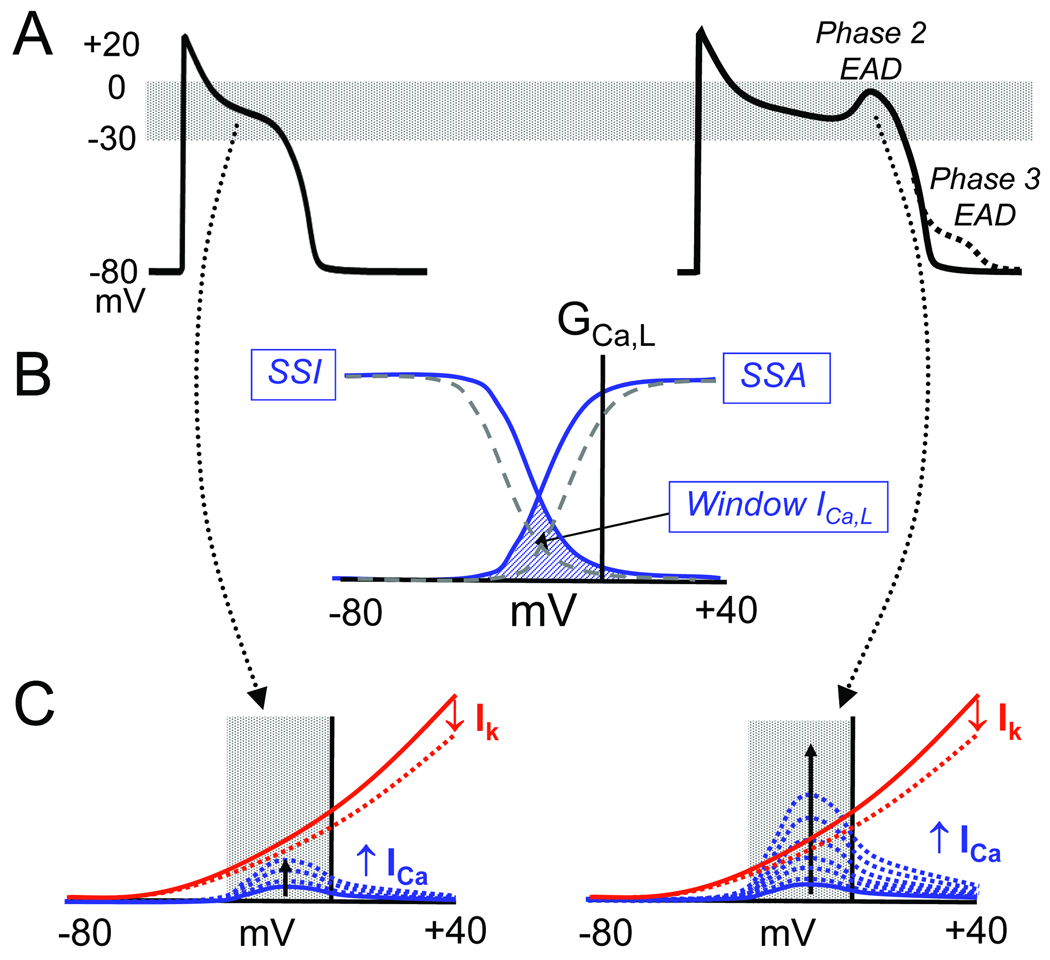
An EAD is defined as a slowing or reversal of normal repolarization during phase 2 or phase 3 of the AP, as illustrated in Fig. 1A (right trace). EADs occur in the setting of reduced repolarization reserve, which can result from a reduction in outward current, an increase in inward current, or both, such that the net outward current required to repolarize the myocyte is compromised. Under these conditions, any mechanism which regeneratively increases net inward current can potentially overcome and reverse repolarization. By regenerative, we mean a current which increases progressively as membrane voltage depolarizes, to form the EAD upstroke. In the voltage range typical for EADs, the L-type Ca current (I_Ca,L) and the Na-Ca exchange current (I_NCX) are the major currents potentially meeting this positive feedback criterion. I_Ca,L exhibits this property in its “window” region (the region of overlap between steady state activation (SSA) and inactivation (SSI), approximately −30 to 0 mV, as shown in Fig. 1B). As the AP repolarizes into the window region, I_Ca,L increases due to both the negative slope region in the I–V curve and increased driving force for Ca entry (Fig. 1C). If the K conductance, which during the early plateau is much lower than the resting K conductance ⁵, gathers force too slowly when the voltage enters the window voltage range, the time- and voltage-dependent recovery from inactivation can allow I_Ca,L to self-amplify sufficiently to reverse repolarization, generating the EAD upstroke (Fig. 1C). Countervailing factors are also present, however: as membrane potential depolarizes during the EAD, I_Ca,L inactivates, and time-dependent outward currents such as I_Kr and I_Ks are further activated. If the outward currents predominate, the EAD is followed by eventual repolarization back to the resting membrane potential. However, if I_Ca,L predominates, repolarization can be altogether aborted, producing a I_Ca,L-mediated AP upstroke that can result in a triggered beat, or a run of triggered beats.

Fig. 1.

A. Normal AP (left) and an AP with a phase 2 EAD (solid) or phase 3 (dashed) EAD (right). B. A schematic plot of L-type Ca channel conductance (G_Ca,L) vs membrane voltage (mV) showing the window I_Ca,L region (cross-hatched) where the steady state activation (SSA) and steady state inactivation (SSI) curves overlap and a fraction of Ca channels remain continuously open. Dashed lines show a potential therapeutic intervention that shifts the SSA and SSI curves to reduce the overlapping window current region. C. Schematic diagram illustrating the interaction between time-dependent I_Ca,L reactivation (blue dashed lines) and time-dependent deactivation of repolarizing currents (I_K) (dashed red lines) in the window voltage range during AP repolarization. For the normal AP (left), repolarization rate is too fast for I_Ca,L to grow larger than I_K. If repolarization rate is too slow, however, I_Ca,L can grow larger than I_K,, thereby reversing repolarization to cause an EAD.

The second major current that facilitates EAD formation is I_NCX. The cardiac Na-Ca exchanger exchanges 3 Na ions for 1 Ca ion, producing an inward current (forward mode I_NCX) when extruding Ca from the cytoplasm. While intracellular Ca (Ca_i) is still elevated during repolarization, I_NCX becomes larger as membrane potential repolarizes, thereby resisting repolarization. Although I_NCX opposes repolarization, it cannot by itself reverse repolarization unless Ca_i increases further (since at constant Ca and Na concentrations, inward I_NCX becomes smaller with depolarization). However, as the window I_Ca,L regeneratively increases during the initial phase of the EAD, it triggers additional Ca release from the sarcoplasmic reticulum (SR). Thus, as I_Ca,L increases, I_NCX synergistically increases, facilitating EAD formation and increasing the probability of an EAD-triggered AP.

In the scenario described above, the EAD is primarily driven by I_Ca,L reactivation, with I_NCX playing a secondary facilitating role. In principle, the converse can also occur, with I_NCX playing the primary role and I_Ca,L the secondary role. If spontaneous (i.e. non I_Ca,L-gated) Ca-induced Ca release from the SR occurs before repolarization is complete, the consequent stimulation of inward I_NCX (assuming that it dominates over increased Ca-induced inactivation of I_Ca,L) may oppose and reverse repolarization. The delay in repolarization allows more time for I_Ca,L to recover from inactivation and reactivate, secondarily facilitating the EAD upstroke. Evidence supporting both EAD mechanisms has been presented ^{6, 7}. Spontaneous SR Ca release during late diastole can also promote EADs indirectly, by affecting subsequent I_Ca,L inactivation and other Ca-sensitive currents during the subsequent AP (i.e. DADs begetting EADs) ^8–11.

An important caveat is that I_Ca,L and I_NCX are such highly interactive currents that it is generally fruitless to debate whether one or the other causes EADs. The correct viewpoint is that these two currents act synergistically to generate EADs, with their relative contributions varying under specific conditions. Thus, targeting either current alone may suffice to prevent EADs by suppressing their synergy. In general, due its voltage dependence, I_NCX makes an increasingly important contribution as the EAD take-off potential becomes more negative, potentiating inward I_NCX. Suppressing either current may be sufficient to suppress EADs,

Whether the slowing of repolarization during the initiation of an EAD is mediated primarily by I_Ca,L reactivation or by I_NCX, the ability of an EAD to generate a PVC which propagates into adjacent repolarized tissue generally depends on a regenerative AP upstroke mediated by I_Ca,L. In a form of congenital LQTS in which a Na channel mutation shifts the I_Na window current in a depolarized direction, I_Na can also contribute to EAD formation ¹², in concert with I_Ca,L and I_NCX.

Classically, EADs emerge during bradycardia. Repolarization reserve is reduced during bradycardia, since time-dependent K currents such as I_Ks enter more deeply closed states, from which subsequent activation requires more time ¹³. However, any combination of altered currents which reduce repolarization reserve sufficiently can promote EADs, whether the heart rate is slow or fast ¹⁴. For example, in certain congenital LQTS, arrhythmias tend to be exercise-induced, due the failure of sympathetic stimulation to increase I_Ks appropriately to compensate for the APD prolonging effect of enhanced I_Ca,L ^{15, 16}.

Finally, it is important to note that reduced repolarization reserve by itself is not sufficient to cause an EAD. The critical factor is whether the voltage during the AP plateau lingers for a sufficiently long time in the range permitting regenerative reactivation of inward currents. That is, the AP plateau voltage must linger below 0 mV. This explains why EADs are often associated with AP triangulation if the dwell time <0 mV before full repolarization is prolonged^{17, 18}. In contrast, AP prolongation per se is much less prone to cause EADs if the plateau voltage remains >0 mV, as long as full repolarization, when it occurs, is remains rapid..

Chaos and EADs

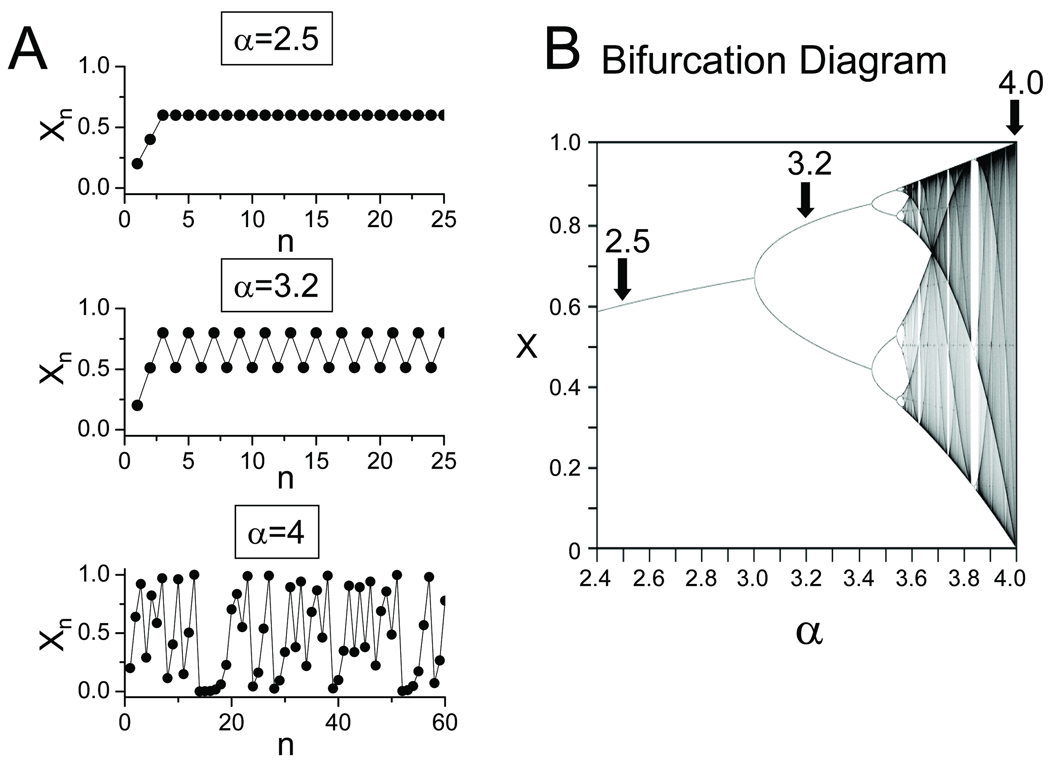
Dynamically, deterministic chaos refers to complex irregular behavior, without a discernibly repeating pattern, which is not due to randomness, but rather results from the inherent dynamics of the system¹⁹ Chaos is a type of behavior that even simple nonlinear systems can develop when the system’s parameters fall in a certain range. One of the simplest examples is the equation for a parabola, also called the logistic equation:

$$x_{n+1}=\alpha ·x_n(1-x_n)$$ (Eq.1)

If this equation is iterated (i.e. assign an initial value to x₀ between 0 and 1, and then use Eq.1 to calculate the next value x₁ from x₀, and then x₂ from x₁, and so forth), the qualitative outcome depends strongly on the value of α. As α increases, the plot of x_n vs n undergoes a series of dramatic qualitative changes in appearance, known as bifurcations in nonlinear dynamics terminology (a period-doubling bifurcation in this case) (Fig. 2A). For most values of α >3.57, successive values of x_n become completely irregular (i.e. chaotic), with no repeating sequences (Fig. 2B). Moreover, the precise pattern (trajectory) is very sensitive to initial conditions, such that very small perturbations to the intitial conditions rapidly cause the system’s behavior (also called its trajectory) to diverge from the unperturbed trajectory. Sensitivity to initial conditions is sometimes called the “butterfly effect”, based on nonlinear atmospheric models predicting that the tiny atmospheric disturbance of a butterfly flapping its wings can result in a completely different weather pattern (e.g. a hurricane that otherwise would not have occurred).

Fig. 2.

Dynamical chaos in the logistic equation. A. Iteration of the logistic equation (Eq.1 in text) produces different behaviors (periodic, alternating, chaotic) depending on the value of α. B. Bifurcation diagram showing the steady state behavior as a function of α.

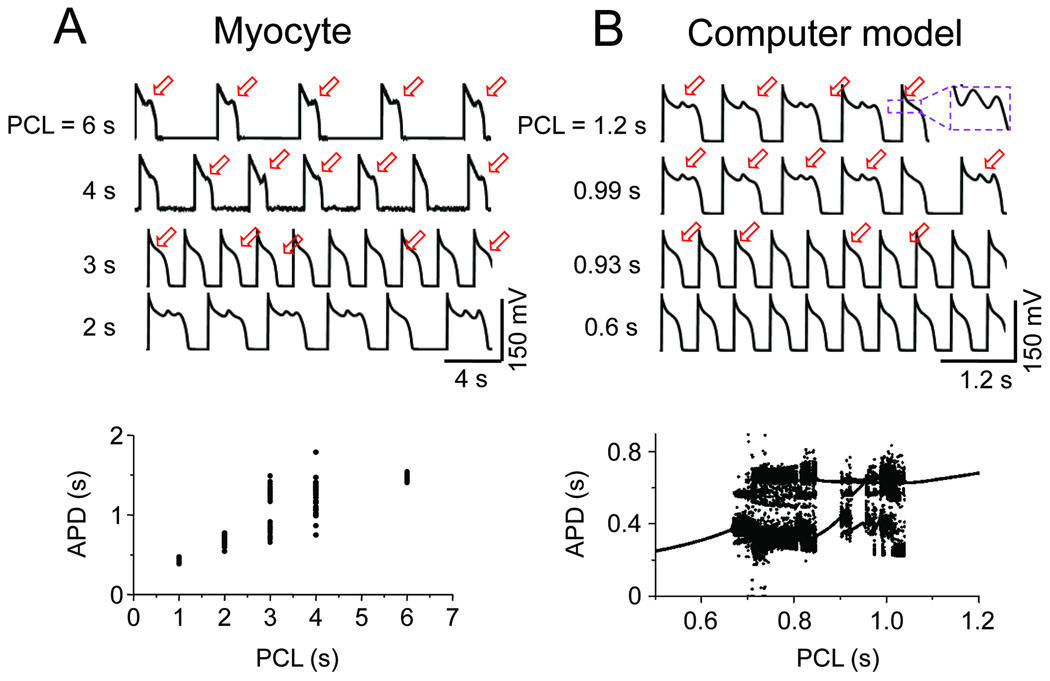
As mentioned above, EADs recorded from isolated myocytes and intact tissue are often irregular, occurring on some beats, but not others ^{20, 21}. In studying EADs induced in isolated rabbit ventricular myocytes by oxidative stress (H₂O₂), BayK8644 or hypokalemia ^{22, 23}, we noted that this irregularity is dependent on heart rate, such that EADs occur on every AP at slow heart rates, irregularly at intermediate rates, and were completely suppressed at faster heart rates (Fig. 3A). Traditionally, the irregularity of EADs has been attributed to random factors, such as stochastic behavior of L-type Ca channels ²⁴. However, the observation that EADs are irregular only over a limited range of heart rates led us to wonder whether the irregularity might be due to dynamical chaos, rather than randomness.

Fig. 3.

A. Rate-dependence of irregular EAD behavior in a patch-clamped rabbit ventricular myocyte. EADs occur on every AP at a pacing cycle length (PCL) of 6s, and are suppressed at PCL 2s, but occur irregularly in between, as illustrated by the variation in APD in the graph below). B. Analogous behavior in a rabbit ventricular AP model with no randomness, indicating that the irregularity is due to dynamical chaos.

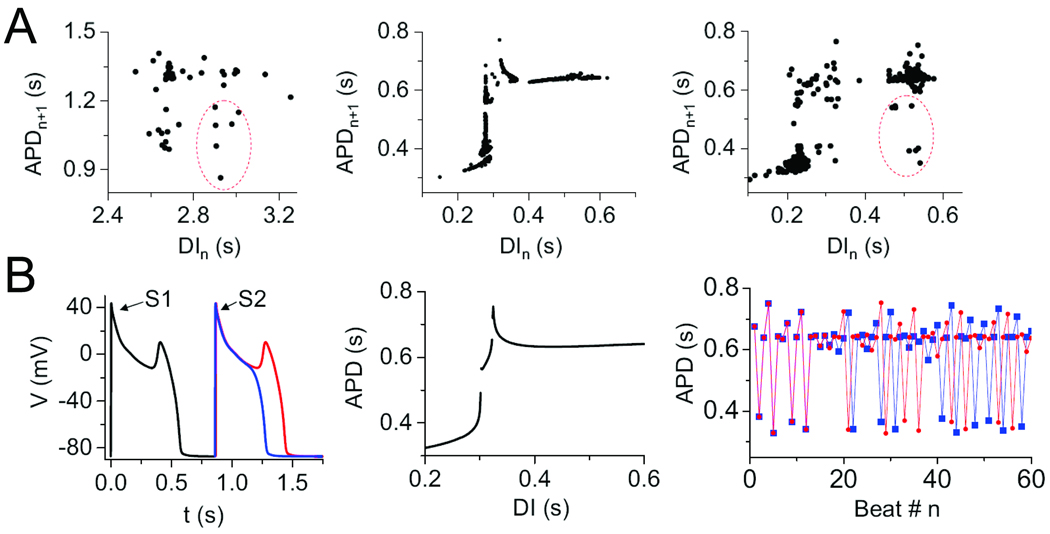
To examine this possibility, we investigated whether the irregularity of EADs could be reproduced in a deterministic computer model of the rabbit ventricular AP, in which no randomness is present. Indeed, this model reproduced that experimental findings demonstrating that irregular EADs occur only in a window of heart rates, with faster heart rates suppressing EADs completely, and slower heart rates producing EADs with every AP (Fig. 3B). The mechanism of chaos is related to the sensitive dependence of EADs on the preceding diastolic interval (DI), as illustrated in APD restitution curves (APD vs DI) shown in Fig. 4A. In both the experimental data and computer model, APD suddenly prolonged due to the occurrence of EADs as the DI lengthened. The formal nonlinear dynamics analysis in the simpler Luo-Rudy 1 AP model (Fig. 4B) revealed that, similar to bursting behavior in neurons ^{25, 26}, chaos arose from a combination of bifurcations: first, a Hopf bifurcation, which is the typical cause for the onset of oscillations in a dynamical system (in this case the voltage oscillations during the EAD); and second, a homoclinic bifurcation, which destroys the stability of the voltage oscillation to induce full repolarization ²⁷. The detailed cardiac AP model is more complex, but contains the same basic elements required to generate the chaotic EAD behavior shown in Fig. 3B, even though additional dynamical mechanisms, e.g. related to SR Ca cycling, may also come into play.

Fig. 4.

Mechanism of EAD chaos. A. During irregular EAD behavior shown in Fig. 3, the APD restitution curve shows a very steep region, indicating a sensitive dependence of APD on DI, for both the real myocyte (left panel) and the rabbit AP model (middle and right panels). The circled points in the real myocyte data were reproduced in the AP model by adding a small amount of random noise (right panel). B. AP traces in a simplified 3-variable AP model illustrating the sensitive dependence of EAD formation on the DI of a premature S2 beat (left). The full APD restitution curve (middle), when iterated, produces the irregular APD variation (right), which exhibits sensitive dependence on initial conditions for a slight difference in the initial DI (blue vs red trace). From ²² with permission

Both cardiac AP models are much more complex than the logistic equation with its single parameter α determining the type of behavior. However, as heart rate is slowed in the AP models, critical parameters analogous to α also change, producing a series of bifurcations from no EADs to irregular EADs to EADs on every beat (compare Fig. 2B and 3B).

The source-sink mismatch in well-coupled cardiac tissue

If a myocyte in well-coupled tissue is primed to develop an EAD, then as soon as its AP repolarization rate begins to slow, electrotonic current will flow into the EAD-generating myocyte through gap junctions from neighboring normally-repolarizing myocytes, in proportion to the voltage difference. If the majority of the neighbors are not predisposed to having an EAD on the same beat, the majority will prevail, forcing the EAD-susceptible myocyte to repolarize along with its unsusceptible neighbors. In other words, a source-sink mismatch is present, such that the depolarizing EAD current from the susceptible myocyte is diluted into too many unsusceptible neighbors to cause a significant delay, much less reversal, of repolarization of the myocyte group. This concept applies generally to any depolarizing current source in coupled tissue, including DADs and external stimulating current, as described originally in the “liminal length” concept ²⁸.

Since the typical ventricular myocyte (the source) is coupled to 11 neighboring myocytes (the sink) ^{29, 30}, the source-sink mismatch is a powerful mechanism preventing an occasional cell predisposed to an EAD from triggering a PVC in tissue. When we performed computer simulations to estimate how many contiguous EAD-generating myocytes are required to generate a PVC that propagates into surrounding non-EAD-generating tissue, the numbers were 70 for a 1D cable, 6,940 for 2D tissue and 696,910 for 3D tissue ³¹. The latter estimate for 3D tissue agrees with experimental data for the number of pacemaker cells required to generate a biological pacemaker ³². Reduced repolarization reserve in the non-EAD-generating tissue, reduced gap junction conductance, and fibrosis significantly decreased these numbers (to as low as 20 contiguous myocytes for a 1D cable, and 40 contiguous myocytes for fibrosed 2D tissue) ³¹. However, the numbers remain large, indicating that the source-sink mismatch in intact tissue is a powerful mechanism preventing unsynchronized EADs from triggering PVCs. For example, if the probability that an individual myocyte will have an EAD is 0.5, then the group probability that 20 contiguous myocytes will all have an EAD on the same beat is (0.5)²⁰=0.000000001. For the group probability to reach 0.5 requires an individual EAD probability of 0.97. Note that the number of contiguous myocytes with EADs required to trigger a PVC increases exponentially with tissue dimension. This may account for the greater EAD susceptibility of the His-Purkinje system (a network of quasi-1D cables) compared to working 3D myocardium, irrespective of the differential susceptibility to EADs of the uncoupled cell types. The important point is that in an isolated myocyte, endogenous membrane currents alone determine whether an EAD occurs or not. In tissue, however, the EAD threshold is set by the sum of endogenous and exogenous currents. For example, adding an externally-applied during an otherwise normally-repolarizing AP plateau is a well-established method to induce EADs ⁴.

EAD synchronization

What factors, then, might cause hundreds or thousands of myocytes to synchronously develop an EAD on the same beat? One obvious possibility is tissue heterogeneity, for example, if the cells in a region larger than the critical size, such as an island of midmyocardial (M) cells ³³, all developed EADs at some critically slow heart rate. In this case, once this critical heart rate was reached, EADs would arise synchronously from this region, and successfully propagate into the surrounding tissue. If the triggered activity persisted, this could result in a focal VT. If the focal VT was rapid enough to cause wavebreak and initiation of a meandering rotor, then PVT or TdP might result ³⁴. Breakup of the meandering rotor could subsequently result in VF. This scenario seems generally plausible in the real hearts, since transmural and base-to-apex electrophysiological heterogeneity are present and exacerbated by heart disease ³⁵. On the other hand, as discussed above, EADs tend to occur irregularly and unpredictably on any given beat ^{20, 21}, reducing the probability that all the cells in a given region will develop an EAD simultaneously on the same beat.

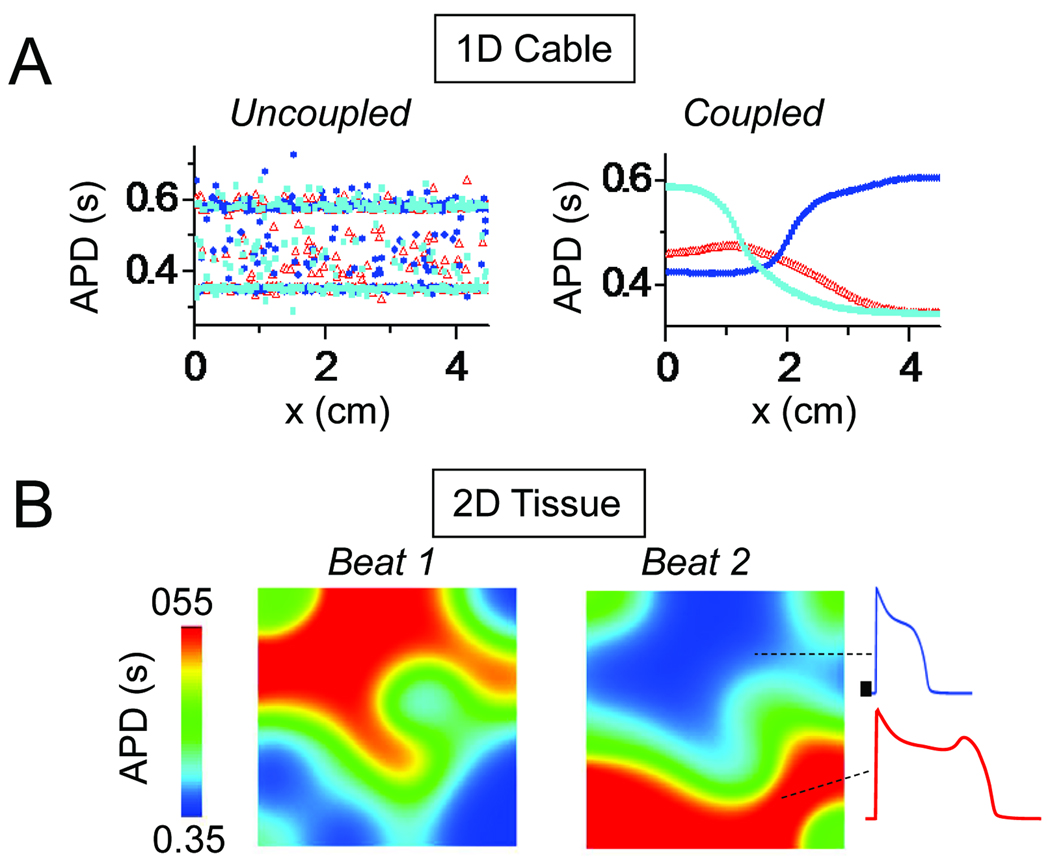
To investigate this issue, we performed simulations of chaotically irregular EADs in coupled tissue. When EADs are chaotic, sensitivity to initial conditions guarantees that small differences in the AP variables will be rapidly amplified. Thus, if slightly different initial conditions are present in 100 otherwise identical cells placed in a line, and the uncoupled cells are paced synchronously at a heart rate generating chaotic EAD behavior, the pattern of EADs (measured by recording the APD) varies wildly from cell-to-cell along the line (Fig. 5A, left). However, if the cells are coupled together by gap junctions, the dispersive force of chaos driving each cell to have a different APD is opposed by the smoothing effect of electrotonic coupling, which minimizes APD differences between adjacent cells. (That is, large differences in membrane voltage during repolarization cause electrotonic current to flow that shortens the long APD and lengthens the short APD, forcing adjacent cells to pick a similar intermediate APD).

Fig. 5.

Synchronization of chaotic EADs. A. In a simulated 1D array of myocytes exhibiting chaotically irregular EADs, slight differences in initial conditions lead to a completely asynchronous and irregular pattern of APD distribution on each beat if the myocytes are uncoupled (left). When myocytes are coupled by gap junctions, however, electronic current flow prevents marked APD differences between adjacent myocytes, creating smooth a APD gradient over the length of the cable, which differs on each beat. B. Same for 2D tissue (4.5×4.5 cm), showing the formation of EAD islands (red) separated by regions without EADs, which vary dramatically from beat-to-beat. From ²² with permission.

The result of this “tug-of-war” between the dispersive force of chaos and the convergent forces of electrotonic coupling is a compromise: a critical length scale emerges, over which the EADs are synchronized, and beyond which they are not. If the 1D cable is shorter than this critical length, then the convergent forces of electrotonic coupling dominate, and the chaotic behavior of EADs becomes spatially synchronized throughout the cable. If this critical length is exceeded, however, the gap junction coupling cannot enforce complete synchronization, and synchronization becomes partial, with APD between adjacent cells changing slowly along the cable (Fig. 5A, right panel). Thus, regions with EADs develop next to regions without EADs, with a different spatiotemporal pattern on each beat.

The spatial profiles of these EAD regions display the characteristic length scale, determined by the the strength of the electrotonic gap junction coupling versus the “wildness” of the chaos, measured by its Lyapunov exponent (i.e. the exponential power by which a small perturbation causes the system’s behavior to diverge or converge, with an absolute value >1 indicating exponential divergence, and <1 indicating exponential convergence). If coupling between cells is decreased, then the critical length decreases, and the spatial scale of regional synchronization also contracts. Similarly, if the Lyapunov exponent of the chaos increases, the spatial scale for the same coupling strength also contracts.

In 2D or 3D tissue, the interaction between chaos and coupling creates “islands” of APs with EADs next to regions without EADs, which shift location dramatically on a beat-to-beat basis (Fig. 5B), markedly increasing tissue APD dispersion. Moreover, if the APD gradients caused by these EAD islands become steep enough, conduction block can lead to initiation of reentry and multiple wavelet fibrillation.

The tug-of-war between the dispersive force of chaos versus the convergent force of electrotonic coupling thus provides a novel answer to the question of how large enough regions of tissue synchronously develop EADs, next to regions without EADs, which is the prerequisite for overt EADs to trigger propagating APs. A key feature in Fig. 5 is that for normal AP cell parameters in well-coupled tissue, the characteristic length scale over which overt EADs become quasi-synchronized is in the centimeter range (with 1 cm corresponding to 50–100 myocytes end-to-end). This is a sufficient length to overcome the source-sink mismatch for an overt EAD to become manifest, trigger an AP and propagate. Equally important, the process of regional EAD synchronization naturally produces both falling and rising APD gradients. Thus, as an impulse propagates into adjacent regions with lengthening APD due to a regional EAD, conduction block may occur if the APD gradient is sufficiently steep.

In summary, the simulations in Fig. 5 demonstrate that during steady pacing in the range of heart rates in which EADs are chaotic, chaos synchronization can create steep enough APD gradients to cause localized conduction block leading to abrupt initiation of reentry from a slow heart rate. In this simulation, the 2D tissue was completely homogeneous, except for tiny differences in initial conditions of each cell. If tissue is heterogeneous, then APD gradients develop even more rapidly, due to the sensitivity to initial conditions.

PVT and TdP due to regional synchronization of EADs

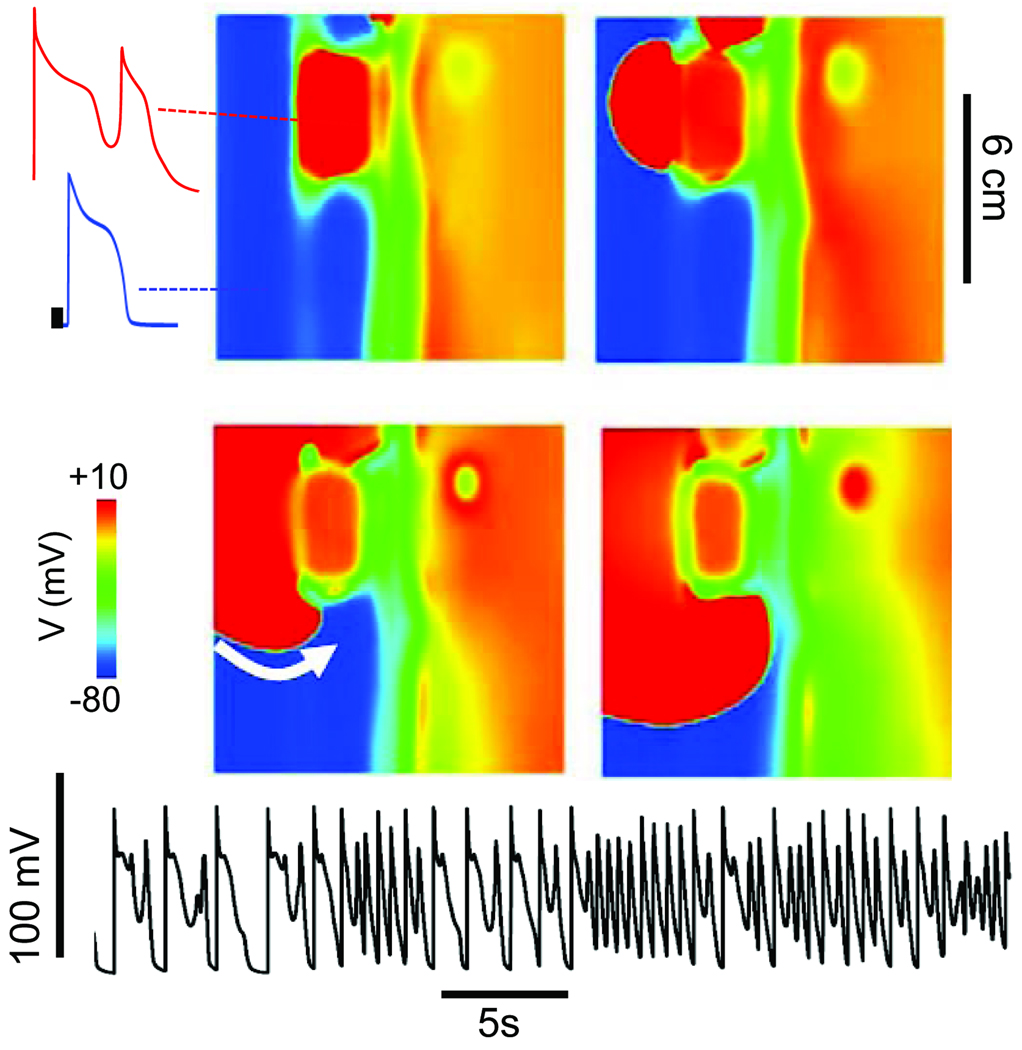
Fig. 6A (see also online movie) illustrates how synchronization of chaotic EADs can trigger APs that propagate into surrounding tissue and induce reentry, simultaneously generating both the triggers and electrophysiological dispersion required for reentry. As EAD-triggered APs conduct into adjoining regions without overt EADs, they induce new EADs, which again trigger propagating APs, in a reciprocating fashion, resulting in a multi-focal self-sustaining arrhythmia. The site of origin of these focal EAD-triggered APs shifts continuously in the tissue. The result is a multi-focal arrhythmia resembling PVT or TdP, as the shifting locations of the foci constantly alter the electrical QRS axis. In addition, after EAD-triggered APs propagate successfully through adjoining regions with shorter APD, they encounter adjacent islands with lengthening APD. If the APD gradients are steep enough, localized conduction block can lead to initiation of reentry. Thus, the characteristic activation pattern is a mixture of focal activity and reentry. Electrocardiographically, the multiple shifting foci produce an arrhythmia resembling PVT or TdP, degenerating to VF when reentry dominates. The same features were observed when a simulation using the AP+EAD cell model was performed in an anatomically realistic ventricles model (Fig. 7A).

Fig. 6.

Mixed focal-reentrant PVT as a result of EAD-mediated PVCs arising from EAD islands in simulated 2D homogeneous tissue. The tissue was paced from the left edge at a slow rate. Four successive voltage snapshots show an EAD (upper left quadrant) that generates a PVC (red trace). The PVC then initiates reentry by reentering (white arrow) the receding waveback of the region without EADs (blue trace). The voltage trace below from a representative cell shows multiple EADs followed by a rapid tachycardia due to a mixture of triggered activity and reentry.

Fig. 7.

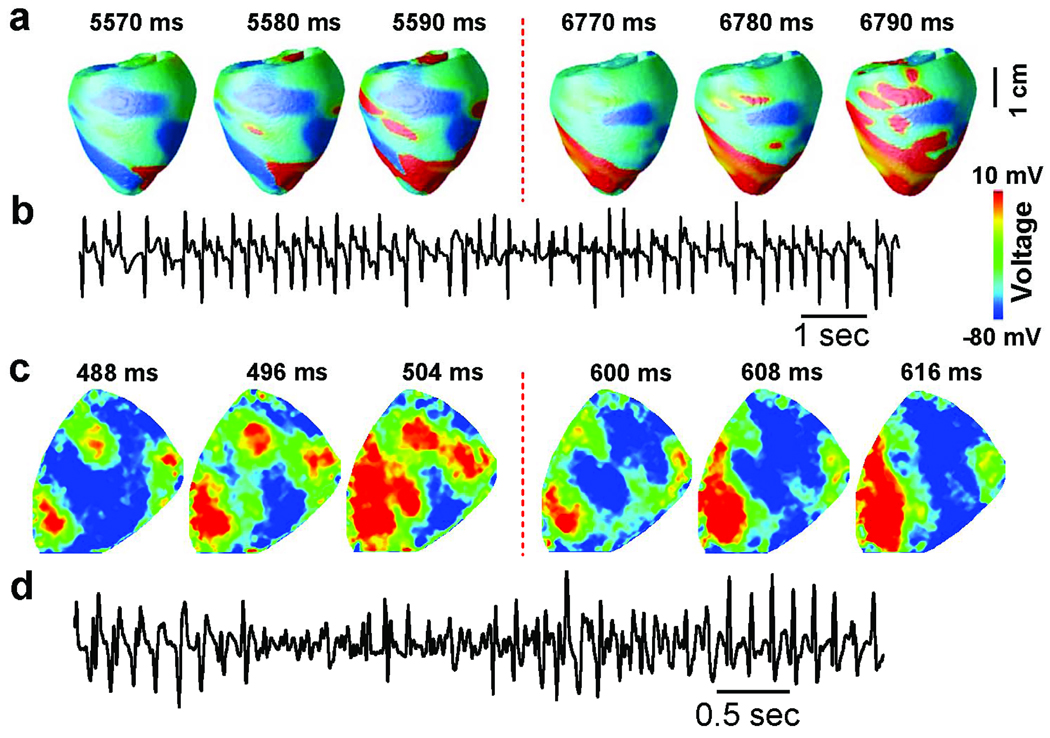
Mixed focal-reentrant PVT due to synchronization of chaotic EADs. A. Simulations in a anatomic rabbit ventricles model. First 3 panels show voltage snapshots of focal activations (red) emerging from 3 discrete sites, which have changed location at the later time (4^th–6^th panels). B. Similar shifting focal activations observed in an optically-mapped Langendorff rabbit heart exposed to H₂O₂ to induce EADs (blue-green-yellow red color scale indicates most repolarized to most derepolarized). Electrocardiographic traces below show PVT. From ²² with permission.

Comparison with experimental arrhythmia mapping studies

Both TdP and PVT are characterized by a shifting electrocardiographic QRS axis. Experimentally, TdP can be produced by pacing the ventricle at two separate sites at different pacing rates, so that the mass of ventricular tissue captured by the two sites fluctuates as they shift in and out of phase ³⁶. Alternatively, a nonstationary reentrant rotor which meanders rapidly over the surface of the ventricle can also produce a shifting electrical axis characteristic of TdP and PVT ³⁴. Mapping studies of pharmacologically-induced long QT syndromes causing TdP and PVT have provided evidence for both shifting foci and reentry. For example, Asano et al ³⁷ described a variable mixture multiple foci and meandering reentry during TdP when Langendorff rabbit ventricles exposed to either low K and quinidine, or to the I_Kr blocker E4031, to induce EADs. Choi and Salama ⁷ also described multiple foci which shifted in location during TdP in rabbit ventricles exposed to E4031 to induce EADs, which persisted when the endocardium was cryoablated. Since H₂O₂ caused EADs in isolated rabbit myocytes (Fig. 2), we tested the effects in Langendorff rabbit ventricles. Fig. 7B shows optical mapping results from a rabbit ventricle exposed to H₂O₂, which induced EADs and PVT. Similar patterns of multiple shifting foci during PVT were observed as in the anatomical ventricles simulation (Fig. 7A).

Summary, clinical relevance and therapeutic implications

The potential significance of chaotic EAD behavior in answering the questions posed in the introduction can be summarized as follows: 1) the tug-of-war between divergent force of chaos driving irregular EADs and the convergent force of electrotonic coupling via gap junctions provides a natural synchronization mechanism to explain how EAD-generating cells overcome local source-sink mismatches in well-coupled tissue and thereby avoid electrotonic suppression by non-EAD-generating cells; 2) synchronization of chaotic EADs amplifies APD dispersion, creating macroscopic “EAD islands” juxtaposed next to regions without EADs, producing a substrate highly vulnerable to conduction block and reentry; 3) when an EAD is robust enough to trigger an AP arising from an EAD island, the AP propagates into adjacent regions without EADs (i.e. down the APD gradient), producing a focal activation pattern; 4) propagation of an EAD-triggered AP into adjacent regions can then induce subsequent EADs in those regions, which then trigger new propagated AP’s, etc. These reciprocating EAD-triggered APs produce an arrhythmia characterized by shifting focal activations, resembling PVT or TdP; 6) regional APD gradients also lead to localized conduction block and initiation of reentry, accounting for the mixture of focal activations and reentry observed with optical mapping in experimental models of EAD-induced TdP and PVT.

A striking feature of chaos synchronization of EADs is that this self-organizing mechanism simultaneously creates both the triggers and the substrate for lethal arrhythmias such as PVT and TdP. Both can be generated purely by the dynamics of the system, since they arise even when the simulated tissue is completely homogeneous, although they develop more rapidly in heterogeneous tissue. The resulting trigger-substrate combination surreptitiously self-organizes in the tissue while the heart is beating at a slow or normal rate, until a triggered AP abruptly emerges to initiate a potentially lethal ventricular arrhythmia. In ambulatory electrocardiographic recordings in which the onset of VT/VF has been captured, most arise from a normal or bradycardic rhythm. It is interesting that in the acquired and congenital long QT syndromes, programmed electrical stimulation (PES) is usually ineffective at inducing PVT or TdP. This is not unexpected if synchronization of chaotic EADs is the underlying mechanism - under typical PES conditions, the heart has not been pre-conditioned at a proper heart rate in which chaos has caused large macroscopic APD gradients to develop. Therefore, the premature extrastimulus does not encounter a sufficiently heterogeneous tissue substrate to induce reentry.

Despite the appealing explanation of many features of EAD-mediated arrhythmias by this synchronization mechanism, its importance to PVT and TdP in LQT syndromes relative to other potential mechanisms remains to be established. Intrinsic tissue heterogeneity accelerates and amplifies the electrophysiological dispersion arising from synchronization of chaotic EADs, but may also be sufficient to cause EAD-related arrhythmias in the absence of chaos. For example, some studies ³³ have reported midmyocardial M cells as being arranged in islands, rather than as a continuous layer insulating the epicardial and endocardial layers. M cells are also more prone to EADs than endocardial or epicardial cells. If an island of M cells all generated EADs at a critical heart rate, they would have sufficient mass to overcome the source-sink mismatch and propagate into adjacent repolarized tissue. Since M cell islands are anatomically-based, it is not clear why this would produce a pattern of shifting foci, unless multiple EAD islands were generated and participated in a revolving sequence. Nevertheless, inherent transmural APD gradients might be sufficient to cause conduction block and initiation of meandering reentrant rotors producing TdP, PVT and/or VF. Increased electrical heterogeneity is well-documented in genetic and drug-induced long QT syndromes, and is enhanced in acquired heart disease by electrical, structural and neural remodeling. How these changes interact dynamically with chaotic AP behavior will be a rich area for further study.

It has been pointed out that electrical remodeling in the failing heart has many of the signatures of acquired long QT syndrome ³⁸. Especially in non-ischemic cardiomyopathy, PES has a low incidence of inducing sustained arrhythmias, as would be predicted if synchronization of chaotic EADs were responsible. Although the observations described above have focused on ventricular arrhythmias, EADs and triggered activity have also been implicated in atrial arrhythmias including atrial fibrillation ³⁹. The same synchronization principles are likely to apply in atrial tissue as well.

Finally, if the synchronization of chaotic EADs is clinically important in EAD-mediated arrhythmias, how can we use this information therapeutically? Given the critical role of window I_Ca,L currents in EAD formation, a therapeutic strategy based on suppression of window I_Ca,L currents may have promise as a pharmacologic or genetic strategy to reduce SCD. For example shifting the steady state activation and inactivation curves by 5–10 mV to minimize overlap in the window voltage range (dashed lines, Fig. 1B), or slowing the kinetics of I_Ca,L recovery from inactivation, might be effective at suppressing EAD formation without significantly altering APD or normal excitation-contraction coupling. Since its synergy with I_Ca,L is also critical for EAD formation, I_NCX is also a potential therapeutic target, if it can be altered without disrupting normal Ca cycling.

Abbreviations

EAD

early afterdepolarization

DAD

delayed afterdepolarization

ICD

implantable cardioverter-defibrillator

LQTS

long QT syndrome

PVC

premature ventricular complex

VF

ventricular fibrillation

PVT

polymorphic ventricular tachycardia

SCD

sudden cardiac death

TdP

Torsades de Pointes