Abstract
Many research institutions have a full suite of preclinical tomographic scanners to answer biomedical questions in vivo. Routine multi-modality imaging requires robust registration of images generated by various tomographs. We have implemented a hardware registration method for preclinical imaging that is similar to that used in the combined positron emission tomography (PET)/computed tomography (CT) scanners in the clinic. We designed an imaging chamber which can be rigidly and reproducibly mounted on separate microPET and microCT scanners. We have also designed a three-dimensional grid phantom with 1288 lines that is used to generate the spatial transformation matrix from software registration using a 15-parameter perspective model. The imaging chamber works in combination with the registration phantom synergistically to achieve the image registration goal. We verified that the average registration error between two imaging modalities is 0.335 mm using an in vivo mouse bone scan. This paper also estimates the impact of image misalignment on PET quantitation using attenuation corrections generated from misregistered images. Our technique is expected to produce PET quantitation errors of less than 5%. The methods presented are robust and appropriate for routine use in high throughput animal imaging facilities.
1. Introduction
Image registration is essential for the interpretation of studies in multi-modality imaging. Molecular images are typically visualized with co-registered anatomical images for improved localization of the molecular signal. This is especially true as molecular probes become more specific in targeting, such as with engineered antibody fragments (Kenanova et al 2005) and reporter gene technologies (Ray et al 2003). Often the anatomical images are also used to improve the quantitation of molecular images, with physical corrections for attenuation and scatter in nuclear imaging (Zaidi and Hasegawa 2003, Chow et al 2005). The quantitative accuracy of the corrected image is thus critically dependent upon the accuracy of the image registration.
A number of sophisticated software techniques to register sets of related intra- and inter-modality images have been developed (Hill et al 2001). However, with the recent introduction of the combined positron emission tomography (PET)/computed tomography (CT) scanners in the clinical environment, hardware registration techniques are being explored (Townsend et al 2004). Here, the patient remains on the same bed for sequential PET and CT scans. As long as the patient does not change position, a predetermined spatial transformation matrix can be applied to the patient data.
This hardware method of registering images has quickly spread into the preclinical arena in both integrated systems (such as in Gamma Medica-Ideas, Inc.’s FLEX™ system combining single-photon emission computed tomography—SPECT, PET and CT) and separate stand-alone systems (combining small animal PET with CT) (Chow et al 2002, Jan et al 2005). The main advantage of a hardware method of registration for preclinical imaging is due to the small subject size. It is easy to transport a 30 g anaesthetized mouse and its bed from one scanner to another. An additional benefit of the hardware method is that registration becomes completely independent of the molecular imaging probe. For example, there are probes for which even a rudimentary manual registration is not possible (Sundaresan et al 2003). Robust hardware registration is also valuable in high throughput imaging facilities where multi-modality imaging is common, saving numerous staff hours performing software or manual alignment.
Determining which image registration technique is best suited for a specific task requires a performance measure. Several techniques for determining the registration accuracy have been described: from visual inspection (Maintz et al 2001), to calculating the average fiducial or target registration error (Lavely et al 2004), to calculating relative entropy from information theory (Kim et al 2005).
Jan et al (2005) described their implementation of the hardware registration for a small animal PET scanner with a combined SPECT/CT scanner. A common mouse holder was described that is positioned manually using alignment markers and a bubble level. The spatial transformation matrix was derived from a scan of a calibration phantom with three line sources. The primary source of registration error was from manual alignment of the holder.
We have implemented the hardware method of image registration at our institution. We designed a mouse-sized imaging chamber that can be rigidly and reproducibly mounted on both PET and CT scanners (Stout et al 2003, 2005, Chatziioannou et al 2004). The spatial transformation matrix is determined from phantom scans on the PET and CT scanners, permitting subsequent animal PET and CT scans to be registered using this predetermined matrix.
Our experience over the past three years using fiducial markers to manually generate the spatial transformation matrix (Chow et al 2002) showed that simple rigid body assumptions (rotations and translations) were producing suboptimal results. Subtle variations in pixel size were observed particularly in the axial direction of the microCT image. Therefore, scans of parallel lines resulted in images with non-parallel lines. This was thought to be due to imperfect alignment of the x-ray detector relative to the x-ray source (von Smekal et al 2004). The use of warping to correct for nonlinear distortions (introduced by the minifying glass fibre bundle in the x-ray detector) in each projection image may also cause voxel size variations in the image. Thus, a more sophisticated method of determining the spatial transformation matrix for PET and CT was desired.
This paper presents a registration phantom used to automatically determine the spatial transformation matrix between separate microPET and microCT scanners, that works in combination with an imaging chamber. Since we are more interested in quantifying the amount of registration error in a routine animal study than in a rigid phantom, a method to quantitatively measure the accuracy of the registration process in vivo is introduced and is used to compare manual with software registration. Furthermore, estimates of the effect of misregistration on subsequent calculations (specifically for attenuation correction in PET) are presented.
2. Materials and methods
All PET data were acquired on a microPET® Focus™ 220 tomograph (Siemens Preclinical Solutions, Knoxville, TN) (Tai et al 2005). The PET imaging field of view was 190 mm diameter in the transverse by 76 mm long in the axial direction. All listmode data were sorted into 3D sinograms using a span of three and a ring difference of 47. All sinograms were Fourier rebinned into 2D sinograms prior to reconstruction (Defrise 1995). Images were reconstructed using 2D filtered backprojection with a ramp filter cutoff at the Nyquist frequency, resulting in an isotropic spatial resolution of 1.7 mm full width at half maximum. The emission data were corrected for detector efficiency, random coincidences, deadtime and isotope decay. The PET image volume (128 × 128 × 95) was reconstructed with a zoom that matched the microCT imaging field of view in the transverse direction and had a voxel size of 0.4 × 0.4 × 0.796 mm3.
All CT data were acquired on a MicroCAT™ II tomograph (Siemens Preclinical Solutions, Knoxville, TN), a step-and-shoot system requiring several milliseconds between radiographs. The six mega-pixel (2048 × 3072) x-ray detector (Dalsa Life Sciences, Waterloo, Ontario, Canada) was positioned with the longer dimension along the axial direction. The source to detector distance was 295.4 mm and the source to imaging centre distance was 218.2 mm. The resulting CT imaging field of view was 52 mm diameter in the transverse by 78 mm long in the axial direction. Projection images were binned, down-sampled and reconstructed using the Feldkamp cone-beam algorithm for filtered backprojection with a ramp filter cutoff at the Nyquist frequency. The CT data were not corrected for scatter or beam hardening artefacts. The CT image volume (256 × 256 × 384) had a voxel size of 0.2 × 0.2 × 0.2 mm3.
2.1. Hardware registration
2.1.1. Imaging chamber
The growth of imaging with immuno-compromised mice has necessitated a bed and isolation chamber arrangement suitable for multimodality and longitudinal studies. We have designed in-house an imaging chamber that is compatible with the PET and CT systems, has reproducible animal positioning for longitudinal studies and is easy to use for high throughput imaging (Stout et al 2003, 2005, Chatziioannou et al 2004). For the purpose of image registration, the most important requirement was the multi-system compatibility. We replaced each tomograph’s system-specific bed with an adapter plate that reproducibly connects the motorized bed stage to our custom-made imaging chamber. The imaging chamber is composed of two main parts: a cylindrical Lucite chamber that fills with gas anaesthesia and a removable bed with alignment posts for the limbs. Figure 1 shows a photograph of the imaging chamber, the bed and the chamber mounted on the microPET and microCT systems. The imaging chamber is made to fit fully in the smaller field of view of the MicroCAT™ II so that all attenuation seen in the PET scanner is seen in the CT as well.
Figure 1.
(a) Photograph of imaging chamber (inset shows the removable bed). Photographs of imaging chamber on PET (b) and CT (c) scanners.
2.1.2. Manual generation of spatial transformation matrix
The manual method of generating the spatial transformation matrix used six point fiducial markers (MMS04-022, Isotope Products Laboratories, Valencia, CA). These fiducial markers were securely fixed to the imaging chamber and bed insert and sequential PET and CT tomograms were acquired. Manual, rigid-body alignment of the images (rotations and translations) was performed using A Medical Image Data Examiner—AMIDE (Loening and Gambhir 2003). Subsequent animal studies were scanned at the same bed location as that of the fiducial marker scan. The PET and CT mouse images were then registered using the predetermined spatial transformation matrix generated from the fiducial marker scan (Chow et al 2002).
2.1.3. Automated generation of spatial transformation matrix
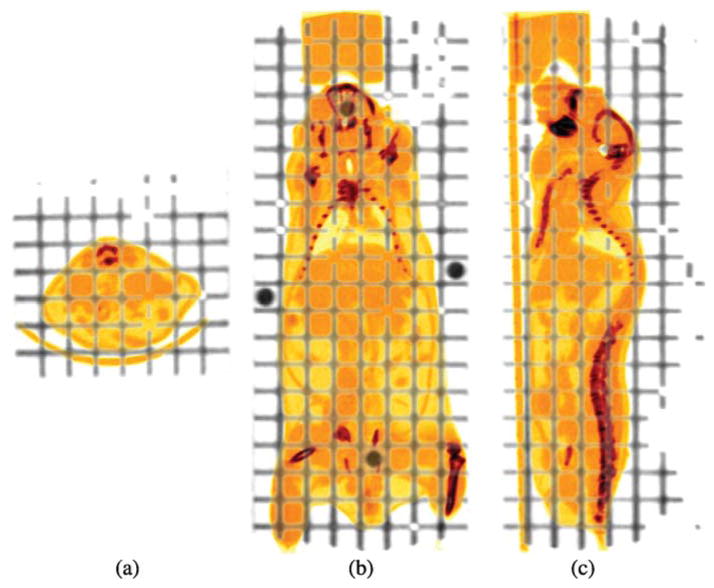
Instead of using a discrete number of fiducial markers to sample a few spatial coordinates, we want to sample (and register) the full, relevant three-dimensional space with a grid of lines. To achieve this, we designed a three-dimensional grid phantom, comprised of a stack of eight rectangular Lucite slabs (40 × 5 × 120 mm3) and a sealable container (60 × 60 × 140 mm3). Since each slab has 1 mm channels milled out of it in all three orthogonal directions spaced 5 mm apart, the assembled phantom has a total of 1288 lines. This phantom is mounted to the same adapter plate as the imaging chamber and covers the same field of view as the imaging chamber. Figure 2 shows an overlay of the grid phantom (showing only the channels) with a mouse CT study. The channels were filled with a solution containing F-18 and Omnipaque™ 350 iodine contrast agent (GE Healthcare, Princeton, NJ) so that the lines were visible in both the PET and CT scans.
Figure 2.
Transverse (a), coronal (b) and sagittal (c) CT images of the grid phantom overlaid with a mouse study in the imaging chamber.
Software registration using the Automated Image Registration 5.0 (AIR) package (Woods et al 1993) determined the spatial transformation matrix from CT to the PET field of view. Some pre-processing of the data was required for a successful registration. Since the grid phantom was larger than the CT field of view, the annular truncation artefact from having attenuation outside the field of view was cropped out of the CT image. The same area in the PET image was also cropped to match the CT. Because the explicit image values of the PET and CT data are very different, while their spatial distribution is highly correlated, the ratio image approach is expected to work well for PET and CT images. Essentially, this cost function uses the relative information content of the two images and not their absolute values. Thus, the magnitude of the cost function (standard deviation of the ratio image) represents the deviation from a perfect registration. A 15-parameter model (perspective transformations were allowed along with rotations, translations, dilation/compression and shear along each of the three orthogonal axes) was used that allowed parallel lines to intersect and was expected to fix the distortions described in section 1. Although this model did not preserve mass and spatial distances, the corrections were small for our fixed geometric object. Other processing steps included: thresholding the CT to use just the contrast-enhanced channels, cropping the noisy end planes of the PET data and reslicing the PET image to CT voxels. The volumetric PET phantom image was used as the reference (standard) image and the volumetric CT phantom image as the mobile (resliced) image.
Subsequent animal studies were scanned at the same bed location as that of the grid phantom scan. The PET and CT mouse images were then registered using the predetermined spatial transformation matrix described above.
2.2. Registration accuracy measurements
2.2.1. Motor accuracy
Since our proposed method of hardware image registration required each tomograph’s motors to position the imaging chamber in the same space accurately, we tested the reproducibility as follows. One to two point fiducial markers were randomly fixed on the bed and tomograms were acquired on the PET and CT scanners. Each acquisition was repeated five times with and without additional homing (a search for the reference position) of both axial and vertical motorized bed stages between acquisitions. A total of six different locations of the fiducial markers were examined. After each fiducial marker was visually identified, the centre of mass was calculated using a cubic region of interest. The centre-of-mass calculation was expected to provide results more accurately than the intrinsic resolution of the PET and CT scanners. The CT data were thresholded to eliminate the background attenuation prior to the centre-of-mass calculation. The average and maximum distances (projected onto each of the three orthogonal axes and in 3D space) between each marker’s centre of mass and the average centre of mass were calculated.
2.2.2. Mounting accuracy
Since the imaging chamber will be unmounted and remounted from the PET and CT scanners for any combined modality study, the positioning reproducibility of the imaging chamber was tested. Sequential scans of fiducial markers were performed on the PET and the CT tomographs and processed as mentioned above. Based on the results of the motor accuracy test, the motors were not additionally homed between acquisitions, while the imaging chamber was unmounted and remounted onto the PET and CT scanner, respectively. The average and maximum distances between each marker’s centre of mass and the average centre of mass were calculated as described above.
2.2.3. Accuracy in rigid phantom
The accuracy of the spatial transformation matrix was first determined for a rigid phantom. The phantom, with six fiducial markers securely fixed to it, was placed on top of the bed inside the imaging chamber and scanned sequentially in the microPET and microCT tomographs. The CT image was registered to the PET image using one of the two spatial transformation matrices: from the manual method with six markers or the automated method with the grid phantom. The PET image was subsequently resliced to CT-sized voxels for comparison. The distance (average and maximum) in the measured centre of mass of each marker in the PET and registered CT images was calculated. Because our imaging chamber has an insert bed to which the mouse is fixed (figure 1), the measured registration error in this experiment includes the inaccuracies mentioned above (motor and chamber removal/repositioning), additional inaccuracies from movements of the bed insert and the spatial transformation matrix.
2.2.4. Accuracy in vivo
We wanted to test the accuracy of our methods for a living, anaesthetized subject to get an estimate of the errors we can expect during routine animal studies, since some of these errors are not seen in measurements of rigid phantoms. Assuming the mouse skeleton attached to our imaging chamber is a rigid structure, we wanted two images sharing as much information content as possible. A 25 g BLK6 mouse was injected with 8.73 MBq (0.236 mCi) [18F] fluoride ion (a bone imaging agent), making the information content of PET and CT images very similar. Following typical imaging protocols, 10 min PET and CT scans were acquired 2 h post-tracer injection. The CT image was registered to the PET using either one of the two spatial transformation matrices (a) the matrix generated manually or (b) the matrix generated automatically. After this first registration step, the data should be ‘perfectly’ aligned.
We then used a residual registration step to measure any errors from our method (i.e. all errors mentioned above plus motions of an anaesthetized mouse). This second software alignment was performed using AIR to align each of the already registered CT mouse volumes (manual or automated method) to the target PET mouse image. The mouse bone images were prepared as input to the AIR program as mentioned above in section 2.1.3, with the exception of cropping since no truncation artefact was present in this case. A threshold was applied to the volumetric CT mouse images to segment the soft tissues and use only the bone for registration, matching the information content of the PET bone scan as closely as possible. The PET image was resliced to CT voxels prior to using it as the target of this second registration. Again, the 15-parameter perspective model was used along with the standard deviation of the ratio image as the cost function to generate two additional spatial transformation matrices, representing the residual registration errors for our two methods (manually and automatically generated matrix).
To quantify the residual registration errors, two computer-generated fields of dots (2 mm apart) representing the mouse skeleton were created using the segmented mouse skeleton from each of the two hardware registered CT images (manual and automated) as a mask. The centre of mass of each of these 211 dots was tracked after applying the corresponding second spatial transformation matrix. The accuracy of the registration of the mouse skeleton for each of the two methods was measured as the average distance that the measured centres of mass of these 211 dots travelled during this second transformation. While these dots do not represent specific features of the mouse skeleton, they can be used to estimate the distance necessary for the skeleton to travel, to cover the residual distance.
2.3. Impact of image misregistration
To estimate the impact of misregistration on PET quantitation, a mouse-sized phantom study was simulated using ideal cylinders and activities. A 25 mm diameter cylinder containing two smaller (10 mm diameter) cylindrical chambers was digitally simulated. In the emission image, a background activity concentration of 100 was used, while one of the smaller cylinders had a four times higher activity concentration. In the transmission image, the above chambers were assigned the theoretical attenuation of water at 511 keV. The remaining small chamber was used to simulate a lung, having 1/3 attenuation and 1/3 activity of the background chamber. These ideal images were smoothed to the spatial resolution of the PET system (to prevent aliasing) and forward projected to create ideal emission and attenuation correction sinograms. By dividing the emission sinogram by the attenuation correction, we obtained the ‘raw’ emission sinogram similar to those from actual microPET measurements. Misregistered transmission images were generated by shifting the transmission image in increments from 0.1 mm to 2.0 mm using the manual reslice tool that is part of the AIR package. Misregistered attenuation correction sinograms were forward projected using each of these misaligned transmission images. Emission image reconstruction with the corresponding attenuation correction sinogram (generated either with the registered transmission image or the intentionally misregistered transmission images) was performed.
3. Results
3.1. Registration accuracy
3.1.1. Motor accuracy
The positioning reproducibility of each scanner’s motors and its effect on the measured location of the fiducial markers is summarized in table 1. The results indicate that on average there is more variation in position when the motorized bed stages were homed (PET: 0.037 mm, CT: 0.021 mm) than when not homed (PET: 0.028 mm, CT: 0.011 mm). This is expected, since homing the stages resets the point of origin of their positioning coordinates. Nonetheless, these results match well with the accuracy reported for the CT motors of 0.021 mm (Parker Hannifin Corporation 2002).
Table 1.
Motor and imaging chamber positioning accuracy.
| Absolute distance (mm) | PET |
CT |
|||
|---|---|---|---|---|---|
| Mean | Max | Mean | Max | ||
| No homing | X | 0.012 | 0.043 | 0.006 | 0.026 |
| Y | 0.014 | 0.047 | 0.007 | 0.028 | |
| Z | 0.016 | 0.054 | 0.003 | 0.007 | |
| 3D | 0.028 | 0.060 | 0.011 | 0.029 | |
| Homing | X | 0.015 | 0.062 | 0.010 | 0.047 |
| Y | 0.025 | 0.076 | 0.015 | 0.044 | |
| Z | 0.013 | 0.054 | 0.005 | 0.022 | |
| 3D | 0.037 | 0.085 | 0.021 | 0.064 | |
| Chamber off/on | X | 0.037 | 0.103 | 0.024 | 0.069 |
| Y | 0.014 | 0.050 | 0.011 | 0.034 | |
| Z | 0.014 | 0.051 | 0.009 | 0.029 | |
| 3D | 0.046 | 0.103 | 0.031 | 0.074 | |
X: left/right; Y: up/down; Z: in/out; 3D: three-dimensional distance.
3.1.2. Mounting accuracy
The positioning reproducibility of the imaging chamber in each scanner is summarized in table 1. The results indicate that the positioning errors when combining motor movements with taking the imaging chamber off and on the tomograph increased slightly (PET: from 0.028 mm to 0.046 mm, CT: from 0.011 mm to 0.031 mm). These positioning errors are attributed to the mechanical variations in the attachment mechanism of the imaging chamber. They are much smaller than the spatial resolution of the PET system, or even the spatial resolution of the CT scan at routine image acquisition settings.
3.1.3. Accuracy in rigid phantom
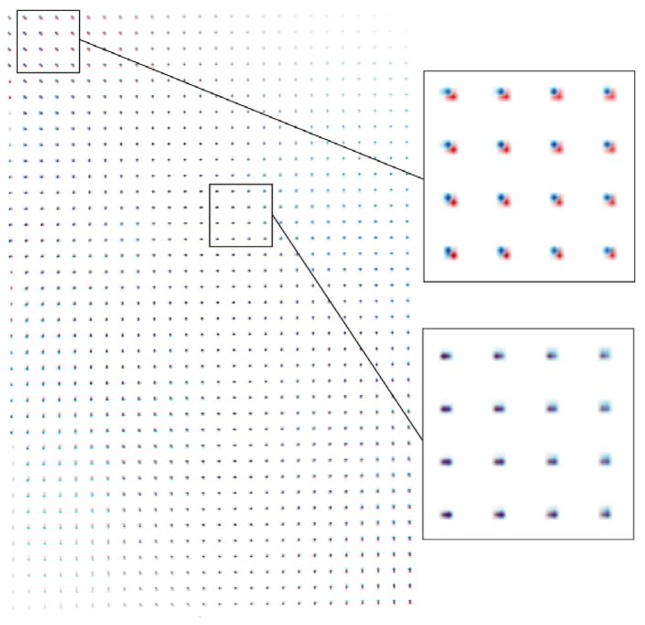
The results of the rigid phantom experiment are summarized in table 2. These positioning errors are the combination of errors from motorized bed stages, imaging chamber mounting accuracy and imaging chamber insert bed positioning. In addition, they also include errors from the estimated spatial transformation matrix. The results indicate that automated registration is more accurate than the manual method of registration (0.573 mm manual versus 0.279 mm automated). The advantages of using a non-rigid spatial transformation matrix are also shown in figure 3. To illustrate the spatial distortions in the reconstructed CT image volume as perceived by the image registration software and the PET image target, we applied both the rigid body (6 parameters) and the non-rigid body (15 parameters) transformation, obtained with our 3D grid phantom, to a computer-generated field of dots (2 mm apart). The average position of the volume is the same for both transformations, but different locations have different location errors. While these errors are still relatively small and difficult to quantitate absolutely as they depend on the specifics of the CT detector, figure 3 indicates that a non-rigid body registration is necessary to improve the results. It can be seen that pairs of dots are not more than 1–2 CT pixels apart.
Table 2.
Registration accuracy in phantom and in vivo.
| Absolute distance (mm) | Manual |
Automated |
|||
|---|---|---|---|---|---|
| Mean | Max | Mean | Max | ||
| Phantom | X | 0.123 | 0.224 | 0.176 | 0.279 |
| Y | 0.351 | 0.594 | 0.109 | 0.236 | |
| Z | 0.402 | 0.639 | 0.125 | 0.376 | |
| 3D | 0.573 | 0.758 | 0.279 | 0.440 | |
| In vivo | X | 0.097 | 0.313 | 0.088 | 0.314 |
| Y | 0.214 | 0.848 | 0.148 | 0.635 | |
| Z | 0.411 | 1.274 | 0.243 | 0.742 | |
| 3D | 0.507 | 1.533 | 0.335 | 0.857 | |
X: left/right; Y: up/down; Z: in/out; 3D: three-dimensional distance.
Figure 3.
Comparison of 6- versus 15-parameter registration model (red and blue dots, respectively) as determined from software alignment of the grid phantom. Insets show enlarged area indicated.
3.1.4. Accuracy in vivo
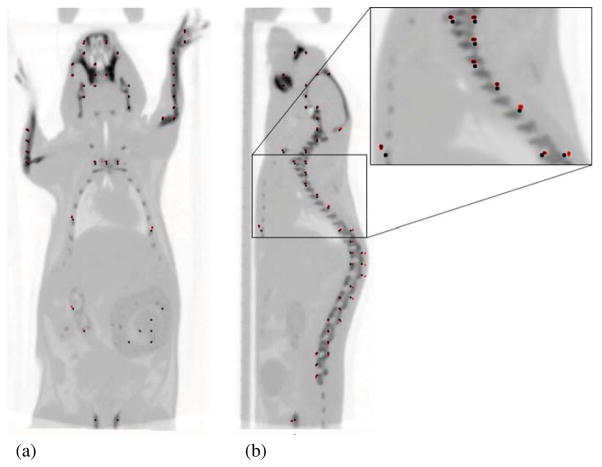
The results of the in vivo experiment are summarized in table 2. Automated registration is more accurate than the manual method of registration (0.507 mm manual versus 0.335 mm automated). Figure 4 shows positions of the dots before and after the second registration overlaid on the CT mouse image aligned using the automatically generated spatial transformation matrix. This in vivo registration error includes all positioning errors mentioned above, errors in the estimated spatial transformation matrix and motions of an anaesthetized mouse. The locations of above average error were in the ribs, where the mouse may be breathing differently in the two tomographic acquisitions. While neither the PET nor the CT data acquisitions were gated for respiration or cardiac motion, the step-and-shoot method of CT acquisition has a similar frequency and tends to synchronize with the mouse respiratory cycle. This effect sometimes causes aliasing artefacts.
Figure 4.
Coronal (a) and sagittal (b) images of dots before (black) and after (red) the second registration, with overlay of CT mouse image aligned using the automatically generated spatial transformation matrix. Inset shows enlarged area indicated.
3.2. Impact of image misregistration
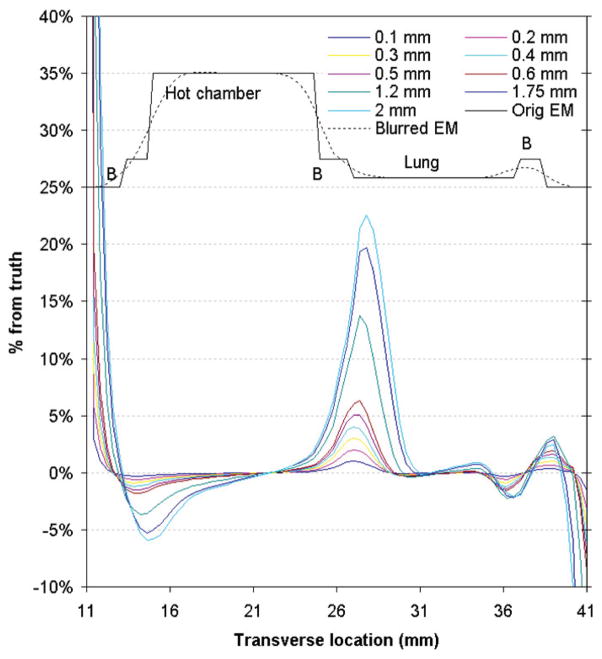
PET data corrected with a significantly misregistered transmission image created non-trivial quantitation errors (>10% for 1.2 mm misalignment). Figure 5 plots the errors in microPET quantitation (from incorrect attenuation correction factors generated by these misregistered transmission images) across different chambers of the simulated phantom. Although errors are high near the boundaries between tissues with varying attenuation coefficients (>20% at the inner lung boundary for 2 mm misregistration), non-trivial errors also exist in regions away from these interfaces (~2.5% near the centre of the hot chamber for 2 mm misregistration).
Figure 5.
Profiles of microPET quantitation error across the different chambers of the simulated mouse-sized phantom for increasing offset from the registered transmission image. The correct emission profiles (perfect and smoothed) are shown in black above the error profiles for reference and are not on the same scale as the error profiles.
4. Discussion and conclusions
As expected, software registration that allows parallel lines in the CT to intersect produces better image registration than manual registration with simple rotations and translations. Our analysis shows that an accuracy of 1.5–2 CT pixels (0.335 mm) is achievable in rigid phantoms and in rigid structures of a mouse. The 15-parameter perspective model was chosen as a way to correct for geometric distortions in the reconstructed CT images. Although we have not quantitatively verified the distortion correction in the CT, our results show that the 15-parameter perspective model is better than the 6-parameter rigid body model for registration to the target PET image. While there might be residual distortions in the imaged field of view, the PET and the anatomical CT data are better registered to each other.
The grid phantom has proven to be a useful tool in multi-modality image registration. This registration procedure only needs to be performed once for a setup. However, filling the phantom was not an easy task, with many channels for air bubbles to get trapped in. A solid grid phantom may prove to be a convenient and practical upgrade.
In summary, we described a hardware registration method that includes both hardware (imaging chamber and registration phantom) and software (manually or automatically generated spatial transformation matrix) components. We described a 3D grid phantom that does not require simple rigid body assumptions for the spatial transformation matrix. Furthermore, we also verified that our hardware method of inter-modality registration using the imaging chamber, grid phantom and automatically generated spatial transformation matrix has an average accuracy of 0.335 mm in vivo. Registration is performed easily and is independent of the user. We also estimated that the effect of misregistration on PET quantitation due to a misaligned attenuation map as acquired with our registration method to be less than 5% from our simulation results. These errors are in addition to those from assuming the wrong attenuation coefficients (Chow et al 2005). Misregistration also affects subsequent calculations (e.g. scatter correction) and additional studies are needed to quantify the magnitude of the errors introduced. The methods described here are extendable to different imaging systems and larger animals (e.g. rats) that can be housed in this or a larger version of the imaging chamber. With this robust technique, staff at high throughput imaging facilities do not have to perform hours of software or manual registration on routine animal studies.
Acknowledgments
The authors thank Michael Kreissl, Judy Edwards and Waldemar Ladno for their invaluable assistance with the animal experiments, Lissa Zyromski and Melanie Harrison from Isotope Products Laboratories for the fiducial markers and Ching-Ti Liu for valuable discussions in statistics. This work was supported in part by the US Department of Energy under contract no. DE-FC03-02ER63420 and by the National Institutes of Health under grant no. R24 CA 92865.
References
- Chatziioannou AF, Stout DB, Silverman RW. Method and apparatus for animal positioning in imaging systems. R268:53028 US Provisional Patent Application. 2004
- Chow PL, Rannou FR, Chatziioannou AF. Molecular Imaging and Biology (San Diego) Vol. 4. New York: Elsevier; 2002. Attenuation correction for a 3D small animal PET tomograph, using x-ray microCT; p. S17. [Google Scholar]
- Chow PL, Rannou FR, Chatziioannou AF. Attenuation correction for small animal PET tomographs. Phys Med Biol. 2005;50:1837–50. doi: 10.1088/0031-9155/50/8/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Defrise M. A factorization method for the 3D x-ray transform. Inverse Problems. 1995;11:983–94. [Google Scholar]
- Hill DLG, Batchelor PG, Holden M, Hawkes DJ. Medical image registration. Phys Med Biol. 2001;46:R1–45. doi: 10.1088/0031-9155/46/3/201. [DOI] [PubMed] [Google Scholar]
- Jan M-L, Chuang K-S, Chen G-W, Ni Y-C, Chen S, Chang C-H, Wu J, Lee T-W, Fu Y-K. A three-dimensional registration method for automated fusion of micro PET-CT-SPECT whole-body images. IEEE Trans Med Imaging. 2005;24:886–93. doi: 10.1109/tmi.2005.848617. [DOI] [PubMed] [Google Scholar]
- Kenanova V, et al. Tailoring the pharmacokinetics and positron emission tomography imaging properties of anti-carcinoembryonic antigen single-chain Fv-Fc antibody fragments. Cancer Res. 2005;65:622–31. [PMC free article] [PubMed] [Google Scholar]
- Kim J, Yin FF, Zhao Y, Kim JH. Effects of x-ray and CT image enhancements on the robustness and accuracy of a rigid 3D/2D image registration. Med Phys. 2005;32:866–73. doi: 10.1118/1.1869592. [DOI] [PubMed] [Google Scholar]
- Lavely WC, Scarfone C, Cevikalp H, Li R, Byrne DW, Cmelak AJ, Dawant B, Price RR, Hallahan DE, Fitzpatrick JM. Phantom validation of coregistration of PET and CT for image-guided radiotherapy. Med Phys. 2004;31:1083–92. doi: 10.1118/1.1688041. [DOI] [PubMed] [Google Scholar]
- Loening AM, Gambhir SS. AMIDE: a free software tool for multimodality medical image analysis. Mol Imaging. 2003;2:131–7. doi: 10.1162/15353500200303133. [DOI] [PubMed] [Google Scholar]
- Maintz JBA, van den Elsen PA, Viergever MA. 3D multimodality medical image registration using morphological tools. Image Vis Comput. 2001;19:53–62. [Google Scholar]
- Parker Hannifin Corporation, Daedal Division. 404/406XR series product manual—Manual no. 100-5320-01 rev. 3. Parker Hannifin Corporation; Irwin, PA: 2002. [Google Scholar]
- Ray P, Wu AM, Gambhir SS. Optical bioluminescence and positron emission tomography imaging of a novel fusion reporter gene in tumor xenografts of living mice. Cancer Res. 2003;63:1160–5. [PubMed] [Google Scholar]
- Stout DB, Chatziioannou AF, Lawson TP, Silverman RW, Gambhir SS, Phelps ME. Small animal imaging center design: the facility at the UCLA Crump Institute for Molecular Imaging. Mol Imaging Biol. 2005 November 1;:1–10. doi: 10.1007/s11307-005-0015-2. Online first. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stout DB, Chow PL, Gustilo A, Grubwieser S, Chatziioannou AF. Molecular Imaging and Biology (Madrid) Vol. 5. New York: Elsevier; 2003. Multimodality isolated bed system for mouse imaging experiments; pp. 128–9. [Google Scholar]
- Sundaresan G, Yazaki PJ, Shively JE, Finn RD, Larson SM, Raubitschek AA, Williams LE, Chatziioannou AF, Gambhir SS, Wu AM. I-124-labeled engineered anti-CEA minibodies and diabodies allow high-contrast, antigen-specific small-animal PET imaging of xenografts in athymic mice. J Nucl Med. 2003;44:1962–9. [PMC free article] [PubMed] [Google Scholar]
- Tai Y-C, Ruangma A, Rowland D, Siegel S, Newport DF, Chow PL, Laforest R. Performance evaluation of the microPET (R) focus: a third-generation microPET scanner dedicated to animal imaging. J Nucl Med. 2005;46:455–63. [PubMed] [Google Scholar]
- Townsend DW, Carney JPJ, Yap JT, Hall NC. PET/CT today and tomorrow. J Nucl Med. 2004;45:4s–14s. [PubMed] [Google Scholar]
- von Smekal L, Kachelriess M, Stepina E, Kalender WA. Geometric misalignment and calibration in cone-beam tomography. Med Phys. 2004;31:3242–66. doi: 10.1118/1.1803792. [DOI] [PubMed] [Google Scholar]
- Woods RP, Mazziotta JC, Cherry SR. MRI-PET registration with automated algorithm. J Comput Assist Tomogr. 1993;17:536–46. doi: 10.1097/00004728-199307000-00004. [DOI] [PubMed] [Google Scholar]
- Zaidi H, Hasegawa B. Determination of the attenuation map in emission tomography. J Nucl Med. 2003;44:291–315. [PubMed] [Google Scholar]