A comparison of the different helices adopted by α- and β-peptides suggests different reasons for their stability

Abstract

The right-handed α-helix is the dominant helical fold of α-peptides, whereas the left-handed 3₁₄-helix is the dominant helical fold of β-peptides. Using molecular dynamics simulations, the properties of α-helical α-peptides and 3₁₄-helical β-peptides with different C-terminal protonation states and in the solvents water and methanol are compared. The observed energetic and entropic differences can be traced to differences in the polarity of the solvent-accessible surface area and, in particular, the solute dipole moments, suggesting different reasons for their stability.

Introduction

β-Peptides are non-natural mimetics of α-peptides. They differ from α-peptides by the insertion of an extra carbon atom between the N and C^α atoms of the peptide group. β-Peptides exhibit a large variety of folded structures, including several types of helices. Their secondary structure is stable even at very short chain lengths. Additionally, helical structures of β-peptides are typically stable in less polar solvents such as methanol, whereas the α-helix of α-peptides is stable in polar solvents such as water. β³-Peptides, in which the C^β atom of the backbone is substituted, have a particular propensity to form 3₁₄-helices. The mechanism by which β³-substitution induces 3₁₄-helix formation has recently been extensively studied by molecular dynamics (MD) simulations.¹

The ability of β-peptides to form secondary structures similar to those of natural peptides, coupled to their resistance to proteases due to their extra backbone carbon atom, make them attractive candidates for rational drug design.² To fulfil their promise in this area, however, further understanding of the relationship between chemical configuration and conformational propensities is required. To address this, we present here an analysis of MD simulations of a set of poly-α-alanine and poly-β-alanine peptide systems in both water and methanol. Because of the particular design of our model systems, we are able to elucidate many of the inherent energetic and entropic differences between helical structures of α- and β-peptides, paying special attention to the reasons for the preferential stability of the 3₁₄-helix of β-peptides in methanol and the α-helix of α-peptides in water.

Results and Discussion

The α- and β-peptides studied here are described in Tables I and II. The lengths of the α- and β-peptides were chosen such that each had the same number of backbone atoms and could form a short helix: a right-handed α-helix for the α-peptide and a left-handed 3₁₄-helix for the β-peptide. The helix-defining NH—CO hydrogen bonds (Table III) were restrained during the simulations. To minimize side-chain effects, all of the amino acids had alanine side-chains. The CH₃ groups at the C^α atoms of the α-peptides and the C^β atoms of the β-peptides were of the L configuration (Fig. 1). The N-termini were always protonated. Two protonation states of the C-termini were investigated: COO—, as is standardly present for α-peptides in water and COOH, typical for β-peptides in methanol. Eight MD simulations were performed, encompassing all combinations of α- and β-peptides, C-termini protonation states and the two solvents, methanol and water. Each simulation started from the helical initial structures defined by the hydrogen bonds given in Table III. Only the helical folded conformations are compared, because a complete characterization of unfolded states is still beyond the currently available computing power.

Table I.

The Characteristic Features of the α- and β-Peptides Studied Here

			Nbb		Ndof
Type	conformation (handedness)	Nres	Total	Per res	Total	Per res	Nhb	Hydrogen bonds
α	α-Helix (RH)	8	24	3	16	2( φ, ψ )	4	i → i − 4
β	314-helix (LH)	6	24	4	18	3( φ, θ, ψ )	4	i → i + 2

N_res is the number of residues, N_bb is the number of backbone atoms, N_dof is the number of torsional-angle degrees of freedom, N_hb is the number of backbone hydrogen bonds, and i is the residue sequence number.

Table II.

The Name and Characteristic Features of Each Peptide System

Name	Type	C-terminus	Solvent
αMO—	α	O—	Methanol
αMOH	α	OH	Methanol
αWO—	α	O—	Water
αWOH	α	OH	Water
βMO—	β	O—	Methanol
βMOH	β	OH	Methanol
βWO—	β	O—	Water
βWOH	β	OH	Water

Table III.

The Hydrogen Bond Distances (nm) Measured from the Starting Structure of Each Type of Peptide

Type	H—O		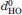H—O		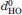H—O		H—O
α	5–1	0.219	6–2	0.199	7–3	0.206	8–4	0.202
β	1–3	0.196	2–4	0.191	3–5	0.223	4–6	0.222

H—O are the residue sequence numbers of the hydrogen- and oxygen-containing residues, respectively, and is the measured distance between the hydrogen and oxygen atoms.

Figure 1.

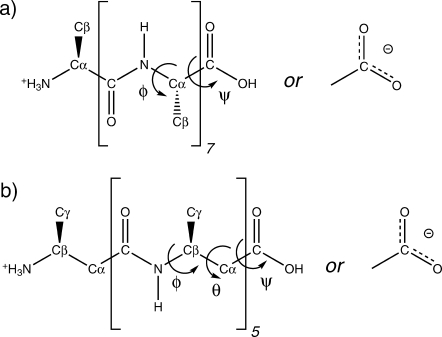
Chemical configuration of the (a) α- and (b) β-peptides. The backbone dihedral angles φ (C—N—C^α—C) and ψ(N—C^α—C—N)(or OH) for the α-peptide and φ(C—N—C^β—C^α), θ (N—C^β—C^α—C) and ψ(C^β—C^α—C—N) (or OH) for the β-peptide are indicated.

Conformational variation

The stability of each helical structure during the simulations was assessed by computing the atom-positional root-mean-square deviation (rmsd) from the energy-minimized initial structure, the root-mean-square fluctuations (rmsf) of the backbone atoms (Fig. 2) and the backbone dihedral angle distributions (Fig. 3 and 4).

Figure 2.

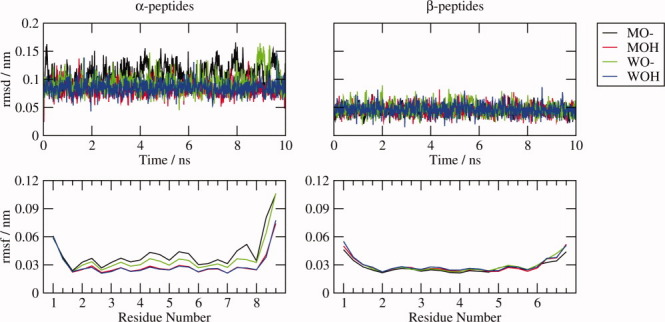
Backbone atom rmsd and rmsf. The atom-positional rmsd from the energy-minimized initial structure and the rmsf were computed for the backbone atoms of each system as labeled after superimposing the backbone atoms of all structures in the 10-ns MD trajectory onto the energy-minimized initial structure.

Figure 3.

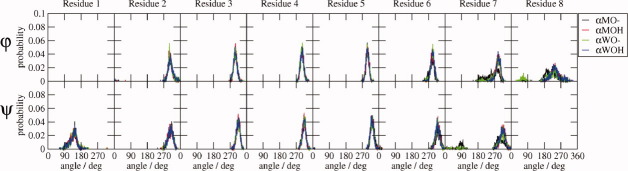
α-peptide dihedral angles. Distributions of the φ and ψ backbone dihedral angle values sampled during the 10-ns MD simulations by the various α-peptide systems as labeled.

Figure 4.

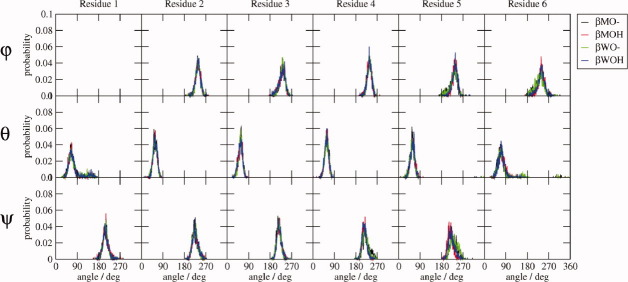
β-peptide dihedral angles. Distributions of the φ and ψ backbone dihedral angle values sampled during the 10-ns MD simulations by the various β-peptide systems as labeled.

The backbone rmsd from the initial structure and rmsf of each helical peptide can be directly compared, as each system has the same number of backbone atoms (Table I). They are both significantly lower for the β-peptides, for which there is also less difference between the rmsd and rmsf of each system. For the α-peptides, the deprotonated systems have larger rmsf than the protonated systems, and this difference is largest in methanol. For both the α- and β-peptides, the rmsf is significantly larger at the termini, in particular the C-termini of the α-peptides.

The dihedral angle distributions of the central residues are relatively narrow, unimodal, and essentially identical for all peptide systems, but the terminal residues exhibit some differences, particularly for the α-peptides. The ψ distributions for residue 1 of the α-peptides are a little broader than those of the other residues. Both the φ and ψ-angle distributions of residue 7 are bimodal, especially for αMO—, and the φ-angle distribution of residue 8 is bimodal for the αXO— (X = M or W) systems. The larger atom-positional rmsf of the terminal backbone atoms of the α-peptides reflects these fluctuations. For the β-peptides, the terminal θ angles gain a tail of larger angle values in all systems, and the dihedral angle distributions for residues 5 and 6 of the βXO— systems broadened a little relative to those of the protonated systems, causing the slight increase in the atom-positional rmsf of the terminal atoms.

The hydrogen bond restraints are barely needed to maintain the helical structure, because the potential energy associated with the hydrogen bond restraint function is low, less than k_BT (Table VI), thus there is little strain on the structures. The main differences between the various systems are the larger fluctuations of the C-terminal atoms of the α-peptides relative to the β-peptides and the greater mobility or entropy, particularly of the α-peptides, when the C-terminus is charged.

Table VI.

Contributions Made by the Covalent Terms and the H-bond Restraint to the Potential Energy (kJ mol ⁻¹) of the Different α- and β-Peptide Systems Described in Table II during 10 ns of MD Simulation with the 53A6 GROMOS Force Field⁷

	Covalent
Peptide	Bond angles	Improper dihedrals	Proper dihedrals	Total	Special H-bond restraints
αMO—	87 (13)	25 (6)	27 (7)	139 (17)	2.0 (2.4)
αMOH	85 (13)	23 (6)	25 (6)	133 (16)	0.9 (1.3)
αWO—	86 (13)	23 (6)	24 (6)	134 (16)	1.5 (2.0)
αWOH	85 (13)	23 (7)	25 (6)	133 (16)	0.9 (1.4)
βMO—	64 (11)	15 (5)	22 (7)	102 (13)	1.2 (1.7)
βMOH	66 (11)	14 (5)	24 (7)	104 (14)	1.0 (1.5)
βWO—	65 (11)	15 (5)	23 (7)	104 (13)	1.2 (1.8)
βWOH	65 (11)	15 (5)	25 (7)	105 (14)	1.1 (1.7)

The rmsf of each value is given in brackets. The covalent bond terms are uniformly zero for all systems.

Dimensions

The propensity of a peptide to form a particular fold is determined in large part by the balance of favorable intrasolute interactions to solute–solvent interactions. The ability of a given atom to interact with the solvent depends on its solvent-accessible surface area (SASA), its type, and the nature of the solvent. Here, the atom types are loosely grouped into hydrophobic and hydrophilic, and the atomic and total SASA is analyzed in terms of atom types (Table IV). The radius of gyration (rgyr) is also given as an alternative measure of the size of each peptide system. Note that the SASA in water will always be smaller than in methanol, because of the smaller probe radius of water compared with methanol.

Table IV.

Contributions Made by the Hydrophobic and Hydrophilic Non-hydrogen Atoms to the SASA (nm²) and the rgyr (nm) of the Different α- and β-peptide Systems Described in Table II During 10 ns of MD Simulation with the 53A6 GROMOS Force Field⁷

	SASA(Whole Peptide)			SASA(Per Atoma)
Peptide	Hydrophobic	Hydrophilic	Total	Hydrophobic	Hydrophilic	Total	rgyr
αMO—	9.42	3.72	13.14	0.39	0.22	0.32	0.40
αMOH	9.78	3.15	12.93	0.41	0.19	0.32	0.40
αWO—	6.70	2.20	8.89	0.28	0.13	0.22	0.40
αWOH	6.87	1.88	8.75	0.29	0.11	0.21	0.40
βMO—	10.03	2.03	12.06	0.42	0.16	0.33	0.35
βMOH	10.26	1.91	12.18	0.43	0.15	0.33	0.35
βWO—	6.59	1.47	8.06	0.27	0.11	0.22	0.35
βWOH	6.81	1.29	8.10	0.28	0.10	0.22	0.35

^aThe α- and β-peptides both have 24 hydrophobic atoms. The α-peptide has 17 hydrophilic atoms and the β-peptide 13.

The total SASA of the non-hydrogen atoms of the α-peptide is larger than that of the β-peptide for each set of conditions, as is the rgyr (Table IV), which is the same for all conditions. The hydrophobic SASA is similar for both α- and β-peptides, particularly in water, whereas the α-peptides have a larger overall and per-atom hydrophilic SASA than the β-peptides. These trends can also be seen when the SASA is plotted separately for each of the non-hydrogen atoms (Fig. 5). The greater hydrophilic SASA of the α-helical α-peptides explains why they are most stable in water, whereas 3₁₄-helical β-peptides are stable in less polar methanol.

Figure 5.

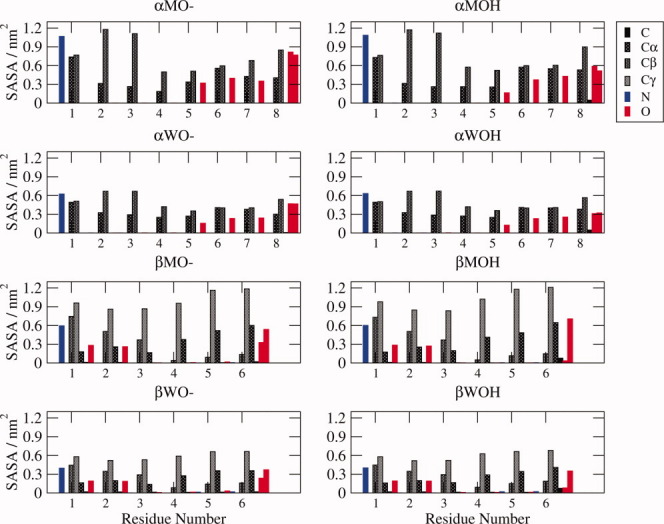
Solvent-accessible surface area (SASA). The SASA of each heavy atom of the different α- and β-peptide systems studied here, averaged over the entire 10-ns MD simulation, and colored according to the type of atom as indicated.

Protonation of the C-terminus lowers the hydrophilic SASA; in Figure 5, it is apparent that this is mostly due to the hydrogen masking part of the SASA of both of the terminal oxygens. Intriguingly, the hydrophobic SASA increases upon protonation. For the α-peptides, the largest increases (0.05–0.13 nm²) are in the Cα and Cβ atoms of residues 4, 7, and 8 in methanol and the Cα and C atoms of residue 8 in water. These increases are counterbalanced to some extent by the decreases in the SASA of the Cα atom of residue 5 and, in methanol, the Cβ atom of residue 7. In comparison, for the β-peptides, there are smaller (>0.01 nm²) increases in the SASA of the carbon atoms of residues 3–6, with the only increases >0.05 nm² being for the Cγ atom of residue 4 and the C atom of residue 6 in methanol and the Cα and C atoms of residue 6 in water. The large-scale changes in the SASA of the hydrophobic atoms of the α-peptides are mediated by the shifting dihedral angle distributions of the terminal residues that occur when the C-terminus is protonated, which alters the SASA not only of atoms localized in the C-terminus but also of residues in the centre of the peptide, through changes in the conformational preferences. The SASA of the β-peptides undergo more subtle changes, which are not so clearly localized to particular residues.

Examining the SASA of each heavy atom also reveals that carbon atoms, particularly the side-chain C^β atoms, are more exposed in the N-termini of the α-peptides, and oxygen atoms are more exposed in the C-termini, meaning that the SASA is more polar at the C-termini of the α-peptides, balanced somewhat by the highly exposed and positively charged NH₃ group at the N-terminus. For the β-peptides, the opposite pattern occurs: the carbon atoms, particularly those of the side-chain, become slightly more solvent exposed toward the C-terminus, and, other than the C-terminal atoms, the carbonyl oxygen atoms are more solvent exposed in the N-terminus. Thus, the overall polarity of the SASA of the β-peptides is distributed quite differently to that of the α-peptides.

Dipole moment

When a set of atoms carries a net charge, which some of the systems described here do, the dipole moment is ill-defined and depends on the choice of coordinate system. For this reason, the solute centre of geometry (COG) was used as an arbitrary common reference point. The COG of each structure in a given trajectory was shifted to the origin before computing the dipole moment. Although the COG of each system will be slightly different, the similarity in size and shape of the systems described here means that the dipole moments of each system calculated in this manner may be compared.

As well as the dipole moment that results from the separation of the positively charged N- and, for some systems, negatively charged C-termini in space, the net dipole moment of peptides is also influenced by the polarity of the peptide bond. For α-helical α-peptides, the dipole moments of the peptide bonds tend to align in the same direction as the COO— → NH₃+ dipole moment of the helix, but for 3₁₄-helical β-peptides, only the central peptide bond dipole moments align with the helix axis, and in the opposite direction to the COO— → NH₃+ dipole moment.

Electron delocalization is not treated explicitly in the standard GROMOS force fields, rather, it is reflected in the partial charges of the individual atoms, thus the dipole moment of the central residues stems from the separation of these partial charges in space. This means that when the central residues are considered, although there is only one peptide bond, the calculated dipole moment takes into account all partially charged atoms within those residues.

The magnitude of the dipole moment of the central pair of residues is identical for all systems (Table V), and remains essentially the same when the central four residues are considered. The NH and carbonyl groups of each amino acid therefore contribute ∼0.08 e nm to the overall dipole moment of the molecule. At this level, the differences in structure induced by the protonation state of the termini, the different environments and the different types of peptide are not sufficient to affect the magnitude of the internal dipole moment of the peptide.

Table V.

Contributions Made by the Specified Subsets of Residues to the Dipole Moment (e nm) of the Different α- and β-peptide systems described in Table II during 10 ns of MD Simulation with the 53A6 GROMOS Force Field⁷

	Residues
Peptide	4–5	3–6	2–7	1–8
αMO—	0.16	0.32	0.46	1.55
αMOH	0.16	0.32	0.48	1.12
αWO—	0.16	0.32	0.48	1.60
αWOH	0.16	0.33	0.49	1.11
	3–4	2–5		1–6
βMO—	0.16	0.32		0.44
βMOH	0.16	0.32		0.25
βWO—	0.16	0.32		0.46
βWOH	0.16	0.32		0.26

When residues 2–7 are included in the calculation of the dipole moment for the α-peptides, the magnitude of the dipole moment is slightly larger when the C-terminus is protonated, indicating that the peptide dipoles of residues 2 and 7 are better aligned in the protonated system.

Upon inclusion of the terminal residues of the β-peptide systems, the magnitude of the dipole moment increases for βXO—, to a value similar to that of residues 2–7 of the α-peptide systems, but decreases for βXOH. This slightly incongruous result can be explained once the directions of the dipole moments are taken into account (see below).

Including the terminal residues increases the dipole moment significantly for both the αXOH and αXO— systems. This is due in part to the inclusion of two more peptide groups (+0.16 e nm), and in part to the inclusion of the charged groups (∼+0.48 e nm per full charge). When the C-terminus is protonated, the dipole moment is essentially the same in both solvents, but for the αXO— systems, for which the magnitude of the dipole moment is greatest, it is larger in water than in methanol. This is because the greater mobility of the C-terminus in methanol means that the directions of the dipole moment vectors of each individual structure in the trajectory are slightly different, so that overall, the average dipole moment vector has a lower magnitude.

The directionality of the dipole moment shows less variation in the α-peptide systems (Fig. 6), where it is similar for all subsets of residues, and only the length of the dipole vector increases as more residues are included. This is because, as mentioned above, the dipole moment of the peptide bond points along the helix axis, as does the dipole moment because of the separation of the charged termini.

Figure 6.

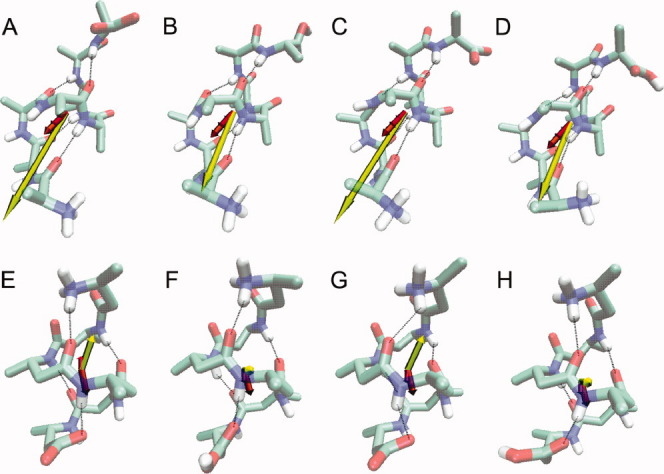
Dipole moment vectors. The final structure and the dipole moment vector averaged over the 10-ns MD simulations of the various α- and β-peptide systems: (A) αMO—, (B) αMOH, (C) αWO—, (D) αWOH, (E) βMO—, (F) βMOH, (G) βWO—, and (H) βWOH. The dipole moment vectors are coloured according to subset of residues included in the calculation. For the α-peptides: (pink) residues 4–5, (red) 3–6, (orange) 2–7 and (yellow) 1–8; for the β-peptides: (red) residues 3–4, (orange) 2–5 and (yellow) 1–6. In the peptide structures, nitrogen atoms are in blue, oxygen atoms in red, polar hydrogens in white, and the hydrogen bonds that were restrained during the simulation are shown as dotted lines. Note that the position of the N- and C-termini of the α- and β-peptide structures are at opposite ends.

For the β-peptide, however, the direction of the dipole moment changes depending on which subset of residues is included in the calculation and is less well aligned with the helix axis than for the α-peptides. This is because upon moving away from the central residues, the peptide bond dipole moment vectors begin to point outward from the central axis of the helix, rather than being aligned with the axis. When all residues are included, the dipole moment vectors of the βXO— systems are aligned with the helix axis. The orientations of the peptide bond dipole moment vectors now cancel, and it is the separation of the terminal charges that determines the overall dipole moment vectors. For the protonated β-peptides, the dipole moment vectors are orthogonal to the helix axis, reflecting the competition between the peptide bond dipole moment vectors, which all point in different directions, and the effect of the single charged terminal atom.

The large dipole moment of the α-peptides, especially those with a deprotonated C-terminus, explains why a deprotonated C-terminus and the α-helix conformation is the preferred state of α-peptides in water, which is a polar solvent, and also accounts for the observed increase in conformational dynamics of the α-peptides, as such a large net dipole moment can have a destabilising effect. β-peptides, on the other hand, tend to be protonated and exist as a 3₁₄-helix in methanol, a less polar solvent in which the low internal dipole moment of this state is favorable.

Energies

The average contributions made by the various terms of the potential energy function over the 10 ns production simulations and their statistical errors are given in Tables VI and VII.

Table VII.

Subtotals and Totals of the Contributions Made by the Covalent and Noncovalent Terms to the Potential Energy (kJ mol ⁻¹) of the Different α- and β-peptide Systems Described in Table II During 10 ns of MD Simulation with the 53A6 GROMOS Force Field⁷

	uu					uu
		Noncov.				Noncov.				vv	uu + uv + v
Peptide	Cov. total	ele	W	Total	Total	ele	ele	Total	uu + uv Total	Noncov. Total	Total
αMO—	139 (17)	77 (25)	−83 (11)	−6 (24)	133 (27)	−1323 (67)	−149 (21)	−1472 (63)	−1339 (58)	−29116 (146)	−30454 (143)
αMOH	133 (16)	−29 (17)	−87 (10)	−116 (18)	17 (18)	−884 (55)	−156 (19)	−1040 (51)	−1023 (50)	−29518 (149)	−30541 (145)
αWO—	134 (16)	114 (28)	−86 (11)	28 (28)	161 (29)	−1561 (82)	−75 (23)	−1637 (76)	−1475 (66)	−76261 (209)	−77736 (202)
αWOH	133 (16)	−25 (17)	−87 (10)	−112 (18)	21 (20)	−944 (61)	−98 (21)	−1043 (55)	−1022 (52)	−76660 (209)	−77682 (202)
βMO—	102 (13)	−608 (31)	−62 (12)	−670 (27)	−569 (29)	−150 (18)	−683 (62)	−683 (62)	−1251 (45)	−21645 (132)	−22896 (127)
βMOH	104 (14)	−507 (23)	−66 (10)	−573 (20)	−469 (24)	−158 (17)	−602 (46)	−602 (62)	−1071 (36)	−22838 (132)	−23908 (128)
βWO—	104 (13)	−582 (33)	−66 (11)	−647 (27)	−544 (33)	−99 (19)	−741 (69)	−741 (69)	−1285 (49)	−58774 (180)	−60058 (177)
βWOH	105 (14)	−488 (23)	−69 (11)	−556 (21)	−452 (24)	−111 (19)	−470 (58)	−470 (58)	−1033 (42)	−61595 (193)	−62627 (189)

The rmsf of each value is given in brackets. The covalent and other intrasolvent molecule contributions to the solvent energy are zero. “uu” refers to the intrasolute interactions, “uv” to the solutesolvent interactions, and “vv” to the solvent–solvent interactions.

The components of the covalent energy (Table VI), the bond, bond-angle, improper and proper dihedral terms, and the total covalent potential energy, are almost identical for all peptides of a given type. The covalent energies for the β-peptide systems are significantly lower than those of the α-peptide systems because of the larger number of bond angle and improper dihedral terms of the latter. As noted earlier, the energies associated with the hydrogen bond restraints are small, less than k_BT, indicating that little force was needed to maintain the helical structure. They are, however, slightly larger for the deprotonated systems, particularly those of the α-peptides, reflecting the greater dynamics of their C-termini.

There is much greater variation in the noncovalent energy terms, particularly the electrostatic terms, between systems (Table VII). Comparing the intrasolute energies (uu), the β-peptides have a much lower energy than the α-peptides, mainly due to the much lower intrasolute electrostatic energy of the β-peptides. For the α-peptides, the deprotonated form has less favorable internal electrostatic energy, but for the β-peptides, the opposite is true.

In contrast, the solute–solvent energy (uv) of the β-peptides is much higher than that of the α-peptides, due to the much higher uv electrostatic energy of the β-peptides, which is only partially compensated for by the lower van der Waals energy. The solute–solvent electrostatic energy of the β-peptides is lower in methanol, whereas for the α-peptides it is lower in water, in keeping with the preferred solvent for helix formation of each type of peptide. The more favorable internal electrostatic potential energy of the β-peptides fits with their lower dipole moment, whereas the α-peptides have more favorable electrostatic interactions with the solvent, mediated by their larger dipole moment and larger hydrophilic SASA.

Overall, once both the intrasolute (uu) and solute–solvent (uv) energies are considered (uu + uv), the total energies of the systems are not markedly different. Note that when comparing the free energy of solvation of different solute molecules in solution, the difference in the contribution to the free energy by the solvent–solvent energy is statistical-mechanically exactly compensated by the difference in the contribution to the free energy by the solvent–solvent entropy.^3–5 This means that the solvent–solvent contributions may be ignored in energetic and entropic considerations regarding the free energy differences between the α- and β-peptides, although they are included in Table VII for completeness.

The αXO— and βXO— systems have a lower uu + uv energy in water, which is more polar solvent than methanol. This effect is greatest for the α—peptides, which have a larger dipole moment than the β-peptides. The αXOH peptides have the same energy in both solvents, whereas the 3₁₄-helical structure of the βXOH peptides is slightly more favorable in methanol, in keeping with the extensive observations of 3₁₄-helical secondary structure for protonated β-peptides in methanol.

Entropy measures

The Schlitter entropy 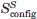provides an upper estimate of the true configurational entropy S_config of a molecule. It was computed for the C^α atoms only, after superposition of the COG followed by a least-squares rotational fit of the C^α atoms, to ensure that the side-chain noise was excluded. The time-series of the entropy (Fig. 7) shows that for the helical fold, it converges within a few nanoseconds, and that the convergence is fastest for the αXO— systems.

Figure 7.

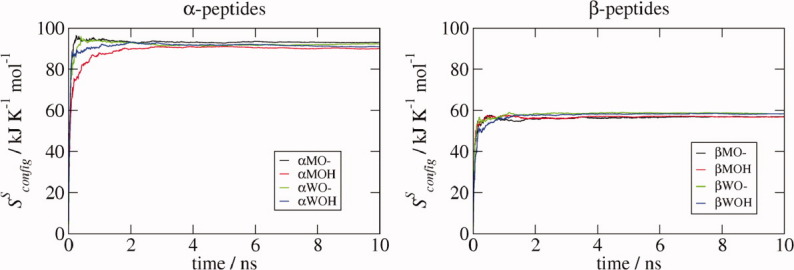
Schlitter entropy 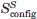. The Schlitter entropy was calculated for the C^α atoms during the 10-ns MD simulations of the various α- and β-peptide systems as labeled. In each case, the structures were first aligned according to the positions of their C^α atoms.

Both the total and atomic Schlitter entropies are higher for the α- than for the β-peptides (Table VIII). For the α-peptides, the entropy is slightly larger when the C-terminus is charged, with a larger difference between the OH and O— systems when they are in methanol. For the β-peptides, the charge of the C-terminus makes no difference, and the entropy is larger in water than in methanol. All of these observations are in keeping with the analysis of the dihedral distributions and atom-positional rmsf.

Table VIII.

Final Values of the Schlitter Entropy 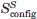(kJ mol ⁻¹ K ⁻¹) and 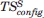(kJ mol ⁻¹) Calculated for the C ^α Atoms and the Sum and Average of the rms Fluctuations of all Dihedral Angles (degrees) for Each of the Different α- and β-Peptide Systems Described in Table II During 10 ns of MD Simulation with the 53A6 GROMOS Force Field⁷

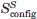				rmsf of Dihedral Angles
Peptide	Per atoma	Total		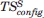Sum	Averageb
αMO—	11.6	93.1	27930	401	19
αMOH	11.3	90.1	27030	269	13
αWO—	11.5	92.3	27690	354	17
αWOH	11.4	90.9	27270	251	12
βMO—	9.5	56.9	17070	348	25
βMOH	9.5	56.8	17040	223	16
βWO—	9.7	58.4	17520	305	22
βWOH	9.7	58.3	17490	205	15

^aThe α-peptides have eight Cα atoms and β-peptides have six Cα atoms

^bThe average is over the total number of dihedral angles in each molecule. Only the φ, ψ and, for the β-peptides, θ backbone dihedral angles were considered, as the ω angles are essentially constant.

The rmsf of the dihedral angles throughout the simulations, excluding the omega angles, which are essentially constant, was also computed as an alternative estimate of the entropy (Table VIII). For the α-peptides, the variation in the rmsf of the dihedral angles shows the same pattern as the variation in the Schlitter entropy for the four systems. For the β-peptides, however, there is much greater variation in the dihedral angle rmsf than in the entropies, indicating that correlations between backbone dihedral angles may play a greater role for β-peptides, as has been noted elsewhere.¹ Unfortunately, as the solute configurational entropy constitutes only part of the total intrasolute and solute–solvent entropy contributions and the latter cannot be reliably calculated, it is not possible to draw any further conclusions from these calculations.

Methods

Molecular systems and simulations

All simulations were performed using MD++ 0.3.0 of the GROMOS05 biomolecular simulation software package⁶ and the 53A6 GROMOS force field.^7,8 Aliphatic CH_n groups of the solute and methanol solvent were treated as united atoms.⁹ The simple point charge (SPC)¹⁰ model was used for water, and the methanol solvent molecules were represented using the rigid three-site model of the standard GROMOS set of solvents.¹¹

The initial coordinates of the α-peptide were those of residues 24–31 of the X-ray crystallographic structure of ubiquitin (PDB entry code 1ubq). Amide hydrogen atoms were added according to standard criteria. The initial coordinates of the β-peptide were those of the first six residues of the NMR structure of the β-heptapeptide H-β-HVal-β-HAla-β-HLeu-(S,S)-β-HAla(αMe)-β-HVal-β-HAla-β-HLeu-OH.^12,13,14 In both cases, all residues were converted to either Ala (α-peptide) or β-HAla (β-peptide) by removing any atoms not present in an Ala or β-HAla residue. The coordinates of the nitrogen of the subsequent residue were used as initial coordinates of the second oxygen of the terminal carboxylic acid group. The protonation state of the C-terminus is indicated by “O—” (deprotonated) or “OH” (protonated) in Table II.

Each peptide was subjected to 2000 steps of steepest descent energy minimization in the GROMOS force field before solvation in a rectangular box of either water or methanol, with a minimum distance of 1.2 nm from any solute atom to the edge of the box and a minimum solute–solvent distance of 0.23 nm. Minimum-image periodic boundary conditions were applied.

All simulations were initiated with the following equilibration scheme: first, the initial velocities were randomly generated from a Maxwell–Boltzmann distribution at 60 K. All solute atoms were restrained to their positions in the corresponding energy-minimized starting structure through a harmonic potential energy term with a force constant of 2.5 × 10⁴ kJ mol⁻¹ nm⁻². The system was simulated with these settings for 20 ps, followed by three consecutive 20 ps simulations; Before each, the temperature was raised by 60 K and the force constant for the positional restraints was reduced by a factor of 10. The position restraints were then removed, and a further 20 ps simulation was carried out at 293 K. The final structure was used as the starting configuration for a 10 ns production run, in which structures were saved every 5 ps.

The SHAKE algorithm¹⁵ was used with a relative tolerance of 10⁻⁴ to constrain bond lengths, allowing for an integration time step of 2 fs. The center of mass motion was removed every 1000 time steps. The temperature and atmospheric pressure were kept constant at 300 K and 1 atmosphere using a weak-coupling approach¹⁶ with relaxation times τ_T = 0.1 ps and τ_p = 0.5 ps and an isothermal compressibility of 4.575 × 10⁻⁴ (kJ mol⁻¹ nm⁻³)⁻¹. Non-bonded interactions were calculated using a triple-range cutoff scheme. The interactions within a cutoff distance of 0.8 nm were calculated at every step from a pair list, which was updated every fifth time step. At this point, interactions between atoms (of charge groups) within 1.4 nm were also calculated and were kept constant between updates. To account for the influence of the dielectric medium outside the cutoff sphere of 1.4 nm, a reaction-field force based on a relative dielectric permittivity ɛ of 61 (water)¹⁷ or 18 (methanol)¹⁸ was added.

To avoid sampling of unfolded structures during the production run, the helix-defining NH—CO hydrogen bonds (Table I) were maintained using a half-harmonic attractive potential energy term with a force constant of 4.0 × 10³ kJ mol⁻¹ nm⁻² for H—O distances larger than the distances 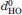given in Table III. For H—O distances greater than 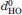+ 0.4 nm, the restraining energy became linear. The values of 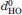were those of the initial structures.

Analysis

All analyses, including the calculation of averages and statistical errors, were carried out using programs in the GROMOS++ 0.3.1⁶ suite of analysis programs. The rmsd, rmsf, and rgyr were computed for the backbone atoms (Cα, C, N, and, for the β-peptides, Cβ). The SASA was computed according to Lee and Richards.¹⁹ For the calculation of the dipole moment, the origin was chosen to be the peptide COG. The Schlitter entropy²⁰ was computed for the C^α atoms (Table VIII) after superposition of the molecular COG and a least-squares rotational fit of the positions of the same set of atoms.

Conclusions

An α-helix of an α-peptide and a 3₁₄-helix of a β-peptide containing an equal number of backbone (non-hydrogen) atoms with two different C-terminus protonation states and in the solvents methanol and water were compared in terms of their dihedral angle distributions, backbone atom-positional fluctuations, hydrophilic and hydrophobic surface areas, solute dipole moments, and energies and entropy measures. With respect to dynamics, the deprotonated α-peptides have more mobile C-termini than the protonated α-peptides, and all α-peptide systems are more flexible and have a higher Schlitter entropy than the β-peptide systems. The two typical structures of the two types of helices compared also possess rather different dipolar and energetic characteristics. In particular, the 3₁₄-helical β-peptides have a more favorable intramolecular electrostatic energy, whereas the α-helical α-peptides have a more favorable solute–solvent electrostatic energy, mediated by their larger hydrophilic SASA and greater dipole moment. Together, these factors explain the greater stability of the α-helix of an α-peptide in water and of the 3₁₄-helix of a β-peptide in methanol and suggest that their helical folds are stable for different reasons: whereas the solute–solvent interaction and intrasolute entropy are larger for α-peptides, the intra-solute interaction is more dominant for β-peptides.