Quantitative assessment of lung microstructure in healthy mice using an MR-based ³He lung morphometry technique

Abstract

The recently developed technique of lung morphometry using hyperpolarized ³He diffusion magnetic resonance (MR) (Yablonskiy DA, Sukstanskii AL, Woods JC, Gierada DS, Quirk JD, Hogg JC, Cooper JD, Conradi MS. J Appl Physiol 107: 1258–1265, 2009) permits in vivo study of lung microstructure at the alveolar level. Originally proposed for human lungs, it also has the potential to study small animals. The technique relies on theoretical developments in the area of gas diffusion in lungs linking the diffusion attenuated MR signal to the lung microstructure. To adapt this technique to small animals, certain modifications in MR protocol and data analysis are required, reflecting the smaller size of mouse alveoli and acinar airways. This is the subject of the present paper. Herein, we established empirical relationships relating diffusion measurements to geometrical parameters of lung acinar airways with dimensions typical for mice and rats by using simulations of diffusion in the airways. We have also adjusted the MR protocol to acquire data with much shorter diffusion times compared with humans to accommodate the substantially smaller acinar airway length. We apply this technique to study mouse lungs ex vivo. Our MR-based measurements yield mean values of lung surface-to-volume ratio of 670 cm⁻¹, alveolar density of 3,200 per mm³, alveolar depth of 55 μm, and mean chord length of 62 μm, all consistent with published data obtained histologically in mice by unbiased methods. The proposed technique can be used for in vivo experiments, opening a door for longitudinal studies of lung morphometry in mice and other small animals.

the efficiency of oxygen delivery through the lung airspaces to the blood vessel network occupying alveolar walls depends mostly on the structure, integrity, and functioning of the pulmonary acinar airways. The morphometry of the pulmonary acinus has been studied in numerous publications. These studies provided invaluable information on lung microstructure that is the basis of the current knowledge on lung structure and function (see, for example, Refs. 7, 15, 16, 23, 35).

Lung stereology, the extraction of the lung spatial geometry from two-dimensional planar sections of tissue, is considered a “gold standard” for lung morphometry (9); however, its clinical applications are limited by its invasive nature. The introduction of hyperpolarized gas magnetic resonance (MR) (19, 27) has opened the door to applications for which gaseous agents are uniquely suited, such as lung MR imaging (MRI) (2). One direction in hyperpolarized ³He gas MRI is lung morphometry that is based on measuring the random atomic motion (diffusion) of ³He gas that is inhaled by a subject. Since the alveolar walls, alveolar ducts, sacs, and respiratory bronchioles serve as obstacles to the path of diffusing ³He atoms, they reduce and restrict the ³He diffusivity. Thus the measured atomic diffusion strongly relates to the lung microstructure. Already, initial publications (5, 25, 26, 37) have demonstrated that the apparent diffusion coefficient (ADC) of hyperpolarized ³He gas in the lungs dramatically increases in emphysema, suggesting a large potential as a diagnostic tool for clinical applications.

Although very encouraging, the ³He gas ADC measurements substantially depend on the details of the technique that is used in MR experiment. Also, ADC does not provide direct measurement of lung geometrical parameters, even though ADC showed correlation with direct morphometric measurements in rats (12, 22), humans (36), and rabbits (18). The ³He lung morphometry technique developed in our laboratory (30, 37, 38) allows MRI-based diffusion measurements to provide unique in vivo information on the lung microstructure at the alveolar level: three-dimensinoal (3D) tomographic images of such geometrical parameters as mean airspace chord length (Lm), lung parenchyma surface-to-volume ratio (S/V), and number of alveoli per unit lung volume (N_a) can be created from a rather short (several seconds) MRI scan. These parameters are most commonly used by lung physiologists to characterize lung morphometry (9) but were not previously available from in vivo studies.

To date, the ³He lung morphometry technique with hyperpolarized ³He diffusion MRI was developed and exploited for human lungs (38). In this study, we use ³He lung morphometry to study lungs in mice. Since mouse lungs have vastly smaller physical parameters, this requires modification of the theoretical equations that relate MRI diffusion measurements to lung microstructural parameters (38). Although the general MRI morphometry theory remains valid, the specific relationships between lung microstructure parameters and diffusion-attenuated MR signal should be modified to fit mouse lungs, which is one of the objectives of this paper. Thus the theoretical model used in our experiment is generalized for the small physical size of mouse lung airways. Also, because the length of acinar airways in mouse lung is much shorter than in humans, the diffusion gradient encoding duration should be shortened to minimize effects of ³He atoms escaping into adjoining airways and distorting the lung morphometry measurements. In this study, we use very short bipolar diffusion-sensitizing gradient pulses (Δ = 440 μs), compared with 1,800 μs in human experiments.

In this paper, we report results obtained with ³He lung morphometry technique in six normal mice and compare them with direct measurements. Our data are in good agreement with the histological values found in the literature for the same mouse strain.

METHODS

Theoretical background.

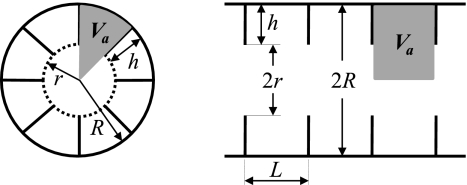
The theoretical background of the ³He lung morphometry technique with hyperpolarized gas MR in mice is similar to that developed in humans (30, 37, 38). Hence, we describe it here only briefly. Measuring the diffusion of ³He gas in lung airspaces can provide valuable information on the lung microstructure. To make the information encoded in the diffusion-attenuated MRI signals quantitative, the relationship between lung microstructural parameters and the MR signal attenuation function is required. In our approach, the lung acinus is treated as a network of acinar airways, cylindrical passages covered with alveolar sleeves (7, 23) where the main geometrical parameters characterizing these airways are the outer radius R and the depth of the alveolar sleeve h (38) (see Fig. 1). Atomic diffusion in each acinar airway is characterized by longitudinal and transverse diffusion coefficients D_L and D_T. Given a large number of acinar airways in lungs (in our experiment, MR signal is collected from the entire mouse lungs, excluding large conducting airways), it is safe to assume a uniform distribution of acinar airway spatial orientations. Accordingly, the diffusion-attenuated MRI signal can be presented as (37):

$$S\left(b\right)=S_{\text{0}}\text{exp}\left(-b·D_T\right){\left(\frac{\pi }{4b{D}_{\text{AN}}}\right)}^{1/2}·\Phi \left[{\left(b{D}_{\text{AN}}\right)}^{1/2}\right],\hspace{0.17em}{D}_{\text{AN}}=D_L-D_T$$ (1)

where b is the so-called b value that depends on the strength and duration of diffusion-weighting gradient waveform (see corresponding expression in the appendix a and Fig. 6) and Φ is the error function. This substantially non-monoexponential dependence of the diffusion-attenuated MR signal on b value was initially confirmed in human (37) and canine (31) lungs. Detail experimental studies were conducted by Jacob et al. (11) in rat lungs, confirming accuracy of Eq. 1 in the broad range of b values. Mathematical equations relating D_L and D_T to acinar airway geometrical parameters R and h that were previously derived for human lungs (30, 38) are modified here in the appendix a to adjust for smaller size of alveoli and acinar airways in mice lungs. Measuring MR signal with multiple b values and fitting theoretical expression in Eq. 1 with D_L and D_T, defined in appendix a by Eqs. A1–A3, to the measured signal, we can find acinar airways geometrical parameters R and h. Finally, knowing these parameters, we can evaluate the lung tissue surface area per alveolus S_a, lung air volume per alveolus V_a, and alveolar number density N_a [the number of alveoli per unit lung volume (38)]:

$$S_{\text{a}}=\frac{\pi }{4}RL+\frac{\pi }{4}h\left(2R-h\right)+2hL;\hspace{0.17em}{V}_{\text{a}}=\frac{\pi }{8}{R}^{2}L;L=2R\sin \frac{\pi }{8};N_{\text{a}}=\frac{1}{V_{\text{a}}}$$ (2)

Fig. 1.

Schematic structure of an acinar airway with eight alveoli distributed along the annular ring (eight-alveolar model). Each airway (duct or sac) can be considered geometrically as a cylindrical object consisting of an alveolar sleeve with alveoli opening toward the internal cylindrical air passage. The diagram defines inner (r) and outer (R) airway radii (as in Fig. 1 in Refs. 7 and 37) and the depth of the alveolar sleeves (h). The ratio L = 0.765R is chosen so that alveolar size is the same along the airway and along the circumference (38). The shaded area shows lung air volume per alveolus V_a that comprises both the volume of alveolus proper and immediately associated duct volume.

Note that the volume V_a comprises both the volume of alveolus proper {π[R² − (R − h)²]L/8} and immediately associated duct volume [π(R − h)²L/8]. Also note that here we are using the acinar airway model with eight alveoli in the cross section (8, 38). Using Eq. 2 that relates acinar airway geometrical parameters R and h to alveoli surface area and volume, and the well known relationship between mean linear intercept and surface-to-volume ratio (34), we can also estimate the mean chord length Lm:

$$S/V=S_{\text{a}}/V_{\text{a}}=4/Lm$$ (3)

Animal preparation.

All experiments were approved by the Washington University Animal Study Committee. We used both lungs excised from freshly euthanized mice (C57BL/6N, males, 3–4 mo of age, food and water provided ad libitum, weight between 21 and 27 g). Each animal was weighed and euthanized with an overdose of anesthetics, 0.1 ml of ketamine cocktail (0.15 ml of xylazine, 1.0 ml of ketamine, and 4.6 ml of sterile saline). The chest cavity was cut open, and the aorta was cut to exsanguinate the animal while the heart was still pumping; clean chest cavity facilitates the lung excision. The trachea was exposed, and the lungs were excised, paying particular attention not to damage the lobes or trachea as the heart and surrounding fat were removed. The trachea was then catheterized by using a plastic needle and ligated (21) to ensure a tight seal. The other end of the plastic needle was sealed with a stopcock valve.

A total of six mice were used for experiments at the same lung inflation pressures; each mouse lung was extracted and prepared using the same protocol.

Gas delivery.

³He gas was hyperpolarized by the spin-exchange technique (33) using a laboratory-built polarizer or a IGI.9600.He commercial polarizer (General Electric Medical, Fairfield, CT) to achieve polarization levels of ∼40%. The hyperpolarized gas from the nearby polarizer was transported in a 1-liter Tedlar bag to the fringe field of the MRI scanner.

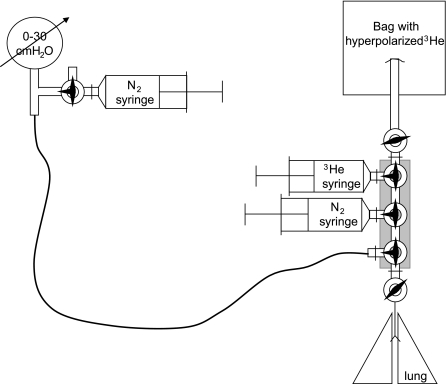
Since oxygen substantially reduces the ³He gas T1 relaxation time constant (24), it was important to reduce the amount of residual oxygen in the lungs before and during delivery of a ³He gas bolus. To achieve that objective, an apparatus for purging and delivering gas was assembled using six valves (Fig. 2). Briefly, the system consists of three syringes, six stopcocks (two on-off and four 3-way valves), a pressure gauge (0–30 cmH₂O), and a Tedlar bag to hold hyperpolarized ³He gas. The syringe close to the pressure gauge is filled with nitrogen and serves to purge the gauge line. The N₂ syringe close to the lungs serves to purge the valve manifold to remove oxygen that enters the manifold after the lungs are disconnected for scanning. The ³He syringe, close to the ³He gas bag, delivers the ³He gas to the lung. To minimize the amount of ³He gas that will be depolarized due to interaction with the walls of small diameter lines, all ³He line connections are made as short as possible (∼14 cm long). To ensure repetitive inflation to the same pressure, a conventional pressure gauge for respiratory research was used.

Fig. 2.

Gas delivery six-valve setup with pressure gauge. The purpose is to allow the lungs to be purged of air multiple times using N₂ and then filled with ³He for the nuclear magnetic resonance (NMR) measurement of diffusion. The 180-cm-long line keeps the pressure gauge containing ferromagnetic parts out of the scanner's fringe field.

The catheterized lungs were immobilized in the center of the ³He coil, and the coil and the lung valve were connected to the six-valve gas delivery setup (Fig. 2). Immediately before the MR experiment, the lungs were purged five times of oxygen to 30 cmH₂O pressure with pure ³He gas. This procedure ensures that the concentration of ³He gas in lungs is practically the same (close to 100%) for all experiments. At this pressure, the typical volume of the C57 mouse lungs is ∼1 ml (29). The first 850 μl of gas delivered to the lung is hyperpolarized ³He, followed by ∼150 μl of N₂. The purpose of this N₂ blanket is to replace ³He gas in the large conducting airways (non-acinar portion of the lungs, typically 11% of mice lungs) (10) with N₂, minimizing the MR signal contribution from large airways and focusing the measurement on the acinar portion of the lungs.

Other than removal of oxygen, the main objectives of the six-valve system are repeatable delivery of hyperpolarized ³He with consistent lung inflation and a precise topping with the N₂ blanket.

MR experiment.

All MR measurements were performed on a Varian 4.7 T scanner with 60 G/cm gradients with 120-mm horizontal bore. The scanner is equipped with broadband capabilities for MR at the ³He frequency of 152.1 MHz. For transmission and reception at the ³He frequency, a dedicated home-built, single-loop coil was used. The coil was manually tuned at the ³He Larmor frequency; the effects of loading by the lungs were small.

B₀ field shimming was conducted using a 17-mm sphere of water in the ³He coil connected to a retuning network. The network allowed the ³He coil to be retuned to the ¹H frequency (199 MHz) for B₀ field shimming without disturbing the ³He coil.

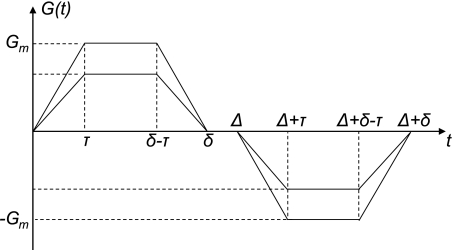
Signal was collected from the whole lung by applying a broad-band radio frequency (RF) pulse and collecting free-induction decay data without any spatial encoding. The bipolar diffusion-sensitizing gradients were inserted between the RF excitation pulse and data acquisition to generate diffusion attenuation of the MR signal. The diffusion gradient waveform had the following parameters: τ = 0.175 ms, Δ = δ = 440 μs, and shape as shown in Fig. 6 (appendix a). Parameters δ and Δ define each gradient pulse duration and the beginning of the second gradient pulse, respectively. As the two gradient pulses are applied consecutively, Δ and δ are the same in our pulse sequence. Time τ is fixed in the sequence; that is, the rise/fall time of each gradient pulse is independent of the gradient strength (see Fig. 6). The gradient waveform slope was controlled to achieve this constant ramp-up and ramp-down time τ, independent of b value; the maximum b value was varied by varying only the maximum gradient amplitude G_m. We assured that the sequence never called for faster gradient ramp rate than the hardware limitation.

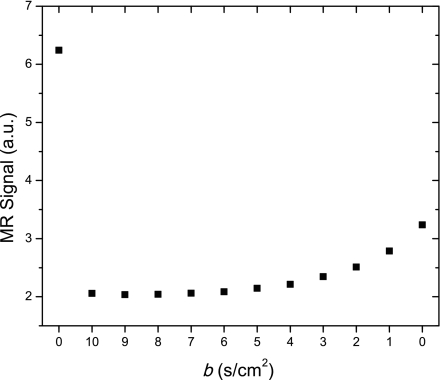
The sequence is a multi-b value experiment that uses 12 measurement with b values (0, 10, 9, 8, 7, …, 2, 1, 0), each with an acquisition time of 50 ms, on a single bolus of helium gas. This descending order for b values was chosen to better use the naturally decreasing SNR in ³He experiments: apply the large b values first while the ³He has strong polarization, and apply the weakest b values last, when the polarization is reduced by ∼60%. Each RF pulse inflicts a loss of nuclear polarization of the hyperpolarized ³He gas. A tradeoff in selecting RF pulse flip angle was made between maximizing the signal extraction from each RF pulse and maintaining polarization for subsequent signals. We chose a flip angle of 20°, leaving ∼45% of the ³He polarization after the last RF pulse. Naturally, the precision of this quantity is dependent on the precision of the flip angle calibration. Preliminary calibration of the flip angle α was conducted using a 10-ml syringe filled with pure hyperpolarized ³He gas, subjected to a train of 20 RF pulses of fixed duration and strength. Final determination of the flip angle was done by comparing the first and the last values of the signal amplitude obtained with zero gradient (b = 0) (see Fig. 3), using s₁ = s₁₂(cos α)¹¹. In all experiments, the flip angle so obtained agreed closely with the value from the calibrating procedure.

Fig. 3.

Example of uncorrected magnetic resonance (MR) signal amplitude (arbitrary units). Data are shown as they were acquired (b = 0, 10, 9, 8, … 2, 1, 0 s/cm²). Two b = 0 signals, at the beginning and the end of the sequence, have different amplitudes since polarization is consumed by radio frequency (RF) pulses during the measurement. These two signals are used to determine the RF pulse flip angle for later correction of the amplitudes.

Each full data set is acquired in <1 s. Each of three axis directions (x, y, and z) is scanned individually with a new batch of hyperpolarized ³He gas.

Data analysis.

The amplitude of each acquired MR signal was estimated using Bayesian analysis software (4) in the time domain. With the true flip angle known (see previous section), each measured signal amplitude is corrected by dividing by (cos α)ⁿ, where n indicates the number of previous RF pulses. The data are then plotted as a function of b value and normalized to 100. The corrected data are analyzed using Eqs. 1 and A1–A3 (as described in the appendix a) to obtain the key lung microstructure parameters, R and h. The data are analyzed using OriginPro 7.5 (OriginLab; Northampton, MA).

The theoretical equations connecting the MR measurements to the lung geometrical parameters (Eqs. 1 and A1–A3) rely on knowledge of the ³He free diffusion coefficient D₀ (recall that, in our experiments, the lungs are filled with pure ³He gas). To measure D₀, ∼10 ml of hyperpolarized ³He gas from the same batch of gas is scanned in a syringe using the same 12 b-value sequence with a substantially lower range of b values, b = 0, 1.5, 1.35, 1.2, …, 0.3, 0.15, 0. The result of this measurement was D₀ = 1.76 cm²/s with very small variation, which is in good agreement with similar values found in the literature (1.8 ± 0.2 cm²/s) (1, 28) for 20°C, the temperature maintained for all our experiments.

RESULTS AND DISCUSSION

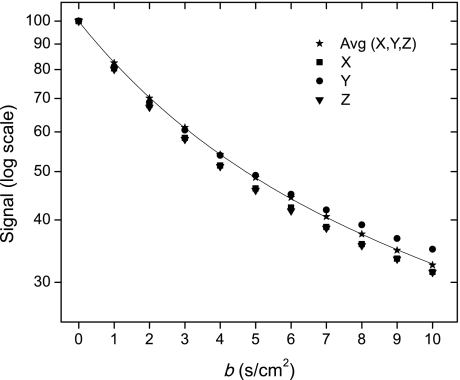
An example of the raw data set corresponding to the MR signal amplitude acquired with the 12b sequence is shown in Fig. 3. A typical dependence of the corrected amplitudes on the b value is shown on a log scale in Fig. 4 (symbols) along with the fitting curve (solid line). Data are presented for three directions of applied diffusion sensitizing gradients and demonstrate a small anisotropy. This is consistent with the results of Mitzner et al. (20) who demonstrated in mice that lung structure is slightly anisotropic even at the macroscopic level. These authors provided evidence that the measured mean linear intercept Lm is dependent on the planar orientation of the sample. Specifically, Lm along the ventral-dorsal axis of the lung tissue was on average 7.4% greater than Lm measured in the perpendicular direction. Our approach takes into account the anisotropic structure of the lung acinar airways at the microscopic level; however, it assumes isotropy of airway orientations at the macroscopic level. That is, the airways are oriented in all directions essentially equally. In principle, we could introduce this anisotropy at the macroscopic level in our equations, which would further increase the model complexity. Instead, to avoid potential bias based on this effect and retain the model's isotropy at the macroscopic level, we collected data for three spatially orthogonal directions of diffusion sensitizing gradients and averaged the MR signals together before data analysis. The result shown in Fig. 4 demonstrates an excellent fit with χ² = 0.045. For this individual measurement, lung microstructure parameters are R = 103.7 ± 2.9 μm and h = 63.1 ± 1.1 μm. An important feature of the diffusion attenuated MR signal dependence on b value is the substantial deviation from the monoexponential behavior (deviation from a straight line on the logarithmic scale in Fig. 4), in agreement with the theoretical prediction and experimental data obtained in human lungs (37).

Fig. 4.

Typical dependence of the corrected diffusion attenuated MR signal amplitude (logarithmic scale) on b value (symbols) for x, y, and z directions of applied diffusion sensitizing gradients. Also shown is the average MR signal with the fitting curve (solid line). Result demonstrates an excellent fit with χ² = 0.045. A very important feature is the substantial deviation of the MR signal from mono-exponential behavior (deviation from straight line), in agreement with theoretical prediction, in Ref. 37 and the theory presented in this paper.

The complete set of morphometric data for all six mice is summarized in Table 1. Our average measurement of the mean linear intercept Lm (computed using Eqs. 2 and 3) is ∼62 μm. This corresponds to a surface-to-volume ratio of the air spaces of 670 cm²/ml. We also found that an average alveolar density, N_a, is ∼3,200 per mm³. The corresponding numbers that we found previously (38) in normal human lungs (S/V of ∼200–240 cm²/ml and N_a of ∼120–150 per mm³) were in good agreement with direct histological measurements.

Table 1.

Summary of geometrical and diffusion parameters from excised lungs of six mice

Mouse No.	R, μm	h, μm	Sa/Va, cm−1	Lm, μm	Na, mm−3	DL0, cm2/s	DT0, cm2/s	βL
1	104 ± 3	63 ± 1	738	54.2	2,984	0.741	0.0114	0.0174
2	108 ± 11	48 ± 5	555	72.1	2,656	0.877	0.0144	0.0081
3	84 ± 5	46 ± 2	836	47.8	5,594	0.642	0.0063	0.0117
4	119 ± 3	64 ± 1	580	69.0	1,969	0.679	0.0235	0.0181
5	109 ± 4	47 ± 1	524	76.4	2,548	0.796	0.0170	0.0075
6	97 ± 10	59 ± 2	788	50.8	3,634	0.486	0.0133	0.0216
Mean	103.5	54.6	670	61.7	3,231	0.704	0.0143	0.0141
SD	11.9	8.3	133	12.2	1,280	0.135	0.0058	0.0058

The table gives values of key parameters in our model: major airway radius (R) and the depth of alveolar sleeve (h) (mean ± fit uncertainty), and mean calculated values of alveolar surface-to-volume ratio (S/V), mean chord length (Lm) and alveolar density (N_a). Average diffusion along and perpendicular to the airways is 0.7 and 0.0143 cm²/s, respectively. Both diffusion parameters, D_L and D_T, are sharply reduced from ³He free diffusion (D₀ = 1.76 cm²/s) as the alveolar ducts and walls present obstacles to diffusing ³He atoms. Quantity β_L is kurtosis factor for longitudinal diffusivity. The variability between different mice most likely reflects variability in the lung inflation level that is difficult to control in excised mice even for a constant inflation pressure.

For comparison with the data reported in Table 1, we have compiled in Table 2 various results from the literature obtained by stereological analysis of mouse lungs (6, 13–17, 20, 29, 32). The studies assessed alveolar number, mean linear intercept of air spaces, and the surface-to-volume ratio, as well as mean alveolar volume [v(alv)]; this latter value allowed obtaining an approximate estimate of h = v(alv)^1/3 assuming a cubic shape of alveoli in first approximation. The data show considerable variation, which may reflect significant differences between animals; but some of this may be due to different inflation levels achieved in fixation since the measured lung volumes varied by a factor of 3. Results obtained in this study for Lm, S/V, and N_a are within the range of published data (Table 2). Some of the differences may also be related to the fact that the lungs prepared for microscopic morphometry are generally fixed by fluid instillation at 20 cmH₂O, whereas in the present study the helium gas was applied at a pressure of 30 cmH₂O, resulting in a larger volume. The lower pressure and the fluid-filled state may have affected some of the microscopic measurements.

Table 2.

Morphometric data from microscopic studies from various literature sources obtained by stereological analysis of mouse lungs using animals of different strain, age, and size

Source	Strain	Age, wk	Mb, g	VL, cm3	Lm, μm	NV(a), 103 mm−3	h, μm	v(a), 103 μm3	Sa/Va, cm−1
Voswinckel (32)	C57BL/6	12–16	24.3	0.721	54		37†	51	740
Knudsen (14)	C57BL/6	12		0.680	35	14.1	39†	59	1150
Soutière (29)	C57BL/6J	6–8		0.95–1.45	45–63
Fehrenbach (6)	C57BL/6	12–14		0.432		2.7
Mitzner (20)	C57BL/6	10–12		1.2	52				770
Knust (16)	C57BL/6	6.5–10	20.6	0.307	85	9.6	39†	59	470
Lee (17)	C57BL/6J	7–9			38
Kang (13)	C57BL/6J	12		1.7	55
Knudsen (15)	C57BL/6*	12		0.64	39				915
Overall range		6–16	20–25	0.4–1.5	40–80	3–14	30–50		500–1000
This study	C57BL/6N	12–16	21–27	∼1.2	61.7 ± 12	3.2 ± 1.3	55 ± 8		670 ± 133

The measured lung volumes varied by a factor of 3, some of which may be due to different inflation levels achieved in fixation.

^*SPD-deficient mice treated with recombinant SPD;

^†h = v(alv)^1/3.

The published data (6, 13–17, 20, 29, 32) do not contain estimates of the morphometric parameters of alveolar ducts, such as their major radius R that comprises both the inner duct radius r and the alveolar sleeve of depth h (Fig. 1). Such data characterizing the structure of acini have been obtained for human, rat, and rabbit lungs (7, 23). Here, for illustration purposes, we present data obtained in an as yet unpublished identical study by one of the co-authors (E. R. Weibel) of the acinus of the mouse lung that provided a limited number of specimens on which the size characteristics of mouse alveolar ducts could be estimated. These studies were based on two types of preparations: silicone rubber casts filled to ∼70% total lung capacity (TLC) (23) and perfusion fixed lungs air-inflated at ∼60% TLC (3); examples of these preparations are shown in Fig. 5, A and B. The specimens were obtained on BALB/6 mice of ∼40 g and a total lung volume of 0.8–1.0 ml following the methods described in Ref. 23. The two specimens are different in terms of preparation artifacts: the silicon rubber cast does not shrink during preparation and thus shows the real size of the structures; in contrast, the lungs fixed by vascular perfusion suffered considerable shrinkage during the preparation procedures, mainly because of critical point drying. We estimate that measurements obtained on the perfusion fixed specimen must be corrected by a factor of 1.6; this is about the difference in the size of alveoli in Fig. 5, A and B. The very small size of mouse acini (mean volume ∼0.1 mm³) rendered a rigorous morphometric analysis of the duct structure, as done for larger lungs (7, 23), difficult, but it was possible to determine an approximate range for the parameters R, r, and h, as marked on a few examples in Fig. 5. We find that the inner duct radius r, marked by double-pointed arrows, measures on the order of 40–75 μm and shows systematic variation being nearly two times as wide in the ducts of the first generations following on the transitional bronchiole (trb) compared with more peripheral ducts; this agrees with the pattern found in rat, rabbit, and human lungs (7, 23). The outer radius R, marked by a bar, varies in the same sense but to a lesser degree with a range of 70–100 μm. The size of alveoli (a) varies considerably in the range of 30–55 μm. These results show a reasonable agreement with our MRI measurements.

Fig. 5.

Left: scanning electron micrograph of segment of a partly dissected silicone-rubber cast of an acinus of a mouse lung showing the transitional bronchiole (trb) as entrance airway and alveoli (a) grouped around alveolar ducts, which have been partly separated. Asterisk marks a transected alveolar duct with diameter 2r. Bars mark approximate outer diameter 2R. Right: scanning electron micrograph of a perfusion-fixed mouse lung air-inflated to ∼60% total lung capacity showing a transitional bronchiole (trb) that opens into the acinus (arrow). Double-pointed arrows mark the inner diameter 2r of alveolar ducts that are wide in the first generations of branching and taper somewhat toward the periphery; the bar marks the outer diameter 2R that comprises the sleeve of alveoli (a). Range of measured values: R = 70–100 μm; r = 40–75 μm; h = 30–55 μm.

Certain phenomena, not taken into consideration by our model and experimental method, can affect the accuracy of the results obtained with ³He lung morphometry technique. First, we mention that our model assumes that during the diffusion experiment of duration 2Δ = 880 μs, most ³He atoms spend their time diffusing in a single airway. Because the average mouse lung mean alveolar diameter and acinar airway length are much smaller than in humans, in this study we used very short bipolar diffusion-sensitizing gradient pulses (δ = Δ = 440 μs) compared with 2Δ = 3,600 μs used in human experiments (38). This decreases the fraction of ³He atoms escaping into adjoining airways and distorting the lung morphometry measurements. In principle, this effect could be further reduced by using still smaller diffusion times; however, hardware limitations in our case would not allow for further improvement.

To minimize the undesirable contribution of ³He gas in conducting airways to our measurements, we followed the ³He gas delivery with 15% of inert N₂. Practically, this may lead to partial mixing of ³He and N₂ gases resulting in a reduced ³He diffusion coefficient D₀ in some regions. If we assume the dilution level of ³He to be 90%, the corresponding reduction in D₀ will be from 1.76 cm²/s for 100% ³He concentration to ∼1.58 cm²/s. Substituting this reduced D₀ in the equations used for data analysis yielded average changes of geometrical parameters R and h of only 3.6% and −4.3%, respectively. Thus we expect that ³He-N₂ gas mixing between large and small airways causes errors no more than 5% in estimation of the geometrical parameters R and h.

Our model is limited to the adopted lung microstructure and its simplified representation. The data analysis provides an overall average of the distribution of the airway and alveolar sizes throughout the lungs. The main geometric parameters characterizing acinar airways are the internal acinar airway radius r and the outer radius R (which includes the sleeve of alveoli with its depth, h) (7). Both of these parameters (R and r, thus R and h) vary depending on the position and branching level of the acinar airway tree. Our method assumes that we can characterize the diffusion attenuated MR signal in terms of the average characteristics across the acinus and, further, across the lung. In humans this is justified by experimental measurements of Haefeli-Bleuer and Weibel who found that the variation in parameter distribution is rather small: the distribution width is 16% for R and 20% for r (7). In this paper, we also make an assumption of the “narrowness” of the distributions of parameters R and r and characterize our result by average parameters R, r, and h in mice.

In this work, we studied only lungs obtained from healthy mice. The theoretical model developed here is suitable to describe deformation/destruction of lung microstructure only in the initial stages of emphysema that can be characterized by airways inflation and retraction of alveolar sleeve (8, 38). At advanced stages of emphysema, characterized by severe destruction of lung parenchyma, lung microstructure can no longer be described in terms of cylindrical acinar airways; hence, parameters of lung airways measured by ³He lung morphometry technique can only be considered as apparent. However, validation data obtained in human lungs (38) demonstrated that the measurements of Lm using ³He lung morphometry even in severely emphysematous lungs were in excellent agreement with direct histological measurements.

Conclusions.

In this paper, we established empirical relationships that connect MRI measurements of ³He gas diffusion-attenuated MRI signal in mouse lungs with the geometrical parameters of lung acinar airways. We have also developed an MR protocol to acquire data with much shorter diffusion times compared with human measurements to accommodate the substantially smaller acinar airway length. We applied this technique to study mouse lungs and demonstrated that MR-based measurements of hyperpolarized ³He diffusion in mouse lungs provides quantitative information on acinar airway dimensions and lung surface-to-volume ratio consistent with published histological values and our direct estimates. Our measurements confirm that the diffusion of ³He gas in the mouse lung is anisotropic at the microscopic level but practically isotropic at the macroscopic level, thus explaining the non-mono-exponential behavior of diffusion-attenuated MR signal in lungs.

The developed method creates a basis for in vivo study of lung microstructure in small animals similar to the previously developed method of ³He lung morphometry in humans (38).

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grants R01 HL-70037 and P50 HL-084922.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX A

Relationships between ³He diffusion attenuated MR signal and acinar airways geometrical parameters in mouse lungs

As mentioned above, the ³He lung morphometry technique developed in (30, 37, 38) is based on considering the lung on the acinar level as a set of airways of cylindrical geometry, covered by alveolar sleeves (7, 23), as in Fig. 1. Diffusion of ³He atoms in the airways is microscopically anisotropic and is described by two principal parameters: longitudinal (D_L) and transverse (D_T) diffusion coefficients (37). The dependence of the MR signal on these parameters is given in Eq. 1. In Ref. 30, the diffusion coefficients D_L and D_T were related to the airways geometrical parameters R and h (see Fig. 1), which made it possible to determine R and h from the diffusion-attenuated multi-b MR experiments. It was further demonstrated in Ref. 38 that the airway geometrical parameters are related to the commonly used morphometric parameters of the lung microstructure, such as mean linear intercept L_m and surface-to-volume ratio S/V (see Eqs. 2 and 3).

It should be noted, however, that the relationships between D_L, D_T, R, and h, obtained in Ref. 38 by means of computer simulations, are not universal and are valid only within the range of the airway size R characteristic of human lungs (R of ∼300 μm). In mice, the airway radii R are substantially smaller (R of ∼100 μm). In the present study, we have found modified relationships between D_L and D_T and R and h for the range of airway radii characteristic for mice and rats: R of ∼60–140 μm and for the pulse sequence parameters with diffusion times corresponding to smaller airway length, as used here. Specifically, the new equations are valid for Δ = δ ∼0.3–0.6 ms. The following relationships were obtained using this approach, based on computer simulations similar to those developed in Ref. 30:

$$\begin{array}{l}{D}_{\text{L}}=D_{\text{L0}}·\left(1-{\beta }_{\text{L}}·b{D}_{\text{L0}}\right)\hfill \\ D_{\text{T}}=D_{\text{T0}}·\left(1+{\beta }_{\text{T}}·b{D}_{\text{T0}}\right)\hfill \end{array}$$ (A1)

where

$$\begin{array}{l}{D}_{\text{L0}}=D_{\text{0}}·\exp \left(-2.99·v^{1.88}\right),v=1-r/R,\hspace{0.17em}{\beta }_{\text{L}}=113.5·{\left(\frac{R}{L_1}\right)}^{1.5}·\exp \left(-5.11/\sqrt{v}\right)\hfill \\ D_{\text{T0}}={\text{D}}_{\text{0}}·\text{F}\left(\text{R}\right)·\left[1+u\left(R,r\right)\right],\hspace{0.17em}F\left(R\right)=\frac{7}{16}·x^{\left(4-3.63\cdot x^{0.6}\right)},x=R/L_2\hfill \\ u\left(R,r\right)=v^{1.75}·\exp \left(A·v\right),A=1.1+3.14·x-18.39·x^2,{\beta }_{\text{T}}=0\hfill \end{array}$$ (A2)

where D₀ is the free diffusion coefficient of ³He gas in lung airspaces. Values

$$L_1={\left(2D_0\Delta \right)}^{1/2},L_2={\left(4D_0\Delta \right)}^{1/2}$$ (A3)

are the characteristic free-diffusion lengths for one- and two-dimensional diffusion. The relationships in Eq. A2 are purely phenomenological; specific mathematical functions are chosen solely to fit the simulations. During the data analysis, we found virtually no transverse diffusion (D_T) dependence on b value; thus the analysis was conducted with β_T = 0.

The b value in the 12b diffusion-attenuated MR experiment is determined by a standard relationship (37):

$$b={\left(\gamma G_{\text{m}}\right)}^2\left[{\delta }^2\left(\Delta -\frac{\delta }{3}\right)+\tau \left({\delta }^2-2\Delta \delta +\Delta \tau -\frac{7}{6}\delta \tau +\frac{8}{15}{\tau }^2\right)\right]$$ (A4)

Using the Eqs. A1–A3 in conjunction with multi-b MR (Fig. 6)) signal measurements in mouse lung acinar airways enables calculation of the geometrical parameters R and h as well as standard morphometric parameters of lung airways: L_m, S/V, N_a (see Eqs. 2 and 3).

Fig. 6.

Bipolar diffusion gradient pulse shape used in our experiment and to derive the relationship between gradient strength and b value. Rise time (τ) remains constant for various gradient values. In experiments, we used waveform without the gap (Δ = δ).

APPENDIX B

Gradient calibration

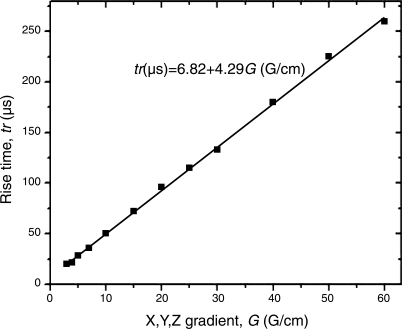
The accuracy of the measurements of the lung microstructural parameters depends in part on the performance of the gradient coils. In particular, precise gradient rise and fall times and gradient strengths should be known accurately for calculation of b values in Eq. A4. To measure and calibrate the gradient coil characteristics, we used an induction-based gradient pickup coil consisting of four spatially offset coils able to record gradients in the x and z (or y and z) directions. The coils feed the gradient signal to electronics for time integration and display on an oscilloscope. The gradient slew rates were measured and tabulated for all three axes through the full range of gradient strengths (Fig. 7). The relationship found in this graph is coded into the pulse sequence to ensure that the calculated slew rate for a given b value never exceeds the slew rate that the system is capable of delivering. After coding the sequence to control the slope, its precision has been confirmed using a gradient pickup coil-oscilloscope setup.

Fig. 7.

Rise times of gradient pulses through the entire range of gradient strengths. Results were identical for all three axes and for negative amplitudes. The solid curve is fit to the data with the expression shown.