Age-related changes in the control of finger force vectors

Abstract

We explored changes in finger interaction in the process of healthy aging as a window into neural control strategies of natural movements. In particular, we quantified the amount of force produced by noninstructed fingers in different directions, the amount of force produced by the instructed finger orthogonally to the task direction, and the strength of multifinger synergies stabilizing the total force magnitude and direction during accurate force production. Healthy elderly participants performed accurate isometric force production tasks in five directions by individual fingers and by all four fingers acting together. Their data were compared with a dataset obtained in a similar earlier study of young subjects. Finger force vectors were measured using six-component force/torque sensors. Multifinger synergies were quantified using the framework of the uncontrolled manifold hypothesis. The elderly participants produced lower force magnitudes by noninstructed fingers and higher force magnitudes by instructed fingers in nontask directions. They showed strong synergies stabilizing the magnitude and direction of the total force vector. However, the synergy indexes were significantly lower than those observed in the earlier study of young subjects. The results are consistent with an earlier hypothesis of preferential weakening of intrinsic hand muscles with age. We interpret the findings as a shift in motor control from synergic to element-based, which may be causally linked to the documented progressive neuronal death at different levels of the neural axis.

aging is associated with major changes in the neuromuscular system (69). In particular, there is a drop in the number of motor units, an increase in the average size of the motor units, and a general slowing of their contractile properties (15, 16, 26, 31, 33, 51). These changes are accompanied by a decline in hand dexterity and strength (5, 21, 25, 28, 30, 53). Several studies reported lower accuracy and higher variability in force production tasks by elderly subjects (6–8, 19, 67, 73). Age-related changes in force variability were most commonly studied in a one-element task, such as index finger abduction.

Most natural human actions involve redundant sets of elements, that is, sets that allow numerous (an infinite number of) solutions for typical motor tasks (4). Recently, the problem of motor redundancy has been revisited based on the principle of motor abundance and the notion of motor synergies (24). Synergies have been defined as neural organizations ensuring covaried adjustments in elemental variables that reduce variability of potentially important performance variables (40, 43, 45). A computational apparatus for quantitative analysis of synergies has been developed within the uncontrolled manifold (UCM) hypothesis framework (57). According to this hypothesis, the central nervous system acts in the space of elemental variables, creates in that space a subspace (UCM) corresponding to a desired value of a performance variable, and then keeps most of the variance within that subspace.

Several studies quantified multidigit synergies in young and elderly subjects during accurate multidigit force and moment-of-force production tasks (50, 61, 63–65). These studies documented an impaired ability of the elderly subjects to organize covariation of commands to individual digits, which would stabilize their combined mechanical output.

Healthy aging is associated with changes in other indexes of finger interaction. In particular, when a person tries to perform an action (movement or force production) with one finger, other fingers of the hand typically show unintended movement or force production (34, 35, 39, 46, 76). Peripheral factors, such as multitendon extrinsic hand muscles and connective tissue links between adjacent fingers, and neural factors, possibly related to overlaps in cortical finger representations, contribute to this phenomenon, which is termed enslaving (55). Several studies have documented a counterintuitive drop in the index of enslaving in older persons (63, 64).

A major limitation of most cited studies is that they used force production tasks in only one direction, typically normal to the contact surface. Most everyday tasks, such as manipulating hand-held objects, pushing a shopping cart, and turning a door knob, require accurate production not only of force magnitude, but also of force direction. The main purpose of the present study was to quantify age-related changes in finger interaction in tasks that require accurate production of force vectors by single fingers and by sets of fingers in three dimensions. At this stage, we limited the study to pressing tasks, which allows standardization of tasks and quantification of finger force components.

Recently, we analyzed the performance of young healthy subjects in one-finger and multifinger tasks that required accurate force vector production (32). Those studies documented and quantified multifinger synergies stabilizing force vector magnitude and direction. They also quantified unintended force production during one-finger tasks. In particular, quantification of unintended production of shear forces demonstrated unusual patterns, with some of the fingers producing unintended shear forces in a direction opposite to the direction of the instructed force by the task finger (52). The study (32) also introduced an index for unintentional force production reflecting forces produced by a task finger in a direction orthogonal to the instructed direction (9).

On the basis of earlier studies (63, 64), we hypothesize that elderly subjects will show lower enslaving for the downward forces.

Similar patterns of enslaving have been documented in young persons for pressing tasks at fingertips and at proximal phalanges (41). Pressing at distal phalanges is produced primarily by extrinsic multitendon muscles, while finger-specific intrinsic muscles serve as prime movers during pressing by proximal phalanges (38, 47). Hence, this finding has been interpreted as an indication that similar neural mechanisms are responsible for the enslaving effects in actions with extrinsic or intrinsic hand muscles as focal force generators. Since shear forces are mostly produced by finger-specific intrinsic hand muscles, we hypothesized that enslaving in shear forces would show a drop with age similar to that documented in the earlier studies of pressing with fingertips (63, 64).

The phenomenon of unintended within-a-finger force production in a direction orthogonal to the required direction likely reflects the coordination of the intrinsic and extrinsic muscles serving the task finger (see discussion). We are unaware of studies that would quantify muscle coordination and its changes with age in accurate force production tasks in specific directions. On the basis of the earlier reports of impaired multifinger synergies in the elderly (50, 63), we hypothesized that changes in this index might be opposite to the changes in enslaving; that is, this index would show an increase with age.

On the basis of earlier studies (9, 65), we expected the elderly to be less accurate in producing force magnitude and direction. We hypothesized that this higher motor variability would be associated with lower indexes of multifinger synergies stabilizing those variables. This hypothesis is not trivial, since the synergy index used in this and earlier studies (32, 42, 63–65) reflects the relative amounts of variance compatible with a certain value of a potentially important performance variable (variance within the UCM or “good variability”) in the total variance. Variability of the performance variable reflects the other component of variance (variance orthogonal to the UCM or “bad variability”). So, in general, it is possible to have a lower index of synergy computed for a particular performance variable because of lower good variability and lower variability of that variable.

METHODS

In this study, we present original data collected in a group of elderly subjects. We compare those data with data from an earlier study of young, healthy subjects (32). This previous study used the same numbers of male and female subjects, the same setup, and the same data-processing methods. The only difference between the present study and our previous study (32) was a larger number of conditions (trials) performed by the young subjects. In the present study, we reduced the number of conditions to ensure that the elderly subjects did not show deterioration of performance due to general fatigue and loss of concentration. The particular conditions were selected to explore age-related changes in the significant effects that were seen across the conditions in the young subjects.

Subjects

Eight elderly subjects (4 men and 4 women) volunteered to participate in the study. Their age was 76.4 ± 2.5 (SD) yr, height was 166.69 ± 13.58 cm, weight was 159.5 ± 34.8 pounds, hand length from the proximal palmar crease to the tip of the middle finger was 18.84 ± 2.36 cm, and hand width at the level of metacarpal heads was 8.33 ± 0.84 cm. All subjects were healthy and right-handed according to their hand usage during writing and eating, and none had diagnosed neurological or peripheral musculoskeletal pathology that could significantly affect the right-hand function. None reported to have been professionally engaged in any activity that might affect hand dexterity (such as being a professional typist or piano player). The elderly subjects were recruited from a local retirement community and passed a screening process that involved a cognition test (mini-mental status exam ≥24 points), a depression test (Beck depression inventory ≤20 points), a quantitative sensory test (monofilaments ≤3.22), and a general neurological examination. Prior to the study, all subjects gave informed consent according to the procedures approved by the Office for Research Protections of The Pennsylvania State University.

Apparatus

Two setups were used in the experiments. The main part of the experiment used four multicomponent force transducers (Nano-17, ATI Industrial Automation, Garner, NC) to measure the three components of force vector applied to the sensor surface by the tip of each finger of the right hand. The transducers were placed within a frame, such that the horizontal distance between the centers of two adjacent transducers was 2 cm. The forward-backward location of the sensors could be adjusted for differences in the length of the subjects' fingers. The sensor surfaces were covered by P-100 sandpaper to increase friction. The transducers were oriented such that the force signals along the three orthogonal axes increased upward (z-axis), to the right (x-axis), and forward (y-axis), as shown in Fig. 1B.

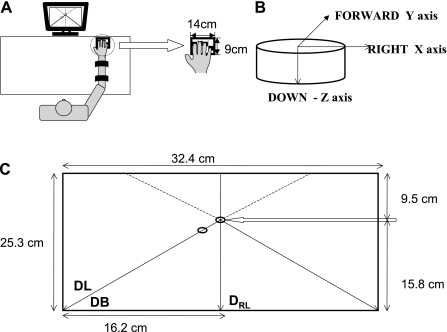
Fig. 1.

A: experimental setup. B: orientation of the 6-component force/torque sensors. C: schematic of feedback screen. Arrow points at the starting location corresponding to zero active force. Vertical line always represented z (downward) direction. Horizontal axis on screen depicted x (right-left) or y (forward-backward) direction, depending on task. Cursor controlled by the subject was expected to follow closely the target circle that moved at a constant rate along the required direction of force production. D_RL, pressing down with feedback on the right-left force changes; DL, downward-leftward; DB, downward-backward.

The frame with the sensors was placed on the surface of a table. The subject sat comfortably in front of the table with the right elbow flexed at ∼90° and the right shoulder slightly flexed and abducted (Fig. 1A). A hand rest was placed below the palm to help maintain a comfortable and constant hand configuration. The subject maintained the same position of the upper extremity throughout the experiment.

The second setup was used only in the tests with downward maximal voluntary force [maximal voluntary contraction (MVC)] production (MVC tests; see Procedure). Finger forces were measured with a set of unidirectional force sensors (model 208C02, PCB Piezotronics), because the multicomponent sensors saturated at high forces. Otherwise, the setup used in the MVC tests was similar to that described above (Fig. 1A).

The signals from the sensors were amplified and sampled at 16 bits using a digital-to-analog converter (model PCI-6225, National Instruments, Austin, TX) at a frequency of 200 Hz. The data were collected on a desktop computer with custom software written in LabView (National Instruments).

Procedure

The experiment consisted of two parts: one- and four-finger pressing tasks. Prior to the main part of the experiment, MVCs were recorded for each of the four fingers and for the four fingers acting together, in a random order. In those trials, the subject had up to 3 s to produce maximal pressing force in the downward direction. The subject was instructed to “press as hard as possible.” Two MVC trials were performed in a row by each finger and by the four fingers together, and the maximum force produced over the two trials was used in the calculations. The MVC trials were separated by 30-s intervals. On the screen, the subject was shown feedback of the downward force produced by the task finger(s) as a function of time. As the MVCs were recorded only for the downward force production, we refer to these values as MVC(z).

The main part of the experiment consisted of one- and four-finger tests with accurate force production in three different directions: downward, downward and leftward, and downward and backward (referred to as D_RL, DL, and DB). The D_RL task was performed under the instruction to keep the force in the right-left direction at zero. In those trials, visual feedback was provided for the force component, which the subjects were instructed to keep at zero level. In all trials, the subject was instructed to keep all the fingers in contact with the sensors at all times and to disregard possible force production by noninstructed fingers.

The targets were set at 22.5% MVC(z) for the downward direction, 3.75% MVC(z) for the right-left force directions, and 10% MVC(z) for the backward direction. These values were the same as those used for the study of young subjects; they were selected on the basis of a set of pilot trials to allow for comparably comfortable performance of all the tasks. The subject had to gradually increase the force during the 5-s trial to eventually reach these targets. The subject was shown the feedback on the computer screen, which was placed in front of the subject at a distance of ∼65 cm. The feedback screen (Fig. 1C) showed a starting point corresponding to zero active force production and three lines passing through the starting point. One line was vertical, and two lines were slanted. A target (a red circle) at the top of one of the lines corresponded to the upcoming task. The target moved at a constant speed along the line, and the task of the subject was to match its motion with the cursor (a black circle) after the target moved through the starting point. The target moved along the vertical line for the D_RL task and along the left-slanted line for the DL and DB tasks.

Feedback gain for movement of the target point along each axis was calculated as percentage of MVC(z) per centimeter. This gain was computed as percentage of MVC(z), set as the target for each direction divided by the length of the line of the screen representing that amount of force. The gains for the three axes were as follows: 1.424% of MVC(z)/cm for the z-axis, 0.231% of MVC(z)/cm for the x-axis, and 0.617% of MVC(z)/cm for the y-axis.

Before each trial, instruction was given for the direction in which the subject had to press and along which of the lines the cursor should be moving. The subject could see the moving target coming toward the starting point and could prepare to start the trial. When the target reached the starting point, the subject had to start pressing, thus moving the cursor in the instructed direction, along the instructed straight line following the moving target. The moving target took 3 s to reach the starting point. From that point, the black circle had to follow the red one over 5 s. Each circle was 3 mm in diameter.

Prior to performing these tasks, the subject was given sufficient practice time (∼10 min), during which the subject practiced accurate force production by individual fingers and by all four fingers along each of the force vector directions. Furthermore, for the one-finger pressing tasks, there was one more practice trial with the moving target followed by three recorded trials for each condition. For these trials, the subject was instructed to “focus only on the task finger,” but not to lift any fingers off the sensors at any time. For the four-finger tasks, there were five practice trials with the moving target followed by 15 recorded trials (more trials were conducted to allow the synergy analyses; see below). The trials were separated by 12-s intervals. A resting time of 1 min was provided between sets of trials. None of the subjects complained of pain or fatigue during or after the experiment. Additional rest periods were given when requested.

Data Processing

One-finger pressing tasks were used for calculation of enslaving indexes, and four-finger pressing tasks were used for computation of sharing indexes and indexes of multifinger synergies (see below). The data were filtered using a two-way second-order Butterworth low-pass filter at 2.5 Hz. We tried other (higher) filtering frequencies and found no significant differences in any of the main outcome variables; the 2.5-Hz filter resulted in the most consistent within-subject data. The data collected at 200 Hz were later resampled into 100 data points for each 5-s trial.

Task Performance

Accuracy of the performance was estimated using the root mean square (RMS) error, which was computed for forces produced in x, y, and z directions for different tasks

$$\text{RMS=}\frac{\text{1}}{{\text{F}}_{\text{P}k}^N}\sqrt{\frac{{\displaystyle \sum _{i=1}^N{\left(F_k^i-F_{\text{P}k}^i\right)}^2}}{N}}$$ (1)

where F_kⁱ is the measured force at sample i along the k-axis, F_Pk is the instructed force shown by the moving target, and N the number of samples (100). The RMS was normalized by the maximum instructed force for each condition.

RMS error was also calculated for the direction of force production

$${\text{RMS}}_{\theta }=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{\left({\tan }^{-1}\left(\frac{{\text{F}}_z^i}{{\text{F}}_z^i}\right)-{\tan }^{-1}\left(\frac{{\text{F}}_{\text{P}z}}{{\text{F}}_{\text{P}k}}\right)\right)}^2}}{N}}$$ (2)

where F_z and F_k are the produced force in the z direction and other (x or y) task directions, respectively. RMS error was calculated for each trial and averaged across all trials within a series and then across the subjects for each condition separately.

Enslaving

Enslaving reflects unintentional force production in one-finger tasks by noninstructed fingers or by the instructed finger in a noninstructed direction. A four-by-four enslaving matrix was computed for each relevant direction (z and/or x or y) for each of the three conditions, resulting in a total of six enslaving matrices (E). Similar to earlier studies of enslaving, we assumed linear relationships among individual finger forces (12, 75, 76). To obtain entries of the enslaving matrix, the forces produced by noninstructed fingers were regressed on the force produced by the task finger over the duration of the trial

$${\text{F}}_{Jk}=a_{jk}+b_{jk}{\text{F}}_k$$ (3)

where F_jk is force produced by finger j when k is the task finger and F_k is the force produced by the task finger in a particular direction. Furthermore, the enslaving matrix was computed as

$$\text{E}=\left[\begin{array}{cccc}{b}_{I,I}& b_{I,M}& b_{I,R}& b_{I,L}\\ b_{M,I}& b_{M,M}& b_{M,R}& b_{M,L}\\ b_{R,L}& b_{R,M}& b_{R,R}& b_{R,L}\\ b_{L,I}& b_{L,M}& b_{L,R}& b_{L,L}\end{array}\right]$$ (4)

where b_j,k is the slope of the regression equation when the force produced by finger j is regressed on force produced by finger k, which is the task finger. We used the best of the three trials for each condition, where best was defined as that with the highest mean R² (square of correlation coefficient) value. Different columns of the enslaving matrix correspond to different task fingers [index (I), middle (M), ring (R), and little (L)], and different rows correspond to different enslaved fingers.

The enslaving index (∣E∣) was calculated as the sum of all nondiagonal entries of the enslaving matrix. Two more indexes, E_j and E_i, were computed for the z direction only. E_j is the measure of how each finger enslaves the other fingers in the z direction (the sum of entries over the corresponding column of the enslaving matrix minus 1). E_i is a measure of how a given finger is enslaved by other fingers in the z direction during different pressing conditions (the sum of entries over the corresponding row of the enslaving matrix minus 1).

Another measure, F_UN, was used to characterize unintended force production within each finger across different directions across one-finger pressing tasks. F_UN reflects the amount of force produced by the task finger acting downward (along the z-axis) in a noninstructed direction (x or y): F_UN = F(non-z,nontask)/F_Z,task.

F_UN was also calculated using linear regressions. Force produced by the task finger in the noninstructed direction was regressed on force produced by the task finger in the z direction. F_UN,ki = a_ki + b_kiF_UN,kz, where F_UN,ki is the force produced by task finger k in the noninstructed direction i, F_UN,kz is the force produced by the task finger k in the z direction, a_ki is a constant, and b_ki is the slope of the regression line. Means and SDs of F_UN in the y direction were computed, across subjects, for each finger individually for two task conditions involving the x-axis (D_RL and DL). It was repeated for F_UN in the x direction for a DB task involving the y-axis.

Analysis of Multifinger Synergies

We quantified multifinger synergies stabilizing the magnitude of total force and its direction in four-finger trials using the framework of the UCM hypothesis (57). This analysis quantifies two components of variance in the space of elemental variables (finger modes; see below): one does not affect a certain value of a performance variable (force magnitude or force direction in our study), and the other does. We will address these two components as variance within the UCM (V_UCM) and variance orthogonal to the UCM (V_ORT). To eliminate the effect of covariation of finger forces due to enslaving, finger forces were transformed into another set of variables, finger modes (12, 42, 75)

$$\text{dF}=\text{Edm}$$ (5)

$$\text{dm}={\text{E}}^{-1}\text{dF}\hspace{0.17em}\left(\text{assuming that E is an invertible matrix}\right)$$

where dF is the change in force produced, E is a 4 × 4 enslaving matrix, and dm is the change in mode magnitude.

Rather than taking the regular matrix inverse, we used the singular value decomposition to calculate the pseudoinverse

$${\text{USV}}^{\text{T}}=\text{E}$$ (6)

The pseudoinverse was then calculated from

$${\text{E}}^{-1}={\text{VS}}^{*}{\text{U}}^{\text{T}}$$ (7)

where S* is the reciprocal of the nonzero elements in S. However, small values (<0.01) in elements of S were set to zero before calculation of S*. For most cases, the result was equivalent to taking the regular matrix inverse, but the removal of small values in S prevented very large values of the inverse of the enslaving matrix in a small number (<10%) of extreme cases.

Before calculating variance, we normalized the forces in each direction with respect to the maximum task force in that direction, i.e., the force magnitude in each direction that the subject was asked to produce. The components of the task force were always considered for each direction separately.

In our study, two performance variables were considered. The first was the sum of the magnitudes of forces (F_TOT) produced by the four fingers in a given task-relevant direction (z and either x or y): F_TOT,k = F_I,k + F_M,k + F_R,k + F_L,k, where F_i,k is the force produced by the i [i = index (I), middle (M), ring (R), and little (L)] finger in the k direction (x, y, or z).

The Jacobian matrix defines the transformation between small changes in the individual finger force magnitudes and changes in F_TOT

$${\text{dF}}_{\text{TOT,}k}=\left[1111\right]\left[\begin{array}{c}d{F}_{Ik}\\ d{F}_{Mk}\\ d{F}_{Rk}\\ d{F}_{Lk}\end{array}\right]$$ (8)

where dF_jk is the change in force produced by the j finger in the k direction (x, y, or z)

$${\text{dF}}_{\text{TOT,}k}=\text{JdF}$$ (9)

In the space of finger modes, we can express this relationship as

$${\text{dF}}_{\text{TOT},k}\text{=JEdm}$$ (10)

The UCM was approximated linearly as the null space of J spanned by basis vectors, e_i, from the following equation

$$0=\text{JE}\hspace{0.17em}{\text{e}}_i$$ (11)

We calculated ∣∣ as the sum of mean free mode vectors projected onto the UCM

$${\text{f}}_{\parallel }={\displaystyle {\sum }_{i-1}^{n-k}\left({\text{e}}_i^{\text{T}}·\text{dm}\right){\text{e}}_i}$$ (12)

where n = 4 is the number of elemental variables and k = 1 corresponds to the one-dimensional performance variable. f⊥ is the component of mode vectors perpendicular to the null space

$${\text{f}}_{\perp }=\text{dm}-{\text{f}}_{\parallel }$$ (13)

Then the variance per degree of freedom (DOF) within the UCM, i.e., V_UCM, was computed as follows

$${\text{V}}_{\text{UCM}}=\frac{{{\displaystyle {\sum }_{\text{trials}}\left|{\text{f}}_{\parallel }\right|}}^2}{\left[\left(n-k\right)N_{\text{trials}}\right]}$$ (14)

Similarly, V_ORT, i.e., variance per DOF orthogonal to the UCM, was calculated as follows

$${\text{V}}_{\text{ORT}}=\frac{{{\displaystyle {\sum }_{\text{trials}}\left|{\text{f}}_{\perp }\right|}}^2}{\left[k{N}_{\text{trials}}\right]}$$ (15)

Furthermore, to allow comparison across subjects, an index ΔV was computed as the difference between the V_UCM and V_ORT divided by the total variance (V_TOT), all computed per DOF

$$\Delta \text{V}=\frac{{\text{V}}_{\text{UCM}}-{\text{V}}_{\text{ORT}}}{{\text{V}}_{\text{TOT}}}$$ (16)

ΔV indexes were computed separately for each of the two relevant directions for each task (z and x or y) and each subject separately. Positive ΔV would indicate a multifinger synergy stabilizing the performance variable; zero or negative ΔV would mean no such synergy.

The second performance variable considered was the ratio between the two vector components reflecting the direction of the vector. It was defined as the force in the non-z task direction k (i.e., x or y) divided by the force in the z direction

$$\text{R}=\frac{{\displaystyle \sum _{i=1}^4{\text{F}}_k^i}}{{\displaystyle \sum _{i=1}^4{\text{F}}_z^i}}$$ (17)

This ratio represents the tangent of the force direction angle. In this analysis, forces, rather than modes, were used to ensure that the units are the same for the numerator and denominator. In this case, the performance variable was R; it depended on eight elemental variables, the eight force components of the four-finger force vectors. For forces in a non-z direction, the elements of the Jacobian matrix were

$$\frac{\partial \text{R}}{\partial {\text{F}}_z^i}=\frac{1}{{\displaystyle \sum _i{\text{F}}_z^i}}$$ (18)

The elements of the Jacobian for the forces in z direction were

$$\frac{\partial \text{R}}{\partial {\text{F}}_z^i}=\frac{-{\displaystyle \sum _i{\text{F}}_k}}{{\displaystyle \sum _i{\left({\text{F}}_z\right)}^2}}$$ (19)

Thus the Jacobian matrix was

$$\left[\frac{1}{{\displaystyle \sum _i{\text{F}}_z^i}}\hspace{0.17em}\frac{-{\displaystyle \sum _i{\text{F}}_k}}{{\displaystyle \sum _i{\left({\text{F}}_z\right)}^2}}\frac{1}{{\displaystyle \sum _i{\text{F}}_z^i}}\hspace{0.17em}\frac{-{\displaystyle \sum _i{\text{F}}_k}}{{\displaystyle \sum _i{\left({\text{F}}_z\right)}^2}}\frac{1}{{\displaystyle \sum _i{\text{F}}_z^i}}\hspace{0.17em}\frac{-{\displaystyle \sum _i{\text{F}}_k}}{{\displaystyle \sum _i{\left({\text{F}}_z\right)}^2}}\frac{1}{{\displaystyle \sum _i{\text{F}}_z^i}}\hspace{0.17em}\frac{-{\displaystyle \sum _i{\text{F}}_k}}{{\displaystyle \sum _i{\left({\text{F}}_z\right)}^2}}\right]$$ (20)

The remainder of the analysis was equivalent to the procedure described above. Briefly, the null space of the Jacobian matrix was used to approximate the UCM. For each sample over the 5-s trial, mean free finger forces were projected onto the UCM and onto the orthogonal complement. Variance was computed within both subspaces and normalized per DOF (the UCM is 7-dimensional and the orthogonal subspace is 1-dimensional). These indexes, V_UCM and V_ORT, were used to compute the index of multifinger synergy (ΔV) stabilizing force vector direction.

Since V_UCM, V_ORT, and V_TOT are computed per DOF, the index of synergy ΔV for stabilizing force magnitude ranges between 1.334 (all variance is within the UCM) and −4 (all variance is in orthogonal subspace). For statistical analysis, the ΔV indexes for force magnitude stabilization were transformed using Fisher's z-transformation, modified according to the boundaries of ΔV

$$z\Delta \text{v}=0.5\text{log}\left(\frac{4+\Delta \text{v}}{1.33-\Delta \text{v}}\right)$$ (21)

The index of synergy ΔV computed for force direction ranges between 1.143 (all variance is within the UCM) and − 8 (all variance is in the orthogonal subspace). For statistical analysis, the ΔV indexes for force direction stabilization were transformed using Fisher's z-transformation, modified according to the boundaries of ΔV

$$z\Delta \text{v}=0.5\text{log}\left(\frac{8+\Delta \text{v}}{1.14-\Delta \text{v}}\right)$$ (22)

Statistics

For all the repeated-measures ANOVAs, the assumptions of sphericity were checked using Mauchly's sphericity test. We used the Greenhouse-Geisser ε-corrections wherever the assumption of sphericity was violated.

Group was a between-subject factor; other factors were within-subject factors. To explore the effects of aging on MVC(z) produced by the subjects, a two-way ANOVA with repeated measures on MVC(z) with factors group [elderly (E) and young (Y)] and finger (I, M, R, L, and IMRL) was used.

To explore the effects of aging on differences in performance between one- and four-finger pressing tasks, a three-way ANOVA with repeated measures was done on the RMS errors of the force vector angle with group, finger (I, M, R, L, and IMRL), and condition (D_RL, DL, and DB) as factors. Two similar ANOVAs were run on the RMS errors of force magnitude in the z direction and in non-z directions. In these ANOVAs, only the first three trials of the four-finger tasks were included to have the same number of trials as in the one-finger tasks and avoid any effects of practice.

To explore the indexes of enslaving, E_j and E_i, across different groups, fingers, and conditions, three-way ANOVAs with repeated measures were done with group, finger (I, M, R, and L), and condition as factors. Another three-way ANOVA with repeated measures was done on the index of unintended force production in the noninstructed directions (F_UN) with factors group, finger (I, M, R, and L), and condition.

To compare the indexes of synergies (ΔV) stabilizing force direction, a three-way ANOVA was done on ΔV with group, condition, and time (10 levels: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%) as factors. The factor time was introduced on the basis of some earlier studies (60, 62) that showed that multifinger synergies take time to emerge and develop. To test the effect of aging on ΔV computed for the synergies stabilizing force magnitude, a three-way ANOVA was run with group, condition, and axis (z and non-z) as factors. To compare the trend of ΔV across time in the two subject groups, another three-way ANOVA was run on ΔV with group, axis (z and non-z), and time as factors.

To explore the effects of aging on variance in force magnitude within the two subspaces (V_UCM and V_ORT), three-way ANOVAs with repeated measures were run separately on V_UCM and V_ORT with the factors group, axis, and condition. To explore possible differential effects of aging on variance in the two subspaces (V_UCM and V_ORT) computed for force direction, a three-way ANOVA was run with the factors group, variance (V_UCM and V_ORT), and condition.

Significant effects were further explored with Tukey's pairwise comparisons. The level of significance was set at P < 0.05.

RESULTS

Maximal Force Production

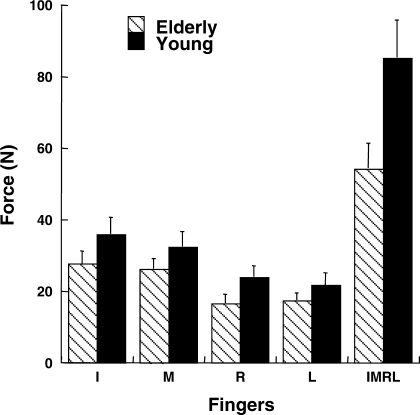
MVC force along the z-axis [MVC(z)] was recorded for each of the individual fingers and for the IMRL task. MVC(z) values were lower for the elderly than for the young subjects, although the difference was significant only for the IMRL task [Fig. 2; main effect of finger in a 2-way group × finger ANOVA (F_1.42,19.92 = 91.3, P < 0.0001), significant group × finger interaction (F_4,56 = 6.53, P < 0.001)]. Tukey's comparisons revealed that MVC(z) was significantly less for the elderly than for the young subjects for the IMRL tasks (P < 0.05). However, MVC(z) was not significantly different between the two groups for the single-finger tasks. Tukey's comparisons revealed that MVC(z) was greater for the I and M than the R and L fingers (P < 0.05) across both groups.

Fig. 2.

Forces produced during maximal voluntary contraction [MVC(z)] for 1-finger [index (I), middle (M), ring (R), and little (L)] and 4-finger (IMRL) tasks for elderly and young groups. Mean values are shown with SE bars.

Accuracy of Performance

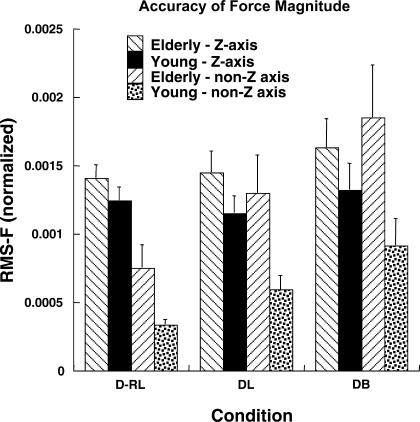
RMS error was used as a measure of accuracy of performance. The RMS indexes were averaged across trials for each subject and then compared across the two groups and tasks. RMS error of force magnitude along the z-axis was similar between the IMRL and one-finger tasks. In Fig. 3, the RMS error of force magnitude along the z-axis and non-z-axes is shown for different conditions for the elderly and young groups. Note the similar RMS indexes for both groups with respect to downward force production [z-axis; main effect of group approached significance in a 3-way group × finger × condition ANOVA (F_1,14 = 4.16, P = 0.06)]. Also, the RMS indexes were larger for the DB condition than for the other two conditions [main effect of condition (F_2,28 = 5.21, P < 0.05)]. Tukey's comparisons revealed that RMS error was greater for the DB condition than for the D_RL and DL conditions (P < 0.05). None of the other effects or interactions were significant.

Fig. 3.

Root mean square (RMS) error of force magnitude [RMS-F (normalized)] along downward direction (z-axis) and relevant non-z axis for different conditions for elderly and young groups. Averaged data across subjects and fingers are shown with SE bars.

In contrast, the RMS indexes for shear (non-z) forces were larger for the elderly group across all the conditions and both shear force directions [main effect of group in a 3-way group × finger × condition ANOVA (F_1,14 = 9.74, P < 0.01)]. Similar to force along the vertical direction, RMS error was greater for the DB condition than for the D_RL and DL conditions [main effect of condition (F_1.15,16.22 = 30.08, P < 0.001); Tukey's comparisons (P < 0.05)].

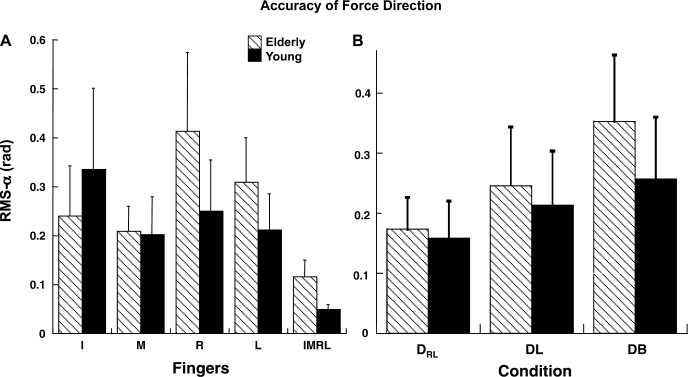
To study how accurately the subjects followed the task direction of force, we computed RMS of force vector angle with respect to the task force direction for one- and four-finger tasks over time. Directional errors were less for the IMRL than for the one-finger tasks for young and elderly groups [Fig. 4A; main effect of finger in a 3-way group × finger × condition ANOVA (F_2.29,32.12 = 3.89, P < 0.05)]. The directional errors were higher for the DB condition, as illustrated in Fig. 4B, which shows values averaged across subjects with SE bars for the two groups separately [main effect of condition (F_2,28 = 7.93, P < 0.01); Tukey's comparisons (P < 0.05)].

Fig. 4.

RMS error of force direction (in radians) averaged across subjects for different fingers (A) and across different conditions (B) for elderly and young groups. Data are shown with SE bars.

Indexes of Finger Interaction

Enslaving.

For each condition, enslaving matrices (E) and indexes of enslaving (∣E∣) were calculated separately for the forces produced along the three axes (see methods). A typical enslaving matrix along the z-axis for the DB task for a typical elderly subject was as follows

$$\left[\begin{array}{cccc}\text{1}.000& 0.112& 0.342& 0.076\\ 0.036& 1.000& 0.745& 0.019\\ 0.034& 0.139& 1.000& 0.124\\ 0.000& 0.039& 0.479& 1.000\end{array}\right]$$

This matrix is strongly nonsymmetrical; i.e., there are large differences between indexes of how a finger enslaves another finger and how it is enslaved by that finger.

Enslaving matrices along a non-z axis could have negative entries, meaning that nontask fingers produced force in a direction opposite to the force produced by the task finger. An example of the enslaving matrix along the x-axis for the DL task (for a typical elderly subject) is as follows

$$\left[\begin{array}{cccc}1.000& -0.050& -0.036& -0.342\\ 0.145& 1.000& -0.204& -0.371\\ 0.061& 0.297& 1.000& -0.150\\ -0.096& 0.065& 0.205& 1.000\end{array}\right]$$

The number of negative entries in the E matrices across the non-D force production tasks (DB and DL) was similar for the elderly and young groups: 5.1 ± 1.8 and 5 ± 1.2 (SD), respectively. Thus, on average, there were five negative entries (of the 12 nondiagonal entries) per participant in elderly and young groups.

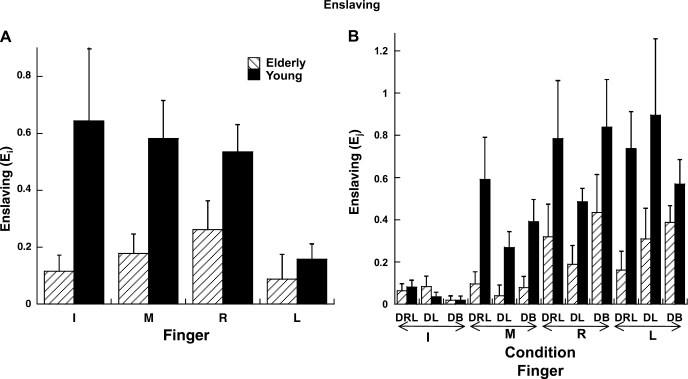
E_j was used as the measure of how a finger enslaves the other fingers in the z direction (it is the sum of entries over a column of the E matrix minus 1). E_i was used as a measure of how a finger is enslaved by other fingers in the z direction (it is the sum of entries over a row of the E matrix minus 1). Figure 5 illustrates that both indexes of enslaving, E_j and E_i were smaller in the elderly than in the young group [main effect of group in 3-way group × finger × condition ANOVAs (F_1,14 = 5.67, P < 0.05 for E_j and F_1,14 = 5.67, P < 0.05 for E_i)]. This trend was consistent across all the conditions (Fig. 5B).

Fig. 5.

Enslaving indexes (dimensionless) for different 1-finger tasks in different conditions for elderly and young groups. Overall, enslaving was lower for elderly than young groups. A: index of how a finger is enslaved by other fingers (E_i). B: index of how a finger enslaves other fingers (E_j). Averaged data across subjects are shown with SE bars.

E_j was less for the I and M than for R and L fingers [main effect of finger (F_3,42 = 12.04, P < 0.001); Tukey's comparisons (P < 0.05)]. There were several condition-dependent differences across the fingers [finger × condition (F_2,84 = 2.45, P < 0.05)]. In particular, E_j was less for the I than for the R finger for the DB and D_RL conditions only. The differences in E_j between the M and L fingers were significant only for the DB condition, while the differences between the M and R finger were significant for only the DL condition (all differences are significant at P < 0.05 based on Tukey's comparisons).

E_i was lower for the L finger than for the other fingers [main effect of finger (F_3,42 = 5.96, P < 0.01), Tukey's comparisons (P < 0.05)]. A significant group × finger interaction (F_3,42 = 2.96, P < 0.05; Fig. 5A) indicated that E_i was less for the elderly than the young group only for I and M fingers [Tukey's comparisons (P < 0.05)].

Unintended force production by a finger across directions.

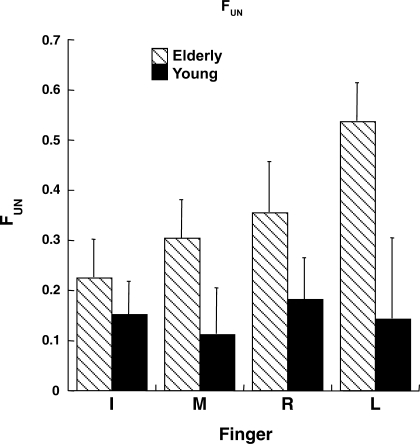
An index of unintended force production in directions orthogonal to the instructed direction (F_UN) was defined as a measure of the amount of force produced by the task finger in a noninstructed direction (x or y) while pressing downward (along the z-axis). In Fig. 6, unintended force production by elderly and young subjects is shown for different fingers. Note the greater magnitude of F_UN for the elderly than for the young group [main effect of group in a 3-way group × finger × condition ANOVA (F_1,14 = 7.23, P < 0.05)]. The F_UN index was lowest for the DB condition [main effect of condition (F_2,28 = 26.66, P < 0.0001); Tukey's comparisons (P < 0.05)]. Effect of finger was close to significance (F_1.92,26.98 = 3.20, P = 0.05), while all the two-factor interactions were significant [group × finger (F_3,42 = 3.07, P < 0.05); group × condition (F_2,28 = 10.11, P < 0.001); finger × condition (F_6,84 = 8.88, P < 0.0001)]. Tukey's comparisons revealed higher F_UN for the elderly than the young group only for the D_RL condition and the L finger (P < 0.05).

Fig. 6.

Unintended force production by task finger in nontask directions (F_UN, dimensionless) averaged across subjects and conditions for different 1-finger tasks for elderly and young groups. F_UN was higher for elderly than young subjects. Data were averaged across conditions for simplification and are shown with SE bars.

Analysis of Multifinger Synergies

To analyze multifinger synergies stabilizing the total force magnitude and force direction, we used the framework of the UCM hypothesis (see methods). Two components of variance across trials, V_UCM and V_ORT, were quantified at each time sample. A normalized difference between V_UCM and V_ORT, ΔV was used as the synergy index. Positive ΔV indicated a synergy stabilizing the performance variable for which ΔV was quantified, while zero or negative ΔV would mean no such synergy.

Across all the task conditions, V_UCM was higher than V_ORT, and ΔV was positive for magnitude and direction of the force vector. Hence, we conclude that strong multifinger synergies stabilized force magnitude and direction in both subject groups.

Force Magnitude Stabilization

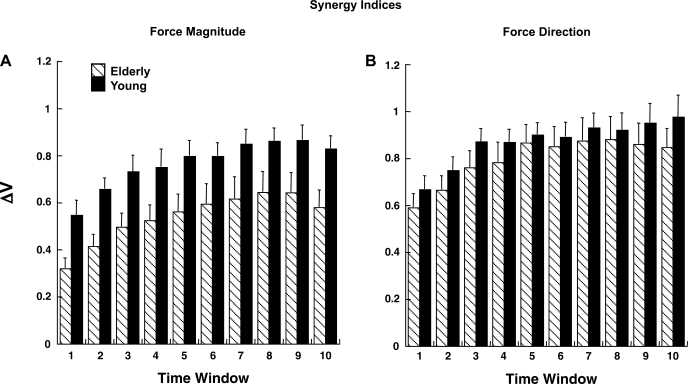
The ΔV values computed for force magnitude as the performance variable were smaller for the elderly than for the young group, and the trend of ΔV across time was similar for both groups (z-transformed ΔV values are shown in Fig. 7A). This was supported by a three-way ANOVA with group, condition, and axis (z and non-z) as factors. There was a significant main effect of group and axis [group (F_1,14 = 4.86, P < 0.05); axis (F_1,14 = 8.07, P < 0.05)]. However, neither the condition effect nor any of the interactions was significant. For the elderly and young groups, ΔV along the relevant non-z axis was higher than that along the z-axis (P < 0.05). Overall, the results show that synergies stabilizing the shear force magnitude are stronger than those stabilizing the magnitude of downward force.

Fig. 7.

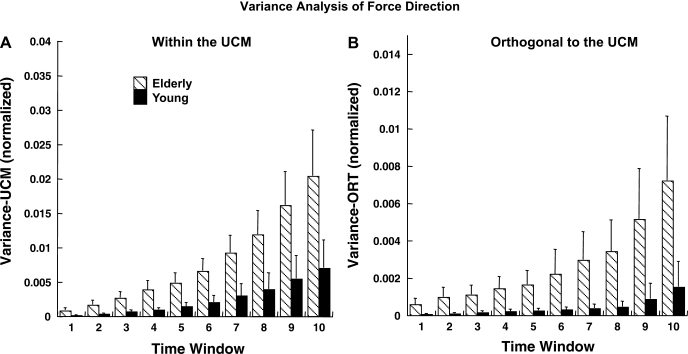
Time changes of index of a multifinger synergy (ΔV, dimensionless) stabilizing force magnitude (A) and of a multifinger synergy stabilizing force direction (B) for elderly and young groups. Data were averaged across the 10 equal time windows over the trial duration and across subjects and are shown with SE bars.

As there was no significant main effect of condition on ΔV related to force magnitude stabilization, ΔV values were averaged across the three conditions. Furthermore, a three-way ANOVA was run with a new factor, time (10 levels: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%) to compare the trend of ΔV over time for the elderly and young groups. There was an increase in the value of ΔV over the first three time intervals (until 30% of total time); thereafter, this index reached a plateau [effect of time in a 3-way group × axis × time ANOVA (F_3.07,42.93 = 41.89, P < 0.0001), Tukey's comparisons (P < 0.05)]. There were also significant effects of group and axis similar to those described above. The group × time interaction was not significant. Thus the elderly and young groups showed similar time trends of ΔV computed for force magnitude stabilization along z- and non-z-axes.

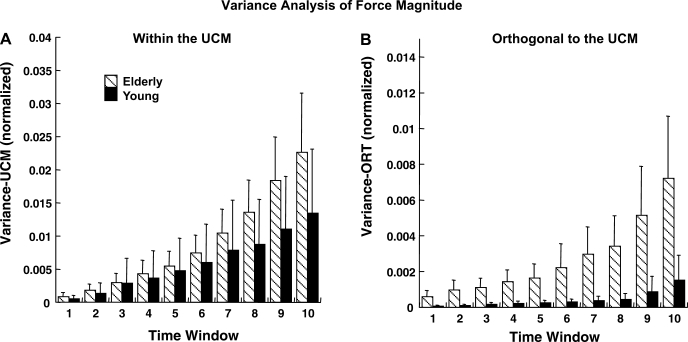
The ANOVA for force magnitude in two subspaces (V_UCM and V_ORT) showed that V_ORT was higher in the elderly than in the young group [main effect of group in a 3-way group × axis × condition ANOVA (F_1,14 = 6.48, P < 0.05)] without a significant difference in V_UCM. Figure 8 illustrates the time profiles of V_UCM and V_ORT for the two groups. Note the higher values of V_ORT in the elderly group. There was a significant difference between the z- and non-z-axes: V_UCM was greater for non-z- than for z-axes, and this was consistent across both groups [main effect of axis (F_1,14 = 14.37, P < 0.01)], while this difference was nearly significant for V_ORT (F_1,14 = 4.58, P = 0.05).

Fig. 8.

Time changes in force mode variance (normalized) within the uncontrolled manifold (UCM; A) and orthogonal to the UCM (B) computed for stabilization of force magnitude for elderly and young groups. Data were averaged across 10 equal time windows over the trial duration and across subjects and are shown with SE bars.

Analysis of V_UCM also showed a significant two-way group × condition interaction (F_2,28 = 5.04, P < 0.05) and a three-way interaction (F_2,28 = 5.43, P < 0.05). Tukey's comparisons revealed that V_UCM was greater for D_RL than for DL and DB, only along the non-z-axes and only for the young group (P < 0.05). No such differences across conditions were found in the elderly group. For V_ORT, the two-way axis × condition interaction was significant (F_2,28 = 3.83, P < 0.05). Tukey's comparisons revealed that V_ORT was greater along the non-z- than z-axis, only for the DB condition.

Force Direction Stabilization

Figure 7B shows the time profile of z-transformed ΔV values computed for force direction as the performance variable for the elderly and young groups. Note the similar trends over time for both groups and smaller synergy indexes for the elderly group [although the difference was statistically significant only for the D_RL condition; no effect of group, but a significant group × condition interaction in a 3-way group × condition × time ANOVA (F_2,28 = 5.07, P < 0.05), Tukey's comparisons (P < 0.05)]. There were significant main effects of condition (F_2,28 = 20.67, P < 0.001) and time (F_3.39,47.54 = 24.79, P < 0.0001). The effect of condition reflected significantly lower ΔV values for the DB than for the DL condition (P < 0.05). Also, the ΔV index for the DB condition was significantly less than for the DL or D_RL condition for the young group, while for the elderly group the significant difference was only between the DB and DL conditions (P < 0.05). Overall, ΔV(DB) < ΔV(D_RL) < ΔV(DL); for the young group, ΔV(DB) < ΔV(DL,D_RL); and for the elderly group, ΔV(DB) < ΔV(DL).

Analysis of the two variance components (V_UCM and V_ORT) showed that although V_UCM and V_ORT were higher in the elderly than in the young group [main effect of group in a 3-way group × variance × condition ANOVA (F_1,14 = 6.96, P < 0.05 for group)], V_UCM was about threefold higher in the elderly group, while the difference in V_ORT was about sixfold [variance × group interaction approached significance (F_2,28 = 4.20, P = 0.059)]. V_UCM was consistently higher than V_ORT [main effect of variance (F_1,14 = 19.53, P < 0.001)]. The variance × condition interaction was also significant (F_2,28 = 4.49, P < 0.05). Tukey's comparisons revealed that V_UCM was greater than V_ORT for all the conditions (P < 0.05), while the difference between V_UCM and V_ORT was higher for the DL and DB conditions than for the D_RL condition. Figure 9 shows the time profiles of V_UCM and V_ORT for both groups.

Fig. 9.

Time changes in force mode variance (normalized) within the UCM (A) and orthogonal to the UCM (B) computed for stabilization of force direction for elderly and young groups. Data were averaged across 10 equal time windows over the trial duration and across subjects and are shown with SE bars.

DISCUSSION

Our observations support the specific hypotheses formulated in the introduction. In particular, we hypothesized that aging would be associated with decreased indexes of unintended force production by nontask fingers. Indeed, indexes of finger enslaving (76, 77) were lower in the elderly than in the young group during force production in all directions. On the other hand, we expected unintended force production by a finger orthogonal to the instructed force direction to be higher in the elderly group. This was also confirmed. Across all the digits, the F_UN index was nearly twice as high in the elderly than in the young group. The third hypothesis was related to possible age-related impairment of multifinger synergies stabilizing force magnitude and direction. The results confirmed smaller indexes of magnitude- and direction-stabilizing synergies in the elderly subjects.

We start with a brief overview of the basic mechanics of force vector production at the end of a kinematic chain. Then we discuss possible contributions of the age-related changes in extrinsic and intrinsic hand muscle groups to the observed patterns of force variability in single-finger tasks. Furthermore, we discuss possible mechanisms of the decreased enslaving and increased F_UN indexes in the elderly subjects, as well as changes in multifinger synergies with age. We also address a possible age-related shift from a synergic hand control to a more somatotopic, element-based control.

Biomechanical Aspects of Force Vector Production

Extrinsic and intrinsic hand muscles are activated during many daily activities, such as grip and pinch (13, 37). Extrinsic flexors [flexor digitorum profundus (FDP) and flexor digitorum superficialis (FDS)] are multidigit muscles, the tendons of which insert at the distal and intermediate phalanges, respectively. This makes the FDP the only focal flexor at the distal interphalangeal (IP) joint, while FDP and FDS contribute to flexion torques at the proximal IP joint. Intrinsic muscles act as digit-specific focal flexors at the metacarpophalangeal (MCP) joints, in addition to their extensor action at more distal joints via the extensor mechanism (38, 47). Abduction and adduction forces are also produced by digit-specific intrinsic hand muscles.

When a vector of force (F) is produced at the end of a kinematic chain in static conditions, the magnitude and direction of the vector define torques in all the joints [the torque vector (T) of the chain, given a joint configuration], according to the following equation

$$\text{T}={\text{J}}^{\text{T}}\text{F}$$ (23)

where J is the Jacobian matrix that links infinitesimal joint rotations to displacements of the end point and the superscript T is the sign of transpose.

In our tasks, the subjects were required to produce force vectors in the plane of finger motion [a sagittal (yz) plane] and also in an orthogonal plane [a frontal (xz) plane]. These tasks involved the intrinsic and extrinsic muscle to different degrees. In particular, forces along the x-axis were primarily produced by activation of intrinsic hand muscles, although one cannot exclude a modest contribution from extrinsic muscles, in particular because finger orientation was defined by the hand anatomy and not exactly parallel to the y-axis of the force sensors. In contrast, shear force production along the y-axis required a coordinated involvement of extrinsic and intrinsic muscles. Since our tasks always involved force production along the z-axis, in addition to shear force production, all the tasks required appropriate scaling of all the joint torques in the IP and MCP joints according to Eq. 23. Note that the conclusions on the role of muscles in different tasks have been drawn on the basis of biomechanical considerations. We did not record muscle activation levels in the study, which may be seen as its drawback.

Force Variability and Effects of Aging on Intrinsic and Extrinsic Hand Muscles

Several previous studies reported stronger age effects on the MVC force of intrinsic than extrinsic muscles. In particular, a significantly larger loss in the MVC force produced during pressing at the proximal phalanges than at the distal phalanges was reported (63). Because of the different sites of tendon attachment, intrinsic muscles are focal force generators during force production at the proximal phalanges, while the extrinsic flexor (FDP) is the focal force generator during force production at the distal phalanges. Hence, these findings suggest a greater force loss with age of intrinsic hand muscles. A palmar bias in the force vector angle during downward force production tasks has been reported (9), also corroborating the idea of a greater impairment of the intrinsic muscles with age.

Our observations further support the hypothesis of greater effects of age of intrinsic hand muscles. In particular, the elderly participants were less accurate in force magnitude production along the nonvertical axes (larger RMS error of shear forces), while there were smaller, statistically nonsignificant effects on accuracy of force production along the vertical axis. The stronger effects of age on intrinsic muscles allow us to expect higher force RMS indexes during force production along the x-axis. The situation is more complex for forces produced along the y- and z-axes. These forces required coordinated activation of extrinsic and intrinsic muscles to ensure appropriate moments of force in the IP and MCP joints. Hence, an increase in force RMS along the y-axis is more likely to reflect impaired coordination of the intrinsic and extrinsic muscles (see Changes in Finger Interaction With Age).

Several studies suggest a relation of force variability to motor unit discharge variability (36, 48, 70). There have been conflicting reports on changes in motor unit discharge variability with age (2, 72, 73). It is difficult, therefore, to link the stronger effects of age on the MVC of intrinsic hand muscles to changes in their motor unit discharge variability. We view this factor as a potential contributor to the higher force variability during tasks that required force production along the x-axis (ulnar-radial deviations).

Effects of aging on the central nervous system are not limited to the segmental spinal apparatus. In particular, aging is associated with progressive death of cortical neurons (18) and cortical reorganization (14). Several studies have suggested that cortical neurons in the motor and premotor areas contribute to multimuscle and multidigit coordination during natural hand tasks (54–56). These observations suggest that aging may be associated with changes in finger interaction and coordination.

Changes in Finger Interaction with Age

Several previous studies report counterintuitive findings of lower indexes of enslaving (higher individuation) in the elderly during downward pressing tasks (63, 65, 75). In the present study, we confirm those observations and extend them to shear force production (Fig. 5). It has been suggested that peripheral factors, such as connective tissue links between fingers and the involvement of multitendon extrinsic hand muscles, and neural factors, including, in particular, overlaps in cortical representations of fingers, contribute to enslaving (55). During movement tasks, peripheral factors are more likely to make a substantial contribution to enslaving (39); during isometric force production tasks, neural factors are more likely to dominate this phenomenon (41).

The drop in the number of cortical neurons, in particular in the motor areas, with age may potentially contribute to the lower enslaving, if it is assumed that this drop is associated with a higher degree of specialization of the surviving neurons in controlling individual digits. The idea of a distributed cortical control of the hand (54) with individual cortical neurons being able to induce activation changes in many different muscles (divergence) and numerous, broadly distributed neurons projecting on the same muscle or effector (convergence) assumes the availability of a hugely redundant set of neurons. When neuronal redundancy decreases with age, a shift toward a more focused, somatotopic control scheme may result in better individuated finger control. A recent study by Yu and colleagues (75) emphasized a negative relationship between enslaving and force deficit (an index reflecting a drop in maximal finger force when it acts simultaneously with other fingers of the hand compared with its single-finger task) and suggested that it might be due to the relative proportion of the amounts of spillover to neighboring digits and neural drive to antagonist muscles. This might occur with aging, as studies have shown lower enslaving and higher force deficits in the elderly (63, 64).

Better individual control of fingers (lower enslaving) does not mean better control of the hand across everyday tasks. It has been shown that patterns of enslaving are organized to stabilize the total moment of force produced by a set of fingers (77), thus helping stabilize rotational action of the hand. It is not surprising, therefore, that lower enslaving in the elderly is associated with worse control of rotational actions, as reflected in indexes of synergies during pressing and prehensile tasks (50, 61). Since rotational hand actions constitute a major component of everyday activities, these changes are likely to contribute to the documented impairment of the hand function with age (5, 21). Also, higher enslaving, by itself, does not predict more or less accurate force production. In earlier studies, we tried to eliminate the direct, task-independent effects of enslaving on force covariation by performing analysis in the space of finger modes (32, 42, 50, 61). In the present study, we used the same method in the analysis of force magnitude-stabilizing synergies.

Young and elderly subjects showed atypical negative entries in the enslaving matrices computed for shear forces. These observations confirm earlier results reported in experiments that used a somewhat different setup and tasks (52). Such negative entries are likely to be mediated by neural factors; in particular, they may reflect the high degree of neural interconnectivity between the intrinsic abductors/adductors (17). They may also reflect synergic control of fingers, with the purpose to avoid large net forces in the ulnar-radial direction.

As suggested by Eq. 23, force vector direction is defined by a combination of torques in all the joints along the finger. Deviations from the task force vector direction reflecting the imperfect balance of the joint torques were quantified in our study using the index F_UN. This index showed changes with age that were opposite to those observed for enslaving: F_UN was higher in the elderly group, supporting earlier observations (9).

The significantly higher F_UN values were accompanied by only minor (nonsignificant) changes in the RMS error computed for force direction. Force direction RMS error was computed in the task plane (e.g., in the xz plane for the DL tasks), while F_UN was computed in a direction orthogonal to that plane. The subjects received visual feedback on deviations of the actual force from the prescribed force only in the task plane. Motor performance of elderly persons is known to show a stronger dependence on visual feedback (58, 68). Hence, it is possible that the lack of visual feedback for forces orthogonal to the task plane was responsible for the stronger effects of age on F_UN compared with RMS error of force direction.

Impaired Synergies in the Elderly

We used the framework of the UCM hypothesis to analyze multifinger synergies (57). This framework allows us to represent variance in the space of elemental variables as consisting of two components: good variance (V_UCM), which does not affect important aspects of performance, and bad variance (V_ORT), which does. A synergy stabilizing a performance variable has been defined as covariation of elemental variables resulting in V_UCM > V_ORT quantified per DOF in the corresponding subspaces (43, 45).

The present study shows similarities and differences in the multifinger synergies in the young and elderly subjects. Both groups were able to demonstrate covariation of forces and modes across trials that stabilized the magnitude and direction of the total force vector. Both groups showed higher synergy indexes for total shear forces than for downward forces. This finding, which may be related to the importance of accurate production of total shear force in typical everyday prehensile tasks, is not trivial. Earlier studies of prehensile synergies showed that during holding of an object with the prismatic grasp, the four-finger normal forces failed to form a synergy stabilizing their total normal force, while the four shear forces did form a synergy stabilizing their total shear force (27). In both groups, synergy indexes grew over the first 30% of the task time, confirming earlier studies that showed that multifinger synergies take time to emerge and develop (60, 62).

The main difference between the two groups was in the significantly lower values of the multifinger synergy indexes for both performance variables. Earlier studies documented lower synergy indexes in elderly subjects during pressing tasks that involved the production of accurate profiles of the total force and total moment of force (50, 61, 63, 65). The present study shows that aging is associated with weakening of multifinger synergies stabilizing other variables, such as shear forces and force vector direction. This may be a reflection of a general trend of a shift from more complex, synergic control to more element-based control, possibly related to the progressive death of neurons at different levels of the neural axis (7, 18). The direction used for visual display under the DB condition did not correspond to the physical direction of force. Indeed, the errors were larger for the DB condition than for the other directions. However, no statistically significant interactions with age for RMS error of force magnitude or its direction would suggest that any incompatibility effects were influencing the elderly more than the young subjects.

Another sign of this trend is the documented loss of complexity in motor signals with age (44, 49, 74). This trend is reflected in the preference for cocontraction motor patterns in the elderly (3, 59) that replace the more typical reciprocal patterns that require accurately timed production of muscle forces. Older adults were also found to differ from younger persons in intersegmental coordination as assessed by accelerometers along the central body axis (1), with older adults tending to sway in an “en bloc” pattern. A previous study (22) found higher cross-correlations between body sway at the shoulder and hip level in older adults than in younger adults. All these results corroborate a suggestion that age-related changes in sensorimotor performance may be due to a reduction in the system's variety of perceptual states and available responses (71).

Synergy index in our study was computed as the normalized difference between V_UCM and V_ORT. As such, its changes may reflect changes in either of the two variance indexes or in both. Both variance indexes were significantly higher in the elderly subjects, but these effects were disproportionate: V_ORT increased more with age (Figs. 8 and 9), leading to the drop in the synergy index.

Use of synergies allows redundant sets of elements to show less variable performance, even if some of the elements show high variability of their outputs. For example, several studies have shown that goal-relevant features of performance are relatively preserved during fatigue of one (or a few) of the elements (10, 11, 20, 23, 29, 66). This strategy, however, is associated with an increase in the corresponding synergy index (66), which was not observed in our study. As a result, the differences between the young and elderly groups in the indexes of variability of total force magnitude and direction were definitely not larger for the single-finger tasks; actually, there was a trend toward somewhat larger differences in the RMS index for total force magnitude across the multifinger tasks (Fig. 3). Hence, the impaired synergic control in elderly persons is an important factor that prevents the use of an adaptive strategy available to young persons when they face a temporary loss of force and an increase in its variability.

Concluding Comments

Taken together, our results suggest a chain of changes triggered by the neuronal loss in the course of healthy aging. Everyday actions are likely to be controlled in a hierarchical way, such that, at higher levels, individual elements (e.g., muscles, joints, and digits) are united into groups recruited using one parameter per group. On the basis of recent studies of the cortical organization, one study (54) suggested a metaphor of a cortical piano: Individual cortical neurons are recruited by inputs into the primary motor cortex (and maybe also premotor cortex) in “chords” that produce elements of meaningful coordinated muscle activations. The neuronal loss with age may force a shift from such synergic control to a more element-specific, somatotopic control. To continue with the cortical piano metaphor, if one loses the ability to play chords, a melody can be constructed from individual notes. In general, any melody can be viewed as a combination of notes; however, use of chords makes learning and performing music much easier.

GRANTS

The study was supported in part by National Institutes of Health Grants AG-018751, NS-035032, and AR-048563.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.