Modulating DNA configuration by interfacial traction: an elastic rod model to characterize DNA folding and unfolding

Abstract

As a continuum model of DNA, a thin elastic rod subjected to interfacial interactions is used to investigate the equilibrium configuration of DNA in intracellular solution. The interfacial traction between the rod and the solution environment is derived in detail. Kirchhoff’s theory of elastic rods is used to analyze the equilibrium configuration of a DNA segment under the action of the interfacial traction. The influences of the interfacial energy factor and bending stiffness on the toroidal spool formation of the DNA segment are discussed. The results show that the equilibrium configuration of DNA is mainly determined by competition between the interfacial energy and elastic strain energy of the DNA itself, and the interfacial traction is one of the forces that drives DNA folding and unfolding.

Introduction

An approach based on Kirchhoff’s theory of elastic rods has been used to model the configuration and stability of the deoxyribonucleic acid (DNA) molecule [1–3]. In this approach, DNA is regarded as a thin elastic rod. Under external loads, the rod exhibits a super-coiling configuration after deformation.

Using the rod model to describe DNA configuration can be traced back to 1970s. In the early stage, Benham [4, 5] and Le Bret [6, 7] first established the elastic rod model of DNA. They showed that the equilibrium configuration of DNA was a toroidal helix under the condition that only deformations of curvature and of twist were permitted. Subsequently, the elastic rod model of DNA was extended and refined in a variety of ways. By introducing shear and extension, Shi et al. expanded the set of allowable deformations of DNA [8]. They found a closed-form solution to the rod model of DNA. Manning et al. [9] and Coleman et al. [10] incorporated the sequence dependence of DNA in the rod model. Tobias, Coleman, and Swigon extended the rod model to include forces of self-contact in the process of DNA deformation [11, 12]. They analyzed the elastic stability of DNA configuration, and pointed out that the stable configuration of DNA would manifest an interwound feature if the self-contact is considered. This results coincides with the observations of small-angle X-ray scattering and cryoelectron microscopy [13, 14].

So far, the thin elastic rod model has been confirmed to be adequate for characterizing the geometrical configuration and stability of DNA. Some reviews and recent advances can be found in references [1–3] and [15, 16].

DNA under physiological conditions is always in an intracellular solution. The interaction of the DNA chain with the intracellular solution (DNA–solution interaction) is a very important determinant of the DNA configuration [1]. If the DNA–solution interaction alters due to the change of the solution, it will cause a restructuring of the DNA conformation. For example, it was discovered that multivalent cations induce DNA to collapse from solution into toroid-shaped condensates [17–19]. However, the DNA–solution interaction is explicitly excluded in the existing rod models of DNA. Macroscopically, we should be able to use the theory of interfacial energy to characterize the interactions of DNA with the intracellular solution if they are short ranged. Due to the background mentioned above, the aim of this contribution is to investigate the influence of the interfacial energy on the equilibrium configuration of DNA based on the elastic rod model. For this, we assume:

1. DNA can be represented as a thin elastic circular rod with initial curvature and twist.

2. The interactions of DNA with the intracellular solution are governed by the interfacial energy of the elastic rod.

3. The interfacial energy factor is homogenous along the length of the rod.

4. The change of environment (solvent concentration, temperature etc.) alters the interfacial energy and bending stiffness of the rod simultaneously.

5. Self-contact, thermal fluctuation, and other loads except interfacial interaction are ignored.

It should be stressed that interfacial energy is a coarse-grained model characterizing interaction potentials between DNA segments and molecules of solution. Therefore, the approach in this paper is complementary to the standard approaches based on the intersegmental interaction potentials of DNA [20]. The paper is divided into four parts. This introductory section shows the background of the paper. In the second section, we firstly discuss the Kirchhoff theory of elastic rods. Then, a set of formulas for the reduced interfacial traction between a circular rod and its solution environment are derived on the basis of the Young-Laplace equation. In the third section, a two-dimensional rod model for a DNA segment is determined. The Runge-Kutta algorithm is used to compute the equilibrium configuration of the DNA segment under the action of the interfacial traction. The influences of the interfacial energy factor and bending stiffness on the DNA segment folding and unfolding are discussed. Finally, some conclusions and comments are drawn.

Basic formulations

Kirchhoff’s equations for elastic rods

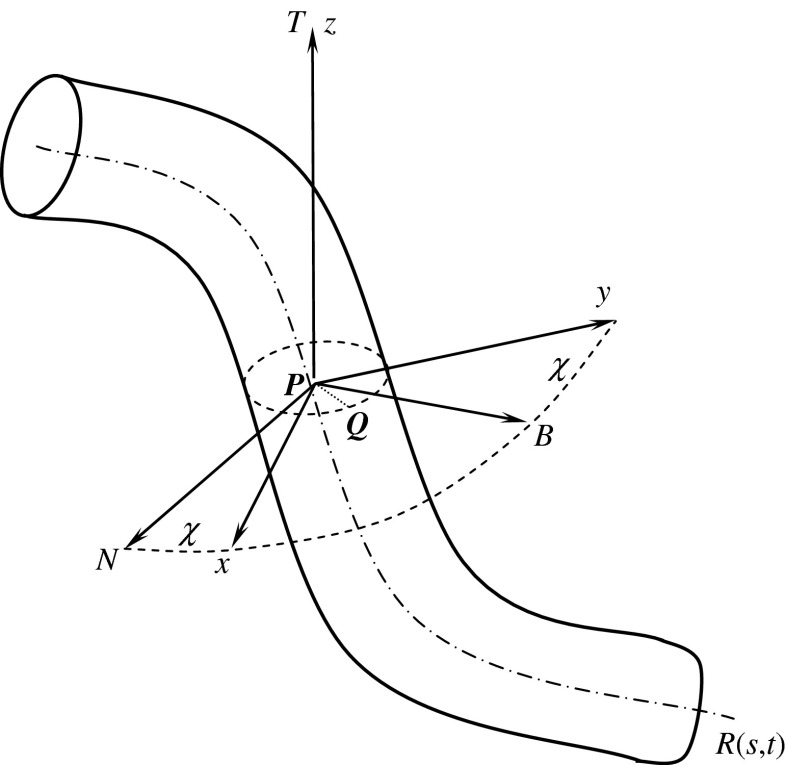
As a coarse-grained description, a DNA can be approximately regarded as a thin flexible circular rod or string [1–16]. The central axis of the rod is a spatial curve R(s, t): R² → R³ parameterized by arc length s and time t. As shown in Fig. 1, the Frenet frame P-NBT and a local orthonormal basis P-xyz are simultaneously set on each cross-section of the rod. P is a point on the curve R(s, t). In P-xyz, the x and y-axes are the two principal inertia axes of the cross-section through the point P. The angle between the principal normal PN and the x-axis (or the binormal PB and y-axis) is called the twisting angle, denoted by χ.

Fig. 1.

Reference frames on rod

In the initial state of rod, the curvature and torsion of the axis are κ₀ and τ₀, respectively. The initial twisting angle is χ₀. Relative to the coordinates P-xyz, the Kirchhoff equations are written with the index symbols as follows [3, 21]:

1

where F_i and M_i are the stress resultant and principal moment acting at the center of the cross-section, ω_i the curvature-twisting vector, and ε_ijk the permutation sign. f_i refers to the traction distributed along the central axis R(s, t). It is equivalent to the external loads applied on the surface of the rod.

2

where denotes the initial curvature-twisting vector. A and B are the bending stiffness with respect to the x-axis and y-axis, respectively. C is the twisting stiffness. Assume the rod is isotropic. Then, A, B, and C are written as

3

where r is the radius of the rod cross-section. E is Young’s modulus, and G the shear modulus. By the curvature κ, torsion τ, and twisting angle χ, the curvature-twisting vector ω_i can be represented as [3, 21]

4

Traction induced by interfacial energy

As shown in Fig. 1, Q is a point on the rod surface. The angle between PQ and PN is θ. Let R and r denote two principal curvature radii at the point Q on the rod surface, respectively. Clearly, r is the circumferential radius of the cross-section of the rod. Since the cross-sections of the rod are the same everywhere, through the point Q, on the rod surface there is an offset curve1 (denoted by c(s, t)) of the central axis curve R(s, t). Let R_l be the curvature radius of c(s, t) at the point Q. It is easy to find that

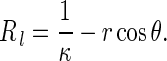5

In terms of the Meusnier’s theorem [22], we have

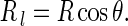6

Inserting Eq. 6 into 5 leads to

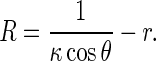7

Macroscopically, interactions of DNA with the intracellular solution can be characterized by interfacial traction between a rod and the solution surrounding the rod. In terms of the Young-Laplace formula [23], the interfacial traction applied on the rod reads

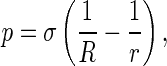8

where p is the normal traction on the interfacial surface between the rod and solution, and σ the interfacial energy factor (also called the interfacial tension), which is a positive constant and represents a composite effect of hydrophilic and hydrophobic patches along the DNA surface. In Eq. 8, we have reckoned a principal curvature radius as positive if it is drawn into the interior of rod. Substituting Eq. 7 into Eq. 8 gives

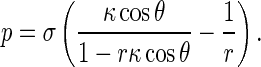9

In coordinates P-xyz, Eq. 9 can be decomposed into

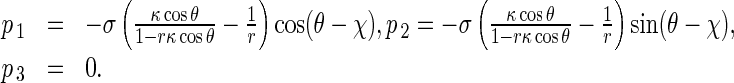10

Integrate Eq. 10 along the perimeter of the cross-section of the rod so that p₁, p₂, and p₃ reduce to the tractions on the central axis curve R(s, t). Thus, we have

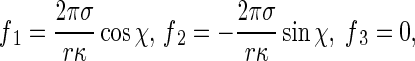11

which are called the reduced interfacial traction. In the formulas above, although the interfacial energy factor σ is very small, f ₁ and f ₂ are much greater than σ in magnitude, because 1/κ > > r. Therefore, influences of the reduced interfacial traction on bending and twisting of a thin curved rod is not negligible.

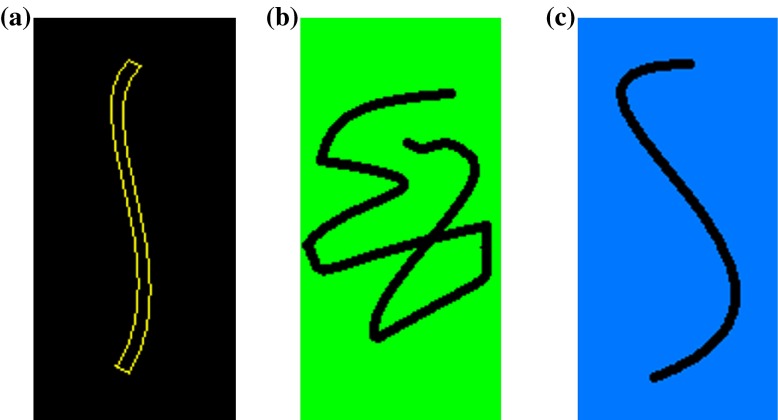
For the convenience of analysis, a thin elastic rod is imagined to form in such way: a rod with the original configuration shown in Fig. 2a is taken out from an ideal bulk material without any change in structure. When the rod breaks away from the bulk material, a new surface will occur on the rod. Due to the interfacial energy produced by the new surface, the rod will deform until it reaches a new equilibrium, to form a new configuration called the condensed configuration (see Fig. 2b). The interfacial energy is directly influenced by the interfacial environment. When the interfacial environment varies, the interfacial energy of the rod will change with it. This causes the rod to be reconfigured to form the so-called relaxed configuration, as shown in Fig. 2c.

Fig. 2.

The configurations of a thin elastic rod subjected to different interfacial tractions

Analysis and discussion

A simplified 2D model

For simplicity, we assume the central axis of the rod is a planar curve from beginning to end. It follows that τ = 0 and χ = 0. Thereby, Eqs. 2 and 4 are written as

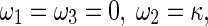12

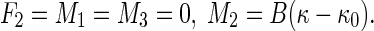13

By the formulas above and Eq. 11, Eq. 1 reduces to

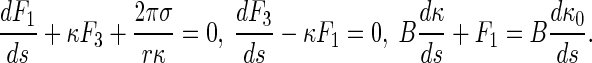14

Let κ = κ₀ + Δκ, where κ₀ denotes the curvature of the original configuration of the rod (see Fig. 2). Then, Eq. 14 leads to

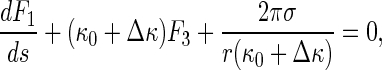15

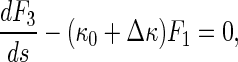16

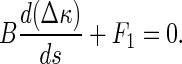17

Under a given initial condition, we can solve the Δκ and κ from Eqs. 15–17. Once κ is given, the configuration of the rod is determined by the equations below:

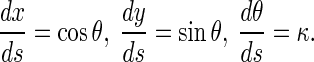18

Clearly, κ depends only on the interfacial energy and the elastic properties of rod. Therefore, the configuration of a rod is completely determined by competition between the interfacial energy and elastic strain energy of the rod.

Numerical results

In this section, we use the theoretical model described by Eqs. 15–18 to solve numerically the equilibrium configuration of DNA under the action of interfacial traction. The aim of this approach is a proof of principles. Therefore, qualitative aspects of the numerical solution are emphasized, regardless of accuracy in details. This is also because we lack accurate data of some parameters such as the interfacial surface energy factor, etc.

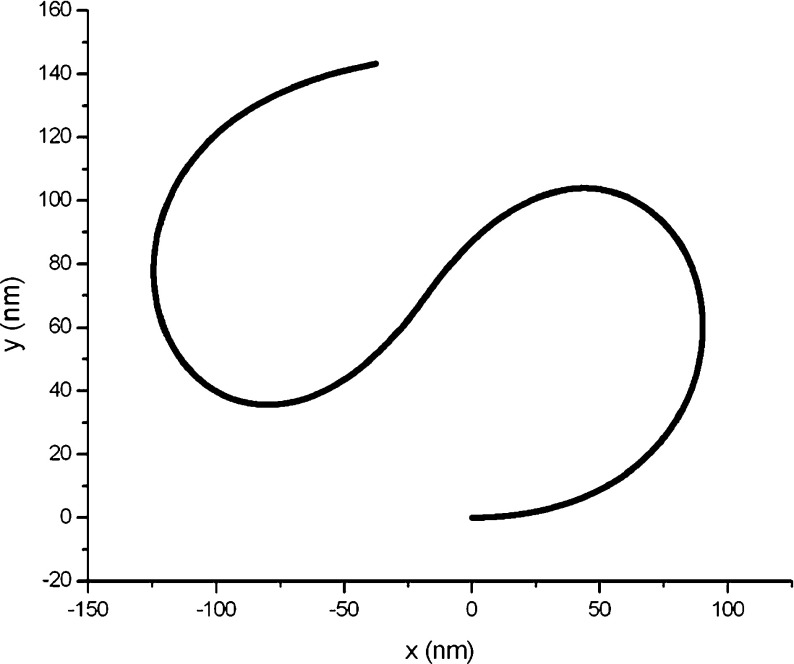
Consider a DNA segment whose original configuration consists of two inextensible circular one-quarter arcs, as shown in Fig. 3. The initial curvatures of both arcs are all 0.006 nm^− 1. Assume this DNA segment is separated from a bulk material. It will then deform from the original configuration into the condensed configuration due to the interfacial traction induced by the new surface. Referring to the relevant data of DNA offered in the reference [24], we take r = 1.0 nm, E = 0.16 nN/nm². Due to the lack of data on the interfacial energy factor between DNA and the intracellular solution, we investigate how the DNA configuration changes with the interfacial energy factor.

Fig. 3.

Original configuration of a DNA segment

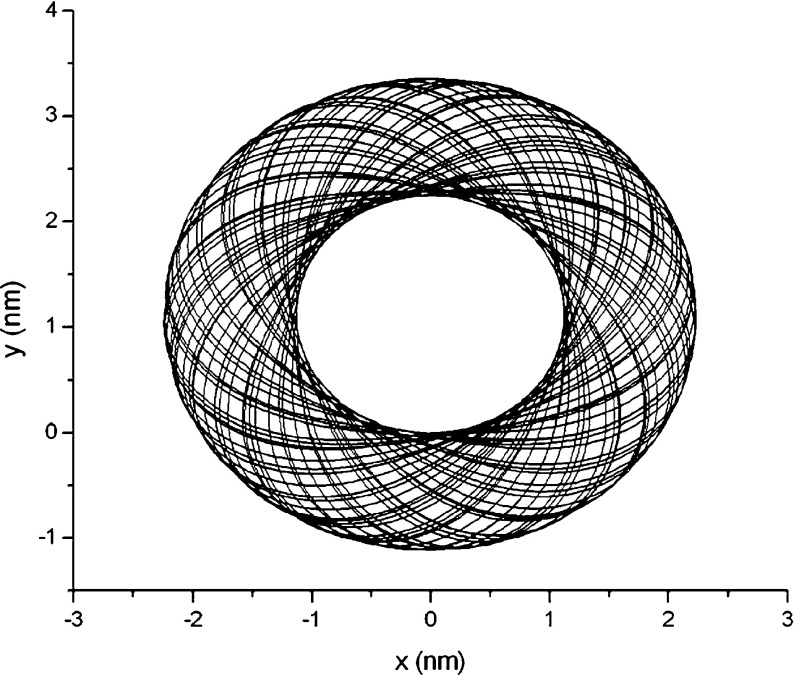
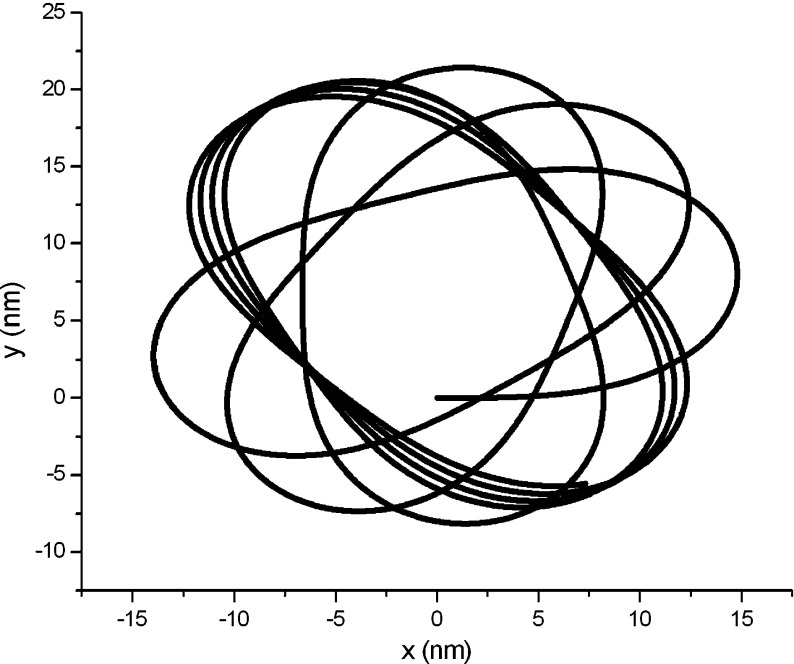
Assume σ = 5.0 ×10^− 4 nN/nm in an intracellular solution. Using the classical Runge-Kutta algorithm, we calculate the condensed configuration corresponding to the original configuration in Fig. 3, under the initial condition of F₁ = F₃ = 0, Δκ = 0, x = y = 0, and θ = 0. The result is shown in Fig. 4. From it, ones see that the DNA segment coils into a “toroid” spontaneously due to the interfacial traction. To one’s surprise, this toroidal DNA was found by many investigators in experiments [17–19, 25]. Hud, Downing, and Balhorn constructed a geometric model (HDB model) as shown in Fig. 4 in terms of their experimental results [18]. Figure 4 reproduces the HDB model in theory.

Fig. 4.

Condensed toroidal configuration corresponding to Fig. 3

The outer diameter of the toroid in Fig. 4 is about 4.5 nm. This magnitude is nearly 120 times smaller than the length of the DNA segment in Fig. 3. So relative to the original configuration, the condensed configuration of the DNA segment seems like a solid grain. As well known, The DNA of any organism must be folded and packed in order to fit inside a cell. For example, the DNA of Escherichia coli is a ring of circumference 1.58 mm that must fit inside a cell of diameter 1 m. This fact seems to be explained by the results in Figs. 3 and 4. Therefore, we infer that the interfacial traction is probably a force to compactify DNA.

With the changes of temperature, concentration, and pH value etc., the DNA chain will undergo a reconfiguration. The reconfiguration shows two results: (1) unfolding of the DNA and (2) stiffening of the DNA. In order to model these phenomena, we investigate the configuration of the DNA segment changes with its interfacial energy factor and bending stiffness.

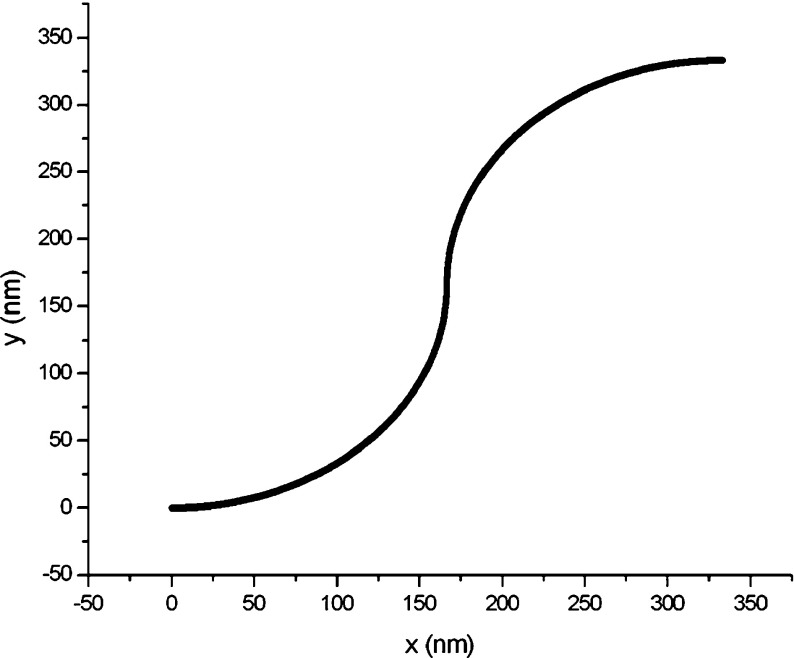
Assume that the interfacial energy factor reduces to 5.0 × 10^− 6 nN/nm and the bending stiffness increases to 1.6 nN/nm². With these changes, the DNA segment will adjust its structure to form the so-called relaxed configuration, illustrated in Fig. 5. Compared with the condensed configuration (see Fig. 4), the relaxed configuration of the DNA segment is sparser in structure, and its size increases about six times due to unfolding. If the interfacial energy factor continues to reduce to 5.0 × 10^− 8 nN/nm and the bending stiffness increases to 16.0 nN/nm², the DNA segment will further unfold to form another new relaxed configuration. The new relaxed configuration is shown in Fig. 6. From Figs. 3–6, it is very clear to see that the DNA segment continues to unfold with the interfacial energy factor decreasing. When the interfacial energy factor drops to zero, the DNA segment will return to its original configuration. Therefore, the relaxation process of DNA is in fact a process returning it to its original state.

Fig. 5.

Relaxed configuration corresponding to Fig. 3 (σ = 5.0 ×10^− 6 nN/nm, E = 1.6 nN/nm²)

Fig. 6.

Relaxed configuration corresponding to Fig. 3 (σ = 5.0 ×10^− 8 nN/nm, E = 16 nN/nm²)

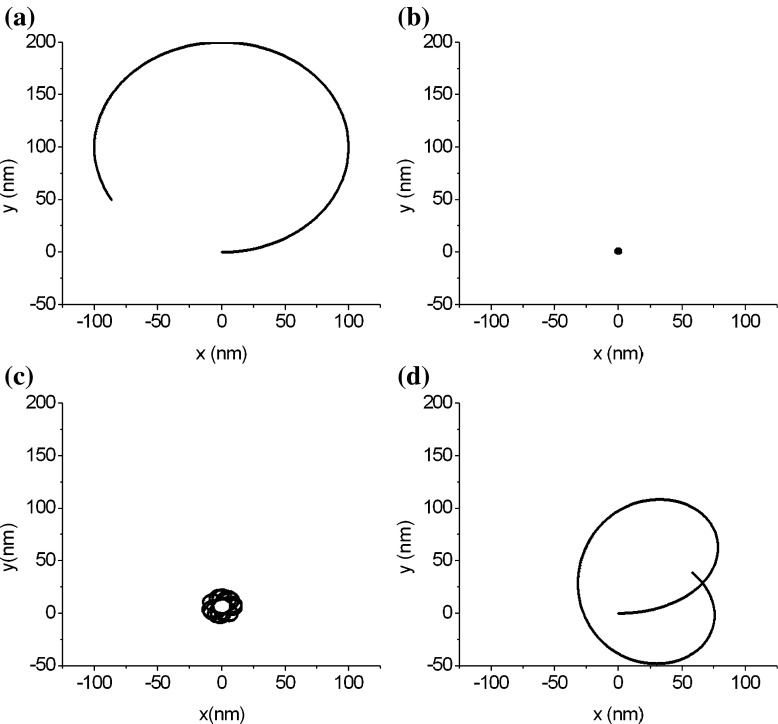
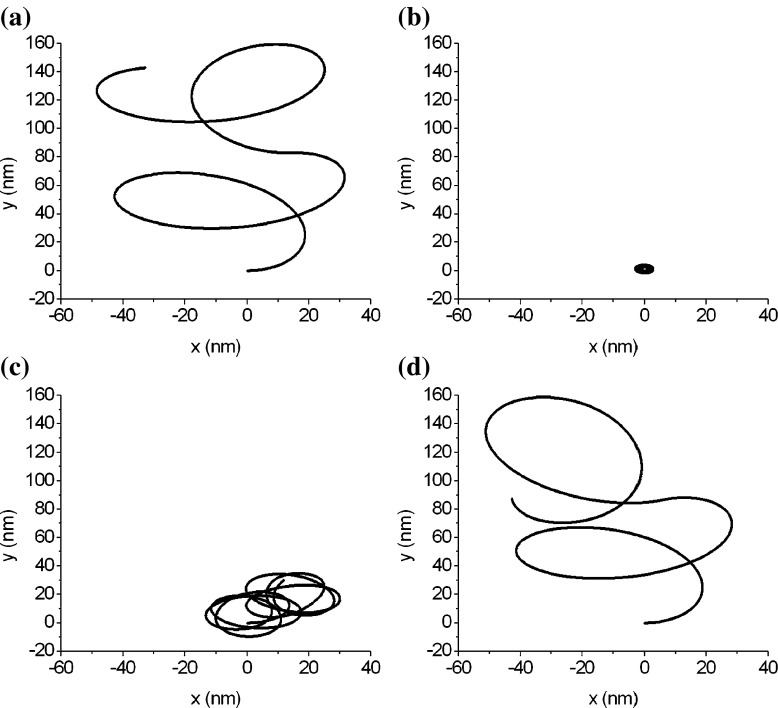
The DNA segments in Figs. 7a and 8a have same physical properties and arc length as that in Fig. 3. Their differences consist only in their configurations. Figure 7a represents a circular arc of three quarters and Fig. 8a is a snake-shaped curve, depicted in terms of the following equation:

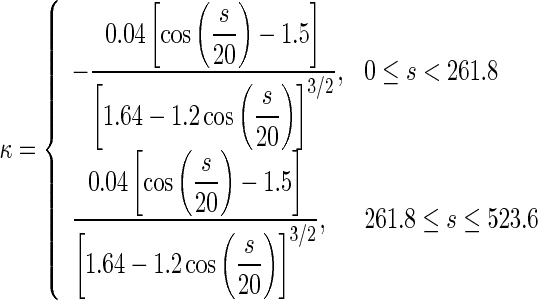19

where κ and s are the curvature and arc length, respectively.

Fig. 7.

The folding and unfolding of an arc-shaped DNA segment

Fig. 8.

The folding and unfolding of a snake-shaped DNA segment

Figures 7 and 8 show the configuration changes, due to folding or unfolding, of two DNA segments. An interesting result is that three DNA segments with different original configurations (see Figs. 3, 7a, and 8a) all fold into a toroidal grain. This means that the condensed configuration of DNA is independent of its original configuration. When unfolding, a DNA changes from its condensed configuration into the relaxed configuration. It is clear that the relaxed configuration of a DNA is correlated with the original configuration of the DNA. Figures 7 and 8 show that, with unfolding, the DNA goes through a series of relaxed configurations to gradually approach its original configuration. Therefore, we conclude that the DNA segments that are different only in the original configuration probably have a condensed toroidal configuration, but their relaxed configurations differ, depending on the original configuration.

Conclusions

A model of a thin elastic rod is established to determine the equilibrium configuration of DNA under the action of interfacial interactions. By the help of this model, we arrive at the following conclusions:

1. Equation 11 characterizes the interfacial traction between a rod and its environment. Although the interfacial energy factor in Eq. 11 is very small, the interfacial traction given by this equation is much greater than the interfacial energy factor in magnitude. So the influence of interfacial traction on deformation of a thin rod is not neglectable.

2. The interfacial traction acts as a source to drive DNA folding and unfolding. The equilibrium configuration of a DNA is completely determined by competition between the interfacial energy and elastic strain energy of the DNA itself.

3. DNA forms its condensed toroidal configuration from an original configuration by folding. The DNAs with different original configurations probably possess the same condensed configuration: a toroidal grain.

4. With the interfacial traction decreasing, DNA unfolds and goes through a series of relaxed configurations to gradually approach its original configuration.

Finally, it should be noted that in the simplified 2D model, two intersecting segments of a curled DNA are allowed to overlap together at the intersecting point. This is a spurious phenomenon that can be eliminated in a 3D model. However, how to remove this phenomenon is still a problem needing further exploration.