Abstract
Computation and information processing are among the most fundamental notions in cognitive science. They are also among the most imprecisely discussed. Many cognitive scientists take it for granted that cognition involves computation, information processing, or both – although others disagree vehemently. Yet different cognitive scientists use ‘computation’ and ‘information processing’ to mean different things, sometimes without realizing that they do. In addition, computation and information processing are surrounded by several myths; first and foremost, that they are the same thing. In this paper, we address this unsatisfactory state of affairs by presenting a general and theory-neutral account of computation and information processing. We also apply our framework by analyzing the relations between computation and information processing on one hand and classicism, connectionism, and computational neuroscience on the other. We defend the relevance to cognitive science of both computation, at least in a generic sense, and information processing, in three important senses of the term. Our account advances several foundational debates in cognitive science by untangling some of their conceptual knots in a theory-neutral way. By leveling the playing field, we pave the way for the future resolution of the debates’ empirical aspects.
Keywords: Classicism, Cognitivism, Computation, Computational neuroscience, Computational theory of mind, Computationalism, Connectionism, Information processing, Meaning, Neural computation, Representation
Information processing, computation, and the foundations of cognitive science
Computation and information processing are among the most fundamental notions in cognitive science. Many cognitive scientists take it for granted that cognition involves computation, information processing, or both. Many others, however, reject theories of cognition based on either computation or information processing [1–7]. This debate has continued for over half a century without resolution.
An equally long-standing debate pitches classical theories of cognitive architecture [8–13] against connectionist and neurocomputational theories [14–21]. Classical theories draw a strong analogy between cognitive systems and digital computers. The term “connectionism” is primarily used for neural network models of cognitive phenomena constrained solely by behavioral (as opposed to neurophysiological) data. By contrast, the term “computational neuroscience” is primarily used for neural network models constrained by neurophysiological and possibly also behavioral data. We are interested not so much in the distinction between connectionism and computational neuroscience as in what they have in common: the explanation of cognition in terms of neural networks and their apparent contrast with classical theories. Thus, for present purposes, connectionism and computational neuroscience may be considered together.
For brevity’s sake, we will refer to these debates on the role information processing, computation, and neural networks should play in a theory of cognition as the foundational debates.
In recent years, some cognitive scientists have attempted to get around the foundational debates by advocating a pluralism of perspectives [22, 23]. According to this kind of pluralism, it is a matter of perspective whether the brain computes, processes information, is a classical system, or is a connectionist system. Different perspectives serve different purposes, and different purposes are legitimate. Hence, all sides of the foundational debates can be retained if appropriately qualified.
Although pluralists are correct to point out that different descriptions of the same phenomenon can in principle complement one another, this kind of perspectival pluralism is flawed in one important respect. There is an extent to which different parties in the foundational debates offer alternative explanations of the same phenomena—they cannot all be right. Nevertheless, these pluralists are responding to something true and important: the foundational debates are not merely empirical; they cannot be resolved solely by collecting more data because they hinge on how we construe the relevant concepts. The way to make progress is therefore not to accept all views at once but to provide a clear and adequate conceptual framework that remains neutral between different theories. Once such a framework is in place, competing explanations can be translated into a shared language and evaluated on empirical grounds.
Lack of conceptual housecleaning has led to the emergence of a number of myths that stand in the way of theoretical progress. Not everyone subscribes to all of the following assumptions, but each is widespread and influential:
Computation is the same as information processing.
Semantic information is necessarily true.
Computation requires representation.
The Church–Turing thesis entails that cognition is computation.
Everything is computational.
Connectionist and classical theories of cognitive architecture are mutually exclusive.
We will argue that these assumptions are mistaken and distort our understanding of computation, information processing, and cognitive architecture.
Traditional accounts of what it takes for a physical system to perform a computation or process information [19, 24–26] are inadequate because they are based on at least some of assumptions 1–6. In lieu of these traditional accounts, we will present a general account of computation and information processing that systematizes, refines, and extends our previous work [27–37].
We will then apply our framework by analyzing the relations between computation and information processing on one hand and classicism, connectionism, and computational neuroscience on the other. We will defend the relevance to cognitive science of both computation, at least in a generic sense we will articulate, and information processing, in three important senses of the term. We will also argue that the choice among theories of cognitive architecture is not between classicism and connectionism or computational neuroscience but rather between varieties of neural computation, which may be classical or nonclassical.
Our account advances the foundational debates by untangling some of their conceptual knots in a theory-neutral way. By leveling the playing field, we pave the way for the future resolution of the debates’ empirical aspects.
Getting rid of some myths
The notions of computation and information processing are often used interchangeably. Here is a representative example: “I ... describe the principles of operation of the human mind, considered as an information-processing, or computational, system” ([38], p. 10, emphasis added). This statement presupposes assumption 1 above. Why are the two notions used interchangeably so often, without a second thought?
We suspect the historical reason for this conflation goes back to the cybernetic movement’s effort to blend Shannon’s information theory [39] with Turing’s [40] computability theory (as well as control theory). Cyberneticians did not clearly distinguish either between Shannon information and semantic information or between semantic and nonsemantic computation (more on these distinctions below). But, at least initially, they were fairly clear that information and computation played distinct roles within their theories. Their idea was that organisms and automata contain control mechanisms: information is transmitted within the system and between system and environment, and control is exerted by means of digital computation [41, 42].
Then the waters got muddier. When the cybernetic movement became influential in psychology, artificial intelligence (AI), and neuroscience, “computation” and “information” became ubiquitous buzzwords. Many people accepted that computation and information processing belong together in a theory of cognition. After that, many stopped paying attention to the differences between the two. To set the record straight and make some progress, we must get clearer on the independent roles computation and information processing can fulfill in a theory of cognition.
The notion of digital computation was imported from computability theory into neuroscience and psychology primarily for two reasons: first, it seemed to provide the right mathematics for modeling neural activity [43]; second, it inherited mathematical tools (algorithms, computer program, formal languages, logical formalisms, and their derivatives, including many types of neural networks) that appeared to capture some aspects of cognition. These reasons are not sufficient to actually establish that cognition is digital computation. Whether cognition is digital computation is a difficult question, which lies outside the scope of this essay.
The theory that cognition is computation became so popular that it progressively led to a stretching of the operative notion of computation. In many quarters, especially neuroscientific ones, the term “computation” is used, more or less, for whatever internal processes explain cognition. Unlike “digital computation,” which stands for a mathematical apparatus in search of applications, “neural computation” is a label in search of a theory. Of course, the theory is quite well developed by now, as witnessed by the explosion of work in computational and theoretical neuroscience over the last decades [20, 44, 45]. The point is that such a theory need not rely on a previously existing and independently defined notion of computation, such as digital computation “or even analog computation” in its most straightforward sense.
By contrast, the various notions of information (processing) have distinct roles to play. By and large, they serve to make sense of how organisms keep track of their environments and produce behaviors accordingly. Shannon’s notion of information can serve to address quantitative problems of efficiency of communication in the presence of noise, including communication between the external (distal) environment and the nervous system. Other notions of information—specifically, semantic information—can serve to give specific semantic content to particular states or events. This may include cognitive or neural events that reliably correlate with events occurring in the organism’s distal environment as well as mental representations, words, and the thoughts and sentences they constitute.
Whether cognitive or neural events fulfill all or any of the job descriptions of computation and information processing is in part an empirical question and in part a conceptual one. It is a conceptual question insofar as we can mean different things by “information” and “computation” and insofar as there are conceptual relations between the various notions. It is an empirical question insofar as, once we fix the meanings with of “computation” and “information,” the extent to which computation and the processing of information are both instantiated in the brain depends on the empirical facts of the matter.
Ok, but do these distinctions really matter? Why should a cognitive theorist care about the differences between computation and information processing? The main theoretical advantage of keeping them separate is to appreciate the independent contributions they can make to a theory of cognition. Conversely, the main cost of conflating computation and information processing is that the resulting mongrel concept may be too messy and vague to do all the jobs that are required of it. As a result, it becomes difficult to reach consensus on whether cognition involves either computation or information processing.
Debates on computation, information processing, and cognition are further muddied by assumptions 2–6.
Assumption 2 is that semantic information is necessarily true; there is no such thing as false information. This “veridicality thesis” is defended by most theorists of semantic information [46–49]. But as we shall point out in Section 4, assumption 2 is inconsistent with one important use of the term “information” in cognitive science [37]. Therefore, we will reject assumption 2 in favor of the view that semantic information may be either true or false.
Assumption 3 is that there is no computation without representation. Most accounts of computation rely on this assumption [19, 24–26, 38]. As one of us has argued extensively elsewhere [27, 28, 50], however, assumption 3 obscures the core notion of computation used in computer science and computability theory—the same notion that inspired the computational theory of cognition—as well as some important distinctions between notions of computation. The core notion of computation does not require representation, although it is compatible with it. In other words, computational states in the core sense may or may not be representations. Understanding computation in its own terms, independently of representation, will allow us to sharpen the debates over the computational theory of cognition as well as cognitive architecture.
Assumption 4 is that cognition is computation because of the Church–Turing thesis [51, 52]. The Church–Turing thesis says that any function that is computable in an intuitive sense is recursive or, equivalently, computable by some Turing machine [40, 53, 54].1 Since Turing machines and other equivalent formalisms are the foundation of the mathematical theory of computation, many authors either assume or attempt to argue that all computations are covered by the results established by Turing and other computability theorists. But recent scholarship has shown this view to be fallacious [29, 55]. The Church–Turing thesis does not establish whether a function is computable. It only says that if a function is computable in a certain intuitive sense, then it is computable by some Turing machine. Furthermore, the intuitive sense in question has to do with what can be computed by following an algorithm (a list of explicit instructions) defined over sequences of digital entities. Thus, the Church–Turing thesis applies directly only to algorithmic digital computation. The relationship between algorithmic digital computation and digital computation simpliciter, let alone other kinds of computation, is quite complex, and the Church–Turing thesis does not settle it.
Assumption 5 is pancomputationalism: everything is computational. There are two ways to defend assumption 5. Some authors argue that everything is computational because describing something as computational is just one way of interpreting it, and everything can be interpreted that way [19, 23]. We reject this interpretational pancomputationalism because it conflates computational modeling with computational explanation. The computational theory of cognition is not limited to the claim that cognition can be described (modeled) computationally, as the weather can; it adds that cognitive phenomena have a computational explanation [28, 31, 34]. Other authors defend assumption 5 by arguing that the universe as a whole is at bottom computational [56, 57]. The latter is a working hypothesis or article of faith for those interested in seeing how familiar physical laws might emerge from a “computational” or “informational” substrate. It is not a widely accepted notion, and there is no direct evidence for it.
The physical form of pancomputationalism is not directly relevant to theories of cognition because theories of cognition attempt to find out what distinguishes cognition from other processes—not what it shares with everything else. Insofar as the theory of cognition uses computation to distinguish cognition from other processes, it needs a notion of computation that excludes at least some other processes as noncomputational (cf. [28, 31, 34]).
Someone may object as follows. Even if pancomputationalism—the thesis that everything is computational—is true, it does not follow that the claim that cognition involves computation is vacuous. A theory of cognition still has to say which specific computations cognition involves. The job of neuroscience and psychology is precisely to discover the specific computations that distinguish cognition from other processes (cf. [26]).
We agree that if cognition involves computation, then the job of neuroscience and psychology is to discover which specific computations cognition involves. But the if is important. The job of psychology and neuroscience is to find out how cognition works, regardless of whether it involves computation. The claim that brains compute was introduced in neuroscience and psychology as an empirical hypothesis to explain cognition by analogy with digital computers. Much of the empirical import of the computational theory of cognition is already eliminated by stretching the notion of computation from digital to generic (see below). Stretching the notion of computation even further, so as to embrace pancomputationalism, erases all empirical import from the claim that brains compute.
Here is another way to describe the problem. The view that cognition involves computation has been fiercely contested. Many psychologists and neuroscientists reject it. If we adopt an all-encompassing notion of computation, we have no way to make sense of this debate. It is utterly implausible that critics of computationalism have simply failed to notice that everything is computational. More likely, they object to what they perceive to be questionable empirical commitments of computationalism. For this reason, computation as it figures in pancomputationalism is a poor foundation for a theory of cognition. From now on, we will leave pancomputationalism behind.
Finally, assumption 6 is that connectionist and classical theories of cognitive architecture are mutually exclusive.2 By this assumption, we do not mean to rule out hybrid theories that combine symbolic and connectionist modules (cf. [59]). What we mean is that, according to assumption 6, for any given module, you must have either a classical or a connectionist theory.
The debate between classicism and connectionism or computational neuroscience is sometimes conflated with the debate between computationalism and anticomputationalism.3 But these are largely separate debates. Computationalists argue that cognition is computation; anticomputationalists deny it. Classicists argue that cognition operates over language-like structures; connectionists suggest that cognition is implemented by neural networks. So all classicists are computationalists, but computationalists need not be classicists, and connectionists and computational neuroscientists need not be anticomputationalists. In both debates, the opposing camps often confusedly mix terminological disputes with substantive disagreements over the nature of cognition. This is why we will begin our next section by introducing a taxonomy of notions of computation.
As we will show in Section 3.4, depending on what one means by computation, computationalism can range from being true but quite weak to being an explanatorily powerful, though fallible, thesis about cognition. Similarly, we will show the opposition between classicists and connectionists to be either spurious or substantive depending on what is meant by connectionism. We will argue that everyone is (or ought to be) a connectionist (or even better, a computational neuroscientist) in the most general and widespread sense of the term, whether they realize it or not.
Computation
Different notions of computation vary along two important dimensions. The first is how encompassing the notion is, that is, how many processes it includes as computational. The second dimension has to do with whether being the vehicle of a computation requires possessing meaning or semantic properties. We will look at the first dimension first.
Digital computation
We use “digital computation” for the notion implicitly defined by the classical mathematical theory of computation, and “digital computationalism” for the thesis that cognition is digital computation. Rigorous mathematical work on computation began with Alan Turing and other logicians in the 1930s [40, 53, 60, 61], and it is now a well-established branch of mathematics [62].
A few years after Turing and others formalized the notion of digital computation, Warren McCulloch and Walter Pitts [43] used digital computation to characterize the activities of the brain. McCulloch and Pitts were impressed that the main vehicles of neural processes appear to be trains of all-or-none spikes, which are discontinuous events [44]. This led them to conclude, rightly or wrongly, that neural processes are digital computations. They then used their theory that brains are digital computers to explain cognition.4
McCulloch and Pitts’s theory is the first theory of cognition to employ Turing’s notion of digital computation. Since McCulloch and Pitts’s theory had a major influence on subsequent computational theories, we stress that digital computation is the principal notion that inspired modern computational theories of cognition [63]. This makes the clarification of digital computation especially salient.
Digital computation may be defined both abstractly and concretely. Roughly speaking, abstract digital computation is the manipulation of strings of discrete elements, that is, strings of letters from a finite alphabet. Here, we are interested primarily in concrete computation or physical computation. Letters from a finite alphabet may be physically implemented by what we call “digits.” To a first approximation, concrete digital computation is the processing of sequences of digits according to general rules defined over the digits [27]. Let us briefly consider the main ingredients of digital computation.
The atomic vehicles of concrete digital computation are digits, where a digit is simply a macroscopic state (of a component of the system) whose type can be reliably and unambiguously distinguished by the system from other macroscopic types. To each (macroscopic) digit type, there correspond a large number of possible microscopic states. Digital systems are engineered so as to treat all those microscopic states in the same way—the one way that corresponds to their (macroscopic) digit type. For instance, a system may treat 4 V plus or minus some noise in the same way (as a “0”), whereas it may treat 8 V plus or minus some noise in a different way (as a “1”). To ensure reliable manipulation of digits based on their type, a physical system must manipulate at most a finite number of digit types. For instance, ordinary computers contain only two types of digit, usually referred to as 0 and 1.5 Digits need not mean or represent anything, but they can; numerals represent numbers, while other digits (e.g., “∣”, “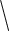 ”) do not represent anything in particular.
”) do not represent anything in particular.
Digits can be concatenated (i.e., ordered) to form sequences or strings. Strings of digits are the vehicles of digital computations. A digital computation consists in the processing of strings of digits according to rules. A rule in the present sense is simply a map from input strings of digits, plus possibly internal states, to output strings of digits. Examples of rules that may figure in a digital computation include addition, multiplication, identity, and sorting.6
When we define concrete computations and the vehicles—such as digits—that they manipulate, we need not consider all of their specific physical properties. We may consider only the properties that are relevant to the computation, according to the rules that define the computation. A physical system can be described at different levels of abstraction. Since concrete computations and their vehicles can be defined independently of the physical media that implement them, we shall call them “medium independent” (the term is due to Justin Garson). That is, computational descriptions of concrete physical systems are sufficiently abstract as to be medium independent.
In other words, a vehicle is medium-independent just in case the rules (i.e., the input–output maps) that define a computation are sensitive only to differences between portions (i.e., spatiotemporal parts) of the vehicles along specific dimensions of variation—they are insensitive to any other physical properties of the vehicles. Put yet another way, the rules are functions of state variables associated with certain degrees of freedom that can be implemented differently in different physical media. Thus, a given computation can be implemented in multiple physical media (e.g., mechanical, electromechanical, electronic, magnetic, etc.), provided that the media possess a sufficient number of dimensions of variation (or degrees of freedom) that can be appropriately accessed and manipulated.
In the case of digits, their defining characteristic is that they are unambiguously distinguishable by the processing mechanism under normal operating conditions. Strings of digits are ordered sets of digits, i.e., digits such that the system can distinguish different members of the set depending on where they lie along the string. The rules defining digital computations are, in turn, defined in terms of strings of digits and internal states of the system, which are simply states that the system can distinguish from one another. No further physical properties of a physical medium are relevant to whether they implement digital computations. Thus, digital computations can be implemented by any physical medium with the right degrees of freedom.
To summarize, a physical system is a digital computing system just in case it is a system that manipulates input strings of digits, depending on the digits’ type and their location on the string, in accordance with a rule defined over the strings (and possibly the internal states of the system).
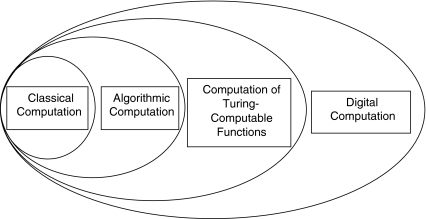
The notion of digital computation here defined is quite general. It should not be confused with three other commonly invoked but more restrictive notions of computation: classical computation (in the sense of Fodor and Pylyshyn [10]),7 computation that follows an algorithm, and computation of Turing-computable functions (see Fig. 1).
Fig. 1.
Types of digital computation and their relations of class inclusion
Let us begin with the most restrictive notion of the three: classical computation. A classical computation is a digital computation that has two additional features. First, it manipulates a special kind of digital vehicle: sentence-like strings of digits. Second, it is algorithmic, meaning that it follows an algorithm—i.e., an effective, step-by-step procedure that manipulate strings of digits and produce a result within finitely many steps. Thus, a classical computation is a digital, algorithmic computation whose algorithms are sensitive to the combinatorial syntax of the symbols [10].8
A classical computation is algorithmic, but the notion of algorithmic computation—i.e., digital computation that follows an algorithm—is more inclusive because it does not require that the vehicles being manipulated be sentence-like.
Any algorithmic computation, in turn, is Turing computable (i.e., it can be performed by a Turing machine). This is a version of the Church–Turing thesis, for which there is compelling evidence [54]. But the computation of Turing-computable functions need not be carried out by following an algorithm. For instance, many neural networks compute Turing-computable functions (their inputs and outputs are strings of digits, and the input–output map is Turing computable), but such networks need not have a level of functional organization at which they follow the steps of an algorithm for computing their functions: no functional level at which their internal states and state transitions are discrete.9
Finally, the computation of a Turing-computable function is a digital computation because Turing-computable functions are by definition functions of a denumerable domain—a domain whose elements may be counted—and the arguments and values of such functions are, or may be represented by, strings of digits. But it is equally possible to define functions of strings of digits that are not Turing-computable and to mathematically define processes that compute such functions. Some authors have speculated that some functions that are not Turing-computable may be computable by some physical systems [55, 64]. According to our usage, any such computations still count as digital computations. Of course, it may well be that only the Turing-computable functions are computable by physical systems; whether this is the case is an empirical question that does not affect our discussion. Furthermore, the computation of Turing-uncomputable functions is unlikely to be relevant to the study of cognition. Be that as it may—we will continue to talk about digital computation in general.
Many other distinctions may be drawn within digital computation, such as hardwired vs. programmable, special purpose vs. general purpose, and serial vs. parallel computation (cf. [30]). Such additional distinctions, which are orthogonal to those of Fig. 1, may be used to further classify theories of cognition that appeal to digital computation. Nevertheless, digital computation is the most restrictive notion of computation that we will consider here. It includes processes that follow ordinary algorithms, such as the computations performed by standard digital computers, as well as many types of neural network computations. Since digital computation is the notion that inspired the computational theory of cognition, it is the most relevant notion for present purposes.
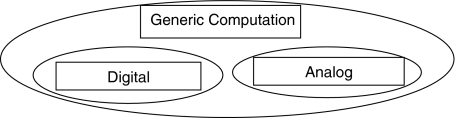
Generic computation
Even though the notion of digital computation is broad, we need an even broader notion of computation. In order to capture all relevant uses of “computation” in cognitive science, we now introduce the notion of generic computation. Generic computation subsumes digital computation, as defined in the previous section, analog computation, and neural computation.
We use “generic computation” to designate the processing of vehicles according to rules that are sensitive to certain vehicle properties and, specifically, to differences between different portions of the vehicles. This definition generalizes the definition of digital computation by allowing for a broader range of vehicles (e.g., continuous variables as well as discrete digits). We use “generic computationalism” to designate the thesis that cognition is computation in the generic sense.
Since the definition of generic computation makes no reference to specific media, generic computation is medium independent—it applies to all media. That is, the differences between portions of vehicles that define a generic computation do not depend on specific physical properties of the medium but only on the presence of relevant degrees of freedom.
Shortly after McCulloch and Pitts argued that brains perform digital computations, others countered that neural processes may be more similar to analog computations [65, 66]. The alleged evidence for the analog computational theory includes neurotransmitters and hormones, which are released by neurons in degrees rather than in all-or-none fashion.
Analog computation is often contrasted with digital computation, but analog computation is a vague and slippery concept. The clearest notion of analog computation is that of Pour-El [67]. Roughly, abstract analog computers are systems that manipulate continuous variables to solve certain systems of differential equations. Continuous variables are variables that can vary continuously over time and take any real values within certain intervals.
Analog computers can be physically implemented, and physically implemented continuous variables are different kinds of vehicles than strings of digits. While a digital computing system can always unambiguously distinguish digits and their types from one another, a concrete analog computing system cannot do the same with the exact values of (physically implemented) continuous variables. This is because the values of continuous variables can only be measured within a margin of error. Primarily due to this, analog computations (in the present, strict sense) are a different kind of process than digital computations.10
The claim that the brain is an analog computer is ambiguous between two interpretations. On the literal interpretation, “analog computer” is given Pour-El’s precise meaning [67]. The theory that the brain is literally an analog computer in this literal sense was never very popular. The primary reason is that, although spike trains are a continuous function of time, they are also sequences of all-or-none signals [44].
On a looser interpretation, “analog computer” refers to a broader class of computing systems. For instance, Churchland and Sejnowski use the term “analog” so that containing continuous variables is sufficient for a system to count as analog: “The input to a neuron is analog (continuous values between 0 and 1)” ([19], p. 51). Under such a usage, even a slide rule counts as an analog computer. Sometimes, the notion of analog computation is simply left undefined, with the result that “analog computer” refers to some otherwise unspecified computing system.
The looser interpretation of “analog computer”—of which Churchland and Sejnowski’s usage is one example—is not uncommon, but we find it misleading because its boundaries are unclear and yet it is prone to being confused with analog computation in the more precise sense of Pour-El’s [67]. Let us now turn to the notion of neural computation.
In recent decades, the analogy between brains and computers has taken hold in neuroscience. Many neuroscientists have started using the term “computation” for the processing of neuronal spike trains, that is, sequences of spikes produced by neurons in real time. The processing of neuronal spike trains by neural systems is often called “neural computation”. Whether neural computation is best regarded as a form of digital computation, analog computation, or something else is a difficult question, which we cannot settle here. Instead, we will subsume digital computation, analog computation, and neural computation under generic computation (Fig. 2).
Fig. 2.
Types of generic computation and their relations of class inclusion. Neural computation is not represented because where it belongs is controversial
While digits are unambiguously distinguishable vehicles, other vehicles are not so. For instance, concrete analog computers cannot unambiguously distinguish between any two portions of the continuous variables they manipulate. Since the variables can take any real values but there is a lower bound to the sensitivity of any system, it is always possible that the difference between two portions of a continuous variable is small enough to go undetected by the system. From this, it follows that the vehicles of analog computation are not strings of digits. Nevertheless, analog computations are only sensitive to the differences between portions of the variables being manipulated, to the degree that they can be distinguished by the system. Any further physical properties of the media implementing the variables are irrelevant to the computation. Like digital computers, therefore, analog computers operate on medium-independent vehicles.
Finally, current evidence suggests that the vehicles of neural processes are neuronal spikes and that the functionally relevant aspects of neural processes are medium-independent aspects of the spikes—primarily, spike rates. That is, the functionally relevant aspects of spikes may be implemented either by neural tissue or by some other physical medium, such as a silicon-based circuit. Thus, spike trains appear to be another case of medium-independent vehicle, in which case they qualify as proper vehicles for generic computations. Assuming that brains process spike trains and that spikes are medium-independent vehicles, it follows by definition that brains perform computations in the generic sense.
In conclusion, generic computation includes digital computation, analog computation, neural computation (which may or may not correspond closely to digital or analog computation), and more.
Semantic vs. nonsemantic computation
So far, we have taxonomized different notions of computation according to how broad they are, namely, how many processes they include as computational. Now, we will consider a second dimension along which notions of computation differ. Consider digital computation. The digits are often taken to be representations because it is assumed that computation requires representation [68]. A similarly semantic view may be taken with respect to generic computation.
One of us has argued at length that computation per se, in the sense implicitly defined by the practices of computability theory and computer science, does not require representation and that any semantic notion of computation presupposes a nonsemantic notion of computation [32, 50]. Meaningful words such as “avocado” are both strings of digits and representations, and computations may be defined over them. Nonsense sequences such as “#r %h@,” which represent nothing, are strings of digits too, and computations may be defined over them just as well.
Although computation does not require representation, it certainly allows it. In fact, generally, computations are carried out over representations. For instance, usually, the states manipulated by ordinary computers are representations.
To maintain generality, we will consider both semantic and nonsemantic notions of computation. In a nutshell, semantic notions of computation define computations as operating over representations. By contrast, nonsemantic notions of computation define computations without requiring that the vehicles being manipulated be representations.
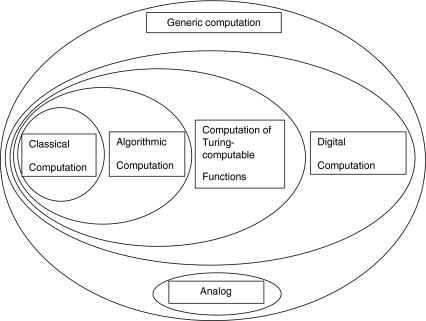
Let us take stock. We have introduced a taxonomy of varieties of computation (Fig. 3). Within each category, we may distinguish a semantic notion of computation, which presupposes that the computational vehicles are representations, and a nonsemantic one, which does not.11
Fig. 3.
Types of computation and their relations of class inclusion. Once again, neural computation is not represented because where it belongs is controversial
Computationalism, classicism, and connectionism reinterpreted
The distinctions introduced so far shed new light on the long-standing debates on computationalism, classicism, connectionism, and computational neuroscience. Computationalism, we have said, is the view that cognition is computation. We can now appreciate that this may mean at least two different things: (1) cognition is digital computation and (2) cognition is computation in the generic sense. Let us consider them in reverse order.
If “computation” means generic computation, i.e., the processing of medium-independent vehicles according to rules, then computationalism becomes the claim that cognition is the manipulation of medium-independent vehicles according to rules. This is not a trivial claim. Disputing generic computationalism requires arguing that cognitive capacities depend in an essential way on some specific physical property of cognitive systems other than those required to distinguish computational vehicles from one another. For instance, one may argue that the processing of spike rates by neural systems is essentially dependent on the use of voltages instead of other physical properties to generate action potentials. Someone might propose that without those specific physical properties it would be impossible to exhibit certain cognitive capacities.
Something along these lines is sometimes maintained for phenomenal consciousness, due to the qualitative feel of conscious states (e.g., [69]). Nevertheless, many cognitive scientists maintain that consciousness is reducible to computation and information processing (cf. [70]). Since we lack the space to discuss consciousness, we will assume (along with mainstream cognitive scientists) that if and insofar as consciousness is not reducible to computation in the generic sense and information processing, cognition may be studied independently of consciousness. If this is right, then, given that cognitive processes appear to be implemented by spike trains and that spike trains appear to be medium independent, we may conclude that cognition is computation in the generic sense.
If “computation” means digital computation, i.e., the processing of strings of digits according to rules, then computationalism says that cognition is the manipulation of digits. As we saw above, this is what McCulloch and Pitts [43] argued. Importantly, it is also what both classical computational theories and many connectionist theories of cognition maintain. Finally, this view is what most critics of computationalism object to [1, 3]. Although digital computationalism encompasses a broad family of theories, it is a powerful thesis with considerable explanatory scope. Its exact explanatory scope depends on the precise kind of digital computing systems that cognitive systems are postulated to be. If cognitive systems are digital computing systems, they may be able to compute a smaller or larger range of functions, depending on their precise mechanistic properties.12
Let us now turn to another debate sometimes conflated with the one just described, namely the debate between classicists and connectionists. By the 1970s, McCulloch and Pitts were mostly forgotten. The dominant paradigm in cognitive science was classical (or symbolic) AI, aimed at writing computer programs that simulate intelligent behavior without much concern for how brains work [9]. It was commonly assumed that digital computationalism is committed to classicism, that is, the idea that cognition is the manipulation of linguistic, or sentence-like, structures. On this view, cognition consists of performing computations on sentences with a logico-syntactic structure akin to that of natural languages but written in the language of thought [71, 72].
It was also assumed that, given digital computationalism, explaining cognition is an autonomous activity from explaining the brain, in the sense that figuring out how the brain works tells us little or nothing about how cognition works: neural descriptions and computational descriptions are at “different levels” [72, 73].
During the 1980s, connectionism reemerged as an influential approach to psychology. Most connectionists deny that cognition is based on a language of thought and affirm that a theory of cognition should be at least “inspired” by the way the brain works [17].
The resulting debate between classicists and connectionists (e.g., [10, 18]) has been somewhat confusing. Part of what’s confusing about it is that different authors employ different notions of computation, which vary in both their degree of precision and their inclusiveness (see [30] for more details). But even after we factor out differences in notions of computation, further confusions lie in the wings.
Digital computationalism and neural network theories are often described as being at odds with one another. This is because it is assumed that digital computationalism is committed to classical computation (the idea that the vehicles of digital computation are language-like structures) and to autonomy from neuroscience, two theses flatly denied by many prominent connectionists and computational neuroscientists. But many connectionists also model and explain cognition using neural networks that perform computations defined over strings of digits, so perhaps they should be counted among the digital computationalists [15–17, 19, 74–77]. To make matters worse, other connectionists and computational neuroscientists reject digital computationalism—they maintain that their neural networks, while explaining behavior, do not perform digital computations [1–3, 5, 7, 78].
In addition, the very origin of digital computationalism calls into question the commitment to autonomy from neuroscience: McCulloch and Pitts initially introduced digital computationalism based on neurophysiological evidence. Furthermore, some form of computationalism or other is now a working assumption of many neuroscientists, and nothing in the notion of digital computation commits us to conceiving of its vehicles as language-like.
To clarify this debate, we need two separate distinctions. One is the distinction between digital computationalism (“cognition is digital computation”) and its denial (“cognition is something other than digital computation”). The other is the distinction between classicism (“cognition is digital computation over linguistic structures”) and connectionist and neurocomputational approaches (“cognition is computation—digital or not—by means of neural networks”).
We then have two versions of digital computationalism—the classical one (“cognition is digital computation over linguistic structures”) and the connectionist and neurocomputational one (“cognition is digital computation by neural networks”)—standing opposite to the denial of digital computationalism (“cognition is a kind of neural network processing that is not digital computation”). This may be enough to accommodate most views in the current debate. But it still does not do justice to the relationship between classicism and connectionist and neurocomputational approaches.
A further wrinkle in this debate derives from the ambiguity of the term “connectionism”. In its original sense, connectionism says that behavior is explained by the changing “connections” between stimuli and responses, which are biologically mediated by changing connections between neurons [79, 80]. This original connectionism is related to behaviorist associationism, according to which behavior is explained by the association between stimuli and responses. Associationist connectionism adds to behaviorist associationism a biological mechanism to explain the associations: the mechanism of changing connections between neurons.
But contemporary connectionism and computational neuroscience are less restrictive than associationist connectionism. In its most general form, contemporary connectionism and computational neuroscience simply say that cognition is explained (at some level) by neural network activity. But this is a truism—or at least it should be. The brain is the organ of cognition, the cells that perform cognitive functions are (mostly) neurons, and neurons perform their cognitive labor by organizing themselves into networks. Modern connectionism in this sense is little more than a platitude.
The relationship between connectionist and neurocomputational approaches on one hand and associationism on the other is more complex than many suppose. We should distinguish between strong and weak associationisms. Strong associationism maintains that association is the only legitimate explanatory construct in a theory of cognition (cf. [81], p. 27). Weak associationism maintains that association is a legitimate explanatory construct along with others such as the innate structure of neural systems.13
To be sure, some connectionists profess strong associationism (e.g., [14], p. 387). But that is beside the point because connectionism per se is consistent with weak associationism or even the complete rejection of associationism. Some connectionist models do not rely on association at all—a prominent example being the work of McCulloch and Pitts [43]. And weak associationism is consistent with many theories of cognition including classicism. A vivid illustration is Alan Turing’s early proposal to train associative neural networks to acquire the architectural structure of universal computing machines [82, 83]. In Turing’s proposal, association may explain how a network acquires the capacity for universal computation (or an approximation thereof), while the capacity for universal computation may explain any number of other cognitive phenomena.
Although many of today’s connectionists and computational neuroscientists emphasize the explanatory role of association, many of them also combine association with other explanatory constructs, as per weak associationism (cf. [77], p. 479; [84], pp. 243–245; [85], pp. xii, 30). What remains to be determined is which neural networks, organized in what way, actually explain cognition and which role association and other explanatory constructs should play in a theory of cognition.
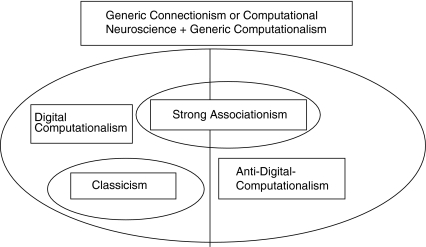
To sum up, everyone is (or should be) a connectionist or computational neuroscientist in the general sense of embracing neural computation, without thereby being committed to either strong or weak associationism. Some people are classicists, believing that, in order to explain cognition, neural networks must amount to manipulators of linguistic structures. Some people are nonclassicist (but still digital computationalist) connectionists, believing that cognition is explained by nonclassical neural network digital computation. Finally, some people are anti-digital-computationalist connectionists, believing that cognition is explained by neural network processes, but these do not amount to digital computation (e.g., because they process the wrong kind of vehicles). To find out which view is correct, in the long run, the only effective way is to study nervous systems at all levels of organization and find out how they produce behavior (Fig. 4).
Fig. 4.
Some prominent forms of generic computationalism and their relations
Information
We now turn our attention to the notion of information. Computation and information processing are commonly assimilated in the sciences of mind. As we have seen, computation is a mongrel concept that comprises importantly different notions. The same is true of information. Once the distinctions between notions of information are introduced, we will be in a position to consider whether the standard assimilation of information processing and computation is warranted and useful for a theory of cognition.
Information plays a central role in many disciplines. In the sciences of mind, information is invoked to explain cognition and behavior (e.g., [86, 87]). In communication engineering, information is central to the design of efficient communication systems such as television, radio, telephone networks, and the internet (e.g., [39, 88, 89]). A number of biologists have suggested explaining genetic inheritance in terms of the information carried by DNA sequences (e.g., [90]; see also [91, 92]). Animal communication theorists routinely characterize nonlinguistic communication in terms of shared information [93]. Some philosophers maintain that information can provide a naturalistic grounding for the intentionality of mental states, namely their being about states of affairs [46, 47]. Finally, information plays important roles in several other disciplines, such as computer science, physics, and statistics.
To account for the different roles information plays in all these fields, more than one notion of information is required. In this paper, we distinguish between three main notions of information: Shannon’s nonsemantic notion plus two notions of semantic information.
Shannon information
We use “Shannon information” to designate the notion of information initially formalized by Shannon [39].14 We distinguish between information theory, which provides the formal definition of information, and communication theory, which applies the formal notion of information to engineering problems of communication. We begin by introducing two measures of information from Shannon’s information theory. Later, we will discuss how to apply them to the physical world.
Let X and Y be two discrete random variables taking values in AX = {a1,...,an} and AY = {b1,...,br} with probabilities p(a1),..,p(an) and p(b1),..,p(br). We assume that p(ai) > 0 for all i = 1,..,n, p(bj) > 0 for all j = 1,..,r, 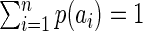 and
and 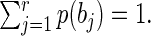
Shannon’s key measures of information are as follows:15
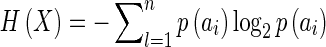 |
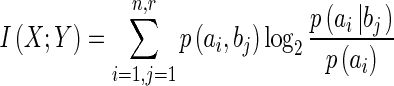 |
H(X) is called “entropy” because it is the same as the formula for measuring thermodynamic entropy; here, it measures the average information produced by the selection of values in AX = {a1,...,an}. We can think of H(X) as a weighted sum of n expressions of the form I(ai) = − log2p(ai). I(ai) is sometimes called the “self-information” produced when X takes the value ai. Shannon obtained the formula for entropy by setting a number of mathematical desiderata that any satisfactory measure of uncertainty should satisfy and showing that the desiderata could only be satisfied by the formula given above.16
Shannon information may be measured with different units. The most common unit is the “bit.”17 A bit is the information generated by a variable, such as X, taking a value ai that has a 50% probability of occurring. Any outcome ai with less than 50% probability will generate more than one bit; any outcome ai with more than 50% probability will generate less than one bit. The choice of unit corresponds to the base of the logarithm in the definition of entropy. Thus, the information generated by X taking value ai is equal to one bit when I(ai) = − log2pi = 1, that is, when pi = 0.5.18
Entropy has a number of important properties. First, it equals zero when X takes some value ai with probability 1. This tells us that information as entropy presupposes uncertainty: if there is no uncertainty as to which value a variable X takes, the selection of that value generates no Shannon information.
Second, the closer the probabilities p1,..,pn are to having the same value, the higher the entropy. The more uncertainty there is as to which value will be selected, the more the selection of a specific value generates information.
Third, the entropy is highest and equal to log2n when X takes every value with the same probability. This occurs when the “freedom of choice” of the selection process represented by X taking values in {a1,...,an} is maximal.
I(X;Y) is called “mutual information”; it is the difference between the entropy characterizing X, on average, before and afterY takes values in AY. Shannon proved that X carries mutual information about Y whenever X and Y are statistically dependent, i.e., whenever it is not the case that p(ai, bj) = p(ai)p(bj) for all i and j. This is to say that the transfer of mutual information between two sets of uncertain outcomes AX = {a1,...,an} and AY = {b1,...,br} amounts to the statistical dependency between the occurrence of outcomes in AX and AY. Information is “mutual” because statistical dependencies are symmetrical.
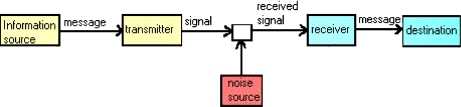
Shannon’s measures of information have many applications. The best-known application is Shannon’s own: communication theory. Shannon was looking for an optimal solution to what he called the “fundamental problem of communication” ([38], p. 379), that is, the reproduction of messages from an information source to a destination. In Shannon’s sense, any device that produces messages in a stochastic manner can count as an information source or destination.
Shannon distinguished three phases in the communication of messages: (a) the encoding of the messages produced by an information source into channel inputs, (b) the transmission of signals across a channel with random disturbances generated by a noise source, (c) the decoding of channel outputs back into the original messages at the destination.
The process is summarized by the picture of a communication system shown in Fig. 5.
Fig. 5.
Shannon’s depiction of a communication system [39]
Having distinguished the operations of coding, transmission, and decoding, Shannon developed mathematical techniques to study how to perform them efficiently. Shannon’s primary tool was the concept of information, as measured by entropy and mutual information.
A common misunderstanding of Shannon information is that it is a semantic notion. This misunderstanding is promoted by the fact that Shannon liberally referred to messages as carriers of Shannon information. But Shannon’s notion of message is not the usual one. In the standard sense, a message has semantic content or meaning—there is something it stands for. By contrast, Shannon’s messages need not have semantic content at all—they need not stand for anything.19
We will continue to discuss Shannon’s theory using the term “message,” but the reader should keep in mind that the usual commitments associated with the notion of message do not apply. The identity of a communication-theoretic message is fully described by two features: it is a physical structure distinguishable from a set of alternative physical structures, and it belongs to an exhaustive set of mutually exclusive physical structures selectable with well-defined probabilities.
Under these premises, to communicate a message produced at a source amounts to generating a second message at a destination that replicates the original message so as to satisfy a number of desiderata (accuracy, speed, cost, etc.). The sense in which the semantic aspects are irrelevant is precisely that messages carry information merely qua selectable, physically distinguishable structures associated with given probabilities. A seemingly paradoxical corollary of this notion of communication is that a nonsense message such as “#r %h@” could in principle generate more Shannon information than a meaningful message such as “avocado”.
To understand why, consider an experiment described by a random variable X taking values a1 and a2 with probabilities p(a1) = 0.9999 and p(a2) = 0.0001, respectively. Before the experiment takes place, outcome a1 is almost certain to occur, and outcome a2 is almost certain not to occur. The occurrence of both outcomes generates information, in the sense that it resolves the uncertainty characterizing the situation before the experiment takes place.
Shannon’s insight was that the occurrence of a2 generates more information than the occurrence of a1 because it is less expectable, or more surprising, in light of the prior probability distribution. This is reflected by the measure of self-information we introduced earlier: I(ai) = − log2p(ai). Given this measure, the higher the p(ai) is, the lower is the I(ai) = − log2p(ai), and the lower the p(ai) is, the higher is the I(ai) = − log2p(ai). Therefore, if “#r %h@” is a more surprising message than “avocado”, it will carry more Shannon information, despite its meaninglessness.
Armed with his measures of nonsemantic information, Shannon proved a number of seminal theorems that had a profound impact on the field of communication engineering. The “fundamental theorem for a noisy channel” established that it was theoretically possible to make the error rate in the transmission of information across a randomly disturbed channel as low as desired up until the point in which the source information rate in bits per unit of time becomes larger than the channel capacity, which is defined as the mutual information maximized over all input source probability distributions.20 Notably, this is true regardless of the physical nature of the channel (e.g., true for electrical channels, wireless channels, water channels, etc.).
Communication theory has found many applications, most prominently in communication engineering, computer science, neuroscience, and psychology. For instance, Shannon information is commonly used by neuroscientists to measure the quantity of information carried by neural signals about a stimulus and estimate the efficiency of coding (what forms of neural responses are optimal for carrying information about stimuli; [44], Chap. 4; [95]). Now, we move on from Shannon information, which is nonsemantic, to semantic information.
Semantic information
Suppose that a certain process leads to the selection of signals. Think, for instance, of how you produce words when speaking. There are two dimensions of this process that are relevant for the purposes of information transmission. One is the uncertainty that characterizes the speaker’s word selection process as a whole—the probability that each word be selected. This is the nonsemantic dimension that would interest a communication engineer and is captured by Shannon’s theory. A second dimension of the word selection process concerns what the selection of each word “means” (in the context of a sentence). This would be the dimension of interest, for example, to a linguist trying to decipher a tribal language.
Broadly understood, semantic notions of information pertain to what a specific signal broadcast by an information source means. To address the semantics of a signal, it is neither necessary nor sufficient to know which other signals might have been selected instead and with what probabilities. Whereas the selection of, say, any of 25 equiprobable but distinct words will generate the same nonsemantic information, the selection of each individual word will generate different semantic information depending on what that particular word means.
Semantic and nonsemantic notions of information are both connected with the reduction of uncertainty. In the case of nonsemantic information, the uncertainty has to do with which among many possible signals is selected. In the case of semantic information, the uncertainty has to do with which among many possible states of affairs is the case.
One of the foundational problems for the sciences of mind is that no uncontroversial theory of semantic information—comparable in rigor and scope to Shannon’s theory—has emerged. This explains the temptation felt in many quarters to appropriate Shannon’s theory of nonsemantic information and squeeze into it a semantic story. The temptation is in effect to understand information transmission in terms of reduction of uncertainty, use Shannon’s measures to quantify the information transmitted, and draw conclusions about the meanings of the transmitted signals.
This will not do. As we have stressed, Shannon information does not capture, nor is it intended to capture, the semantic content, or meaning, of signals. From the fact that Shannon information has been transmitted, no conclusions follow concerning what semantic information, if any, has been transmitted.
To tackle the meaning relation, we begin with Grice’s distinction between two kinds of meaning that are sometimes conflated, namely, natural and nonnatural meaning [96]. Natural meaning is exemplified by a sentence such as “those spots mean measles,” which is true—Grice claimed—just in case the patient has measles. Nonnatural meaning is exemplified by a sentence such as “those three rings on the bell (of the bus) mean that the bus is full” ([96], p. 85), which is true even if the bus is not full.
We extend the distinction between Grice’s two types of meaning to a distinction between two types of semantic information: natural information and nonnatural information.21 Spots carry natural information about measles by virtue of a reliable physical correlation between measles and spots. By contrast, the three rings on the bell of the bus carry nonnatural information about the bus being full by virtue of a convention.22 We will now consider each notion of semantic information in more detail.
Natural (semantic) information
When smoke carries information about fire, the basis for this informational link is the physical relation between fire and smoke. By the same token, when spots carry information about measles, the basis for this informational link is the physical relation between measles and spots. Both are examples of natural semantic information.
The most basic task of an account of natural semantic information is to specify the relation that has to occur between a source (e.g., fire) and a signal (e.g., smoke) for the signal to carry natural information about the source. Following Dretske [46], we discuss natural information in terms of correlations between event types. On the view we propose, an event token a of type A carries natural information about an event token b of type B just in case Areliably correlates with B. (Unlike [46], in addition to natural information, we posit nonnatural information; see below.)
Reliable correlations are the sorts of correlations information users can count on to hold in some range of future and counterfactual circumstances. For instance, smoke-type events reliably correlate with fire-type events, spot-type events reliably correlate with measles-type events, and ringing doorbell-type events reliably correlate with visitors at the door-type events. It is by virtue of these correlations that one can dependably infer a fire-token from a smoke-token, a measles-token from a spots-token, and a visitors-token from a ringing doorbell-token.
Yet correlations are rarely perfect. Smoke is occasionally produced by smoke machines, spots are occasionally produced by mumps, and doorbell rings are occasionally produced by naughty kids who immediately run away. Dretske [46] and most subsequent theorists of natural information have disregarded imperfect correlations, either because they believe that they carry no natural information [49] or because they believe that they do not carry the sort of natural information necessary for knowledge [46]. Dretske [46] focused only on cases in which signals and the events they are about are related by nomically underwritten perfect correlations.
We consider this situation unfortunate because, although not knowledge causing, the transmission of natural information by means of imperfect yet reliable correlations is what underlies the central role natural information plays in the descriptive and explanatory efforts of cognitive scientists. In other words, most of the natural information signals carry in real-world environments is probabilistic: signals carry natural information to the effect that o is probablyG, rather than natural information to the effect that, with nomic certainty, o is G.23
Unlike the traditional (all-or-nothing) notion of natural information, this probabilistic notion of natural information is applicable to the sorts of signals studied by cognitive scientists. Organisms survive and reproduce by tuning themselves to reliable but imperfect correlations between internal variables and environmental stimuli, as well as between environmental stimuli and threats and opportunities. In comes the sound of a predator, out comes running. In comes the redness of a ripe apple, out comes approaching.
But organisms do make mistakes, after all. Some mistakes are due to the reception of probabilistic information about events that fail to obtain.24 For instance, sometimes nonpredators are mistaken for predators because they sound like predators; or predators are mistaken for nonpredators because they look like nonpredators.
Consider a paradigmatic example from ethology. Vervet monkeys’ alarm calls appear to be qualitatively different for three classes of predators: leopards, eagles, and snakes [97, 98]. As a result, vervets respond to eagle calls by hiding behind bushes, to leopard calls by climbing trees, and to snake calls by standing tall.
A theory of natural information with explanatory power should be able to make sense of the connection between the reception of different calls and different behaviors. To make sense of this connection, we need a notion of natural information according to which types of alarm call carry information about types of predators. But any theory of natural information that demands perfect correlations between event types will not do because, as a matter of empirical fact, when the alarm calls are issued the relevant predators are not always present.
The theory of natural information one of us has developed [36], on the other hand, can capture the vervet monkey case with ease because it only demands that informative signals change the probability of what they are about. This is precisely what happens in the vervet alarm call case, in the sense that the probability that, say, an eagle/leopard/snake is present is significantly higher given the eagle/leopard/snake call than in its absence.
Notably, this notion of natural information is graded: signals can carry more or less natural information about a certain event. More precisely, the higher the difference between the probability that the eagle/leopard/snake is present given the call and the probability that it is present without the call, the higher is the amount of natural information carried by an alarm call about the presence of an eagle/leopard/snake.
This approach to natural information allows us to give an information-based explanation of why vervets take refuge under bushes when they hear eagle calls (mutatis mutandis for leopard and snake calls). They do because they have received an ecologically significant amount of probabilistic information that an eagle is present.
To sum up, an event’s failure to obtain is compatible with the reception of natural information about its obtaining, just like the claim that the probability that o is G is high is compatible with the claim that o is not G. No valid inference rules take us from claims about the transmission of probabilistic information to claims about how things turn out to be.25
Nonnatural (semantic) information
Cognitive scientists routinely say that cognition involves the processing of information. Sometimes, they mean that cognition involves the processing of natural information. At other times, they mean that cognition involves the processing of nonnatural information. This second notion of information is best understood as the notion of representation, where a (descriptive) representation is by definition something that can get things wrong.26
We should point out that some cognitive scientists simply assimilate representation with natural semantic information, assuming in effect that what a signal represents is what it reliably correlates with. This is a weaker notion of representation than the one we endorse. Following the usage that prevails in the philosophical literature, we reserve the term “representation” for states that can get things wrong or misrepresent (for further discussion, see for instance [47]).
Bearers of natural information, we have said, “mean” states of affairs in virtue of being physically connected to them. We have provided a working account of the required connection: there must be a reliable correlation between a signal and its source. Whatever the right account may be, one thing is clear: in the absence of the appropriate physical connection, no natural information is carried.
Bearers of nonnatural information, by contrast, need not be physically connected to what they are about in any direct way. Thus, there must be an alternative process by which bearers of nonnatural information come to bear nonnatural information about things they may not reliably correlate with. A convention, as in the case of the three rings on the bell of the bus, is a clear example of what may establish a nonnatural informational link. Once the convention is established, error (misrepresentation) becomes possible.
The convention may either be explicitly stipulated, as in the rings case, or emerge spontaneously, as in the case of the nonnatural information attached to words in natural languages. But we do not wish to assume that nonnatural information is always based on convention (cf. [96]). There may be other mechanisms, such as learning or biological evolution, through which nonnatural informational links may be established. What matters for something to bear nonnatural information is that, somehow, it stands for something else relative to a signal recipient.
An important implication of our account is that semantic information of the nonnatural variety does not entail truth. On our account, false nonnatural information is a genuine kind of information, even though it is epistemically inferior to true information. The statement “water is not H2O” gets things wrong with respect to the chemical composition of water, but it does not fail to represent that water is not H2O. By the same token, the statement “water is not H2O” contains false nonnatural information to the effect that water is not H2O.
Most theorists of information have instead followed Dretske [46–48] in holding that false information, or misinformation, is not really information. This is because they draw a sharp distinction between information, understood along the lines of Grice’s natural meaning, and representation, understood along the lines of Grice’s nonnatural meaning.
The reason for drawing this distinction is that they want to use natural information to provide a naturalistic reduction of representation (or intentionality). For instance, according to some teleosemantic theories, the only kind of information carried by signals is of the natural variety, but signals come to represent what they have the function of carrying natural information about. According to theories of this sort, what accounts for how representations can get things wrong is the notion of function: representations get things wrong whenever they fail to fulfill their biological function.
But our present goal is not to naturalize intentionality. Rather, our goal is to understand the central role played by information and computation in cognitive science. If cognitive scientists used “information” only to mean natural information, we would happily follow the tradition and speak of information exclusively in its natural sense. The problem is that the notion of information as used in the special sciences often presupposes representational content.
Instead of distinguishing sharply between information and meaning, we distinguish between natural information, understood roughly along the lines of Grice’s natural meaning (cf. Section 4.2.1), and nonnatural information, understood along the lines of Grice’s nonnatural meaning. We lose no conceptual distinction, while we gain an accurate description of how the concept of information is used in the sciences of mind. We take this to be a good bargain.
We are now in a position to refine the sense in which Shannon information is nonsemantic. Shannon information is nonsemantic in the sense that Shannon’s measures of information are not measures of semantic content or meaning, whether natural or nonnatural. Shannon information is also nonsemantic in the sense that, as Shannon himself emphasized, the signals studied by communication theory need not carry any nonnatural information.
But the signals studied by communication theory always carry natural information about their source when they carry Shannon information. When a signal carries Shannon information, there is by definition a reliable correlation between source events and receiver events. For any source event, there is a nonzero probability of the corresponding receiver event. In addition, in virtually all practical applications of communication theory (as opposed to information theory more generally), the probabilities connecting source and receiver events are underwritten by a causal process.
For instance, ordinary communication channels such as cable and satellite television rely on signals that causally propagate from the sources to the receivers. Because of this, the signals studied by communication theory, in addition to producing a certain amount of Shannon information based on the probability of their selection, also carry a certain amount of natural semantic information about their source (depending on how reliable their correlation with the source is). Of course, in many cases, signals also carry nonnatural information about things other than their sources—but that is a contingent matter, to be determined case by case.
Other notions of information
There are other notions of information, such as Fisher information [100] and information in the sense of algorithmic information theory [101]. There is even an all-encompassing notion of information. Physical information may be generalized to the point that every state of a physical system is defined as an information-bearing state. Given this all-encompassing notion, allegedly, the physical world is, at its most fundamental level, constituted by information [56, 57]. Since these other notions of information are not directly relevant to our present concerns, we set them aside.
In what follows, we focus on the relations between computation and the following three notions of information: Shannon information (information according to Shannon’s communication theory), natural information (truth-entailing semantic information27), and nonnatural information (non-truth-entailing semantic information).
The differences between these three notions can be exemplified as follows. Consider an utterance of the sentence “I have a toothache.” It carries Shannon information just in case the production of the utterance is a stochastic process that generates words with certain probabilities. The same utterance carries natural information about having a toothache just in case utterances of that type reliably correlate with toothaches. Carrying natural information about having a toothache entails that a headache is more likely given the signal than in the absence of the signal. Finally, the same utterance carries nonnatural information just in case the utterance has nonnatural meaning in a natural or artificial language. Carrying nonnatural information about having a toothache need not raise the probability of having a toothache.
How computation and information processing fit together
Do the vehicles of computations necessarily bear information? Is information processing necessarily carried out by means of computation? What notion of information is relevant to the claim that a cognitive system is an information processor? Answering these questions requires combining computation and information in several of the senses we have discussed.
We have distinguished two main notions of computation (digital and generic) and three main notions of information processing (processing Shannon information, processing natural semantic information, and processing nonnatural semantic information). It is now time to see how they fit together.
We will argue that the vehicles over which computations are performed may or may not bear information. Yet, as a matter of contingent fact, the vehicles over which cognitive computations are performed generally bear information, in several senses of the term. We will also argue that information processing must be carried out by means of computation in the generic sense, although it need not be carried out by computation in either the digital or the analog sense.
Before we begin, we should emphasize that there is a trivial sense in which computation entails the processing of Shannon information. We mention it now but will immediately set it aside because it is not especially relevant to cognitive science.
Consider an electronic digital computer. Each of its memory cells is designed to stabilize on one of two thermodynamically macroscopic states, called “0” and “1”. Suppose that, as soon as the computer is switched on, each memory cell randomly goes into one of those states. A nonzero Shannon entropy is associated with this state initialization process, since it is a random process, and manipulation of randomly generated initial states by the computer amounts to the processing of Shannon information in this trivial sense.
Note, however, that the digits created by random initialization of the memory cells carry no nonnatural semantic information, since the digits in question do not have any conventional semantic content. They carry no functionally relevant natural semantic information either, since they do not reliably correlate with any source other than the thermal component of the electrons’ dynamics in the memory cell at power up. Random noise is not the kind of source of natural information that is relevant to the theory of cognition. Thus, the digits do not carry any natural semantic information beyond the theoretically unimportant natural information they carry about what caused them—whatever that may be.
Since a computer manipulates its digits and, in the above sense, a nonzero Shannon information is associated with randomly generated digits, it follows that a computer processing randomly generated digits is processing information-bearing states. In this trivial sense, such a computer is necessarily a processor of Shannon information. But here we are not interested in whether computation can be regarded as processing information in this trivial sense. We are interested in how computation fits with the processing of Shannon information, natural semantic information, and nonnatural semantic information about sources in the system’s distal environment—the sources the system needs to respond to. We will take up each of these in turn.
Computation and the processing of Shannon Information
Cognitive scientists are generally interested in computational vehicles that bear semantic information; they rarely worry about whether computation is the processing of Shannon information, which is not semantic. Nevertheless, it is useful to briefly examine the relationship between computation and Shannon information.
We emphasize at the outset that the notion of processing Shannon information is not entirely clear. Shannon information is not a property of individual signals, which can be manipulated as the signal is manipulated. Instead, Shannon entropy and mutual information quantify statistical properties of a selection process and a communication channel as a whole.
The first thing to note is that, strictly speaking, computational vehicles need not carry Shannon information at all. This is because Shannon information requires random variables—deterministic variables carry no Shannon information whatsoever—whereas computation is compatible with deterministic variables. For instance, consider again a digital computer. For its inputs to be regarded as carriers of Shannon information, they have to be selected in a stochastic way. But the computer works just the same whether its inputs are selected deterministically or probabilistically. The same point can be made about other computing devices, such as analog computers and neural networks. Thus, computation need not entail the processing of Shannon information.
Another relevant observation is that computation need not create Shannon information. This is because computation may be either probabilistic or deterministic—in most real-world applications, computation is deterministic. Deterministic computation cannot create Shannon information—it can only conserve it or destroy it. More precisely, Shannon information is conserved in logically reversible computations (which are necessarily deterministic), is reduced in logically irreversible deterministic computations, and may be created, conserved, or destroyed in noisy computations.
These points should not obscure the fundamental importance of communication theory to the understanding of computing systems. Even though, strictly speaking, computing systems need not process Shannon information, it is useful to assume that they do. That is, it is useful to characterize the inputs, internal states, and outputs of computing systems and their components stochastically and analyze system performance and resource requirements using information-theoretic measures and techniques. On this view, the components of computing systems may be treated as sources and receivers in the sense of communication theory [102]. This allows engineers to design efficient computer codes and effective communication channels within computing systems. The same techniques may be used to analyze neural codes and signal transmission within the nervous system.
So far, we have discussed whether computation is the processing of Shannon information. What about the converse? Processing Shannon information may or may not be done by means of digital computation. First, for Shannon information processing to be done by digital computing, the information must be produced and carried by strings of digits. But Shannon information can also be produced and carried by continuous signals, which may be processed by analog means. Second, even when the bearers of Shannon information are digits, there exist forms of processing of such digits other than digital computation. Just to give an example, a digital-to-analog converter transforms digits into analog signals.
Shannon information processing is, however, a form of computation in the generic sense. As we defined it, generic computation is the functional manipulation of any medium-independent vehicle. Shannon information is a medium-independent notion, in the sense that whether Shannon information can be associated with a given vehicle does not depend on its specific physical properties, but rather on its probability of occurrence relative to its physically distinguishable alternatives. Thus, generic computation is broad enough to encompass the processing of Shannon information. In other words, if a vehicle carries Shannon information, its processing is a computation in the generic sense.28
The bottom line is this: although, strictly speaking, computation need not process vehicles that carry Shannon information, it usually does, and at any rate, it is useful to assume that it does. Conversely, the processing of Shannon information amounts to some form of generic computation. Communication theory places constraints on any kind of signal transmission (and hence on the processing of any information carried by the transmitted signals) within computing systems, including cognitive ones. This does not yet tell us what we are most interested in: how does computation relate to semantic information?
Computation and the processing of natural information
Many people use “computation” and “information processing” interchangeably. What they often mean by “information processing”, we submit, is the processing of natural semantic information carried by the computation vehicles. This use of “information processing” is especially common in the behavioral and brain sciences. It is thus important to examine whether and in what sense computation is the processing of natural information.
The notion of digital computation does not require that the computation vehicles carry natural information—or more precisely, digits are not required to carry natural information about the computing system’s distal environment.29 In this section, we will focus on whether digital computation entails the processing of natural information about the system’s distal environment.
Granted, natural information is virtually ubiquitous—it is easy enough to find reliable correlations between physical variables. This being the case, the digits within a digital computer may well carry natural information about cognitively relevant sources, such as environmental stimuli that the computer responds to. Consider a car’s computer, which receives and responds to natural information about the state of the car. The computer uses feedback from the car to regulate fuel injection, ignition timing, speed, etc. In such a case, a digital computation will be a case of natural information processing.
But digits—the vehicles of digital computation—need not correlate reliably with anything (in the distal environment) in order for a digital computation to be performed over them. Thus, a digital computation may or may not constitute the processing of natural information (about the distal environment). If the computation vehicles do carry natural information (about the distal environment), this may be quite important. In our example, that certain digits carry natural information about the state of the car explains why the car’s computer can regulate, say, fuel injection successfully. Our point is simply that digital computation does not entail the processing of natural information about the distal environment.
This point is largely independent of the distinction between semantic and nonsemantic digital computation. A semantic digital computation is generally defined over the nonnatural information carried by the digits—independently of whether they carry natural information (about the distal environment) or what specific natural information they carry. For instance, ordinary mathematical calculations carried out on a computer are defined over numbers, regardless of what the digits being manipulated by the computer reliably correlate with. Furthermore, it is possible for a digital computation to yield an incorrect output, which misrepresents the outcome of the operation performed. As we have seen, natural information cannot misrepresent. Thus, even semantic digital computation does not entail the processing of natural information (about the distal environment). (More on the relation between natural and nonnatural information below.)
This point generalizes to generic computation, which includes, in addition to digital computation, at least analog computation and neural computation (i.e., the processing of neuronal spike trains). Nothing in the notions of analog computation or neural computation mandates that the vehicles being manipulated carry natural information (about the distal environment). More generally, nothing in the notion of manipulating medium-independent vehicles mandates that such vehicles carry natural information (about the distal environment). Thus, computation may or may not be the processing of natural information.
What about the converse claim: that the processing of natural information must be carried out by means of computation? The answer is that yes, it must, although the computation need not be digital or of any specific kind. Natural information may be encoded by continuous variables, which cannot be processed by digital computers. Or it may be encoded by strings of digits, whose processing consists in converting them to analog signals. In both of these cases, natural information is processed, although not by means of digital computation.
But if natural information is processed, some kind or other of generic computation must be taking place. Natural information, like Shannon information, is a medium-independent notion. As long as a variable reliably correlates with another variable, it carries natural information about it. Any other physical properties of the variables are immaterial to whether they carry natural information. Since generic computation is just the processing of medium-independent vehicles, any processing of natural information amounts to a computation in the generic sense.
What about cognition? Does it involve the processing of natural information? Intuitively, our perceptual states seem to reliably correlate with our environment. But we do not have to stop at appearances. Large portions of neurophysiology are devoted to the detection, description, and explanation of the detailed causal correlations that exist between neural responses and variables in the external (distal) environment of organisms [20, 44]. Thus, cognition involves the processing of natural information. This is another way to reach the conclusion that cognition is computation in the generic sense.
In sum, computation vehicles need not carry natural information, but natural information processing is necessarily some kind of generic computation—though not necessarily either digital or analog computation. Since cognition involves the processing of natural information, it amounts to computation in the generic sense, though it does not follow that cognition is some more specific kind of computation, such as digital or analog computation.
Computation and the processing of nonnatural information
Nonnatural information is a central notion in our discourse about minds and computers. We attribute representational contents to each other’s minds. We do the same with the digits manipulated by computers. We will now examine whether and in what sense computation is the processing of nonnatural information and what this has to do with theories of cognition.
Digital computation may or may not be the processing of nonnatural information and vice versa. This case is analogous to that of natural information, with one difference. In the case of semantic digital computation—digital computation that has semantic content by definition—most notions of semantic content turn digital computation into nonnatural information processing. (The primary exception are notions of semantic content based solely on natural information; but since natural information is not representational, such notions would be inadequate to capture the main notion of semantic content—representational semantic content.) As a matter of fact, almost all (digital) computing conducted in artifacts is information processing, at least in the ordinary sense of nonnatural information.
But the main question we are trying to answer is whether necessarily, digital computation is the processing of nonnatural information. It is if we define a notion of digital computation that entails that the digits are representations. But, as pointed out in Section 3.4, nothing in the notion of digital computation used by computer scientists and computability theorists mandates such a definition. So, in the theoretically most important sense of digital computation—digital computation as implicitly defined by the practices of computability theory and computer science; digital computation in the sense that provides a mechanistic explanation for the behavior of digital computers—digital computation need not be the processing of nonnatural information.
Conversely, the processing of nonnatural information need not be carried out by means of digital computation. Whether it is depends on whether the nonnatural information is digitally encoded and how it is processed. It may be encoded either digitally, by continuous variables, or by other vehicles. Even when encoded digitally, nonnatural information may be manipulated by digital computation or by other processes, as in digital-to-analog conversion.
Generic computation may or may not constitute the processing of semantic information, for similar reasons. Nothing in the notions of analog computation or neural computation mandates that the vehicles being manipulated carry nonnatural information. They could be entirely meaningless and the computations would proceed just the same. More generally, nothing in the notion of manipulating medium-independent vehicles mandates that such vehicles carry nonnatural information.
As in the case of natural information, the converse does not hold. Instead, nonnatural semantic information processing is necessarily done by means of computation in the generic sense. For medium-independent nonnatural semantic information, it is defined in terms of the association between an information-carrying vehicle and what it stands for, without reference to any physical properties of the vehicles. Since generic computation is defined as the processing of medium-independent vehicles, the processing of nonnatural semantic information (i.e., the processing of vehicles carrying nonnatural semantic information) is computation in the generic sense.
The connection between nonnatural information processing and generic computation provides yet another route for establishing a generic form of computationalism. All that is required is that cognition involves the processing of nonnatural information. That seems plausible enough. Intuitively, our thoughts appear to have non-natural semantic contents. For example, Violet’s thought that angels are unhelpful has semantic content, but its content appears to constitute nonnatural information. There is no immediate correlation between Violet’s thought and anything in her environment, which would be required to turn the content of her thought into natural information. In addition, mainstream theories of language and cognition individuate concepts and cognitive processes at least in part by their nonnatural semantic contents (cf. [103]).
Nevertheless, the reality, or at least the scientific explanatory value, of nonnatural information has been denied [104, 105]. Since we lack room to defend the explanatory value of nonnatural information, we will simply assume that at least some cognitive systems do process nonnatural information at least some of the time. Our main reason for this assumption is that our current best theories of cognition are largely built on it. As long as we lack a better alternative, we propose to explore the commitments and viability of our best theories.
Our work is not done yet. We defined nonnatural information in terms of the association between bearers of nonnatural information and what they stand for. This representation relation requires explication.
In recent decades, philosophers have devoted a large literature to representation. They have articulated several theoretical options. One option is antinaturalism: representation cannot and need not be explained or reduced in naturalistic or mechanistic terms—the representational character of cognition simply shows that psychology and perhaps neuroscience are sui generis sciences. A second option is antirealism: representation is not a real (i.e., causally efficacious and explanatory) feature of cognition, although ascriptions of nonnatural information-bearing states may be heuristically useful [106]. Finally, naturalists look for explanations of representation in nonintentional terms [107].
A prominent family of naturalistic theories attempts to reduce nonnatural information to natural information—plus, perhaps, some other naturalistic ingredients. As we mentioned earlier, several efforts have been made to this effect [46, 47, 108–110]. According to these theories, nonnatural information is, at least in part, natural information. But theories according to which nonnatural information reduces to natural information are only one family of naturalistic theories among others. According to other naturalistic theories, nonnatural information reduces to things other than natural information (e.g., [111–115]).
Again, we lack the space to discuss accounts of nonnatural information in detail. We do wish to point out, however, that a complete theory of cognition cannot simply postulate that cognition involves the processing of nonnatural information and take the notion of nonnatural information for granted. On the contrary, a complete theory needs to take a stance on nonnatural information—what it amounts to, whether it is causally efficacious, and if so, how it may be naturalistically explainable.
Summing up the contents of this section, we have reached three main conclusions. First, computation may or may not be the processing of nonnatural information—with the exception of semantic computation, which is not the core notion of computation. Second, the processing of nonnatural information is a kind of generic computation. Third, although our best theories of cognition postulate that cognition involves the processing of nonnatural information, the notion of nonnatural information may require a naturalistic explanation. So it is not a conceptual truth that cognitive computation involves the processing of nonnatural information, but it is (plausibly) a contingent empirical truth that holds at least in some cases.
Conclusion
In our paper, we have offered a comprehensive account of both computation and information processing. We then charted the conceptual relations (or lack thereof) between computation and information processing, addressing along the way what lies behind the six widespread myths we discussed in Section 2.
“Computation” and “information processing” are commonly used interchangeably, which presupposes that they are roughly synonymous terms. If that were true, computation would entail information processing, and information processing would entail computation. Alas, things are not so simple. We have argued that each of the two assimilated notions has more than one meaning, and the entailment relations do not hold on many legitimate ways of understanding computation and information processing.
If it is unclear which notions of information and computation different theorists employ and how they are related, cross-purpose talk lurks at every corner. It is difficult to compare and contrast theories; nonequivalent theories may be taken to be equivalent and equivalent theories may be taken to be nonequivalent. The notion of nonnatural information may be used without realizing that it is different from natural information and may require naturalization. In addition, it may be difficult to integrate findings and explanations from different research areas because authors working in different areas may use key terms in different senses.
For instances, many psychologists use “computation” to mean digital computation, while many neuroscientists use it to mean computation in the generic sense. Similarly, many neuroscientists and computer scientists use “information” to mean nonnatural information, while many philosophers use “information” to mean natural information. Making progress in our understanding of cognition requires clarity and precision on what kind of computation and information processing are involved in cognition and on whether the two are related. If they are related, it is also important to understand whether they are related conceptually because of how we use the notions of computation and information processing or whether they are related in ways that constitute an empirical discovery about cognition.
The conflation of computation with information processing leads to fallacious arguments. Here is an example among many. Since many cognitive and neural events reliably correlate with environmental events and since such correlations seem to have much to do with the production of behavior, we may conclude that the brain processes natural information. Since information processing is carried out by means of computations, in turn, we may further conclude that the brain is a computing system. So far, so good—except that we did not specify which notion of computation we were using. Since we know there is a mathematical theory of computation that establishes many of the properties and limitations of computation, we may be tempted to appeal to such a theory in characterizing neural computation. This line of reasoning can be seen at work in some contemporary neuroscience literature (e.g., [19, 52, 76]).
But the last step is fallacious: at best, we are entitled to the conclusion that the brain performs computations in the generic sense—once again, a relatively weak claim. Whether and in what way neural computations are characterized by the results of computability theory—i.e., whether neural computations are a kind of digital computation—is a matter that needs to be established independently.
The above mistake is further compounded by the tendency, present in some of the same authors, to describe neural systems as analog as opposed to digital (e.g., [19], p. 51). Analog variables are generally assumed to take any real values (within a relevant interval), which entails that they can take uncountably many values. Since computability theory is defined in terms of variables that can take only countably many values, computability theory does not apply to analog variables in any direct way ([31], Section 3.5).
At this point, some people might be tempted to short-cut this discussion by appealing to the Church–Turing thesis, which says that any computable function is computable by some Turing machine. Since Turing machines and other equivalent formalisms are the foundation of computability theory, doesn’t it follow that all computations are covered by the results established by Turing and other computability theorists? Not quite. The Church–Turing thesis applies directly only to algorithmic digital computation. The relationship between algorithmic digital computation and digital computation simpliciter, let alone other kinds of computation, is complex, and the Church–Turing thesis does nothing to settle it.30
So one important consequence of our analysis is that the common view that cognition involves computation simply because it processes information is liable to generate serious mistakes. Nevertheless, there are three important senses—corresponding to the notion of Shannon information and the two notions of natural and nonnatural information—in which, plausibly, cognition involves information processing. Neither of these senses entails that cognition is computation in the historically and theoretically most significant sense of the term, i.e., digital computation (which includes many important cases of neural network computation). All that follows is that cognition is computation in the weak sense that it involves the processing of medium-independent vehicles.
To sum up, here is how the landscape looks at the end of our survey:
Question: Is digital computation the same as information processing?
- Thesis 1:
- Digital computation vs. processing Shannon information
- Digital computation (semantic or nonsemantic) does not entail the processing of Shannon information.
- The processing of Shannon information does not entail digital computation (semantic or nonsemantic).
- Thesis 2:
- Digital computation vs. processing natural information
- Digital computation (semantic or nonsemantic) does not entail the processing of natural information (about the distal environment).
- The processing of natural information does not entail digital computation (semantic or nonsemantic).
- Thesis 3:
- Digital computation vs. processing nonnatural information
- Nonsemantic digital computation does not entail the processing of nonnatural information.
- Semantic digital computation entails the processing of nonnatural information.
- The processing of nonnatural information does not entail digital computation (semantic or nonsemantic).
Question: Is generic computation the same as information processing?
- Thesis 4:
- Generic computation vs. processing Shannon information
- Generic computation (semantic or nonsemantic) does not entail the processing of Shannon information.
- The processing of Shannon information entails generic computation (semantic or nonsemantic).
- Thesis 5:
- Generic computation vs. processing natural information
- Generic computation (semantic or nonsemantic) does not entail the processing of natural information (about the distal environment).
- The processing of natural information entails (semantic) generic computation.
- Thesis 6:
- Generic computation vs. processing nonnatural information
- Nonsemantic generic computation does not entail the processing of nonnatural information.
- Semantic generic computation entails the processing of nonnatural information.
- The processing of nonnatural information entails (semantic) generic computation.
These six theses summarize the relations of conceptual entailment, or lack thereof, between computation and information processing, depending on what each notion is taken to mean.
Question: Does cognition involve computation, information processing, or both?
- Thesis 7:
- Cognition, computation, and information processing
- Cognition involves the transmission of signals, which are subject to the constraints of communication theory (Shannon information).
- Cognition involves the processing of natural information.
- Cognition, at least in some important cases, involves the processing of nonnatural information.
- Cognition is a form of computation in the generic sense.
Thesis 7 summarizes what we take to be the clearest, most general, and most plausible formulation of the information processing and computational approach to cognition. Within such an approach, there is room for disagreement among theories of cognitive architecture.
Theories of cognitive architecture are traditionally divided into classical and neural network-based. As we have argued, the contrast implied in this division is misleading. If “connectionism” means strongly associationist connectionism, then there is a genuine contrast with classical theories. But if a connectionist or neurocomputational theory is simply a theory committed to an explanation in terms of neural networks, as the most common use of “connectionism” and “computational neuroscience” suggests, then all cognitive scientists—including classicists—ought to embrace neural computation. Thus, the choice among theories of cognitive architecture is not between classicism and connectionism, but rather between varieties of neural computation, which may be classical or nonclassical.
The account we presented advances two foundational debates in cognitive science: the debate about whether cognition involves computation and the debate about whether cognitive architecture is classical or connectionist. It does so by untangling some of their conceptual knots in a theory-neutral way. We have leveled the playing field on which cognitive science is built and sharpened our understanding of some foundational questions. Doing so is a necessary step towards resolving the empirical aspects of the foundational debates. Many additional questions about cognition, computation, and information processing remain to be investigated and can now be pursued in a more fruitful way. One question that seems especially pressing to us is whether neural computation is a form of digital computation, analog computation, or neither.
Acknowledgements
An abbreviated ancestor of some portions of this paper appeared in G. Piccinini and A. Scarantino, “Computation vs. information processing: why their difference matters to cognitive science,” Stud. Hist. Philos. Sci. (2010, in press). Thanks to our audience at the 2009 meeting of the Southern Society for Philosophy and Psychology and to Ken Aizawa, Sonya Bahar, Mark Collier, Carrie Figdor, Robert Gordon, Corey Maley, Alex Morgan, Brad Rives, Martin Roth, Anna-Mari Rusanen, Dan Ryder, Oron Shagrir, Susan Schneider, Eric Thomson, and several anonymous referees for helpful comments and encouragement. Special thanks to Neal Anderson for his extensive and insightful comments. Thanks to Matthew Piper and James Virtel for editorial assistance. This material is based upon work supported by the National Science Foundation under grant no. SES-0924527 to Gualtiero Piccinini.
Footnotes
The Church–Turing thesis properly so-called—i.e., the thesis supported by Church, Turing, and Kleene’s arguments—is sometimes confused with the Physical Church–Turing thesis. The Physical Church-Turing thesis [58] lies outside the scope of this paper. Suffice it to say that the Physical Church–Turing thesis is controversial and in any case does not entail that cognition is computation in a sense that is relevant to cognitive science [29].
Classical theories are often referred to as “symbolic.” Roughly speaking, in the present context, a symbol is something that satisfies two conditions: (1) it is a representation and (2) it falls under a discrete (or digital) linguistic type. As we will argue below, conceptual clarity requires keeping these two aspects of symbols separate. Therefore, we will avoid the term “symbol” and its cognates.
Sometimes, the view that cognition is dynamical is presented as an alternative to the view that cognition is computational (e.g., [4]). This is simply a false contrast. Computation is dynamical too; the relevant question is whether cognitive dynamics are computational.
Did McCulloch and Pitts really offer a theory of cognition in terms of digital computation? Absolutely. McCulloch and Pitts’ work is widely misunderstood; for a detailed study, see [63].
The term “digit” is used in two ways. It may be used for the discrete variables that can take different values; for instance, binary cells are often called bits, which can take either 0 or 1 as values. Alternatively, the term digit may be used for the values themselves. In this second sense, it is the 0s and 1s that are the bits. We use digit in the second sense.
Addition and multiplication are usually defined as functions over numbers. To maintain consistency in the present context, they ought to be understood as functions over strings of digits.
The term “classical computation” is sometimes used as an approximate synonym of digital computation. Here, we are focusing on the more restricted sense of the term that has been used in debates on cognitive architecture at least since [10].
Fodor and Pylyshyn [10] restrict their notion of classical computation to processes defined over representations because they operate under assumption 3—that computation requires representation. In other words, the sentence-like symbolic structures manipulated by Fodor and Pylyshyn’s classical computations must have semantic content. Thus, Fodor and Pylyshyn’s classical computations are a kind of “semantic computation.” Since assumption 3 is a red herring in the present context, we avoided assumption 3 in the main text. We will discuss the distinction between semantic and nonsemantic computation in Section 3.3.
Two caveats: First, neural networks should not be confused with their digital simulations. A simulation is a model or representation of a neural network; the network is what the simulation represents. Of course, a digital simulation of a neural network is algorithmic; it does not follow that the network itself (the system represented by the simulation) is algorithmic. Second, some authors use the term “algorithm” for the computations performed by all neural networks. In this broader sense of algorithm, any processing of a signal follows an algorithm, regardless of whether the process is defined in terms of discrete manipulations of strings of digits. Since this is a more encompassing notion of algorithm than the one employed in computer science—indeed, it is even broader than the notion of computing Turing-computable functions—our point stands. The point is that the notion of computing Turing-computable functions is more inclusive than that of algorithmic computation in the standard sense [30].
For more details on the contrast between digital and analog computers, see [31, Section 3.5].
One terminological caveat. Later on, we will also speak of semantic notions of information. In the case of nonnatural semantic information, by “semantic,” we will mean the same as what we mean here, i.e., representational. A representation is something that can misrepresent, i.e., may be unsatisfied or false. In the case of natural information, by “semantic,” we will mean something weaker, which is not representational because it cannot misrepresent (see below).
Digital computing systems belong in a hierarchy of systems that are computationally more or less powerful. The hierarchy is measured by the progressively larger classes of functions each class of system can compute. Classes include the functions computable by finite automata, pushdown automata, and Turing machines [62].
We should also note that there are different associative mechanisms, some of which are more powerful than others; comparing associative mechanisms lies outside the scope of this paper.
Shannon was building on important work by Boltzmann, Szilard, Hartley, and others [89].
The logarithm to the base b of a variable x—expressed as logbx—is defined as the power to which b must be raised to get x. In other words, logbx = y if and only if by = x. We stipulate that the expression 0 logb 0 in any of the addenda of H(X) is equal to 0. Shannon ([39], p. 379) pointed out that in choosing a logarithmic function he was following Hartley [94] and added that logarithmic functions have nice mathematical properties, are more useful practically because a number of engineering parameters “vary linearly with the logarithm of the number of possibilities,” and are “nearer to our intuitive feeling as to the proper measure” of information.
The three mathematical desiderata are the following: (1) The entropy H should be continuous in the probabilities pi; (2) The entropy H should be a monotonic increasing function of n when pi = 1/n; and (3) If n = b1 + .. + bk with bi positive integer, then  Shannon further supported his interpretation of H as the proper measure of information by demonstrating that the channel capacity required for most efficient coding is determined by the entropy ([39], see Theorem 9 in Section 9).
Shannon further supported his interpretation of H as the proper measure of information by demonstrating that the channel capacity required for most efficient coding is determined by the entropy ([39], see Theorem 9 in Section 9).
Shannon credited John Tukey, a computer scientist at Bell Telephone Laboratories, with introducing the term in a 1947 working paper.
− log2 0.5 = 1.
Furthermore, Shannon’s messages do not even have to be strings of digits of finitely many types; on the contrary, they may be continuous variables. We gave the definitions of entropy and mutual information for discrete variables, but the definitions can be modified to suit continuous variables ([39], part III).
Shannon defined the channel capacity C as follows:  The conditional entropy is calculated as follows:
The conditional entropy is calculated as follows: 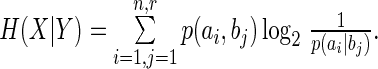
By calling this kind of information nonnatural, we are not taking a stance on whether it can be naturalized, that is, reduced to some more fundamental natural process. We are simply using Grice’s terminology to distinguish between two importantly different notions of semantic information. We will briefly discuss the naturalization of nonnatural information in Section 4.3
This is not to say that conventions are the only possible source of nonnatural meaning. For further discussion, see [96].
For a more precise and detailed theory of probabilistic information, see [36, 37]. The probabilistic notion of information we employ includes all-or-nothing natural information—roughly, the natural information that o is G with certainty—as a special, limiting case. For a critique of approaches focusing solely on all-or-nothing natural information, see [99].
This is not to say that natural information is enough to explain why acting on the basis of received natural information sometimes constitutes a mistake and sometimes it does not. We briefly discuss conditions of correctness for information-based behaviors below.
A consequence of this point is that the transmission of natural information entails nothing more than the truth of a probabilistic claim [37]. It follows that our distinction between natural and nonnatural meaning/information differs from Grice’s original distinction in one important respect. On our view, there is nothing objectionable in holding that “those spots carry natural information about measles, but he doesn’t have measles,” provided measles are more likely given those spots than in the absence of those spots.
There are also imperative representations, such as desires. And there are representations that combine descriptive and imperative functions, such as honeybee dances and rabbit thumps (cf. [47]). For simplicity, we will continue to focus on descriptive representations.
See [37] for an explanation of the limited sense in which we take natural information to be truth entailing.
In this section, we have not discussed the distinction between semantic and nonsemantic notions of computation, as it makes no difference to our present concerns.
At least for deterministic computation, there is always a reliable causal correlation between later states and earlier states of the system as well as between initial states and whatever caused those initial states—even if what caused them are just the thermal properties of the immediate surroundings. In this sense, (deterministic) digital computation entails natural information processing. But the natural information that is always “processed” is not about the distal environment, which is what theorists of cognition are generally interested in.
Contributor Information
Gualtiero Piccinini, Email: piccininig@umsl.edu.
Andrea Scarantino, Email: ascarantino@gsu.edu.
References
- 1.Perkel DH. Computational neuroscience: scope and structure. In: Schwartz EL, editor. Computational Neuroscience. Cambridge: MIT Press; 1990. pp. 38–45. [Google Scholar]
- 2.Edelman GM. Bright Air, Brilliant Fire: on the Matter of the Mind. New York: Basic Books; 1992. [Google Scholar]
- 3.Globus GG. Towards a noncomputational cognitive neuroscience. J. Cogn. Neurosci. 1992;4(4):299–310. doi: 10.1162/jocn.1992.4.4.299. [DOI] [PubMed] [Google Scholar]
- 4.Port RF, Gelder T. Mind as Motion: Explorations in the Dynamics of Cognition. Cambridge: MIT Press; 1995. [Google Scholar]
- 5.Freeman WJ. How Brains Make Up Their Minds. New York: Columbia University Press; 2001. [Google Scholar]
- 6.Wallace B, Ross A, David J, Anderson T, editors. The Mind, The Body and the World: Psychology after Cognitivism? Exeter: Imprint Academic; 2007. [Google Scholar]
- 7.Spivey M. The Continuity of Mind. Oxford: Oxford University Press; 2007. [Google Scholar]
- 8.Miller GA, Galanter EH, Pribram KH. Plans and the Structure of Behavior. New York: Holt; 1960. [Google Scholar]
- 9.Newell A, Simon HA.Computer science as an empirical enquiry: symbols and search Commun. ACM 197619113–126.464629 [Google Scholar]
- 10.Fodor JA, Pylyshyn ZW. Connectionism and cognitive architecture. Cognition. 1988;28:3–71. doi: 10.1016/0010-0277(88)90031-5. [DOI] [PubMed] [Google Scholar]
- 11.Newell A. Unified Theories of Cognition. Cambridge: Harvard University Press; 1990. [Google Scholar]
- 12.Pinker S. How the Mind Works. New York: Norton; 1997. [DOI] [PubMed] [Google Scholar]
- 13.Gallistel CR, King AP. Memory and the Computational Brain: Why Cognitive Science will Transform Neuroscience. Malden: Wiley-Blackwell; 2008. [Google Scholar]
- 14.Rosenblatt F.The perceptron: a probabilistic model for information storage and organization in the brain Psychol. Rev. 195865386–408.1529895 [DOI] [PubMed] [Google Scholar]
- 15.Feldman JA, Ballard DH. Connectionist models and their properties. Cogn. Sci. 1982;6:205–254. [Google Scholar]
- 16.Hopfield JJ.Neural networks and physical systems with emergent collective computational abilities Proc. Natl. Acad. Sci. U.S.A. 1982792554–2558.6520331982PNAS...79.2554H [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rumelhart DE, McClelland JM, et al. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge: MIT Press; 1986. [DOI] [PubMed] [Google Scholar]
- 18.Smolensky P.On the proper treatment of connectionism Behav. Brain Sci. 19881111–23.1220075 [Google Scholar]
- 19.Churchland PS, Sejnowski TJ. The Computational Brain. Cambridge: MIT Press; 1992. [Google Scholar]
- 20.O’Reilly RC, Munakata Y. Computational Explorations in Cognitive Neuroscience: Understanding the Mind by Simulating the Brain. Cambridge: MIT Press; 2000. [Google Scholar]
- 21.Rogers TT, McClelland JL. Semantic Cognition: a Parallel Distributed Processing Approach. Cambridge: MIT Press; 2006. [DOI] [PubMed] [Google Scholar]
- 22.Dale R. The possibility of a pluralist cognitive science. J. Exp. Theor. Artif. Intell. 2008;20(3):155–179. [Google Scholar]
- 23.Edelman S. On the nature of minds, or: truth and consequences. J. Exp. Theor. Artif. Intell. 2008;20(3):181–196. [Google Scholar]
- 24.Fodor JA. LOT 2: the Language of Thought Revisited. Oxford: Oxford University Press; 2008. [Google Scholar]
- 25.Pylyshyn ZW. Computation and Cognition. Cambridge: MIT Press; 1984. [Google Scholar]
- 26.Shagrir O.Why we view the brain as a computer Synthese 20061533393–416.2290008 [Google Scholar]
- 27.Piccinini G.Computing mechanisms Philos. Sci. 2007744501–526.2387334 [Google Scholar]
- 28.Piccinini G.Computational modeling vs. computational explanation: is everything a Turing machine, and does it matter to the philosophy of mind? Australas. J. Philos. 200785193–115.2293976 [Google Scholar]
- 29.Piccinini G.Computationalism, the Church-Turing thesis, and the Church-Turing fallacy Synthese 2007154197–120.1120.030052293976 [Google Scholar]
- 30.Piccinini G. Some neural networks compute, others don’t. Neural Netw. 2008;21(2–3):311–321. doi: 10.1016/j.neunet.2007.12.010. [DOI] [PubMed] [Google Scholar]
- 31.Piccinini G. Computers. Pac. Philos. Q. 2008;89(1):32–73. [Google Scholar]
- 32.Piccinini G.Computation without representation Philos. Stud. 20081372205–241.2384219 [Google Scholar]
- 33.Piccinini G.Computationalism in the philosophy of mind Philos. Comp. 200943515–532.880124 [Google Scholar]
- 34.Piccinini, G.: The mind as neural software? Understanding functionalism, computationalism, and computational functionalism. Philos. Phenomenol. Res. 81(2) (2010)
- 35.Piccinini, G.: The resilience of computationalism. Philos. Sci. (2010, in press)
- 36.Scarantino, A.: A theory of probabilistic information. Unpublished
- 37.Scarantino A, Piccinini G. Information without truth. Metaphilosophy. 2010;41:313–330. [Google Scholar]
- 38.Edelman S. Computing the Mind: How the Mind Really Works. Oxford: Oxford University Press; 2008. [Google Scholar]
- 39.Shannon CE.A mathematical theory of communication ATT Tech. J. 194827379–423623–656.26286 [Google Scholar]
- 40.Turing A. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc., ser. 2. 1936–37;42:230–265. [Google Scholar]
- 41.Wiener N. Cybernetics: or Control and Communication in the Animal and the Machine. Cambridge: MIT Press; 1948. [Google Scholar]
- 42.McCulloch WS. The brain as a computing machine. Electr. Eng. 1949;68:492–497. [Google Scholar]
- 43.McCulloch WS, Pitts WH.A logical calculus of the ideas immanent in nervous activity Bull. Math. Biol. 19437115–133.10388 [PubMed] [Google Scholar]
- 44.Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge: MIT Press; 2001. [Google Scholar]
- 45.Eliasmith C, Anderson CH. Neural Engineering: Computation, Representation, and Dynamics in Neurobiological systems. Cambridge: MIT Press; 2003. [Google Scholar]
- 46.Dretske F. Knowledge and the Flow of Information. Oxford: Blackwells; 1981. [Google Scholar]
- 47.Millikan RG. Varieties of Meaning. Cambridge: MIT Press; 2004. [Google Scholar]
- 48.Floridi L. Is semantic information meaningful data? Philos. Phenomenol. Res. 2005;70(2):351–370. [Google Scholar]
- 49.Cohen J, Meskin A. An objective counterfactual theory of information. Australas. J. Philos. 2006;84:333–352. [Google Scholar]
- 50.Piccinini G. Functionalism, computationalism, and mental contents. Can. J. Philos. 2004;34(3):375–410. [Google Scholar]
- 51.Baum EB. What is Thought? Cambridge: MIT Press; 2004. [Google Scholar]
- 52.Churchland PM. Neurophilosophy at Work. Cambridge: Cambridge University Press; 2007. [Google Scholar]
- 53.Church A.An unsolvable problem in elementary number theory Am. J. Math. 193658345–363.1507159 [Google Scholar]
- 54.Kleene SC. Introduction to Metamathematics. New York: Elsevier; 1952. [Google Scholar]
- 55.Copeland BJ.Narrow versus wide mechanism: including a re-examination of Turing’s views on the mind-machine issue J. Philos. 2000XCVI15–32.1741438 [Google Scholar]
- 56.Wolfram S. A New Kind of Science. Champaign: Wolfram Media; 2002. [Google Scholar]
- 57.Lloyd S. Programming the Universe: a Quantum Computer Scientist Takes on the Cosmos. New York: Knopf; 2006. [Google Scholar]
- 58.Pitowsky I. The physical Church thesis and physical computational complexity. Iyyun. 1990;39:81–99. [Google Scholar]
- 59.Jilk DJ, Lebiere C, O’Reilly RC, Anderson JR. SAL: an explicitly pluralistic cognitive architecture. J. Exp. Theor. Artif. Intell. 2008;20:197–218. [Google Scholar]
- 60.Gödel K. On undecidable propositions of formal mathematical systems. In: Davis M, editor. The Undecidable. Ewlett: Raven; 1934. pp. 41–71. [Google Scholar]
- 61.Post E.Finite combinatory processes - formulation I J. Symb. Log. 19361103–105.0015.19301 [Google Scholar]
- 62.Davis MD, Sigal R, Weyuker EJ. Computability, Complexity, and Languages. Boston: Academic Press; 1994. [Google Scholar]
- 63.Piccinini G.The first computational theory of mind and brain: a close look at McCulloch and Pitts’s “Logical calculus of ideas immanent in nervous activity” Synthese 20041412175–215.2101909 [Google Scholar]
- 64.Penrose R. Shadows of the Mind. Oxford: Oxford University Press; 1994. [Google Scholar]
- 65.Gerard RW. Some of the problems concerning digital notions in the central nervous system. Cybernetics. In: Foerster HV, Mead M, Teuber HL, editors. Circular Causal and Feedback Mechanisms in Biological and Social Systems. Transactions of the Seventh Conference. New York: Macy Foundation; 1951. pp. 11–57. [Google Scholar]
- 66.Rubel LA. The brain as an analog computer. J. Theor. Neurobiol. 1985;4:73–81. [Google Scholar]
- 67.Pour-El MB.Abstract computability and its relation to the general purpose analog computer (some connections between logic, differential equations and analog computers) Trans. Am. Math. Soc. 19741991–28.0296.02022347575 [Google Scholar]
- 68.Fodor JA. The mind-body problem. Sci. Am. 1981;244:124–132. doi: 10.1038/scientificamerican0181-114. [DOI] [PubMed] [Google Scholar]
- 69.Block N. Troubles with functionalism. In: Savage CW, editor. Perception and Cognition: Issues in the Foundations of Psychology, vol. 6. Minneapolis: University of Minnesota Press; 1978. pp. 261–325. [Google Scholar]
- 70.Baars BJ, Banks WP, Newman JB, editors. Essential Sources in the Scientific Study of Consciousness. Cambridge: MIT Press; 2003. [Google Scholar]
- 71.Harman G. Thought. Princeton: Princeton University Press; 1973. [Google Scholar]
- 72.Fodor JA. The Language of Thought. Cambridge: Harvard University Press; 1975. [Google Scholar]
- 73.Marr D. Vision. San Francisco: W.H. Freeman; 1982. [Google Scholar]
- 74.Bechtel W, Abrahamsen A. Connectionism and the Mind: Parallel Processing, Dynamics, and Evolution in Networks. Malden: Blackwell; 2002. [Google Scholar]
- 75.Koch C. Biophysics of Computation: Information Processing in Single Neurons. New York: Oxford University Press; 1999. [Google Scholar]
- 76.Marr D, Poggio T.Cooperative computation of stereo disparity Science 19761944262283–287.1976Sci...194..283M [DOI] [PubMed] [Google Scholar]
- 77.Smolensky P, Legendre G. The Harmonic Mind: From Neural Computation to Optimality-Theoretic Grammar, vol. 1: Cognitive Architecture; vol. 2: Linguistic and Philosophical Implications. Cambridge: MIT Press; 2006. [Google Scholar]
- 78.Horgan T, Tienson J. Connectionism and the Philosophy of Psychology. Cambridge: MIT Press; 1996. [Google Scholar]
- 79.Thorndike E. The Fundamentals of Learning. New York: Columbia University Press; 1932. [Google Scholar]
- 80.Hebb D. The Organization of Behavior: a Neuropsychological Theory. New York: Wiley; 1949. [Google Scholar]
- 81.Fodor JA. The Modularity of Mind. Cambridge: MIT Press; 1983. [Google Scholar]
- 82.Turing, A.M.: Intelligent Machinery. Mechanical Intelligence, pp. 117–127. D. Ince. Amsterdam, North-Holland (1948)
- 83.Copeland BJ, Proudfoot D.On Alan Turing’s anticipation of connectionism Synthese 1996113361–377.1412786 [Google Scholar]
- 84.Trehub A. The Cognitive Brain. Cambridge: Cambridge, MIT Press; 1991. [Google Scholar]
- 85.Marcus GF. The Algebraic Mind: Integrating Connectionism and Cognitive Science. Cambridge: MIT Press; 2001. [Google Scholar]
- 86.Miller GA. Language and Communication. New York: McGraw-Hill; 1951. [Google Scholar]
- 87.Minsky M. Semantic Information Processing. Cambridge: MIT Press; 1968. [Google Scholar]
- 88.Fano RM. Transmission of Information; a Statistical Theory of Communications. New York: MIT Press; 1961. [Google Scholar]
- 89.Pierce JR. An Introduction to Information Theory. New York: Dover Publications; 1980. [Google Scholar]
- 90.Smith JM.The concept of information in biology Philos. Sci. 2000672177–194.1783357 [Google Scholar]
- 91.Godfrey-Smith P.On the theoretical role of “genetic coding” Philos. Sci. 20006726–44.1783357 [Google Scholar]
- 92.Griffiths PE. Genetic information: a metaphor in search of a theory. Philos. Sci. 2001;68(3):394–412. [Google Scholar]
- 93.Bradbury JW, Vehrencamp SL. Economic models of animal communication. Anim. Behav. 2000;59(2):259–268. doi: 10.1006/anbe.1999.1330. [DOI] [PubMed] [Google Scholar]
- 94.Hartley RV. Transmission of information. ATT Tech. J. 1928;7:535–563. [Google Scholar]
- 95.Baddeley R, Hancock P, et al., editors. Information Theory and the Brain. Cambridge: Cambridge University Press; 2000. [Google Scholar]
- 96.Grice P. Meaning. Philos. Rev. 1957;66:377–388. [Google Scholar]
- 97.Struhsaker TT. Auditory communication among vervet monkeys (Cercopithecus aethiops) In: Altmann SA, editor. Social Communication Among Primates. Chicago: University of Chicago Press; 1967. pp. 281–324. [Google Scholar]
- 98.Seyfarth RM, Cheney DL. Meaning and mind in monkeys. Sci. Am. 1992;267:122–129. doi: 10.1038/scientificamerican1292-122. [DOI] [PubMed] [Google Scholar]
- 99.Scarantino A. Shell games, information, and counterfactuals. Australas. J. Philos. 2008;86(4):629–634. [Google Scholar]
- 100.Fisher R. The Design of Experiments. Edinburgh: Oliver and Boyd; 1935. [Google Scholar]
- 101.Li M, Vitányi P. An Introduction to Kolmogorov Complexity and its Applications. 2. New York: Springer; 1997. [Google Scholar]
- 102.Winograd S, Cowan JD. Reliable Computation in the Presence of Noise. Cambridge: MIT Press; 1963. [Google Scholar]
- 103.Margolis E, Laurence S, editors. Concepts: Core Readings. Cambridge: MIT Press; 1999. [Google Scholar]
- 104.Quine WVO. Word and Object. Cambridge: MIT Press; 1960. [Google Scholar]
- 105.Stich S. From Folk Psychology to Cognitive Science. Cambridge: MIT Press; 1983. [Google Scholar]
- 106.Egan, F.: A modest role for content. Stud. Hist. Philos. Sci. (2010, in press)
- 107.Rupert RD.Causal theories of mental content Philos. Comp. 200832353–380.2382973 [Google Scholar]
- 108.Dretske F. Explaining Behaviour. Cambridge: Bradford Press; 1988. [Google Scholar]
- 109.Barwise J, Seligman J. Information Flow: The Logic of Distributed Systems. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- 110.Fodor J. A Theory of Content and Other Essays. Cambridge: MIT Press; 1990. [Google Scholar]
- 111.Millikan RG. Language, Thought, and Other Biological Categories. Cambridge: MIT Press; 1984. [Google Scholar]
- 112.Harman G. (Nonsolipsistic) conceptual role semantics. In: LePore E, editor. New Directions in Semantics. London: Academic Press; 1987. pp. 55–81. [Google Scholar]
- 113.Papineau D. Reality and Representation. Oxford: Blackwell; 1987. [Google Scholar]
- 114.Grush R. The emulation theory of representation: motor control, imagery, and perception. Behav. Brain Sci. 2004;27(3):377–442. doi: 10.1017/s0140525x04000093. [DOI] [PubMed] [Google Scholar]
- 115.Ryder D. SINBAD neurosemantics: a theory of mental representation. Mind Lang. 2004;19(2):211–240. [Google Scholar]