Experimental observation of increased fluctuations in an order parameter before epochs of extended brain synchronization

Abstract

The identification of epileptic seizure precursors has potential clinical relevance. It is conjectured that seizures may be represented by dynamical bifurcations and that an adequate order parameter to characterize brain dynamics is the phase difference in the oscillatory activity of neural systems. In this study, the critical point hypothesis that seizures, or more generally periods of widespread high synchronization, represent bifurcations is empirically tested by monitoring the growth of fluctuations in the putative order parameter of phase differences between magnetoencephalographic and electroencephalographic signals in nearby brain regions in patients with epilepsy and normal subjects during hyperventilation. Implications of the results with regard to epileptic phenomena are discussed.

Introduction

The increase in fluctuations of order parameters near a dynamical bifurcation (or phase transition), originally described and studied in the context of periodic behaviour [1, 2], is a well-known phenomenon in complex systems theory [3]. However, experimental demonstrations of the pre-bifurcation enhancement of fluctuations have rarely been reported. In neuroscience, the question of finding adequate order parameters to unravel brain dynamics and the related notion of dynamical bifurcations in neural activity are profusely discussed in the neuroscientific literature, as these are presumed to be fundamental aspects in the characterization of brain activity. The concept of order parameters is widely used in physics in studies of phase transitions. While control parameters induce transitions in the system’s behaviour, order parameters are defined as those that are able to capture the macroscopic behaviour resulting from microscopic fluctuations, thus allowing for a description of the dynamics using few variables. In this regard, differences in the oscillating phase extracted from neural signals or from specific oscillatory behaviours have been proposed to be an adequate order parameter [4, 5]. With regards to bifurcations, there is wide evidence from theoretical studies demonstrating bifurcations in neural dynamics [6].

In a previous study, we reported the observation of an absolute minimum in the values of a phase synchronization index immediately before or after epileptic seizures [7]. This phenomenon is already indicative of the amplification of fluctuations in phase differences (particularly the appearance of more jumps in phase and phase slips) at those time points. Furthermore, other studies reported decreases in synchronization preceding seizures [8]. It is then conceivable to test the critical point hypothesis (that the seizure represents a bifurcation) by monitoring the growth of fluctuations in an order parameter (the phase difference in brain signals). This procedure has been used to address similar questions in, for example, seismic studies, specifically whether an earthquake represents a critical phase transition [3, 9].

Hence, in this study we sought to address the hypothesis that there is a growth of the fluctuations in the phase differences immediately preceding moments of long-lasting and spatially extended brain synchronization, in particular spontaneous seizures in patients and hypersynchronous events in normal subjects during hyperventilation. Thus, we are testing two complementary premises: that phase difference extracted from brain signals is an adequate order parameter and that seizures (or long-lasting high-synchrony episodes) represent critical points in brain dynamics. To this end, we calculate the amplitude of the fluctuations in phase synchronization during epileptiform activity in patients and that of normal subjects while they hyperventilate. The reason for the latter is that hyperventilation is a common activation technique in the evaluation of seizures in patients and the electroencephalographic (EEG) changes during hyperventilation have been well documented [10]. In other words, hyperventilation represents a “control parameter” that brings about a transitory period of higher synchronization (in our cases these were not seizures because they were non-epileptic individuals). The EEG changes consist of transient bilateral medium and high amplitude delta and theta slow waves during hyperventilation. This slowing and synchronization of cortical rhythms during hyperventilation is believed to be related to the effects of hypocapnia and the resulting cerebral vasoconstriction that decreases activity in the mesencephalic reticular formation [11, 12]. Hence, while we cannot operate a control parameter during the spontaneous transition to seizures, we can manipulate the transition to a higher synchronous state by using hyperventilation as a control parameter.

Methods

Recordings were analysed from six patients: three with magnetoencephalographic (MEG) and three with intracranial EEG recordings; and from five normal control subjects during hyperventilation (scalp EEG recordings). Details of the patients’ epilepsies, seizure types and number of seizures recorded are presented in Table 1. The MEG recordings were obtained in one patient with primary generalized epilepsy and absence seizures, in one patient with symptomatic generalized epilepsy and tonic motor seizures, and in one patient with frontal lobe epilepsy and tonic motor seizures. The intracranial EEG recordings were obtained from patients with medically refractory temporal lobe epilepsy as part of their routine clinical pre-surgical investigations. MEG recording sensors covered the whole cerebral cortex, whereas intracranial EEG electrodes were positioned bilaterally in the amygdala and hippocampal structures of the temporal lobes. There were 19 EEG scalp electrodes for the normal subject recordings. The duration of the recordings was 120 s for the MEG studies, 54 min for the intracranial EEG epochs, and 5 to 7 min for the normal subject EEGs of which 3 min were recorded during hyperventilation. MEG signals were obtained as described previously [13]. Phase differences between two signals were estimated from the instantaneous phases extracted using the Hilbert transform [14]. Several central wavelengths were chosen with a bandpass of 2 Hz on either side; specifically, the selected frequencies ranged from 5 to 30 Hz, and so, for instance, a central frequency of 5 Hz would include the range 5 ± 2 Hz. One example is shown in Fig. 1 as the unwrapped phase difference: note the phase jumps and the fluctuating time series. Then, the fluctuations in the phase difference time series were estimated as the absolute value of the derivative of the time series: 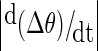where Δθ is the phase difference between two selected signals. In this manner, both small fluctuations and large ones (phase slips) are captured. Phase differences were studied at frequencies from 10 to 30 Hz, except in the case of the absence epilepsy patient where these were calculated at 5 and 15 Hz (because absence seizures occur typically at ∼3–4 Hz, we chose to focus on lower frequencies in this case, and so for the central frequency of 5 Hz the range 5 ± 2 Hz is covered). Phase differences for the normal subjects’ recordings were calculated at 5 Hz as well, to reflect the frequency slowing during hyperventilation to ∼4 Hz. In addition, a phase synchrony index (R), using a 1-s running window, was obtained from the phase differences using the mean phase coherence statistic [8, 13], which is a measure of phase locking and is defined as .

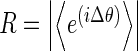Table 1.

Patients’ epilepsies, seizure types and number of seizures

Patient	Epilepsy type	Seizure type	Recording type	Number of seizures	Mean (± SD) time before seizures of global maxima in fluctuations of phase differences (seconds)	Pair-wise electrode combinations with pre-seizure increase in fluctuations (%)
1	TLE	CPS	ICEEG	4	74 (±17)	73.7 (14 of 19)
2	TLE	CPS	ICEEG	5	56.7 (±49)	38 (10 of 26)
3	TLE	CPS	ICEEG	5	435 (±240)	50 (12 of 24)
4	PGE	Absence	MEG	1	5.2 (±3.8)	72.7 (16 of 22)
5	FLE	Tonic	MEG	2	6.4 (±4.5)	50 (6 of 12)
6	SGE	Tonic	MEG	7	1.6 (±1.2)	38.5 (10 of 26)

CPS complex partial seizures, ICEEG Intracranial EEG, FLE frontal lobe epilepsy, PGE primary generalized epilepsy, SGE symptomatic generalized epilepsy, TLE temporal lobe epilepsy

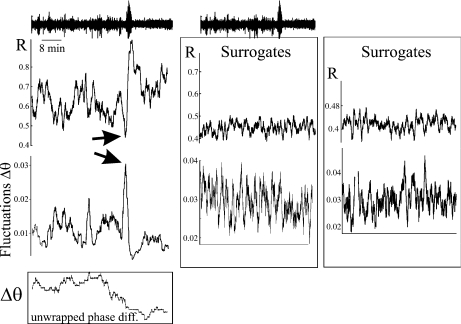
Fig. 1.

Growth of the fluctuations in phase difference between two intracerebral electrodes located in the left hippocampus of patient 1 suffering from temporal lobe epilepsy. Upper trace is the 54 min recording from one of the electrodes, with the seizure visible as the large amplitude signal located at minute 36 and lasting ∼55 s. The phase synchrony index R between the two signals is plotted (upper graph) for the duration of the recording: note the increase in R during the seizure and the drop immediately before the seizure, the latter coinciding with the growth of the fluctuations in phase difference (lower graph, evaluated at 30 ± 2 Hz) seen just before the seizure (arrows). Insetat the bottom shows the time evolution of the unwrapped phase difference between the two signals, exhibiting phase jumps and the relatively “flat” region coinciding with the seizure. Time scale (x-axes) is the same for all panels. Right-hand side graphs represent the same analysis done using phase-randomised surrogates of the two signals. Two examples are shown: note that the increase in synchrony at the time of the seizure disappears and that there is no absolute maximum of the fluctuations preceding an absolute maximum in R

Results

An increase in the fluctuations of the phase differences before seizure onset was noted in all patients. Figure 1 shows an example derived from an intracranial EEG recording in patient 1 (see Table 1) and Fig. 2 shows a similar pattern derived from two MEG recordings in patients 4 and 5. Absolute maxima of the fluctuations were sought in the fluctuation time series corresponding to the whole recording period, and of particular interest are those cases in which the absolute maximum occurred before the seizure (or equivalently, before the increase in the phase synchrony index R) within a relatively short time window. The peaks in fluctuation shown in Figs. 1 and 2, occurring just ahead of the large increase in the synchrony index (corresponding to the seizure), are representative illustrations of what was found. It should be noted that the growth of the fluctuations before a seizure was not always observed in every pair-wise combination assessed: for the patients with focal or symptomatic generalized epilepsy it occurred in 73.7%, 50%, 50%, 38%, and 38.5% of the pair-wise combinations of signals assessed. In the case of the patient with primary generalized absence epilepsy, the growth of fluctuations occurred more frequently at 5 Hz (perhaps because it is closer to the absence seizure frequency aforementioned): 72.7% of the inspected pair-wise combination of sensors at 5 Hz, compared with 62% at 15 Hz. Surrogate signals were obtained from each of the original recordings using phase randomization, and the same analyses applied. Figure 1 shows two examples using surrogates for the particular intracranial electrodes (details in the figure legend). To confirm that the association between R maxima and fluctuations observed in the recordings was not due to chance, we took into consideration the time window during which these global maxima occurred, and the likelihood of their being as close to the seizures as actually observed, which can be assessed by considering a variable x defined as the fraction between the time in which absolute maxima occurred before the seizure in relation to the total time examined (the length of the recording): x = t_before / t_total . If the locations of these maxima were not related to the seizures, then x should behave as a random event evenly distributed in the segment [0, 1] with approximate mean 0.5. The total mean in our data was 0.0469. A Kolmogorov–Smirnov test was used to validate the hypothesis that the maxima do not follow this distribution, resulting in a p value of 0.00001. Thus, we can conclude that the maxima in the series of fluctuations of phase differences are, with very high probability, effectively linked to the seizure occurrences.

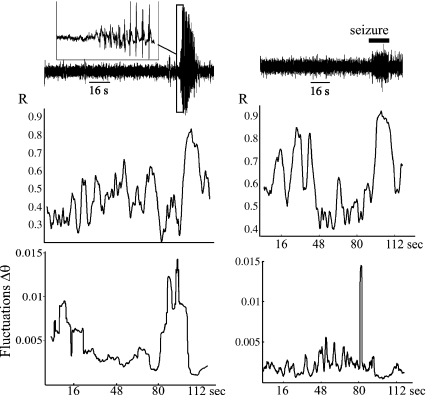
Fig. 2.

Growth of the fluctuations in phase difference between two MEG sensors in patient 4, with absence epilepsy (left), and patient 5, with frontal lobe epilepsy (right). The two sensors were located on the left frontal cortex (left) and in the central midline (right). Upper traces are the MEG recording in one sensor, and the inset denotes the start of the spike-and-wave absence seizure. Graphs show the phase synchrony index (R) and the fluctuations in phase difference (evaluated at 5 ± 2 Hz and 30 ± 2 Hz, respectively) showing a similar pattern to that revealed in Fig. 1. Note, however, that the absolute minimum of the R values coinciding with the increase in fluctuations is not clearly seen in the right-hand side case. Time scale (x-axes) is the same for allpanels in each column

When detected, the presence of the absolute maximum in fluctuations before seizures occurred between 2 and 74 s in all patients except for one (patient 3) in whose recordings this phenomenon took place 435 ± 240 s (about 7 min) prior to seizures. It should be noted that this particular patient’s seizures showed a specific intracranial EEG pattern in which the fast oscillatory activity universally recognized as seizure onset is preceded by a sustained period of rhythmic focal spiking between 0.5 and 2 Hz in the same region. This pattern, which has been called “pre-ictal spiking” or “rhythmic limbic spiking” is occasionally encountered as a variant in hippocampal seizure onsets in some patients with temporal lobe epilepsy, and it is debated as to whether or not the “pre-ictal spiking” itself marks in some way the actual beginning of the seizure [15–17]. The presence of this particular seizure pattern might somehow bear relevance to the much longer pre-seizure maximum fluctuation times in this patient (the R maxima coincided with the onset of the classical fast rhythmic ictal pattern, and not the “pre-ictal spiking”). However, it must be acknowledged that the pre-seizure spiking never lasted more than 1 min (mean 33 s) and so any relationship is speculative. The other average times (in seconds) pre-seizure at which the absolute maxima of phase difference fluctuations was observed, for each case, were: 74 ± 17, 56.7 ± 49, 5.2 ± 3.8, 6.4 ± 4.5, and 1.6 ± 1.2 s. One can see that the pre-seizure times appear longer in the patients with temporal lobe epilepsy, investigated with intracranial EEG, than in the patients with other epilepsies, investigated with MEG, which may reflect either the differences in epilepsy syndromes and their respective regions of seizure generation or the differences in recording techniques between extracranial MEG and intracranial EEG. It must be acknowledged that the quantification of these pre-seizure times would make more sense if there were access to a control parameter, which we do not have, as discussed below. Whereas many times the absolute maximum of fluctuations in phase difference coincided with an absolute minimum in the phase synchrony index R, as depicted in Fig. 1 (these absolute minima in R shown here are qualitatively similar to what was shown in Fig. 4 in [7]), this was not always the case (Fig. 2, right-hand side). Obviously, the R index is related to the phase difference Δθ as shown in the equation above at the end of Section 2..

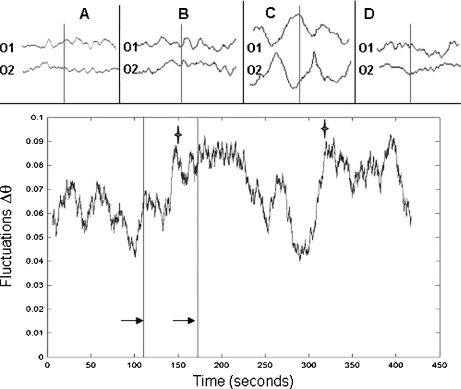
Fig. 4.

Rate of phase fluctuations for an EEG recording of a normal subject hyperventilating. Note how the fluctuations increase as the subject starts to hyperventilate. The first maximum (marked with a star) occurs between the initiation of hyperventilation in the subject (indicated by the first arrow at 110 s) and the onset of slow waves on EEG (indicated by the second arrow at 175 s and shown in upper panel, trace B). The second star marks the cessation of hyperventilation and return to normal baseline EEG. The panel above shows 3-s epochs of raw EEG recordings of the occipital lobes at baseline (A), onset of slow waves after 1 min of hyperventilation (B), high amplitude slow waves at 2 min of hyperventilation (C) and return to baseline after cessation of hyperventilation (D)

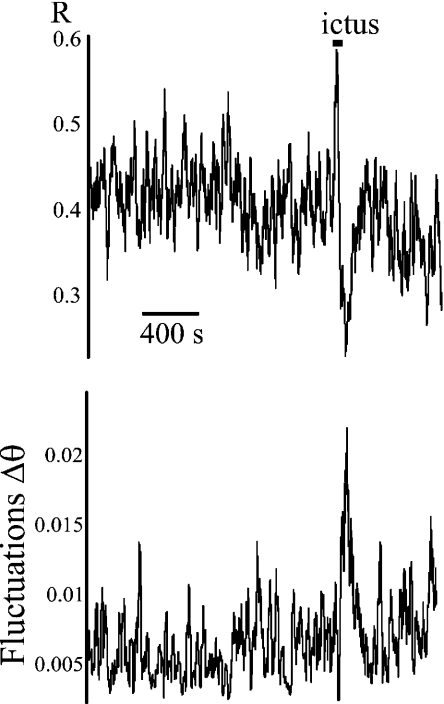
Since seizure onset is considered a bifurcation, then, conceivably, seizure offset is also a bifurcation—the qualitative behaviour in the signal changes equally abruptly at seizure offset as at seizure onset. In this case, an increase in the noise of the order parameter is also expected. In fact, we observed a growth of the fluctuations in phase locking at seizure offset as well, as shown in Fig. 3.

Fig. 3.

Increased fluctuations in phase difference associated with the end of a seizure, in patient 3, with temporal lobe epilepsy. The upper plot shows the phase locking value between two electrodes located in the right hippocampus, and the lower graph represents the fluctuations in phase difference, evaluated at 20 ± 2 Hz. The seizure is marked by a horizontal line (‘ictus’). Note, in this case, the decrease in synchrony (R) associated with the growth of fluctuations at the end of the ictal event

In the hyperventilating control subjects, the magnitude of phase synchronization (R) increased throughout the 19 EEG sensors during the slow wave activity (data not shown), indicating that this enhanced synchrony during hyperventilation is a global brain phenomenon, as is well known. As in the case of seizures described above, maxima of the fluctuations were observed after the onset of hyperventilation and just before the emergence of high amplitude slow waves (Fig. 4). Maxima were observed again after the cessation of hyperventilation, when the EEG waveforms reverted to baseline. The average time of the appearance of the maxima before the extended slow wave synchronization was 29.3 ± 5 s. To address the likelihood of this event, we applied a binomial test similar to the one used above for the seizure recordings. Because in this case we have a “control parameter”, the hyperventilation, the EEG was divided into two time windows: the first was the period of recording prior to the onset of the hyperventilation, and the second was the period from the onset of the hyperventilation to the onset of the slow wave pattern. The probability of success under the null hypothesis of finding the peak within the second period is simply the ratio of the second period over the total period (second+first). Using this test, we found that identifying a peak across all cases studied at those temporal distances from the start of the slow wave activity is highly significant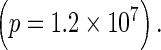

Discussion

In this study, we used EEG and MEG recordings to identify increases in fluctuations of an order parameter prior to changes in human brain states, including the transition to epileptic seizures. Our main goal was not to present a new epileptic seizure prediction algorithm but rather to provide experimental evidence for the existence of this basic phenomenon in a biological system, an observation that may have relevance not only to the dynamics of human epilepsy—specifically the starting, and stopping, of seizures—but also to non-pathological changes in brain states associated with something as seemingly innocuous as over-breathing. We discuss our findings in the following.

A bifurcation occurs because control parameters vary, and if they scale beyond a critical value, a transition in the system dynamics occurs. One limitation of our in vivo study of patients with epilepsy is that there is no access to possible control parameters, as the brain activity unfolds continuously. Thus, the only manner to correlate the measured increase of fluctuations as the seizure approaches would be to simultaneously measure one, or more, of the possible control parameters, which can rarely be done in the clinical setting. Some conceivable candidates as parameters thought to be involved in seizure generation include extracellular potassium concentration [18] or the balance between excitatory and inhibitory neurotransmission [19, 20]. The search for control parameters might also take advantage of the observation that certain opiate medications [21] and general anaesthetics [22] can cause transitions to seizures. In the latter case, experimental modeling has suggested that enflurane-induced alterations in the shape of inhibitory post-synaptic potentials may be the specific parameter facilitating the development of pre-seizure bifurcations in the setting of this general anaesthetic. Of course, this would be but one of many possible control parameters that might have a role in seizure generation, and is mentioned here only as an example, as our patients did not receive anaesthetic medications. On the other hand, hyperventilation, an activation procedure known to induce seizures in susceptible subjects, allows us to manipulate a “control parameter”, which could be the CO₂ levels, hypocapnia and vasoconstriction, or any other caused by the hyperventilation. Even when seizures are not induced, as in our cases here reported, the EEG changes are well documented [10, 11], and the change from baseline brain activity to high amplitude slow waves is believed to be a thalamus-mediated response and results in an extended cortical synchronization.

Order parameters are used in physics in studies of phase transitions. Order parameters are defined as those that capture the macroscopic behaviour resulting from microscopic fluctuations, which are different from control parameters, those that induce transitions in the system’s behaviour. Several experimental order parameters have been used in neuroscience, from phase differences in motor coordination [4] to the amplitudes of grasping movements [23]. Model-based quantification of neurophysiologic parameters from EEG signals has been used to monitor temporal changes in the signals [24, 25]. Within the framework of complex systems, an order parameter should increase its fluctuations before a critical point [3], as has been shown numerous times in theoretical models and computer simulations. Empirical demonstrations, however, do not abound. These include the experimental observation of the fluctuations in the injected current to a diode laser before a period-doubling bifurcation [26], the flow rate fluctuations in a chemical oscillator before a subcritical bifurcation [27], the accelerating cumulative energy release before earthquakes [9], and the increase in the fluctuations of the relative phase between EEG signals and auditory stimuli presented in a sensorimotor coordination task before a behavioural bifurcation [28]. The amplification of fluctuations has been shown, in theoretical models, to be dependent on the rate of transition through the bifurcation point [29].

Our observations are complementary to those that reported a decrease in phase synchrony before seizures [7, 8], for, after all, a decrease in phase synchrony is associated with an increased rate of phase slips. At the cellular level, a decrease in firing synchrony at seizure onset was reported to occur in vitro [30]. However, as aforementioned, we observe this phenomenon more clearly by monitoring the fluctuations in phase differences directly to assess the changes in the amplitude of the fluctuations, rather than by monitoring the phase synchrony index. The decrease of the magnitude of the synchrony index, R, could be due mostly to the increase of the fluctuation amplitude of the phase difference, and the bifurcation leads to higher synchrony but is preceded by a period of higher fluctuations.

Our results indicate that there are measurable precursors of seizure events, as also recently suggested by the use of recurrence plot-based measures, where some precursors of ictal events were observed [31]. That seizures can be anticipated, or predicted, based on deviations from scale-free characteristics, has been suggested recently analysing inter-seizure interval distributions [32, 33]. Deviations from self-organized criticality preceding large earthquakes have been identified as potential predictive indicators in seismic studies and may ultimately be applicable to neurophysiologic studies attempting to anticipate analogous changes to synchronized regimes, representing seizures (rather than earthquakes), in epilepsy [33, 34]. Since the early work in this field it has been suggested that measuring noise amplification experimentally might be a useful tool for revealing a forthcoming bifurcation [1, 2]. For instance, it has been proposed that monitoring fluctuations in muscle motility could be used to predict parturition [35]. Thus, although our study was not intended to focus on the potential seizure prediction value of this phenomenon, monitoring of fluctuations in phase synchrony could represent another method to be added to the already abundant arsenal of algorithms that try to anticipate seizure occurrence.

We have considered in this study seizures as possible bifurcations, as other studies have done as well [36, 37]. However, as with other studies exploring the dynamics of human epileptic phenomena, we have based our designation of a seizure on the appearance of typical, rhythmic, oscillatory high amplitude waveforms in the MEG and EEG recordings, as is done in clinical practice (Figs. 1 and 2). And yet, is this actually the onset of the bifurcation? As briefly alluded to above for one particular intracranial EEG pattern, there is still debate on what a seizure onset really is, and some consider that seizures may start some time before the classical oscillatory activity first becomes visually apparent in MEG and EEG recordings. We must acknowledge that the recordings we have at our disposal are, basically, field potentials, manifestations of synchronized population activity and that to correlate these events with potential bifurcations cannot be done accurately, but only qualitatively. This is of importance because the amplification of fluctuations we observed in our study occurred at different times for each patient, which is something to be expected as every patient is a different case. What can be assumed without risk is that the onset of the bifurcation (or the seizure) should occur some time before the visible high amplitude waveforms. The perspective adopted here so far has been to consider one seizure, or a period of extended synchronization, as a dynamical bifurcation; however, another perspective could consider that the whole brain can undergo a re-organization, as is typical in self-organising phenomena. This is a sort of local versus global phenomenon, both of these levels being complementary, and perhaps for this reason the non-reductionistic, global view on brain activity and the epileptic condition in particular as being governed by scale-free mechanisms [32] may offer new avenues to address matters related to the anticipation and control of epileptic events.

One scenario that emerges from this and similar studies is that epileptic phenomena (and perhaps most brain activity) can be conceptualised in terms of the statistical physics of critical phase transitions, as the picture is qualitatively similar in all these phenomena: upon approaching a bifurcation there is an increase in the fluctuations [3]. The growth of the phase difference slips before the ictal event could be due to the increase in tonic (continuous) neuronal action potential discharges that precede or occur at seizure onset, while as the seizure progresses the neuronal activity becomes intermittent (bursting) and more correlated amongst cells. Thus, seizures may follow periods of increasing cell activity, much as earthquakes follow periods of accelerating seismicity [9]. Possible scenarios at the network level to explain the decrease in synchrony before seizures have been advanced, wherein there could be several small regions that are experiencing synchronization, but only locally, which become more globally synchronized as the seizure advances [8, 38]. Because criticality entails large susceptibility to external influences and long-range correlation between constituents of the system, it represents a cooperative phenomenon, and the sudden and seemingly unpredictable occurrence of seizures can be considered a natural consequence of these critical phenomena. In summary, the observed growth of the fluctuations in phase synchrony prior to periods of extended brain synchrony indicates that this is a generic phenomenon, regardless of whether these periods are classified as seizures or not, and that these prolonged and extensive “hypersynchronous” states may represent dynamical bifurcations.