Optimal Partitioning for Linear Mixed Effects Models: Applications to Identifying Placebo Responders

Abstract

A long–standing problem in clinical research is distinguishing drug treated subjects that respond due to specific effects of the drug from those that respond to non-specific (or placebo) effects of the treatment. Linear mixed effect models are commonly used to model longitudinal clinical trial data. In this paper we present a solution to the problem of identifying placebo responders using an optimal partitioning methodology for linear mixed effects models. Since individual outcomes in a longitudinal study correspond to curves, the optimal partitioning methodology produces a set of prototypical outcome profiles. The optimal partitioning methodology can accommodate both continuous and discrete covariates. The proposed partitioning strategy is compared and contrasted with the growth mixture modelling approach. The methodology is applied to a two-phase depression clinical trial where subjects in a first phase were treated openly for 12 weeks with fluoxetine followed by a double blind discontinuation phase where responders to treatment in the first phase were randomized to either stay on fluoxetine or switched to a placebo. The optimal partitioning methodology is applied to the first phase to identify prototypical outcome profiles. Using time to relapse in the second phase of the study, a survival analysis is performed on the partitioned data. The optimal partitioning results identify prototypical profiles that distinguish whether subjects relapse depending on whether or not they stay on the drug or are randomized to a placebo.

1 Introduction

Patients suffering from mental illnesses and treated with a drug may respond due to the specific effects of the drug as well as non-specific effects (or placebo effects) of treatment that include expectations of improvement from taking a pill and receiving attention from clinicians. A major problem in psychiatric research is to determine the degree to which subjects respond due to specific and non-specific aspects of treatment. Answers to questions pertaining to drug efficacy (e.g., Kirsch et al., 2008), treatment decisions, and trial design depend on the degree to which subjects respond due to non-specific effects of treatment as well as the specific effects of a drug. Investigators have long struggled with the problem of differentiating these two effects when treating mental illnesses such as depression (e.g., Quitkin et al., 1987a,b, 2000; Stewart et al., 1998; Ross et al., 2002). A drawback to these approaches is that they do not adequately accommodate the possibility that subjects may experience both non-specific and specific effects.

The problem of identifying specific and non-specific responders to treatment in longitudinal studies can be formulated in terms of identifying prototypical profiles with clinically meaningful interpretations. One approach is to cluster the data. For instance, Lipkovich et al. (2008) cluster curves from a longitudinal study of acute bipolar mania to identify distinct response patterns to treatment. A closely related methodology that has become very popular is model-based clustering using a finite mixture model (e.g., Titterington et al., 1985). For longitudinal data, growth mixture models (GMM) have been used to incorporate random effects into the finite mixture model (Muthén and Shedden, 1999; James and Sugar, 2003; Elliott et al., 2005). Finite mixture models that incorporate random effects have also been developed for analyzing gene expression data (e.g., Luan and Li, 2003; Celeux et al., 2005; Qin and Self, 2005; Eng et al., 2008). A major problem with the use of GMM is that these models assume the existence of distinct latent sub-groups in the population. If the population is homogeneous and does not consist of distinct sub-populations, then the GMM approach is not appropriate. As is well known, finite mixture models can provide very good fits to homogenous distributions (e.g. Bauer and Curran, 2003; Tarpey et al., 2008); however, attaching meaning to the mixture components in these cases reinforces an erroneous interpretation that the investigators have discovered distinct and well-defined sub-populations. For instance, in the placebo response problem, there may not be distinct classes of specific and non-specific responders to treatment, in which case a GMM approach would not be appropriate. A different scenario is that all patients may experience some degree of both specific and non-specific responses and the extent of these effects could vary continuously.

An alternative to the GMM for estimating prototypical curve profiles in longitudinal studies is to partition the data. For example, Tarpey et al. (2003) analyzed data from a longitudinal depression trial using quadratic outcome profiles where the distribution of the estimated regression coefficients appeared homogeneous and consistent with a normal distribution. Nonetheless, a variety of distinct profile shapes existed in the data (e.g. flat, decreasing, concave up and down) corresponding to distinctly different clinical interpretations (e.g., non-responder, drug responder, placebo responder, a mixture of a drug/placebo responder).

In this paper, we present a methodology for optimal partitioning for mixed effects (OPME) models. The OPME approach incorporates random effects, accommodates covariate information and can handle missing observations. We develop and illustrate the methodology for linear mixed effects models and discuss the extension to nonlinear mixed effects models in Section 8.

The problem of optimal partitioning, stratification or grouping is a classic statistical problem with a long history (e.g., Cox, 1957; Connor, 1972; Dalenius, 1950; Dalenius and Gurney, 1951; Fang and He, 1982; Mease et al., 2004). The optimality criterion usually refers to finding a partition of a distribution into k strata (or clusters) that minimizes the within strata variances. The means of the strata (cluster means) obtained from an optimal partitioning of a theoretical distribution are called principal points (Flury, 1990, 1993). The optimal partitioning methodology presented in this paper is based on estimating the principal points for mixed effects models.

In the information theory and signal processing literature, the term vector quantization is used to represent the mathematically equivalent problem to optimal partitioning (e.g. see the March 1982 issue of the IEEE Transactions on Information Theory which is devoted to the subject of quantization or the more recent article Perlmutter et al. (1998) which provides a nice overview of vector quantization and its relationship to research in the statistical literature). Vector quantization in signal processing has been developed primarily for data reduction whereas the focus of optimal partitioning in the statistical literature is mostly focused on inference.

This paper has the following organization: Section 2 describes a trial where the drug fluoxetine was used to treat depression; Section 3 presents a Bayesian GMM and applies the model to the depression trial. The GMM results indicate that after accounting for covariates, there are no distinct mixture components. This provides the motivation for the OPME approach of this paper. In Section 4, the notion of self-consistency is presented that provides the basis for determining an optimal partitioning for a linear mixed effects model. Classification based on the optimal partitioning is described in Section 5. A small simulation example is provided in Section 6. In Section 7, the optimal partitioning approach is applied to the depression trial data to differentiate specific and non-specific responses among subjects treated with drug. The paper is concluded in Section 8. All data analysis is performed using the R software (R Development Core Team, 2009)

2 The Depression Treatment Study

A study was conducted to determine optimal treatment duration for depression with fluoxetine using a randomized discontinuation trial design (Stewart et al., 1998). Study subjects were outpatients aged 18 to 65 years, meeting diagnostic criteria for major depression with severity scores of 16 or more on a modified 17-item Hamilton Depression Rating Scale (HAM-D). The study had two phases: a 12 week open phase and a 90 day discontinuation phase. In the open phase, all patients were treated openly with fluoxetine, 20 mg/day, for 12 weeks. The HAM-D scores were assessed at weeks 0, 1, 2, 3, 4, 6, 8, 10, 11, 12. Remission was defined as HAM-D scores of 7 or less and failure to meet the diagnostic criteria for major depression for the last 2 weeks. Demographic (gender, age) and clinical characteristics (such as persistency of depression, age-at-onset, melancholia type, chronicity, neurovegetative type, number of previous episodes, and many others), were recorded at baseline. Of 839 patients who openly received fluoxetine in the study, 395 completed the 12 weeks open treatment phase, met the remission criteria and agreed to be enrolled in a double blind discontinuation phase. In the discontinuation phase, these remitters were randomized to either continue taking fluoxetine or to be switched to placebo. They were followed for 90 days and the time to relapse was recorded. Subjects still in remission were censored at 90 days.

If subjects relapsed when switched to placebo, it can be inferred that their remission was due to a large extent to the specific effect of the drug. If subjects relapsed while continuing on fluoxetine, it is reasonable to assume that their remission was largely due to the non-specific aspects of the treatment, i.e. placebo effects, which are unstable in the sense that these non-specific effects of treatment are not constant over time.

The goal is to partition the remitters with respect to their outcome profiles during the open treatment phase. The partitioning should be useful in explaining relapse during the discontinuation phase. For example, subjects with a specific outcome profile shape during the open treatment phase might have a high probability of relapse if they are switched to placebo but a low relapse probability if they are maintained on fluoxetine – such subjects might be considered to have experienced strong specific treatment effect and, possibly, only minimal non-specific treatment effect. Alternatively, subjects with a different outcome profile shape during the open treatment phase might have similar relapse probabilities whether they are switched to placebo or maintained on fluoxetine – such individuals can be considered to have benefitted from non-specific effects of the treatment.

3 A Growth Mixture Model (GMM) Approach

The assumption underlying finite mixture models is that the population consists of J homogeneous latent sub-populations. In this section we describe a Bayesian approach to estimating a growth mixture model for longitudinal data that can incorporate covariates both in the classification model and in the model for the longitudinal trajectories. The approach is similar to Elliott et al. (2005) who modeled simultaneously continuous and discrete longitudinal outcomes. In our approach we only model a single continuous longitudinal outcome variable but we allow the trajectories of this outcome over time to depend on baseline covariates. Full details on this procedure are in Lu (2006).

For the ith subject, a q × 1 vector of covariates w_i at the baseline is observed and a vector of responses y_i = (y_i,1, ···, y_i,ri)′ is observed at time points t_i,1 < ··· < t_i,ri. Given J, define a latent group indicator variable c_i with c_i = j denoting that the ith subject belongs to the jth mixture component, j < J. Conditional on J and c_i,

$${\mathit{y}}_i={\mathit{S}}_i{\mathit{\beta }}_{c_i}+{\mathit{Z}}_i{\mathit{b}}_i+{\mathit{\epsilon }}_i,$$ (1)

where S_i is a design matrix with time effects and may incorporate a subset of the covariates and β_ci is a vector of fixed effects associated with the c_ith mixture component; Z_i is the design matrix for the random effects b_i ~ N (0, D) and ε ~ N (0, σ²I).

The covariates are also used to model the classification variables c_i using a multinomial logistic model as follows:

$$c_i\sim Mn(1;{\pi }_{i,1},\dots ,{\pi }_{i,J}),\text{with}log\frac{{\pi }_{i,j}}{{\pi }_{i,J}}={\mathit{w}}_{1i}^{\prime }{\mathit{\gamma }}_j\text{for}j=1,\cdots ,J-1,$$

where π_i,j denotes the probability of c_i = j, j = 1, …, J, w_1i is a sub-vector of w_i and Mn(···) denotes a multinomial distribution. In addition, γ_J is set to 0 for identifiability purposes. Then for j = 1, ···, J − 1, γ_j is a vector of unknown parameters describing the odds of c_i = j relative to c_i = J.

A Bayesian estimation is implemented using a Gibbs sampler (Gelfand and Smith, 1990; Robert and Casella, 2004) to obtain random samples of the model parameters, the random effects and the classification variables from the posterior distribution. Conjugate prior distributions are used for the model parameters: normal priors are used for the regression coefficients β and γ; a gamma distribution for σ² and an inverse Wishart distribution for D. Details for specifying the hyperparameters of the prior distributions are specified in Lu (2006).

The number of mixture components J was determined based on two criteria: (1) The Deviance Information Criterion (DIC) as a goodness-of-fit criterion, and (2) a fully Bayesian estimation procedure using a reversible jump MCMC to find a posterior distribution on J (Richardson and Green, 1997).

In Bayesian analysis of mixture models with J components, the problem of non-identifiability of mixture components, called label switching, arises from the invariance of the log-likelihood function to any permutation in the parameter labelling. A relabelling algorithm proposed by Stephens (2000) is used whereby the MCMC output is postprocessed to minimize the posterior expected loss (risk).

The growth mixture model was applied to the first 6-weeks of the fluoxetine trial data using orthogonal quadratic profiles to fit the curves to the HAM-D response. The Gibbs sampler was run three times with widely different starting points to avoid possible dependence of the results on the starting values. The method was robust to both the initial values of unknown parameters and their prior distributions. Trace plots for each sampled parameter showed that the three MCMC chains converge in a few hundred iterations. The Gibbs sampler was run with 5, 000 iterations after a burn-in of 5, 000 sweeps. Estimates of the parameters and group allocations were based on the average of the 3 runs of the Gibbs sampler. The mixture random effect models were fit with J = 1, 2, 3, 4 to the fluoxetine data and the DIC was computed for each model.

First, when fitting the growth mixture model without covariate effects on trajectories, the lowest DIC occurred for J = 4 groups. The DIC values for models without covariate effects on trajectories were much larger than those based on models that do account for covariate effects. Second, with the binary melancholia covariate for the trajectories and the age-at-onset covariate for class membership, the data strongly supported the model with J = 1, which gave the smallest DIC. Other baseline covariates were also considered such as age and gender. In each case, the one-component mixture model had the smallest DIC values. Models with more covariates had much larger DIC values than the model with only age-at-onset and melancholia type to predict class membership and mean trajectories.

In this example, the finite mixture model is appealing for solving the problem of identifying specific and non-specific responders because this is truly a latent characteristic. However, once covariates are entered into the model, evidence of distinct mixture components vanishes. This illustrates the fact that finite mixture models identify the effect of discrete covariates which might be unknown and unmeasured (latent) or, as in this case, which might be measured. Additionally, the mixture model is defined in terms of a indicator variable specifying that subjects belong to one and only one component of the mixture. Consequently, the mixture model stipulates a strict dichotomy that individuals must belong to one or the other category (e.g. must either be specific or non-specific responders); in the case of the depression treatment with fluoxetine example, the mixture model does not allow for the possibility that subjects may experience both effects. In this example, as we will see, there exists a variety of different response profile shapes even though the growth mixture analysis indicates that there are no distinct mixture components after accounting for the covariates. It is important to note that even if a population is a finite mixture of say 2 mixture components, there may very well exist more than two clinically meaningful outcome profiles. Therefore in cases where fitting a growth mixture model is appropriate, the mixture model by itself will not always be sufficient for identifying the variety of distinct outcome profiles in the distribution. In the following sections, we describe an alternative to the growth mixture model based on an optimal partition of the underlying distribution.

4 Self-Consistency for Mixed Effects Models

An underlying principle of statistics is to extract the relevant information available in the data, typically through some summarization process, such as fitting a model. Given a random variable X, Tarpey and Flury (1996) defined a random variable Y to be a self-consistent approximation to X if Y is a measurable function of X and

$$E[\mathit{X}\mid \mathit{Y}]=\mathit{Y}\text{almost}\text{surely}$$ (2)

Examples of self-consistency are principal components, principal curves (Hastie and Stuetzle, 1989), principal variables (McCabe, 1984), and principal points (Flury, 1990, 1993). Our focus will be on principal points. Let X denote a random vector. Given a set of k points ξ₁, …, ξ_k, define Y = ξ_j if ||X − ξ_j|| < ||X − ξ_h||, for h ≠ j. If Y is self-consistent for X, then the points ξ₁, …, ξ_k, are called k self-consistent points of X (Flury, 1993). If E||X − Y ||² ≤ E||X − Y^*||² for any other k point approximation Y^*to X, then the k points ξ₁, …, ξ_k are called k principal points of X (Flury, 1990).

A set of k principal points induces an optimal partition (in terms of mean square error) of a distribution into k strata according to the minimal distance to the closest principal point. The problem of determining and estimating principal points of different distributions has been studied by many authors (Eubank, 1988; Gu and Mathew, 2001; Iyengar and Solomon, 1983; Li and Flury, 1995; Graf and Luschgy, 2000; Luschgy and Pagés, 2002; Pötzelberger and Felsenstein, 1994; Rowe, 1996; Stampfer and Stadlober, 2002; Su, 1997; Tarpey, 1997; Yamamoto and Shinozaki, 2000a,b; Zoppé, 1995, 1997). Principal points can be regarded as cluster means for theoretical distributions. Nonparametric estimators of principal points can be obtained using cluster means from the k-means algorithm (Hartigan and Wong, 1979). The efficiency of estimating principal points can be greatly increased by taking advantage of parametric assumptions. For example, Flury (1993) derives maximum likelihood estimators of principal points in the simple case of a univariate normal distribution. This section describes a method of obtaining maximum likelihood estimators of principal points for linear mixed effects models.

The complication in mixed effects models is that the random effects are not observed. The following observation will be useful in this regard: suppose Y is self-consistent for X, but that X is not directly observed. Instead X + ε is observed where ε is a mean zero error. If ε is independent of X, then ε will be independent of Y and hence, by (2)

$$E[\mathit{X}+\mathit{\epsilon }\mid \mathit{Y}]=E[\mathit{X}\mid \mathit{Y}]+E[\mathit{\epsilon }\mid \mathit{Y}]=\mathit{Y}+\mathbf{0}=\mathit{Y}\text{almost}\text{surely}.$$ (3)

Therefore, if Y is self-consistent for X, then Y is also self-consistent for X + ε.

4.1 Longitudinal Mixed Effect Models Without Covariates

Let x denote a vector of outcomes for an individual observed over a period of time. Then the standard linear mixed effects model is expressed as:

$$\mathit{x}=\mathit{S}\mathit{\beta }+\mathit{Zb}+\mathit{\epsilon },$$ (4)

where β is a vector of fixed effects, b is a vector of random effects assumed to have mean zero and covariance matrix D, ε is a mean zero vector of random errors with covariance matrix σ²R assumed to be independent of b. The S and Z are design matrices.

For this subsection, we consider the case of S and Z consisting of the same q factors, i.e. S = Z. More general cases will be examined below. By (3), a self-consistent approximation to Zβ + Zb will be self-consistent for the outcome vector x.

Because the regression curves in (4) are determined by β + b, a self-consistent approximation to x by k curves can be obtained by estimating the k principal points of the N(β, D) distribution, assuming the random effects are normally distributed. Let η = β + b ~ N(β, D) be the vector of regression coefficients. Let ξ₁, …, ξ_k denote k principal points of N(β, D). Define

$$\mathit{u}={\mathit{\xi }}_j\text{if}{\left|\right|\mathit{\eta }-{\mathit{\xi }}_j\left|\right|}^2<{\left|\right|\mathit{\eta }-{\mathit{\xi }}_h\left|\right|}^2,h\ne j.$$

Then by (3)

$$E[\mathit{x}\mid \mathit{Zu}=\mathit{Z}{\mathit{\xi }}_j]=E[\mathit{Z}(\mathit{\beta }+\mathit{b})+\mathit{\epsilon }\mid \mathit{u}={\mathit{\xi }}_j]=\mathit{Zu},$$

provided Z is of full column rank. Thus, Zu is a self-consistent k-point approximation to x. Because principal points are a special case of self-consistent points (Flury, 1993), this method can be used to determine the principal points for a mixed model.

Maximum likelihood estimators of k principal points for the linear mixed effects model are obtained by first fitting a linear mixed effects model to obtain β̂ and D̂, the maximum likelihood estimates of β and D in (4), and then determining the k principal points of the distribution N(β̂, D̂).

Analytical expressions for the k principal points of N(β̂, D̂) do not exist except in very simple cases (e.g. small values of k in low dimensions). A straightforward Monte Carlo approach to estimating the principal points, called the parametric k-means algorithm (Tarpey, 2007b), employs the k-means algorithm on a very large sample simulated from the distribution in N(β̂, D̂). Because cluster means from the k-means algorithm are strongly consistent estimators of the principal points (Pollard, 1981), the cluster means from the simulated sample are essentially maximum likelihood estimators of the principal points of the linear mixed effects model (Tarpey, 2007b, Section 3) for a sufficiently large simulated sample. A similar approach to estimating the principal points of a distribution is the LBG algorithm proposed by Linde et al. (1980) in the signal processing literature in the context of vector quantization. The LBG algorithm is very similar to the well-known k-means algorithm (Hartigan and Wong, 1979) and Linde et al. (1980) also suggested a parametric clustering approach by applying the algorithm directly to a known distribution.

A more straightforward approach to estimating k principal points for (4) is to fit a curve individually for the ith subject using ordinary least squares to obtain ${\widehat{\mathit{\beta }}}_i={({\mathit{Z}}_i^{\prime }{\mathit{Z}}_i)}^{-1}{\mathit{Z}}_i^{\prime }{\mathit{x}}_i$ where Z_i is the design matrix for the ith subject. This approach is frequently called filtering. The principal points can then be estimated by clustering the estimated coefficients (e.g. Abraham et al., 2003) or by assuming the estimated coefficients follow some parametric distribution (e.g. normal) and then finding the principal points of the corresponding normal distribution (Tarpey et al., 2003). However, there are several drawbacks to this approach. From (4)

$${\widehat{\mathit{\beta }}}_i=(\mathit{\beta }+{\mathit{b}}_i)+{({\mathit{Z}}^{\prime }\mathit{Z})}^{-1}{\mathit{Z}}^{\prime }\mathit{\epsilon }.$$

Thus, estimating principal points based on the least-square coefficients β̂_i’s will produce estimates of the principal points of a N(β, D + σ²(Z′Z)⁻¹ R(Z′Z)⁻¹), assuming the random effects and the errors are normally distributed. If σ is large, the filtering approach will produce principal point estimates that are too spread out. Secondly, it is difficult to accommodate covariates (although Section 6 illustrates one possible approach) and to account for missing outcome values by working directly with β̂_i’s.

4.2 Optimal Partitioning with Covariates

If covariates are available for the linear mixed effects, then the more general model (4) can be used where S and Z are not necessarily equal and the fixed effect vector β has components corresponding to the covariate effects. First consider the case that the covariates are categorical. If the discrete covariates correspond to M categories, then the regression coefficients conditional on belonging to the mth category can be written β_m + b, where β_m is the fixed effect regression coefficient vector for the mth category, m = 1, …, M. Let π_m, m = 1, …, M, denote the probabilities for the M categories.

Assuming the random effects b are normally distributed, the distribution for the regression coefficients η is a finite mixture

$$\sum _{m=1}^M{\pi }_{m}N(\mathit{\eta };{\mathit{\beta }}_m;\mathit{D}),$$ (5)

where N(·; μ, Ψ) denotes a multivariate normal density with mean μ and covariance matrix Ψ. A self-consistent approximation to the response vector x can be estimated by determining the k principal points of

$$\sum _{m=1}^M{\widehat{\pi }}_{m}N({\widehat{\mathit{\beta }}}_m;\widehat{\mathit{D}}),$$ (6)

where maximum likelihood is used to estimate the parameters in the mixed effects model.

Consider now the case where an r-dimensional continuous covariate w is available. The linear mixed effects model (4) can be expressed as

$$\mathit{x}=\mathit{Z}(\mathit{\beta }+\mathit{b}+\mathbf{\Gamma }\mathit{w})+\mathit{\epsilon },$$ (7)

where Γ is a q × r matrix of regression coefficients corresponding to the continuous covariate. The density for the distribution of the regression coefficient η = β + b + Γw can be expressed as

$$f(\mathit{\eta })=\int f(\mathit{\eta }\mid \mathit{w})g(\mathit{w})d\mathit{w},$$

where g(w) is the density for the continuous covariates. Let μ_w and Ψ_w denote the mean and covariance matrix for w respectively. If w has a normal distribution, independent of b, then estimators of the k principal points of the coefficient distribution η = β + b + Γw can be found by determining the k principal points of

$$N(\widehat{\mathit{\beta }}+\widehat{\mathbf{\Gamma }}{\widehat{\mathit{\mu }}}_{\mathit{w}},\widehat{\mathit{D}}+\widehat{\mathbf{\Gamma }}{\widehat{\mathbf{\Psi }}}_{\mathit{w}}{\widehat{\mathbf{\Gamma }}}^{\prime }).$$ (8)

If the continuous covariates are not independent of the random effects, then the covariance matrix for the coefficient distribution would need to be augmented by the covariance between the continuous covariates and the random effects. If w does not have a normal distribution, then the marginal density for η will be a convolution which may not admit a closed form expression. The case of both discrete and continuous covariates will result in a combination of (6) and (8).

The parametric k-means algorithm, as described in the previous section, can be used to estimate the principal points of (6) and (8). Optimal partitioning can also be obtained for models with non-normal random effects (Zhang and Davidian, 2001; Arellano-Valle et al., 2005); the only requirement is to be able to simulate from these distributions. If the distribution is a mixture, then k principal points can still be estimated (Tarpey, 2007b). For instance, if data from a longitudinal clinical study is consistent with a 2-component mixture, there may very well exist more than two distinct profile shapes of clinical importance. In these cases, k principal points can be estimated by first fitting a GMM and then by applying the parametric k-means algorithm to the estimated GMM.

4.3 Choosing the number of clusters k

In a finite mixture model, there may exist a well-defined number of groups. However, for homogeneous distributions there will exist k principal points for each value of k ≥ 1. The goal of partitioning based on principal points is to find an interpretable partitioning and to identify the corresponding representative cluster means. Choosing k depends on the following considerations: First, in a functional data analysis setting, the value of k should be chosen so that all distinct curve shapes in the data are captured by the k principal points. If k is too large, several of the principal point curve profiles will have similar features; if k is too small, existing distinct features will not be represented. Second, a value of k can be chosen that is meaningful for the particular application at hand. For instance, in Tarpey et al. (2003), a value of k = 5 was chosen because the five principal points represented the distinct curve shapes in the data and the principal points corresponded to different clinical outcomes (non-responders, non-responders with an initial placebo response, placebo responders, drug-responders and combination of a drug/placebo responders). Third, k can be chosen so that the percentage of variability R² in the underlying distribution explained by the k principal points is large. The percentage of variability explained can be based on the usual ANOVA sum of squares: the within group sum of squares is computed by squaring the distance between an observation and the principal point to which it is classified; the total sum of squares is computed by squaring the distance between each observation and the overall mean. Thus, the proportion of variability explained by k principal points is

$$R^2=1-[\text{SS}(\text{within}\text{group})/\text{SS}(\text{total})].$$ (9)

The within and between sum of squares can be computed from the simulation sample used for the parametric k-means algorithm. As k → ∞, R² → 1. Often values of k as small as 4 or 5 can explain up to 70–80% of the total variability.

4.4 Principal Points for Linearly Transformed Data

Like principal components, principal point solutions are not invariant to linear transformations of the data. With functional data, the choice of a set of basis functions determines the design matrix and different design matrices correspond to different linear transformations of the data. However, when partitioning functional data using the k-means algorithm, one will obtain essentially the same results regardless of the choice of a basis as long as orthogonal design matrices are used. Additionally, when using an orthonormal basis to represent functions, the squared Euclidean distance between regression coefficients corresponds to the usual L² distance between functions (Tarpey, 2007a). Frequently with functional data, the intercept term will account for most of the variability in the curves. In these cases, the k-means algorithm tends to produce cluster mean curves that are essentially vertical translations of one another. Linear transformations can be used in these settings to tamp down the variability of the intercept. Finally, interest sometimes lies in clustering derivatives of functions. Because derivatives can often be obtained by via a linear transformation of the design matrix, clustering derivatives of functions often amounts to applying the k-means algorithm to an appropriate linear transformation of the data.

5 Classification Based on Principal Points

The goal of the OPME models approach is to identify non-overlapping strata in a distribution such that the points in a given stratum have similar characteristics. In the depression example discussed here, the purpose of the partitioning is to identify the prototypical treatment response trajectories. In order to associate clinical significance to the different prototypical trajectories, we must be able to associate subjects with these trajectories. To relate an observed outcome x_i to a particular principal point ξ_j, we shall define a posterior probability π_ij as the probability that the ith observation is represented by the jth principal point, j = 1, …, k. Let the indicator variable d_ij equal 1 if x_i belongs to the stratum defined by the jth principal point function/curve and 0 otherwise. That is, d_ij = 1 if x_i(t) is closest to ξ_j(t) with respect to the L² metric, where t denotes time. Let β + b_i ∈ ℜ^q denote the q-dimensional regression coefficients (fixed effects plus random effects) for the ith subject. Define a “domain of attraction” D_j for the jth principal point as the subset of the sample space ℜ^q closest to the jth principal point. Then d_ij = 1 if ||(β + b_i) − ξ_j||² is less than the squared Euclidean distance between β + b_i and any other principal point coefficient vector ξ_h, h ≠ j, i.e. if (β + b_i) ∈ D_j. From well-known results on the multivariate normal distribution, the conditional distribution of (β + b_i) given x_i is

$$(\mathit{\beta }+{\mathit{b}}_i)\mid {\mathit{x}}_i\sim N(\mathit{\beta }+{({\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\sigma }^2{\mathit{D}}^{-1})}^{-1}{\mathit{S}}_i^{\prime }({\mathit{x}}_i-{\mathit{S}}_i\mathit{\beta }),{({\sigma }^{-2}{\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\mathit{D}}^{-1})}^{-1}).$$ (10)

Therefore the posterior probability π_ij that the ith observation is associated with the jth principal point can be defined as

$$\begin{array}{l}{\pi }_{ij}=E[d_{ij}\mid {\mathit{x}}_i]\\ =Pr[(\mathit{\beta }+{\mathit{b}}_i)\in D_j\mid {\mathit{x}}_i]\\ ={\int }_{D_j}N(\mathit{w};\mathit{\beta }+{({\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\sigma }^2{\mathit{D}}^{-1})}^{-1}{\mathit{S}}_i^{\prime }({\mathit{x}}_i-{\mathit{S}}_i\mathit{\beta }),{({\sigma }^{-2}{\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\mathit{D}}^{-1})}^{-1})d\mathit{w},\end{array}$$

where w is the integration variable. Typically the q-dimensional regions D_j will be complicated convex subsets of ℜ^q and analytical evaluations of this integral will not be possible. However, the posterior probabilities can be estimated via a Monte Carlo simulation. For each observed outcome x_i, simulate a large sample from the conditional distribution (10) with maximum likelihood estimates plugged in for the parameters in (10). Then the estimated posterior probability π̂_ij is computed as the proportion of the simulated sample that is closer to ξ̂_j than to ξ̂_h, h ≠ j.

Unlike typical k–means clustering settings, the proposed classification rule based on posterior probabilities acknowledges the fact that many observations may straddle classification boundaries with nearly equal probabilities to be represented by several different principal points. In addition, the posterior probabilities can be used to classify new observations. In this regard, the proposed classification rule for mixed effects models is analogous to the posterior probabilities for finite mixtures.

6 A Simulation Illustration

A small simulation experiment was run to illustrate how different estimators of principal point curves for mixed effects models perform. In this illustration, data sets were simulated from (5) using a quadratic model with a binary covariate with a fixed effect curve x = 20 − 8t + t² when the binary covariate is zero and x = 22 − 7.5t + t² when the binary covariate is one. The probabilities for the two levels of the binary covariate were set to π₁ = π₂ = 0.5. The standard deviation of the error was set to σ = 3.5 and the covariance matrix of the random effects for the intercept, slope and curvature was set to

$$\mathit{D}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 4& -0.25\\ 0& -0.25& 4\end{array}\right).$$

The simulated curves were sampled from seven equally spaced time points t = 0, 1, …, 6. The parametric k-means algorithm was used to determine k = 4 principal points for this model using a large sample of n_s = 2,000,000. One hundred data sets of sample size 50 were simulated.

The purpose of the simulation was to compare estimators of principal points, in particular, (i) the OPME approach of Section 4.2 and (ii) a “filtering” approach based on fitting individual curves to each of the 50 response vectors for each simulated data set using least-squares.

In the OPME approach (i), for each simulated data set, maximum likelihood estimates of the mixed effects model parameters were computed using the EM algorithm. Next, the parametric k-means algorithm was applied to (6) using n_s = 500, 000 to obtain k = 4 principal point profile estimates.

For the filtering approach (ii), least squares were used to obtain a vector of individual parabola coefficient estimates β̂₁, …, β̂₅₀ for each of the 50 response vectors in a given simulated data set. A straightforward approach to estimating k = 4 principal points is to simply plug these 50 estimated regression coefficient vectors into the k-means algorithm. However, this approach ignores the information on the binary covariate. A more efficient approach is to compute the sample mean ${\overline{\widehat{\mathit{\beta }}}}_j$ and covariance matrix S_j, for the two levels of the binary covariate (j = 1, 2) using the 50 estimated regression coefficient vectors and then applying the parametric k-means algorithm to the mixture distribution ${\widehat{\pi }}_{1}N({\overline{\widehat{\mathit{\beta }}}}_1,{\mathit{S}}_1)+{\widehat{\pi }}_{2}N({\overline{\widehat{\mathit{\beta }}}}_2,{\mathit{S}}_2)$.

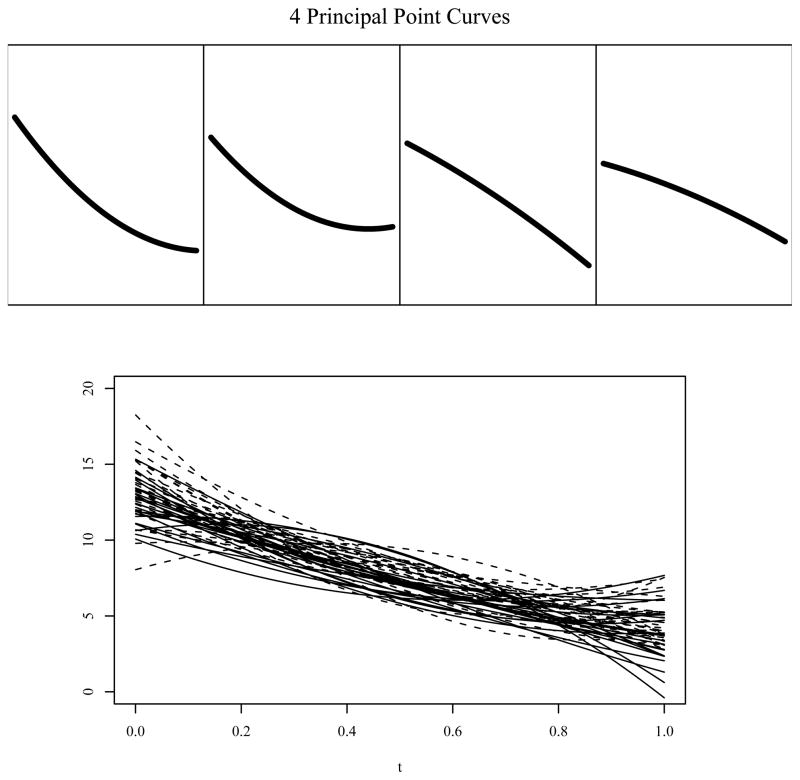
Figure 1 shows the 50 parabolas from a simulated data set in the bottom panel where the solid and dashed lines correspond to curves for the two different levels of the binary covariate. The four top panels show the true k = 4 principal point curves. The two leftmost curves in the top panel are concave down, one steeper than the other. The two rightmost curves are concave up again with one steeper than the other.

Figure 1.

Quadratic curves from a linear mixed effects model with a single binary covariate. The top panels show k = 4 principal point curves obtained using the parametric k-means algorithm for the true model. The bottom panel shows n = 50 parabolas from a simulated data set: the solid and dashed curves correspond to the two levels of the binary covariate.

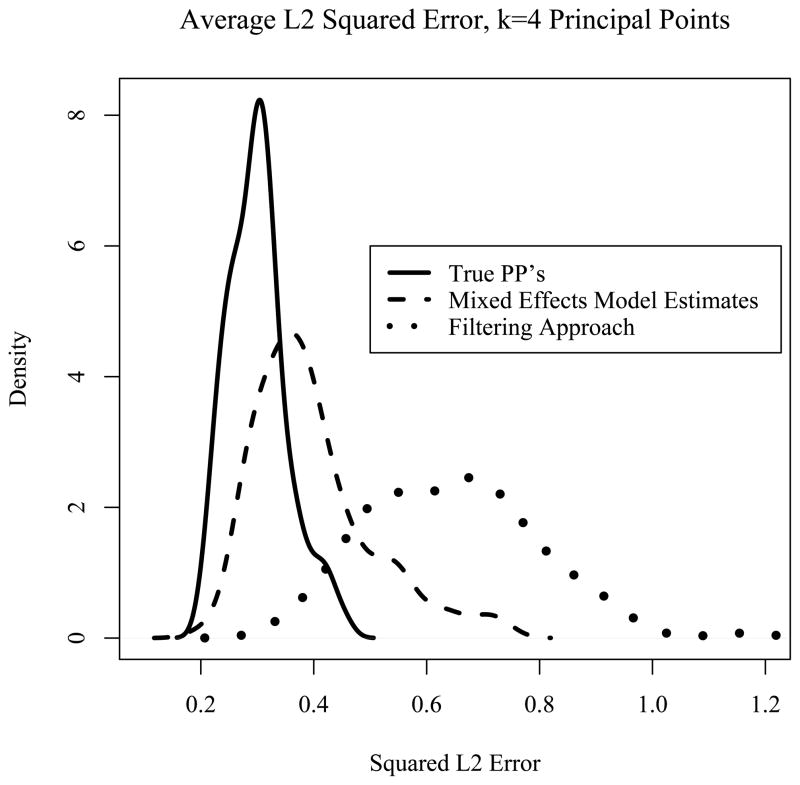
The two methods of estimating principal point curves (OPME and the filtering approach) were compared using a squared L² distance. For each parabola in a simulated data set, three squared L² distances were computed: the squared L² distance between the parabola and the nearest true principal point curve, the nearest maximum likelihood estimated principal point curve estimated via the linear mixed effects model, and the nearest principal point curve estimated via the filtering method. These squared distances were averaged over all n = 50 curves in the data set, resulting in measures of “goodness of fit” for these three methods. From the 100 simulated data sets, we obtained 100 squared L² averages distances using the three methods. Figure 2 shows nonparametric density estimates based on the 100 average squared L² distances for: the true principal points (solid curve), the maximum likelihood OPME approach (dashed curve), and the filtering approach (dotted curve). As expected, the average squared L² distances of the curves to the true principal points were lowest. Figure 2 shows that the method of estimating principal point profiles using the OPME approach performs much better than the filtering approach because the density of squared L² distances for the OPME approach (dashed curve) is shifted considerably further to the left compared the filtering approach (dotted curve). In fact, averaging over all 100 data sets, the squared L² error is 0.398 for the OPME approach compared to 0.647 for the filtering approach That is, the average L² distance of curves to the nearest principal point estimated curve is about twice as high using the filtering approach compared to the OPME approach. Another simulation was run using 100 data sets of larger sample size (n = 100 instead of n = 50), which produced very similar results.

Figure 2.

Nonparametric densities obtained from the 100 simulated data sets of the average squared L² distances to the nearest principal point curve estimate (k = 4) using: the true principal points (solid curve), the principal point curves estimated using the OPME approach (dashed curve), and principal point curves estimated using the filtering approach (dotted curve).

7 The Depression Treatment Study Revisited

A linear mixed effects model was fit to the longitudinal depression severity data (HAM-D) from the 12 week open phase described in Section 2. Time was modelled using a B-spline basis with five basis functions with a single knot for the cubic splines at the half-way time point, 6 weeks. Of all baseline covariates available in this study, the indicator for depression with melancholia features was the most significant in the linear mixed effects model using a likelihood ratio test. Subjects’ age was also significant but it had little influence on the fitted curves, after accounting for melancholia features. Thus the linear mixed effects model was fit using only melancholia as a binary covariate.

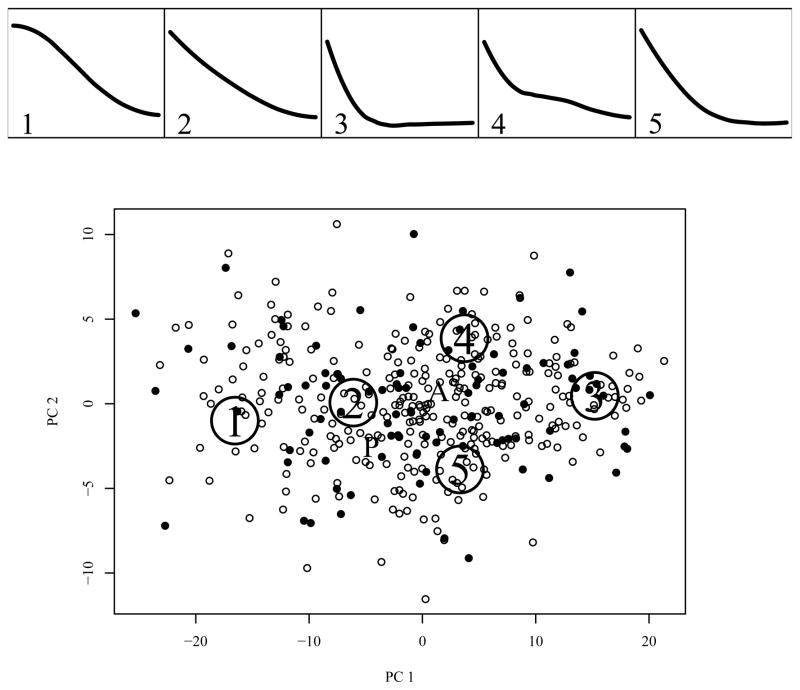
The parametric k-means algorithm used a simulation sample size of one million and the posterior probabilities were estimated for each observation using a simulated sample of size 10000. For this analysis, a value of k = 5 was chosen. From (9), k = 5 principal points is accounts for 74% of the total random effect variability, while an increase of k to 8 brings R² only up to 0.8. The top panels of Figure 3 show the k = 5 principal point profile curves estimated from the initial 12 week open phase of the study. Each curve is represented by five B-spline coefficients. The first two principal components for the five dimensional coefficient distribution explain 94.3% of the total variability of the random effects distribution. The bottom panel of Figure 3 shows the B-spline coefficients for the k = 5 estimated principal points, projected into the subspace of the first two principal components of the coefficients distribution. The small dots represent the Best Linear Unbiased Predictors (BLUPs) for individual subjects where the solid and open points correspond to subjects with and without melancholia respectively. The “A” and “P” in the bottom panel indicate the fixed effect means for the two levels (absence and presence) of the melancholia.

Figure 3.

Top panels: k = 5 principal point profile curves fit to depression severity during the open treatment phase of the study using a B-spline basis. Bottom panel: a scatterplot of the best linear unbiased predictors (solid = melancholia, open = no melancholia) in the principal component subspace spanned by the first two principal components of the coefficient distribution: The “A” and the “P” mark the estimated fixed effects for absence and presence respectively of the melancholia features.

For each subject, posterior probabilities (Section 5) were computed to indicate the principal point profile from the open phase that best represents the subject. The posterior probabilities for each subject add to one over the k = 5 principal points and, for the analysis that follows, a subject was classified to the principal point according to the largest posterior probability.

Recall that in the discontinuation phase of the study, remitters in the open phase were randomized to either stay on fluoxetine or to be switched to a placebo. The original goal of the discontinuation study was to establish whether responders to open treatment (12 weeks) for depression could be discontinued from the drug without increasing their risk for relapse as compared to the risk for relapse with continued drug. After responding to 12 weeks of open treatment for depression, a longer time to relapse on drug would indicate that subjects should be maintained on the drug. However, if the time to relapse on drug and placebo are the same, this would indicate that no maintenance treatment is needed. The followup problem is to identify subjects who would need the drug to stay in remission (specific responders to treatment) versus those that would relapse whether or not they are maintained on the drug (nonspecific responders).

Using the OPME results from the pre-randomization data, we now compare relapse on drug and placebo separately in each stratum. Kaplan-Meier estimates of time to relapse in the two treatment groups are computed and Log-rank tests are used to compare relapse on drug and placebo within each stratum.

Survival analysis results for subjects associated with the principal points 2 and 4 (see Figure 3) are shown in Figure 4. For reference, the left panels show the principal point profiles using the numbering shown in Figure 3. The p-values for the Log-rank tests comparing time to relapse for fluoxetine versus placebo in the discontinuation phase are p = 0.0574 with n₂ = 97 for principal point 2 and p = 0.210 with n₄ = 86 for principal point 4. Subjects associated to principal points 2 and 4 have similar relapse rates in the discontinuation phase whether they were randomized to a placebo or remained on fluoxetine. Based on the preceding discussion, we therefore label these subjects as “Predominantly non-specific responders.” We note that principal point profiles 2 and 4 show immediate improvement after treatment began in the open phase which is consistent with clinicians’ observations that while specific antidepressants take time to exert their effects, non-specific effects are usually immediate.

Figure 4. Predominantly Non-specific Responders.

Left panels show the principal point profile curves estimated from the open phase of the study. The right panels show the Kaplan-Meier survivorship curves for subjects associated to these two principal point trajectories broken down by treatment (drug versus placebo) in the discontinuation phase.

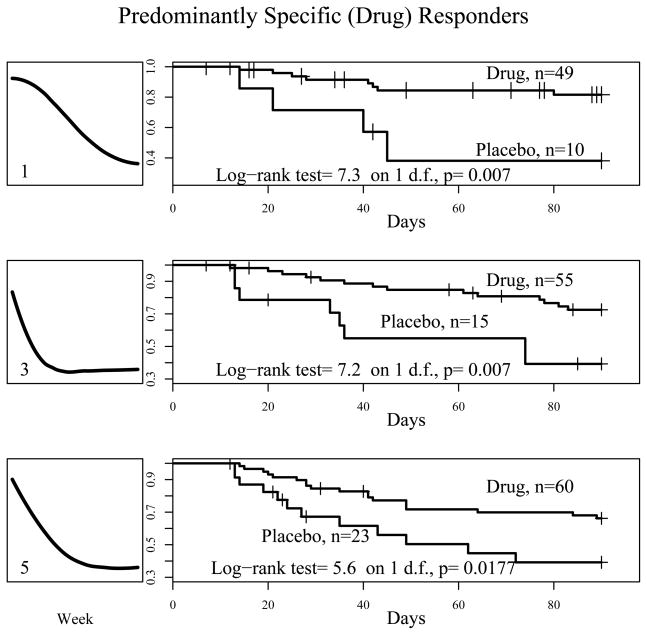
Figure 5 shows the the Kaplan-Meier survivorship curves comparing fluoxetine and placebo treatment during the discontinuation phase for subjects associated to principal point profiles 1, 3 and 5 from the open phase. Within these three strata, there were significant differences in time to relapse between drug and placebo. Since remaining on fluoxetine results in lower relapse rates compared to placebo, it can be inferred that subjects in these strata experienced a substantial benefit from the drug. Therefore, we have labelled them “predominantly specific responders”. The curve corresponding to principal point curve 1 exhibits little to no initial improvement followed by steady reduction in depression severity – this is considered a typical drug- response profile. Principal point profile 3 is similar in shape to the mixed responder of Tarpey et al. (2003), i.e. benefitting from both specific and non-specific aspects of treatment. Principal point profile 5 also shows an immediate strong and steady improvement through the 12 week open phase, but compared with profiles 1 and 3, the rate of relapse for subjects continuing drug treatment is higher; this might be indicative of only transient specific response.

Figure 5. Predominantly Specific Responders.

Left panels show the principal point profile curves estimated from the open phase of the study. The right panels show the Kaplan-Meier survivorship curves for subjects associated with these three principal point trajectories broken down by treatment (drug versus placebo) in the discontinuation phase.

8 Discussion

The problem of determining an optimal partition of a distribution is one of the classic statistical problems. This paper provides a solution to this problem in the setting of mixed effects models. The optimal partitioning results produce a set of prototypical curve profiles in longitudinal studies that can identify distinct types of outcomes. We have contrasted the optimum partitioning approach with the alternative growth mixture model approach. It is interesting to note that in the depression example of Section 7, if the melancholia covariate were not measured, then the underlying distribution would appear to be a two-component growth mixture model corresponding to the two levels of the melancholia covariate. The fitted GMM should approximately reproduce the mean curves corresponding to the absence and presence of melancholia, represented by the “A” and “P” points in the coefficient space in the bottom panel of Figure 3. The curves corresponding to the absence and presence of the melancholia have very similar shapes. Thus, a GMM in this case would fail to discover the full variety of outcome profile shapes in the distribution. However, the OPME approach described in this paper could be applied to the estimated 2-component GMM in order to estimate a wider variety of distinct outcome profiles.

It should be noted that the partitioning based on the principal point methodology is not expected to produce pure groups of specific and non-specific responders. The degree to which a subject experiences a specific and a non-specific effect could vary continuously in which case distinct classes of specific and non-specific responders will not exist. The principal point methodology is well-suited for this type of problem by identifying representative profiles from the continuum of response profile shapes.

Early work on optimal stratification (e.g., Dalenius, 1950; Dalenius and Gurney, 1951) was focused on improving precision of estimators and increasing statistical power. Future research plans are to investigate potential increases in estimation precision and power in survival analysis by applying the optimal stratification methods based on principal points using a stratified Cox model.

The OPME methodology described in this paper can be extended to nonlinear mixed effects models as well as generalized linear mixed effects models. For example, in a mixed effects logistic growth model, the response for the ith “subject” at the jth time point can be written

$$y_{ij}=\frac{{\beta }_1+b_{1i}}{1+e^{-(t_{ij}-{\beta }_2-b_{2i})/({\beta }_3+b_{3i})}}+{\epsilon }_{ij},$$

where β′ = (β₁, β₂, β₃) is a coefficient vector of fixed effects and ${\mathit{b}}_i^{\prime }=(b_{1i},b_{2i},b_{3i})$ is a random effect vector assumed to be normal with mean zero. Once maximum likelihood estimates of β and the covariance matrix D of b_i are obtained, the parametric k-means algorithm can be applied to N(β̂, D̂) to obtain a set of k prototypical logistic growth profiles. However, a complication that arises in the context of nonlinear and generalized linear mixed effects models is that an optimal partition obtained in the coefficient space via the parametric k-means algorithm does not necessarily correspond to an optimal partition in function space. A solution to this problem is to run the parametric k-means algorithm directly in function space, e.g., to cluster the logistic growth functions directly using an L² metric instead of the coefficients using a Euclidean metric.