How Do Plants Achieve Tolerance to Phosphorus Deficiency? Small Causes with Big Effects

Abstract

Genotypic differences in phosphorus (P) uptake from P-deficient soils may be due to higher root growth or higher external root efficiency (micrograms of P taken up per square centimeter of root surface area). Both factors are highly interrelated because any additional P provided by externally efficient roots will also stimulate root growth. It will be necessary to separate both factors to identify a primary mechanism to formulate hypotheses on pathways and genes causing genotypic differences in P uptake. For this purpose, a plant growth model was developed for rice (Oryza sativa) grown under highly P-deficient conditions. Model simulations showed that small changes in root growth-related parameters had big effects on P uptake. Increasing root fineness or the internal efficiency for root dry matter production (dry matter accumulated per unit P distributed to roots) by 22% was sufficient to increase P uptake by a factor of three. That same effect could be achieved by a 33% increase in external root efficiency. However, the direct effect of increasing external root efficiency accounted for little over 10% of the 3-fold increase in P uptake. The remaining 90% was due to enhanced root growth as a result of higher P uptake per unit root size. These results demonstrate that large genotypic differences in P uptake from a P-deficient soil can be caused by rather small changes in tolerance mechanisms. Such changes will be particularly difficult to detect for external efficiency because they are likely overshadowed by secondary root growth effects.

P deficiency is a major abiotic stress that limits plant growth and crop productivity throughout the world (Sanchez and Salinas, 1981). It is associated with highly weathered soils, a high capacity to fix P in forms that are generally not available to plants, and low fertilizer use particularly in areas commonly inhabited by resource-poor farmers. Some efforts have been directed at improving the tolerance to P deficiency in rice (Oryza sativa) cultivars, because it was shown that considerable genotypic variation for the ability to take up P from a highly P-fixing soil exists in GenBank accessions (Wissuwa and Ae, 2001a). However, progress in breeding has been slow. The availability of rice genome sequence data could lead to further advances because they will facilitate identifying genes for tolerance to P deficiency, which may then be manipulated to attain levels of tolerance that are presently not achievable. In that regard, it will be crucial to gain a better understanding of the physiological processes involved.

Diffusion rates of P in the soil solution are generally very low because soil particles easily bind P. If P does not move freely into the rhizosphere, plants may increase P uptake by expanding their root system, thereby exploring a greater soil volume. The size of the root system is consequently considered to be an important characteristic of plants that tolerate P deficiency (Ermani et al., 1994; Wissuwa and Ae, 2001a). However, severe P deficiency limits total plant growth including root growth. To maintain relatively high root growth rates despite P deficiency would therefore be of higher importance than a general ability to produce a large root system. Alternatively, tolerance could be achieved by an increase in external P uptake efficiency, defined as plant P uptake per unit root size (root surface area [RSA]). Plants may play an active role in acquiring hardly soluble P by excreting organic compounds capable of releasing soil-bound P. Kirk et al. (1999) estimated that P solubilization due to organic anion excretion was responsible for the bulk of P uptake by rice from a P-deficient soil. Root hairs have also been shown to improve P acquisition in a wider variety of plant species, and their effect is thought to be due to an increase in the soil volume explored by the root (Föhse et al., 1991).

Any genotype with higher external P uptake efficiency is also likely to show higher relative root growth because the additional P taken up will allow further biomass accumulation including root growth. Both factors, root growth and external P uptake efficiency, are therefore highly interrelated, and the complexity of this relation complicates the identification of a primary factor that may have initially caused genotypic differences in P uptake. It will therefore be necessary to separate root growth from external efficiency effects to formulate hypotheses on pathways and genes that are most likely involved. Without such a hypothesis, the risk of pursuing an exceeding number of potential target genes is likely to limit any progress in finding genes that would be useful in improving tolerance to P deficiency.

Previous genetic studies on tolerance to P deficiency in rice have identified a major quantitative trait locus (QTL) for P uptake, Pup1, which has subsequently been mapped to a small marker interval on the long arm of chromosome 12 (Wissuwa et al., 2002). The secondary mapping population used in that study had been developed by backcrossing a near isogenic line (NIL-C443) containing the QTL from the donor parent to the recurrent parent, rice cv Nipponbare. NIL-C443 exceeded rice cv Nipponbare in P uptake from a highly P-deficient soil by a factor of three (Wissuwa and Ae, 2001b). The low P uptake of rice cv Nipponbare was accompanied by a severe reduction in root growth, whereas NIL-C443 maintained relatively higher root growth rates but only as it started to diverge from rice cv Nipponbare in P uptake. It was thus not possible to determine whether differences in root growth preceded and caused differences in P uptake or vice versa.

To completely separate root growth from external P uptake efficiency effects will be difficult in experiments that closely resemble natural growth conditions. A mathematical plant growth model based on empirical data measured under such conditions, however, may offer an alternative way to assess the contribution of several factors to P deficiency tolerance without confounding primary causes with secondary effects. The objective of this study was the development of such a plant growth model for highly P-deficient soil conditions using data from a set of experiments conducted with rice cv Nipponbare. A first set of model simulations examined the potential importance of several growth and efficiency parameters on tolerance to P deficiency. Subsequently, the question was addressed as to how much parameters would have to change to explain the observed increase in growth and P uptake of NIL-C443 in an attempt to identify potential target mechanisms that could be attributed to Pup1.

MODEL DESCRIPTION AND SPECIFICATION

The model P-LIM-GROW (P limited growth) describes growth and P uptake of the rice cv Nipponbare on a severely P-deficient soil that is not known to have any other growth-limiting properties. Rice cv Nipponbare possesses low tolerance to P deficiency and may show a reduction in growth of up to 90% relative to a control supplied with P (Wissuwa and Ae, 2001b). The model was developed using the software Stella (v7.0.2, High Performance Systems, Hanover, NH). Figure 1 illustrates the principal components of P-LIM-GROW, and Table I gives a summary of variables and parameters used in the model. All model processes run on daily time steps. Two basic assumptions were made in developing the model: (a) The severity of P deficiency causes growth processes to depend on the amount of P available to the plant; and (b) because P is the growth-limiting factor, plants will rapidly use P influxes for biomass accumulation. It is therefore assumed that P taken up by the plant is distributed to roots and shoots and converted to dry matter with a time lag of only 1 d.

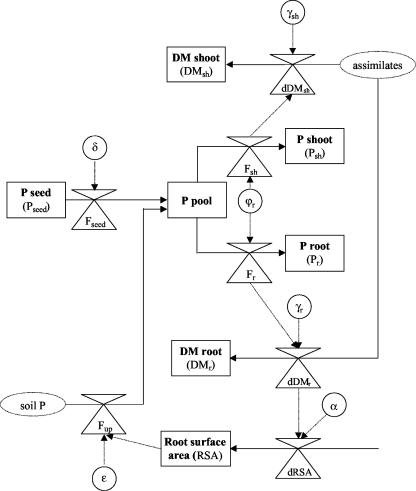
Figure 1.

P-LIM-GROW, a model to simulate plant growth under highly P-deficient growth conditions. Boxes represent state variables, and valve-like symbols represent rate variables. The flow of substances (P and dry matter) is indicated by solid lines. The rate of a flow is influenced by model parameters or constants (circles), and that influence is represented by broken lines. “Sources” that are not quantified and that are not used in model calculations are shown as broken ovals. The modeling process at t = 0 starts with germination and seed P translocation as the initial influx of P into the seedling. The process of P redistribution within the plant and more complex P uptake scenarios of the two- and three-step sub-models are not shown for the sake of simplicity.

Table I.

State variables, rate variables, and other parameters or constants used by the model

	Nomenclature	Value or Function	Unit
Ppool	P available for plant growth		μg
Pseed	Seed P	43	μg
P(r,sh)	P in roots, shoots		μg
DM(r,sh)	Dry matter (root, shoot)		mg
RSA(n,a,m)	Root surface area (new, active, mature)		cm2
Fup	Flux of P due to uptake by roots		μg d−1
Fseed	Flux of P due to translocation from seeds		μg d−1
F(r,sh)	Flux of P due to distribution to roots, shoots		μg d−1
Pred(r,sh)	P redistributed within roots, shoots		μg
δ	Seed P fraction mobilized	0.0954 + 0.00095 × t2.5	d−1
ϕr	P partitioning factor	(0.2112 − 0.1216 × t0.5 + 0.0369 × t − 0.00559 × t1.5 + 0.00032 × t2) / (1 − 0.69427 × t0.5 + 0.206 × t − 0.0286 × t1.5 + 0.00152 × t2)	d−1
γr	Internal P efficiency (root)	0.255 + 0.0367 × t − 0.000555 × t2 + 0.000003 × t3	mg DMr μg−1 P
γsh	Internal P efficiency (shoot)	(0.0774 + 0.01285 × t2) / (1 + 0.00781 × t2)	mg DMsh μg−1 P
α	Specific root surface area	1.05	cm2 mg−1
εn	External P uptake efficiency of new roots	0.49a	μg P cm−2 d−1
εa	External P uptake efficiency of active roots	0.14a	μg P cm−2 d−1
εm	External P uptake efficiency of mature roots	0.025a	μg P cm−2 d−1

^aValues shown are for three-step base model.

The flow of P in this model is given by two influx components: (a) F_seed, the P translocated from the seed during germination, and (b) F_up, the P uptake by roots. Both influxes supply free P to a pool of P that is available for growth (P_pool). As assumed under (b), P effluxes from that pool to roots (F_r) and shoots (F_sh) will be equal to influxes of the previous day. The distribution of P to roots and shoots depends on a time-dependent partitioning factor ϕ_r. Fluxes into and out of the pool can be described by the following equations:

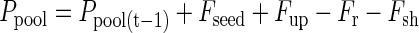1

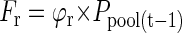2

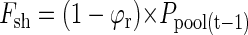3

The modeling process starts with germination and translocation of the P stored in the seed (P_seed) as the initial flux (at time = 0) into the pool. Over time, an increasing fraction (δ) of P_seed is transferred to the seedling until seed P reserves are exhausted on d 15:

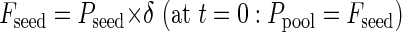4

At time t = 1, the seed P translocated on the previous day P_pool(t-1) is distributed to shoots and roots. The P flux to roots and shoots is then converted to root or shoot dry matter by multiplication with internal P efficiency coefficients for dry matter accumulation γ_r or γ_sh (milligrams of dry matter per microgram of P):

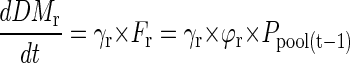5

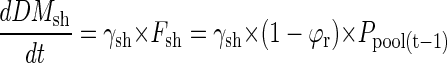6

Internal P efficiency increases over time as tissue matures under P deficiency, and in consequence, some P (P_red) will be redistributed within roots and shoots. This will be a gradual process, and here, it is assumed that only a fraction (25%) of the theoretical amount is redistributed per day. P_red is then used to form additional dry matter (by adding P_red(r,sh) to F_r, F_sh). The process of P redistribution is exemplified for roots by the following equation (the same principle applies for shoots):

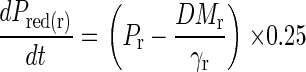7

The influx due to P uptake by roots (F_up) is considered to be more closely related to the RSA in contact with the soil solution than to root biomass. Newly formed root biomass (dDM_r/dt) is therefore converted into RSA by multiplication with the specific RSA, α (square centimeters per milligram):

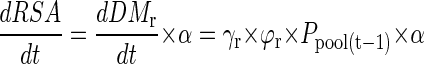8

In its simplest form, hereafter referred to as the one-step sub-model (illustrated in Fig. 1), the model assumes that the entire RSA contributes to P uptake (F_up) with a constant external P uptake efficiency of roots, ε, (micrograms of P per square centimeter per day) from the day of formation until the end of the model cycle:

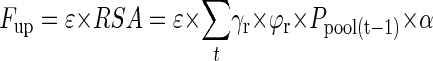9

This obviously is an oversimplification because it ignores that older roots may cease to take up P due to maturation of the rhizodermis, that newly formed roots may grow into unexplored soil with a higher P concentration in the soil solution, and that P uptake by roots will cause P depletion in the rhizosphere.

Two additional sub-models that account for the complexity of P uptake processes were therefore developed. Both sub-models calculate F_seed as described above but differ in the way the second influx component (F_up) is computed. A two-step model assumes that newly formed RSA (RSA_n = dRSA/dt) is developed in previously unexplored soil. There, all readily available P in the rhizosphere is taken up with the external efficiency ε_n that is equal to the amount of readily available P in the soil volume in contact with RSA_n. After 1 d, the readily available P is depleted, and roots enter a pool of “mature” roots (RSA_m) that continue P uptake with a constant but lower external efficiency (ε_m) until the end of the model cycle. P uptake per day in this two-step sub-model is the sum of uptake by new and mature roots:

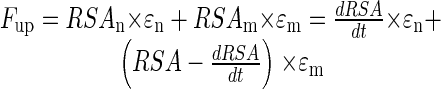10

Additional effects are taken into consideration in the more complex three-step sub-model. The first step is equivalent to uptake of readily available P by new roots as described for the two-step sub-model. After 1 d, RSA_n(t-1) is shifted to a pool of “active” RSA (RSA_a) that contributes to P uptake with the external efficiency ε_a. Processes that may affect ε_a would be related to rhizosphere changes in pH and excretion of P-solubilizing agents like organic acids or phosphatases. After 14 d in the pool of active RSA, roots enter a pool of mature roots (RSA_m). As in the two-step sub-model, that pool contributes to P uptake with the much lower efficiency ε_m until the model cycle ends at d 98. The limited life span of root hairs, a decreasing permeability for nutrients of the rhizodermis, and an increasing depletion of P in the rhizosphere would be factors responsible for lower ε_m. Daily uptake of P by roots in the three-step model therefore is envisioned to occur in three phases:

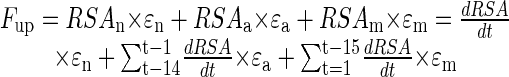11

The model was solved numerically by Stella. A copy of the model can be obtained from the author upon request.

RESULTS

Input Parameters

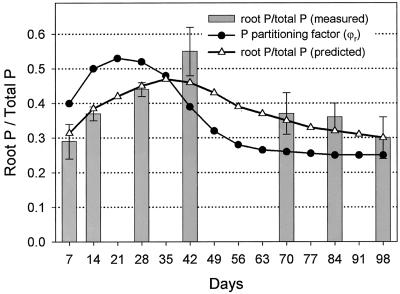
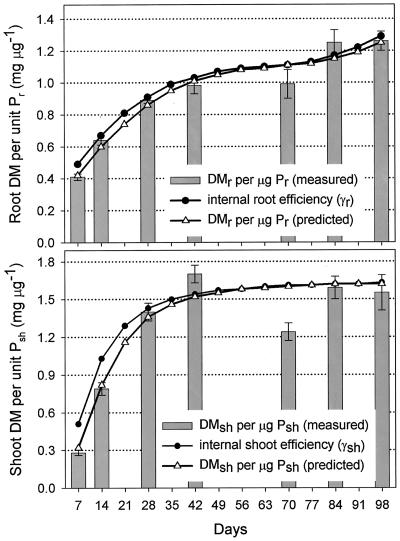
Rice cv Nipponbare seeds contained on average 43 μg of P that was translocated to the seedling within 15 d. An estimate for δ, the fraction of seed P mobilized, is given in Table I together with measured values or derived equations of other input parameters. Empirical data for the portion of total P found in roots are shown in Figure 2. These values represent the average over the period of growth until sampling at time t. On the basis of these data, an equation was derived for the P partitioning factor (ϕ_r, Table I) that describes P partitioning per day. Using this equation in model calculations gave estimates of the portion of total P found in roots that closely matched measured values. At each sampling date, total root or shoot dry matter was divided by total root or shoot P to obtain estimates of the average internal efficiency over growth periods. Derived equations for internal efficiencies at a given day (γ_r, γ_sh) are given in Table I and calculated input values for γ_r and γ_sh are shown in Figure 3 together with the average internal efficiency predicted by the model. The α, used to convert root dry matter (DM_r) to RSA, was obtained by dividing RSA by DM_r. Newly formed roots had an α of 1.05 cm² mg^-1 DM_r, and this value was used throughout the modeling process.

Figure 2.

Fraction of total P in roots at a given time (bars represent values measured for rice cv Nipponbare; triangles are model predictions) and P partitioning factor (model input parameter, ϕ_r). The difference between ϕ_r and root P/total P is due to the factor time: ϕ_r determines how much of the P taken up is partitioned to roots at time t, whereas values for root P/total P are the result of partitioning over the whole growth period.

Figure 3.

Internal P efficiency for root dry matter production or shoot dry matter production. Bars represent measured values, triangles are model predictions, and solid circles represent model inputs for γ_r and γ_sh, respectively. Input parameters γ_r and γ_sh represent instantaneous values, whereas measured and predicted values for DM_r/P and DM_sh/P are the result of changes in γ_r and γ_sh from d 1 until sampling.

The three-step model required three inputs for external P uptake efficiency (ε). The value for newly formed roots that grow into unexplored soil (ε_n) is based on the soil volume explored by the root and the amount of available P in that soil volume. The content of plant-available P in the andosol used here was 1.04 μg P cm^-3 as determined by a resin extraction method (Hedley et al., 1994). In samples of young plants, a RSA of 1 cm² was equal to 11.42 cm root length with a radius of 0.014 cm. Rice cv Nipponbare produced root hairs in high density with an average length of 0.1 cm, which increased the radius for the root cylinder with hairs to 0.114 cm. A young rice cv Nipponbare root with a surface area of 1 cm² would therefore explore 0.47 cm³ soil (11.42 ^* π ^* 0.114²) containing 0.49 μg of P. This value was used for the input parameter ε_n in calculations for the two- and three-step models.

A suitable experimental procedure was not available to estimate the external P uptake efficiency of active (ε_a) and mature roots (ε_m). Instead, a series of permutations were used to determine the one combination that best fit observed data and that exactly matched total P uptake of rice cv Nipponbare at the final sampling time on d 98. The range of values used in permutations was from 0.117 to 0.163 μg P cm^-2 for ε_a and 0.001 to 0.05 μg P cm^-2 for ε_m. The combination that produced the best fit of model outputs with empirical data for P uptake and biomass was 0.14 μg P cm^-2 for ε_a and 0.025 μg P cm^-2 for ε_m. The model based on this combination is referred to as the three-step base model. The value for external ε_m in the two-step model was obtained by feeding estimates into the model until one (0.06 μg P cm^-2) resulted in a final P uptake that matched the observed value for rice cv Nipponbare. In a similar fashion, the best fit for ε of the one-step model was found to be 0.112 μg P cm^-2.

Comparison of Empirical and Predicted Growth Patterns

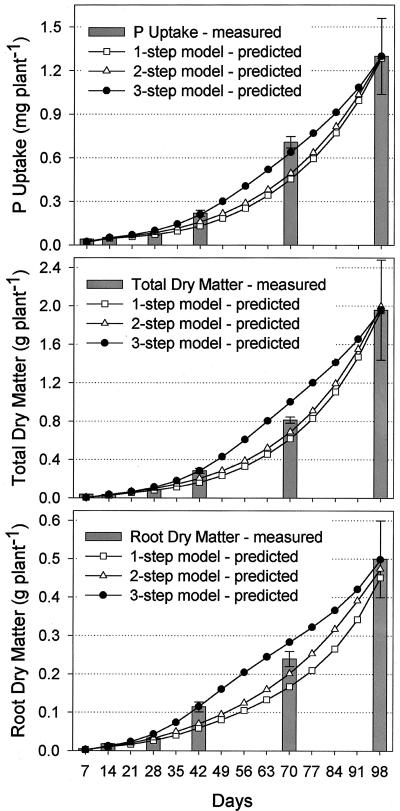
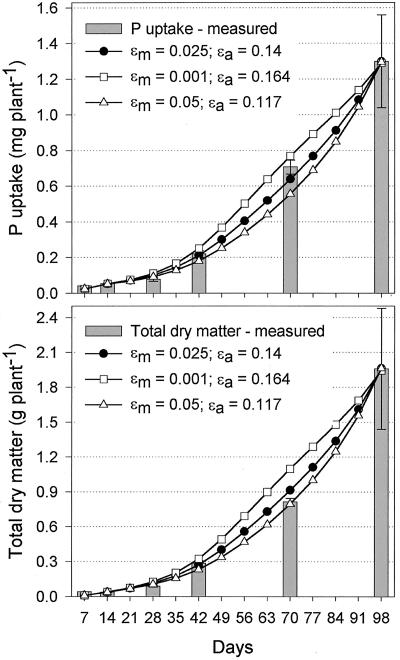
All plant growth parameters used as input variables for the model were based directly on empirical data and their derived functions. The process of P uptake itself, however, was difficult to measure experimentally, at least over a 98-d growth period as used in this study. To take account of the relative uncertainty regarding uptake processes, three alternative sub-models were developed. Outputs from model calculations shall now be compared with empirical rice cv Nipponbare data for P uptake, total dry matter (TDM) and root dry matter (DM_r) to determine which sub-model best fitted observed data (Fig. 4). All sub-models converged on d 98 with a P uptake of 1,290 to 1,300 μg of P because external efficiency parameters were fitted to coincide with the final P uptake of rice cv Nipponbare of 1,298.3 μg of P. Sub-models differed, however, in how closely they matched the development in P uptake over time. The three-step model showed closest agreement with empirical data, whereas the other sub-models notably underestimated P uptake on days 42 and 70. Similar results were obtained for DM_r and TDM. Growth curves predicted by the one- and two-step models followed an exponential pattern that misrepresented empirical data for DM_r and P uptake. The three-step sub-model shall therefore be used in further simulations.

Figure 4.

Comparison of observed and predicted P uptake, total dry matter (TDM), and root dry matter (DM_r) for three sub-models that differ in complexity of the P uptake process. The one-step model assumes roots take up P at a constant rate regardless of root age, whereas the two-step model assumes that newly formed roots have higher P uptake because they grow into soil not yet depleted of its available P. The three-step model adds a third uptake element. After new roots have depleted readily available P and before they have reached full maturation characterized by very low uptake, roots are considered to actively influence rhizosphere processes, providing additional P for uptake.

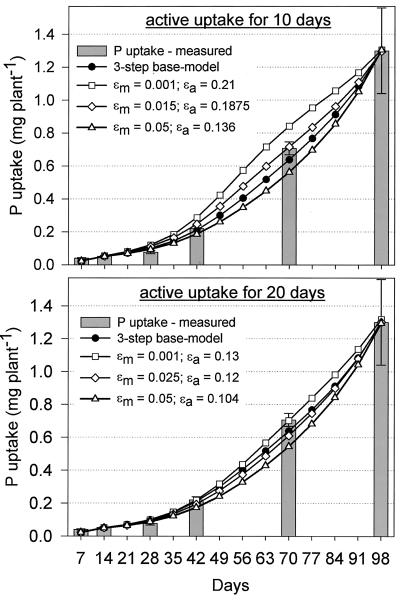
Output data presented in Figure 4 were based on values of 0.14 μg P cm^-2 for ε_a and 0.025 μg P cm^-2 for ε_m. How alternative combinations affected model predictions is shown in Figure 5. Doubling ε_m to 0.05 μg P cm^-2 led to an underestimation of P uptake at d 70 similar to the two-step model, whereas reducing ε_m to 0.001 μg P cm^-2 slightly overestimated P uptake and significantly overestimated TDM. A factor that will influence external efficiency values is how long roots remain active. An additional simulation was run using durations of 10 or 20 d instead of the 14 d used in the three-step model discussed so far. The simulation varied ε_m from 0.001 to 0.05 μg P cm^-2 and adjusted ε_a to give a final P uptake of 1,300 μg of P. A good fit of model and empirical data was obtained with ε_m values between 0.015 and 0.03 μg P cm^-2 for an active duration of 10 d and between 0.001 and 0.025 μg P cm^-2 for 20 d (Fig. 6). An ε_m of 0.05 μg P cm^-2 underestimated P uptake by the same magnitude in all simulations and should be considered too high.

Figure 5.

Effect of changing values of model inputs for the external efficiency of active (ε_a) and mature (ε_m) roots on P uptake and total dry matter. Bars represent measured values and black circles are simulation outputs of the three-step base model (ε_a = 0.14 and ε_m = 0.025 μg P cm^-2). Squares represent model predictions under the assumption that the contribution of mature roots to P uptake is small (ε_m = 0.001 μg P cm^-2), triangles show predictions if mature roots contribute much (ε_m = 0.05 μg P cm^-2).

Figure 6.

Simulations of P uptake using alternative combinations for external efficiencies of active (ε_a) and mature (ε_m) roots. The duration roots remain active was varied from 10 to 20 d. Squares represent model predictions under the assumption that the contribution of mature roots to P uptake is small (ε_m = 0.001 μg P cm^-2), and triangles show predictions if mature roots contribute much (ε_m = 0.05 μg P cm^-2).

Sensitivity Analysis

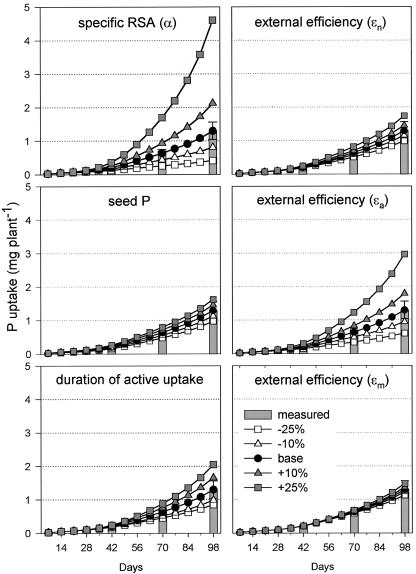
Parameter sensitivity analysis was conducted by increasing or decreasing input parameters by 10% or 25% and by evaluating the effect of that change on final P uptake. Increasing seed P reserves by 10% affected P uptake by the same percentage and this almost linear relation remained over a wide range of seed P increases (Fig. 7). The rate of seed P translocation (δ) had no effect on final P uptake (data not shown). Very influential parameters were those directly related to root growth. Increasing the portion of P partitioned to roots (ϕ_r), the internal efficiency for DM_r production (γ_r), or the α by 10% led to 62% to 64% higher P uptake (only data for α are shown in Fig. 7 because ϕ_r and γ_r gave almost identical results). A 25% increase even raised P uptake from about 1,300 to 4,500 μg of P. Changes in the external efficiency on the other hand had markedly different effects depending on which root fraction was analyzed. P uptake was not sensitive to variation in the efficiency of mature roots (ε_m) and only slightly sensitive to changes in new roots (ε_n), whereas the efficiency of active roots (ε_a) was very influential. Prolonging the period roots remain active had an intermediate effect.

Figure 7.

Parameter sensitivity analysis for the three-step sub-model. The effect of increasing or decreasing input parameters by 10% or 25% on P uptake is shown over a 98-d period.

The structural sensitivity analysis examined how changes in assumptions on the P uptake process would affect parameter sensitivities. The contrasting set of extreme border values for ε_m and ε_a described earlier was used to examine whether parameter sensitivities were affected by model assumptions. The parameters α, ϕ_r, and γ_r again behaved very similarly and were most influential, regardless of which combination of ε_m and ε_a was used (Table II). Because of this similarity, values are only shown for α as representative of root growth-related parameters. Among external efficiencies, ε_a remained the dominant parameter. Its influence increased when less importance was placed on P uptake by mature roots (ε_m = 0.001 μg P cm^-2) and decreased when ε_m was raised to 0.05 μg P cm^-2. However, even in that extreme situation, P uptake was five times more sensitive to changes in ε_a compared with changes in ε_m. The sensitivity to ε_n remained largely unaffected by structural changes.

Table II.

Results of structural sensitivity analysis using extreme border values for ε_a and ε_m

Within alternative ε_a and ε_o combinations, the active period was altered from 14 d to 10 or 20 d, respectively. Values in brackets show changes in P uptake (%) for the three-step base model.

Parameter		Parameter Increase	P Uptake
			Final	Change
		%	μg	%
εa = 0.163; εm = 0.001	α	10	2,316.3	78.4 (64.0)
	εa	10	2,005.1	54.5 (38.1)
	εn	10	1,475.5	13.6 (12.2)
	εm	10	1,301.5	0.2 (5.4)
Active duration 10 d	εa	10	2,124.7	63.6 (38.1)
Active duration 20 d	εe	10	1,921.9	48.0 (38.1)
εa = 0.117; εm = 0.05	α	10	1,988.6	53.2 (64.0)
	εa	10	1,642.7	26.5 (38.1)
	εn	10	1,435.5	10.6 (12.2)
	εm	10	1,368.5	5.4 (5.4)
Active duration 10 d	εa	10	1,628.3	25.4 (38.1)
Active duration 20 d	εa	10	1,666.6	28.4 (38.1)
One-step model	ε	10	1,764.6	35.9
	α	10	1,764.6	35.9
Rice cv Nipponbare		-	1,298.3	-

The effect of altering the duration of active uptake on the sensitivity to ε_a was examined within extreme combinations of ε_m and ε_a (Table II). Increasing the duration to 20 d had opposite effects because the sensitivity to ε_a decreased at an ε_m of 0.001 μg P cm^-2 but increased when ε_m = 0.05. These changes were, however, relatively small. An additional sensitivity analysis was conducted on the one-step model. P uptake was equally sensitive to changes in external efficiency and in root growth parameters (represented by α). The sensitivity to root growth was reduced compared with the three-step model, whereas sensitivity to external efficiency remained at a relatively similar level.

Comparison of Rice cv Nipponbare to NIL-C443

A final set of simulations was run to determine to what extent parameters would have to change to explain the genotypic difference in P uptake between rice cv Nipponbare (1,298.3 μg of P) and NIL-C443 (3,998.2 μg of P). Results indicated that a 22% increase in root growth-related parameters (ϕ_r, γ_r, and α) would suffice to account for a 3-fold higher final P uptake (Table III). Seed P reserves would have to increase 3-fold to explain that difference, whereas the duration roots remain active would have to double from 14 to 28 d. Changes required in external root efficiencies varied greatly with root fractions from 280% for mature roots (ε_m) to only 33.5% in active roots (ε_a). Altering the duration roots remain active to 10 or 20 d at a constant value for ε_m of 0.025 μg P cm^-2 gave equally low estimates for ε_a, whereas changes in ε_m caused ε_a to vary from 25% to 45% with little effect on α.

Table III.

Change required in input parameter to account for a 3-fold higher P uptake of NIL-C443 compared with rice cv Nipponbare

Parameter		Value	Change	P Uptake	Direct Effecta		Secondary Root Effectb
			%	μg P	μg P	%	μg P	%
Seed P	Pseed	129	200	3,894.6	86	6.6	2,447.3	188.5
SRSA	α	1.28	22	3,983.8	2,685.5	206.8
Internal efficiency (root)	γr		22	3,914.1	2,615.8	201.5
P partitioning factor	θr		22	3,911.6	2,613.3	201.3
Root activity (duration)		28	100	3,993.0	454.0	35.3	1,764.2	137.3
External P uptake efficiency	εn	0.93	86	3,987.7	201.0	15.4	2,035.3	156.8
(εa = 0.14; εm = 0.025)	εa	0.187	33.5	3,961.9	244.4	19.0	1,875.4	145.9
	εm	0.095	280	3,949.0	658.2	50.7	1,524.6	117.4
εa for 10d (εa = 0.172; εm = 0.025)	εa	0.228	32.6	3,939.9	225.6	17.3	2,003.7	154.3
εa for 20d (εa = 0.1167; εm = 0.025)	εa	0.157	34.8	3,957.3	290.5	22.3	1,758.2	135.4
εa = 0.163; εm = 0.001	εa	0.204	25	3,955.4	212.8	16.4	1,935.2	149.1
	α	1.25	19	3,988.4	2,690.1	207.2
εa = 0.117; εm = 0.05	εa	0.169	45	3,986.3	226.8	17.5	1,837.8	141.6
	α	1.31	25	3,919.7	2,621.4	201.9
One-step model	α		37	3,972.0	395.5	30.8	1,480.5	115.2
NIL-C443				3,998.2
Rice cv Nipponbare			—	1,298.3	—		—	—

^a Direct effects were estimated by using root growth estimates of the rice cv Nipponbare base model as direct inputs in simulation runs with altered input parameters. ^b Secondary root growth effects were estimated by using root growth estimates of simulation runs with altered parameters as direct inputs in further simulation runs while reversing the change in the parameter under investigation.

One purpose of employing a modeling approach was to separate direct effects of parameter changes on P uptake from subsequent root growth effects. This separation was achieved by uncoupling dRSA/dt from dDM_r/dt (see Fig. 1). The direct effect of a parameter change was then estimated by maintaining root growth rates of the base model (using dRSA/dt values of the base model as direct inputs). The secondary root growth effect was estimated using dRSA/dt values of a simulation run with altered parameters as direct inputs while changing the parameter under investigation back to its original value. Although a 33.5% increase in ε_a was sufficient to explain 3-fold higher P uptake, only 19% of that increase was due to the direct effect of ε_a (Table III). Secondary root growth effects contributed almost eight times more to final P uptake compared with the primary effect (change in ε_a). Alternative model assumptions had little effect on this relation, because the direct effect of increasing ε_a was very small compared with the secondary root growth effect in all simulations.

DISCUSSION

Model Structure

Mathematical models on P uptake are generally developed and tested on soils with adequate P status and simulate uptake and growth for relatively short periods usually not exceeding 50 d. P uptake is assumed to be a function of P concentrations in the soil solution, of diffusion rates in soil, and of soil buffering capacity (Nye et al., 1975; Itoh and Barber, 1983; Föhse et al., 1991; Teo et al., 1992). Plant or root growth is either used as a fixed input independent of P uptake (Itoh and Barber, 1983) or simulated as a function of photosynthesis that may depend on P concentrations in the shoot (Nye et al., 1975). These models closely predict observed P uptake in a variety of soils with medium to high P content but tend to underestimate uptake from P-deficient soils by as much as 65% (Ermani et al., 1994) or even 90% (Brewster et al., 1976). Several factors may be responsible for this discrepancy. Plant roots may be more than passive sinks for P as assumed in these models and Kirk et al. (1999) showed that the exudation of solubilizing agents could greatly increase P availability. A second important factor may be related to the ability of plants to react to nutrient deficiencies by increasing the internal efficiency for the limiting nutrient. Using growth functions as fixed model inputs that do not account for these effects would therefore underestimate plant growth and ultimately P uptake.

The model developed here uses a radically different approach from models discussed above. It is specifically designed to simulate growth under conditions where P is the growth-limiting factor. Consequently, no single predetermined function is used to describe plant or root growth. Instead, growth itself is simulated using empirical data for P partitioning and internal efficiencies that have been measured over the entire vegetative growth period. Using these parameters therefore takes account of adaptive changes that plants undergo in response to P deficiency.

One assumption made in developing the model is that the amount of P taken up would drive all growth processes. This assumption would not be justified if declining growth rates under P deficiency were caused by insufficient assimilate supply to growing plant parts. Furbank et al. (1987) suggested that P deficiency would reduce photosynthetic efficiency but Plénet et al. (2000) found no evidence of reduced radiation use efficiency in P-deficient maize (Zea mays). Instead, it has been reported that lower total light interception by the smaller canopy of a P-deficient plant may reduce root growth because of insufficient assimilate supply (Pellerin et al., 2000). Studies with rice cv Nipponbare, however, showed that carbohydrate concentrations increased in P-deficient roots (M. Wissuwa, unpublished data), suggesting that a decline in growth was not caused by lack of assimilates. Insufficient P supply thus appeared to have a more direct effect on growth that preceded effects of decreasing photosynthetic efficiency. Parameters related to photosynthesis and assimilate flows were therefore not included in the present model.

The only soil parameter used in this model was an estimate for available P. The principal reason for omitting other soil factors is that processes involved in P uptake are not sufficiently understood. The underestimation of P uptake under P-deficient conditions by models that envision P uptake as a function of P concentrations in the soil solution, of diffusion rates in soil, and of soil buffering capacity shows that additional factors have to be involved. Kirk et al. (1999) expanded a conventional model to include solubilization of P by organic acids excreted by roots. They concluded that citrate excretion at rates observed in rice genotypes was sufficient to account for the discrepancy between observed P uptake rates and those predicted by a standard model that treats roots as passive sinks for P. Root exudates collected from rice cv Nipponbare and NIL-C443, however, did not contain a significant amount of organic acids (M. Wissuwa, unpublished data). Furthermore, genotypic differences in citrate excretion detected by Kirk et al. (1999) did not correspond to differences in P uptake reported in a field study conducted on the same soil used to determine model input parameters (Wissuwa and Ae, 2001a). In that study, IAC 47 was one of the best genotypes in P uptake, yet it had the lowest rate of citrate excretion (Kirk et al., 1999). Factors not accounted for in P uptake models may therefore be of considerable importance.

The approach chosen in this model, using estimates for external ε, acknowledges uncertainty about the uptake process but attempts to guard against that uncertainty by simulating a range of scenarios. Two of these scenarios, the one- and two-step sub models, underestimated P uptake and growth during the tillering stages of plant development, whereas the three-step model more accurately predicted observed values (Fig. 4). Additional simulations showed that the advantage of the three-step model was due to limiting the contribution of mature roots to P uptake. All simulations with high external efficiencies for mature roots (ε_m = 0.05) led to underestimations of P uptake that were comparable with the one-step model (Figs. 4 and 5). Three important input parameters needed for the three-step model, ε_a, ε_m, and the duration roots remain active, were not based on empirical data. Values for ε_a and ε_m were determined by a series of permutations to identify the one combination that best fit observed data and that exactly matched total P uptake of rice cv Nipponbare on d 98. Alternative combinations were then used in additional simulations to validate conclusions drawn with values used in the base-model. All combinations that led to close agreement of model predictions with measured data on P uptake and TDM also gave comparable results regarding the relative importance of other parameters on P uptake.

The developmental stage at which individual roots have reached a degree of maturity that reduces the ability to take up P has been studied in a variety of plant species. Bhat and Nye (1974) detected a significant drop in P uptake rates in 11-d-old onion roots and 8-d-old rape roots, whereas Kraus et al. (1987) reported continued P uptake up to 20 d by maize roots. In both studies, an initial phase of high P uptake was followed by a second phase of lower but constant uptake rates that would correspond to distinction between ε_n and ε_a made in this model. Comparable data for rice grown under upland conditions are not available. Yoshida (1995) pointed out, however, that P uptake was highest near the root tip and that uptake rates would drop by 80% and more in mature roots as root hairs and rhizodermis are shed and replaced by a suberized layer of exodermis during the maturation process. The factor largely responsible for the duration of P uptake would be the longevity of root hairs. To account for this uncertainty, model simulations were run using a duration for ε_a of 10 and 20 d in addition to the 14 d used in the base model, and results indicated that such changes did not have a big influence on the relative importance of other parameters. The three-step base model was thus very robust, and conclusions drawn from simulations were not affected by assumptions made about the P uptake process.

A possible limitation of the present model that does not account for detailed root-soil interactions lies in the potential development of overlapping depletion zones around roots. Their existence would cause lower than expected P uptake, particularly if newly developed roots would grow into zones already depleted by older roots. Huguenin-Elie et al. (2002) estimated that depletion zones around roots would overlap at a root length density of 3,000 dm root length dm^-3 soil volume. Above that value, P uptake would not increase linearly with root size, and P uptake would be overestimated by the model. Due to the severe P deficiency that highly reduced root growth and due to the large soil volume used here, rice cv Nipponbare only reached a maximum root length density of around 350 dm dm^-3 at 98 d. NIL-C443 reached a root length density of 1,200 dm dm^-3. Both values are well below the critical value given by Huguenin-Elie et al. (2002) thus overlapping depletion zones are not expected to cause significant overestimation of P uptake in the present study.

Sensitivity Analysis: Parameters of Importance for Tolerance to P Deficiency

The most influential parameters in all model simulations were the P partitioning factor (ϕ_r), the internal efficiency in DM_r production (γ_r), and the specific RS4(α). Raising these parameters by 10% in the base model led to almost identical (62%-64%) improvements in P uptake. The similarity among these factors was due to their linear influence on RSA. Data presented in Table III further showed that a 22% increase in these root growth-related parameters would be sufficient to triple P uptake in NIL-C443. Changing model assumptions had small effects, because the change required in α to triple P uptake varied by only ±3%. The model therefore quite clearly shows that improving root growth would be the most efficient way to enhance tolerance to P deficiency. Similar results were obtained by Teo et al. (1992) for lowland rice and by Ermani et al. (1994) for maize grown in P-deficient soil. There may be limitations, however, as to which of the root growth-related parameters would be most suitable for genotypic improvements. Greater P partitioning to roots may have limitations if plants have already optimized the fine balance in P partitioning. Further reductions of P supply to shoots could then lead to insufficient photosynthesis and assimilate supply for root growth with negative effects on P uptake. Theoretically such limitations should not exist for γ_r or α. Selecting genotypes with a low internal P requirement for DM_r production may thus be an efficient way to improve tolerance to P deficiency. My studies have shown that genotypic variation existed for γ_r and that landraces such as Kasalath generally required less P per unit dry matter compared with modern varieties (X. XXX, unpublished data). Producing finer roots or more and longer root hairs would increase α at little or no additional cost to the plant (Föhse et al., 1991). The difficulty of screening for these traits may, however, make it less likely that α would become a selection criterion in breeding programs.

The second most influential parameter in all simulations was the external efficiency of active roots (ε_a). An increase in ε_a of about 33% was sufficient to explain the difference in P uptake between rice cv Nipponbare and the NIL, and this was not affected by assumptions about the duration of active uptake as similar results were obtained with 10 and 20 d (Table III). Changing model assumptions about the relative importance of ε_m had bigger consequences on ε_a with estimates for required changes ranging from 25% (ε_m = 0.001) to 45% (ε_m = 0.05). But because an ε_m of 0.05 did not show close agreement with measured values for P uptake, more realistic estimates for the necessary increase in ε_a would be closer to 30% than to 45%.

Seed P reserves were less influential but nevertheless deserve some attention if farmers in P-deficient environments use their own harvest as seed sources for following crops. Any reduction in the amount of P stored in the seed would negatively affect growth of a subsequent crop, and this could be aggravated if the genotype used possesses high internal efficiency in all of its tissue. An ideal genotype would therefore be internally efficient in vegetative tissue only but would maintain relatively high P concentrations in the seed. Little is known about the relation between internal efficiencies in different tissues, but this question may be worth further investigations.

Implications for Physiological Studies Aimed at Identifying Target Mechanisms

Near isogenic lines are powerful tools in investigating the physiological basis of complex traits such as P uptake. An important question that has nevertheless rarely been addressed is how big differences in potentially important mechanisms would have to be between a pair of NILs to confidently establish a causal relation between that mechanism and the complex trait of interest. Answering that question has been one of the main objectives of this study. The modeling approach chosen here yielded two important results. First, a 3-fold genotypic difference in P uptake can be attributed to a mere 22% change in root growth-related parameters or to about 33% increases in external P uptake efficiency. Experimenters therefore have to guard against the assumption that large differences in a trait would also have to be caused by relatively large genotypic differences in potentially important mechanisms.

The second important conclusion of this study is related to the other main objective of separating primary causes from secondary effects. Particularly noteworthy was the observation that direct effects of increasing ε_a were about seven times smaller compared with secondary root growth effects (Table III). That previous attempts to link the Pup1 locus to a specific mechanism did not yield conclusive answers (Wissuwa and Ae, 2001b) may have been due to the inter-relatedness of external P uptake efficiency and root growth. The detection of small differences in external efficiency will be more difficult if these were overshadowed by subsequently larger effects on root growth.

This has important implications for physiological studies aimed at identifying target mechanisms. Having an estimate for the magnitude of genotypic difference in potential mechanisms that would suffice to explain genotypic differences in the target trait would facilitate any search for target mechanisms for several reasons. First, it will prevent disregarding small differences as insignificant. Furthermore, it will help in specifically designing experiments to allow for significant detection of small differences between genotypes. Detecting such small increases in external efficiency experimentally will be difficult considering that measurements on root size are bound to contain relatively large experimental error. Finally, it may be necessary to eliminate potentially confounding secondary effects through experimental design. Previous results of experiments comparing rice cv Nipponbare with NIL-C443 strongly support this point. When external root efficiency was determined by dividing total P uptake over the whole growth period by RSA at the end of the growth period, differences in external efficiency were not significant. However, if lines were transplanted with roots trimmed to eliminate effects of seedling root growth, NIL-C443 had about 35% higher external efficiency compared with rice cv Nipponbare. As model predictions showed, this difference would be sufficiently large to account for observed differences in P uptake. External efficiency may therefore be the mechanism directly affected by the Pup1 locus.

MATERIALS AND METHODS

All model parameters were measured in pot experiments conducted at the National Institute for Agro-Environmental Sciences (Tsukuba, Japan). The rice (Oryza sativa) variety Nipponbare of the japonica subspecies was used in all experiments because it had been well characterized on this soil (Wissuwa and Ae, 2001b). The second genotype used was a near isogenic line (NIL-C443) containing the P uptake QTL, Pup1, in a rice cv Nipponbare genetic background (Wissuwa et al., 2002). Pots were filled with a highly P-deficient soil (Humic haplic andosol) collected from a field that had not received P fertilizer for more than 30 years. Whole plants were harvested after growth periods of 7, 14, 28, 42, 70, 85, and 98 d. To allow for full root development, various pot sizes were used: 3-L pots for harvests up to 28 d, 10-L pots for 42 d, and 60-L buckets for 70 to 98 d. Pots of each subexperiment were arranged in a randomized complete block design with four replications. Pots were watered on alternate days with tap water and once a week with one-half-strength, P-free nutrient solution (Arnon, 1938). At the end of each growth period, shoots were harvested, and pots were tilted to wash out soil with running water. Roots were then rinsed over a sieve to remove attached soil, blotted dry with paper towels, and weighed to determine fresh weight. RSA and root fineness were determined on a sub-sample of 1 g (fresh weight). To obtain a representative sub-sample, pieces of 1 cm length were cut at 5, 10, and 15 cm from the crown and analyzed using a digital scanner and the software package WinRhizo (Regent, Quebec, Canada). Software parameters were set to measure and calculate roots in 0.1-mm-diameter increments. After oven-drying samples (65°C for 3 d), dry weight was recorded, and samples were ground to pass a 1-mm mesh. The tissue P concentration of root, shoot, and seed samples was determined colorimetrically by the phosphovanadate method (Hanson, 1950) after digestion in a mixture of HNO₃:HClO₄:H₂SO₄ (3:1:1, v/v). To estimate seed P translocation, seedlings were grown in P-free nutrient solution and sampled after 7, 14, and 21 d. The P remaining in the seed attached to seedlings was determined in addition to root and shoot P concentrations.