Influence of Fatigue on Hand Muscle Coordination and EMG-EMG Coherence During Three-Digit Grasping

Abstract

Fingertip force control requires fine coordination of multiple hand muscles within and across the digits. While the modulation of neural drive to hand muscles as a function of force has been extensively studied, much less is known about the effects of fatigue on the coordination of simultaneously active hand muscles. We asked eight subjects to perform a fatiguing contraction by gripping a manipulandum with thumb, index, and middle fingers while matching an isometric target force (40% maximal voluntary force) for as long as possible. The coordination of 12 hand muscles was quantified as electromyographic (EMG) muscle activation pattern (MAP) vector and EMG-EMG coherence. We hypothesized that muscle fatigue would cause uniform changes in EMG amplitude across all muscles and an increase in EMG-EMG coherence in the higher frequency bands but with an invariant heterogeneous distribution across muscles. Muscle fatigue caused a 12.5% drop in the maximum voluntary contraction force (P < 0.05) at task failure and an increase in the SD of force (P < 0.01). Although EMG amplitude of all muscles increased during the fatiguing contraction (P < 0.001), the MAP vector orientation did not change, indicating that a similar muscle coordination pattern was used throughout the fatiguing contraction. Last, EMG-EMG coherence (0–35 Hz) was significantly greater at the end than at the beginning of the fatiguing contraction (P < 0.01) but was heterogeneously distributed across hand muscles. These findings suggest that similar mechanisms are involved for modulating and sustaining digit forces in nonfatiguing and fatiguing contractions, respectively.

INTRODUCTION

Muscle fatigue is an exercise-induced reduction in the muscle's capability to generate force (Bigland-Ritchie and Woods 1984; Gandevia 2001) and depends on the details of the task (Bigland-Ritchie et al. 1995; Enoka and Duchateau 2008; Enoka and Stuart 1992). The cause of muscle fatigue is complex but appears to be due to both peripheral and central mechanisms (Bigland-Ritchie et al. 1983a,b; Gandevia et al. 1996; Taylor and Gandevia 2008; Taylor et al. 2000). Muscle fatigue has been studied extensively during submaximal isometric contractions. Under these conditions, fatigue leads to an increase in muscle force fluctuations (Cresswell and Loscher 2000; Ebenbichler et al. 2000; Hunter et al. 2002), motor unit recruitment (Carpentier et al. 2001; Christova and Kossev 2001; Fallentin et al. 1993; Mottram et al. 2005b), EMG amplitude (Fuglevand et al. 1993), and motor unit discharge variability (Mottram et al. 2005b) as well as a decrease in motor unit discharge rates (Carpentier et al. 2001; Mottram et al. 2005b). These adjustments are associated with an increase in descending drive (Hunter and Enoka 2003; Klass et al. 2008; Levenez et al. 2008), increased motor neuron excitability (Klass et al. 2008; Levenez et al. 2008), and decreased excitatory Ia input onto motor neurons (Bigland-Ritchie et al. 1986; Bongiovanni and Hagbarth 1990; Bongiovanni et al. 1990; Martin et al. 2006).

Another adjustment that occurs during submaximal fatiguing contractions is a change in the muscle coordination patterns (Enoka and Stuart 1992). For example, several studies have provided evidence of alternating levels of muscle activity among synergists (Kouzaki and Shinohara 2006; Kouzaki et al. 2002–2004; Shinohara et al. 2009) and motor unit substitution (Person 1974; Westgaard and de Luca 1999) or rotation (Fallentin et al. 1993; Kato et al. 1981; Sale 1987; Sjogaard et al. 1986) during fatiguing contractions within a single muscle. These phenomena, however, are observed only at very low forces (<5% of maximal voluntary contraction, MVC) (Kouzaki et al. 2002) and are considered strategies adopted by the CNS to maintain the same task performance, i.e., force.

Several gaps exist in the understanding of how fatigue influences voluntary control of muscle activity. Specifically, the aforementioned studies have generally focused on the motor output and electromyographic (EMG) activity of a single agonist muscle or a small group of agonist muscles around a single joint. However, often force production in everyday tasks such as object grasping and manipulation involves the recruitment of multiple muscles acting across multiple joints. Although some studies have investigated the effects of fatigue on digit force coordination patterns (Danion et al. 2000, 2001; Singh et al. 2010), the extent to which fatigue influences muscle coordination as measured by EMG in tasks involving a large number of muscles and/or multi-joint muscles remains to be determined. Furthermore, studies on the coordination and modulation of the neural drive to muscles have focused primarily on the temporal characteristics of single or multiunit EMG recordings (Kouzaki and Shinohara 2006; Kouzaki et al. 2002–2004; Person 1974; Shinohara et al. 2009; Westgaard and de Luca 1999). However, an additional tool for studying the effect of fatigue on muscle coordination is EMG-EMG coherence.

Coherence can be used as an index of muscle coordination between pairs of muscles by identifying the strength and periodicity of common frequency characteristics between two EMG signals (Farmer 1998; Farmer et al. 1993; Grosse et al. 2002; Rosenberg et al. 1989). Furthermore, the strength and frequency band distribution of the coherence spectrum has been shown to reflect common neural inputs to motor neurons pools, which are primarily from the direct corticospinal pathway (Brown 2000; Farmer et al. 1993; Fisher et al. 2002; Grosse et al. 2002; Kilner et al. 2004; Riddle and Baker 2005). It has been proposed that the functional role of coherent oscillations in the motor system may be to bind remote groups of neurons (Farmer 1998; Schoffelen et al. 2005), efficiently recruit motor units (Baker et al. 1999; Kattla and Lowery 2009; Kilner et al. 1999), or coordinate activity of multiple muscles (Kidgell et al. 2006; Kilner et al. 2002; Semmler et al. 2004).

To our knowledge, only one study has examined the effect of fatigue on EMG-EMG coherence in hand muscles. Kattla and Lowery (2009) found that EMG-EMG coherence between an intrinsic and extrinsic index flexor muscle significantly increased in the 15–60 Hz frequency range when comparing pre- and postfatigue EMG signals from an isometric index finger flexion task. However, this study only investigated coherence across one pair of muscles acting at a single joint. Therefore it remains unknown how coherence among many multi-joint muscles changes throughout the duration of a fatiguing contraction. Based on the preceding considerations, it is necessary to further examine coherence across a larger number of muscles to gain insight into the effect of fatigue on the CNS's ability to coordinate multiple, concurrently active muscles.

The present study was designed to quantify the extent to which muscle fatigue influences the coordination of simultaneously active hand muscles. The hand was used as a model for two reasons: the complex anatomy of its muscles (large number of muscles and joints) and coherence modulation due to fatigue should be most evident in hand muscles due to their direct corticospinal inputs (Palmer and Ashby 1992).

Studies that have examined submaximal fatiguing contractions in two to four agonist muscles have found relatively similar rates of increase in the EMG amplitude (Hunter et al. 2002; Mottram et al. 2005a,b, 2006; Rudroff et al. 2004, 2007). In nonfatiguing submaximal and maximal force production tasks by a single digit (Valero-Cuevas 2000), EMG amplitude of all seven muscles of the index finger scaled uniformly when force was increased ≤100% of maximum. Similar results have recently been reported for the coordination of 12 muscles acting on the thumb, index, and middle fingers during three-digit grasping (Poston et al. 2010). Based on these findings and the known fatigue-dependent increase in EMG amplitude, our first hypothesis was that the neural drive aimed at maintaining a constant force throughout a fatiguing contraction would elicit a uniform increase in EMG amplitude across all muscles studied, this phenomenon being similar to that in the preceding text described for voluntary modulation of digit forces. Our second hypothesis, based on the study by Kattla and Lowery (2009), was that longer contraction durations would be accompanied by an increase in EMG-EMG coherence in the higher frequency bands, e.g., >15 Hz. Based on the results on EMG-EMG coherence reported by Poston et al. (2010), our third hypothesis was that fatigue would not affect the heterogeneous distribution of coherence across extrinsic and intrinsic muscle pairs, the former functional group being characterized by stronger coherence. This expectation was based on the observation that voluntary force modulation does not affect the distribution of correlated neural input to hand muscle motor nuclei. Preliminary accounts of these results have been presented in abstract form (Poston et al. 2009).

METHODS

Subjects

Eight young adults [5 men, 3 women; age 27 ± 6 (SD) yr] participated in the study. All subjects reported being healthy, without known neurological disorders or musculoskeletal injuries of the hand, and right handed. Subjects gave written informed consent in accordance with the Declaration of Helsinki before participating in the study, and the experimental procedures were approved by the Institutional Review Board at Arizona State University.

Experimental procedures

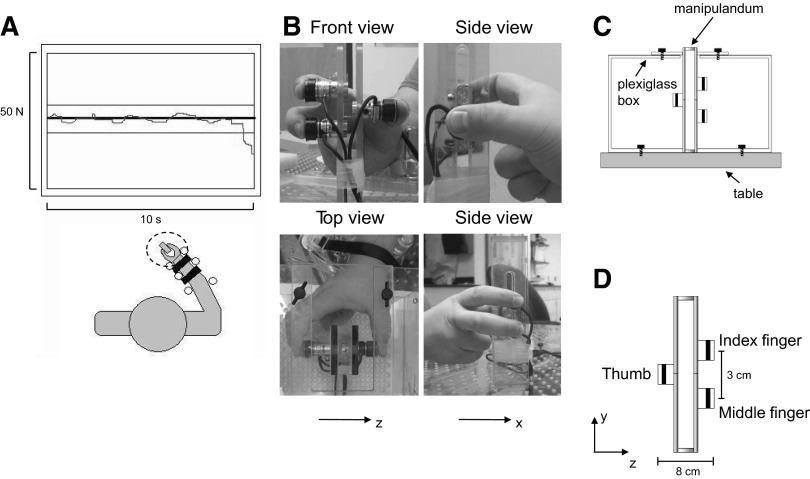
Subjects performed two isometric force production tasks with the right hand: MVCs and a submaximal fatiguing contraction. For both tasks, subjects generated isometric normal forces simultaneously with the thumb, index, and middle fingers on a grip manipulandum (Fig. 1, B–D). The forces exerted by each digit were measured by three-dimensional (3D) force/torque transducers (ATI Nano-17, Apex, NC) mounted on the manipulandum (Fig. 1D). Subjects sat in an adjustable chair and faced a computer monitor that was located ∼1 m away at eye level (Fig. 1A). The right forearm was placed on a flat, rigid platform, and a soft pad was placed under the forearm to prevent discomfort. The hand was kept semi-supinated while the wrist was kept in a neutral position. The forearm was immobilized by adjustable rigid dowels fastened to the platform on both sides of the wrist and forearm (Fig. 1A). The contact surfaces of the sensors for the fingertips of the index and middle fingers were 3 cm apart vertically and 8 cm apart horizontally from the thumb (Fig. 1, B and D). This arrangement ensured that the index and middle fingers did not rest against each other.

Fig. 1.

Experimental setup. Subjects sat in front of a monitor that displayed the target and actual force (thick and thin lines, respectively; A), the latter being the sum of thumb, index, and middle finger normal forces exerted on the grip manipulandum (B and D). Subjects' forearm and wrist were immobilized on the table during the entire duration of the fatiguing contraction trial. B: front, top, and side views of the grip manipulandum together with their antero-posterior and lateral frames of reference (x and z, respectively). A Plexiglas box anchored to the table (C) secured the manipulandum in place during the execution of the tasks. Note that for the side views of the manipulandum (B), the plexiglass box is not shown for clarity. D: the grip manipulandum with three force/torque sensors, their relative distances, and the sensor-based frame of reference.

To allow placement of the distal pads of the three digits on their respective force/torque sensors, the distance between the wrist and the grip device was adjusted to allow subjects to grip the device using a natural hand posture. Specifically, the index finger metacarpal-phalangeal (mcp) joint was abducted and extended (∼10 and 30°, respectively), whereas the proximal and distal interphalangeal (pip and dip, respectively) joints were flexed and in a neutral posture (∼40 and ∼0°, respectively). The middle finger mcp joint was in a neutral adduction/abduction posture and extended (∼0 and 30°, respectively), flexed at the pip and dip joints (∼50 and 30°, respectively); the thumb mcp joint was abducted and flexed (∼50 and 35°, respectively) and the interphalangeal joint angle was set at a neutral posture (∼0°). Finally, the uninvolved ring and little fingers were flexed (curled against the palm of the hand).

The experimental apparatus consisted of a Plexiglas box attached to the table (Fig. 1C). This device and the controls used to maintain an invariant hand posture have been described in detail in Poston et al. (2010). Briefly, rigid dowels were used to immobilize the forearm, the finger pad position was constantly monitored by the experimenters to ensure consistent forearm, hand, and digit posture. Most importantly, digit posture was verified off-line by quantifying the center of pressure of each digit relative to the center of its sensor (see following text). Finally, we analyzed the orientation of the 3D force vector during the fatiguing contraction trial.

MVCs

We instructed subjects to increase the isometric force exerted by the three digits (in the flexion direction) from baseline (∼1 N following the initial contact with all sensors) to their maximum over a 3-s period and maintain this maximum for 6 s. All subjects were encouraged verbally to maximize digit force production while minimizing the tangential components of the digit forces (antero-posterior and vertical, x- and y- components, respectively; Fig. 1, B and D). Visual feedback of the total digit force (sum of normal force exerted by the 3 digits) was not provided to the subjects. Subjects performed three MVC trials before performing the fatiguing submaximal contraction. The trial with the largest total normal force was used as the reference value to compute the target force for the submaximal fatiguing contraction (note that EMG recorded during this trial was also used to normalize the EMG amplitude recorded during the fatiguing contraction). Subjects were given a rest period of 3 min between each MVC trial to minimize fatigue and ensure that subjects were producing maximum force on each trial. Additionally, subjects performed one MVC immediately following the submaximal fatiguing contraction to quantify the drop in MVC force induced by the fatiguing trial.

Submaximal fatiguing contraction

Subjects were required to grip the manipulandum with the thumb, index, and middle fingers and to perform a sustained isometric contraction for as long as possible at a target force of 40% of MVC. A target force of 40% of MVC was chosen to allow the CNS the capability of modulating motor unit recruitment and rate coding, to minimize the duration of the contraction and to allow for comparison with the majority of fatigue studies, which have employed target forces of 20–50% of MVC.

To initiate the task, subjects gradually increased the total digit normal force from baseline (∼1 N) to the target force. Data collection started as soon as the subject reached the target force and was able to maintain the force for ≥3 s. Visual feedback of the target force level was provided on a computer monitor throughout the fatiguing contraction. A horizontal line in the center of the monitor denoted the target force, whereas the sum of the three digits' normal forces was displayed as a red trace in real-time (Fig. 1A). The termination criteria for this task were an inability to maintain the force exerted within 10% of the target force for 3 s (determined on-line by the data acquisition software) or failure to maintain the same hand or forearm posture throughout the trial despite strong verbal encouragement. However, all subjects failed due to an inability to maintain the target force. The time between the start of data collection and the time of task failure was denoted as the time to task failure.

Force and EMG measurement

Normal and tangential forces of the thumb, index, and middle fingers were measured by three Nano17/SI-25-250 force/torque sensors (ATI Industrial Automation; diameter: 17 mm; nominal resolution: 0.0015 N) mounted on the manipulandum (height: 20 cm; width: 2.2 cm; depth: 4.4 cm; Fig. 1D). The center of the thumb sensor was aligned with the midpoint of the vertical distance between the index and middle finger sensors (Fig. 1, B–D). The contact surface of the sensor was covered with a 7-mm thick circular plate covered with sandpaper (80 grit silicon carbide D-Weight resine, Alligator; coefficient of friction between finger pads and sandpaper: 1.08 ± 0.02). Intramuscular EMG recordings were obtained using monopolar electrodes from 12 muscles of the right hand. We used 27-gauge hypodermic needles to insert fine-wire electrodes (50 μm diam; California Fine Wire, Grover Beach, CA) into the muscle bellies of six intrinsic and six extrinsic muscles of the thumb, index, and middle fingers. The intrinsic hand muscles were: first and second dorsal interosseus (FDI, 2DI), abductors of the index and middle fingers, respectively; first and second palmar interosseus (FPI, 2PI), adductors of the index and middle fingers, respectively; abductor pollicis brevis (ABPB), abductor of the thumb; and flexor pollicis brevis, a flexor of the thumb. The extrinsic hand muscles were flexor pollicis longus (FPL), a flexor of the thumb; extensor pollicis longus (EPL), extensor of the thumb; index and middle finger compartments of flexor digitorum superficialis (FDS2 and FDS3), flexors of the index and middle fingers, respectively; and index and middle finger compartments of extensor digitorum (ED2, ED3), extensors of the index and middle finger, respectively.

The procedures used to record EMG, assess cross-talk among the EMG recordings, and verify electrode placement in the target muscles have been described in details elsewhere (Poston et al. 2010). Briefly, to increase the recording volume of the electrode ∼2 mm of insulation from the tip of the fine-wire were removed before inserting the fine-wire into the belly of each muscle or muscle compartment using either a ½ or 1½ inch 27-gauge hypodermic needle. The approximate location of the target muscle was located using maps obtained by previous studies (Poston et al. 2010; Winges et al. 2004, 2008) and palpation while the muscle was voluntarily activated. The quality of the EMG signal was then inspected while subjects performed voluntary isometric contractions and the depth and/or angle of insertion of the electrode were adjusted to maximize and minimize the signal-to-noise ratio of the EMG signal of the target and neighboring muscle(s), respectively. Electrode placement was verified using electrical stimulation (for more details, see Poston et al. 2010). After these procedures, the needle was removed and the wire remained in the muscle belly for the remainder of the experiment.

Two surface electrodes (10 mm-diam gold-plated silver disc, Model F-E5GH, Grass Instruments; West Warwick, RI) were placed on the radial styloid. The skin was prepared with iodine and alcohol and abraded with Nuprep to lower skin impedance. Each surface electrode served as a reference electrode for six of the intramuscular electrodes. To verify the quality of the EMG signals throughout data collection, EMG signals from all muscles were displayed on a computer monitor using a data acquisition interface (Micro 1401, Cambridge Electronic Design, Cambridge, UK). The EMG signals were amplified (× 2,000) and band-pass filtered (3–3,000 Hz; Neurodata Acquisition System model 12, Grass Instruments). Off-line analyses revealed that ∼99% of the power spectral density of our EMG data were <500 Hz.

Data acquisition

Force and EMG data were acquired with a 12-bit A/D converter boards (PCI-6225, National Instrument, Austin, TX; sampling frequency: 2 kHz), displayed, and stored on a computer with a custom data acquisition interface (LabView version 6.0, National Instrument).

Data analysis

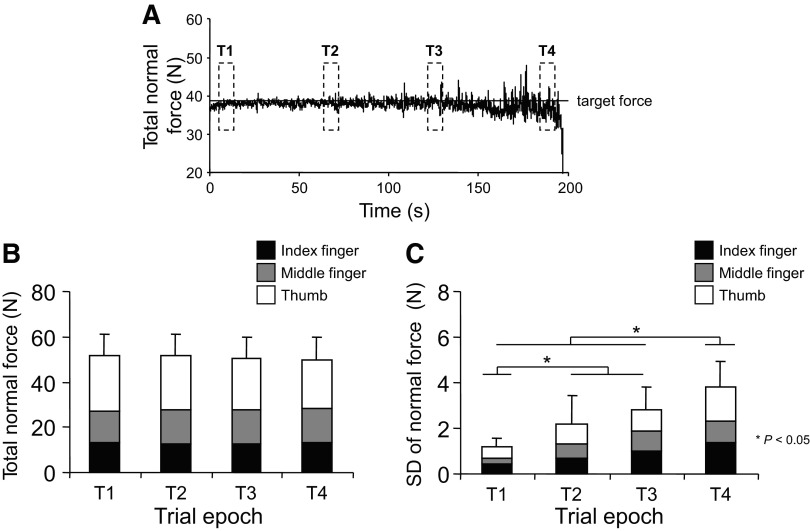
Data were analyzed off-line with custom-written software (Matlab, The Mathworks, Natick, MA). To analyze the change in EMG amplitude and digit forces during the fatiguing contractions, each trial was split into four time epochs of 6 s each (Fig. 2A): the first time epoch (T1) began a half second after subjects initially reached the target force required for the fatiguing contraction; the second and third time epochs (T2 and T3, respectively) were centered around 33 and 66% of the time to task failure, respectively; the fourth time epoch (T4) was defined as the last 6 s before the final 3 s of the task, i.e., before one of the task failure criteria was met.

Fig. 2.

Digit forces and force variability. A: the time course of total normal force during the fatiguing contraction trial from 1 representative subject. —, the target force equivalent to 40% of the total normal force measured during the maximal voluntary contraction (MVC) trial characterized by the largest force. - - -, the epochs used for analyses of digit forces and electromyographic (EMG) amplitude. This subject was able to maintain a constant total normal force for ∼190 s after which task failure occurred (see text for details). B and C: the magnitude of total and individual digit normal forces and the SD of total normal force, respectively, measured at each time epoch. Data in B and C are averages of all subjects (±SE).

DIGIT FORCES.

Force/torque data in the antero-posterior, vertical, and normal directions (x-, y-, and z-force and torque components; Fig. 1, B and C) were filtered (20 Hz low-pass, 2nd order, 0-lag Butterworth filter) before further processing. For each of the four time epochs, we computed the average normal and tangential forces (vertical and antero-posterior, respectively), and the SD of average normal force exerted by each digit as well as of the sum of normal forces exerted by the three digits.

We used the force and torque outputs of each sensor also to verify repeatability of digit position and force direction during the fatiguing contraction trial. For each digit, changes in the position of the finger pad relative to the sensor that might have occurred across time epochs were quantified by computing differences in the digit center of pressure (for details, see Poston et al. 2010). By definition, the magnitude of normal forces was constrained to remain relatively constant throughout the fatiguing contraction trial. However, fatigue might have affected force production along directions whose control was not explicitly constrained by the task, i.e., tangential force components. To quantify changes in the orientation of the 3D force vector at each time epoch, we computed the angle between its projections on the xz and xy planes and the x- and y-axis (angles 1 and 2, respectively) of a coordinate system with its origin located at the center of the force/torque sensor.

HAND MUSCLE COORDINATION: EMG TIME DOMAIN ANALYSIS.

Before processing, the EMG recordings were visually inspected to verify the absence of artifacts. EMG signals were then rectified, averaged over a 6-s second time interval centered around each of the preceding four time epochs (Fig. 3A) and normalized by the mean EMG amplitude recorded during the MVC trial characterized by the largest normal force. We will refer to EMG amplitude averaged within each time epoch and normalized to the MVC EMG as aEMG.

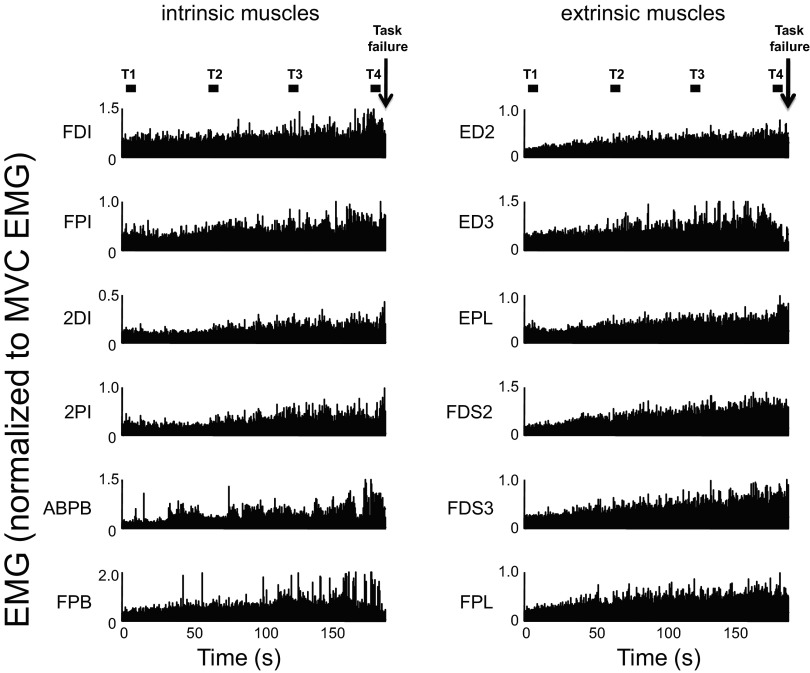
Fig. 3.

EMG activity during the fatiguing contraction trial. Rectified EMG from 1 subject (S3) is shown for each of the 12 muscles that were simultaneously recorded during the fatiguing contraction trial. The 4 epochs used for analysis are (■; T1–T4). EMG amplitude is shown in normalized form relative to EMG recorded during the MVC trial characterized by the largest force (see text for more details). Left and right: EMG from intrinsic and extrinsic hand muscles (see text for muscle abbreviations). ↓, the instant of time to failure.

Using the approach adopted by Valero-Cuevas and colleagues (1998), the aEMG obtained for each muscle and subject during the sub-maximal fatiguing contraction was used to assemble a 12-dimensional vector referred to as muscle activation pattern (MAP) vector (for more details, see Poston et al. 2010). Briefly, the magnitude of each MAP vector (the square root of the sum of the squares of its aEMG elements) was computed within each time epoch to quantify changes in the aEMG amplitude that might have occurred across time epochs. Note that changes in the MAP vector magnitude during the fatiguing contraction denote changes in aEMG amplitude in one or more muscles which, in turn, may also affect the angle between MAP vectors measured at different time epochs. To quantify the extent to which the relative aEMG contribution of each muscle to the MAP vector changed across time epochs, we computed the dot product (cosine of the angle, equivalent to the Pearson's correlation coefficient) between MAP vectors obtained from pair-wise comparisons of time epochs. As the magnitude of aEMG components can only be greater than or equal to 0, the comparisons between MAP vector pairs yield cosine values that span a limited range, i.e., between 0 and 1 (maximum dissimilarity and similarity, respectively). Therefore for statistical purposes the absolute cosine values were transformed using Fisher's z-transformation: z = 0.5 · log{[1 + cos(α)]/[1 − cos(α)]}.

HAND MUSCLE COORDINATION: FREQUENCY DOMAIN ANALYSIS (COHERENCE).

We quantified correlations of muscle activations in the frequency domain by computing EMG-EMG coherence. Before computing coherence, the stationarity of EMG signals was verified by using the procedures described by Halliday and colleagues (2009). Stationarity was tested across the 0–55 Hz frequency range on nonoverlapping segments (1 s each) for each of the four time epochs (T1–T4). The intermediate time epochs (T2 and T3) tended to be nonstationary in most of our subjects. Therefore we tested stationarity iteratively on time epochs of different durations to determine the longest time epochs during which we could establish stationarity for most (>90%) of our EMG signals. Two time epochs that fitted this criterion were the first and last 25% of the fatiguing contraction trial (174 of 192 time epochs; ∼91%). For the first 25% of the trial, coherence analysis was performed on EMG data starting half a second after the initiation of the fatiguing contraction and ending at 25% of the trial duration. The average (±SE) duration of each of the first and last 25% of the fatiguing contraction trial was 36.40 ± 7.11 s. Coherence analysis was performed only on the stationary EMG data.

EMG-EMG coherence was performed on interference EMG data as described in Poston et al. (2010). Briefly, we computed coherence separately for each of 66 pairs of EMG signals, i.e., all possible pair combinations of the 12 muscles we recorded from (see Table 1 for the list and labels of muscle pairs) as follows

$${\left|R_{xy}\left(\lambda \right)\right|}^2={\left|f_{xy}\left(\lambda \right)\right|}^2/\left[f_{xx}\left(\lambda \right)f_{yy}\left(\lambda \right)\right]$$ (1)

where f_xy is the cross-spectrum of two EMG signals, and f_xx and f_yy are the auto-spectra of each signal at frequency λ. Coherence was estimated from 1-s segments of nonoverlapping data (2,000 samples per segment; frequency bin resolution: 1 Hz) between a frequency range of 0–55 Hz. The individual estimates of coherence were used to compute pooled coherence (Amjad et al. 1997)

$$\frac{{\left|{\displaystyle \sum _{t=1}^k{f}_{xy}\left(\lambda \right)L_i}\right|}^2}{\left({\displaystyle \sum _{t=1}^k{f}_{xx}\left(\lambda \right)L_i}\right)\left({\displaystyle \sum _{t=1}^k{f}_{yy}\left(\lambda \right)L_i}\right)}$$ (2)

where i is the trial number, k is the total number of coherence estimates (k = 66, 1 per muscle pair) used to compute the average, and Li is the number of disjoint segments used in the spectra calculations for coherence estimate i.

Table 1.

Muscle pair groupings and labels used in Fig. 7

Muscle Pair	Intrinsic-Intrinsic	Muscle Pair	Intrinsic-Extrinsic
	FDI-FPI	31	FDI-ED2
	FDI-2DI	32	FDI-ED3
	FDI-2PI	33	FDI-EPL
	FDI-ABPB	34	FDI-FDS2
	FDI-FPB	35	FDI-FDS3
	FPI-2DI	36	FDI-FPL
	FPI-2PI	37	FPI-ED2
	FPI-ABPB	38	FPI-ED3
	FPI-FPB	39	FPI-EPL
	2DI-2PI	40	FPI-FDS2
	2DI-ABPB	41	FPI-FDS3
	2DI-FPB	42	FPI-FPL
	2PI-ABPB	43	2DI-ED2
	2PI-FPB	44	2DI-ED3
	ABPB-FPB	45	2DI-EPL
		46	2DI-FDS2
Muscle Pair	Extrinsic-Extrinsic	47	2DI-FDS3
	ED2-ED3	48	2DI-FPL
	ED2-EPL	49	2PI-ED2
	ED2-FDS2	50	2PI-ED3
	ED2-FDS3	51	2PI-EPL
	ED2-FPL	52	2PI-FDS2
	ED3-EPL	53	2PI-FDS3
	ED3-FDS2	54	2PI-FPL
	ED3-FDS3	55	ABPB-ED2
	ED3-FPL	56	ABPB-ED3
	EPL-FDS2	57	ABPB-EPL
	EPL-FDS3	58	ABPB-FDS2
	EPL-FPL	59	ABPB-FDS3
	FDS2-FDS3	60	ABPB-FPL
	FDS2-FPL	61	FPB-ED2
	FDS3-FPL	62	FPB-ED3
		63	FPB-EPL
		64	FPB-FDS2
		65	FPB-FDS3
		66	FPB-FPL

Pooled coherence was computed on individual subjects and the two epochs (1st and last 25% of the fatiguing contraction trial) separately to determine the effect of fatigue on EMG-EMG coherence 1) across all muscle pairs combined and within the 0–55 Hz frequency range, 2) at frequency ranges of 0–5 (common drive), 6–15 (alpha), 16–35 (gamma), and 36–55 Hz (high gamma) identified based on the presumed source and task dependency of coherent oscillations (Brown 2000) and for all muscle pairs combined, and 3) across 0–55 Hz frequency range within each of three muscle groups (see following text).

For analysis 2), we computed pooled coherence within frequency bands. For analysis 3), the 66 muscle pairs were separated into three functional groups: intrinsic-intrinsic muscle group (muscle pairs 1–15), extrinsic-extrinsic muscle group (muscle pairs 16–30), and the intrinsic-extrinsic muscle group (muscle pairs 31–66; Table 1).

For statistical purposes, we z-transformed individual and pooled coherence estimates (Fisher transformation of coherency, Rxy). The integral of z-transformed coherence estimates was computed for values above significance level over the entire frequency range (0–55 Hz; analyses 1) and 3) in the preceding text) and within four frequency bands (analysis 2) in the preceding text). The effect of fatigue on the magnitude of these integrals of coherence was analyzed using nonparametric statistics (see following text).

Statistical analysis

A two-tailed paired t-test was used to compare the MVC force before and after the fatiguing contraction. We performed one-way ANOVAs with repeated measures to test the effect of time epoch (T1–T4; 4 levels) on the sum of normal forces exerted by the three digits (total normal force), the SD of total normal force, the MAP vector magnitude, and the z-transformed cosines of the angle between the MAP vector from the first versus the vector from each of the last three epochs (T1 vs. T2, T1 vs. T3, and T1 vs. T4). Two-way ANOVAs with repeated measures were used to test the effect of fatigue on individual digit forces (within-subject factors: digit, 3 levels; time epoch, 4 levels) and normalized EMG amplitude (aEMG) from each muscle (within-subject factors: muscle, 12 levels; time epoch, 4 levels). When appropriate, post hoc comparisons (Tukey's pair-wise comparisons with Bonferroni correction when necessary) were performed. The level of significance was set as P = 0.05 for all statistical tests. Data are reported as means ± SE.

The effect of fatigue on the integral of z-transformed EMG-EMG coherence was further quantified using nonparametric statistical analysis (Nichols and Holmes 2002) as described in Poston et al. (2010). Briefly, the observations from all subjects (n = 8) were randomly assigned across the two time epochs. For each of all possible permutations (₁₆C₈ = 256), the total number of observations for each epoch remains the same (i.e., 8 for each epoch) and the mean difference between the integrals of coherence from the two epochs is calculated. The Monte Carlo P value is calculated as the proportion of mean differences obtained from all permutations that are larger than the absolute value of the experimentally observed mean difference (Maris et al. 2007). A P value ≤0.05 is considered significant. These procedures were used for all preceding coherence analyses.

RESULTS

MVC force, digit forces, and force variability

The MVC force produced by the three digits significantly declined 12.5% from 134.68 ± 19.01 N before the fatiguing contraction to 117.98 ± 8.22 N immediately after the contraction (P = 0.025). ANOVA confirmed that the subjects complied with the task requirement of maintaining the same total normal force across all trial epochs up to the point of task failure [no significant effect of time epoch: F(3,28) = 0.375; P = 0.772; Fig. 2B]. Although the thumb exerted significantly larger normal force than the index and middle fingers [main effect of digit: F(2,84) = 65.87; P < 0.01 for both comparisons], this sharing pattern was consistent throughout the fatiguing contraction [no significant interaction digit × time epoch: F(6,84) = 0.456; P = 0.839]. In contrast, variability (SD) of total and individual digit normal force progressively increased across time epochs (significant main effect of time epoch: F(3,28) = 5.81; P = 0.003; significant differences among time epochs are shown in Fig. 2C] but uniformly across digits [no significant main effect of digit: F(2,84) = 2.14; P = 0.124; or interaction digit × time epoch: F(6,84) = 0.448; P = 0.845].

Analysis of digit center of pressure revealed that no significant changes occurred across time epochs (P > 0.05 for all digits). Analyses of the two angles of the 3D force vector projections revealed that the orientation of the force vector of the index and middle fingers was not significantly affected by fatigue (no significant main effect of time epoch: all P > 0.3). For the thumb, only the angle between the projection of the 3D force vector on the xz plane and the x axis changed significantly during the fatiguing contraction trial [main effect of time epoch: F(2,28) = 8.257; P < 0.001]. This effect was due to a larger contribution of the x component of the thumb force vector (flexion direction) but did not affect the uniform scaling of EMG amplitude across all muscles (see following text).

Hand muscle activation patterns

AMPLITUDE DOMAIN ANALYSIS.

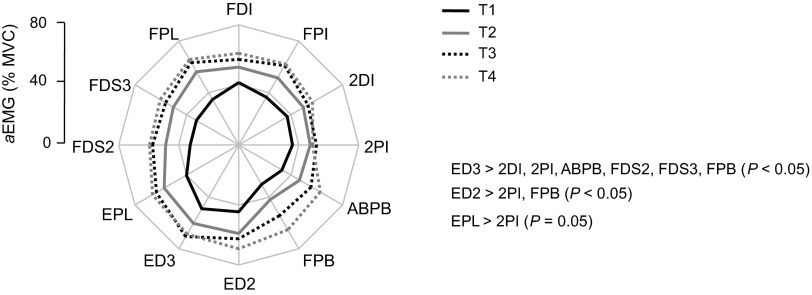
Figure 3 shows rectified EMG from 12 muscles of a representative subject during the execution of the submaximal fatiguing contraction. As expected, EMG amplitude of both intrinsic and extrinsic muscles increased throughout the fatiguing contraction up to the time of task failure. Figure 4 shows aEMG averaged across all subjects for each time epoch. Similarly to the data shown for one subject in Fig. 3, aEMG progressively increased throughout the fatiguing contraction [significant main effect of time epoch; F(3,336) = 75.48; P < 0.001]. Tukey's pair-wise comparisons indicated that aEMG was significantly larger for T4 and T3 compared with T2 and T1 (P < 0.05 for all comparisons). The amplitude of aEMG was also significantly different across muscles [significant main effect of muscle; F(11,336) = 4.72; P < 0.001; the results of post hoc comparisons are shown in Fig. 4]. Closer inspection of the data in Fig. 4 shows that aEMG increased with time in all muscles uniformly as indicated by the similarity in the shape of the EMG polygon. This was confirmed by a lack of significant interaction time epoch × muscle [F(33,336) = 0.486; P = 0.993].

Fig. 4.

EMG amplitude (aEMG) as a function of time epoch and muscle. The EMG amplitude from each muscle is shown as percentage of EMG recorded during MVC (aEMG) for each time epoch during the fatiguing contraction trial. Significant differences in EMG amplitude among muscles are indicated on the right side of the plot. Data are averages of all subjects.

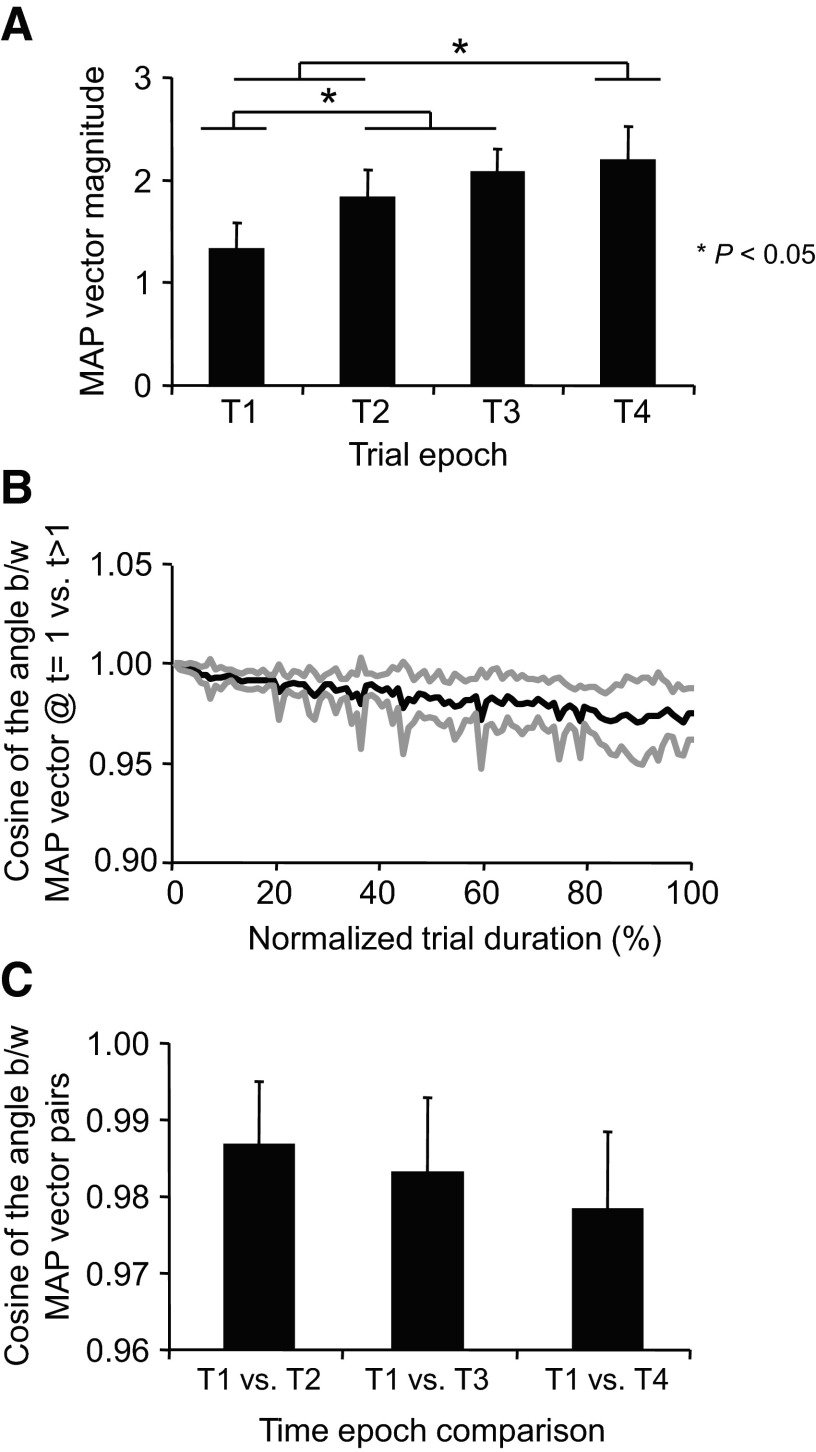
To further quantify the effect of fatigue on EMG activity, we computed the magnitude and orientation of the 12-dimensional MAP (see methods). As expected, the MAP vector magnitude increased during the fatiguing contraction [F(3,28) = 15.91; P < 0.001; Fig. 5A]. Except for T3 versus T4, the remainder of the pair-wise comparisons between time epochs revealed significant differences in MAP vector magnitudes (P < 0.001). The orientation of the MAP vector changed little during the fatiguing contraction, thus suggesting that the relative aEMG contribution of each muscle to the vector orientation remained relatively invariant. Figure 5B shows the cosine of the angle (equivalent to the correlation coefficient) between the MAP vector at the beginning of the trial (t = 0) and the MAP vector computed throughout the trial averaged across all subjects. Although a progressive decrease in similarity between MAP vectors at the beginning versus later epochs in the trial occurred, the fatiguing contraction had little affect on the orientation of the MAP vector as indicated by the large cosine values (>0.95) at the end of the trial [no significant main effect of time epoch, F(2,21) = 1.49; P = 0.248; Fig. 5C].

Fig. 5.

Magnitude and similarity of muscle activation pattern vectors. A: the magnitude of 12-dimensional muscle activation pattern (MAP) vector computed at each time epoch. B: mean ± SE (black and gray traces, respectively) of cosines of the angle between the MAP vector at the beginning of the fatiguing contraction trials (t = 1) vs. the MAP vector at subsequent time-normalized points (t = 2–100) of the fatiguing contraction trial. C: the cosines of the angle between the MAP vector at T1 vs. the MAP vector at T2–T4. Data in all panels are averages of all subjects (±SE).

FREQUENCY DOMAIN ANALYSIS.

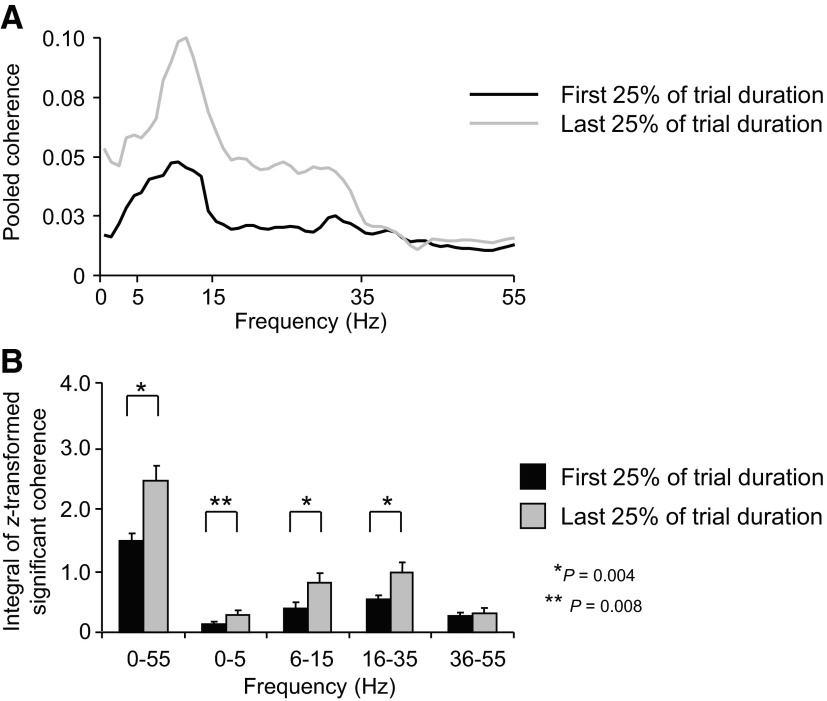
Figure 6A shows pooled coherence computed across all 66 muscle pairs (Table 1) over the 0–55 Hz frequency range for the first and last 25% of the fatiguing contraction (black and grays traces, respectively; see methods for the rationale for using the 1st and last quarter of the trial). The overall profile of pooled coherence remained fairly constant from the first to the last quarter of the trial, the strongest coherence occurring within the common drive and alpha frequency range (<15 Hz). Nonparametric statistics performed on the z-transformed integrals of coherence (0–55 Hz range) revealed that pooled coherence was significantly stronger on the last versus first quarter of the trial (P = 0.004; Fig. 6B).

Fig. 6.

EMG-EMG pooled coherence across all muscle pairs. A: EMG-EMG pooled coherence computed across all muscle pairs (n = 66) for the 1st and last 25% of the fatiguing trial (black and gray traces, respectively) and averaged across subjects. B: the integral of the z-transformed significant coherence computed for the 1st and last 25% of the fatiguing trial within the 0–55 Hz frequency range and within 0–5, 6–15, 16–35, and 36–55 Hz pooled across all muscles. Data in B are averages of all subjects (±SE).

To determine whether the fatiguing process might have caused coherence to shift across frequency ranges, we compared the integrals of z-transformed coherence estimates from the first versus the last quarter of the trial within each of four different frequency ranges (0–5, 6–15, 16–35, and 36–55 Hz; Fig. 6B). Nonparametric statistical analysis revealed significantly larger differences in the integral of z-transformed coherence on the last versus first quarter of the trial at frequency bands of 0–5, 6–15, and 16–35 Hz (P = 0.008, 0.004, and 0.004, respectively) but not for the 35–55 Hz band (P > 0.05).

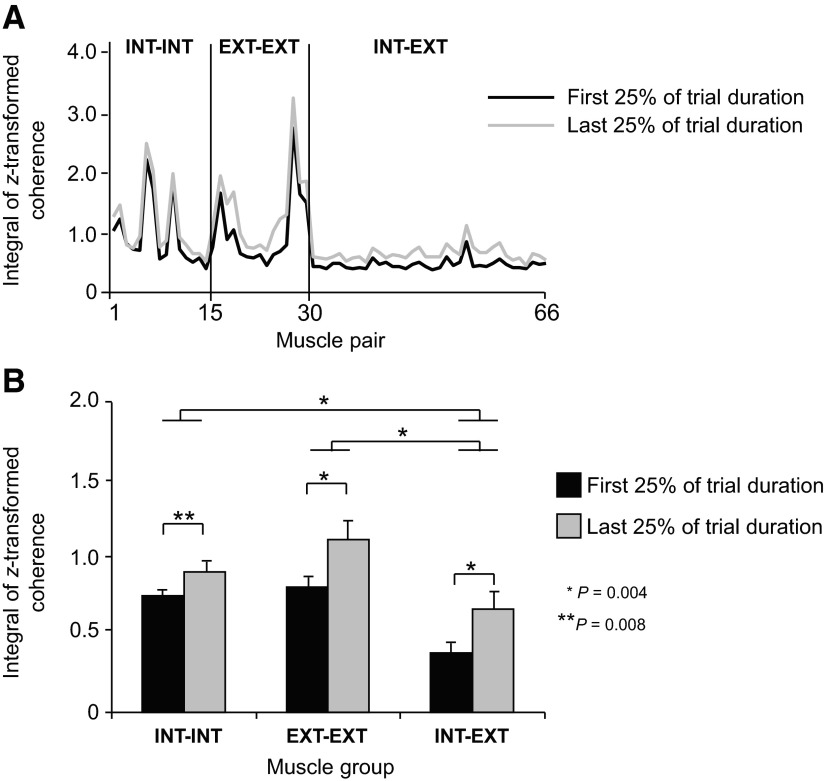
Figure 7A shows the integrals of z-transformed coherence computed on individual muscle pairs over the frequency range of 0–55 Hz and averaged across all subjects for the first and last quarter of the fatiguing contraction trial. To visualize possible across-muscle differences in the effect of fatigue on coherence, data are plotted as a function of muscle groups (extrinsic-extrinsic, intrinsic-intrinsic, and intrinsic-extrinsic; see Table 1 for muscle pair labels). The effect of fatigue on coherence was similar regardless of muscle group. However, coherence was greater for most extrinsic-extrinsic and intrinsic-intrinsic muscle pairs than for intrinsic-extrinsic muscle pairs. Nonparametric statistical analysis on the integrals of z-transformed pooled coherence computed within each muscle group confirmed a significant effect of time epoch for each muscle group (P = 0.004 for both extrinsic-extrinsic and intrinsic-extrinsic muscle groups; P = 0.008 for the intrinsic-intrinsic muscle group). We also found significantly stronger coherence for the extrinsic-extrinsic and intrinsic-intrinsic muscle groups than intrinsic-extrinsic muscle groups (P = 0.004 for both comparisons; Fig. 7B).

Fig. 7.

EMG-EMG pooled coherence for individual muscle pairs and muscle groups. A: the integral of z-transformed significant coherence computed for the 1st and last 25% of the fatiguing trial over the 0–55 Hz frequency range for each muscle pair. Data are ordered based on the muscle pair anatomical/functional characteristics: extrinsic-extrinsic, intrinsic-intrinsic, and intrinsic-extrinsic muscle pairs (EXT-EXT, INT-INT, and INT-EXT, respectively; see Table 1 for muscle pair labels). Note the stronger coherence found for the majority of muscle groups during the last 25% of the fatiguing trial (gray trace). B: the integral of z-transformed significant pooled coherence computed over the frequency range of 0–55 Hz within EXT-EXT, INT-INT, and INT-EXT muscle groups for the 1st and last quarter of the fatiguing contraction trial (black and gray bars, respectively). Significant differences and P values are shown for time epochs and muscle group comparisons. Data are averages of all subjects. Vertical bars in B denote SE.

DISCUSSION

The purpose of the present study was to quantify the extent to which muscle fatigue influences the coordination of multiple, simultaneously active hand muscles during a grasping task. As expected, the fatiguing contraction resulted in a decline in MVC force, an increase in digit force variability, and an increase in EMG amplitude. Surprisingly, however, the increase in EMG amplitude was relatively uniform across all 12 hand muscles, suggesting the involvement of fatigue-independent neural mechanisms constraining the concurrent activation pattern of multiple hand muscles. The strength of correlated neural input at frequencies <35 Hz increased throughout the contraction, whereas the heterogeneous distribution of coherence across muscle pairs remained unchanged. These results are discussed in the context of differences and similarities with mechanisms underlying voluntary modulation of digit forces during nonfatiguing contractions.

Effects of fatigue on force production

The increase in force variability with fatigue is consistent with previous reports (Cresswell and Loscher 2000; Ebenbichler et al. 2000; Mottram et al. 2005b) and is thought to be associated with the recruitment of additional motor units (Mottram et al. 2005b) as well as contributions from peripheral afferent feedback (Cresswell and Loscher 2000; McAuley and Marsden 2000; McAuley et al. 1997). In the current study, the relative contribution of each digit to the total force was similar across the four time epochs. Similarly, Danion et al. (2000) found a similar force sharing patterns during multi-finger MVCs performed before and after a multi-finger sustained MVC. Subsequent studies (Danion et al. 2001; Singh et al. 2010) showed changes in other indices of digit force coordination that could not be accounted for by peripheral mechanisms alone. These studies (Danion et al. 2001; Singh et al. 2010) provide evidence that in both maximal and submaximal fatiguing contractions descending commands responsible for digit force coordination are sensitive to fatigue.

Fatigue-induced modulation of EMG amplitude

As expected, EMG amplitude (aEMG) for all 12 muscles acting on the three digits, quantified as a 12-D MAP vector, increased progressively and at a relatively uniform rate during the fatiguing contraction (Fig. 5A). The increase in aEMG was likely due to a progressive recruitment of larger motor units (Carpentier et al. 2001; Christova and Kossev 2001; Fallentin et al. 1993; Hunter and Enoka 2003; Klass et al. 2008; Levenez et al. 2008; Mottram et al. 2005b) to maintain the target force and offset declines in motor unit discharge rate (Mottram et al. 2005b). Small hand muscles have been shown to have an upper motor unit recruitment limit of ∼50–60% of MVC (De Luca et al. 1982; Moritz et al. 2005). Therefore during nonfatiguing contractions, increases in force production ≤50–60% of MVC in hand muscles are accomplished through motor unit recruitment and increases in discharge rate while further force increases must be due solely to increases in discharge rate. Thus the initial target force of 40% of MVC provided the opportunity for the CNS to maintain the target force via increased motor unit recruitment and modulation of the discharge rate of these additional motor units as the fatiguing contraction progressed.

Motor unit discharge rate and variability can increase or decrease during a fatiguing contraction depending on the task, the type of motor unit, and the time at which the unit is sampled during the contraction. Nonetheless, the discharge rate of earlier recruited motor units generally declines with fatigue (Mottram et al. 2005b), whereas newly recruited units show an initial increase in discharge rate followed by a decrease (Carpentier et al. 2001). Furthermore, the discharge variability of both types of units generally increases with duration of the contraction. Regardless of the exact pattern of motor unit discharge activity in the present study, coherence analysis demonstrated that the progression of fatigue was accompanied by a stronger common modulation of motor unit activity (see following text).

Fatigue-independent muscle activity coordination patterns

The invariant orientation of the 12-D MAP EMG vector across the four time epochs (Fig. 5, B and C), indicating a generally uniform increase in EMG amplitude across all muscles, supports our first hypothesis. This finding is reminiscent to that described for voluntary modulation of single and multi-digit forces (Valero-Cuevas 2000 and Poston et al. 2010; respectively). To the best of our knowledge, this is the first report describing a fatigue-independent EMG coordination pattern across a large number of hand muscles. The current findings suggest that fatiguing and nonfatiguing contractions share similar neural mechanisms for constraining the uniform modulation of neural activity across simultaneously active hand muscles. This similarity is, however, striking as different neural mechanisms are involved in these two tasks. Therefore we interpret the present and previous findings as evidence for a task-independent organization of neural drive to hand muscles. The existence of correlated neural inputs to hand muscle motor nuclei is consistent with such an organization (see following text) (for a more detailed discussion, see Poston et al. 2010; Winges et al. 2008).

Studies examining changes in muscle coordination patterns occurring during fatigue have also reported changes in muscle activity coordination among synergistic muscles. However, these changes were quantified as the number of occurrences of alternate increases and decreases in aEMG of knee extensors (Kouzaki and Shinohara 2006; Kouzaki et al. 2002–2004; Shinohara et al. 2009) rather than changes in MAP vector length or orientation. Changes in coordination patterns within a single muscle, quantified as motor unit rotation or substitution, have also been reported (Fallentin et al. 1993; Kato et al. 1981; Person 1974; Sale 1987; Sjogaard et al. 1986; Westgaard and de Luca 1999). In both cases, however, these changes in muscle coordination patterns are found only at forces of 5% MVC or below. The reasons for the lack of changes in muscle coordination in these studies at higher forces are unclear but could be due to methodological limitations. For example, single motor unit recordings are difficult to maintain and discriminate at high forces. Furthermore, motor unit rotation or substitution would escape detection when using interference EMG recordings. Therefore, further investigation is required to determine whether these fatigue-induced changes are limited to very low forces.

Effect of fatigue on EMG-EMG coherence

Our results indicate that fatigue leads to a widespread strengthening of correlated neural inputs to motor nuclei of hand muscles even though this occurs in a muscle pair-specific fashion (see following text). Interestingly, the fatigue-induced increase in coherence did not interfere with the coordination of neural drive to hand muscles as quantified by the invariant orientation of the MAP EMG vector (see preceding text). These observations suggest that the mechanisms constraining the simultaneous modulation of EMG amplitude can operate independently from those modulating the strength of correlated neural inputs.

In accordance with the involvement of mechanisms binding the simultaneous activity of all muscles during muscle fatigue, the integral of the z-transformed pooled coherence across all 66 pairs of muscles was greater at the end than at the beginning of the fatiguing contraction at frequencies <35 Hz (Fig. 6B). However, this finding only partially supports our second hypothesis that EMG-EMG coherence would increase with fatigue only at frequencies >15 Hz. This hypothesis was based on the study by Kattla and Lowery (2009), who observed an increase in coherence within a frequency range of 15–60 Hz between the 1DI and FDS muscles before and immediately after sustained isometric contractions performed with the index finger. However, the discrepancy between the present task and that studied by Kattla and Lowery (2009) in the frequency bands at which EMG-EMG coherence exhibited fatigue-induced changes might be due to methodological differences. Specifically, Kattla and Lowery (2009) measured coherence before and after a fatiguing contraction and at a different target force than during the fatiguing contraction. Another difference between the two studies consists of different muscle actions during a multi-digit grip versus single digit force production.

When comparing the force ramp and constant force phases of isometric muscle contractions, Kilner et al. (1999) reported that EMG-EMG and EMG-magnetoencephalography (MEG) coherence of wrist and hand muscles modulated to task phase (stronger for constant force than ramp contractions), indicating that part of the EMG-EMG coherence was cortical in origin. These authors further proposed that the functional role of MEG-EMG coherence might be to improve the efficiency with which motor neurons are recruited (Kilner et al. 1999). Consistent with this assertion, it has also been shown that oscillatory inputs can more efficiently drive motor neurons than asynchronous inputs (Baker 1997; Murthy and Fetz 1994). Assuming that EMG-EMG coherence partly reflects cortical oscillations, the proposed role of coherence as a means to efficiently recruit motor neurons would be especially advantageous for maintaining the target force during fatiguing contractions. This is because the goal of generating a constant force has to be maintained despite a reduction in motor unit discharge rate (Carpentier et al. 2001; Mottram et al. 2005b) through the recruitment of additional motor units (Carpentier et al. 2001; Christova and Kossev 2001; Fallentin et al. 1993; Mottram et al. 2005b).

With regard to the interpretation of the sources of coherence, it has been suggested that the source of the 16–32 Hz band coherence is of central origin (Farmer et al. 1993), in particular the direct corticospinal pathways, and to a lesser extent, the somatosensory pathway (Fisher et al. 2002; Kilner et al. 2004; Riddle and Baker 2005). Others have asserted that the source of the coherent oscillations in the alpha band are not yet known but may arise from the inferior olive or thalamo-cortical loop (Llinas and Jahnsen 1982; Llinas and Yarom 1981; Mima et al. 1999). Lastly the source of the coherent oscillations between 0 and 5 Hz often termed common drive (De Luca et al. 1982) remains unknown and may originate from sources other than the corticospinal system as it is preserved in patients with cortical or capsular strokes (Farmer et al. 1993; Grosse et al. 2002), e.g., spinal mechanisms. Taken together, the increased coherence with fatigue in the 0–5, 6–15, and 16–35 Hz bands indicate that there is an increase in coherent oscillations to the muscles of the hand arising from cortical and subcortical inputs onto the motor neuron pool. Furthermore, it is possible that other spinal mechanisms may contribute to the increase in coherence observed with fatigue (Klass et al. 2008).

Effect of fatigue on the heterogeneous distribution of correlated neural input to hand muscles

As predicted by our third hypothesis, we found that the heterogeneous distribution of EMG-EMG coherence among muscle pairs was not affected by fatigue despite a significant increase in the strength of correlated neural inputs (Fig. 7, A and B). Specifically, the EMG-EMG coherence was greater across the extrinsic-extrinsic and intrinsic-intrinsic muscle pairs compared with intrinsic-extrinsic muscle pairs both in the first and last quarter of the fatiguing trials. The existence of a heterogenous distribution of EMG-EMG coherence among hand muscles is similar to that we have recently reported in a study examining EMG-EMG coherence as a function of digit force (Poston et al. 2010; but see following text). The previous and present findings suggest that the CNS binds the neural drive to hand muscles that are anatomically and/or functionally similar during constant force isometric contractions in both fatiguing and nonfatiguing contractions. These observations suggest that the distribution of correlated neural inputs remains invariant regardless of whether coherence strength remains constant across the voluntary force range (Poston et al. 2010) or increases during fatiguing contractions (present findings).

Even though coherence tended to be greater across extrinsic-extrinsic muscle pairs than intrinsic-intrinsic muscle pairs, this difference was not statistically significant (Fig. 7B). In contrast, Poston et al. (2010) found significant differences between these muscle pairs across a wide range of forces (5–80% of MVC). This small discrepancy is difficult to explain but may be due to methodological differences and thus may offer insights into the factors that influence the distribution of coherence among motor neurons supplying hand muscles. A key difference between the two studies is that the present work examined continuous fatiguing contractions, whereas Poston et al. (2010) examined brief, nonfatiguing contractions. Therefore it appears that EMG-EMG coherence distribution may be sensitive to the above-described fatigue-dependent mechanisms. Taken together, these findings suggest that the distribution of correlated input to hand muscles is not obligatory. Nonetheless the overall findings are consistent with the general framework that correlated neural input to hand muscles is heterogeneously distributed (McIssac and Fuglevand 2008; Poston et al. 2010; Winges et al. 2008). However, further work is needed to better understand the task dependency of the coherence strength and distribution to hand muscles.

Conclusions

We found that fatiguing contractions elicited phenomena similar to those associated with tasks involving voluntary force modulation: 1) an invariant muscle activity coordination pattern that scaled in magnitude, but not in the relative EMG amplitude contribution of individual muscles, and 2) an invariant distribution of neural common inputs to hand muscles. An important difference, however, was that fatigue led to an increase in coherence, whereas production of forces of different magnitudes did not. Although central and peripheral mechanisms are involved in both tasks, the difference in coherence modulation suggest the selective involvement of neural mechanisms for maintaining a constant force output while accommodating the progression of muscle fatigue versus generating forces in nonfatiguing contractions.

GRANTS

This publication was made possible by National Institute of Arthritis, Musculoskeletal and Skin Diseases Grant 2R01 AR-47301. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NIAMSD or NIH.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).