Classifying Facial Actions

Abstract

The Facial Action Coding System (FACS) [23] is an objective method for quantifying facial movement in terms of component actions. This system is widely used in behavioral investigations of emotion, cognitive processes, and social interaction. The coding is presently performed by highly trained human experts. This paper explores and compares techniques for automatically recognizing facial actions in sequences of images. These techniques include analysis of facial motion through estimation of optical flow; holistic spatial analysis, such as principal component analysis, independent component analysis, local feature analysis, and linear discriminant analysis; and methods based on the outputs of local filters, such as Gabor wavelet representations and local principal components. Performance of these systems is compared to naive and expert human subjects. Best performances were obtained using the Gabor wavelet representation and the independent component representation, both of which achieved 96 percent accuracy for classifying 12 facial actions of the upper and lower face. The results provide converging evidence for the importance of using local filters, high spatial frequencies, and statistical independence for classifying facial actions.

1 Introduction

Facial expressions provide information not only about affective state, but also about cognitive activity, temperament and personality, truthfulness, and psychopathology. The Facial Action Coding System (FACS) [23] is the leading method for measuring facial movement in behavioral science. FACS is currently performed manually by highly trained human experts. Recent advances in image analysis open up the possibility of automatic measurement of facial signals. An automated system would make facial expression measurement more widely accessible as a tool for research and assessment in behavioral science and medicine. Such a system would also have applications in human-computer interaction.

This paper presents a survey and comparison of recent techniques for facial expression recognition as applied to automated FACS encoding. Recent approaches include measurement of facial motion through optic flow [44], [64], [54], [26], [15], [43] and analysis of surface textures based on principal component analysis (PCA) [17], [48], [40]. In addition, a number of methods that have been developed for representing faces for identity recognition may also be powerful for expression analysis. These approaches are also included in the present comparison. These include Gabor wavelets [20], [39], linear discriminant analysis [8], local feature analysis [49], and independent component analysis [5], [4]. The techniques are compared on a single image testbed. The analysis focuses on methods for face image representation (generation of feature vectors) and the representations are compared using a common similarity measure and classifier.

1.1 The Facial Action Coding System

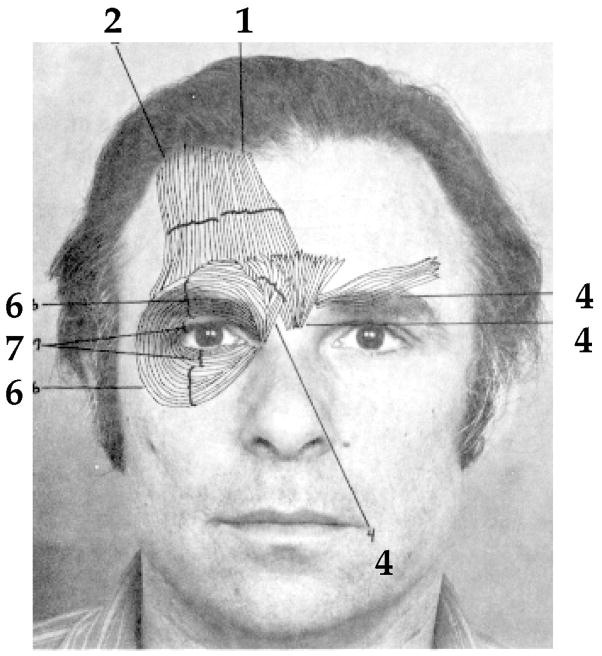
FACS was developed by Ekman and Friesen [23] in 1978 to objectively measure facial activity for behavioral science investigations of the face. It provides an objective description of facial signals in terms of component motions, or “facial actions.” FACS was developed by determining from palpation, knowledge of anatomy, and videotapes how the contraction of each of the facial muscles changed the appearance of the face (see Fig. 1). Ekman and Friesen defined 46 Action Units, or AUs, to correspond to each independent motion of the face. A trained human FACS coder decomposes an observed expression into the specific AUs that produced the expression. FACS is coded from video and the code provides precise specification of the dynamics (duration, onset, and offset time) of facial movement in addition to the morphology (the specific facial actions which occur).

Fig. 1.

The Facial Action Coding System decomposes facial motion into component actions. The upper facial muscles corresponding to action units 1, 2, 4, 6, and 7 are illustrated. Reprinted with permission from Ekman and Friesen (1978).

FACS continues to be the leading method for measuring facial expressions in behavioral science (see [25] for a review). This system has been used, for example, to demonstrate differences between genuine and simulated pain [19], differences between when people are telling the truth versus lying [22], and differences between the facial signals of suicidal and nonsuicidally depressed patients [34]. Although FACS is a promising approach, a major impediment to its widespread use is the time required to both train human experts and to manually score the video tape. It takes over 100 hours of training to achieve minimal competency on FACS and each minute of video tape takes approximately one hour to score. Automating FACS would make it more widely accessible as a research tool. It would not only increase the speed of coding, it would also improve the reliability, precision, and temporal resolution of facial measurement.

Aspects of FACS have been incorporated into computer graphic systems for synthesizing facial expressions (e.g., Toy Story [38]) and into facial muscle models for parameterizing facial movement [55], [44]. It is important to distinguish FACS itself from facial muscle models that employ aspects of FACS. In particular, there has been a tendency to confuse FACS with CANDIDE [55]. FACS is performed by human observers using stop-motion video. Although there are clearly defined relationships between FACS and the underlying facial muscles, FACS is an image-based method. Facial actions are defined by the image changes they produce in video sequences of face images.

1.2 Automated Facial Expression Measurement

Recent advances have been made in computer vision for automatic recognition of facial expressions in images. The approaches that have been explored include analysis of facial motion [44], [64], [54], [26], measurements of the shapes of facial features and their spatial arrangements [40], [66], holistic spatial pattern analysis using techniques based on principal component analysis [17], [48], [40], graylevel pattern analysis using local spatial filters [48], [66], and methods for relating face images to physical models of the facial skin and musculature [44] [59], [42], [26]. The image analysis techniques in these systems are relevant to the present goals, but the systems themselves are of limited use for behavioral science investigations of the face (see [31] for a discussion). Many of these systems were designed with an objective of classifying facial expressions into a few basic categories of emotion, such as happy, sad, or surprised. For basic science investigations of facial behavior itself, such as studying the difference between genuine and simulated pain, an objective and detailed measure of facial activity such as FACS is needed. Several computer vision systems explicitly parameterize facial movement [64] and relate facial movements to the underlying facial musculature [44], [26], but it is not known whether these descriptions are sufficient for describing the full range of facial behavior. For example, movement parameters that were estimated from posed, prototypical expressions may not be appropriate descriptors for spontaneous facial expressions, which differ from posed expressions in both their morphology and their dynamics [31]. Furthermore, the relationship between these movement parameters and internal state has not been investigated to the extent that FACS has been. There is over 20 years of behavioral data on the relationships of facial action codes to emotion and to state variables such as deceit, interest, depression, and psychopathology.

In addition to providing a tool for basic science research, a system that outputs facial action codes would provide a strong basis for human-computer interaction systems. In natural interaction, prototypic expressions of basic emotions occur relatively infrequently. Annoyance, for example, may be indicated by just a lowering of the brows or tightening of the mouth. FACS provides a description of the basic elements of any facial movement, analogous to phonemes in speech. Facial action codes also provide more detailed information about facial behavior, including information about variations within an emotional category (e.g., vengeance vs. resentment), variations in intensity (e.g., annoyance vs. fury), blends of two or more emotions (e.g., happiness + disgust → smug), facial signals of deceit, signs of boredom or interest, and conversational signals that provide emphasis to speech and information about syntax.

Explicit attempts to automate the facial action coding system involved tracking the positions of dots attached to the face [35], [37]. A system that detects facial actions from image sequences without requiring application of dots to the subjects face would have much broader utility. Efforts have recently turned to measuring facial actions by image processing of video sequences [6], [4], [15]. Cohn et al. [15] achieved some success for automated facial action coding by feature point tracking of a set of manually located points in the face image (fiducial points). Here, we explore image representations based on full field analysis of the face image, not just displacements of selected feature points. Techniques employing 2D filters of image graylevels have proven to be more effective than feature-based representations for identity recognition [13], [40] and expression recognition [66]. In our previous work on automatic facial action coding [6], [3], [2], we found that full-field representations of image textures and image motion provided more reliable indicators of facial actions than task-specific feature measurements such as the increase of facial wrinkles in specific facial regions.

Several facial expression recognition systems have employed explicit physical models of the face [44], [59], [42], [26]. There are numerous factors that influence the motion of the skin following muscle contraction, and it is difficult to accurately account for all of them in a deterministic model. Here, we take an image-based approach in which facial action classes are learned directly from example image sequences of the actions, bypassing the physical model. Image-based approaches have recently been advocated [11] and can successfully accomplish tasks previously assumed to require mapping onto a physical model, such as expression synthesis, face recognition across changes in pose, and synthesis across pose [12], [61].

2 Overview

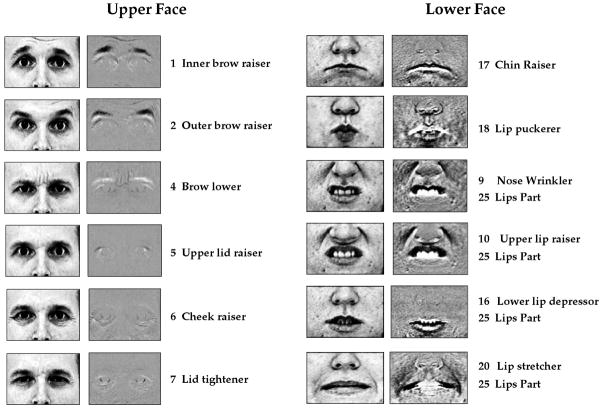
This paper explores and compares approaches to face image representation. Section 3 presents the image database used for the comparative study and the image preprocessing techniques. We examined a number of techniques that have been presented in the literature for processing images of faces and compare their performance on the task of facial action classification. These approaches were grouped into the following classes: analysis of facial motion, holistic spatial analysis, and local spatial analysis. Section 4 examines a representation of facial motion based on optic flow. The technique is a correlation-based method with subpixel accuracy [58]. Because local smoothing is commonly imposed on flow fields to clean up the signal, we also examined the effects of local smoothing on classification of facial motion. Holistic spatial analysis is an approach that employs image-dimensional graylevel texture filters. Many of these approaches employ data-driven kernels learned from the statistics of the face image ensemble. These approaches include eigenfaces [60], [17], [48], [40] and local feature analysis (LFA) [49], in which the kernels are learned through unsupervised methods based on principal component analysis (PCA). Eigenface and LFA kernels are derived from the second-order dependencies among the image pixels, whereas independent component analysis (ICA) learns kernels from the high-order dependencies in addition to the second-order dependencies among the pixels [5], [4], [2]. Another class of holistic kernel, Fisher’s linear discriminants (FLD) [8], is learned through supervised methods, and finds a class-specific linear projection of the images. Section 5 compares four representations derived from holistic spatial analysis: eigenfaces (PCA), LFA, ICA, and FLD. Local spatial analysis is an approach in which spatially local kernels are employed to filter the images. These include predefined families of kernels, such as Gabor wavelets [20], [39], [66], and data-driven kernels learned from the statistics of small image patches, such as local PCA [48]. Section 6 examines two representations based on the outputs of local spatial filters: local PCA and a Gabor wavelet representation. The two local representations were further compared via a hybrid representation, local PCA jets. Section 7 provides benchmarks for the performance of the computer vision systems by measuring the ability of naive and expert human subjects to classify the facial actions.

3 Image Database

We collected a database of image sequences of subjects performing specified facial actions. The full database contains over 1,100 sequences containing over 150 distinct actions, or action combinations, and 24 different subjects. Each sequence contained six images, beginning with a neutral expression and ending with a high magnitude muscle contraction. Trained FACS experts provided demonstrations and instructions to subjects on how to perform each action. The selection of images was based on FACS coding of stop motion video. The images were coded by three experienced FACS coders certified with high intercoder reliability. The criterion for acceptance of images was that the requested action and only the requested action was present. Sequences containing rigid head motion detectable by a human observer were excluded. For this investigation, we used data from 20 subjects and attempted to classify 12 actions: six upper face actions and six lower face actions. See Fig. 2 for a summary of the actions examined. There were a total of 111 action sequences, (9, 10, 18, 20, 5, 18), respectively, of the six upper face actions, and (8, 4, 4, 5, 4, 6) of the six lower face actions. The actions were divided into upper and lower-face categories because facial actions in the lower face have little influence on facial motion in the upper face and vice versa [23], which allowed us to treat them separately.

Fig. 2.

List of facial actions classified in this study. From left to right: Example cropped image of the highest magnitude action, the δ image obtained by subtracting the neutral frame (the first image in the sequence), Action Unit number, and Action Unit name.

The face was located in the first frame in each sequence using the centers of the eyes and mouth. These coordinates were obtained manually by a mouse click. Accurate image registration is critical to holistic approaches such as principal component analysis. An alignment procedure similar to this one was found to give the most accurate image registration during the FERET test [50]. The variance in the assigned feature location using this procedure was 0.4 pixels in the 640 × 480 pixel images. The coordinates from Frame 1 were used to register the subsequent frames in the sequence. We found in pilot investigations that rigid head motion was smaller than the positional noise in the registration procedure. The three coordinates were used to align the faces, rotate the eyes to horizontal, scale, and, finally, crop a window of 60 × 90 pixels containing the region of interest (upper or lower face). The aspect ratios of the faces were warped so that the eye and mouth centers coincided across all images. It has been found that identity recognition performance using principal component-based approaches is most successful when the images are warped to remove variations in facial shape [11], [62].

To control the variation in lighting between frames of the same sequence and in different sequences, we applied a logistic filter with parameters chosen to match the statistics of the grayscale levels of each sequence [46]. This procedure enhanced the contrast, performing a partial histogram equalization on the images.

4 Optic Flow Analysis

The majority of work on facial expression recognition has focused on facial motion analysis through optic flow estimation. In an early exploration of facial expression recognition, Mase [44] used optic flow to estimate the activity in a subset of the facial muscles. Essa and Pentland [26] extended this approach, using optic flow to estimate activity in a detailed anatomical and physical model of the face. Motion estimates from optic flow were refined by the physical model in a recursive estimation and control framework and the estimated forces were used to classify the facial expressions. Yacoob and Davis [64] bypassed the physical model and constructed a mid-level representation of facial motion, such as “right mouth corner raises,” directly from the optic flow. These mid-level representations were classified into one of six facial expressions using a set of heuristic rules. Rosenblum et al. [54] expanded this system to model the full temporal profile of facial expressions with radial basis functions, from initiation, to apex, and relaxation. Cohn et al. [15] are developing a system for automatic facial action classification based on feature-point tracking. The displacements of 36 manually located feature points are estimated using optic flow and classified using discriminant functions.

Here, optic flow fields were estimated by employing a correlation-based technique developed by Singh [58]. This algorithm produces flow fields with subpixel accuracy and is comprised of two main components: 1) local velocity extraction using luminance conservation constraints, 2) local smoothing.

4.1 Local Velocity Extraction

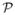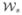We start with a sequence of three images at time t = t₀ − 1, t₀, t₀ + 1 and use it to recover all the velocity information available locally. For each pixel (x, y) in the central image (t = t₀), 1) a small window () of 3 × 3 pixels is formed around , 2) a search area () of 5 × 5 pixels is considered around location (x, y) in the other two images, 3) the correlation between (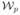) and the corresponding window centered on each pixel in (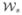) is computed, thus giving the matching strength, or response, at each pixel in the search window ().

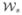At the end of this process, (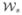) is covered by a response distribution (ℛ) in which the response at each point gives the frequency of occurrence, or likelihood, of the corresponding value of velocity. Employing a constant temporal model, the response distributions for the two windows corresponding to t₀ − 1 and t₀ + 1, (ℛ₋₁ and ℛ₊₁), are combined by R = ℛ₊₁ + πℛ₋₁. Velocity is then estimated using the weighted least squares estimate in (1). Fig. 3 shows an example flow field obtained by this algorithm.

Fig. 3.

Optic flow for AU1 extracted using local velocity information extracted by the correlation-based technique, with no spatial smoothing.

$$\widehat{u}=\frac{{\sum }_u{\sum }_v\mathcal{R}(u,v)u}{{\sum }_u{\sum }_v\mathcal{R}(u,v)}\widehat{v}=\frac{{\sum }_u{\sum }_v\mathcal{R}(u,v)v}{{\sum }_u{\sum }_v\mathcal{R}(u,v)}u,v\in [-2,2].$$ (1)

4.2 Local Smoothing

To refine the conservation constraint estimate 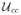= (û, v̂) obtained above, a local neighborhood estimate of velocity, 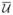, is defined as a weighted sum of the velocities in a neighborhood of 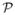using a 5 × 5 Gaussian mask. An optimal estimate 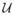of (u, v) should combine the two estimates 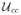and 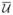, from the conservation and local smoothness constraints respectively. Since 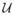is a point in (u, v) space, its distance from 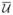, weighted by its covariance matrix 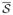, represents the error in the smoothness constraint estimate. Similarly, the distance between 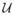and 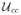weighted by 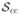represents the error due to conservation constraints. Computing 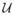, then, amounts to simultaneously minimizing the two errors:

$$\mathcal{U}=argmin\{{\left|\right|\mathcal{U}-{\mathcal{U}}_{cc}\left|\right|}_{{\mathcal{S}}_{cc}}\wedge {\left|\right|\mathcal{U}-\overline{\mathcal{U}}\left|\right|}_{\overline{\mathcal{S}}}\}.$$ (2)

Since we do not know the true velocity, this estimate must be computed iteratively. To update the field, we use the equations [58]:

$$\begin{array}{l}{\mathcal{U}}^0={\mathcal{U}}_{cc}\\ {\mathcal{U}}^{k+1}={\left[{\mathcal{S}}_{cc}^{-1}+{\overline{\mathcal{S}}}^{-1}\right]}^{-1}\left[{\mathcal{S}}_{cc}^{-1}{\mathcal{U}}_{cc}+{\overline{\mathcal{S}}}^{-1}{\overline{\mathcal{U}}}^k\right],\end{array}$$ (3)

where 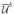is the estimate derived from smoothness constraints at step k. The iterations stop when

$$\left|\right|{\mathcal{U}}^{k+1}-{\mathcal{U}}^k\left|\right|<\epsilon ,$$

with ε ∝ 10⁻⁴.

4.3 Classification Procedure

The following classification procedures were used to test the efficacy of each representation in this comparison for facial action recognition. Each image analysis algorithm produced a feature vector, f. We employed a simple nearest neighbor classifier in which the similarity S of a training feature vector, f^t, and a novel feature vector, fⁿ, was measured as the cosine of the angle between them:

$$S(f^n,f^t)=\frac{\langle f^n,f^t\rangle }{\left|\right|f^n\left|\right|·\left|\right|f^t\left|\right|}\in [-1,1].$$ (4)

Classification performances were also evaluated using Euclidean distance, instead of cosine, as the similarity measure and template matching, instead of nearest neighbor as the classifier, where the templates consisted of the mean feature vector for the training images. The similarity measure and classifier that gave the best performance is indicated for each technique.

The algorithms were trained and tested using leave-one-out cross-validation, also known as the jack-knife procedure, which makes maximal use of the available data for training. In this procedure, the image representations were calculated multiple times, each time using images from all but one subject for training and reserving one subject for testing. This procedure was repeated for each of the 20 subjects and mean classification accuracy was calculated across all of the test cases.

Table 1 presents classification performances for the medium magnitude facial actions, which occur in the middle of each sequence. Performance was consistently highest for the medium magnitude actions. Flow fields were calculated from frames 2, 3, and 4 of the image sequence and the performance of the brightness-based algorithms is presented for frame 4 of each sequence. A class assignment is considered “correct” if it is consistent with the labels assigned by human experts during image collection. The consistency of human experts with each other on this image set is indicated by the agreement rates also shown in Table 1.

TABLE 1.

Best Performance for Each Classifier

Optic Flow	Correlation	85.6% ± 3.3
	Smoothed	53.1% ± 4.7
Holistic Spatial Analysis	PCA	79.3% ± 3.9
	LFA	81.1% ± 3.7
	FLD	75.7% ± 4.1
	ICA	95.5% ± 2.0
Local Spatial Analysis	Gaussian Kernel	70.3 ± 4.
	PCA Shift-inv	73.4% ± 4.2
	PCA Shift-var	78.3% ± 3.9
	PCA Jets	72.1% ± 4.2
	Gabor Jets	95.5% ± 2.0
Human Subjects	Naive	77.9% ± 2.5
	Expert	94.1% ± 2.1

PCA: Principal component analysis. LFA: Local feature analysis. FLD: Fisher’s linear discriminant. ICA: Independent component analysis. Shift-inv: Shift-invariant. Shift-var: Shift-variant.

4.4 Optic Flow Performance

Best performance for the optic flow approach was obtained using the the cosine similarity measure and template matching classifier. The correlation-based flow algorithm gave 85.6 percent correct classification performance. Since optic flow is a noisy measure, many flow-based expression analysis systems employ regularization procedures such as smoothing and quantizing. We found that spatial smoothing did not improve performance and, instead, degraded it to 53.1 percent. It appears that high spatial resolution optic flow is important for facial action classification. In addition, the motion in facial expression sequences is nonrigid and can be highly discontinuous due to the formation of wrinkles. Smoothing algorithms that are not sensitive to these boundaries can be disadvantageous.

There are a variety of choices of flow algorithms, of which Singh’s correlation-based algorithm is just one. Also, it is possible that adding more data to the flow field estimate could improve performance. The results obtained here, however, were comparable to the performance of other facial expression recognition systems based on optic flow [64], [54]. Optic flow estimates can also be further refined, such as with a Kalman filter in an estimation-and-control framework (e.g., [26]). The comparison here addresses direct, image-based representations that do not incorporate a physical model. Sequences of flow fields can also be analyzed using dynamical models, such as an HMMs or radial basis functions (e.g., [54]). Such dynamical models could also be employed with texture-based representations. Here, we compare all representations using the same classifiers.

5 Holistic Analysis

A number of approaches to face image analysis employ data-driven kernels learned from the statistics of the face image ensemble. Approaches such as eigenfaces [60] employ principal component analysis, which is an unsupervised learning method based on the second-order dependencies among the pixels. Second-order dependencies are pixelwise covariances. Representations based on principal component analysis have been applied successfully to recognizing facial identity [18], [60], classifying gender [17], [29], and recognizing facial expressions [17], [48], [6].

Penev and Atick [49] recently developed a topographic representation based on second-order image dependencies called local feature analysis (LFA). A representation based on LFA gave the highest performance on the March 1995 FERET face recognition competition [51]. The LFA kernels are spatially local, but, in this paper, we class this technique as holistic since the image-dimensional kernels are derived from statistical analysis over the whole image. Another holistic image representation that has recently been shown to be effective for identity recognition is based on Fisher’s Linear discriminants (FLD) [8]. FLD is a supervised learning method that uses second-order statistics to find a class-specific linear projection of the images. Representations such as PCA (eigenfaces), LFA, and FLD do not address high-order statistical dependencies in the image. A representation based on independent component analysis (ICA) was recently developed which is based on the high-order, in addition to the second-order dependencies in the images [5], [4], [2]. The ICA representation was found to be superior to the eigenface (PCA) representation for classifying facial identity.

The holistic spatial analysis algorithms examined in this section each found a set of n-dimensional data-driven image kernels, where n is the number of pixels in each image. The analysis was performed on the difference (or δ) images (Fig. 2), obtained by subtracting the first image in a sequence (neutral frame) from each of the subsequent frames in each sequence. Advantages of difference images include robustness to changes in illumination, removal of surface variations between subjects, and emphasis of the dynamic aspects of the image sequence [46]. The kernels were derived from low, medium, and high magnitude actions. Holistic kernels for the upper and lower-face subimages were calculated separately.

The methods in this section begin with a data matrix X where the δ-images were stored as row vectors x_j, and the columns had zero mean. In the following descriptions, n is the number of pixels in each image, N is the number of training images and p is the number of principal components retained to build the final representation.

5.1 Principal Component Analysis: “EigenActions”

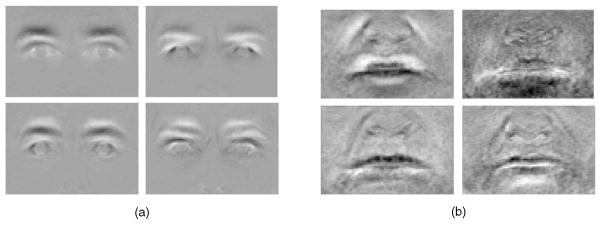
This approach is based on [17] and [60], with the primary distinction in that we performed principal component analysis on the dataset of difference images. The principal components were obtained by calculating the eigenvectors of the pixelwise covariance matrix, S, of the δ-images, X. The eigenvectors were found by decomposing S into the orthogonal matrix P and diagonal matrix D: S = PDP^T. Examples of the eigenvectors are shown in Fig. 4. The zero-mean δ-frames of each sequence were then projected onto the first p eigenvectors in P, producing a vector of p coefficients for each image.

Fig. 4.

First four principal components of the difference images for the (a) upper face actions and (b) lower face actions. Components are ordered left to right, top to bottom.

Best performance with the holistic principal component representation, 79.3 percent correct, was obtained with the first 30 principal components, using the Euclidean distance similarity measure and template matching classifier. Previous studies (e.g., [8]) reported that discarding the first one to three components improved performance. Here, discarding these components degraded performance.

5.2 Local Feature Analysis (LFA)

Local Feature Analysis (LFA) defines a set of topographic, local kernels that are optimally matched to the second-order statistics of the input ensemble [49]. The kernels are derived from the principal component axes and consist of “sphering” the PCA coefficients to equalize their variance [1], followed by a rotation to pixel space. We begin with the zero-mean matrix of δ-images, X, and calculate the principal component eigenvectors P according to S = PDP^T. Penev and Atick [49] defined a set of kernels, K as

$$K={\mathit{PVP}}^T\text{where}V=D^{-\frac{1}{2}}=\text{diag}\left(\frac{1}{\sqrt{{\lambda }_i}}\right)i=1,\dots ,p,$$ (5)

where λ_i are the eigenvalues of S. The rows of K contain the kernels. The kernels were found to have spatially local properties and are “topographic” in the sense that they are indexed by spatial location [49]. The kernel matrix K transforms X to the LFA output O = KX^T (see Fig. 5). Note that the matrix V is the inverse square root of the covariance matrix of the principal component coefficients. This transform spheres the principal component coefficients (normalizes their output variance to unity) and minimizes correlations in the LFA output. Another way to interpret the LFA output O is that it is the image reconstruction using sphered PCA coefficients, O = P(V P^TX^T).

Fig. 5.

(a) An original δ-image, (b) its corresponding LFA output O(x), and (c) the first 155 filter locations selected by the sparsification algorithm superimposed on the mean upper face δ-image.

5.2.1 Sparsification of LFA

LFA produces an n-dimensional representation, where n is the number of pixels in the images. Since we have n outputs described by p ≪ n linearly independent variables, there are residual correlations in the output. Penev and Atick presented an algorithm for reducing the dimensionality of the representation by choosing a subset ℳ of outputs that were as decorrelated as possible. The sparsification algorithm was an iterative algorithm based on multiple linear regression. At each time step, the output point that was predicted most poorly by multiple linear regression on the points in ℳ was added to ℳ. Due to the topographic property of the kernels, selection of output points was equivalent to selection of kernels for the representation.

The methods in [49] addressed image representation but did not address recognition. The sparsification algorithm in [49] selected a different set of kernels, ℳ, for each image, which is problematic for recognition. In order to make the representation amenable to recognition, we selected a single set ℳ of kernels for all images. At each time step, the kernel corresponding to the pixel with the largest mean reconstruction error across all images was added to ℳ.

At each step, the kernel added to ℳ is chosen as the kernel corresponding to location

$$argmax\langle {\left|\right|O-O^{\mathit{rec}}\left|\right|}^2\rangle ,$$ (6)

where O^rec is a reconstruction of the complete output, O, using a linear predictor on the subset of the outputs O generated from the kernels in ℳ. The linear predictor is of the form:

$$\mathcal{Y}=\beta \mathcal{X},$$ (7)

where 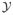= O^rec, β is the vector of the regression parameters, and = O(ℳ, N). Here, O(ℳ, N) denotes the subset of O corresponding to the points in ℳ for all N images.¹

β is calculated from:

$$\beta =\frac{\mathcal{Y}\mathcal{X}}{({\mathcal{X}}^T\mathcal{X})}=\frac{{(O^{\mathit{rec}})}^{T}O(\mathcal{M},\mathcal{N})}{O{(\mathcal{M},\mathcal{N})}^{\mathcal{T}}\mathcal{O}(\mathcal{M},\mathcal{N})}.$$ (8)

Equation (8) can also be expressed in terms of the correlation matrix of the outputs, C = O^TO, as in [49]:

$$\beta =C(\mathcal{M},\mathcal{N})C{(\mathcal{M},\mathcal{M})}^{-1}.$$ (9)

The termination condition was |ℳ| = N. Fig. 5 shows the locations of the points selected by the sparsification algorithm for the upper-face images. We evaluated classification performance using the first i kernels selected by the sparsification algorithm, up to N = 155.

The local feature analysis representation attained 81.1 percent correct classification performance. Best performance was obtained using the first 155 kernels, the cosine similarity measure, and nearest neighbor classifier. Classification performance using LFA was not significantly different from the performance using global PCA. Although a face recognition algorithm related to LFA outperformed eigenfaces in the March 1995 FERET competition [51], our results suggest that an aspect of the algorithm other than the LFA representation accounts for the difference in performance. The exact algorithm used in the FERET test has not been disclosed.

5.3 “FisherActions”

This approach is based on the original work by Belhumeur et al. [8] that showed that a class-specific linear projection of a principal components representation of faces improved identity recognition performance. The method is based on Fisher’s linear discriminant (FLD) [28], which projects the images into a subspace in which the classes are maximally separated. FLD assumes linear separability of the classes. For identity recognition, the approach relied on the assumption that images of the same face under different viewing conditions lie in an approximately linear subspace

$$1.O(\mathcal{M},N)=O(i,j),\forall i\in \mathcal{M},\forall j=1,\dots ,N.$$

of the image space, an assumption which holds true for changes in lighting if the face is modeled by a Lambertian surface [56], [32]. In our dataset, the lighting conditions are fairly constant and most of the variation is suppressed by the logistic filter. The linear assumption for facial expression classification is that the δ-images of a facial action across different faces lie in a linear subspace.

Fisher’s Linear Discriminant is a projection into a subspace that maximizes the between-class scatter while minimizing the within-class scatter of the projected data. Let ( $\chi \triangleq \{{\chi }_1,{\chi }_2,\dots ,{\chi }_c\}$) be the set of all N = |χ| data, divided into c classes. Each class χ_i is composed of a variable number of images x_i ∈ Rⁿ. The between-class scatter matrix S_B and the inter-class scatter matrix S_W are defined as

$$\begin{array}{l}{S}_B\triangleq \sum _{i=1}^c\mid {\chi }_i\mid ({\mu }_i-\mu ){({\mu }_i-\mu )}^T\text{and}\\ S_W\triangleq \sum _{i=1}^c\sum _{x_k\in {\chi }_i}(x_k-{\mu }_i){(x_k-{\mu }_i)}^T,\end{array}$$ (10)

where μ_i is the mean image of class χ_i and μ is the mean of all data. W_opt projects (Rⁿ↦R^c−1) and satisfies

$$\begin{array}{l}{W}_{\mathit{opt}}=arg\underset{W}{max}J(W)\triangleq arg\underset{W}{max}\frac{det(W^T{S}_{B}W)}{det(W^T{S}_{W}W)}\\ =\{w_1,w_2,\dots ,w_{c-1}\}.\end{array}$$ (11)

The {w_i} are the solutions to the generalized eigenvalues problem S_Bw_i = λ_iS_W w_i for i = 1, …, c − 1. Following [8], the calculations are greatly simplified by first performing PCA on the total scatter matrix (S_T = S_W + S_B) to project the feature space to R^p. Denoting the PCA projection matrix W_pca, we project S_W and S_B:

$${\stackrel{\sim }{S}}_B\triangleq W_{\mathit{pca}}^T{S}_B{W}_{\mathit{pca}}\text{and}{\stackrel{\sim }{S}}_W\triangleq W_{\mathit{pca}}^T{S}_W{W}_{\mathit{pca}}.$$ (12)

The original FLD problem is thus reformulated as:

$$\begin{array}{l}{W}_{\mathit{fld}}=arg\underset{W}{max}J(W)\triangleq arg\underset{W}{max}\frac{det(W^T{\stackrel{\sim }{S}}_{B}W)}{det(W^T{\stackrel{\sim }{S}}_{W}W)}\\ =\{w_1^{\prime },w_2^{\prime },\dots ,w_{c-1}^{\prime }\}.\end{array}$$ (13)

From (11) and (13), W_opt = W_pcaW_fld, and the { $w_i^{\prime }$} can now be calculated using ${\stackrel{\sim }{S}}_W^{-1}{\stackrel{\sim }{S}}_B{w}_i^{\prime }={\lambda }_i{w}_i^{\prime }$, where S̃_W is full-rank for p ≤ N − c.

Best performance was obtained by choosing p = 30 principal components to first reduce the dimensionality of the data. The data was then projected down to five dimensions via the projection matrix, W_fld. Best performance of 75.7 percent correct was obtained with the Euclidean distance similarity measure and template matching classifier.

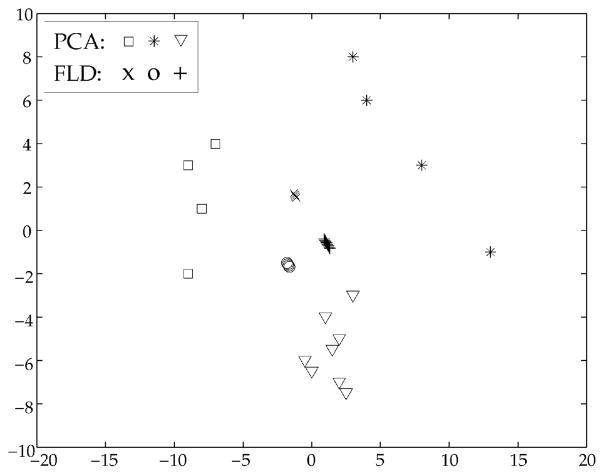
Clustering with FLD is compared to PCA in Fig. 6. As an example, three lower face actions were projected down to c − 1 = 2 dimensions using FLD and PCA. The FLD projection virtually eliminated within-class scatter of the training set and the exemplars of each class were projected to a single point. The three actions in this example were 17, 18, and 9 + 25.

Fig. 6.

PCA and FLD projections of three lower-face action classes onto two dimensions. FLD projections are slightly offset for visibility. FLD projected each class to a single point.

Contrary to the results obtained in [8], Fisher’s Linear Discriminants did not improve classification over basic PCA (eigenfaces), despite providing a much more compact representation of the data that optimized linear discrimination. This suggests that the linear subspace assumption was violated more catastrophically for our dataset than for the dataset in [8] which consisted of faces under different lighting conditions. Another reason for the difference in performance may be due to the problem of generalization to novel subjects. The FLD method achieved the best performance on the training data (close to 100 percent), but generalized poorly to new individuals. This is consistent with other reports of poor generalization to novel subjects [14] (also H. Wechsler, personal communication). Good performance with FLD has only been obtained when other images of the test subject were included in the training set. The low dimensionality may provide insufficient degrees of freedom for linear discrimination between classes of face images [14]. Class discriminations that are approximately linear in high dimensions may not be linear when projected down to as few as five dimensions.

5.4 Independent Component Analysis

Representations such as eigenfaces, LFA, and FLD are based on the second-order dependencies of the image set, the pixelwise covariances, but are insensitive to the high-order dependencies of the image set. High-order dependencies in an image include nonlinear relationships among the pixel grayvalues, such as edges, in which there is phase alignment across multiple spatial scales, and elements of shape and curvature. In a task such as facial expression analysis, much of the relevant information may be contained in the high-order relationships among the image pixels. Independent component analysis (ICA) is a generalization of PCA which learns the high-order moments of the data in addition to the second-order moments. In a direct comparison, a face representation based on ICA outperformed PCA for identity recognition. The methods in this section are based on [5], [4], [2].

The independent component representation was obtained by performing “blind separation” on the set of face images [5], [4], [2]. In the image synthesis model of Fig. 7, the δ-images in the rows of X are assumed to be a linear mixture of an unknown set of statistically independent source images S, where A is an unknown mixing matrix. The sources are recovered by a learned unmixing matrix W, which approximates A⁻¹ and produces statistically independent outputs, U.

Fig. 7.

Image synthesis model for the ICA representation.

The ICA unmixing matrix W was found using an unsupervised learning algorithm derived from the principle of optimal information transfer between neurons [9], [10]. The algorithm maximizes the mutual information between the input and the output of a nonlinear transfer function g. A discussion of how information maximization leads to independent outputs can be found in [47], [9], [10]. Let u = Wx, where x is a column of the image matrix X and y = g(u). The update rule for the weight matrix, W, is given by

$$\begin{array}{l}\mathrm{\Delta }W=(I+y^{\prime }{u}^T)W\\ \text{where}{y}^{\prime }=\frac{\partial }{\partial y_i}\frac{\partial y_i}{\partial u_i}=\frac{\partial }{\partial u_i}ln\frac{\partial y_i}{\partial u_i}.\end{array}$$ (14)

We employed the logistic transfer function, $g(u)=\frac{1}{1+e^{-u}}$, giving y′ = (1 − 2y_i). Convergence is greatly speeded by including a “sphering” step prior to learning [10], in which the zero-mean dataset X is passed through the whitening filter, $W_Z=2\ast {\langle {XX}^T\rangle }^{-\frac{1}{2}}$. This removes both the first and the second-order dependencies from the data. The full transform was, therefore, W = W_I * W_Z, where W_I is the weight obtained by information maximization in (14).

The projection of the image set onto each weight vector in W produced an image of the statistical dependencies that each weight vector learned. These images are the rows of the output matrix U and examples are shown in Fig. 8. The rows of U are the independent components of the image set and they provided a basis set for the expression images. The ICA representation consisted of the coefficients, a, for the linear combination of basis images in U that comprised each face image in X. These coefficients were obtained from the rows of the estimated mixing matrix $A\triangleq W^{-1}$ [4]. The number of independent components extracted by the ICA algorithm corresponds with the dimensionality of the input. Two hundred independent components were extracted for the upper and lower face image sets, respectively. Since there were more than 200 images, ICA was performed on 200 linear mixtures of the faces without affecting the image synthesis model. The first 200 PCA eigenvectors were chosen for these linear mixtures since they give the combination of the images that accouts for the maximum variability among the pixels. The eigenvectors were normalized to unit length. Details are available in [24

Fig. 8.

Sample ICA basis images.

Unlike PCA, there is no inherent ordering to the independent components of the dataset. We therefore selected as an ordering parameter the class discriminability of each component. Let ā_k be the overall mean of coefficient a_k and ā_jk be the mean for action j. The ratio of between-class to within-class variability, r, for each coefficient is defined as

$$r=\frac{{\sigma }_{\mathit{between}}}{{\sigma }_{\mathit{within}}},$$ (15)

where σ_between = Σ_j(ā_jk − ā_k)² is the variance of the j class means and σ_within = Σ_jΣ_i(a_ijk − ā_jk)² is the sum of the variances within each class. The first p components selected by class discriminability comprised the independent component representation.

Best performance of 95.5 percent was obtained with the first 75 components selected by class discriminability, using the cosine similarity measure and nearest neighbor classifier. Independent component analysis gave the best performance among all of the holistic classifiers. Note, however, that the independent component images in Fig. 8 were local in nature. As in LFA, the ICA algorithm analyzed the images as whole, but the basis images that the algorithm learned were local. Two factors contributed to the local property of the ICA basis images: Most of the statistical dependencies were in spatially proximal image locations and, second, the ICA algorithm produces sparse outputs [10].

6 Local Representations

In the approaches described in Section 5, the kernels for the representation were learned from the statistics of the entire image. There is evidence from a number of sources that local spatial filters may be superior to global spatial filters for facial expression classification. Padgett and Cottrell [48] found that “eigenfeatures,” consisting of the principal components of image subregions containing the mouth and eyes, were more effective than global PCA (full-face eigenfaces) for facial expression recognition. Furthermore, they found that a set of shift-invariant local basis functions derived from the principal components of small image patches were more effective than both eigenfeatures and global PCA. This finding is supported by Gray et al. [30], who found that a similar local PCA representation gave better performance than global PCA for lipreading from video. Principal component analysis of image patches sampled from random locations such that the image statistics are stationary over the patch describes the amplitude spectrum [27], [53].

An alternative to adaptive local filters such as local PCA are predefined wavelet decompositions such as families of Gabor filters. Gabor filters are obtained by modulating a 2D sine wave with a Gaussian envelope. Such filters remove most of the variability in images due to variation in lighting and contrast, and closely model the response properties of visual cortical cells [52], [36], [21], [20]. Representations based on the outputs of families of Gabor filters at multiple spatial scales, orientations, and spatial locations have proven successful for recognizing facial identity in images [39], [50]. In a direct comparison of face recognition algorithms, Gabor filter representations gave better identity recognition performance than representations based on principal component analysis [65]. A Gabor representation was also more effective than a representation based on the geometric locations of facial features for expression recognition [66].

Section 6 explores local representations based on filters that act on small spatial regions within the images. We examined three variations on local filters that employ PCA and compared them to the biologically inspired Gabor wavelet decomposition.

A simple benchmark for the local filters consisted of a single Gaussian kernel. The δ-images were convolved with a 15 × 15 Gaussian kernel and the output was down-sampled by a factor of 4. The dimensionality of the final representation was $\frac{n}{4}$. The output of this basic local filter was classified at 70.3 percent accuracy using the Euclidean distance similarity measure and template matching classifier.

6.1 Local PCA

This approach is based on the local PCA representation that was found to outperform global PCA for expression recognition [48]. The shift-invariant local basis functions employed in [48] were derived from the principal components of small image patches from randomly sampled locations in the face image. A set of more than 7,000 patches of size 15 × 15 was taken from random locations in the δ-images and decomposed using PCA. The first p principal components were then used as convolution kernels to filter the full images. The outputs were subsequently down-sampled by a factor of 4 such that the final dimensionality of the representation was isomorphic to R^p×n/4. The local PCA filters obtained from the set of lower-face δ-images are shown in Fig. 9.

Fig. 9.

(a) Shift-invariant local PCA kernels. First nine components, order left to right, top to bottom. (b) Shift-variant local PCA kernels. The first principal component is shown for each image location.

Performance improved by excluding the first principal component. Best performance of 73.4 percent was obtained with principal components 2–30, using Euclidean distance and template matching. Unlike the findings in [48], shift invariant basis functions obtained through local PCA were no more effective than global PCA for facial action coding. Performance of this local PCA technique was not significantly higher than that obtained using a single 15 × 15 Gaussian kernel.

Because the local PCA implementation differed from global PCA in two properties, spatial locality and image alignment, we repeated the local PCA analysis at fixed spatial locations. PCA of location-independent images captures amplitude information without phase, whereas alignment of the images provides implicit phase information [27], [10]. Local PCA at fixed image locations is related to the eigenfeatures representation addressed in [48]. The eigenfeature representation in [48] differed from shift-invariant local PCA in image patch size. Here, we compare shift-invariant and shift-variant versions of local PCA while controlling for patch size.

The images were divided into $m\ll \frac{n}{4}$ 15 × 15 fixed regions. The principal components of each region were calculated separately. Each image was thus represented by p × m coefficients. The final representation consisted of p = 10 principal components of m = 48 image regions.

Classification performance was tested using up to the first 30 components of each patch. Best performance of 78.3 percent was obtained with the first 10 principal components of each image patch, using Euclidean distance and the nearest neighbor classifier. There is a trend for phase alignment to improve classification performance using local PCA, but the difference is not statistically significant. Contrary to the findings in [48], neither local PCA representation outperformed the global PCA representation. It has been proposed that local representations reduce sensitivity to identity-specific aspects of the face image [48], [30]. The success of global PCA here could be attributable to the use of δ-images, which reduced variance related to identity specific aspects of the face image. Another reason for the difference in findings could be the method of downsampling. Padgett and Cottrell selected filter outputs from seven image locations at the eyes and mouth, whereas here, downsampling was performed in a grid-wise fashion from 48 image locations.

6.2 Gabor Wavelet Representation

Here, we examine predefined local filters based on the Gabor wavelet decomposition. This representation was based on the methods described in [39]. Given an image ℐ(x⃗) (where x⃗ = (x, y)), the transform 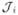is defined as a convolution

$${\mathcal{J}}_i=\int ℐ(\overrightarrow{x}){\psi }_i(\overrightarrow{x}-{\overrightarrow{x}}^{\prime })d^2{\overrightarrow{x}}^{\prime }$$ (16)

with a family of Gabor kernels ψ_i

$${\psi }_i(\overrightarrow{x})=\frac{{\left|\right|{\overrightarrow{k}}_i\left|\right|}^2}{{\sigma }^2}{e}^{-\frac{{\left|\right|{\overrightarrow{k}}_i\left|\right|}^2{\left|\right|\overrightarrow{x}\left|\right|}^2}{2{\sigma }^2}}\left[e^{j{\overrightarrow{k}}_i\overrightarrow{x}}-e^{-\frac{{\sigma }^2}{2}}\right].$$ (17)

Each ψ_i is a plane wave characterized by the vector k⃗_i enveloped by a Gaussian function, where the parameter σ = 2π determines the ratio of window width to wavelength. The first term in the square brackets determines the oscillatory part of the kernel and the second term compensates for the DC value of the kernel [39]. The vector k⃗_i is defined as

$${\overrightarrow{k}}_i=\left(\begin{array}{c}{f}_{\nu }cos{\varphi }_{\mu }\\ f_{\nu }sin{\varphi }_{\mu }\end{array}\right),$$ (18)

where

$$f_{\nu }=2^{-\frac{\nu +2}{2}}\pi ,\text{and}{\varphi }_{\mu }=\mu \frac{\pi }{8}.$$

The parameters ν and μ define the frequency and orientation of the kernels. We used five frequencies, (ν = 0 – 4), and eight orientations, (μ = 1 – 8), in the final representation, following the methods in [39]. Example filters are shown in Fig. 10. The Gabor filters were applied to the δ-images. The outputs {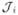} of the 40 Gabor filters were downsampled by a factor q to reduce the dimensionality to $40\times \frac{n}{q}$ and normalized to unit length, which performed a divisive contrast normalization. We tested the performance of the system using q = 1, 4, 16 and found that q = 16 yielded the best generalization rate. Best performance was obtained with the cosine similarity measure and nearest neighbor classifier.

Fig. 10.

(a) Original δ-image. (b) Gabor kernels (low and high frequency) with the magnitude of the filtered image to the right. (c) Local PCA kernels (large and small scale) with the corresponding filtered image.

Classification performance with the Gabor filter representation was 95.5 percent. This performance was significantly higher than all other approaches in the comparison except independent component analysis, with which it tied. This finding is supported by Zhang et al. [65], who found that face recognition with the Gabor filter representation was superior to that with a holistic principal component-based representation. To determine which frequency ranges contained more information for action classification, we repeated the tests using subsets of high frequencies (ν = 0, 1, 2) and low frequencies, (ν = 2, 3, 4). Performance with the high frequency subset was 92.8 percent, almost the same as for ν = 0, , 4, whereas performance with the low frequency subset was 83.8 percent. The finding that the higher spatial frequency bands of the Gabor filter representation contain more information than the lower frequency bands is consistent with our analysis of optic flow, above, in which reduction of the spatial resolution of the optic flow through smoothing had a detrimental effect on classification performance. It appears that high spatial frequencies are important for this task.

6.3 PCA Jets

We next investigated whether the multiscale property of the Gabor wavelet representation accounts for the difference in performance obtained using the Gabor representation and the local PCA representation. To test this hypothesis, we developed a multiscale version of the local PCA representation, PCA jets. The principal components of random subimage patches provide the amplitude spectrum of local image regions. A multiscale local PCA representation was obtained by performing PCA on random image patches at five different scales chosen to match the sizes of the Gaussian envelopes (see Fig. 10). Patch sizes were chosen as ±3σ, yielding the following set: [9 × 9, 15 × 15, 23 × 23, 35 × 35, and 49 × 49]. The number of filters was matched to the Gabor representation by retaining 16 principal components at each scale, for a total of 80 filters. The downsampling factor q = 16 was also chosen to match the Gabor representation.

As for the Gabor representation, performance was tested using the cosine similarity measure and nearest neighbor classifier. Best results were obtained using eigenvectors 2 to 17 for each patch size. Performance was 64.9 percent for all five scales, 72.1 percent for the three smaller scales, and 62.2 percent for the three larger scales. The multiscale principal component analysis (PCA jets) did not improve performance over the single scale local PCA. It appears that the multiscale property of the Gabor representation does not account for the improvement in performance obtained with this representation over local representations based on principal component analysis.

7 Human Subjects

The performance of human subjects provided benchmarks for the performances of the automated systems. Most other computer vision systems test performance on prototypical expressions of emotion, which naive human subjects can classify with over 90 percent agreement (e.g., [45]). Facial action coding is a more detailed analysis of facial behavior than discriminating prototypical expressions. The ability of naive human subjects to classify the facial action images in this set gives a simple indication of the difficulty of the visual classification task and provides a basis for comparing the results presented here with other systems in the literature. Since the long-term goal of this project is to replace human expert coders with an automated system, a second benchmark was provided by the agreement rates of expert human coders on these images. This benchmark indicated the extent to which the automated systems attained the goal of reaching the consistency levels of the expert coders.

Naive subjects

Naive subjects were 10 adult volunteers with no prior knowledge of facial expression measurement. The upper and lower face actions were tested separately. Subjects were provided with a guide sheet which contained an example image of each of the six upper or lower face actions along with a written description of each action and a list of image cues for detecting and discriminating the actions from [23]. Each subject was given a training session in which the facial actions were described and demonstrated and the image cues listed on the guide sheet were reviewed and indicated on the example images. The subjects kept the guide sheet as a reference during the task.

Face images were preprocessed identically to how they had been for the automated systems, as described in Section 3, and printed using a high resolution HP Laserjet 4si printer with 600 dpi. Face images were presented in pairs, with a neutral expression image and the test image presented side by side. Subjects were instructed to compare the test image with the neutral image and decide which of the actions the subject had performed in the test image. Ninety-three image pairs were presented in both the upper and lower face tasks. Subjects were instructed to take as much time as they needed to perform the task, which ranged from 30 minutes to one hour. Naive subjects classified these images at 77.9 percent correct. Presenting uncropped face images did not improve performance.

Expert coders

Expert subjects were four certified FACS coders. The task was identical to the naive subject task with the following exceptions: Expert subjects were not given a guide sheet or additional training and the complete face was visible, as it would normally be during FACS scoring. Although the complete action was visible in the cropped images, the experts were experienced with full face images and the cropping may bias their performance by removing contextual information. One hundred and fourteen upper-face image pairs and 93 lower-face image pairs were presented. Time to complete the task ranged from 20 minutes to 1 hour and 15 minutes. The rate of agreement of the expert coders with the assigned labels was 94.1 percent.

8 Discussion

We have compared a number of different image analysis methods on a difficult classification problem, the classification of facial actions. Several approaches to facial expression analysis have been presented in the literature, but until now, there has been little direct comparison of these methods on a single dataset. These approaches include analysis of facial motion [44], [64], [54], [26], holistic spatial pattern analysis using techniques based on principal component analysis [17], [48], [40], and measurements of the shapes and facial features and their spatial arrangements [40], [66]. This investigation compared facial action classification using optic flow, holistic spatial analysis, and local spatial representations. We also included in our comparison a number of representations that had been developed for facial identity recognition and applied them for the first time to facial expression analysis. These representations included Gabor filters [39], Linear Discriminant Analysis [8], Local Feature Analysis [49], and Independent Component Analysis [4].

Best performances were obtained with the local Gabor filter representation and the Independent Component representation, which both achieved 96 percent correct classification. The performance of these two methods equaled the agreement level of expert human subjects on these images. Image representations derived from the second-order statistics of the dataset (PCA and LFA) performed about as well as naive human subjects on this image classification task, in the 80 percent accuracy range. Performances using LFA and FLD did not significantly differ from PCA nor did spatially local implementations of PCA. Correlation-based optic flow performed at a level between naive and expert human subjects, at 86 percent. Classification accuracies obtained here compared favorably with other systems developed for emotion classification, despite the additional challenges of classifying facial actions over classifying prototypical expressions reviewed in [31].

We obtained converging evidence that local spatial filters are important for analysis of facial expressions. The two representations that significantly outperformed the others, the Gabor representation [39] and the Independent Component representation [4], were based on local filters. ICA was classified as a holistic algorithm since the analysis was performed over the images as a whole. The basis images that the algorithm produced, however, were local. Our results also demonstrated that spatial locality of the image filters alone is insufficient for good classification. Local principal component representations such as LFA and local PCA performed no better than the global PCA representation (eigenfaces).

We also obtained multiple sources of evidence that high spatial frequencies are important for classifying facial actions. Spatial smoothing of optic flow degraded performance by more than 30 percent. Second, classification with only the high frequencies of the Gabor representation was superior to classification using only the low spatial frequencies. A similar result was obtained with the PCA jets. These findings are in contrast to a recent report that the information for recognizing prototypical facial expressions was carried predominantly by the low spatial frequencies [66]. This difference in findings highlights the difference in the task requirements of classifying facial actions versus classifying prototypical expressions of emotion. Classifying facial actions is a more detailed level of analysis. Our findings predict, for example, that high spatial frequencies would carry important information for discriminating genuine expressions of happiness from posed ones, which differ in the presence of AU 6 (the cheek raiser) [24].

The relevance of high spatial frequencies has implications for motion-based facial expression analysis. Since optic flow is a noisy measure, many flow-based expression analysis systems employ regularization procedures such as smoothing and quantizing to estimate a principal direction of motion within an image region. The analysis presented here suggests that high spatial resolution optic flow is important for analysis of facial behavior at the level of facial action coding.

In addition to spatial locality, the ICA representation and the Gabor filter representation share the property of redundancy reduction and have relationships to representations in the visual cortex. The response properties of primary visual cortical cells are closely modeled by a bank of Gabor filters [52], [36], [21], [20]. Relationships have been demonstrated between Gabor filters and independent component analysis. Bell and Sejnowski [10] found, using ICA, that the filters that produced independent outputs from natural scenes were spatially local, oriented edge filters, similar to a bank of Gabor filters. It has also been shown that Gabor filter outputs of natural images are at least pairwise independent [57]. This holds when the responses undergo divisive normalization, which neurophysiologists have proposed takes place in the visual cortex [33]. The length normalization in our Gabor representation is a form of divisive normalization.

The Gabor wavelets, PCA, and ICA each provide a way to represent face images as a linear superposition of basis functions. Gabor wavelets employ a set of predefined basis functions, whereas PCA and ICA learn basis functions that are adapted to the data ensemble. PCA models the data as a multivariate Gaussian and the basis functions are restricted to be orthogonal [41]. ICA allows the learning of nonorthogonal bases and allows the data to be modeled with non-Gaussian distributions [16]. As noted above, there are a number of relationships between Gabor wavelets and the basis functions obtained with ICA. The Gabor wavelets are not specialized to the particular data ensemble, but would be advantageous when the amount of data is too small to estimate filters.

The ICA representation performed as well as the Gabor representation, despite having two orders of magnitude fewer basis functions. A large number of basis functions does not appear to confer an advantage for classification. The PCA-jet representation, which was matched to the Gabor representation for number of basis functions as well as scale, performed at only 72 percent correct.

Each of the local representations underwent down-sampling. The effect of downsampling on generalization rate was examined in the Gabor representation and we found downsampling improved generalization performance. The downsampling was done in a grid-wise fashion and there was no manual selection of facial features. Comparison to representations based on individual facial features (or fiducial points) has been addressed in recent work by Zhang [66] which showed that multiresolution Gabor wavelet coefficients give better information than the geometric positions of fiducial points for facial expression recognition.

9 Conclusions

The results of this comparison provided converging evidence for the importance of using local filters, high spatial frequencies, and statistical independence for classifying facial actions. Best performances were obtained with Gabor wavelet decomposition and independent component analysis. These two representations are related to each other. They employ graylevel texture filters that share properties of spatial locality, independence, and have relationships to the response properties of visual cortical neurons.

The majority of the approaches to facial expression recognition by computer have focused exclusively on analysis of facial motion. Motion is an important aspect of facial expressions, but not the only cue. Although experiments with point-light displays have shown that human subjects can recognize facial expressions from motion signals alone [7], recognition rates are just above chance and substantially lower than those reported for recognizing a similar set of expressions from static graylevel images (e.g., [45]). In this comparison, best performances were obtained with representations based on surface graylevels. A future direction of this work is to combine the motion information with spatial texture information. Perhaps combining motion and graylevel information will ultimately provide the best facial expression recognition performance, as it does for the human visual system [7], [63].

Biographies

Gianluca Donato received his Laurea degree in electrical engineering from the University of Padova, Italy, in 1999. He was an exchange student at the University of California San Diego in 1996–1997 and a visiting researcher at the Computational Neurobiology Laboratory at the Salk Institute in 1997. He specialized in control systems and digital signal processing. His thesis work dealt with the recognition of facial actions. He is currently employed at Digital Persona, Inc.

Marian Stewart Bartlett received her Bachelor’s degree in mathematics and computer science from Middlebury College in 1988 and her PhD in cognitive science and psychology from the University of California, San Diego in 1998. She is a postdoctoral researcher at the Institute for Neural Computation, University of California, San Diego. Her dissertation work was conducted with Terrence Sejnowski at the Salk Institute. Her interests include approaches to image analysis through unsupervised learning, with a focus on face recognition and expression analysis. She is presently exploring probabilistic dynamical models and their application to video analysis at the University of California, San Diego.

Joseph C. Hager earned his PhD in psychology from the University of California, San Francisco in 1983, where he later managed a computer services unit and worked on a U.S. National Science Foundation grant studying classification of facial behaviors with computers. He is acting CEO and Director of Research at Network Information Research Corporation in Salt Lake City, Utah. His interests include applying computational technology to behavioral science issues.

Paul Ekman is a professor of psychology and director of the Human Interaction Laboratory at the University of California, San Francisco. In 1991, he received the Distinguished Scientific Contribution Award of the American Psychological Association, the highest award given for basic research. In 1994, he was given an honorary Doctor of Humane Letters from the University of Chicago. In 1998, he was named a William James Fellow of the American Psychological Society. Ekman is co-author of Emotion in the Human Face (1971), Unmasking the Face (1975), Facial Action Coding System (1978), editor of Darwin and Facial Expression (1973), co-editor of Handbook of Methods in Nonverbal Behavior Research (1982), Approaches to Emotion (1984), The Nature of Emotion (1994), What the Face Reveals (1997), and author of Face of Man (1980), Telling Lies (1985, second edition, 1992), and Why Kids Lie (1989). He is the editor of the third edition of Charles Darwin’s The Expression of the Emotions in Man and Animals (1998). He has published more than 100 articles.

Terrence J. Sejnowski received his BS in physics from the Case-Western Reserve University and his PhD in physics from Princeton University in 1978. Dr. Sejnowski is an investigator with the Howard Hughes Medical Institute and a professor at The Salk Institute for Biological Studies, where he directs the Computational Neurobiology Laboratory, and professor of biology at the University of California, San Diego. In 1982, he joined the faculty of the Department of Biophysics at Johns Hopkins University before moving to San Diego in 1988. Dr. Sejnowski founded Neural Computation in 1988, the leading journal in the area of neural networks and computational neuroscience. The long-range goal of Dr. Sejnowski’s research is to build linking principles from brain to behavior using computational models. This goal is being pursued with a combination of theoretical and experimental approaches at several levels of investigation ranging from the biophysical level to the systems level. The issues addressed by this research include how sensory information is represented in the visual cortex.