Fast Bound Pool Fraction Imaging of the In Vivo Rat Brain: Association with Myelin Content and Validation in the C6 Glioma Model

Abstract

Cross-relaxation imaging (CRI) is a quantitative magnetic resonance technique that measures the kinetic parameters of magnetization transfer between protons bound to water and protons bound to macromolecules. In this study, in vivo, four-parameter CRI of normal rat brains (N=5) at 3.0 T was first directly compared to histology. The bound pool fraction, f, was strongly associated with myelin density (Pearson’s r = 0.99, p <0.001). The correlation persisted in separate analyses of gray matter (GM; r = 0.89, p =0.046) and white matter (WM; r = 0.97, p =0.029). Subsequently, a new time-efficient approach for solely capturing the whole-brain parametric map of f was proposed, validated with histology, and used to estimate myelin density. Since the described approach for the rapid acquisition of f applied constraints to other CRI parameters, a theoretical analysis of error was performed. Estimates of f in normal and pathologic tissue were expected to have <10% error. A comparison of values for f obtained from the traditional four-parameter fit of CRI data versus the proposed rapid acquisition of f was within this expected margin for in vivo rat brain gliomas (N=4; mean ± SE; 3.9 ± 0.2% vs. 4.0 ± 0.2%, respectively). In both whole-brain f maps and myelin density maps, replacement of normal GM and WM by proliferating and invading tumor cells could be readily identified. The rapid, whole-brain acquisition of the bound pool fraction may provide a reliable method for detection of glioma invasion in both GM and WM during animal and human imaging.

1. Introduction

Quantitative magnetization transfer (qMT) extracts the parametric indices that govern magnetization exchange in tissues. In the two-pool model of magnetization transfer (Edzes and Samulski, 1978; Grad et al., 1991; Morrison and Henkelman, 1995), magnetization exchange occurs between protons bound to water (i.e. the free pool) and protons bound to macromolecules (i.e. the bound pool). Mapping of the various tissue-specific parameters that govern magnetization transfer has been accomplished by a variety of techniques (Cercignani et al., 2005; Gloor et al., 2008; Gochberg and Gore, 2003; Helms and Piringer, 2005; Ramani et al., 2002; Ropele et al., 2003; Sled and Pike, 2001; Tozer et al., 2003; Yarnykh, 2002; Yarnykh and Yuan, 2004) that make use of various pulse sequences, sampling schemes and reconstruction algorithms.

A key parameter of qMT captured by all approaches is the molar fraction of protons bound to macromolecules (i.e. bound pool fraction), f. The acquisition of f has been shown to be obtainable with reasonable accuracy regardless of methodology (Portnoy and Stanisz, 2007). In the brain, f has been associated with white matter (WM) fiber tracts (Yarnykh and Yuan, 2004). However, in contrast to quantitative diffusion imaging techniques, f provides data that is not associated with directional coherence of fibers (Underhill et al., 2009). In multiple sclerosis (MS), in vivo alterations to the bound pool fraction have been identified in WM (Davies et al., 2004; Sled and Pike, 2001; Tozer et al., 2003; Yarnykh, 2002). The decrease in bound pool fraction from within MS lesions has been attributed to a localized reduction in the rich macromolecular content of myelin (Fralix et al., 1991; Koenig, 1991; Wolff and Balaban, 1989) associated with demyelination. These in vivo observations have been supported by ex vivo human studies and in vivo animal models. Schmierer et al. imaged post-mortem ex vivo brains afflicted with MS and found significant differences in the bound pool fraction when measured from histologically identified normal-appearing WM, remyelinated WM lesions, and demyelinated WM lesions (Schmierer et al., 2007). Rausch et al. has produced demyelinating lesions in the rat brain by inducing an experimental autoimmune encephalitis (Rausch et al., 2009). A decrease in the bound pool fraction from regions of interest (ROIs) within demyelinated lesions compared to ROIs from unaffected WM within the same animal and corresponding WM from healthy animals was reported (Rausch et al., 2009). Samsonov et al. demonstrated a dramatic and uniform decrease of the bound pool fraction in demyelinated WM using the mutant canine model (Samsonov et al., 2006; Samsonov et al., 2010). While the evidence indicates an association between myelin content and the bound pool fraction, the data (Rausch et al., 2009; Samsonov et al., 2006; Samsonov et al., 2010; Schmierer et al., 2007) were derived from the assessment of abnormal tissues. As such, the dominant underlying tissue property that governs bound pool fraction variations in normal brain tissues remains ambiguous since factors such as inflammation, edema, or genetically-determined structural myelin disorganization may confound observations based on post-mortem diseased brain or animal models.

While the major field of application of qMT methods has been historically associated with demyelinating disorders (Davies et al., 2004; Rausch et al., 2009; Schmierer et al., 2007; Sled and Pike, 2001; Tozer et al., 2003; Yarnykh, 2002), another area of considerable interest is related to brain tumors, especially those of glial origin. The devastating mortality associated with gliomas, particularly high-grade gliomas (5-year survival <3%) (Laws et al., 2003), has been attributed to tumor cell invasion of normal parenchyma, particularly WM (Giese and Westphal, 2001). Understanding glioma cell invasion is a key aspect necessary to improve survival, which has remained unchanged for more than 30 years (Polin et al., 2005; Scanlon and Taylor, 1979). Accordingly, animal models have been developed to characterize and study in vivo glioma cell invasion (Barth, 1998). Development of a technology that allows non-invasive detection of glioma spread across normal brain tissues would not only enrich animal studies, but may also improve treatment planning and prognostic guidance for clinical decision making (Giese et al., 2003). qMT methods have a promising potential for this purpose due to a high sensitivity of cross-relaxation parameters to WM organization (Underhill et al., 2009; Yarnykh and Yuan, 2004). Current knowledge about cross-relaxation in brain tumors and associated effects on surrounding tissues is very limited. The distinctions in the two-pool model parameters between glioma and normal brain tissues were first demonstrated using a well-established C6 rat glioma model based on continuous wave Z-spectroscopic data acquisition (Quesson et al., 1997). Parametric maps of the bound pool fraction and cross-relaxation rate constant in the single-case human observation (Yarnykh, 2002) identified clear contrast between the glioma tissue, surrounding edema, and normal brain. Recently, Garcia et al. and Tozer et al. reported preliminary data identifying alterations in qMT parametric maps associated with low-grade and high-grade gliomas, respectively (Garica et al., 2010; Tozer et al., 2007). In the former study, parametric maps appeared heterogenous compared to the relatively homogenous appearance of corresponding contrast-enhanced T1-weighted and T2-weighted images suggesting qMT may provide additional information for diagnostic tumor characterization (Garica et al., 2010). Additionally, the bound pool fraction appeared to differentiate better in gliomas between tumor and perifocal edema compared to other qMT parameters (Garica et al., 2010). These preliminary findings warrant further investigation of CRI in gliomas, and particularly, a detailed study of histological correlations using a well-established animal model.

From a technical standpoint, qMT remains a rather challenging experimental approach due to time-consuming multi-point data acquisition and sophisticated reconstruction algorithms utilizing voxel-based fit of several parameters (from two to five, depending on the model parameterization) (Cercignani et al., 2005; Gloor et al., 2008; Gochberg and Gore, 2003; Helms and Piringer, 2005; Ramani et al., 2002; Ropele et al., 2003; Sled and Pike, 2001; Tozer et al., 2003; Yarnykh, 2002; Yarnykh and Yuan, 2004). This circumstance to a large extent restricts clinical qMT applications. Several studies have been focused on the improvement of time efficiency of qMT techniques (Gloor et al., 2008; Ropele et al., 2003; Yarnykh and Yuan, 2004). Collectively, these approaches are aimed to reduce the parameter space of the two-pool MT model by focusing on the parameters which are assumed to be most clinically informative, while introducing certain model simplifications to avoid estimation of other parameters. In the cross-relaxation imaging (CRI) method (Yarnykh and Yuan, 2004), a reduction of the number of adjustable parameters to two (bound pool fraction, f, and forward cross-relaxation rate constant, k, defined for magnetization transfer from free to bound pool) in conjunction with constraining the remaining parameters (transverse relaxation times of the free and bound pool, T₂^F and T₂^B) has been shown to allow the use of four data points with variable off-resonance saturation, and therefore, provide considerable total scan time shortening as compared to multi-point Z-spectroscopic techniques. Ropele et al. proposed an inversion-based pulse sequence and a simplified theoretical model for determination of the bound pool fraction from two images (Ropele et al., 2003). Recently, Gloor et al. introduced the technique based on the on-resonance MT effect induced by the fast SSFP sequence with multi-point data acquisition for reconstruction of the two MT parameters (bound pool fraction and cross-relaxation rate constant) (Gloor et al., 2008). The above techniques still suffer from a relatively long scan time if used for whole-brain imaging (at least 25-30 min for human brain studies) due to the need of either several data points with 3D acquisition (Gloor et al., 2008; Yarnykh and Yuan, 2004) or sequential 2D acquisition with a long repetition time (Ropele et al., 2003). To further improve time efficiency of qMT, a modified CRI technique for rapid acquisition of f maps has been recently proposed in human brain imaging at 3.0 T (Underhill et al., 2010b; Yarnykh et al., 2010). This method applies average-brain constraints for the parameter T₂^B and the product of the longitudinal relaxation rate and transverse relaxation time of the free pool, R₁^FT₂^F, similar to the earlier approach (Underhill et al., 2009; Yarnykh and Yuan, 2004), and additionally utilizes a constrained value for the parameter combination k(1−f)/f, which physically corresponds to the inverse cross-relaxation rate constant describing magnetization transfer from bound to free pool. This approach (Underhill et al., 2010b; Yarnykh et al., 2010) is particularly fast, since only two off-resonance saturation data points are required, and all images are acquired using a spoiled gradient-echo sequence with a short repetition time. However, the accuracy of this method has not been studied in detail, and its further validation is needed.

In accordance with the above, we hypothesized that the bound pool fraction would be the most robust parameter for relating qMT to histology in the brain. In this study, we first aimed to determine associations between the parameters of the two-pool model (f, k, T₂^F, and T₂^B) and key histological characteristics (myelin density, axonal content, and cellularity) in the normal rat brain in vivo at 3.0 T. Second, we sought to identify histopathological correlations of cross-relaxation parameters in the C6 rat glioma model. Then, we aimed to validate with histology a recent time-efficient methodology for single-parameter bound pool fraction mapping in both normal and pathologic brain tissues. Lastly, this single-parameter bound pool fraction mapping method was compared to the magnetization transfer ratio (MTR) mapping, a widely used simple semi-quantitative magnetization transfer technique that describes the relative change in image contrast after a single off-resonance RF saturation pulse (Dousset et al., 1992). MTR has been previously used to study diseases associated with alterations to WM, such as MS (Dousset et al., 1992; Loevner et al., 1995), metastatic lesions (Boorstein et al., 1994), and progressive multifocal leukoencephalopathy (Dousset et al., 1997).

2. Methods

2.1 Animal Procedures

Nine adult male Wistar rats (Charles River Laboratories, Wilmington, MA) were used in this study five healthy rats and four rats imaged two weeks after intracranial inoculation with C6 cells. Weight range for all animals at the time of imaging was 315–335 g. The C6 cell line was established from a glioma generated by intravenous exposure of random-bred Wistar-Furth rats to N,N′-nitrosomethylurea (Benda et al., 1971), and has been widely used as an animal model of glioma (Bernstein et al., 1990; Chicoine and Silbergeld, 1995).

C6 cells were grown in Dulbecco’s modified Eagle’s medium (DMEM; Gibco, Gaithersburg, MD) with 5% fetal calf serum and 100 μg/ml streptomycin. Cells were maintained in a humidified incubator at 37° C in 5% CO₂. For implantation, nearly confluent cells were harvested by scraping, counted using a hemocytometer, and 1×10⁶ cells were resuspended in 10 μL of DMEM.

Rats were anesthetized with 60 mg/kg ketamine and 5 mg/kg xylazine administered IP. The head was immobilized in a stereotactic head set with ear bars and a teeth bar. The skull was exposed by a 2 cm midline incision, and a burr hole was created on the right side 1 mm anterior and 2 mm lateral to the bregma. A microsyringe (Hamilton, Reno, NV) was used to inject the 10 μL aliquot of 10⁶ C6 cells into the frontal lobe at a depth of 5 mm from the skull surface over a period of 5 minutes. The needle was kept in place 2 minutes after injection to prevent backflow prior to removal. The burr hole was filled with bone wax (Ethicon, Somerville, NJ). The skin was closed with surgical staples that were removed prior to MR imaging.

After imaging, the rats were anesthetized with 100 mg/kg pentobarbital and then euthanized by intravascular perfusion of the animal with 10% neutral buffered formalin via an open-chest, left cardiac ventricle puncture approach. Brains were subsequently removed intact and maintained in 10% neutral buffered formalin.

2.2 MRI Acquisition

Rats were imaged on a 3.0 T Philips Achieva whole-body scanner (Philips Medical Systems, Best, Netherlands) using a dual coil approach. A quadrature transmit/receive head coil (Philips Medical Systems, Best, Netherlands) was utilized for RF transmission, and an in-house-built combined solenoid-surface coil (Underhill et al., 2010a) dedicated to high spatial resolution whole-brain rat imaging was used for RF reception. All images were acquired in the coronal plane.

After induction in an anesthesia chamber with 5% isoflurane mixed with oxygen, the rats were positioned within the dual coils and maintained on 2% isoflurane mixed with oxygen via nose cone inhalation. Animals were placed on an isothermal pad (Deltaphase®, Braintree Scientific, Inc., Braintree, MA) to maintain core body temperature during scanning.

Fifteen Z-spectral data points were acquired for each rat using a 3D MT-prepared spoiled gradient echo (GRE) sequence with TR/TE = 42/4.6 ms and excitation flip angle α = 10°. The sampling scheme included five variable offset frequencies (Δ = 0.6, 1, 2, 4, and 8 kHz) of the off-resonance saturation pulse. At each offset frequency, a single-lobe sinc saturation pulse with Gaussian apodization was applied with duration 18 ms utilizing three separate nominal effective flip angles of 950°, 800°, and 650° corresponding to the root-mean-square amplitudes (ω_1rms/2π) = 169.2 Hz, 142.5 Hz, and 115.8 Hz. Reference images for data normalization were obtained using the same sequence with Δ = 96 kHz (no MT effect is observed at this frequency) for each effective flip angle to ensure that the transmitter operates with identical gain settings. Complementary R₁ maps necessary for parameter fitting were obtained using the variable flip angle (VFA) method (Haacke et al., 1999) with a 3D spoiled GRE sequence (TR/TE = 20/2.3 ms, α = 4, 10, 20, and 30°). All Z-spectral and VFA images were acquired with a FOV = 29×29×19.8 mm³, matrix = 97×97×66, acquisition resolution = 0.3×0.3×0.3 mm³ (zero-interpolated to 0.15×0.15×0.15 mm³), and full-Fourier acquisition. Z-spectroscopic data were acquired with one excitation (NEX = 1). VFA data were acquired with variable signal excitations so that signal-to-noise ratio (SNR) for 4° (NEX = 3), 20° (NEX = 2) and 30° (NEX = 3) were similar to the SNR for 10° (NEX = 1). Scan time for each Z-spectral and VFA data point per excitation was 4.4 minutes and 2.1 minutes, respectively. Total scan time for Z-spectral and VFA images was 79.2 minutes and 18.9 minutes, respectively.

Additionally, whole-brain 3D B₀ and B₁ maps were acquired to correct for field heterogeneities. For B₀ mapping, the GRE-based dual-TE phase-difference method (Skinner and Glover, 1997) was used with TR/TE₁/TE₂ = 20/4.7/5.7 ms and α = 10°. B₁ maps were obtained using the actual flip angle imaging (AFI) method (Yarnykh, 2007) with recent optimal spoiling modifications (Yarnykh, 2010) and following sequence parameters: TR₁/TR₂/TE = 25/125/6.6 ms and α = 60°. 3D B₀ and B₁ maps were acquired with a FOV = 29×29×19.8, matrix = 64×64×33, acquisition resolution = 0.45×0.45×0.6 mm³ (zero-interpolated to 0.15×0.15×0.15 mm³), and NEX = 1. Total scan time for B₀ and B₁ maps was 2.8 minutes and 10.5 minutes, respectively.

2.3 Image Processing

CRI parametric maps were reconstructed by voxel-based fitting of the previously described matrix model of pulsed magnetization transfer that approximates a shaped off-resonance saturation pulse by a rectangular pulse with the same ω_1rms (Yarnykh and Yuan, 2004) to signal intensities obtained at variable Δ and ω_1rms. Two fit options were applied after normalization of signal intensities to the intensity corresponding to Δ = 96 kHz at a particular ω_1rms. First, all data points (15 points) were processed to obtain the maps of four parameters (f, k, T₂^F, and T₂^B) of the two-pool model similar to the previously described procedure for the human brain (Underhill et al., 2009). Subsequently, constraints for T₂^B, the product T₂^FR₁^F, and the inverse rate constant k(1−f)/f were determined from these data as detailed in Section 2.4 Image Analysis. A second fit utilizing two data points taken sufficiently far from resonance (Δ = 4 and 8 kHz, ω_1rms/2π = 169.2 Hz) was performed to solely reconstruct f maps using the identified constraints for T₂^B, the product T₂^FR₁^F, and the constant k(1−f)/f.

R₁ maps were reconstructed from VFA data using a linear fit to the signal intensities (S) transformed into the coordinates [S(α) / sin α, S(α) / tan α] (Haacke et al., 1999). Prior to fit of both CRI parametric maps and R₁ maps, B₀ and B₁ corrections were applied as previously described (Underhill et al., 2009). Briefly, B₀ maps were used to determine the actual voxel-based Δ in the presence of field heterogeneity. B₁ maps were used to correct the voxel-based nominal values of ω_1rms and excitation flip angles for both Z-spectral and VFA datasets.

MTR images were reconstructed using the Δ = 2 kHz (S_m) image and the reference image Δ = 96 kHz (S₀) acquired at ω_1rms/2π = 169.2 Hz with the following equation: MTR = 100 × (S₀ S_m) / S₀. This calculation of MTR is consistent with previous publications (Blezer et al., 2007; Dousset et al., 1992; Loevner et al., 1995).

All CRI and MTR processing was performed using in-house written Matlab (The Mathworks, Natick, MA) and C/C++ language software. Nonlinear least squares fitting for the matrix model of magnetization transfer was performed with a Levenberg-Marquardt algorithm (Press et al., 1992). To improve SNR during whole-brain voxel-based fitting, two adjacent slices were averaged and then a 3×3 median filter was applied to raw images from Z-spectral and VFA datasets. After maps were produced, a 3×3 median filter was applied prior to image display to minimize noise contribution and to average outlying voxels mostly occurring on the edges of anatomic structures in the proximity of CSF spaces and brain surfaces.

The regression equation (see Section 2.7 Statistical Analysis) defining the association between myelin density determined from histology and f determined from the two-point, single-parameter fit of Z-spectra was used to produce whole-brain, voxel-based estimations of myelin density. Using red-green-blue (RGB) intensity values obtained from Luxol-Fast blue slides (see Section 2.6 Quantitative Histology) a linear scale was produced based on the structures with the most and least myelin density, expressed as a percent. Voxel-based bound pool fraction values were mapped to corresponding myelin density values using the regression equation. Voxel-based estimates of myelin density were then assigned the appropriate RGB value. The colorized representation of myelin density derived from the bound pool fraction is subsequently referred to as myelin maps.

2.4 Image Analysis

Utilizing a rat brain atlas (Paxinos and Watson, 2004) for reference, ROIs were manually outlined within a number of GM and WM structures. Relatively large (present on three continuous slices) structures were selected to minimize the partial volume effect. Signal intensities for these anatomic structures were sampled on all source images and the mean value from each ROI was used for four-parameter (f, k, T₂^F, and T₂^B) model fitting as described in Section 2.3 Image Processing. Constraints for T₂^B, the product T₂^FR₁^F, and the constant k(1−f)/f were then determined as the mean values across all anatomic structures listed in Table 1 after weighting the mean value for GM and WM structures evenly. Constraints identified for T₂^B, T₂^FR₁^F, and k(1−f)/f were subsequently used for the single-parameter fit of f from two data points (4 and 8 kHz). In animals with implanted glioma, data were also sampled in ROIs from bulk tumor and processed similarly. Identical ROIs used during CRI were used for determination of MTR as described in Section 2.3 Image Processing.

Table 1.

CRI (mean ± SE) and histology results for anatomic structures in the normal (N=5) and diseased (N=4) rat brain.

	R1 (s−1)	Four-Parameter Fit (15 pt)a				One-Parameter Fit (2 pt)bf (%)	Myelin Content (%)	Axon Content (%)	Cell Count
		k (s−1)	f (%)	T2F (ms)	T2B (μs)
Gray Matter
Caudate/Putamen	0.77±0.02	2.34±0.25	7.0±0.2	40.7±2.4	10.7±0.7	7.2±0.4	14.0	7.5	45
Cerebellar Gray Matter	0.67±0.02	2.17±0.41	5.7±0.1	54.9±1.6	9.7±0.4	5.8±0.3	8.7	0.1	26
Cortical Gray Matter	0.67±0.01	2.77±0.25	6.3±0.2	41.9±1.1	9.3±0.3	6.7±0.2	11.8	2.9	37
Superior Colliculus	0.81±0.02	3.66±0.44	7.3±0.1	41.2±1.3	9.9±0.4	7.9±0.2	19.2	5.5	71
Thalamus	0.77±0.04	3.77±0.79	6.6±0.3	42.0±1.5	10.5±0.5	7.0±0.2	17.4	10.6	43
White Matter
Anterior Limb, Anterior Commissure	0.93±0.03	3.10±0.48	12.8±0.4	26.6±1.0	11.1±0.5	11.6±0.6	37.2	16.6	60
Corpus Callosum	0.95±0.01	3.38±0.46	13.9±0.5	33.2±2.2	11.1±0.4	12.7±0.7	39.6	14.5	79
Internal Capsule	0.96±0.06	3.69±0.37	13.7±0.4	28.1±0.7	11.4±0.5	12.7±0.6	41.2	19.5	51
Ventral Hippocampal Commissure	0.87±0.05	2.71±0.12	11.3±0.3	32.1±1.6	11.5±0.2	10.9±0.5	31.4	9.4	62
Bulk Tumor	0.59±0.02	1.88±0.85	3.9±0.2	59.7±3.6	10.3±0.5	4.0±0.2	9.7	1.4	338

^aΔ = 0.6, 1, 2, 4, and 8 kHz with nominal effective flip angles of 950°, 800°, and 650°

^bΔ = 4 and 8 kHz with nominal effective flip angle of 950°

2.5 Error Analysis in Fast f Mapping

To evaluate the impact of parameter constraints during one-parameter fit on the accuracy of the bound pool fraction estimation from two data points, a series of simulations were performed using model datasets as previously described (Underhill et al., 2009; Yarnykh, 2002). In these simulations, two (Δ = 4 and 8 kHz, nominal flip angle of the saturation pulse 950°) normalized intensities of Z-spectra were numerically generated based on a predefined set of model parameters (R₁, f, k, T₂^F, and T₂^B) and the actual imaging parameters described in Section 2.2 MRI Acquisition using numerical solution of Bloch equations with cross-relaxation for the actual shape of the saturation pulse. The model parameters for GM and WM were the average values of the corresponding structures listed in Table 1. For the tumor, these values were the mean values obtained from the four-parameter fit of the 15 point data set acquired from an ROI in a bulk tumor from four different animals (Table 1). Computations for numerical simulation were carried out using in-house written Matlab and C language software.

For error analysis, simulations were performed using fixed values for R₁ and f. For the remaining parameters, T₂^B, T₂^F, or the constant k(1−f)/f, two parameters were fixed while the other was varied across a series of values that exceeded the expected range of physiological variability based on the literature (Cercignani et al., 2005; Gloor et al., 2008; Gochberg and Gore, 2003;

Helms and Piringer, 2005; Ramani et al., 2002; Ropele et al., 2003; Sled and Pike, 2001; Tozer et al., 2003; Underhill et al., 2009; Yarnykh, 2002; Yarnykh and Yuan, 2004) and observations of this study. Subsequently, each synthetic Z-spectrum was processed by the one-parameter fit with fixed constraints of T₂^B, T₂^FR₁^F, and k(1−f)/f yielding a potentially biased estimation of f. Results were plotted as the percent difference in f (relative error) determined from a one-parameter fit relative to the actual values utilized in the simulation versus the range of the parameter that was varied. Simulations were performed for GM, WM, and a tumor.

2.6 Quantitative Histology

After fixation, normal brains were sectioned to provide orthogonal sections through WM fiber tracts. Brains with tumor were sectioned in the coronal plane. All brains were subsequently embedded in paraffin. Sections (5 μm thick) were stained with hematoxylin-eosin, Luxol-Fast blue, and Bielchowsky’s silver impregnation. All normal and pathologic specimens were processed and stained during the same session.

All stained slides were subsequently scanned using an Olympus VS110 virtual microscopy system (Olympus, Center Valley, PA) for display on NDP.view (v1.2.25). Anatomic structures corresponding to ROIs from MRI were evaluated in the tissue plane orthogonal to axonal direction at 20x and exported as RGB images. A circular ROI of identical size (radius = 93 μm) was used for each structure. The size of the ROI was the largest possible size to fit within the smallest structure. A large ROI was selected to account for heterogeneity that may exist within a structure, particularly GM. For example, the caudate/putamen was characterized by GM with localized clusters of WM (Figure 1B). Myelin density was quantified in all structures by measuring the mean intensity of the red channel (I_R) in an ROI on Luxol-Fast blue images after subtracting the nuclei from the image. The red channel is complementary to the hue of LFB myelin staining and is a measure of blue saturation purity, since using blue-channel intensity may actually correspond to whiteness if all channels are of similar intensity (Gonzalez and Woods, 2002). Myelin density was subsequently represented for each structure by 100% × [1(I_R / 256)], which yields a higher myelin content for increasing values. Axonal density was obtained by identifying pixels with an intensity < 90 in all color channels on images of Bielchowsky’s silver impregnation in corresponding ROIs after subtraction of nuclei from the image. Axonal density was subsequently represented by the proportion of the ROI occupied by the selected pixels. Cellularity was determined by manual nuclear count on hematoxylin-eosin images also from a corresponding ROI. On the slides containing tumor, myelin and axonal density were determined after manual subtraction of nuclei from the image. In-house written software in Matlab was used for image analysis of histology specimens.

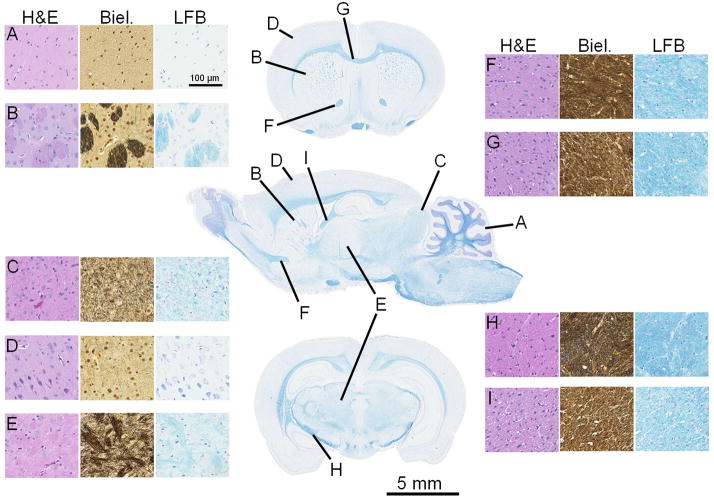
Figure 1.

A single sagittal section and two coronal sections of the normal rat brain stained with Luxol-Fast blue (center column). Anatomic structures that correspond to Table 1 are indicated (A I). For each structure, representative stains of hematoxylin and eosin (H&E), Bielchowsky’s silver impregnation (Biel.), and Luxol-Fast blue (LFB) are provided. A = cerebellar GM; B = caudate/putamen; C = superior colliculus; D = cortical GM; E = thalamus; F = anterior limb, anterior commissure; G = corpus callosum; H = internal capsule; I = ventral hippocampal commissure

2.7 Statistical Analysis

Mean and standard error (SE) of CRI parameters (R₁, f, k, T₂^F, and T₂^B) were calculated for each anatomic structure. Pearson’s correlation coefficient and linear regression analysis was used to determine associations between CRI parameters and histology (myelin density, axon density, and cellularity), and to characterize the strength of correlation between f estimates obtained from four- and single-parameter fits. Scatter plots were also utilized and error bars represent the 95% confidence interval (95% CI = ±1.96×SE). The paired Student’s t-test was used to assess for bias between CRI-based estimate of myelin density and myelin density determined by histology. All statistical analysis was carried out in SPSS 12.0 for Windows. Statistical significance was defined as a value of P < 0.05.

3. Results

3.1 CRI versus Histology

Representative histology sections from each stain are presented in Figure 1. Quantitative histology data and two-pool model parameters for each anatomic structure and tumors are reported in Table 1. Fits of sample experimental Z-spectra from GM, WM, and glioma ROIs are presented in Figure 2. Correlations between two-pool model parameters and quantitative histology are summarized in Table 2, and associations for the bound pool fraction are also exemplified in Figure 3.

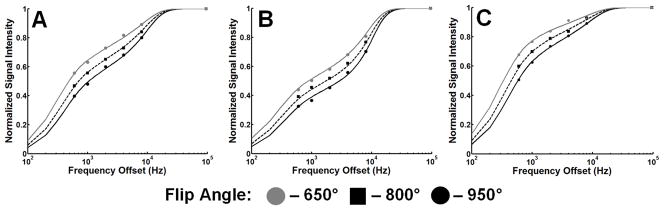
Figure 2.

Z-spectra of GM (cortical gray matter, A), WM (corpus callosum, B) and glioma (bulk tumor, C). The discrete points correspond to experimental data from various offset frequencies and nominal flip angles of the saturation pulse. The lines represent theoretical values corresponding to parameters derived from a four-parameter fit.

Table 2.

Pearson’s correlations (r) between CRI (four-parameter fit and single-parameter f estimation) and histology.

	Four-parameter fit				Single- parameter fit
	k	f	T2F	T2B	f
Myelin Content
GM + WM	0.49 (p = 0.17)	0.99 (p < 0.001)	0.90 (p = 0.001)	0.84 (p = 0.005)	0.99 (p < 0.001)
GM	0.88 (p = 0.048)	0.89 (p = 0.046)	0.73 (p = 0.16)	0.46 (p = 0.44)	0.91 (p = 0.030)
WM	0.97 (p = 0.026)	0.97 (p = 0.029)	0.30 (p = 0.70)	0.48 (p = 0.52)	0.95
Axon Content
GM + WM	0.59 (p = 0.09)	0.88 (p = 0.002)	0.89 (p = 0.001)	0.84 (p = 0.005)	0.88 (p =0.002)
GM	0.63 (p = 0.25)	0.66 (p = 0.23)	0.72 (p = 0.18)	0.79 (p = 0.11)	0.61 (p = 0.28)
WM	0.88 (p = 0.12)	0.79 (p = 0.22)	0.67 (p = 0.33)	−0.38 (p = 0.62)	0.74 (p = 0.26)
Cell Count
GM + WM	0.52 (p = 0.15)	0.66 (p = 0.052)	0.64 (p = 0.064)	0.55 (p = 0.13)	0.70 (p = 0.037)
GM	0.67 (p = 0.22)	0.92 (p = 0.029)	0.64 (p = 0.24)	0.23 (p = 0.70)	0.95 (p = 0.012)
WM	0.15 (p = 0.85)	0.20 (p = 0.80)	0.75 (p = 0.25)	0.51 (p = 0.49)	0.13 (p = 0.87)

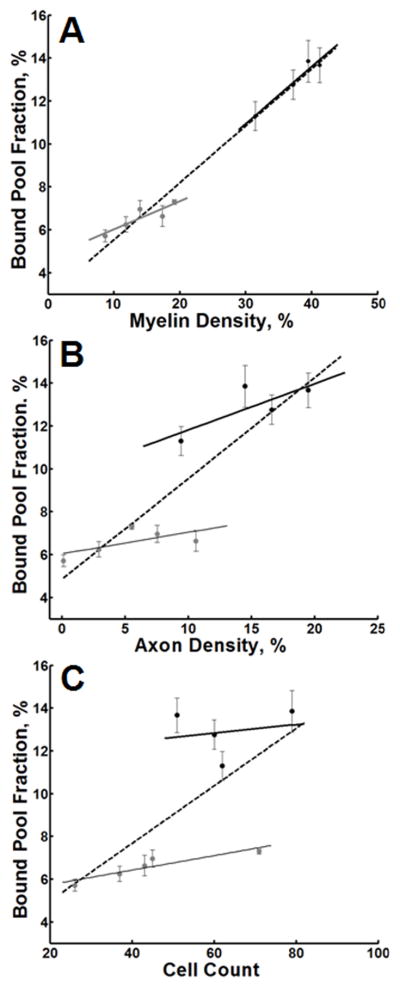
Figure 3.

Scatter plots of the bound pool fraction vs. myelin density (A), axonal density (B), and cell count (C) for GM (gray dots) and WM (black dots). In each plot, the dotted line represents the linear regression of all data points (GM + WM). The solid gray and black lines represent the linear regression through GM and WM, respectively. Error bars represent the 95% CI (±1.96 × SE).

Across all non-tumor anatomic structures identified in Table 1, there was a significant association between myelin content and both f and T₂^B. For the bound pool fraction (Figure 3), but not for T₂^F or T₂^B (Table 2), these relationships persisted within tissues specific to either GM or WM. Although k was not significantly associated with myelin content across all structures combined (Table 2), k was associated with myelin content separately for GM and WM. A significant association was observed between myelin content and axon content. In accord, similar relationships between axon content and f, T₂^F and T₂^B across all structures were identified (Table 2). Although there were trends for an association between f and k and axon content within GM and WM, corresponding correlations were not statistically significant (Table 2). The bound pool fraction was associated with cell count in GM, however, other statistically significant associations were not identified between two-pool model parameters and cell count (Table 2).

Notably, recalculation of associations using bulk tumor glioma as an additional data point did not substantially alter the strength of the correlations or the statistical significance between CRI and both myelin content and axon content (data not shown). However, association with cell count and each CRI parameter was inverted after inclusion of bulk tumor data. For example, across all structures and bulk tumor, the correlation between cell count and f shifted from r = 0.66 (p = 0.052) to r = 0.36 (p = 0.30). Classifying bulk tumor as GM found a similar inversion of the association between cell count and the bound pool fraction of GM structures (r = 0.92 vs. r = 0.84). Accordingly, the suggested association between f and cell count in Table 2 for normal anatomic tissues may be driven by factors beyond tissue cellularity.

3.2 Validation of the Time-Efficient f-mapping CRI Technique

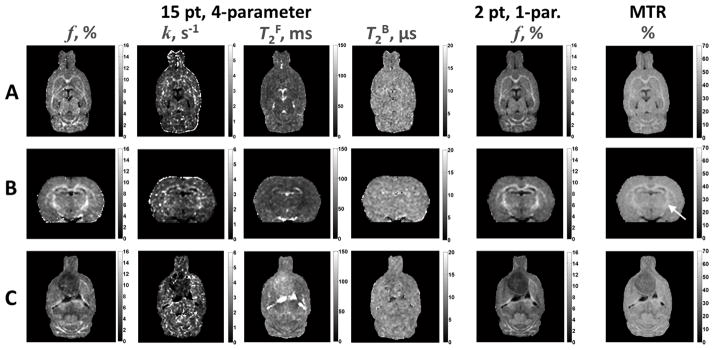
Orthogonal sections from voxel-based, whole-brain maps of the two-pool model parameters are shown in Figure 4A and B. The f map demonstrated a strong contrast between GM and WM. Although there was evidence of WM structures in the k map, overall the image appeared noisy compared to the other parametric maps obtained from a four-parameter fit. The T₂^F map was consistent with a T₂-weighted image showing WM as hypointense relative to GM, and CSF was hyperintense. The T₂^B map was relatively homogenous and had poor differentiation between GM and WM structures. Implanted glioma tumors appeared hypointense relative to GM on both the f and k maps (Figure 4C). On the T₂^F map the tumor was heterogenous and slightly hyperintense relative to GM and WM, but hypointense compared to cerebrospinal fluid. The tumor was similar in contrast to surrounding GM and WM on the T₂^B map.

Figure 4.

CRI parametric maps. Images in Row A represent the original plane of acquisition. Panel B are reconstructed images in the coronal plane. Images in Row C are from an animal implanted with a C6 glioma. The tumor is the large hypointense region most easily visualized on f maps in the anterior forebrain. Within each parameter, images are displayed at the identical window and level settings. There is a strong visual correspondence between f maps obtained from a 15 point, 4-parameter fit and a 2 point, 1-parameter fit. Compared to f maps, MTR has a decreased differentiation between GM and WM. This is most notable in the internal capsule (arrow) present in Row B.

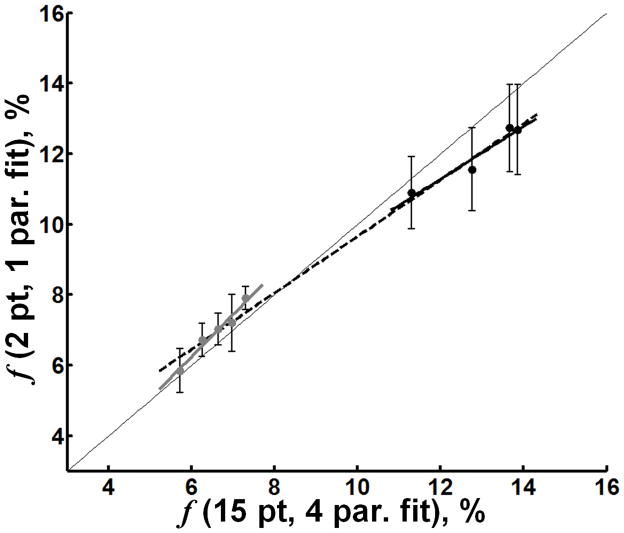
From Table 1, the mean values from non-tumor tissues of T₂^B, the product T₂^FR₁^F, and the constant k(1−f)/f determined for constrained single-parameter fitting were 10.7 μs, 0.030, and 29 s⁻¹, respectively. Comparing ROI-based results in non-tumor tissue from the 15 point, four-parameter fit and the 2 point, one-parameter fit of f yielded strong associations (Figure 5) across all structures (r = 0.996, p < 0.001), as well as separately within GM (r = 0.98, p = 0.003), and within WM (r = 0.97, p = 0.031). There was excellent visual agreement between the four-parameter f map and the one-parameter f map (Figure 4). Additionally, one-parameter f maps demonstrated more homogenous contrast within tissues suggestive of improved SNR that may result from reduced errors imposed by subtle mis-registrations between images, increased stability associated with single-parameter fitting compared to the fit of multiple parameters, or both. Finally, it should be noted that correlations of f estimates obtained by the single-parameter fit with quantitative histology closely reproduce (in terms of statistical significance and correlation strengths, see Table 2) those described above for the f values determined from the four-parameter fit.

Figure 5.

Scatter plots of CRI parameters derived from constrained 2 point, one-parameter fit (y-axis) versus 15 point, four-parameter fit (x-axis). The 2 point, one-parameter fit of f is in strong agreement with the 15 point, four-parameter fit of f in both GM and WM. A slight underestimation of f is evident in WM. In each plot, the dotted line represents the linear regression of all data points (GM + WM). The solid gray and black lines represent the linear regression through GM and WM, respectively. The thin gray line is the line of unity. Error bars represent the 95% CI (±1.96 × SE).

3.3 Analysis of Fast f Mapping Accuracy

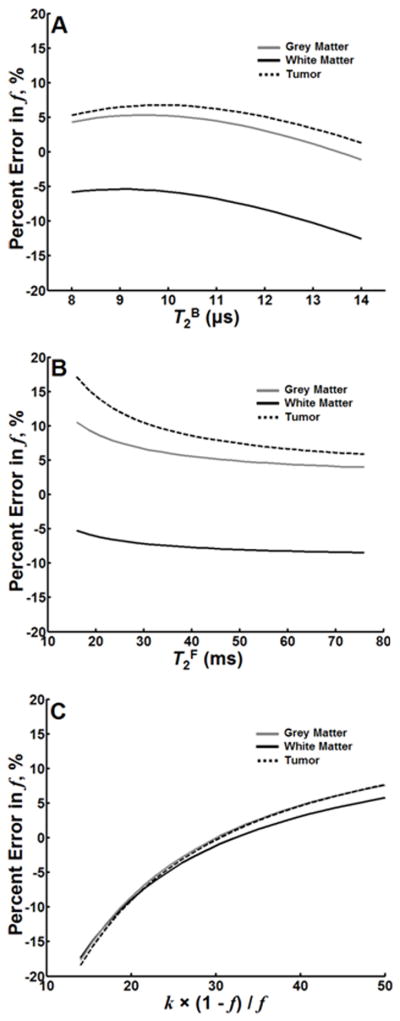
The parameter sets for error analysis of GM, WM and bulk tumor across ranges of T₂^B, T₂^F, and the constant k(1−f)/f were constructed from mean values within each category of tissues identified in Table 1. For GM: R₁ = 0.74 s⁻¹, f = 6.6 %, k = 2.94 s⁻¹, T₂^F = 44.1 ms, T₂^B = 10.0 μs. For WM: R₁ = 0.93 s⁻¹, f = 12.9 %, k = 3.22 s⁻¹, T₂^F = 30.0 ms, T₂^B = 11.3 μs. For bulk tumor: R₁ = 0.59 s⁻¹, f = 3.9 %, k = 1.88 s⁻¹, T₂^F = 59.7 ms, T₂^B = 10.3 μs.

Simulations found that errors in f in response to changes in T₂^B and T₂^F caused overestimation in GM and bulk tumor and underestimation in WM (Figure 6). In general, however, the relative error in f was less than 10% across the range of physiologically reasonable values considered for T₂^B and T₂^F. Errors in f consequent of change in the constant k(1−f)/f were similar for GM, WM and bulk tumor (Figure 6C). The theoretical predictions shown in Figure 6 are consistent with experimental data (Figure 5). Notably, values for constraints were determined from normal tissues, however, errors in f were not substantially different for tumor tissue. In fact, values of f derived from the one-parameter fit were in strong agreement with f derived from the four-parameter fit for an ROI taken from within bulk tumor (Table 1). Furthermore, there was strong visual agreement between the four-parameter f map and the one-parameter f map of the in vivo rat brain glioma (Figure 4C).

Figure 6.

Relative error in f across serial values of T₂^B (A), T₂^F (B), and k(1−f)/f (C) for GM, WM and a tumor. Relative error was calculated as the difference between output of the one-parameter fit performed on simulated data and the initial value of f (used to simulate the Z-spectra) normalized to the initial value of f.

3.4 Whole-Brain Myelin Mapping

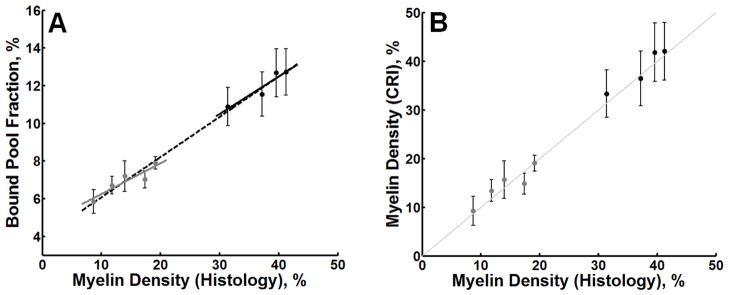
There was a strong association between 2 point, one-parameter fit of the bound pool fraction and myelin density in normal brain tissues (r = 0.99, p < 0.001; Figure 7A). This association also persisted in both GM (r = 0.91, p = 0.030) and WM (r = 0.95, p = 0.047) anatomic structures taken separately. The strength of these correlations suggests the possibility of using the bound pool fraction as a non-invasive surrogate measure of myelin density based on the linear regression approach. The regression equation defining the association between f and myelin density (MD) was: f = 0.21 × MD + 3.9 . Using this regression equation, estimates of expected myelin density were obtained from f and tested against quantitative histological measurements (Figure 7B). CRI-based myelin measurements and quantitative histology demonstrated excellent agreement (r = 0.993, p < 0.001) with no significant bias (mean ± SD, 25.1 ± 13.1 vs. 24.5 ± 12.8, respectively; p = 0.27).

Figure 7.

In (A), a scatter plot of the bound pool fraction derived from two-point, one-parameter fit versus myelin density. The dotted line represents the linear regression of all data points (GM + WM). The solid gray and black lines represent the linear regression through GM (gray dots) and WM (black dots). In (B), a scatter plot of myelin density derived from histology versus myelin density derived from CRI using the regression equation associated with the dashed line in (A). The thin gray line in (B) is the line of unity. Error bars represent the 95% CI (±1.96 × SE).

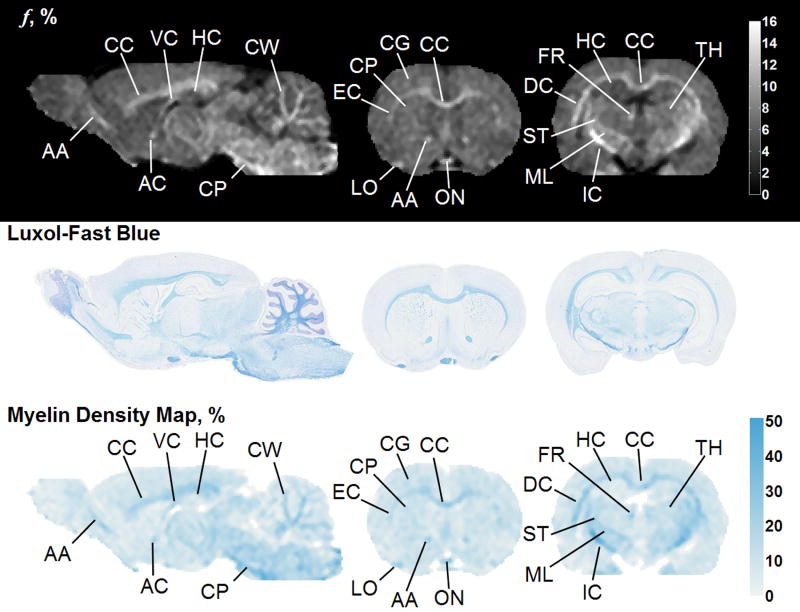
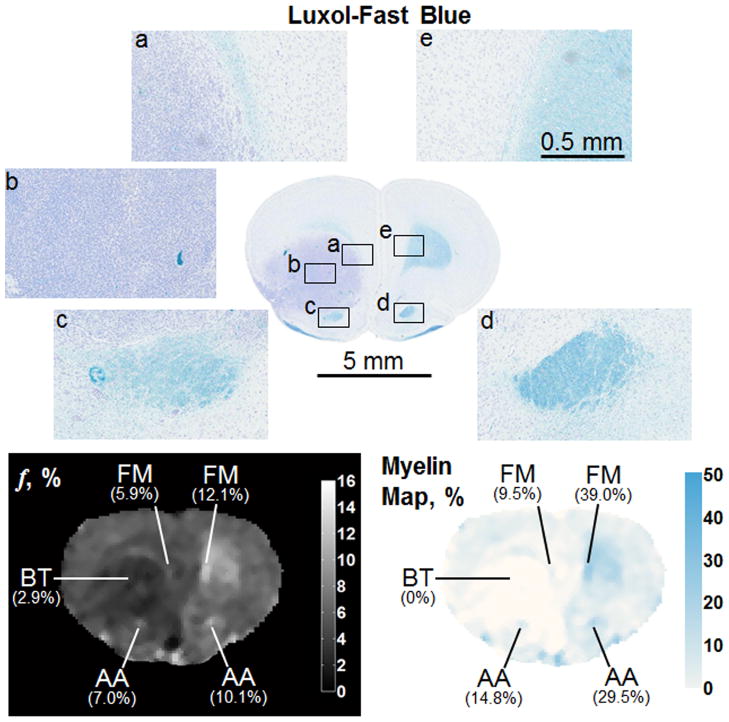
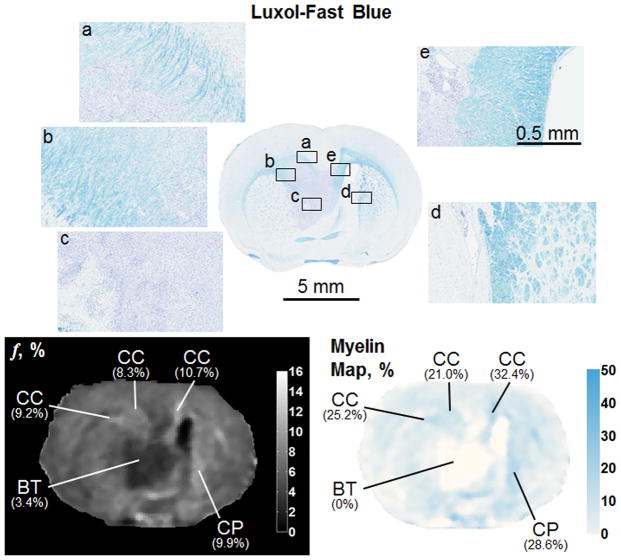
Subsequently, whole-brain CRI-based myelin maps were produced for both normal and pathologic brains and compared to registered histological sections stained with Luxol-Fast blue. In the normal brain, there is a strong visual correspondence between histology, bound pool fraction maps, and myelin maps (Figure 8). In brains with tumor present (Figures 9 and 10), there is a similar visual agreement. The bulk tumor is characterized by a negligibly low myelin density (Figures 9b and 10c). Differences in GM and WM resulting from pathologic changes induced by the tumor were detectable. Mass effect of the tumor was observed to compress contralateral tissues, which in one instance resulted in an increase in myelin density in the caudate putamen (Figure 10d) causing an elevation in the bound pool fraction from the corresponding region compared to the expected value based on normal animals (9.9% vs. 7.1%, respectively). In WM adjacent to bulk tumor a marked decrease of myelin content as identified by both CRI-based myelin maps and histology is suggestive of tumor infiltration (Figures 10a and 10b). Effects of tumor infiltration were also evident in WM fiber tracts. A decrease in myelin density was observed in the anterior limb of the anterior commissure adjacent to tumor growth (Figure 9c) compared to the unaffected contralateral side (Figure 9d). This relative decrease in myelin density manifested as a decrease of the structure’s mean value in the CRI-based bound pool fraction (7.0% vs. 10.1%, respectively; Figure 9) and myelin maps (14.8% vs. 29.5%, respectively; Figure 9).

Figure 8.

Bound pool fraction maps (top row), Luxol-Fast blue stain (middle row), and myelin maps (bottom row) of a normal rat brain presented in sagittal and coronal planes. AA = anterior limb, anterior commissure; AC = anterior commissure; CC = corpus callosum; CG = cortical gray matter; CP = cerebral peduncle; CW = cerebellar white matter; DC = deep cerebral white matter; EC = external capsule; FR = fasciculus retroflexus; HC = hippocampus; IC = internal capsule; LO = lateral olfactory tract; ML = medial lemniscus; ON = optic nerve; ST = superior thalamic radiations; thalamus; VC = ventral hippocampal commissure

Figure 9.

Comparison of Luxol-Fast blue stain, bound pool fraction map, and myelin map of a coronal section in a rat brain with a tumor. The bulk tumor (BT, b) is characterized by a very low bound pool fraction and myelin density. The tumor is also affecting WM density adjacent to its growth. The fimbria minor of the corpus callosum (FM) and the anterior limb of the anterior commissure (AA) are less dense adjacent to the tumor (a and c, respectively) compared to the contralateral side (e and d, respectively). Changes in myelin density on histology are captured by differences in the bound pool fraction map and myelin density.

Figure 10.

Comparison of Luxol-Fast blue stain, bound pool fraction map, and myelin map of a coronal section in a rat brain with a tumor. In this example, the tumor has penetrated the corpus callosum (CC) and is causing the fibers to separate. The WM superior (a) and inferior (b) to the separation exhibits a differential myelin density, which is detectable with CRI and lower than the contralateral side (e). The tumor is also causing deformation of the contralateral caudate/putamen (CP, d), which is resulting in an increase in f and myelin density. The bulk tumor (BT, b) is characterized by a very low bound pool fraction and myelin density.

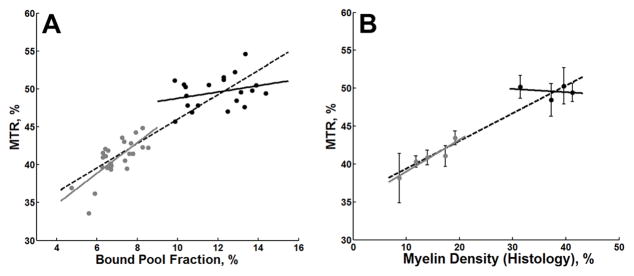
3.5 Fast f mapping vs. MTR

There was a strong association between the two-point, one-parameter fit of the bound pool fraction and MTR for GM and WM structures (r = 0.90, p < 0.001; Figure 11A). While this association persisted in GM only (r = 0.73, p < 0.001), there was not a statistically significant association in WM (r = 0.29, p = 0.21). Similarly, there was a strong correspondence between myelin density and MTR (Figure 11B) across all structures combined (r = 0.96, p < 0.001) and separately for GM (r = 0.93, p = 0.021), but not for WM (r = 0.21, p = 0.79). MTR images were remarkable for an apparent decrease in the dynamic range with poorer distinction between GM and WM structures compared to f maps (Figure 4). Although bulk tumor was readily detectable on MTR images (Figure 4), differences in fiber tracts affected by tumor were less apparent. For example, there was only a 9.5 % relative decrease between the MTR values in the anterior limb of the anterior commissure adjacent to tumor growth (Figure 9c) compared to the unaffected contralateral side (Figure 9d) (43.6% vs. 48.2% in absolute MTR measurements, respectively) For comparison, the bound pool fraction decreased by 30.1% in the same structures as described in Section 3.4 Whole-Brain Myelin Mapping.

Figure 11.

In (A), a scatter plot of all individual data points of MTR versus bound pool fraction determined from identical ROIs obtained from the same nine anatomic structures in five healthy rat brains. The dotted black line represents the linear regression of all data points (GM + WM). The solid gray and black lines represent the linear regression through GM (gray dots) and WM (black dots), respectively. In (B), a scatter plot of myelin density derived from histology versus the mean MTR for each anatomic structure. Error bars represent the 95% CI (±1.96 × SE).

4. Discussion

In this study, the bound pool fraction obtainable with CRI in the in vivo normal rat brain at 3.0 T was found to correspond to myelin density on histology across all combined tissue types, and separately within GM and WM. This relationship was further substantiated by whole-brain bound pool fraction maps from animals with gliomas. Alterations in the in vivo bound pool fraction in WM structures consequent of bulk tumor mass effect, tumor cell invasion, or both was readily identifiable. These statistical and visual associations between myelin density and the bound pool fraction were realized despite a larger MRI slice thickness compared to histological sections, which may have reduced correlations due to the partial volume effect in the MRI data. From in vivo and ex vivo studies of demyelination, the bound pool fraction has been shown to be sensitive to the destruction of the rich macromolecular proton pool inherent to myelin (Rausch et al., 2009; Schmierer et al., 2007). In addition, during ex vivo imaging of a model of neural inflammation, Stanisz et al. found a pronounced reduction in the bound pool fraction, which was attributed to reduced density of myelin caused by edema without demyelination (Stanisz et al., 2004). Accordingly, alterations to the measurable bound pool fraction may not be specific to a particular etiology of myelin density change, but rather susceptible to change incurred by a loss of myelin, an increase in separation of myelin fibers, or both. Previous investigations have indicated that multi-compartmental analysis of T₂ decay curves for measuring myelin water content may be a more specific indicator of myelin integrity (Odrobina et al., 2005) and density (Dula et al., 2010). However, acquisition of myelin water content requires an SNR of around 500 for adequate precision (Odrobina et al., 2005) and exhibits larger inter-subject variations than the bound pool fraction (Tozer et al., 2005). As such, measuring the in vivo bound pool fraction may represent a viable approach for monitoring the evolution of a variety of pathologies that afflict WM and alter myelin density in both small animal models and in human disease. In addition, the error analysis described herein supports the constrained (two-point, one-parameter fit of Z-spectra) estimation of the bound pool fraction enabling a rapid, whole-brain acquisition and production of in vivo myelin density maps of both normal and pathologic tissue. Importantly, whole-brain acquisition of the bound pool fraction should not be limited solely to the study of WM disease. While the density of myelin appears to dominate the measured bound pool fraction signal, the absence of myelin from normal (e.g. cerebellar GM) and diseased tissue (e.g. bulk tumor) did not preclude the acquisition of a signal. In tissue devoid of myelin, the principal tissue component that contributes the signal remains ambiguous. However, from previous studies (Garica et al., 2010; Quesson et al., 1997; Tozer et al., 2007; Yarnykh, 2002) and our study it is apparent that the signal is consequent of extracellular, rather than intracellular, components since measurements from bulk glioma tumor with a high cellular content have the lowest measurable bound pool fraction in comparison to both GM and WM. Future studies using immunohistochemistry to quantify the components of the extracellular matrix would be beneficial. Nevertheless, perturbations in the normal extracellular matrix of GM by glioma cell infiltration were detectable. As such, whole-brain bound pool fraction imaging may be useful for studying GM disease.

Although a strong association between myelin density and axonal content was present, the association between the bound pool fraction and axonal content was weaker compared to myelin density, particularly within the subcategories of GM and WM. Similar observations have been identified in studies using MTR. MTR is more sensitive to demyelinating lesions than conventional MRI techniques (Dousset et al., 1992; Horsfield, 2005). In a primate model of experimental autoimmune encephalomyelitis, Blezer et al. did not find a significant correspondence between MTR and axonal density (Blezer et al., 2007). Recently, similar findings have been reported for the bound pool fraction (Rausch et al., 2009). To differentiate the effects of demyelination versus axonal pathology, Ou et al. induced unilateral retinal ischemia in shiverer mice, an animal model with intact axons, but devoid of myelin (Ou et al., 2009). Differences in the bound pool fraction between optic nerves undergoing axonal degeneration versus intact optic nerves were not identified (Ou et al., 2009). Additional evidence for the primary role of myelin as a key factor determining variations of the bound pool fraction in the brain is provided by observations in the “shaking pup” canine mutant model (Samsonov et al., 2006; Samsonov et al., 2010). In this model, widespread myelin deficiency occurs across WM, while the axonal organization is almost unaffected (Lunn et al., 1995). CRI of the “shaking pup” model (Samsonov et al., 2006; Samsonov et al., 2010) revealed a dramatic decrease of the bound pool fraction in WM as compared to normal animals. Accordingly, the bound pool fraction appears rather specific for myelin content, but it may not provide a reliable measure of axonal degeneration or density.

In comparison to fast bound pool fraction mapping, MTR imaging affords a more rapid acquisition since this semi-quantitative technique requires only two images with and without a magnetization transfer saturation pulse. However, MTR has several inherent limitations. MTR has a complex dependence on all parameters of the two-pool model, but for discussion purposes the primary factors affecting MTR can be conceptualized in terms of the approximated theory of the pulsed MT effect (Yarnykh, 2002). In the typical conditions of MTR imaging, MTR values are inversely proportional to a weighted sum of two factors: 1/(f × T₁) and 1/(k × T₁), where their relative weights depend on pulse sequence parameters. As such, an expected pathological decrease of f and k can be offset by an increase in T₁, which will result in reduced sensitivity of MTR to tissue changes. This theoretical approach explains the absence of a statistically significant association between MTR and myelin density in normal WM found in the present study, while detecting more robust differences in myelin density that occur between WM and GM or bulk tumor. The observation that MTR has reduced sensitivity to myelin density compared to bound pool fraction is substantiated by Rausch et al. in their study of experimental autoimmune encephalomyelitis in rats (Rausch et al., 2009), where MTR was reported to have a decreased dynamic range and decreased sensitivity for detecting early changes in areas of demyelination. Further, MTR cannot be consistently interpreted without knowledge of the pathological trends in the parameters f, k, and T₁. Finally, contributions of f, k and T₁ into MTR vary between imaging protocols due to different sequence parameters, such as TR, excitation flip angle, and properties of a saturation pulse. Collectively, these findings suggest that bound pool fraction imaging may provide earlier detection of abnormal tissue and a more accurate estimate of tissue involvement, which may prove beneficial in diseases that are diffuse and have variable alterations to myelin density such as invasive gliomas.

While the described method for fast bound pool fraction mapping provides good accuracy and excellent time efficiency, these advantages are achieved at the cost of losing information about other two-pool model parameters. According to previous studies (Odrobina et al., 2005; Sled and Pike, 2001; Stanisz et al., 2004; Yarnykh, 2002), the pathological changes in these parameters are more difficult to interpret, and their determination is associated with larger errors and technical difficulties. Particularly, for the CRI method allowing simultaneous determination of two parameters (f and k) (Yarnykh and Yuan, 2004), recent error analysis based on human brain data at 3.0 T (Underhill et al., 2009) revealed up to a 40 % error in k from both normal tissues and a simulated model of multiple sclerosis across a similar range of deviations from constrained parameter values. At the same time, the accuracy of f estimation by the two-parameter fit technique is not improved, as compared to the single-parameter method. This conclusion follows from the comparison between error analyses for the parameter f performed using the same methodology in the present study and in the previous publication (Underhill et al., 2009), where relative f errors of ±10–20% were reported. Notably, in contrast to the bound pool fraction, the rate of magnetization transfer has demonstrated variability in sensitivity to WM pathology depending on the acquisition technique (Odrobina et al., 2005; Sled and Pike, 2001; Stanisz et al., 2004; Yarnykh, 2002). In accord, a comparison between qMT methodologies found the rate of magnetization transfer to exhibit the highest variability amongst fitted parameters (Portnoy and Stanisz, 2007). Collectively, these findings draw into question the utility of k maps for imaging normal and diseased tissue.

Overall there was a general correspondence in distinctions between WM and GM for myelin density and the transverse relaxation time of both the free (T₂^F) and bound (T₂^B) pools. In particular, T₂^F maps provided reasonable contrast between GM and WM structures. However, associations with myelin density weakened substantially for T₂^F and T₂^B within the individual subtypes of GM and WM. Although, similar to the bound pool fraction, T₂^B can be evaluated with reasonable accuracy regardless of acquisition technique (Portnoy and Stanisz, 2007), evidence indicates that T₂^B may not be sensitive to pathologic changes (Rausch et al., 2009). This parameter has a minor physiological variability across brain anatomic structures and lesions as indicated by earlier studies (Cercignani et al., 2005; Sled and Pike, 2001; Tozer et al., 2003; Underhill et al., 2009; Yarnykh, 2002) and the present work (Figure 4C). In contrast, T₂^F is model dependent, although potentially sensitive to demyelination (Portnoy and Stanisz, 2007). The absence of a stronger correlation within WM may have resulted from the application of a two-pool model of magnetization transfer. As described earlier, accurate determination of T₂ in WM requires a multi-compartment model due to the additional unique contribution of water from myelin (MacKay et al., 2006; Odrobina et al., 2005). To adequately represent the separate T₂ components, four-pool models of magnetization transfer have been proposed to specifically account for myelin water content (Bjarnason et al., 2005; Levesque and Pike, 2009; Stanisz et al., 2005). However, technical limitations and imaging time constraints make acquisition of the sufficient data points necessary to fit a four-pool model impractical for whole brain imaging. Accordingly, acquisition of T₂^F via magnetization transfer may have limited applicability, particularly when traditional spin-echo sequences offer a viable alternative.

The complexity of the theoretical model describing two-pool magnetization transfer in pulsed experiments (Yarnykh, 2002; Yarnykh and Yuan, 2004) warrants a discussion regarding the validity of approximation of certain model parameters by their fixed values in order to solely extract the parameter f from a limited number of experimental measurements. Of note, the idea of uncoupling the bound pool fraction from other model parameters and measuring this parameter in a single-offset off-resonance saturation experiment was proposed earlier (Lee and Dagher, 1997) based on the continuous wave Z-spectroscopic technique. For this type of experiment, the mathematical model is described by the closed-form solution of stationary Bloch equations, and approximations allowing f estimation are easy to derive algebraically (Lee and Dagher, 1997). First, direct saturation of the free pool is considered negligible which can be achieved by applying RF irradiation at low power and sufficiently far from resonance. Second, the parameter T₂^B determining the spectral line width for the bound pool is assumed constant across tissues. Third, the exchange rate R (which is equivalent to the inverse rate constant k(1−f)/f in terms of this publication) is assumed infinitely fast in the timescale of applied RF irradiation. Fourth, the relaxation rate R₁ and equilibrium magnetization in the absence of saturation need to be measured in independent experiments. Based on the simplified first-order model of pulsed MT (Yarnykh, 2002), it is easy to show that the same assumptions would allow independent f estimation using pulsed MT data. While some of the above approximations may be rather unrealistic from a practical standpoint, the general idea of sole f measurements from off-resonance pulsed MT data has its mathematical rationale, since the simplified pulsed MT theory (Yarnykh, 2002) provides a good approximation at certain experimental conditions (particularly, at high offset frequencies >2 kHz and short sequence timing). In our implementation of the fast f measurement technique, we relied on the accurate exponential matrix model of pulsed MT (Yarnykh and Yuan, 2004) and less restrictive assumptions, which are also supported by numerous literature data. Particularly, since the direct saturation effect on the free pool may be non-negligible (especially if T₂^F is short), the fixed constraint T₂^FR₁^F was used in the model to avoid fitting of the parameter T₂^F. This option provides a rather accurate correction for direct saturation far from resonance and reduces tissue dependent variations of the direct effect related to the variability of T₂^F, as detailed earlier (Yarnykh and Yuan, 2004). It also should be noted that the specific value of T₂^FR₁^F strongly depends on magnetic field strength (Underhill et al., 2009). Similar to earlier studies (Underhill et al., 2009; Yarnykh, 2002; Yarnykh and Yuan, 2004), we assumed that the constant value of T₂^B defined for the superLorentzian line shape (Morrison and Henkelman, 1995) satisfactorily describes line shapes of the bound pool for a variety of tissues. As noted above, this assumptions is in good agreement with previous publications (Cercignani et al., 2005; Quesson et al., 1997; Sled and Pike, 2001; Tozer et al., 2003; Underhill et al., 2009; Yarnykh, 2002) and results of this study, which generally confirm a minor variability of T₂^B in brain tissues. While some tissue-dependent variations of this parameter still persist, their effect on the single-parameter fit of f can be alleviated by using an appropriate sampling scheme. Referring to the analysis by Yarnykh (Yarnykh, 2002), the effect of T₂^B on a Z-spectrum is minimized in the intermediate-frequency region (offset frequencies in a range 4-8 kHz, see Fig. 1h in (Yarnykh, 2002)). The choice of frequency sampling points in this region therefore reduces a bias caused by a deviation of fixed T₂^B from its actual value (see Figure 6A, where relative f errors caused by T₂^B demonstrate a minor dependence on T₂^B). Finally, it should be noted that the above-mentioned assumption about the infinitely fast k(1−f)/f does not hold for brain tissues, where this parameter is comparable to typical saturation rates in pulsed MT experiments (Yarnykh, 2002; Yarnykh and Yuan, 2004). Instead, the approach used in this study and briefly reported previously (Underhill et al., 2010b; Yarnykh et al., 2010) utilizes the fixed value of k(1−f)/f across a group of tissues to constrain k during the model fit. The rationale behind this approximation is based on the fact that both f and k exhibit similar global trends across brain tissues (i.e. a reduction in GM and lesions compared to WM) (Garica et al., 2010; Gloor et al., 2008; Sled et al., 2004; Sled and Pike, 2001; Underhill et al., 2009; Yarnykh, 2002; Yarnykh and Yuan, 2004). Therefore, the tissue-dependent variability of k(1−f)/f is expected to be smaller than that of k alone. Correspondingly, the constant value of k(1−f)/f provides a pseudo-estimate of k, which absorbs a part of the variance of signal intensities that is unexplained by changes in f alone during the fitting process. In summary, the above approximations in the fast f estimation method may introduce a bias caused by deviations of fixed parameters from their true values, but this bias is relatively small (<10–15% of the measured value) as confirmed by experiments and theoretical error analysis in this study. Furthermore, the f estimates obtained by the fast technique completely preserve physiological trends determining the variability of this parameter in normal and pathological tissues.

5. Conclusions

The bound pool fraction obtainable with in vivo, whole-brain CRI in the rat at 3.0 T corresponds to myelin density. A time-efficient acquisition directed at solely acquiring the bound pool fraction yields a similar correspondence with myelin density without substantial errors in the estimation of the bound pool fraction induced by the application of a constrained parametric model. The improved time-efficiency may enable improvements in resolution, SNR, or both. The in vivo production of whole-brain bound pool fraction maps and myelin density maps identified changes in both GM and WM associated with the presence of a tumor. Bound pool fraction imaging and myelin density maps may be beneficial in clinical and animal studies aimed at detecting and monitoring neurological diseases that affect GM, WM, or both.

Abbreviations

CRI

cross-relaxation imaging

GM

gray matter

MS

multiple sclerosis

MTR

magnetization transfer ratio

qMT

quantitative magnetization transfer

RGB

red-green-blue

SNR

signal-to-noise ratio

WM

white matter