Abstract
The mammalian inner ear is remarkably sensitive to quiet sounds, exhibits over 100dB dynamic range, and has the exquisite ability to discriminate closely spaced tones even in the presence of noise. This performance is achieved, in part, through active mechanical amplification of vibrations by sensory hair cells within the inner ear. All hair cells are endowed with a bundle of motile microvilli, stereocilia, located at the apical end of the cell, and the more specialized outer hair cells (OHC’s) are also endowed with somatic electromotility responsible for changes in cell length in response to perturbations in membrane potential. Both hair bundle and somatic motors are known to feed energy into the mechanical vibrations in the inner ear. The biophysical origin and relative significance of the motors remains a subject of intense research. Several biological motors have been identified in hair cells that might underlie the motor(s), including a cousin of the classical ATP driven actin-myosin motor found in skeletal muscle. Hydrolysis of ATP, however, is much too slow to be viable at audio frequencies on a cycle-by-cycle basis. Heuristically, the OHC somatic motor behaves as if the OHC lateral wall membrane were a piezoelectric material and the hair bundle motor behaves as if the plasma membrane were a flexoelectric material. We propose these observations from a continuum materials perspective are literally true. To examine this idea, we formulated mathematical models of the OHC lateral wall “piezoelectric” motor and the more ubiquitous “flexoelectric” hair bundle motor. Plausible biophysical mechanisms underlying piezo- and flexoelectricity were established. Model predictions were compared extensively to the available data. The models were then applied to study the power conversion efficiency of the motors. Results show that the material properties of the complex membranes in hair cells provide them with the ability to convert electrical power available in the inner ear cochlea into useful mechanical amplification of sound induced vibrations at auditory frequencies. We also examined how hair cell amplification might be controlled by the brain through efferent synaptic contacts on hair cells and found a simple mechanism to tune hearing to signals of interest to the listener by electrical control of these motors.
Introduction
The inner ear is capable of detecting signals less than one-billionth that of atmospheric pressure and has a dynamic range extending more than three orders of magnitude. A major contribution toward achieving this performance comes from active amplification of sound by the sensory-motor receptors, hair cells, themselves. At least five biological motors have been identified in these cells: three residing in the stereocilia bundle positioned at the apex of the hair cell and two residing in the soma1. Stereocilia bundle based amplification is currently thought to include a slow adaptation (10–100 ms) mediated by a calcium sensitive actin/myosin motor complex2–4 and faster (<ms) temporal contributions from calcium regulated mechanotransducer channel (MET) re-closure and, the subject of this study, flexoelectric generated bundle movements. Somatic motor based electromotility includes both a slow and a fast acting mechanism5. The slow mechanism occurs on the order of seconds due to cytoskeletal rearrangements/remodeling6. Fast motility, occurring at speeds up to 10 micro-seconds, is dependent on the transmembrane protein prestin and produces isochoric, transmembrane potential dependent dimensional changes7, 8 here examined as occurring due protein-dependent piezoelectricity.
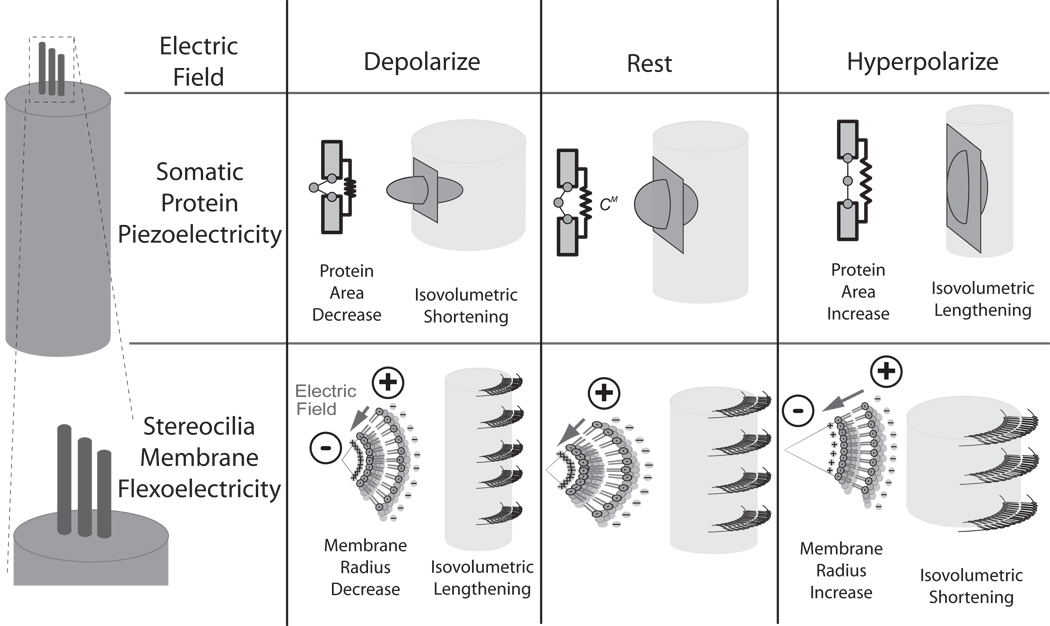
Flexoelectricity and piezoelectricity function in both the forward direction, to produce electrical polarization from deformation, and the reverse direction to produce mechanical deformation from polarization. We examined the theoretical contributions of flexoelectricity to the motility of hair bundles and of piezoelectricity to the motility of OHC somata. Flexoelectricity was first discovered in liquid-crystals but was later found to also function in biological membranes9. Here, flexoelectricity of the stereocilia membrane manifests as a converse effect in which electrical polarization compels a change in the curvature of the membrane10, 11 due to the interplay between the charged lipid-membrane heads and extra-cellular ionic solution (figure 1). The flexoelectric effect is especially large in the stereocilia because of the small radius of curvature of the membrane (~10−7 m). In contrast, electromotility of OHC somata cannot be explained by flexoelectricity alone because the effect produces movements that are much too small and in the wrong direction with respect to experimental data. Instead, OHC somata behave as if piezoelectric. Similar to flexoelectricity, piezoelectricity functions to produce mechanical strain and associated displacement current from changes in membrane potential. In the OHC case, charge displacement perpendicular to the plasma membrane compels a change in membrane surface area. Although the microscopic effect is piezoelectric in nature, the precise nanoscopic molecular origin(s) remains a subject of debate. In the simplest model, somatic piezoelectricity is described as due to charge driven conformational change in the transmembrane protein prestin and concomitant change in the surface area occupied by the protein. The area model is schematized in the center row of Fig. 1. More complex models include extrinsic voltage sensors or membrane curvature as key contributors to OHC lateral wall piezoelectric function12,13.
Figure 1.
Illustration of how somatic protein-based piezoelectricity (2nd row) and stereocilia membrane flexoelectricity (3rd row) might operate during changes in transmembrane potential (1st row). It is interesting to note that OHC somatic piezoelectricity and membrane flexoelectricity may compel length changes opposite in directions.
In the present report we briefly review a piezoelectric model of the OHC soma and a flexoelectric model of hair cell stereocilia bundle with specific attention to the efficiencies of these motors. For both the stereocilia and the somata, the peak efficiency of the electrical to mechanical conversion was found to occur at a specific frequency dependent upon hair bundle and cell body lengths respectively. Correspondingly, for maximum efficiency these models predict a gradation in length of hair bundles and somata that would map onto the tonotopic place principle within hearing organs. Peak efficiency predictions of the models were compared with morphological and neurophysiological frequency sensitivity data and were found to compare favorably. Results suggest that the lengths of stereocilia and the lengths of somata may be optimized to maximize the power output of flexo- and piezoelectric hair cell motors in the ear. The analysis also shows that efficiency of electromechanical conversion would be lost upon lowering the electrical impedance of the hair cell body, thus providing an explanation for how the brain may control hair cell organs to tune sensitivity to signals of interest to the animal.
Theory
To examine behavior of the prestin-dependent OHC somatic motor, we modeled the lateral wall as an electrically leaky piezoelectric material in series with a passive elastic material 14. This material model was coupled to the passive elasticity of the cortical lattice and to the intracellular voltage as shown schematically in Fig. 2a. The model structure is similar to the classic cable commonly used to model passive axons15, but with piezoelectric electro-mechanical equations appearing for the membrane instead of a simple parallel resistor-capacitor circuit. The model has been applied previously to explain how the displacement, isometric force and piezoelectric charge displacement (so called non-linear capacitance) depend upon morphometric's of the OHC14. Briefly, depolarizing current entering the cell body from the stereocilia compels somatic shortening due to the piezoelectric effect. When the cell is mechanically loaded, the cell shape change can do useful mechanical work on its surroundings. The magnitude and frequency dependence of the power output is critical to the ability of the motor to amplify auditory signals and therefore key for analysis.
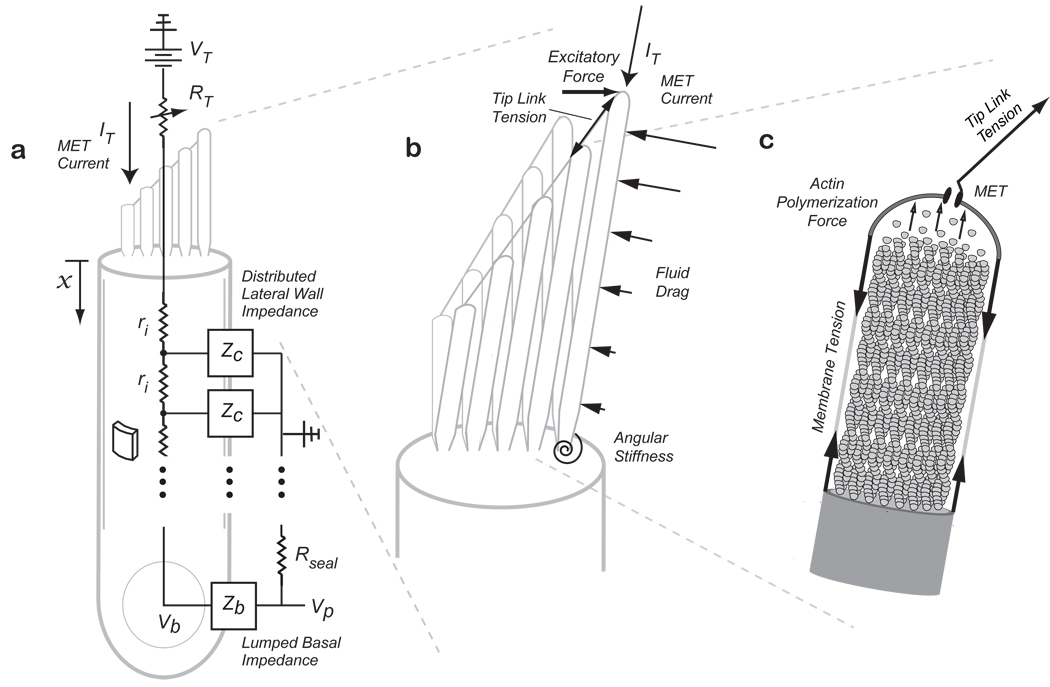
Figure 2.
Model Schematic showing (a) somatic piezoelectricity represented as a distributed lateral wall piezoelectric element ZC, with an intracellular fluid resistance, ri, and a lumped basal impedance, Zb. Input MET current, IT, enters the apically positioned stereocilia bundle with a variable resistance at their tips representing the MET. Stereocilia bundle flexoelectricity (b) is represented as stereocilia connected by tip-links with input MET current at their tips. An excitatory force tilts the bundle and is resisted by tension in the tip-links, fluid-drag forces along the length of the stereocilia, and angular stiffness at the base. The stereocilia core is filled with actin filaments (c) and the actin polymerization force required to maintain the stereocilium height generates the resting membrane tension (based on 14,16).
To examine bundle-based flexoelectric amplification, stereocilia were modeled as constant-volume cylinders with an actin core as shown in figure 2b,c 16. Briefly, the resting membrane tension was related, by Newton’s first law, to the force of actin polymerization at the tip that is necessary to maintain the stereocilium height. The stereocilia bundles are arranged in a staircase architecture with heights going from short to tall and are connected by angled tip-links. During hair cell excitation, the bundle is pushed in the direction of the tallest stereocilium causing an increase in the tip-link tension, opening of the mechanoelectric transducer (MET), and an influx of cationic (depolarizing) current. For flexoelectric stereocilia, transmembrane depolarization would cause a decrease in the radius and isochoric lengthening. The magnitude of the height increase would be volume-dependent such that taller stereocilia would elongate more than shorter stereocilia leading to an increase in the tip-link tension. Because of the angled tip-link connections, axial bundle height increases would lead to transverse bundle deflections in the negative direction. During inhibitory stimulation, transmembrane hyperpolarization would occur causing an increase in the radius, a decrease in the height, a reduction in the tip-link tension and, ultimately, further relaxation of the bundle in the negative direction. The sign of the flexoelectric effect is intrinsic to the distribution of charge induced by curvature of the membrane, such that depolarization of the stereocilia induces lengthening16.
Results
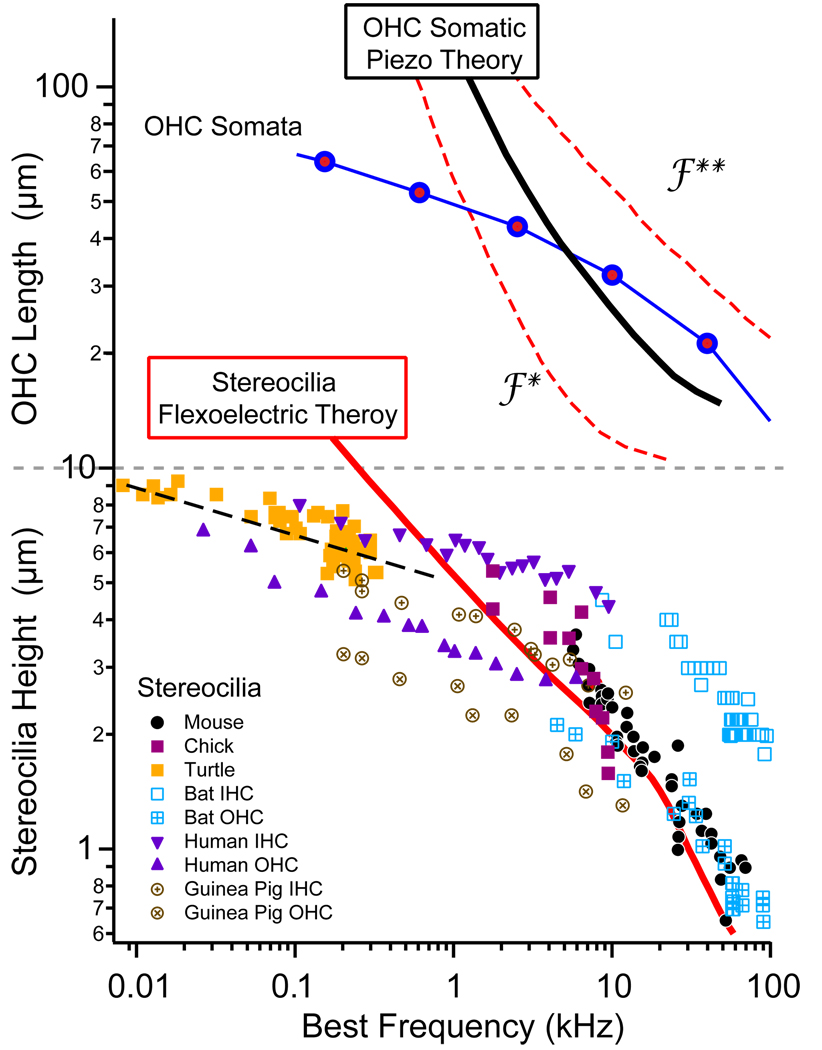
The efficiency of electrical to mechanical conversion was analyzed for both the somatic piezoelectric motor14 and for the stereocilia flexoelectric motor16. In auditory hair cell organs, there is a standing electro-chemical potential across hair cells that serves as the source of potential energy (a battery) that drives the transduction current into the stereocilia. This is the power source for the piezo- and flexo-electric motors discussed here. The input electrical power was computed from the transduction current and voltage, while the output mechanical power was computed from the force and velocity exerted by the cell or bundle on the surroundings. We focused on the real component of the power, which measures the ability of the cell to deliver real power vs. the reactive cycling of power associated with elements like capacitors or springs. For both motors, the analysis produced a peak efficiency at a specific frequency, dependent on the length of the OHC or stereocilium. The problem is fundamentally one of impedance matching the motor to the load. In our analysis we adjusted the mechanical impedance of the load to maximize the real power output (at each frequency). Even with this matching, the stiffness of the soma or hair bundle always caused poor power delivery at low frequencies. Viscosity was the primary loss mechanism near the best frequency and mass became important only at very high frequencies. The frequency where peak efficiency occurred is the most interesting. If the piezo- and flexo-electric motors are physiologically important in hearing organs one would expect hair cells to operate at frequencies near the peak efficiency. From the theoretical analysis, shorter bundles and shorter somata would have peak efficiencies at higher frequencies. As illustrated in Fig. 4, this quantitative theoretical prediction corresponds reasonably well with lengths of hair cells and bundles appearing in nature. Power output at peak efficiency for the stereocilia bundle and somata were nearly the same, about 1-2aW per pA of input transduction current.
Figure 4.
Predictions of the most efficient frequency of operation for a given height OHC (top) or stereocilia (bottom) were compared with morphological measurements of neural “best” frequency sensitivities (place-principle, based on 14, 16). Model predictions correspond well with lengths occurring in nature at frequencies above 1kHz. Divergence at lower frequencies suggests other mechanisms may be at play, or that delivering maximum piezo/flexoelectric power is not the limiting step at low frequencies.
Discussion
Membrane piezoelectricity and flexoelectricity both present mechanisms capable of cycle-by-cycle motility at frequencies that span the range of hearing (up to 100kHz). Piezoelectric analysis shows the OHC somata are capable of efficiently converting the MET current into useful power output even at frequencies higher than the membrane RC time constant. The same high frequency efficiency applies to membrane flexoelectricity. Both mechanisms show reasonable correlations with the length/ frequency tonotopy seen in nature at frequencies above 200 Hz. Our results suggest piezo- and flexoelectricity, both faster biophysics-based mechanisms, may dominate at high frequencies while other motors, such as unconventional myosin’s 3, may be more important at lower frequencies.
Experimental data show that the power output of ear hair cell motors is controlled by the brain via an extensive centripetal efferent innervation17–19. Our analysis shows that the flexo-and piezoelectric motors may be quickly shut down by efferent activation due to a decrease in the basal impedance of the soma evoked by efferent transmitter action on hair cells20, 21. In essence, short circuit of the soma by the efferent system allows the MET current to flow out the base of the cell rather than powering the piezo- and flexo-electric motors.
Conclusions
Piezoelectricity and flexoelectricity are efficient, fast membrane-related motor mechanisms capable of working on a cycle-by-cycle basis up to the limits of the hearing range. Estimations of the length vs. frequency relationship for most efficient motor prediction correlate well with the tonotopy measured in nature. Efferent activation serves to attenuate and detune these motors consistent with experimental data. The analysis predicts 1-2aW of useful power output for each pA of transduction current input consistent with experimental measurements of hair cell work16,22. Piezoelectricity and flexoelectricity provide simple explanations for the voltage-dependent movements seen in OHC somata and stereocilia bundles and provide a potential explanation for the tonotopic organization of hair bundle and cell body size observed in hair cell organs in nature. Of the two mechanisms, flexoelectricity in the stereocilia has the potential to apply across a broader range of organs and species but numerous questions remain and a discriminating experiment testing the flexoelectric hypothesis in hair bundles has not yet been reported.
Figure 3.
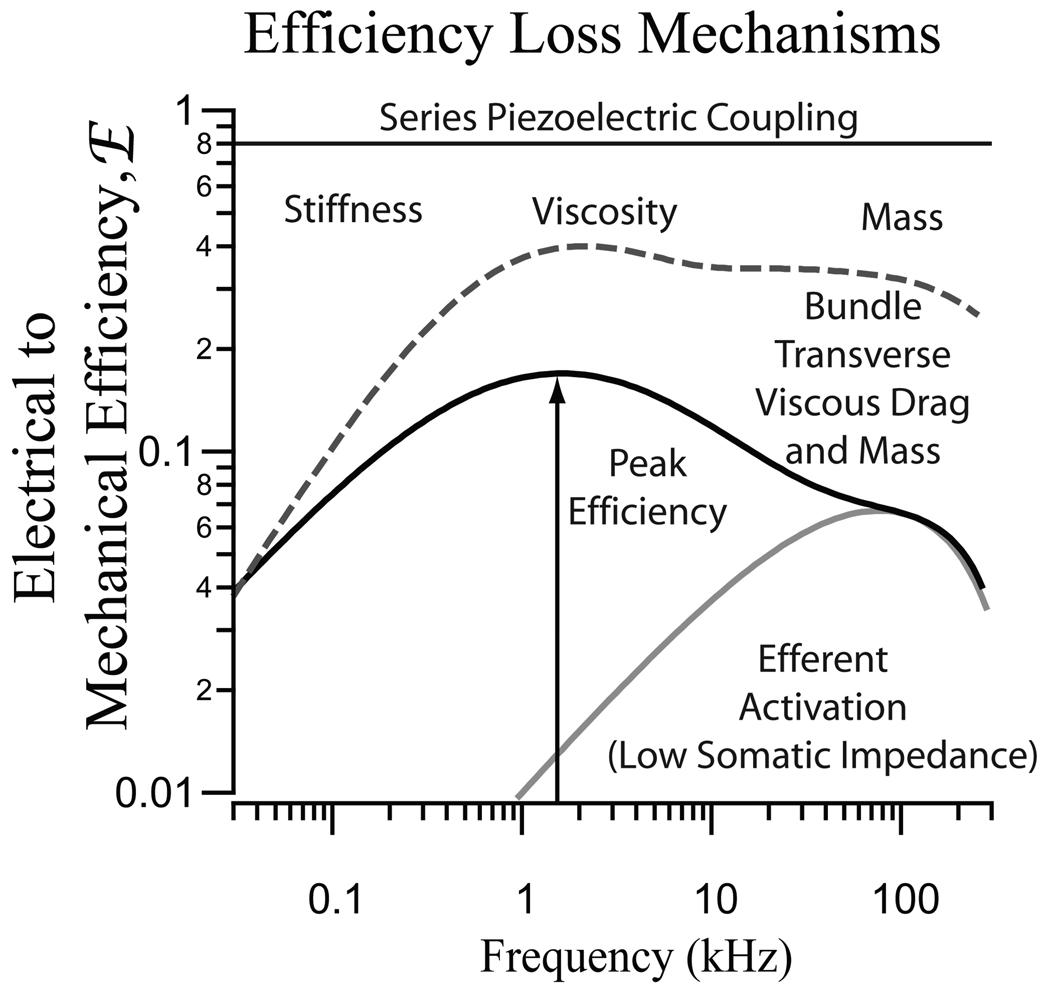
Illustration demonstrating mechanisms that produce a loss of efficiency. For both OHC protein piezoelectricity and bundle flexoelectricity, power is lost at low frequencies due mechanical stiffness, in the mid-band to viscosity, and at high frequencies due to viscosity and mass. For the bundle, transverse viscous drag causes even more power loss relative to axial movements at high frequencies. Efferent activation causes a decrease in the efficiency and a change in the frequency of peak efficiency for both the hair bundle and the soma. (Based on results from14, 16).
Acknowledgements
Supported by NIDCD R01 DC04928, R01 DC06685, and NASA Ames GSRA56000135 and NSF IGERT DGE9987616.
References
- 1.Rabbitt RD, Clifford S, Breneman KD, Farrell BF, Brownell W. PLoS Comput Biol. 2009;5(7):e1000444. doi: 10.1371/journal.pcbi.1000444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hudspeth AJ, Gillespie PG. Neuron. 1994;12(1):1–9. doi: 10.1016/0896-6273(94)90147-3. [DOI] [PubMed] [Google Scholar]
- 3.Holt JR, Gillespie SK, Provance DW, Shah K, Shokat KM, Corey DP, Mercer JA, Gillespie PG. Cell. 2002;108(3):371–381. doi: 10.1016/s0092-8674(02)00629-3. [DOI] [PubMed] [Google Scholar]
- 4.Gillespie PG, Cyr JL. Annu Rev Physiol. 2004;66:521–545. doi: 10.1146/annurev.physiol.66.032102.112842. [DOI] [PubMed] [Google Scholar]
- 5.Matsumoto N, Kalinec F. Biophys J. 2005;89(6):4343–4351. doi: 10.1529/biophysj.105.064626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Frolenkov GI, Mammano F, Kachar B. Cell Calcium. 2003;33(3):185–195. doi: 10.1016/s0143-4160(02)00228-2. [DOI] [PubMed] [Google Scholar]
- 7.Brownell WE, Bader CRB, D, De Ribaupierre Y. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- 8.Kachar B, Brownell WE, Altschuler R, Fex J. Nature. 1986;322(6077):365–368. doi: 10.1038/322365a0. [DOI] [PubMed] [Google Scholar]
- 9.Petrov AG. In: Physical and Chemical Basis of Biological Information Transfer. V. J., editor. New York: Plenum Press; 1975. pp. 111–125. [Google Scholar]
- 10.Petrov AG. Biochim Biophys Acta. 2002;1561(1):1–25. doi: 10.1016/s0304-4157(01)00007-7. [DOI] [PubMed] [Google Scholar]
- 11.Petrov AG. Anal Chim Acta. 2006;568(1–2):70–83. doi: 10.1016/j.aca.2006.01.108. [DOI] [PubMed] [Google Scholar]
- 12.Raphael RM, Popel AS, Brownell WE. Biophysical journal. 2000;78(6):2844–2862. doi: 10.1016/S0006-3495(00)76827-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Spector AA, Brownell WE, Popel AS. J Acoust Soc Am. 2003;113(1):453–461. doi: 10.1121/1.1526493. [DOI] [PubMed] [Google Scholar]
- 14.Rabbitt RD, Clifford S, Breneman KD, Farrell BF, Brownell W. PLoS Comput Biol. 2009;5(7):e1000444. doi: 10.1371/journal.pcbi.1000444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weiss T. Cellular Biophysics. Vol. 2: Electrical Properties. Cambridge: MIT Press; 1996. [Google Scholar]
- 16.Breneman K, Brownell WE, Rabbitt RD. PLoS One. 2009;4(4):e5201. doi: 10.1371/journal.pone.0005201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Murugasu E, Russell IJ. J Neurosci. 1996;16(1):325–332. doi: 10.1523/JNEUROSCI.16-01-00325.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Russell IJ, Murugasu E. J Acoust Soc Am. 1997;102(3):1734–1738. doi: 10.1121/1.420083. [DOI] [PubMed] [Google Scholar]
- 19.Liberman MC. Hearing research. 1980;3(3):189–204. doi: 10.1016/0378-5955(80)90046-5. [DOI] [PubMed] [Google Scholar]
- 20.Flock A, Russell I. J Physiol. 1976;257(1):45–62. doi: 10.1113/jphysiol.1976.sp011355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Boyle R, Rabbitt R, Highstein S. J. Neurophysiol. 2009;102(3):1513–1525. doi: 10.1152/jn.91367.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Martin P, Hudspeth AJ. Proc Natl Acad Sci U S A. 1999;96(25):14306–14311. doi: 10.1073/pnas.96.25.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]