Abstract
Animal research and computational modeling have indicated an important role for the neuromodulatory locus coeruleus–norepinephrine (LC–NE) system in the control of behavior. According to the adaptive gain theory, the LC–NE system is critical for optimizing behavioral performance by regulating the balance between exploitative and exploratory control states. However, crucial direct empirical tests of this theory in human subjects have been lacking. We used a pharmacological manipulation of the LC–NE system to test predictions of this theory in humans. In a double-blind parallel-groups design (N = 52), participants received 4 mg reboxetine (a selective norepinephrine reuptake inhibitor), 30 mg citalopram (a selective serotonin reuptake inhibitor), or placebo. The adaptive gain theory predicted that the increased tonic NE levels induced by reboxetine would promote task disengagement and exploratory behavior. We assessed the effects of reboxetine on performance in two cognitive tasks designed to examine task (dis)engagement and exploitative versus exploratory behavior: a diminishing-utility task and a gambling task with a non-stationary pay-off structure. In contrast to predictions of the adaptive gain theory, we did not find differences in task (dis)engagement or exploratory behavior between the three experimental groups, despite demonstrable effects of the two drugs on non-specific central and autonomic nervous system parameters. Our findings suggest that the LC–NE system may not be involved in the regulation of the exploration–exploitation trade-off in humans, at least not within the context of a single task. It remains to be examined whether the LC–NE system is involved in random exploration exceeding the current task context.
Keywords: norepinephrine, locus coeruleus, cognitive control, exploration, decision making, reboxetine
Introduction
The locus coeruleus (LC) is one of the major brainstem neuromodulatory nuclei, with widely distributed, ascending projections throughout the neocortex. LC activation results in the release of norepinephrine (NE) in cortical areas, which increases the responsivity of these areas to their afferent input (Servan-Schreiber et al., 1990; Berridge and Waterhouse, 2003). Traditionally, the LC–NE system has been associated with basic functions such as arousal and the sleep–wake cycle (Jouvet, 1969; Aston-Jones et al., 1984), but recent studies have suggested that this system also plays a more specific role in the control of behavior (Aston-Jones et al., 1997; Usher et al., 1999; Clayton et al., 2004). According to an influential recent theory of LC function, the adaptive gain theory (Aston-Jones and Cohen, 2005), the LC–NE system plays an important role in regulating the balance between exploiting known sources of reward versus exploring alternative options.
Neurophysiological studies in monkeys have revealed spontaneous fluctuations of tonic (baseline) LC activity over the course of a test session (Kubiak et al., 1992; Aston-Jones et al., 1996). Interestingly, these variations in tonic LC activity were closely related to the monkeys’ control state: periods of moderate tonic LC activity were consistently associated with task engagement and accurate task performance, whereas periods of elevated tonic LC activity were associated with distractible behavior and poor task performance. Periods of very low or absent tonic LC activity were associated with drowsiness and inattention. Furthermore, periods of moderate tonic LC activity were accompanied by large phasic increases in LC activity following task-relevant stimuli, whereas such phasic LC responses were diminished during periods of elevated or low tonic LC activity. Thus, during alert task performance, the pattern of LC activity varied between moderate tonic/large phasic activity, and elevated tonic/small phasic activity, which are referred to as the phasic and the tonic LC mode, respectively.
According to the adaptive gain theory (Aston-Jones and Cohen, 2005), the phasic and tonic LC modes promote, respectively, exploitative and exploratory control states. In the phasic mode, NE is released selectively in response to task-relevant events, which promotes task engagement and the optimization of performance in the current task (exploitation). In the tonic mode the sustained release of NE indiscriminately facilitates processing of all events, including non-task-related events, which promotes task disengagement and exploration. The theory further proposes that transitions between the phasic and tonic LC modes are driven by assessments of task-related costs and rewards (task utility), carried out in ventral and medial frontal structures.
The adaptive gain theory has been supported by computational modeling and neurophysiological studies in monkeys (Usher et al., 1999; Aston-Jones and Cohen, 2005) and, indirectly, by recent pupillometry studies in humans (Gilzenrat et al., 2010; Jepma and Nieuwenhuis, in press). However, crucial direct empirical tests of the theory in human participants have been lacking.
In the present study, we used a pharmacological manipulation to test in humans one of the central tenets of the adaptive gain theory, namely the assumption that the tonic LC mode promotes an exploratory control state. Participants received a single dose of reboxetine (a selective NE reuptake inhibitor), citalopram (a selective serotonin reuptake inhibitor), or placebo. Acute administration of reboxetine has opposing effects in the forebrain (increased NE levels via the inhibition of NE reuptake) and in the LC (reduction of firing activity via the increased activation of inhibitory α2-autoreceptors; Szabo and Blier, 2001). However, microdialysis studies have shown that the net effect of these two actions is an increase in NE levels in various regions of the brain (for a wide range of reboxetine doses; Page and Lucki, 2002; Invernizzi and Garattini, 2004), which supposedly resembles the effects of elevated NE release in the tonic LC mode. To determine whether potential effects were selective for manipulations of the LC–NE system, we used citalopram as a control drug; it increases serotonin but not NE levels (Bymaster et al., 2002). To confirm that these drugs at the doses employed in this study were pharmacologically active, we determined pupil size and several of the most drug-sensitive central nervous system (CNS) effects, including adaptive-tracking performance (index of visuomotor coordination and vigilance; Van Steveninck et al., 1991, 1993) and saccadic peak velocity (index of alertness; Van Steveninck et al., 1991, 1999).
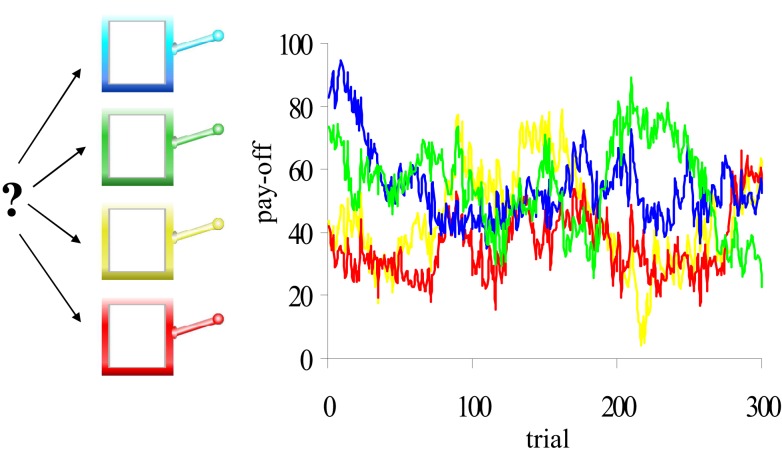
The adaptive gain theory predicted that the increased tonic NE levels that were presumably induced by reboxetine would result in more task disengagement and exploratory behavior in the reboxetine group compared to the citalopram and placebo groups. We used two cognitive tasks to test these predictions. We measured task (dis)engagement using a diminishing-utility task (Gilzenrat et al., 2010), in which task difficulty and potential reward – two determinants of task utility – increased over time. Importantly, participants had the opportunity to reset the level of task difficulty and reward, and hence disengage from the current task set. We measured exploratory behavior using a gambling task with a gradually changing pay-off structure (Daw et al., 2006; Figure 2), in which optimal performance required a delicate balance between exploitative and exploratory choices.
Figure 2.
The four-armed bandit task. Participants made repeated choices between four slot machines. Unlike standard slots, the mean pay-offs of the four machines changed gradually and independently from trial to trial (four colored lines). Participants were encouraged to earn as many points as possible during the task. Each choice was classified as exploitative or exploratory, using a computational model of reinforcement learning.
Materials and Methods
Participants
Fifty-two healthy university students, aged 18–25 years, took part in a single experimental session in return for €100,-. After signing an informed consent, participants were medically screened within 3 weeks before study participation. Exclusion criteria included history or presence of psychiatric disease and evidence of relevant clinical abnormalities.
Participants received a single oral dose of 4 mg reboxetine, 30 mg citalopram, or placebo in a double-blind, parallel-groups design. The doses of reboxetine and citalopram were based on previous studies that have found significant behavioral effects using these doses of reboxetine (e.g., Tse and Bond, 2002; Miskowiak et al., 2007; De Martino et al., 2008) and citalopram (e.g., Chamberlain et al., 2006). Unfortunately, the random-block design intended to produce equal numbers of men and women in each treatment group was thwarted by early dropouts and planning problems, causing a somewhat unbalanced sex distribution. The reboxetine group (8 men, 10 women, mean age = 20.6), the citalopram group (8 men, 8 women, mean age = 21.6), and the placebo group (10 men, 8 women, mean age = 21.5) had similar mean ages (F(2, 49) = 1.66, p = 0.20). The study was approved by the medical ethics committee of the Leiden University Medical Center and conducted according to the Declaration of Helsinki.
Procedure
All participants came to the research center at 8 AM after an overnight fast (except from water). We instructed participants to abstain from caffeine, nicotine, alcohol and other psycho-active substances from 10 PM the night prior to the study day. On arrival, participants underwent a medical screening. Approximately 1 h after arrival, participants in the citalopram group received a capsule with 2 mg granisetron, to prevent nausea as a potential side effect of citalopram. Participants in the reboxetine and placebo groups received a placebo capsule instead of granisetron. Sixty minutes later, participants received a capsule with reboxetine, citalopram or placebo.
Peak plasma concentrations of reboxetine and citalopram occur, respectively, 2 and 2–4 h after drug administration (Hyttel, 1994; Edwards et al., 1995; Dostert et al., 1997; Noble and Benfield, 1997). Accordingly, the experimental tasks designed to measure task (dis)engagement and exploratory behavior were performed between 2 and 3 h post-treatment. All participants started with the diminishing-utility task, followed by the gambling task1. We measured participants’ pupil–iris ratio (Twa et al., 2004) and subjective state at several time points during the study day. Subjective state was assessed by means of sixteen 100-mm visual analog scales measuring alertness, calmness and contentment (Bond and Lader, 1974). In addition, at several time points during the study day, we measured participants’ adaptive-tracking performance (Borland and Nicholson, 1984; see Supplementary Material for a description of the task) and saccadic eye movements (Van Steveninck et al., 1989). These measures were part of a more extensive CNS test battery, the results of which will be reported more comprehensively elsewhere. To assess drug-related effects on subjective state, pupil size, adaptive-tracking performance, and saccadic eye movements, we compared the pre-treatment values with the average values from the time points surrounding performance of the diminishing-utility task and the gambling task (i.e., 2-3 h post-treatment). The complete time courses of these measures will be reported elsewhere.
Diminishing-utility task
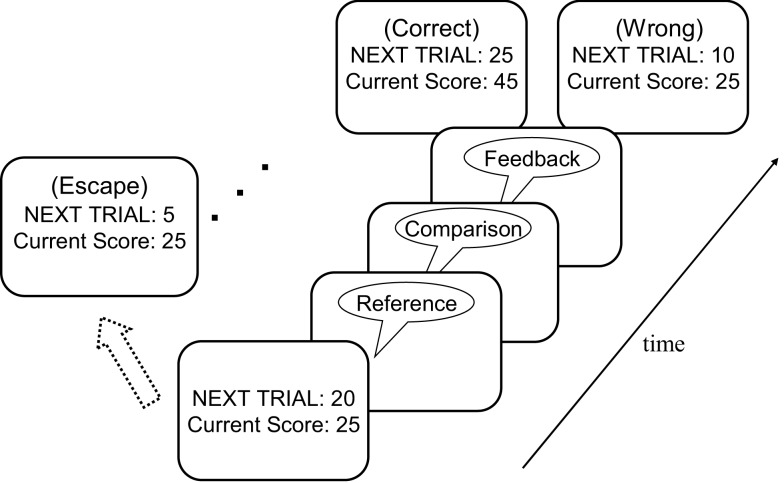
Participants performed an auditory pitch-discrimination task (Gilzenrat et al., 2010). Each trial began with a sequence of two 250-ms sinusoidal tones: a reference tone, followed 3 s later by a comparison tone. Participants were instructed to indicate whether the comparison tone was higher or lower in pitch than the reference tone, and earned points for each correct response. If participants responded correctly on a particular trial, the value of that trial was added to the participant's total score. In addition, in the next trial, the reward that could be earned increased by five points, and the pitch discrimination was made more difficult by halving the difference in pitch between the reference and comparison tones. Following an incorrect response, the reward value of the subsequent trial decreased by 10 points (but with a floor value of zero points), and the level of task difficulty remained the same. Importantly, prior to each trial, participants had the opportunity to “escape” from the current series of discriminations without score penalty and receive a new discrimination task (i.e., comparison against a new reference tone), with the point value reset to five points and the easiest pitch discriminability. Participants were instructed to maximize their total score over the 20 min of the experiment.
The task procedure is illustrated in Figure 1. At the start of each trial participants were shown a score/value screen that displayed the total score accumulated thus far and the point value of the next trial. Participants then indicated with a key press whether they wanted to “accept” this trial or “escape”. If the participant accepted the trial, a reference/comparison tone pair followed after a delay of 1 s. Participants were instructed to indicate as quickly and accurately as possible whether the comparison tone was lower or higher in pitch than the reference tone. After a delay of 1 s, the accuracy of the participant's response was indicated by a 250-ms feedback sound: a bell sound for correct responses and a buzzer sound for incorrect responses. Two seconds after the feedback sound, the next trial started. If participants pressed the “escape” button at the score/value screen, a 250-ms “escape sound” was played, immediately followed by a new score/value screen. We refer to a series of trials accepted by a participant as an “epoch” of play. Electing to escape begins a new epoch. We considered the average number of trials in an epoch as an index of task (dis)engagement.
Figure 1.
Illustration of a sample trial in the diminishing-utility task. See text for further details.
In the first trial of each epoch, the difference in pitch between the two tones was 64 Hz. As noted above, this difference was halved following each correct response. If participants correctly discriminated a ¼-Hz difference, the tones presented in the next trial were impossible to discriminate (i.e., 0 Hz difference), and impossible discrimination trials continued to be presented until the participant elected to escape. Accordingly, participants would exhaust any real discriminable differences between reference and comparison tone after nine correct trials; the tenth and subsequent trials within an epoch were impossible to discriminate. The feedback signal on impossible-discrimination trials was randomly picked. The same reference tone was presented on each trial within a given epoch. After an escape, a new reference tone was selected randomly without replacement from the set (400, 550, 700, and 850 Hz). The set was replenished if all reference tones were exhausted. On 50% of the trials, the comparison tone was higher in pitch and on the remaining trials it was lower in pitch than the reference tone.
Gambling task
Participants performed a “four-armed bandit” task (Daw et al., 2006). On each trial, participants were presented with pictures of four different-colored slot machines, and selected one by pressing the “q”-, “w”-, “a”-, or “s”- key. Participants had a maximum of 1.5 s in which to make their choice; if no choice was made during that interval, a red X appeared in the center of the screen for 4.2 s to signal a missed trial (average number = 2.5). If participants responded within 1.5 s, the lever of the chosen slot machine was lowered and the number of points earned was displayed in the chosen machine for 1 s after which the next trial started. The task consisted of 300 trials. Importantly, the number of points paid off by the four slot machines gradually and independently changed from trial to trial (Figure 2; Supplementary Material).
Before the start of the experimental session, participants were given 24 practice trials. We instructed the participants that, on top of the standard payment for participation in the study, they would receive a bonus sum of money that depended on the number of points they would obtain in this task, and that the average bonus earned in this task was 9 euros. However, we did not tell participants how the number of points was converted into euros, or what their cumulative point total was. After completion of the study, each participant received a bonus of 10 euros.
Analysis
We fitted three reinforcement-learning models to the data. All models estimated the pay-offs of each machine on each trial, and selected a machine based on these estimations. The models differed in how they calculated the estimated pay-offs (Supplementary Material). All models selected a machine according to the “softmax” rule. This rule assumes that choices between different options are made in a probabilistic manner, such that the probability that a particular machine is chosen depends on its relative estimated pay-off. The exploitation–exploration balance is adjusted by a parameter referred to as gain, or inverse temperature: with higher gain, action selection is determined more by the relative estimated pay-offs of the different options (exploitation), whereas with lower gain, action-selection is more evenly distributed across the different options (exploration). We classified each choice as exploitative or exploratory according to whether the chosen slot machine was the one with the maximum estimated pay-off (exploitation) or not (exploration). In addition, we calculated the degree of exploration for each exploratory choice, by subtracting the estimated pay-off of the chosen machine from the maximum estimated pay-off. We assessed the value of the gain parameter and the proportion of exploratory choices as a function of pharmacological treatment. Only the results from the best-fitting model are reported, although the other models yielded similar results.
Results
Subjective state
The participants assigned to the three treatment groups did not differ in their pre-treatment ratings of alertness, calmness or contentment (all ps > 0.7; Table 1). To asses the effects of reboxetine and citalopram on subjective state we conducted analyses of covariance (ANCOVAs) on the subjective ratings of alertness, calmness and contentment, with treatment and sex as between-subject factors, and the pre-treatment ratings as covariate. There were no main effects of treatment or sex, and no treatment by sex interactions on any of these ratings (all ps > 0.16), suggesting that reboxetine and citalopram did not affect subjective state.
Table 1.
Pre- and post-treatment ratings of alertness, calmness, and contentment in the placebo, citalopram and reboxetine group (SD in parentheses).
| Time of measurement | Placebo | Citalopram | Reboxetine | |
|---|---|---|---|---|
| Alertness (mm) | Pre-treatment | 51.2 (7.9) | 52.2 (5.3) | 50.6 (4.4) |
| Post-treatment | 50.2 (8.9) | 52.4 (6.4) | 48.6 (5.5) | |
| Calmness (mm) | Pre-treatment | 57.5 (9.9) | 57.9 (10.2) | 56.2 (4.4) |
| Post-treatment | 59.2 (10.7) | 54.9 (9.4) | 56.3 (6.1) | |
| Contentment (mm) | Pre-treatment | 55.9 (7.4) | 56.7 (9.1) | 55.9 (4.1) |
| Post-treatment | 57.5 (8.3) | 56.4 (8.6) | 56.9 (5.2) |
Non-specific central and autonomic nervous system effects
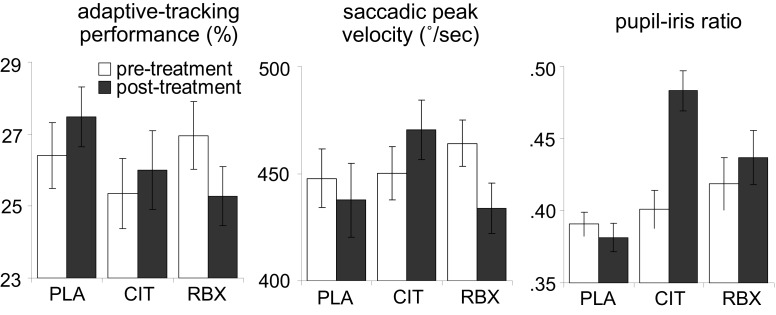
Figure 3 (left panel) shows the adaptive-tracking performance pre-treatment (averaged across 1.5 and 0.5 h pre-treatment) and post-treatment (averaged across 2 and 3 h post-treatment) for each treatment group. We conducted an ANCOVA on the post-treatment adaptive-tracking performance with treatment and sex as between-subjects factors and pre-treatment performance as covariate. This analysis revealed a main effect of treatment [F(2, 45) = 5.2, p = 0.009]. There was no main effect of sex [F(1, 45) = 0.8, p = 0.4] and no interaction between treatment and sex [F(2, 45) = 1.1, p = 0.3]. Follow-up comparisons indicated that the reboxetine group showed worse post-treatment adaptive-tracking performance than the placebo group [F(1, 31) = 12.0, p = 0.02], whereas there was no difference between the citalopram and the placebo group [F(1, 29) = 0.5, p = 0.5]. The difference in post-treatment adaptive-tracking performance between the reboxetine and the citalopram group just failed to reach significance [F(1, 29) = 3.8, p = 0.06]. These results suggest that reboxetine led to a decrease in adaptive-tracking performance.
Figure 3.
Adaptive-tracking performance, saccadic peak velocity and pupil–iris ratio pre-treatment and post-treatment, separately for each treatment group (error bars indicate standard errors of the mean). PLA, placebo; CIT, citalopram; RBX, reboxetine.
Figure 3 (middle panel) shows the saccadic peak velocity measured pre-treatment (averaged across 1.5 and 0.5 h pre-treatment) and post-treatment (averaged across 2 and 3 h post-treatment) for each treatment group. An ANCOVA on the post-treatment saccadic peak velocity with treatment and sex as between-subjects factors and pre-treatment saccadic peak velocity as covariate revealed a main effect of treatment [F(2, 45) = 15.3, p < 0.001]. There was no main effect of sex [F(1, 45) = 1.8, p = 0.2] and no significant interaction between treatment and sex [F(2, 45) = 0.6, p = 0.6]. Follow-up comparisons indicated that the reboxetine group showed smaller post-treatment saccadic peak velocity than the placebo group [F(1, 31) = 5.1, p = 0.03], whereas the citalopram group showed larger post-treatment saccadic peak velocity than the placebo group [F(1, 29) = 8.6, p = 0.007]. Thus, both reboxetine and citalopram affected saccadic eye movements, but the effects were in opposite directions. The time courses of saccadic peak velocity and adaptive-tracking performance showed that the effects of reboxetine and citalopram on these measures were maximal at the time points surrounding performance of the diminishing-utility task and the gambling task, suggesting that the drug-related CNS effects were maximal during performance of these tasks.
Figure 3 (right panel) shows the pupil–iris ratio measured pre-treatment (averaged across 1.5 and 0.5 h pre-treatment) and post-treatment (averaged across 2, 2.5 and 3 h post-treatment) for each treatment group. An ANCOVA on the post-treatment pupil–iris ratio with treatment and sex as between-subjects factors and pre-treatment pupil–iris ratio as covariate revealed a main effect of treatment [F(2, 45) = 22.1, p < 0.001]. There was no main effect of sex [F(1, 45) = 0.1, p = 0.7] and no significant interaction between treatment and sex [F(2, 45) = 2.8, p = 0.07]. Follow-up comparisons indicated that both the reboxetine group and the citalopram group had larger post-treatment pupil–iris ratios than the placebo group [F(1, 31) = 7.1, p = 0.01 and F(1, 29) = 44.4, p < 0.001, respectively]. In addition, post-treatment pupil–iris ratio was larger in the citalopram group than the reboxetine group [F(1, 29) = 13.7, p = 0.001]. Thus, consistent with previous studies (Phillips et al., 2000; Schmitt et al., 2002), both citalopram and reboxetine led to an increase in pupil diameter, and this effect was more pronounced in the citalopram group. There is no reliable evidence for direct projections from the LC to the autonomic nuclei that control the pupil (Aston-Jones, 2004), but there are a number of possible indirect pathways by which LC manipulation could affect the sympathetic nervous system (cf. Berntson et al., 1998). Therefore, it is possible that the increase in pupil diameter in the reboxetine group reflects drug-induced changes in LC activity. However, it is also possible that the pharmacological effects on pupil diameter were produced at the level of the autonomic nuclei controlling the pupil, and thus reflect other drug actions than changes in LC activity.
Diminishing-utility task
The progressive increase in both task difficulty and potential reward during each series of tone discriminations produces a non-linear development of task-related utility. Initially, the increases in reward value for correct performance outpace the increases in difficulty, such that the expected value (utility) of task performance progressively increases. However, after several trials, the increases in difficulty will lead to sufficient number of errors as to reduce the expected value of performance, even in the face of increasing reward value for correct responses.
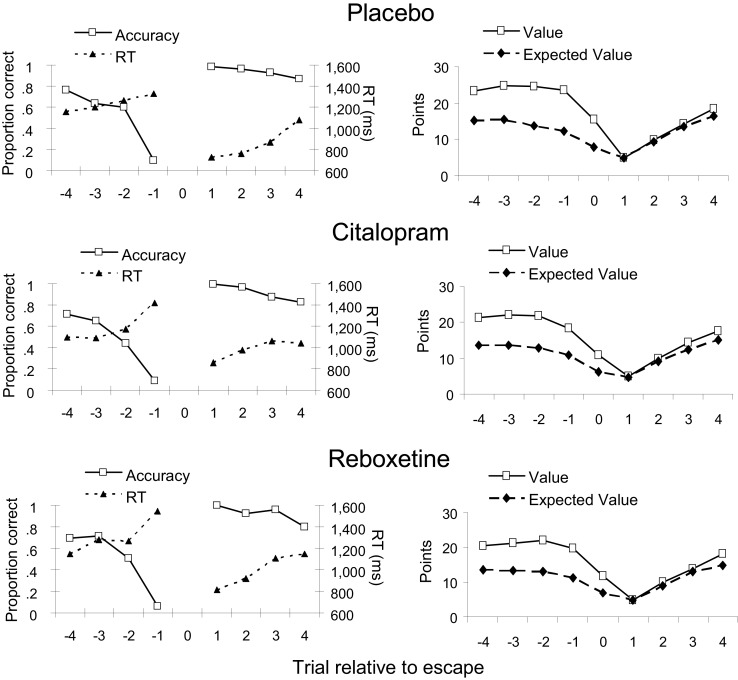
To examine changes in performance and task-related utility leading up to and following participants’ choice to “escape” (i.e., abandon the current series and start a new one), we averaged trials as a function of their position relative to the escape events. For this analysis, we considered only escape events that were preceded and followed by a minimum of four regular (i.e., non-escape) trials. As a measure of task utility, we calculated an estimate of expected value for each trial. For a given trial, expected value was computed individually for each participant by multiplying the point value of the trial (representing the potential reward value if the trial was accepted) by the expected accuracy on that trial for that participant. Expected accuracy was defined as the probability that the participant would give a correct response, given the level of difficulty of the required pitch discrimination. To determine this, we averaged the accuracy of all other trials for that participant with the same frequency difference between reference and comparison tones.
Figure 4 (left panels) shows the average accuracy and RT on the trials flanking an escape for each treatment group. All treatment groups showed a sharp decrease in accuracy and an increase in RT over the trials leading up to an escape, which was confirmed by significant linear trends [F(1, 44) = 462.5, p < 0.001 and F(1, 44) = 14.3, p < 0.001, respectively]. As expected, performance was best on the first trial following an escape, after which accuracy gradually decreased and RT increased again [F(1, 44) = 54.5, p < 0.001 and F(1, 44) = 35.1, p < 0.001, respectively]. Figure 4 (right panels) shows how our measure of expected value and the actual point value varied across the trials surrounding an escape. In all treatment groups, participants on average selected to escape when expected value approached the start value of a new series of discriminations. Both expected value and point value gradually decreased over the trials leading up to an escape [F(1, 44) = 100.1, p < 0.001 and F(1, 44) = 30.5, p < 0.001, respectively], and gradually increased again over the trials following an escape [F(1, 44) = 422.1, p < 0.001 and F(1, 44) = 1079.0, p < 0.001, respectively]. Importantly, the effects of peri-escape trial position on performance and task utility did not interact with treatment or sex (all ps > 0.3).
Figure 4.
Dependent measures for peri-escape trials in the three treatment groups. Trial number “0” indicates the escape trial. Left panels: accuracy and response time (RT). Right panels: Trial value and its computed expected value. Note that no measures of accuracy and RT are available for escape trials, because, on these trials, no comparison tone was presented.
We next examined the average number of accepted trials in an epoch. The average number of trials in an epoch did not differ between the three treatment groups [F(2, 44) = 0.26, p = 0.77]. There was no main effect of sex either [F(1, 44) = 1.08, p = 0.30], and no interaction between treatment and sex [F(2, 44) = 0.33, p = 0.72]. Furthermore, there was no significant across-subject correlation between the mean epoch length and the reboxetine-related change in adaptive-tracking performance [r = 0.43, p = 0.08]. Note that, if anything, this correlation showed a trend in the opposite direction than predicted by the adaptive gain theory. Mean epoch length was not significantly correlated with the drug-related increase in pupil diameter either [r = −0.13, p = 0.62 in the reboxetine group; r = 0.24, p = 0.38 in the citalopram group].
There were no effects of treatment or sex on the total number of trials completed or total number of points obtained (all ps > 0.3), except for a significant interaction between treatment and sex on the total number of point obtained [F(2, 44) = 3.68, p = 0.03]. Follow-up contrasts indicated that the male participants obtained significantly more points than the female participants in the reboxetine group [t(16) = 3.08, p = 0.007], whereas there were no significant sex effects in the placebo and citalopram groups (ps > 0.48). An overview of the dependent variables in this task as a function of treatment and sex is shown in Table 2. An analysis of the improvement in tone-discrimination performance over the course of the task (i.e., learning curve) is reported in the Supplementary Material.
Table 2.
Overview of the dependent variables in the diminishing-utility task, as a function of treatment and sex (SD in parentheses).
| Placebo | Citalopram | Reboxetine | ||||
|---|---|---|---|---|---|---|
| Men | Women | Men | Women | Men | Women | |
| Mean epoch length (trials) | 10.3 (2.3) | 12.1 (4.3) | 9.9 (2.5) | 10.9 (4.1) | 11.0 (3.8) | 11.0 (2.3) |
| Number of escapes | 12.8 (3.1) | 11.5 (4.0) | 13.4 (3.7) | 12.9 (5.1) | 13.3 (5.9) | 11.8 (4.7) |
| Total score | 1694 (380) | 1749 (418) | 1496 (537) | 1674 (404) | 1904 (353) | 1356 (391) |
| Total number of trials | 136 (3) | 136 (3) | 135 (3) | 136 (3) | 138 (3) | 132 (3) |
Gambling task
Each participant's tendency to make exploratory choices is reflected in the estimated gain parameter of the reinforcement-learning model: a lower value of the gain parameter indicates a more exploratory choice strategy (Materials and methods; Supplementary Material). The value of the gain parameter did not differ between the three treatment groups [F(2, 45) = 0.70, p = 0.51; Table S1] or between the male and female participants [F(2, 45) = 2.50, p = 0.12]. In addition, we classified each choice as exploitative or exploratory according to whether the chosen slot machine was the one with the maximum estimated pay-off (exploitation) or not (exploration). The proportion of exploratory choices did not differ between the three treatment groups [28%, 32%, and 27% in the placebo, citalopram and reboxetine group, respectively; F(2, 45) = 0.92, p = 0.41] or between male and female participants [26% versus 31%; F(2, 45) = 2.43, p = 0.13]. The three treatment groups did not differ in the degree of exploration of the exploratory choices either (section Analysis); the degrees of exploration in the placebo, citalopram and reboxetine groups were 0.39, 0.37, and 0.37, respectively (F(2, 45) = 0.43, p = 0.65).
Neither the value of the gain parameter nor the proportion of exploratory decisions was significantly correlated with the reboxetine-related change in adaptive-tracking performance [gain parameter: r = 0.41, p = 0.09; proportion exploration: r = −0.25, p = 0.32]. Our measures of exploration were not significantly correlated with the drug-related increase in pupil diameter either (ps > 0.15 in the reboxetine group; ps > 0.35 in the citalopram group).
There were no across-subject correlations between our measure of task disengagement in the diminishing-utility task (mean epoch length) and our measures of exploration in the gambling task (value gain parameter and proportion of exploratory choices; ps > 0.8). This suggests that the disengagement and exploration measures in these tasks reflect separate aspects of the exploratory control state hypothesized to be mediated by the tonic LC mode.
Discussion
The present study provided the first direct test in humans of one of the central tenets of the adaptive gain theory of LC function (Aston-Jones and Cohen, 2005), namely the assumption that an elevated level of tonic LC–NE activity (tonic LC mode) promotes a more exploratory control state. Contrary to predictions of the adaptive gain theory, we found no evidence that the increased NE levels induced by reboxetine were associated with task disengagement or exploratory behavior in our experimental tasks.
Our null effects cannot be explained by a general ineffectiveness of our pharmacological manipulations, since there were significant drug effects on several central and autonomic nervous system parameters. Reboxetine caused reductions in adaptive-tracking performance and in saccadic peak velocity, which corroborates previous findings suggesting the involvement of the noradrenergic system in visuomotor control of movements (Wang et al., 2009). Citalopram increased saccadic peak velocity, which is in line with the mild stimulating properties of the SSRI on the electroencephalogram (Itil et al., 1984; Saletu et al., 2002). The time course of the effects suggests that reboxetine was maximally effective during performance of the diminishing-utility task and gambling task. In addition, both citalopram and reboxetine resulted in an increase in pupil diameter, but it is unknown whether these pupil modulations were produced by changes in LC activity or by other drug influences peripheral to the LC (e.g., on lower medullary NE cell groups or autonomic nervous system). Furthermore, previous studies using the same dose of reboxetine, between-subject designs, and similar group sizes have found significant group differences in behavioral measures (Tse and Bond, 2002; Miskowiak et al., 2007; De Martino et al., 2008). The absence of significant across-subject correlations between our measures of disengagement/exploration and the reboxetine-related effects on adaptive-tracking performance suggests that the effectiveness of the reboxetine manipulation in individual participants did not predict their tendency to disengage or explore.
The two experimental tasks we used to measure exploratory behavior and task (dis)engagement seem well suited for detecting individual differences in control state. The n-armed bandit task with non-stationary pay-off structure is the most commonly used paradigm for studying the exploration–exploitation trade-off in reinforcement-learning research (Sutton and Barto, 1998). Combined with computational modeling, it allows a formal description of participants’ choice behavior and provides an index of their tendency to explore. The diminishing-utility task is a more novel paradigm in which task engagement is modulated by means of dynamic changes in task-related utility. Importantly, the opportunity to “escape” from the current task set provides an overt behavioral index of disengagement. In line with a previous study using this task (Gilzenrat et al., 2010), we found that participants behaved optimally on average, and chose to disengage from the current task set when estimated task utility approached the baseline utility of a new task set. In addition, in a recent study using the same gambling task as used here (Jepma and Nieuwenhuis, in press) we have found that changes in utility measures and pupil diameter leading up to the switch from an exploitative to an exploratory choice strategy were similar to those leading up to an “escape” in the diminishing-utility task (Gilzenrat et al., 2010). This suggests that disengagement in the diminishing-utility task and exploration in the gambling task are both driven by decreases in task utility. That said, optimal exploration strategies in our experimental tasks may differ from those needed in the real world; the changes in pay-offs and task-related utility in our tasks developed gradually and relatively slowly over time, which may not correspond to the dynamics of utility changes in real-world environments (Cohen et al., 2007).
Although disengagement and exploration are both considered behaviors indicative of an exploratory control state associated with the tonic LC mode, it is important to note that disengagement in the diminishing-utility task (i.e., choosing to “escape” from the current series of tone discriminations) is not equivalent to exploration in the gambling task, which may explain the absence of a correlation between our measures of disengagement and exploratory behavior. The development of a computational model for the diminishing-utility task is an important objective for future studies, as this will allow a more formal description of participants’ behavior in this task and a better comparison with exploratory behavior in other tasks.
One possible explanation for the absence of reboxetine effects on our measures of task disengagement and exploratory behavior is that the LC–NE system is not involved in regulating the balance between exploitative and exploratory control states in humans. The adaptive gain theory is based on findings from neurophysiological studies in monkeys using relatively simple target-detection tasks, and it is possible that the results from these studies cannot be generalized to the regulation of control state in humans. Moreover, although it is intuitively appealing to interpret the observations of increased distractibility, labile attention, and impaired focused performance during elevated tonic LC–NE activity in animals as reflections of an exploratory control state (Aston-Jones and Cohen, 2005), it is important to note that the neurophysiological studies did not explicitly investigate the exploration–exploitation trade-off; the proposed link between the tonic LC mode and an exploratory control state is an assumption. Because we did not find evidence for this assumption, it seems appropriate to consider alternative explanations for the distractible behavior associated with the tonic LC mode. When taking a reinforcement-learning model perspective, it may be possible to explain the behaviors observed in the tonic LC mode by changes in reinforcement-learning parameters other than the exploration parameter. One possibility is that high LC–NE activity increases the rate at which action values are updated based on new information (i.e., the learning rate parameter). This hypothesis would be compatible with a recent proposal that increased NE levels boost the learning of new task contingencies (Yu and Dayan, 2005). In line with this hypothesis, the estimated learning rate of the reinforcement-learning model that we fit to the choice data of the gambling task was somewhat larger in the reboxetine group than in the other treatment groups (Table S2 and Figure S1 in Supplementary Material). However, because of the very high learning rates associated with this task, this result must be interpreted with caution. Alternatively, high LC–NE activity may increase the importance attached to immediate versus delayed rewards (i.e., the future-reward discount factor). Support for this hypothesis comes from findings from a recent study in mice that suggest that drug-induced increases in NE levels impair the ability to take future rewards into account, which would lead to the impulsive selection of options with short-term rewards (Luksys et al., 2009). Luksys et al. suggested that the distractible behavior observed in animals with elevated LC–NE activity can be produced by an increased devaluation of future, relative to immediate, rewards combined with high exploitation (as opposed to exploration; see Doya, 2002, for a similar proposal). Thus, the behaviors associated with the tonic LC mode that have been interpreted as indices of an exploratory control state by the adaptive gain theory may also be explained by modulations of other reinforcement-learning parameters. To further address this issue, future studies need to dissociate the role of the LC–NE system and other neuromodulatory systems in the regulation of different components of reinforcement learning and decision making.
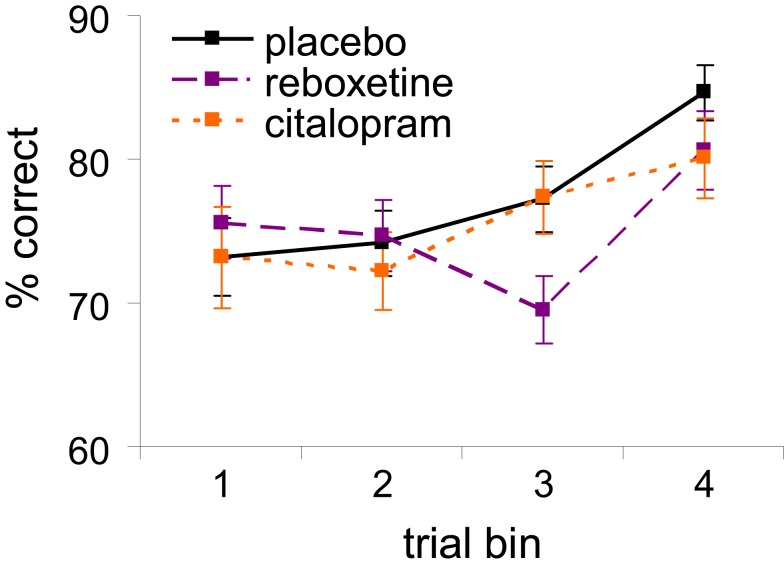
Figure S1.
Learning curves illustrating the change in tone-discrimination performance over the four consecutive trial bins in the diminishing-utility task, separately for each treatment group (error bars indicate standard errors of the mean).
Another possibility is that the tonic LC mode promotes a type of exploratory behavior and disengagement that was not measured in the present study. It is likely that exploration is not a single process but comprises several distinct functions involving different neural mechanisms. An important aspect may be whether exploration is driven by top–down motives or by bottom–up stimulation. Exploratory behavior in the four-armed bandit task may be referred to as “controlled” or “systematic” exploration, since it is aimed at obtaining information in order to optimize performance in the current task. Similarly, disengaging from the current task set in the diminishing-utility task serves the higher-level goal of maximizing the total score obtained in the task. Such controlled, top–down driven exploration and disengagement within the current task context might be mediated by different neural mechanisms and/or neuromodulatory systems than random, bottom–up driven exploration exceeding the current task context. Controlled exploration presumably requires cognitive control functions that rely on the prefrontal cortex (PFC), which is supported by the finding of PFC activation during exploratory decisions in the four-armed bandit task (Daw et al., 2006). There is also some evidence that the dopamine system plays a role in the regulation of a particular type of controlled exploration (Frank et al., 2009). Our findings suggest that the LC–NE system may not be involved in controlled exploration. However, our study leaves open the possibility that the LC–NE system is involved in random exploration exceeding the current task context. Random exploration is likely to be associated with an increased sensitivity to bottom–up activation, resulting from a global increase in neuronal responsivity. The widespread projection system of the LC and the neuromodulatory effects of NE on cortical neurons suggest that the LC–NE system is well suited to produce such global changes in responsivity.
The idea that the tonic LC mode promotes a more random type of exploration outside the current task context is supported by findings that drug-related increases in tonic NE levels improve attentional-set shifting and reversal learning in rats and monkeys (Devauges and Sara, 1990; Lapiz and Morilak, 2006; Lapiz et al., 2007; Seu et al., 2008), whereas noradrenergic lesions impair attentional-set shifting (Tait et al., 2007; McGaughy et al., 2008; Newman et al., 2008). These functions require the adaptation of behavior according to unexpected changes in the task environment, which depends on a shift of attention to previously irrelevant stimulus dimensions. These types of attention shifts are likely to be facilitated by random exploration (although an increased learning rate may provide an alternative explanation). Investigating the noradrenergic modulation of random exploration outside the current task context in humans is an important objective for future studies.
The distinction between controlled and random exploration might be related to the proposed distinction between expected and unexpected uncertainty (Yu and Dayan, 2005). Yu and Dayan have proposed that acetylcholine signals expected uncertainty (i.e., anticipated variation in task outcome), whereas NE signals unexpected uncertainty (i.e., unanticipated changes in the task context resulting in strong violations of top–down expectations; see Bouret and Sara, 2005, for a similar account). Yu and Dayan have also proposed that the NE-related signaling of unexpected uncertainty facilitates the learning of predictive relationships within a behavioral context, and therefore accelerates the detection of a change in task contingencies, which could explain the improvements in attentional-set shifting associated with increased tonic NE levels. Yu and Dayan's account thus suggests that the tonic LC mode boosts learning about new predictive relationships in noisy and changing environments. This account is closely related to the adaptive gain theory's assumption that the tonic LC mode promotes exploration, at least when applied to random exploration exceeding the current task context, since this type of exploration is likely to facilitate the learning of contextual changes. The detection of unexpected uncertainty might be an important factor in driving the LC towards a more tonic LC mode. However, how assessments of unexpected uncertainty interact with assessments of task-related utility on different timescales to regulate LC mode and control state remains to be investigated. An interesting speculation is that the degree of unexpected uncertainty determines how much weight is given to assessments of long versus short-term utility, such that long-term utility has relatively less influence in situations of high unexpected uncertainty. In terms of reinforcement-learning models, this would be similar to the suggested modulation of the learning rate parameter by the volatility of the environment (Behrens et al., 2007).
Finally, it is important to note that although microdialysis studies have shown that a single dose of reboxetine increases NE concentrations, these studies, due to their limited temporal resolution, do not provide unequivocal evidence that this reflects purely an increase in tonic NE levels. Since the effects of selective NE reuptake inhibitors on the phasic LC response in awake animals are not known, we cannot exclude the possibility that our reboxetine manipulation also affected phasic LC activity and NE release, for example via modulations of the electrotonic coupling strength between LC neurons (Alvarez et al., 2002). Thus, determining the exact effects of selective NE reuptake inhibitors on the phasic and tonic components of LC–NE activity will be important for a better understanding of their effects on cognition. In addition, the effects of pharmacologically increasing NE levels on control state might depend on individual differences in baseline (pre-treatment) NE level. Accordingly, individual differences in baseline NE level could have been partly responsible for the absence of group differences on our measures of disengagement and exploration. Consistent with this possibility, a recent study in mice has shown that pharmacological manipulations of the LC–NE system interact with several other factors, such as individual differences in genotype and trait anxiety, stress and motivation, in modulating the exploration–exploitation trade-off (Luksys et al., 2009). Thus, it seems that multiple factors need to be taken into account to enable predictions of exploratory behavior and its modulation by NE.
To conclude, our findings suggest that the acute induction of an elevated tonic NE level does not affect people's tendency to explore or disengage, at least not within the current task context. These findings challenge the adaptive gain theory's claim that the LC–NE system regulates the balance between exploitative and exploratory control states (Aston-Jones and Cohen, 2005). It remains to be examined whether the LC–NE system is involved in random exploration outside the current task context, possibly driven by the detection of unexpected uncertainty. The present study contributes to our understanding of the noradrenergic modulation of human control state, and hopefully encourages further investigation of this topic.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
Adaptive-tracking task
The adaptive-tracking task is a pursuit-tracking task (Borland and Nicholson, 1984). A target circle moves randomly on a computer screen, and the participant must try to keep a marker dot inside the moving circle by operating a joystick. The mean velocity of the moving circle is automatically adjusted to match the participant's skill. If the participant is successful in maintaining the dot inside the circle, the velocity of the moving circle gradually increases. Conversely, if the participant cannot maintain the dot inside the circle, the velocity is reduced. The task lasts 3.5 min, including a run-in period of 0.5 min during which no data is recorded. Performance is measured as the percentage of time that the participant is able to keep the dot in the circle. The adaptive-tracking task has proved to be useful for measurement of CNS effects of alcohol, various psychoactive drugs, and sleep deprivation (Cohen et al. 1985; Van Steveninck et al., 1991, 1999).
Pay-off structure of the gambling task
The number of points paid off by slot machine i on trial t ranged from 1 to 100, drawn from a Gaussian distribution (standard deviation σo = 4) around a mean μi,t and rounded to the nearest integer. At each trial, the means diffused in a decaying Gaussian random walk:
μi,t + 1 = λμi,t + (1 − λ)θ + ν
The decay parameter λ was 0.9836, the decay center θ was 50, and the diffusion noise ν was zero-mean Gaussian (standard deviation σd = 2.8). We used three instantiations of this process; one is illustrated in Figure 2.
Description of the reinforcement-learning models
We fitted three reinforcement-learning models to the choice data of the gambling task. All models consisted of a mean-tracking rule that tracked the expected pay-offs of each machine (), and a choice rule that selected a machine based on these estimations. The estimated pay-offs were calculated as follows:
Model 1 (mean pay-off estimation without decay; dayan and abbott, 2001)
When a participant chooses machine c on trial t and receives pay-off r, the estimated pay-off of the chosen machine is updated according to:
with prediction error and learning rate parameter . The estimated pay-offs of the unchosen machines do not change.
Model 2 (mean pay-off estimation with decay)
The chosen machine's estimated pay-off is updated as in model 1:
In addition, the estimated pay-offs of all machines, regardless of choice, are updated in time according to:
in which is the decay parameter (a smaller value of indicates a faster decay rate) and is the decay-center parameter.
Model 3 (kalman filter; Daw et al., 2006)
The pay-offs of the machines are updated as in model 2. In addition to tracking the mean pay-offs (), this model also tracks the uncertainties about these pay-offs (, i.e., the variance of the expected pay-off distributions) which determine the trial-specific learning rates κt. When a participant chooses machine c on trial t and receives pay-off r, the estimated pay-off distribution of the chosen machine () is updated according to:
with prediction error and learning rate .
Then, the estimated prior pay-off distributions of all machines on the subsequent trial (trial t + 1) are updated in time according to:
In all models, the selection of a machine on each trial was determined by a softmax rule; the probability Pi,t of choosing machine i on trial t as the function of the estimated pay-offs was:
with exploration parameter β (referred to as the gain, or inverse temperature).
We fitted each model to the participants’ choice data by maximizing the log-likelihood of the observed choices. To optimize the parameter fits, we used a non-linear optimization algorithm (Matlab's Fmin search function; Lagarias et al., 1998), together with a search of different starting values. The trials in which no response was made within the 1.5-s time limit were omitted. The pay-off tracking parameters () were shared by all participants that had received the same pharmacological treatment, whereas the exploration parameter (β) was estimated separately for each participant. Parameter in model 3 was fixed at 4. Estimation of parameter in model 3 resulted in extreme values for most of the participants, suggesting unreliable fits. Therefore, we fixed this parameter at 50, which is similar to the best fitting parameter found in a previous study (Daw et al., 2006). Large values of induce high learning rates, indicating that the expected pay-offs are determined primarily by the most recent experience with each machine. Given that the estimated learning rate parameters in models 1 and 2 were very near or even slightly above 1 as well (Table S1), and that previous studies have also associated this task with high learning rates (Daw et al., 2006; Jepma and Nieuwenhuis, in press), the oversensitivity to the most recent pay-off of each machine seems to be characteristic of participants’ choice behavior in this task.
Table S1.
Mean parameter estimates and fit information for the three models, separately for each treatment group (SD in parentheses).
| Model 1 | Model 2 | Model 3 | ||
|---|---|---|---|---|
| β | Placebo | 0.095 (0.028) | 0.137 (0.042) | 0.197 (0.058) |
| Reboxetine | 0.105 (0.039) | 0.152 (0.081) | 0.245 (0.129) | |
| Citalopram | 0.093 (0.035) | 0.135 (0.053) | 0.157 (0.061) | |
| Placebo | − | 0.73 | 0.70 | |
| Reboxetine | − | 0.73 | 0.65 | |
| Citalopram | − | 0.85 | 0.84 | |
| Placebo | − | 45.9 | 45.6 | |
| Reboxetine | − | 45.6 | 45.3 | |
| Citalopram | − | 49.7 | 49.5 | |
| Placebo | 0.93 | 1.07 | − | |
| Reboxetine | 1.03 | 1.17 | − | |
| Citalopram | 0.86 | 1.01 | − | |
| −LL | Placebo | 4380 | 3789 | 3821 |
| Reboxetine | 4415 | 3751 | 3780 | |
| Citalopram | 4349 | 3858 | 3901 | |
| BIC | Placebo | 8913 | 7757 | 7804 |
| Reboxetine | 8994 | 7691 | 7732 | |
| Citalopram | 8842 | 7885 | 7954 | |
| p | Placebo | <0.001 | >0.999 | <0.001 |
| Reboxetine | <0.001 | >0.999 | <0.001 | |
| Citalopram | <0.001 | >0.999 | <0.001 |
Model 2 provided the best fit to the data.
Note: Model 1, mean pay-off estimation without decay; Model 2, mean pay-off estimation with decay; Model 3, pay-off distribution estimation with decay; -LL, negative log likelihood (smaller values indicate better fit); BIC, Bayesian information criterion; p, BIC model weight.
To compare the adequacy of the three models in explaining the observed data we used the Bayesian information criterion (BIC; Raftery, 1996), a statistical criterion for model selection. The BIC is an increasing function of the residual sum of squares from the estimated model, and an increasing function of the number of free parameters to be estimated. Thus, the best model is the model with the lowest BIC value. In addition, the raw BIC values were transformed to a probability scale (BIC model weights or “Schwarz weights”), enabling a more intuitive comparison of the probabilities of each model being the best model, given the data and the set of candidate models (Wagenmakers and Farrell, 2004). Table S1 shows the estimated parameter values and the BIC values and model weights of each model. Model 2 (mean pay-off estimation with decay) provided by far the best fit to the choice data.
Tone-discrimination learning curves in the diminishing-utility task
To examine whether the three treatment groups showed different rates of improvement in tone-discrimination performance over the course of the task (i.e., different learning curves), we divided all trials in four equally sized consecutive trial bins, separately for each participant and each level of task difficulty, and assessed the mean percentage of correct tone discriminations in each trial bin (Figure S1). The trials with impossible discriminations (i.e., 0 Hz tone differences) were excluded from the analysis. There was a significant main effect of trial bin on tone-discrimination performance [F(3, 132) = 10.1, p < 0.001], which was best described by a linear improvement over the four sequential bins [F(1, 44) = 15.9, p < 0.001]. This learning effect interacted with treatment at a trend level [F(6, 132) = 2.1, p = 0.057], but did not differ between the male and female participants (p = 0.48). Follow-up comparisons indicated that the learning curve in the reboxetine group differed from those in the placebo and citalopram groups [F(3, 93) = 2.5, p = 0.07 and F(3, 87) = 2.7, p = 0.05, respectively]; whereas the placebo and citalopram groups showed a significant linear improvement over the four consecutive bins (linear trend effect ps < 0.002 for both groups), the effect of trial bin in the reboxetine group was best described by a cubic trend [F(1, 17) = 11.8, p = 0.003] reflecting the initial decrease in performance in trial bins 2 and 3 followed by an increase in performance in the last bin.
Bootstrap analysis of the shared parameters in the reinforcement-learning model
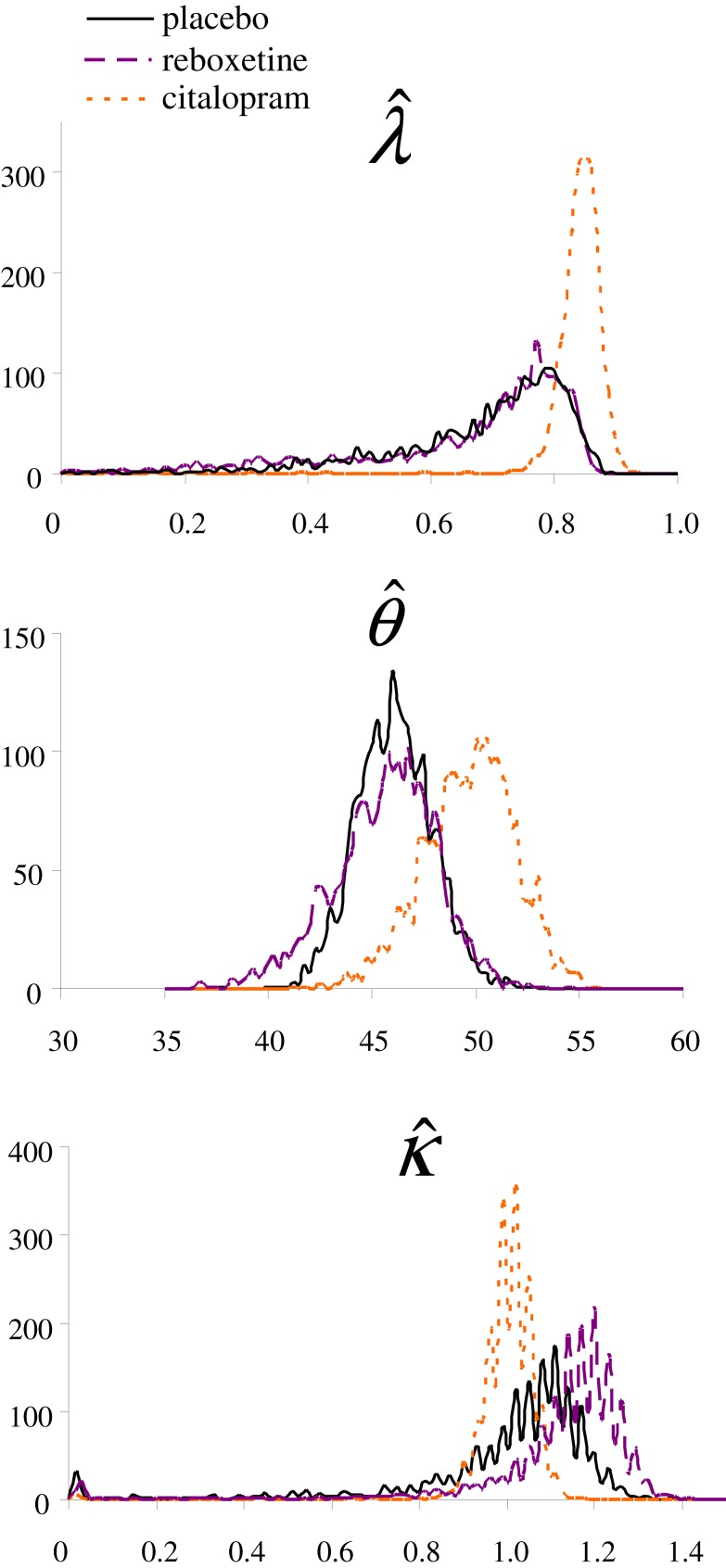
To approximate the distribution of the shared parameters, (), we conducted a bootstrap analysis (Efron and Tibshirani, 1993). For each treatment group, the computer generated 2162 bootstrap sets by sampling with replacement from the original group of participants; each bootstrap set had the same number of “participants” as the original data set. Model 2 was fitted to the choice data from each bootstrap set, which resulted in a bootstrap sampling distribution for each parameter in each treatment group (Figure S2).
Figure S2.
Bootstrap distributions of the (decay parameter; larger values indicate slower decay rate), (decay center), and (learning rate) parameters in each treatment group.
To assess whether the parameter values differed between the three treatment groups we determined the 95% confidence interval of each parameter in each group (Table S2). The distributions of the parameter suggest that is larger in the citalopram group than in the other two groups, indicating a slower decay rate (i.e., slower forgetting of the estimated values) in the citalopram group. However, the bootstrap-based 95% confidence interval of the citalopram group partly overlaps with that of the other treatment groups, hence the difference misses significance. The trend for a slower decay rate in the citalopram group may be consistent with findings that serotonin manipulations affect the sensitivity for short- versus long-term consequences of actions (e.g., Schweighofer et al., 2008). The values of and did not differ significantly between the three groups, although there was a trend for a somewhat higher learning rate in the reboxetine group.
Table S2.
The 2.5, 50 and 97.5 percentile of the bootstrap sampling distributions of the parameters.
| Percentile | ||||||
|---|---|---|---|---|---|---|
| 2.5 | 50 | 97.5 | ||||
| Placebo | 0.31 | 0.73 | 0.85 | |||
| Reboxetine | 0.20 | 0.73 | 0.84 | |||
| Citalopram | 0.78 | 0.85 | 0.89 | |||
| Placebo | 42.4 | 45.9 | 49.6 | |||
| Reboxetine | 40.1 | 45.7 | 49.9 | |||
| Citalopram | 45.1 | 49.7 | 53.5 | |||
| Placebo | 0.17 | 1.05 | 1.22 | |||
| Reboxetine | 0.49 | 1.16 | 1.30 | |||
| Citalopram | 0.89 | 1.00 | 1.09 | |||
The 2.5 and 97.5 percentiles indicate the lower and upper bound of the 95% confidence interval.
Acknowledgments
This research was supported by the Netherlands Organization for Scientific Research. We thank Rafal Bogacz for providing the scripts for fitting the reinforcement-learning models to the behavioral data, Thijs Schrama for his help with the bootstrap analyses, and Marieke de Kam for her statistical advice.
Footnotes
1Due to technical problems, three participants did not complete one of the tasks and were excluded from the corresponding analyses. For the diminishing-utility task this was the case for one female participant in the citalopram group and one male participant in the placebo group, and for the four-armed bandit task this was the case for one male participant in the placebo group.
References
- Alvarez V. A., Chow C. C., Van Bockstaele E. J., Williams J. T. (2002). Frequency-dependent synchrony in locus ceruleus: role of electrotonic coupling. Proc. Natl. Acad. Sci. U.S.A. 99, 4032–4036 10.1073/pnas.062716299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aston-Jones G. (2004). “Locus coeruleus, A5 and A7 noradrenergic cell groups,” In The Rat Nervous System, 3rd Edn ed. Paxinos G. (San Diego: Elsevier Academic Press; ), 259–294 [Google Scholar]
- Aston-Jones G., Cohen J. D. (2005). An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci. 28, 403–450 10.1146/annurev.neuro.28.061604.135709 [DOI] [PubMed] [Google Scholar]
- Aston-Jones G., Foote S. L., Bloom F. E. (1984). “Anatomy and physiology of locus coeruleus neurons: functional implications,” in Frontiers of Clinical Neuroscience: Vol. 2, Norepinephrine, eds Ziegler M., Lake C. R. (Baltimore: Williams and Wilkins; ), 92–116 [Google Scholar]
- Aston-Jones G., Rajkowski J., Kubiak P. (1997). Conditioned responses of monkey locus coeruleus neurons anticipate acquisition of discriminative behavior in a vigilance task. Neuroscience 80, 697–715 10.1016/S0306-4522(97)00060-2 [DOI] [PubMed] [Google Scholar]
- Aston-Jones G., Rajkowski J., Kubiak P., Valentino R. J., Shipley M. T. (1996). Role of the locus coeruleus in emotional activation. Prog. Brain Res. 107, 379–402 10.1016/S0079-6123(08)61877-4 [DOI] [PubMed] [Google Scholar]
- Behrens T. E., Woolrich M W., Walton M. E., Rushworth M. F. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221 10.1038/nn1954 [DOI] [PubMed] [Google Scholar]
- Berntson G. G., Sarter M., Cacioppo J. T. (1998). Anxiety and cardiovascular reactivity: the basal forebrain cholinergic link. Behav. Brain Res. 94, 225–248 10.1016/S0166-4328(98)00041-2 [DOI] [PubMed] [Google Scholar]
- Berridge C. W., Waterhouse B. D. (2003). The locus coeruleus-noradrenergic system: modulation of behavioral state and state-dependent cognitive processes. Brain Res. Brain Res. Rev. 42, 33–84 10.1016/S0165-0173(03)00143-7 [DOI] [PubMed] [Google Scholar]
- Bond A., Lader M. (1974). The use of analogue scales in rating subjective feelings. Br. J. Psychol. 47, 211–218 [Google Scholar]
- Borland R. G., Nicholson A. N. (1984). Visual motor co-ordination and dynamic visual acuity. Br. J. Clin. Pharmacol. 18(Suppl. 1), 69S–72S [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouret S., Sara S. J. (2005). Network reset: a simplified overarching theory of locus coeruleus noradrenaline function. Trends Neurosci. 28, 574–582 10.1016/j.tins.2005.09.002 [DOI] [PubMed] [Google Scholar]
- Bymaster F. P., Zhang W., Carter P. A., Shaw J., Chernet E., Phebus L., Wong D. T., Perry K. W. (2002). Fluoxetine, but not other selective serotonin uptake inhibitors, increases norepinephrine and dopamine extracellular levels in prefrontal cortex. Psychopharmacology (Berl.) 160, 353–361 10.1007/s00213-001-0986-x [DOI] [PubMed] [Google Scholar]
- Chamberlain S. R., Müller U., Blackwell A. D., Clark L., Robbins T. W., Sahakian B. J. (2006). Neurochemical modulation of response inhibition and probabilistic learning in humans. Science 311, 861–863 10.1126/science.1121218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton E. C., Rajkowski J., Cohen J. D., Aston-Jones G. (2004). Phasic activation of monkey locus coeruleus neurons by simple decisions in a forced choice task. J. Neurosci. 24, 9914–9920 10.1523/JNEUROSCI.2446-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. D., McClure S. M., Yu A. J. (2007). Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 933–942 10.1098/rstb.2007.2098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw N. D., O'Doherty J. P., Dayan P., Seymour B., Dolan R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–479 10.1038/nature04766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino B., Strange B. A., Dolan R. J. (2008). Noradrenergic neuromodulation of human attention for emotional and neutral stimuli. Psychopharmacology (Berl.) 197, 127–136 10.1007/s00213-007-1015-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devauges V., Sara S. J. (1990). Activation of the noradrenergic system facilitates an attentional shift in the rat. Behav. Brain Res. 39, 19–28 10.1016/0166-4328(90)90118-X [DOI] [PubMed] [Google Scholar]
- Dostert P., Benedetti M. S., Poggesi I. (1997). Review of the pharmacokinetics and metabolism of reboxetine, a selective noradrenaline reuptake inhibitor. Eur. Neuropsychopharmacol. 7(Suppl. 1), S23–S35 10.1016/S0924-977X(97)00417-3 [DOI] [PubMed] [Google Scholar]
- Doya K. (2002). Metalearning and neuromodulation. Neural Netw. 15, 495–506 10.1016/S0893-6080(02)00044-8 [DOI] [PubMed] [Google Scholar]
- Edwards D., M, Pellizzoni C., Breuel H. P., Berardi A., Castelli M. G., Frigerio E., Poggesi I., Rocchetti M., Dubini A., Strolin Benedetti M. (1995). Pharmacokinetics of reboxetine in healthy volunteers. Single oral doses, linearity and plasma protein binding. Biopharm. Drug Dispos. 16, 443–460 10.1002/bdd.2510160603 [DOI] [PubMed] [Google Scholar]
- Frank M. J., Doll B. B., Oas-Terpstra J., Moreno F. (2009). Prefrontal and striatal dopaminergic genes predict individual differences in exploration and exploitation. Nat. Neurosci. 12, 1062–1068 10.1038/nn.2342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilzenrat M. S., Nieuwenhuis S., Jepma M., Cohen J. D. (2010). Pupil diameter tracks changes in control state predicted by the adaptive gain theory of locus coeruleus function. Cogn. Affect Behav. Neurosci. 10, 252–269 10.3758/CABN.10.2.252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyttel J. (1994). Pharmacological characterization of selective serotonin reuptake inhibitors (SSRIs). Int. Clin. Psychopharmacol. 9(Suppl. 1), 19–26 10.1097/00004850-199403001-00004 [DOI] [PubMed] [Google Scholar]
- Invernizzi R. W., Garattini S. (2004). Role of presynaptic alpha2-adrenoceptors in antidepressant action: recent findings from microdialysis studies. Prog. Neuropsychopharmacol. Biol. Psychiatry 28, 819–827 10.1016/j.pnpbp.2004.05.026 [DOI] [PubMed] [Google Scholar]
- Itil T. M., Menon G. N., Bozak M. M., Itil K. Z. (1984). CNS effects of citalopram, a new serotonin inhibitor antidepressant (a quantitative pharmaco-electroencephalography study). Prog. Neuropsychopharmacol. Biol. Psychiatry 8, 397–409 [PubMed] [Google Scholar]
- Jepma M., Nieuwenhuis S. (in press). Pupil diameter predicts changes in the exploration-exploitation trade-off: Evidence for the adaptive gain theory. J. Cogn. Neurosci. [DOI] [PubMed] [Google Scholar]
- Jouvet M. (1969). Biogenic amines and the states of sleep. Science 163, 32–41 10.1126/science.163.3862.32 [DOI] [PubMed] [Google Scholar]
- Kubiak P., Rajkowski J., Aston-Jones G. (1992). Behavioral performance and sensory responsiveness of LC neurons in a vigilance task varies with tonic LC discharge rate. Soc. Neurosci. Abstr. 18, 538 [Google Scholar]
- Lapiz M. D., Bondi C. O., Morilak D. A. (2007). Chronic treatment with desipramine improves cognitive performance of rats in an attentional set-shifting test. Neuropsychopharmacology (Berl. Ger.) 32, 1000–1010 [DOI] [PubMed] [Google Scholar]
- Lapiz M. D., Morilak D. A. (2006). Noradrenergic modulation of cognitive function in rat medial prefrontal cortex as measured by attentional set shifting capability. Neuroscience 137, 1039–1049 10.1016/j.neuroscience.2005.09.031 [DOI] [PubMed] [Google Scholar]
- Luksys G., Gerstner W., Sandi C. (2009). Stress, genotype and norepinephrine in the prediction of mouse behavior using reinforcement learning. Nat. Neurosci. 12, 1180–1186 10.1038/nn.2374 [DOI] [PubMed] [Google Scholar]
- McGaughy J., Ross R. S., Eichenbaum H. (2008). Noradrenergic, but not cholinergic, deafferentation of prefrontal cortex impairs attentional set-shifting. Neuroscience 153, 63–71 10.1016/j.neuroscience.2008.01.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miskowiak K., Papadatou-Pastou M., Cowen P. J., Goodwin G. M., Norbury R., Harmer C. J. (2007). Single dose antidepressant administration modulates the neural processing of self-referent personality trait words. Neuroimage 37, 904–911 10.1016/j.neuroimage.2007.05.036 [DOI] [PubMed] [Google Scholar]
- Newman L. A., Darling J., McGaughy J. (2008). Atomoxetine reverses attentional deficits produced by noradrenergic deafferentation of medial prefrontal cortex. Psychopharmacology (Berl.) 200, 39–50 10.1007/s00213-008-1097-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble S., Benfield P. (1997). Citalopram: a review of its pharmacology, clinical efficacy and tolerability in the treatment of depression. CNS Drugs 8, 410–431 10.2165/00023210-199708050-00009 [DOI] [Google Scholar]
- Page M. E., Lucki I. (2002). Effects of acute and chronic reboxetine treatment on stress-induced monoamine efflux in the rat frontal cortex. Neuropsychopharmacology 27, 237–247 10.1016/S0893-133X(02)00301-9 [DOI] [PubMed] [Google Scholar]
- Phillips M. A., Bitsios P., Szabadi E., Bradshaw C. M. (2000). Comparison of the antidepressants reboxetine, fluvoxamine and amitriptyline upon spontaneous pupillary fluctuations in healthy human volunteers. Psychopharmacology (Berl.) 149, 72–76 10.1007/s002139900334 [DOI] [PubMed] [Google Scholar]
- Saletu B., Anderer P., Saletu-Zyhlarz G. M., Arnold O., Pascual-Marqui R. D. (2002). Classification and evaluation of the pharmacodynamics of psychotropic drugs by single-lead pharmaco-EEG, EEG mapping and tomography (LORETA). Methods Find Exp. Clin. Pharmacol. 24(Suppl. C), 97S–120S [PubMed] [Google Scholar]
- Schmitt J. A., Riedel W. J., Vuurman E. F., Kruizinga M., Ramaekers J. G. (2002). Modulation of the critical flicker fusion effects of serotonin reuptake inhibitors by concomitant pupillary changes. Psychopharmacology (Berl.) 160, 381–386 10.1007/s00213-001-0993-y [DOI] [PubMed] [Google Scholar]
- Servan-Schreiber D., Printz H., Cohen J. D. (1990). A network model of catecholamine effects: gain, signal-to-noise ratio, and behavior. Science 249, 892–895 10.1126/science.2392679 [DOI] [PubMed] [Google Scholar]
- Seu E., Lang A., Rivera R. J., Jentsch J. D. (2008). Inhibition of the norepinephrine transporter improves behavioral flexibility in rats and monkeys. Psychopharmacology (Berl.) 202, 505–519 10.1007/s00213-008-1250-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton R. S., Barto A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press [Google Scholar]
- Szabo S. T., Blier P. (2001). Effect of the selective noradrenergic reuptake inhibitor reboxetine on the firing activity of noradrenaline and serotonin neurons. Eur. J. Neurosci. 13, 2077–2087 10.1046/j.0953-816x.2001.01583.x [DOI] [PubMed] [Google Scholar]
- Tait D. S., Brown V. J., Farovik A., Theobald D. E., Dalley J. W., Robbins T. W. (2007). Lesions of the dorsal noradrenergic bundle impair attentional set-shifting in the rat. Eur. J. Neurosci. 25, 3719–3724 10.1111/j.1460-9568.2007.05612.x [DOI] [PubMed] [Google Scholar]
- Tse W. S., Bond A. J. (2002). Difference in serotonergic and noradrenergic regulation of human social behaviours. Psychopharmacology (Berl.) 159, 216–221 10.1007/s00213-001-0926-9 [DOI] [PubMed] [Google Scholar]
- Twa M. D., Bailey M. D., Hayes J., Bullimore M. (2004). Estimation of pupil size by digital photography. J. Cataract Refract. Surg. 30, 381–389 10.1016/S0886-3350(03)00619-9 [DOI] [PubMed] [Google Scholar]
- Usher M., Cohen J. D., Servan-Schreiber D., Rajkowski J., Aston-Jones G. (1999). The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554 10.1126/science.283.5401.549 [DOI] [PubMed] [Google Scholar]
- Van Steveninck A. L., Cohen A. F., Ward T. (1989). A microcomputer based system for recording and analysis of smooth pursuit and saccadic eye movements. Br. J. Clin. Pharmacol. 27, 712–713 [Google Scholar]
- Van Steveninck A. L., Gieschke R., Schoemaker H. C., Pieters M. S., Kroon J. M., Breimer D. D., Cohen A. F. (1993). Pharmacodynamic interactions of diazepam and intravenous alcohol at pseudo steady state. Psychopharmacology (Berl.) 110, 471–478 10.1007/BF02244655 [DOI] [PubMed] [Google Scholar]
- Van Steveninck A. L., Schoemaker H. C., Pieters M. S., Kroon R., Breimer D. D., Cohen A. F. (1991). A comparison of the sensitivities of adaptive tracking, eye movement analysis and visual analog lines to the effects of incremental doses of temazepam in healthy volunteers. Clin. Pharmacol. Ther. 50, 172–180 10.1038/clpt.1991.122 [DOI] [PubMed] [Google Scholar]
- Van Steveninck A. L., Van Berckel B. N., Schoemaker R. C., Breimer D. D., Van Gerven J. M., Cohen A. F. (1999). The sensitivity of pharmacodynamic tests for the central nervous system effects of drugs on the effects of sleep deprivation. J. Psychopharmacol. 13, 10–17 10.1177/026988119901300102 [DOI] [PubMed] [Google Scholar]
- Wang L. E., Fink G. R., Dafotakis M., Grefkes C. (2009). Noradrenergic stimulation and motor performance: differential effects of reboxetine on movement kinematics and visuomotor abilities in healthy human subjects. Neuropsychologia 47, 1302–1312 10.1016/j.neuropsychologia.2009.01.024 [DOI] [PubMed] [Google Scholar]
- Yu A. J., Dayan P. (2005). Uncertainty, neuromodulation, and attention. Neuron 46, 681–692 10.1016/j.neuron.2005.04.026 [DOI] [PubMed] [Google Scholar]
Supplementary References
- Cohen A. F., Ashby L., Crowley D., Land G., Peck A. W., Miller A. A. (1985). Lamotrigine (BW430C), a potential anticonvulsant. Effects on the central nervous system in comparison with phenytoin and diazepam. Br. J. Clin. Pharmacol. 20, 619–629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P., Abbott L. F. (2001): Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems (Chapter 9). London: The MIT Press [Google Scholar]
- Efron B., Tibshirani R. J. (1993). An Introduction to the Bootstrap. London: Chapman & Hall [Google Scholar]
- Lagarias J. C., Reeds J. A., Wright M. H., Wright P. E. (1998). Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 9, 112–147 10.1137/S1052623496303470 [DOI] [Google Scholar]
- Raftery A. E. (1996). Approximate Bayes factors and accounting for model uncertainty in generalized linear models. Biometrika 83, 251–266 10.1093/biomet/83.2.251 [DOI] [Google Scholar]
- Schweighofer N., Bertin M., Shishida K., Okamoto Y., Tanaka S. C., Yamawaki S., Doya K. (2008). Low-serotonin levels increase delayed reward discounting in humans. J. Neurosci. 28, 4528–4532 10.1523/JNEUROSCI.4982-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenmakers E. J., Farrell S. (2004). AIC model selection using Akaike weights. Psychon. Bull. Rev. 11, 192–196 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1.
Mean parameter estimates and fit information for the three models, separately for each treatment group (SD in parentheses).
| Model 1 | Model 2 | Model 3 | ||
|---|---|---|---|---|
| β | Placebo | 0.095 (0.028) | 0.137 (0.042) | 0.197 (0.058) |
| Reboxetine | 0.105 (0.039) | 0.152 (0.081) | 0.245 (0.129) | |
| Citalopram | 0.093 (0.035) | 0.135 (0.053) | 0.157 (0.061) | |
| Placebo | − | 0.73 | 0.70 | |
| Reboxetine | − | 0.73 | 0.65 | |
| Citalopram | − | 0.85 | 0.84 | |
| Placebo | − | 45.9 | 45.6 | |
| Reboxetine | − | 45.6 | 45.3 | |
| Citalopram | − | 49.7 | 49.5 | |
| Placebo | 0.93 | 1.07 | − | |
| Reboxetine | 1.03 | 1.17 | − | |
| Citalopram | 0.86 | 1.01 | − | |
| −LL | Placebo | 4380 | 3789 | 3821 |
| Reboxetine | 4415 | 3751 | 3780 | |
| Citalopram | 4349 | 3858 | 3901 | |
| BIC | Placebo | 8913 | 7757 | 7804 |
| Reboxetine | 8994 | 7691 | 7732 | |
| Citalopram | 8842 | 7885 | 7954 | |
| p | Placebo | <0.001 | >0.999 | <0.001 |
| Reboxetine | <0.001 | >0.999 | <0.001 | |
| Citalopram | <0.001 | >0.999 | <0.001 |
Model 2 provided the best fit to the data.
Note: Model 1, mean pay-off estimation without decay; Model 2, mean pay-off estimation with decay; Model 3, pay-off distribution estimation with decay; -LL, negative log likelihood (smaller values indicate better fit); BIC, Bayesian information criterion; p, BIC model weight.
Table S2.
The 2.5, 50 and 97.5 percentile of the bootstrap sampling distributions of the parameters.
| Percentile | ||||||
|---|---|---|---|---|---|---|
| 2.5 | 50 | 97.5 | ||||
| Placebo | 0.31 | 0.73 | 0.85 | |||
| Reboxetine | 0.20 | 0.73 | 0.84 | |||
| Citalopram | 0.78 | 0.85 | 0.89 | |||
| Placebo | 42.4 | 45.9 | 49.6 | |||
| Reboxetine | 40.1 | 45.7 | 49.9 | |||
| Citalopram | 45.1 | 49.7 | 53.5 | |||
| Placebo | 0.17 | 1.05 | 1.22 | |||
| Reboxetine | 0.49 | 1.16 | 1.30 | |||
| Citalopram | 0.89 | 1.00 | 1.09 | |||
The 2.5 and 97.5 percentiles indicate the lower and upper bound of the 95% confidence interval.