Multisite Reliability of Cognitive BOLD Data

Abstract

Investigators perform multi-site functional magnetic resonance imaging studies to increase statistical power, to enhance generalizability, and to improve the likelihood of sampling relevant subgroups. Yet undesired site variation in imaging methods could off-set these potential advantages. We used variance components analysis to investigate sources of variation in the blood oxygen level dependent (BOLD) signal across four 3T magnets in voxelwise and region of interest (ROI) analyses. Eighteen participants traveled to four magnet sites to complete eight runs of a working memory task involving emotional or neutral distraction. Person variance was more than 10 times larger than site variance for five of six ROIs studied. Person-by-site interactions, however, contributed sizable unwanted variance to the total. Averaging over runs increased between-site reliability, with many voxels showing good to excellent between-site reliability when eight runs were averaged and regions of interest showing fair to good reliability. Between-site reliability depended on the specific functional contrast analyzed in addition to the number of runs averaged. Although median effect size was correlated with between-site reliability, dissociations were observed for many voxels. Brain regions where the pooled effect size was large but between-site reliability was poor were associated with reduced individual differences. Brain regions where the pooled effect size was small but between-site reliability was excellent were associated with a balance of participants who displayed consistently positive or consistently negative BOLD responses. Although between-site reliability of BOLD data can be good to excellent, acquiring highly reliable data requires robust activation paradigms, ongoing quality assurance, and careful experimental control.

Introduction

Several multi-site functional magnetic resonance imaging (fMRI) studies are currently in process or are being planned (Van Horn and Toga 2009). The larger samples made possible by multi-site studies can potentially increase statistical power, enhance the generalizability of study results, facilitate the identification of disease risk, increase the odds of finding uncommon genetic variations, make rare disease and subgroup identification possible, help justify multivariate analyses, and support cross-validation designs (Cohen 1988; Friedman and Glover 2006a; Jack et al., 2008; Mulkern et al., 2008; Van Horn and Toga 2009). Yet the potential advantages of multi-site functional imaging studies could be off-set by unwanted variation in imaging methods across sites. Even when the same activation task is used at different sites and the same image processing path is employed, potential site differences might arise from differences in stimulus delivery and response recording, head stabilization method, field strength, the geometry of field inhomogeneity, gradient performance, transmit and receive coil configuration, system stability, shimming method, type and details of the image sequence including K-space trajectory, type of K-space filtering, system maintenance, and environmental noise (Friedman and Glover 2006a, 2006b; Ojemann et al., 1998; Van Horn and Toga 2009; Voyvodic 2006). A large number of experimental factors that might differ between-sites could introduce unwanted variation related to site and its interactions into in a multi-site fMRI study. This unwanted variation may, in turn, undermine the advantages of increased statistical power and enhanced generalizability that would otherwise be associated with large-sample studies. Given that unwanted between-site variation is itself likely to vary from multi-site study to multi-site study, determining the magnitude of site variation and evaluating its impact on the consistency of results across sites has become a critical component of multi-site fMRI studies (Friedman et al., 2008; Pearlson 2009).

The consistency of blood oxygen-level dependent (BOLD) fMRI values across sites has been studied for a variety of behavioral activation tasks using several different statistical approaches. One common approach is to measure between-site consistency by assessing the extent of overlap of either observed or latent activation regions (Casey et al., 1998; Gountouna et al. 2010; Vlieger et al., 2003; Zou et al., 2005). These studies find only a modest degree of overlap in the extent of activation, with the number of regions found to be significantly activated varying by five-fold across sites in one study (Casey et al., 1998). Differences in field strength and k-space trajectory have accounted for significant between-site variation in some studies (Cohen et al., 2004; Voyvodic 2006; Zou,et al., 2005). Even when Cartesian K-space trajectories are used at all sites, differences in the type of image acquisition protocol can produce differences in the spatial extent and magnitude of the BOLD signal, as studies comparing gradient-recalled echo protocols with spin echo and asymmetric spin echo protocols show (Cohen et al., 2004; Ojemann et al., 1998).

Methods that measure the overlap of activation extent and volume across MR systems have been criticized for assuming invariant null-hypothesis distributions across sites and for the use of a specific threshold to determine statistical significance (Suckling et al., 2008; Voyvodic 2006). The distributions of the test statistics, however, can be checked and if differences in distributions are found, methods are available to adjust the activation maps or modify the statistical analysis (Miller 1986; Voyvodic 2006). With regard to the second criticism, overlap consistency can be investigated across a range of thresholds, as in the Zou study (Zou et al., 2005). A more fundamental limitation of overlap methods is that they do not provide a standard against which to judge the importance of a particular degree of overlap. The question of how much overlap is necessary to produce statistically robust and generalizable findings typically remains after percent overlap statistics are presented. In addition, overlap methods do not address the question of how consistently subjects can be rank-ordered by their brain response across sites. For example, in a study involving assessment of the same subjects scanned at multiple sites, a high degree of overlap in regional activation might be observed in group-level mean statistical maps across sites even though the rank-ordering of the brain response of subjects changes randomly from site to site. This possibility underscores the point that cross-site reliability of fMRI measurements cannot be determined solely by examining the consistency of group activation maps across sites using repeated measures ANOVA model.

Variance components analysis (VCA), which assesses components of systematic and error variance by random effects models, is another commonly used method to assess cross-site consistency of fMRI data (Bosnell et al., 2008; Costafreda et al., 2007; Dunn 2004; Friedman et al., 2008; Gountouna et al.,; Suckling et al., 2008). VCA provides several useful standards against which to judge the importance of consistency findings. For investigators interested in studying the brain basis of individual differences, one natural standard is to compare variance components of nuisance factors against the person variance. This strategy of assessing the importance of between-site variation in fMRI studies has been used in several studies. Costafreda and colleagues, for example, found that between-subject variance was nearly seven-fold larger than site-variance in the region of interest (ROI) they studied (Costafreda et al., 2007). In the Gountouna et al. study, site variance was virtually zero for several ROIs with the ratio of subject variance to site variance as large as 44 to 1 in another especially reliable ROI (Gountouna et al., 2010). Suckling and colleagues reported a value of between-subject variance that was slightly more than 10 times greater than the between-site variance (Suckling et al., 2008). Using a fixed effect ANOVA model, Sutton and colleagues found effect sizes for between-subject differences to be seven to sixteen times larger than the between-site effect for the ROIs studied (Sutton et al., 2008).

Variance components are also commonly used to calculate intraclass correlations (ICC) that can be compared with the intraclass correlations of other, perhaps more familiar, variables (Brennan 2001; Dunn 2004). Between-site intraclass correlations of ROIs have been reported in the .20 to .70 range for fMRI data, depending on the activation measure, behavioral task, and degree of homogeneity of the magnets studied (Bosnell et al., 2008; Friedman et al., 2008). For clinical ratings of psychiatric symptoms, ICCs in the .20 to .70 range would be rated as ranging from poor to good (Cicchetti and Sparrow 1981). The intraclass correlation can also be used to assess the impact of measurement error on the statistical power of between-site studies, providing a third method to assess the importance of VCA results (Bosnell et al., 2008; Suckling et al., 2008).

In the present study, healthy volunteers were scanned once at three sites and twice at a fourth site while performing a working memory task with emotional or neutral distraction. We investigated the between-site reliability of BOLD/fMRI data by calculating variance components for voxel-wise data. Voxel-wise VCA and ICC maps are presented in order to identify voxel clusters where particular components of variation were most prominent and where between-site reliability was largest. Presenting data for all voxels avoided limitations of generalization associated with the use of specific statistical thresholds. We also present findings obtained by averaging beta-weights over voxels within selected regions of interest (ROI) to simplify the comparison of our results with those of other studies that presented ROI results. The main study hypotheses follow:

1. Clusters of voxels will be identified where the between-subject variation will be more than 10-fold the value of the between-site variation. This hypothesis is derived from the VCA studies discussed above.

2. Variation attributed to the person-by-site interaction will be greater than variation associated with the site factor. Because person-by-site interactions occur when the rank ordering and/or distance of the BOLD response of subjects differs across sites, this source of variation reflects a broader array of potential sources of error than site variation alone.

3. The magnitude of the ICC will depend on whether the functional contrast involved a low-level or high-level control condition, where a low level control involves only orientation, attention, and basic perceptual processing, and a high level control condition involves additional cognitive processes (Donaldson and Buckner 2001). High level control conditions are likely to share a larger number of neural processes with the experimental condition than low level control conditions leading to a larger subtraction of neural activity and a smaller BOLD signal, especially for brain regions that participate in a multiplicity of neurocognitive functions engaged by the experimental task. The smaller magnitude of the BOLD response is likely to restrict the range of person variance, reducing the between-site ICC (Cronbach 1970; Magnusson 1966).

4. The between-site intraclass correlation will increase as the number of runs averaged increases. Although this hypothesis has been supported by a previous study involving a sensorimotor task, it has not been tested in BOLD data generated by a cognitive task (Friedman et al., 2008).

We also investigated the relationships among between-site reliability, effect size, and sample size. A previous within-site reliability study found correlations greater than .95 between the median within-site ICC and the activation-threshold t-test value for both an auditory target detection task and an N-back working memory task (Caceres et al., 2009). We will examine the relationship between reliability and effect size for the between-site case. Although we anticipate that median effect size calculated across voxels will be strongly related to the magnitude of between-site reliability for those voxels, dissociations might be observed. If voxels with large activation effect sizes and poor reliability are observed, we will investigate the possibility that these voxels have poor reliability due to reduced variation among people (Brennan 2001; Magnusson 1966). If voxels with small activation effect sizes and good between-site reliability are observed, we will investigate the possibility that activation magnitude within subjects is consistent across sites, yet balanced between negative and positive activation values.

In the present study, the specific form of the ICC we calculated assessed between-site consistency at an absolute level (Brennan 2001; Friedman et al., 2008; Shrout and Fleiss 1979). High between-site ICC values, therefore, would support the interchangeability of data and justify the pooling of fMRI values across sites (Friedman et al., 2008; Shavelson et al., 1989). There are, of course, alternative definitions of the ICC (Shrout and Fleiss 1979) and it is useful here to provide some discussion of the factors that would affect the choice to assess reliability based on absolute or relative agreement of measurements at different sites. The appropriate reliability measure will depend on the type of study being designed and the intended analysis. Suppose that "site" is explicitly considered as a design factor and that as a result "site" is explicitly accounted for in the data analysis. Then it might seem that the site factor will address consistent differences across site and that an ICC measuring relative agreement would be appropriate. This argument is plausible as long as "site" is orthogonal or independent of other design/analysis factors. For such studies, the Pearson correlation, the generalizability coefficient of Generalizability Theory or the ICC(3,1) statistic of Shrout and Fleiss (all of which look for relative rather than absolute agreement) would be appropriate statistics to assess reliability (Brennan 2001; Shavelson et al., 1989; Shrout and Fleiss 1979). If on the other hand there are associations between-site and other factors, e.g., there is variation in the patient/control mix cross sites or there is variation in a genotype of interest, then adjusting for site in the analysis is not enough to eliminate all site effects and it is valuable to consider an ICC measuring absolute consistency. In these circumstances, having established in a reliability study that site variation contributes only a small amount of variation to the pooled variance would permit the pooling, which in turn should increase the likelihood that important subgroups will be detected and would enhance both statistical power and the generalizability of results. The reliability results of the present study were used to design a large study where the range of genetic variation and relevant symptom subtypes could not be determined a priori. We therefore calculated ICCs to assess the consistency of the absolute magnitude of the fMRI/BOLD response in order to determine whether data pooling would be justified.

Materials and Methods

Participants

Nine male and nine female, healthy, right-handed volunteers were studied once at each of three magnet sites and twice at a fourth site (mean [range], age: 34.44 [23 – 53] years; education: 17.06 [12–23] years). The sample size was chosen so that the lower .01 confidence interval for an ICC at the lower limits of excellent reliability (.75) would exceed ICC values at poor levels of reliability (< .40) (Walter 1998). All participants were employed, with the largest number of individuals (eight) working in business, finance, or management jobs. To be enrolled, an individual needed to have eyesight correctable to 20/20 and be fluent in English. Individuals were excluded from the study if they had a current or past history of major medical illness, head injury with loss of consciousness > 24 hours, diagnosis of a current Axis I psychiatric disorder based on a Structured Clinical Interview for DSM-IV, color blindness, hearing loss, and/or a verbal intellectual quotient less than 75 on the North American Adult Reading Test (Blair and Spreen 1989; First et al., 1997). Although individuals with a past diagnosis of substance dependence were excluded, those with a history of substance abuse that did not occur during the past three months were studied.

Study Design

All participants were recruited at a single site where, with one exception, they were initially scanned. Scan order was then randomized across the four 3T magnet sites, with five individuals receiving their first and second scans at the recruitment site (See Table 1 for site descriptions). After site staff received training through webcasts, in-person meetings and teleconferences, the study quality officer (BM) qualified each site following an in-person visit, where the officer himself was scanned. His scans were not included in the analysis. The order of events at each scan session was documented on a detailed scanning checklist. Participants were asked to refrain from the use of recreational drugs two weeks prior to each scan session. They were also to have a normal night of sleep and no more than one alcoholic drink the day before each scan session and to abstain from caffeine consumption two hours before each session, with smokers avoiding smoking cigarettes in the 40 minute period prior to entering the scanner room.

Table 1.

Scanner Characteristics

Site Number	Vendor	Model	PACE	Coil Type
A	General Electric	Signa Excite	Not available	8 channel
B	General Electric	Signa Excite	Not available	8 channel
C	Siemens	TIM Trio	OFF	12 channel
D	Siemens	Trio	OFF	8 channel

Procedures

Behavioral Tasks

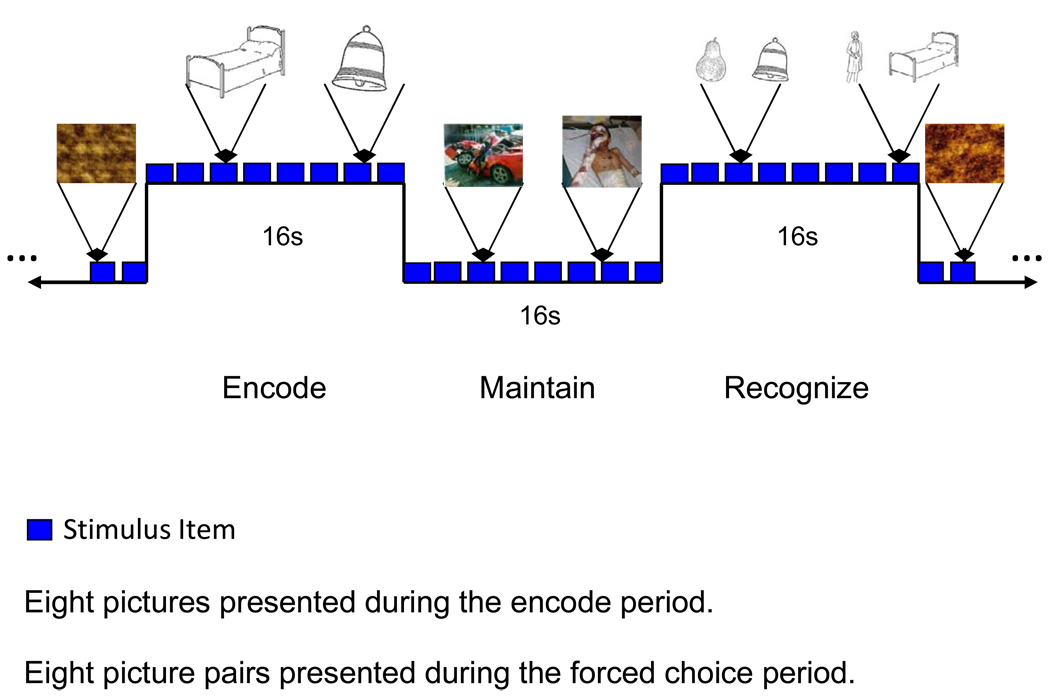
Participants performed a breath hold study and an emotional working memory task (EWMT). The results of the breath hold study will be reported elsewhere. A central aim in the development of the EWMT was to create a task that would determine the impact of attending to negative emotional stimuli during the maintain-period on subsequent recognition (Figure 1). Each EWMT block was divided into passive viewing – fixation; passive viewing – scrambled pictures; encode; maintain; and recognition periods. During the encode period participants were asked to memorize eight line drawings of common objects presented serially at two second intervals (Snodgrass and Vanderwart 1980). During the maintain period, eight neutral or eight negatively valenced photographs were presented, and participants decided whether the photograph included a human face. Intervening photographs were obtained from the International Affective Pictures System (Neutral – Mean Valence Rating: 5.48, Mean Arousal Rating: 3.40; Negative – Mean Valence Rating: 2.95, Mean Arousal Rating: 5.43) (Lang 2005). Subjects were asked to detect the presence/absence of a human face in order to ensure that they viewed and processed the content of each photograph. During the recognition period participants were presented every two seconds with a screen containing two pictures: one from the previous encode set and one that had never been presented to the subject. The subject responded by indicating which of the two pictures they had seen in the previous encode period. Choices were indicated by a button-press response. Passive viewing of a fixation cross, not shown, occurred during the initial and final six seconds; passive viewing of scrambled pictures presented every two seconds over a 16 second interval, served as the baseline condition and separated each encode-maintain-recognize cycle. The order of the two neutral and two emotional maintain-blocks within each 284 s run was pseudo-randomized across the eight study runs. The EWMT was programmed in CIGAL by the developer (JV) (www.nitric.org/projects/cigal). At the entry into the study, participants viewed a webcast to instruct them on how to perform the EWMT. Directions were reviewed prior to each study session at the remaining sites.

Figure 1.

Working Memory Task (WM) with Emotional Distraction. Each blue square represents an acquired echo-planar volume. Every WM epoch is preceded and followed by passively viewed scrambled faces. During the encode period, eight line drawings of common objects are presented at a 2 s rate. During the maintain period, individuals are instructed to remember the eight learned pictures while deciding whether intervening pictures included a human face. The block of pictures presented during the maintain period was composed of either emotionally aversive or neutral pictures. During the recognition probe period, individuals decided which of two line drawing pictures was studied during the encode period. Decisions during the maintain and recognition periods were indicated by a button press. An orientation cross was presented 6 s before and after each WM-scrambled faces cycle.

Imaging Protocols

After obtaining localizer scans to confirm head placement, a high resolution, 3D sagittal T₁ weighted image was obtained using an inversion-recovery prepared, fast spoiled gradient-recalled sequence with ASSET calibration at General Electric sites and a magnetization-prepared rapid acquisition gradient echo sequence at Siemens sites (GE: FOV 256 mm × 256 mm, matrix 256 × 256, 170 slices, 1.2 mm slice thickness, TR 7.5 ms, TE minimum full, flip angle 12°, NEX 1, ASSET two phase acceleration, scan time 4:39; Siemens: FOV 220 mm × 220 mm, matrix 256 × 192, 160 slices, 1.2 mm slice thickness, TR 2300 ms, TE 2.94 ms (Site C) or 2.92 ms (Site D), flip angle 9°, GRAPPA factor 2, scan time 4:20). Axial T₂ weighted structural images were acquired in AC-PC alignment using a fast spin echo protocol (GE: FOV 220 mm × 220 mm, matrix 256 × 256, 30 slices, 4 mm slice with 1 mm skip, NEX 2, TR 6000 ms, TE 120 ms, flip angle 149°, echo train 24, ASSET two phase acceleration, total scan time 1:20; Siemens: FOV 220 mm × 220 mm, matrix 256 × 256 (Site C) or 256 × 192 (Site D), 30 slices, 4 mm slice with 1 mm skip, TR 6310 ms, TE 68 ms, flip angle 149° degrees, turbo factor 13, GRAPPA factor 2, total scan time 1:24 (Site C) and 1:10 (Site D)). Sites used the vendor standard method for slice select for the vendor platform employed in the study.

Time series of the ${\mathrm{T}}_2^{*}$ – weighted images were obtained while participants performed eight runs of the EWMT. Scan parameters for both GE and Siemens were: gradient echo single shot echoplanar image sequence, axial AC-PC aligned, FOV 220 mm by 220 mm, matrix 64 × 64, 30 slices in ascending order, 4 mm slice thickness with 1 mm skip, TR 2000 ms, TE 30 ms, flip angle 77°, 139 active frames with three equilibration acquisitions with NEX = 1 and ramp sampling. Siemens sites did not use PACE. Images were reconstructed without the use of k-space or apodization filters, with all filters turned off at Siemens sites and Fermi filters turned off at GE sites. Throughout the duration of the experiment, weekly quality assurance scans of an agar phantom were acquired at all sites to monitor scanner performance. A detailed report of these quality assurance data has been submitted for publication (Greve et al., submitted). A pdf of the complete imaging parameters can be obtained from the authors.

Images were shared across sites by registering the locally stored image using the Storage Resource Broker (SRB) (www.sdsc.edu/srb/index.php/Main_Page) using upload scripts and procedures developed by the Function Biomedical Informatics Research Network (fBIRN) (Keator et al., 2009). Upload scripts were developed to register locally stored images and to convert images into the NIfTI-1 format (http://nifti.nimh.nih.gov). FIPS XML files were generated that linked the image analysis with the registered study ID and stored basic information about the image protocol, the image analysis and the behavioral task (Keator et al., 2006).

Functional Contrast

Images were processed with a second generation version of the FBIRN Image Processing Scripts (http://nbirn.net/research/function/fips.shtm), an image analysis pipeline primarily using routines from the FMRIB Software Library (FSL) (www.fmrib.ox.ac.uk). For each run, consisting of two neutral and two maintain blocks, the functional time series was motion and slice-time corrected, high pass filtered, smoothed by 5 mm FWHM, intensity normalized to 10,000, and spatially normalized by a 12-parameter affine transformation to MNI-152 atlas space (Collins et al., 1994). The fMRI time series analysis was performed using FSL’s FEAT routine (www.fmrib.ox.ac.uk/fsl/feat5/), modeling each block type (encode; maintain during presentation of emotional pictures; maintain during presentation of neutral pictures; recognition probe following an emotional maintain picture; and recognition probe following a neutral maintain picture) as separate explanatory variables using FEAT’s default gamma hemodynamic response model and pre-whitened residuals. The amplitude of functional contrasts, represented by model regression weights, were derived.

Scan data were not successfully obtained for 14 runs. The missing runs occurred both early and late in the run series and were distributed over seven subjects. Because dropping subjects with missing data from the analysis would have reduced the sample size to 11, we used an in-house regression method to impute voxel-wise values for the missing runs (2.4%). To obtain an estimate of the missing runs, we formulated a regression model that included 17 indicator variables to code for the effect of subject, 3 indicator variables to code for the effect of site, and 7 indicator variables to code for the effect of run. For each voxel, we used R’s linear model routine lm to regress the data available for each contrast analyzed at the run level onto the above model to obtain 27 regression weights and an additive constant (http://cran.r-project.org/web/packages/nlme/index.html). The constant term represented the BOLD response of the 18^th subject on the 8^th run at the 4^th site. Using these regression model parameters and AFNI’s 3dcalc we estimated BOLD maps for each of the 14 missing runs (Cox, 1996). This imputation method would tend to stabilize the variance components estimates for person, site, and run, reducing their standard error, while slightly underestimating the person-by-site variance compared with a full data set. Given the small amount of missing data, these imputation effects are likely to be small.

Statistical Analysis

Two functional contrasts were analyzed: recognition versus scrambled pictures and recognition following emotional distraction versus recognition following neutral distraction. Findings related to other contrasts can be obtained from the first author. Given space limitations, the full analysis is reported only for the recognition versus scrambled picture contrast. The BOLD response during the recognition probe was chosen for a complete discussion because performance in the recognition period reflects the integration of processes occurring throughout the task and, therefore, is a summary measure of task functioning.

Voxel-wise variance component maps for each of these contrasts were estimated using in-house scripts calling R’s lmer routine. We used commands from the “Analysis of fMRI Experiments” package to read AFNI volumes into and out from R routines (http://www.wias-berlin.de/projects/matheon_a3/) (http://cran.r-project.org/web/packages/nlme/index.html).

We analyzed the impact of run averaging on between-site reliability for the two contrasts. In these variance components analyses person and site were crossed, with run nested under person-site combinations (Friedman et al., 2008). The nesting assumed that the BOLD response for runs occurring at a particular site shared common site variation that made them more similar to one another than were runs collected at different sites. Including run in the model permitted the person-by-site variance component to be estimated separately from the unexplained term, because variation related to run and its interactions can be used to estimate unexplained (residual) variance (Brennan 2001). Given this design, the total session variance is: Session variance_{#run_ave} =

$$\text{VD}\_\text{person}+\text{VD}\_\text{site}+\text{VD}\_\text{person }\times \text{ site}+(\text{VD}\_\text{unexplained}/\#\text{ runs})$$ (1)

where VD stands for “variance due to”. Between-site intraclass correlations for different numbers of runs averaged were calculated as:

$$\text{Between}-{\text{site reliability}}_{\_\#\text{runs ave}}=\text{VD}\_\text{person}/{\text{Session variance}}_{\_\#\text{runs ave}}.$$ (2)

Within-site reliability for the two scans obtained at the recruitment site was calculated in the same manner except that there were no site or person × site terms to include in the definition of session variance.

All variance components were estimated by a restricted maximum likelihood method (Brennan 2001). We adopted Cicchetti and Sparrow’s (1981) guidelines for judging the clinical significance of inter-rater agreement as a validated criterion against which to judge the clinical importance of a particular ICC value: < .40 poor; .40 – .59 fair, .60 – .74 good, > .74 excellent (Cicchetti and Sparrow 1981).

In addition to calculating variance components for voxel-wise data, variance components of the mean beta weight for regions of interest were calculated by averaging over voxels. Anatomical regions of interest relevant to working memory were identified from the literature and selected for the MNI152 template using the Wake Forest University PickAtlas (Maldjian et al., 2003; Maldjian et al., 2004). ROI findings were provided only for the recognition versus scrambled pictures contrast.

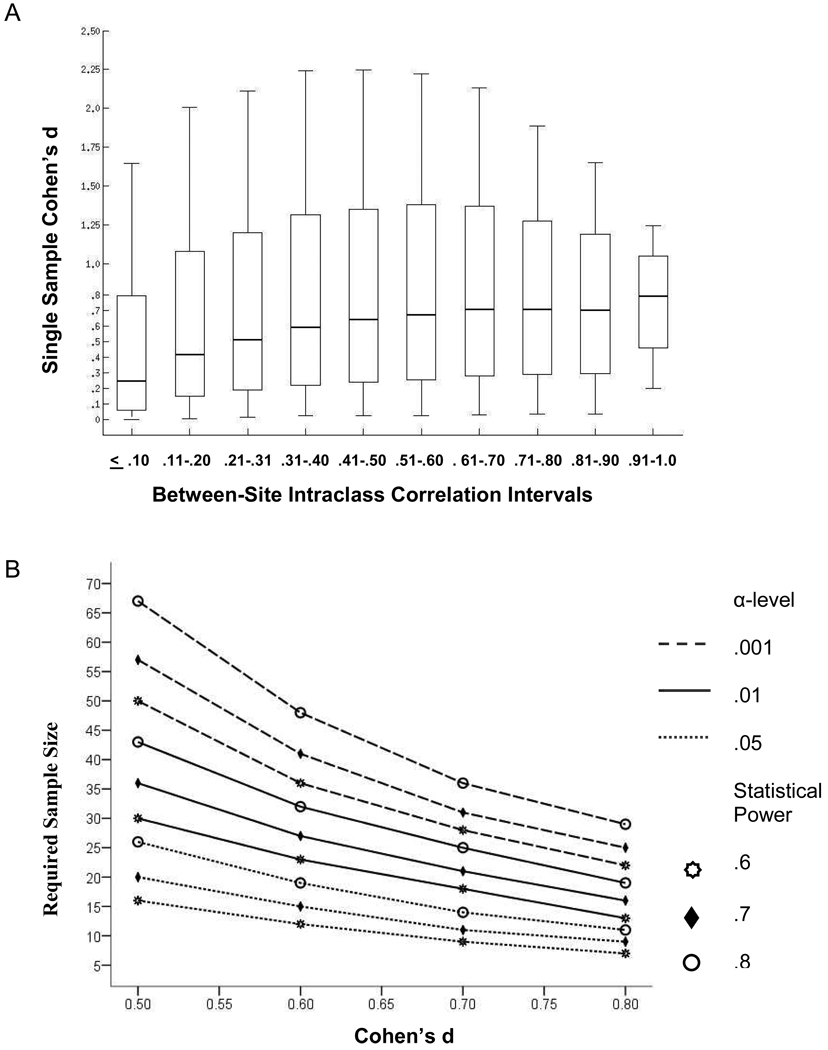
To determine how a voxel’s between-site reliability was related to the magnitude of activation in pooled data, we calculated a standardized effect size, Cohen’s d, for averaged data. We first calculated a pooled t-test map by averaging the recognition versus scrambled picture contrast over run and sites for each person then calculated a single sample t-value against the null hypothesis of no activation. From these t-values we calculated Cohen’s d to estimate effect sizes at each voxel (Cohen 1988). To test the hypothesis that the observed effect size was determined at least in part by the between-site ICC, we binned voxels from the between-site ICC_{_8 runs ave} map into ten masks where the ICC was ≤ .10, .11 – .20, .21 – .30, .31 – .40, .41 – .50, .51 – .60, .61 –. 70, .71 – .80, .81 – .90, or .91 – 1.0 (Caceres et al., 2009). Each mask was applied to the Cohen d map described above with distributions of the resulting values within each ICC bin presented as box and whisker plots. Plots are also provided for the number of significantly activated voxels found in each ICC bin for three significance levels, .05, .01, and .001, uncorrected for multiple statistical tests. To develop some of the implications associated with different levels of between-site reliability, we calculated sample sizes required to detect significant activation for different levels of reliability. Sample size estimates were derived for Cohen d values in the medium to large range (.5, .6, .7, .8) at three different α-levels (.05, .01, .001) and three levels of statistical power (.6, .7, .8) for a one-tailed, single-sample test. The formula used for the sample size estimates was:

$$\frac{{\mathrm{Z}}_{1-\alpha }+{\mathrm{Z}}_{1-\beta }}{{\mathrm{d}}_{\text{Cohen}}}=\frac{(\mathrm{n}-1)\sqrt{\mathrm{n}}}{(\mathrm{n}-1)+1.21({\mathrm{Z}}_{1-\alpha }-1.06)}$$ (3)

where d_Cohen is Cohen’s d for the one-sample t-test; α is a one-tailed significance value; Z_{1 - α} is the value from the cumulative normal distribution associated with the α-level, and Z_(1-β) is the cumulative distribution value for a particular level of power, 1 - β. Equation 3 was derived from Dixon and Massey’s discussion of statistical power and is an one-sample modification of a formula provided by Cohen (Cohen, 1998, p. 545; Dixon and Massey 1983, p. 310). Specific values of the left side of the equation were derived from hypothesized values of significance level, power, and effect size. Sample size values were found by using the R routine nls to estimate n (Ritz & Streibig, 2008). Sample size estimates produced by equation 3 were very similar to values Cohen provides when the hypothesized conditions overlapped with those of Cohen’s tables (Cohen, 1988). The sample plots are approximations that are meant to provide heuristic information about the relationships among the concepts of between-site reliability, effect size, and sample size. The plots should not be used to plan studies.

Voxel-wise significance tests were adjusted to protect against false positives due to multiple statistical tests by using AFNI’s AlphaSim to determine a cluster volume threshold. Assuming a voxel-wise p = .01 for a 2-tailed test, the AlphaSim simulation set a volume threshold of 1115 mm³ to provide a family-wise error rate of p = .05. Under the assumptions given, the simulation determined that at least one cluster 1115 mm³ or larger will occur in less than 5% of replications under the null hypothesis that no significant activation clusters would be observed in any brain region.

Results

Recognition Probe Events versus Scrambled Pictures

Voxel-wise Maps

To determine whether the BOLD response changed merely by being repeated across the four sites, the effect of session order on the recognition versus scrambled faces contrast was tested with a voxel-wise repeated measures analysis. Because the test revealed no significant clusters, session order was ignored in the following analyses.

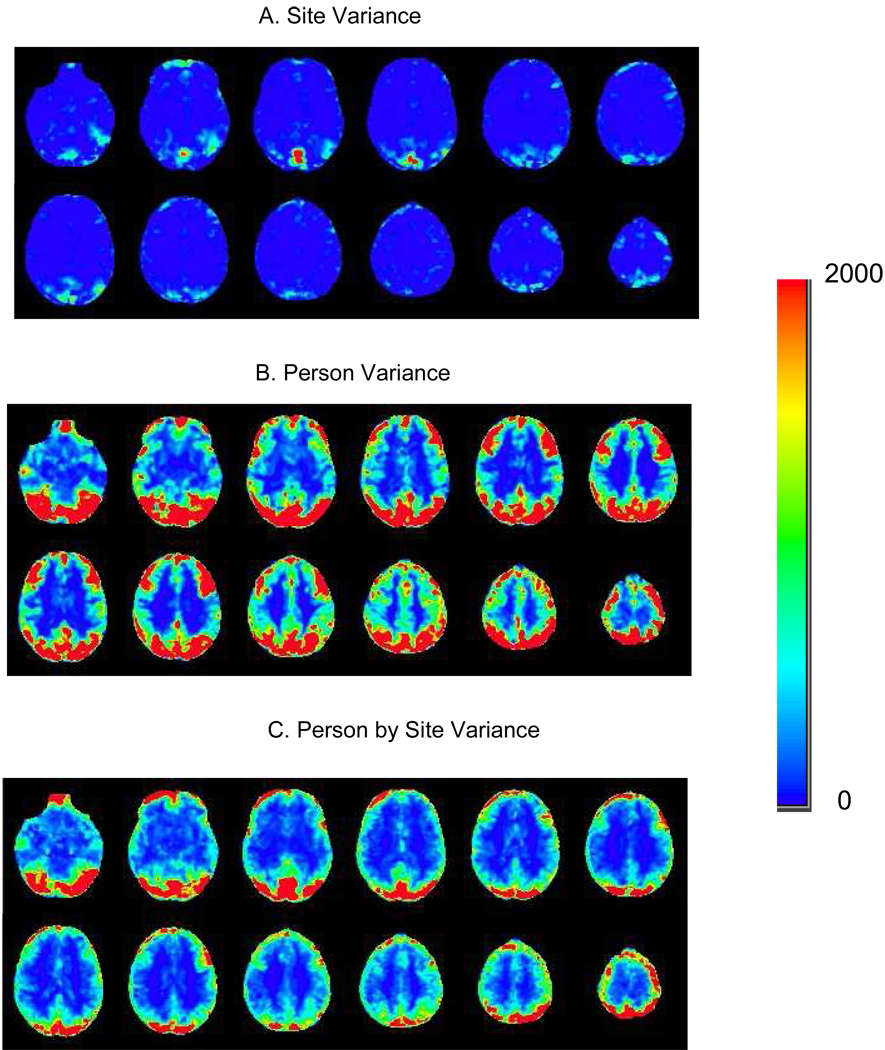
Voxel-wise plots of the site variance component revealed little variation in most brain regions (Figure 2A). Voxels in the superior sagittal sinus, in the most dorsal portion of the superior parietal cortex, and in the inferior portion of the frontal pole appeared to show the largest amount of site variation. Voxels in the dorsolateral prefrontal cortex, superior parietal lobule, angular gyrus, and supramarginal gyrus showed substantial person variance (Figure 2B). Although site variation was generally small compared with person variation, the person-by-site variance was moderately large in many brain voxels (Figure 2C).

Figure 2.

Variance components for the recognition probe versus scrambled faces contrast.

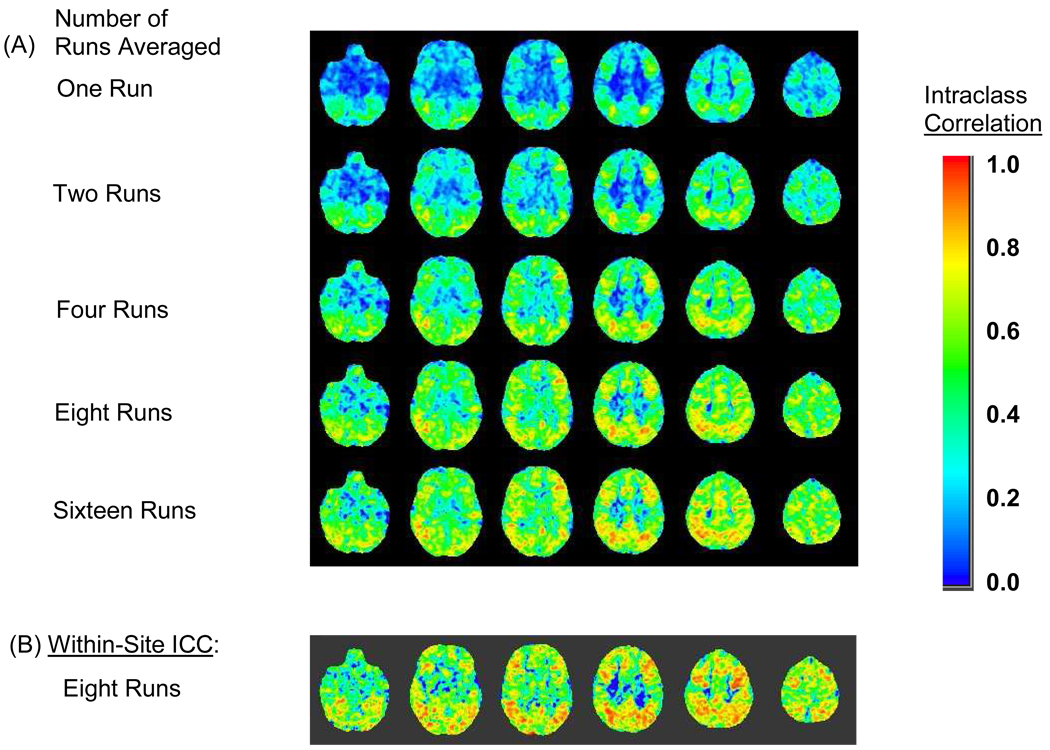
Figure 3 displays the projected impact of run averaging on voxelwise between-site intraclass correlations. These maps were calculated from equations 1 and 2. Run averaging increased the between-site intraclass correlations in most voxels and increased the spatial extent of regions with good to excellent reliability. Few brain areas reached an excellent level of between-site reliability unless at least four runs were averaged. The eight-run ICC (Figure 3A) showed good (.60 to .74) to excellent (≥.75) between-site reliability in many voxel clusters, including the dorsolateral prefrontal cortex, superior parietal lobule, angular gyrus, and supramarginal gyrus, areas where the person variance was also large (Cicchetti and Sparrow 1981). For voxels in regions, such as the lateral prefrontal cortex and posterior parietal cortex, where working memory recognition probes would be expected to activate the brain substantially, the between-site reliability approached the within-site, test-retest reliability at site D in magnitude though not in spatial extent (Figure 3B) (D'Esposito 2001). Areas where the within-site reliability exceeded the between-site reliability included voxels along brain edges, especially the brain/background edge of the medial frontal cortex, the vertex of the brain, the roof of the lateral ventricles, and the left caudate/ventricular edge. Within-site reliability also exceeded between-site reliability in anterior temporal region, orbital-frontal cortex, inferior frontal pole, left occipital-temporal cortex, and cerebellum.

Figure 3.

Data from the recognition probe versus scrambled faces contrast. (A) Between-site reliability for increasing numbers of runs averaged. (B) Within-site, between-session reliability for eight runs averaged at the site where scans were repeated (Site D).

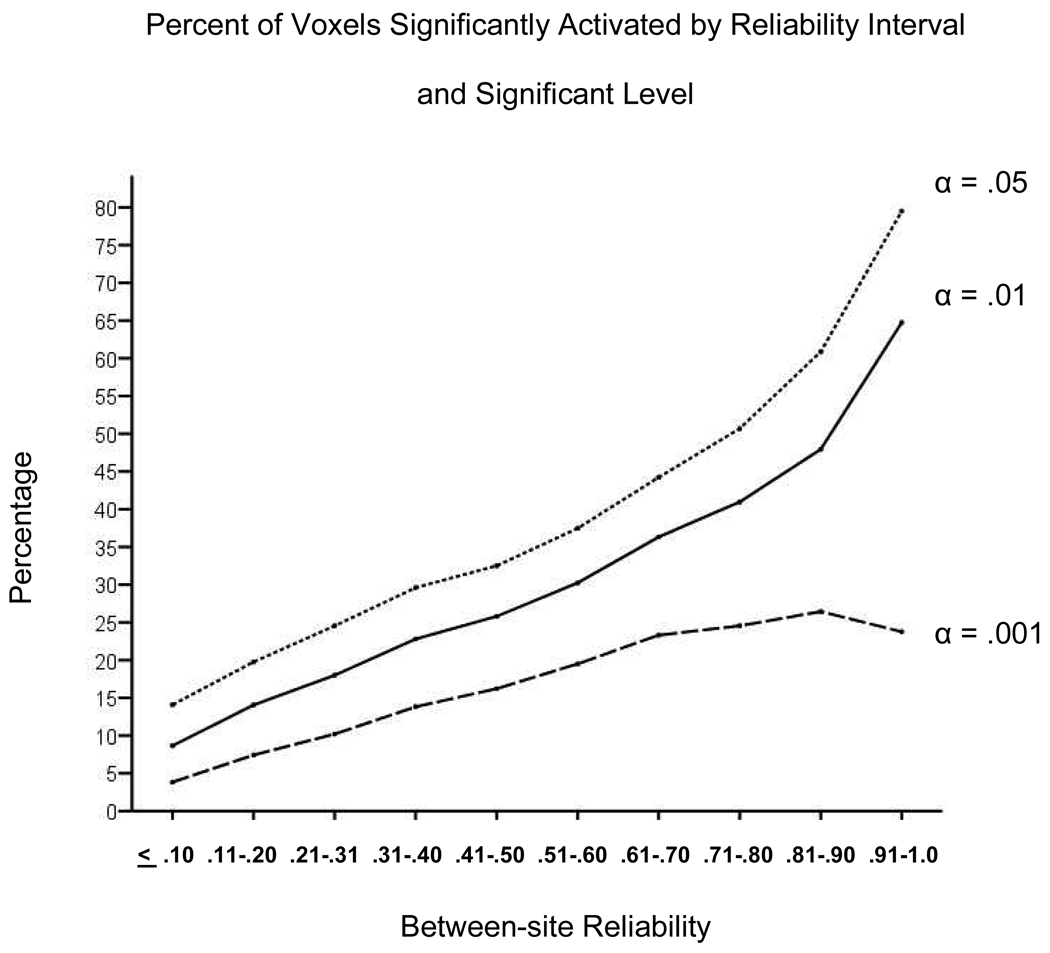
Figure 4 shows the percentage of voxels found to be significantly activated as between-site reliability increases for α = .05, .01, .001. In general, a greater percentage of voxels were found to be significantly activated as reliability increased. The one exception occurred at the data point for the largest reliability interval with the most stringent α-level, where few voxels were observed. For the two lower α-values, the majority of voxels with excellent levels of between-site reliability showed significant BOLD responses. Although reliability and likelihood of activation were found to be related, Figure 4 implies that between reliability and activation significance were dissociated for some voxels. To examine the relationship between activation effect size and between-site reliability in more detail, we calculated at each voxel the Cohen’s d associated with a one-sample t-test of the recognition probes versus scrambled pictures contrast. As shown in Figure 5A the relationship of the median Cohen’s d to the between-site ICC is curvilinear, with a model including both linear and quadratic terms fitting the median Cohen’s d value very well, R² = .96, p < .001. Figure 5B shows the sample size required to detect a significant effect for effect sizes that vary across the medium to large range. The sample size required depends on the α-level and the statistical power desired. For all combinations of statistical power and significance level, sample size requirements dropped most rapidly as the effect size improved from .50 to .60.

Figure 4.

Percent of voxels in a particular between-site reliability bin significantly activated at three different levels of significance based on the pooled t-test of recognition versus scrambled contrast. Reliability intervals were based on the eight-run between-site reliability map.

Figure 5.

(A). Effect size (Cohen’s d) by binned intervals of between-site reliability. The effect size value was derived from the single-sample t-test comparing recognition probes with scrambled pictures. The between-site reliability values were obtained from the eight-run between-site reliability maps. See Figure 3A. (B) Sample sizes required to detect a significant effect for a one-tailed test at three α-levels and three levels of power for medium to large effect sizes (Cohen’s d .5 to .8).

Although the relationship between median effect size and between-site ICC was very strong, there were many voxels where dissociations between ICC and effect size occurred. We predicted that regions with poor between-site reliability and large effect sizes would show attenuated person variation. To investigate this hypothesis, we created a mask of voxels where the between-site ICC was less than .40 and Cohen’s d was greater than or equal to 2.0. This mask included several large, spatially coherent regions. We then applied the mask to the variance components maps. The mean person variance for voxels with poor between-site reliability and very large effect sizes was only 42% as large as the mean person variance averaged over all brain voxels. The mean of all of the other sources of variation in the mask was only 4% less than the mean non-person variance sources for all brain voxels. As predicted, regions with poor between-site reliability were characterized by greatly reduced variation among people.

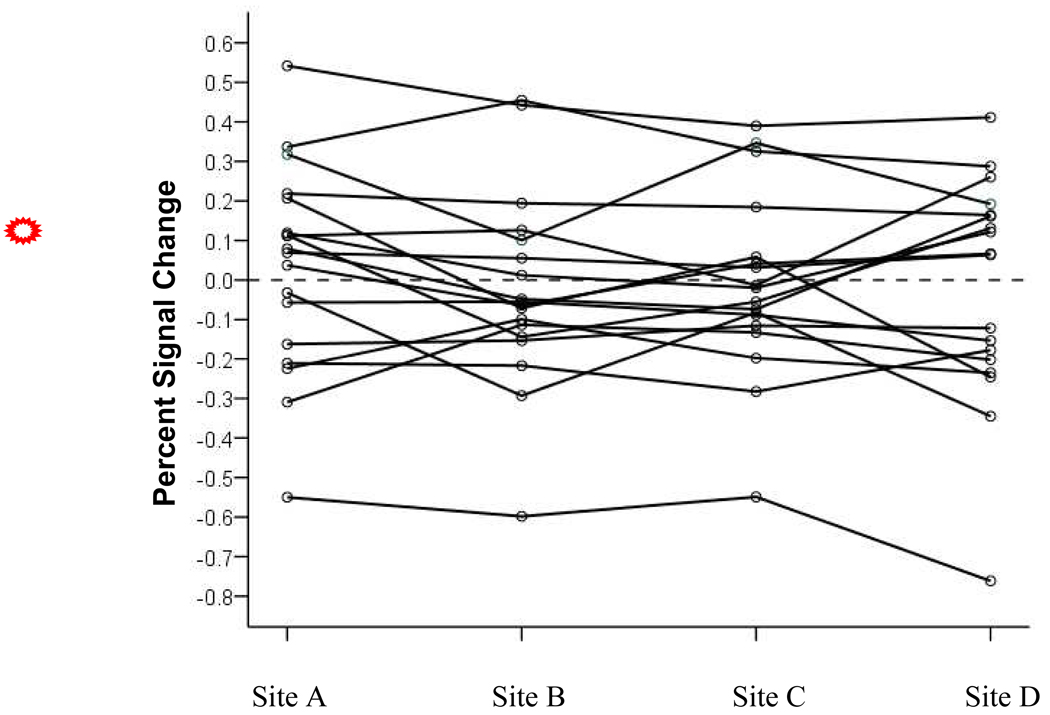
Voxels were also observed where between-site reliability was excellent and yet effect sizes were small. These voxels tended to group into small spatially disparate clusters or appear as isolated voxels. We predicted that for these voxels participants would show consistent levels of BOLD response within-subjects across sites, but that the number of individuals with positive BOLD response would be balanced by the number of individuals showing negative BOLD responses. To investigate this hypothesis we created a mask of all voxels where Cohen’s d was less than or equal to .20 (small effect) and the between-site ICC was greater than or equal to .80 (excellent clinical reliability). The mask was then applied to the subject-level percent signal change maps to obtain a mean percent signal change for each subject at each site. These means are plotted in Figure 6. As the figure shows, when ICC is large yet effect size is small, many participants displayed consistent BOLD response across sites, with nearly equal numbers of individuals having displayed positive responses as displayed negative responses. To determine whether the consistently negative values across sites might be associated with consistently poorer model fits across sites, we compared the squared standard error of the contrast of recognition probe versus scrambled pictures for the subject with the most extreme negative BOLD value against the subject with the most extreme positive value. The squared standard error for the subject with the most negative BOLD response was 53% to 91% greater across the four sites than the squared standard error for the subject with the largest positive BOLD response.

Figure 6.

Mean percent signal change for voxels with high between-site reliability and small effect sizes. Solid lines represent the performance of each subject at each of the four study sites.

Regions of Interest

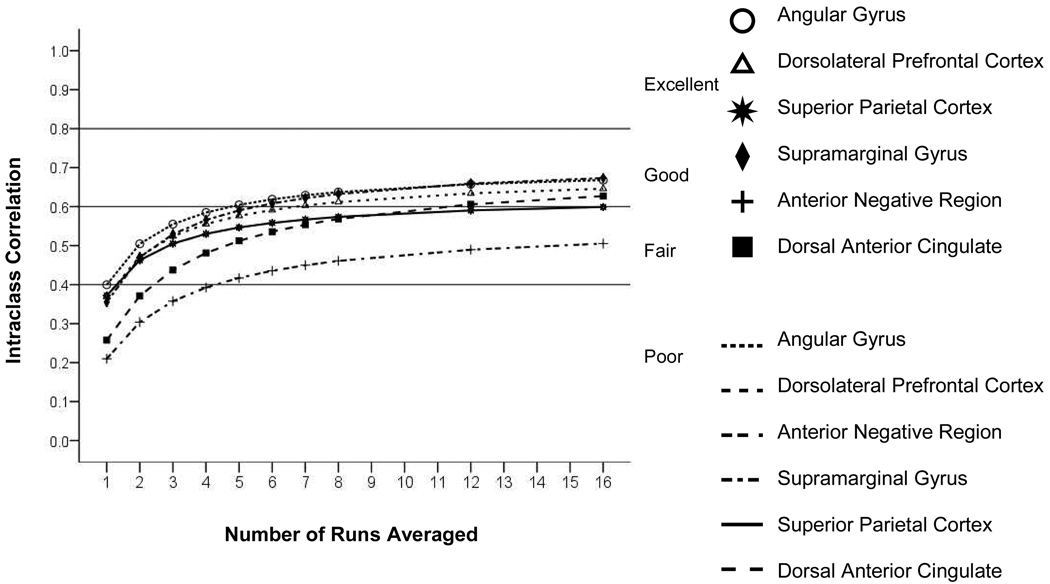
The five a priori identified ROIs were studied, as well as a large area of significantly negative BOLD response in the ventral medial prefrontal cortex. In five of six ROIs, the person variation was at least 10-fold larger than the site variation (Table 2). The person variation was more than 20-fold larger than the site variation in four ROIs. Residual variance was the largest source of variation for all ROIs (Table 2). Figure 7 shows the rate of increase in the between-ICC reliability due to run averaging for the six ROIs. For all ROIs, the projected between-site reliability of a single run was poor (See http://www.bieegl.net/fbirn/ects/predicted vs true.zip for additional detail). For all ROIs, the between-site ICC reached a fair level of between-site reliability by four runs, though seven to eight runs were required to attain a good level of reliability for the more reliable ROIs.

Table 2.

Between-site variance component estimates as a % of total raw variance for various regions of interest: Recognition versus scrambled faces contrast

	Source of Variation
Region of Interest	Person Variance	Site Variance	Person-by-Site Variance	Residual Variance
Dorsolateral Prefrontal Cortex	37.54	2.32	14.28	46.91
Anterior Negative Response Region	20.89	2.14	15.04	60.81
Dorsal Anterior Cingulate	27.28	0.83	8.42	62.79
Angular Gyrus	38.71	0.58	15.57	44.96
Supramarginal Gyrus	33.06	0.60	12.39	53.71
Superior Parietal Lobule	39.03	1.55	18.41	40.57

Figure 7.

Intraclass correlation (ICC) for the recognition probe versus scrambled faces contrast in selected regions of interest as a function of the number of runs averaged.

Recognition following Emotional Distraction versus Neutral Distraction

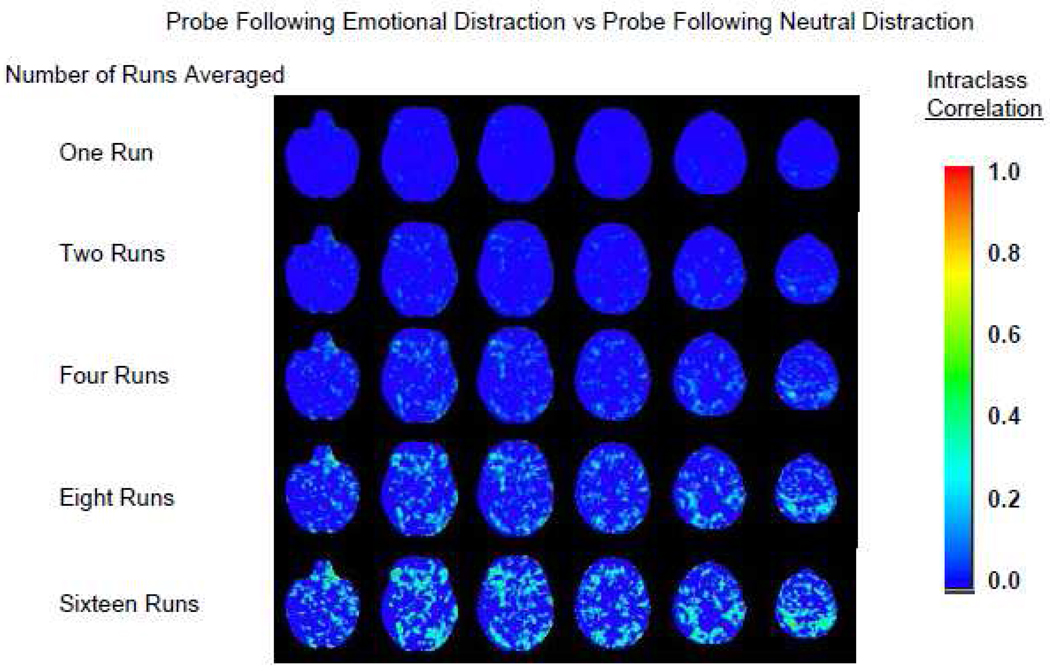
Voxel-wise between-site ICCs for the contrast of recognition probes following emotional versus neutral distraction are presented in Figure 8. Although run averaging increased the between-site ICCs, between-site reliability in most voxels was much lower when contrasting BOLD response for recognition probes following emotional versus neutral distraction than when recognition probes were contrasted with scrambled pictures. When averaging reached eight runs, ICCs in some areas approached the lower limit of the fair reliability range. The difference between within-site and between-site reliability (not shown) revealed the brain edge effects seen in the previously described contrast and edge effects at gray matter/white matter boundaries. Greater within-site reliability was also observed in the orbital frontal cortex, in a few voxels in the left amygdala, in the body of the cingulate gyrus, and in the inferior parietal cortex.

Figure 8.

Between-site reliability for increasing numbers of runs averaged. Recognition probe following emotional distraction versus recognition probe following neutral distraction.

Discussion

Between-site reliability of the BOLD response elicited by working memory conditions can be good to excellent in many brain regions, though the extent of reliability depends on the specific cognitive contrast studied, the number of runs averaged, and the brain area investigated. In five of six regions of interest studied, variance associated with people exceeded site variance by least 10-fold. There is now evidence from several multisite variance components analyses of BOLD data showing that mean differences in BOLD response across sites need not overwhelm the measurement of individual differences (Costafreda et al., 2007; Gountouna et al., 2010; Suckling et al., 2008). When adding the results of the present study to previous studies, variance components analysis has found person variance to be much larger than site variance in the primary motor region, striatum, prefrontal cortex, dorsal anterior cingulate, amygdala, angular gyrus, and supramarginal gyrus (Costafreda et al., 2007; Gountouna et al., 2010). In the present study we also found a medial prefrontal region where the BOLD response was negative yet the ratio of person to site variance was large (~9.8), suggesting that at least some areas involved in resting or intrinsic networks might also be reliably suppressed with external stimulation. It is likely that individual differences in BOLD response in other brain areas will similarly be found to be consistently measured in future multisite reliability studies.

There are several qualifications to the generalization that individual differences can outweigh site differences by an order of magnitude in fMRI studies. Because the magnitude of the BOLD signal is strongly dependent on field strength, the finding that site variation contributes only a small portion to the total measured variation in multisite fMRI studies is likely to be limited to studies using scanners at the same field strength (Cohen et al., 2004; Ogawa et al., 1998). Additionally, the amount of potentially observable person variation, and therefore the size of the associated multisite ICC, can be limited by a restriction of range associated with oversampling very similar people (Brennan 2001; Cronbach 1970). Restriction of range might have constrained between-site reliability in a previously published fBIRN study, where only well educated males in their twenties were studied (Friedman et al., 2008). In that study, magnets not persons were the targeted objects of measurement In the present study, a considerable effort was invested into maintaining high image quality across magnet sites. Probably as a result of this quality assurance effort, the percent variation associated with site was generally smaller in the present study than in our previous variance components study (Friedman et al., 2008). When careful quality assurance methods are in place, demographically varied people are enrolled, and magnets at the same field strength are used, studies of between-site reliability of fMRI data are likely to find much smaller site variance than person variance.

There were, nonetheless, brain regions were site variation was relatively large. One area of relatively large site variation followed the expected course of large veins along the medial brain surface. The greater content of deoxyhemoglobin in these large sagittal veins is likely to reduce signal intensities within the veins relative to arteries and arterioles and to create susceptibility differences that would alter signal in surrounding tissue (Haacke et al., 2004; Kawabori et al., 2009). Signal drop out was apparent on our echoplanar images in the regions of the superior sagittal sinus and in the confluence of the superior, straight, occipital and transverse sinuses. Such physiological susceptibility effects might have intensified native differences in field homogeneity at different magnet sites (DeGuio, Denoit-Cottin and Davenel, 2008). Variation in the superior parietal regions appeared to be related, on occasion, to site differences in the care taken to place participants inside the field of view. The larger site variation observed in the frontal pole might have been due to different tendencies of the head to pitch at difference sites as a result of differences in neck support and to differences in shim quality.

Although differences in the mean BOLD signal across sites contributed little to the overall variation in BOLD values in most brain areas, in both the voxel-wise maps and ROI analyses the person-by-site interaction contributed substantial variation to the total. Person-by-site variation is introduced whenever the rank ordering and/or distance of the BOLD response among individuals varies across magnet sites, producing a second unwanted source of variation involving site. For the ROIs studied, the person-by-site interactions were at least 6-fold greater than site variation for the more reliable of the two functional contrasts studied. Person-by-site effects might have been mediated in part by long term learning effects present in the data if session order had been fixed across sites. Although there was no evidence of substantial long-term learning effects in our activation data, the permutation of session order across sites in the present study would have reduced the impact of long-term learning effects on estimates of the magnitude of the person-by-site interaction.

Large person-by-site interactions would depress the between-site reliability coefficient, if all other sources of variance are equal (Brennan, 2001). When the person-by-site interaction is large relative to person variance, the ordering and/or distance among people will vary across site. The lack of stability introduced by the person-by-site interaction would attenuate correlations between the BOLD response and external variables, such as symptom scales, and would reduce the accuracy of predictions about treatment response or illness course (See Costafreda, Khanna, Mourao-Miranda, & Fu, 2009 for an example of a treatment response study). Large person-by-site variance relative to person variance, therefore, is a threat to the robustness of data collected in multi-site studies even when site variance is small. There are many potential sources of person-by-site variance in fMRI studies, including evolving differences in the stability of study magnets or differential care in subject placement within the field of view at the various study sites. Individual differences in performance consistency and compliance across study sessions could also alter the rank ordering of the BOLD response of individuals across sites and lead to an increase in person-by-site variance (Carron 1971; Nevill and Copas 1991; Shavelson et al., 1989; Shoda et al., 1993).

In a previous fBIRN variance components analysis of BOLD percent signal change data, person-by-site interactions exceeded site variation only for 3T magnets (Friedman et al., 2008). In Gountouna’s study of 1.5T scanners, the person-by-site interaction was greater than the site variance for only one of the three ROIs studied (Gountouna et al., 2010). As the sensitivity of the BOLD signal to small signal changes increases with increasing field strength, subtle differences in the between subject rank order or between subject distance across sites seems to become more apparent. As fMRI research moves to higher field strengths, person-by-site interactions are likely to contribute an increasing amount of unwanted variance to total study variation, unless steps are taken to counter this source of variability. Experimental control of the subject’s physiological state, standardized study conditions and instructions, and quality assurance monitoring and correction of equipment drift might prove to be useful methods to reduce person-by-site variation.

For contrasts that lead to robust activation, between-site reliability approached or equaled within-site reliability in some voxels. There were many areas, nonetheless, where within site reliability was greater than between-site reliability. For most of the contrasts studied, within-site reliability was greater than between-site reliability along brain edges. This effect was commonly observed on the mid-sagittal slice. These edge effects suggest that when multiple images obtained from a single subject are registered into standard space, the registration process might be somewhat less successful when images are collected at different sites than when they are collected at the same site. Other regions where within site reliability exceeded between-site reliability included frontal areas where signal dropout is typically observed. The lower between-site reliability in areas of signal dropout might be due to differences in signal attenuation geometry across magnet sites. For contrasts that involved the comparison of negatively valenced and neutral pictures, within-site reliability was greater than between-site reliability in areas involving the processing of emotional stimuli, such as the amygdala and subgenual cingulate cortex. Possibly environmental differences between-sites evoked somewhat different baseline emotional states that interacted with the emotional content of the experimental stimuli. Alternatively, differing degrees of susceptibility related drop out might have caused the MR signal to vary in the amygdala and subgenual cingulate cortex across magnet sites. In the present study assessment of the stability of data across occasions was only assessed at one site. To determine whether within-site reliability varied across sites, we would have had to scan participants on at least two occasions at each site. Given the variance components model described in equation 1, the impact of potential site-by-occasion interactions on our data would have been included in the unexplained term with larger interactions reducing between-site reliability if other variance components terms were unchanged.

Increasing the number of runs averaged during a scanning session has been found to increase between-site reliability and statistical power of BOLD data obtained from regions of interest (Friedman et al., 2008; Suckling et al., 2008). The present study corroborates the beneficial effect of run averaging on between-site reliability of ROI data and extends the finding to the voxel level of analysis. In the present study, one run of a working memory task with emotional distraction led to poor ICCs in nearly all brain areas, even for the more reliable of the functional contrasts studied. Moreover, few brain areas reached a good to excellent level of between-site reliability on the ICC maps unless at least four runs were averaged. The general principle that greater run averaging improves reliability assumes that all runs are sampled from the same population of runs (Brennan 2001; Magnusson 1966). Systematic run effects such as practice effects, attention level and fatigue, dissimilarities in the items presented across runs, varying intervals between runs, and equipment drift are examples of factors that might undermine the run sampling assumption (Cronbach 1970). Some of these potentially confounding factors can be lessened by considering the impact of massing versus distributing runs within a session and by practicing subjects to a criterion level of performance before each scan. Run averaging increases between-site reliability by increasing within site reliability and by reducing measurement errors within a site (Suckling et al., 2008). In addition to run averaging, the behavioral literature discusses techniques, such as item analysis and tailored testing, that might be usefully explored in future reliability studies of functional brain imaging (Cronbach 1970; Wainer 1990).

Because run averaging improved between-site reliability, the results of the present study have implications for study design, especially when considering the trade-offs between the duration of a task and the number of subjects to be studied given a fixed budget (Mumford & Nichols, 2008). The effect of between-site reliability on sample size was indirect, reflecting the influence of reliability on effect size and the impact of effect size on sample size. Figure 3A shows that the between-site reliability of most voxels fell below .5 when only one run was averaged even in areas where the task would be expected to activate the brain. For the ROI data, reliability was even worse when one run was averaged (Figure 7). What then is a reasonable tradeoff between number of runs and sample size for fMRI studies using our emotional working memory task? This question is easier to answer for the ROI data. In Figure 7, a single run is associated with a median between-site reliability value of about .35. Figure 5A shows that a between-site reliability value of .35 fell into a reliability interval associated with a median Cohen’s d of about .57. This effect size is associated with a required sample size of approximately 54 to detect a significant effect at α = .001 with a power of .80. What if the number of runs were increased to four? Four runs averaged is associated with a median between-site reliability of about .58 across the six ROIs in Figure 7, which in turn is associated with an effect size of about .68. To detect a significant effect of .68 requires a sample size of approximately 38 at α = .001 with a power of .80, a savings of about 30%. Further increases in reliability related to run averaging produces diminishing returns with the median effect size not exceeding .70 for reliability values less than .90. It appears, then, that for a fixed budget the investigator might more efficiently increase statistical power by doubling the sample size, producing a $\sqrt{2}$ increase in effect size, rather than doubling the number of runs for each subject from four to eight. Mumford and Nichols (2008) provide a systematic framework from which to consider the tradeoff between task duration and sample size. For the task they studied, there was little gain in power for each on/off cycle after acquiring about 14 cycles. For our task, each run contained four recognition probe cycles. Fourteen cycles would be achieved between three and four runs. The results from the present study converge with Mumford and Nichols’ analysis to show that there are limits to the use of run averaging to increase statistical power. The present results, however, are limited to the question of the power to detect whether mean activation differs from zero and limited to the recognition versus scrambled pictures contrast. A second important question is how reliable a measure should be to provide robust correlations with an external variable. The present study does not address that question.

Between-site reliability varied across the two functional contrasts studied. The contrast comparing recognition against scrambled pictures was associated with larger between-site ICCs than the contrast comparing recognition probes following emotional versus neutral distraction. These results supported the hypothesis that contrasting an experimental condition against a low level control task is likely to lead to larger between-site reliability coefficients than contrasting an experimental task with a high level control task. The more reliable contrast, however, was also driven by data from twice as many trials within a run than was the less reliable contrast. Greater trial run density as well as the nature of the control condition might have contributed to the larger between-site ICCs of our more reliable functional contrast.

In both the present study and in Caceres and colleagues’ within-site reliability study, central tendency summaries of effect size were strongly related to reliability (R > .95), though the relationship in the Caceres study was more linear (Caceres et al., 2009). In both studies, nonetheless, moderately large effects were observed in some brain regions even when associated reliabilities were in the .3 to .5 range. Among voxels in the current study where effect sizes were large even though between-site reliability was poor, between-subject variation tended to be small. For voxels where effect sizes were small even though between-site reliability was large, individuals with consistently negative and consistently positive BOLD responses across sites tended to be equally represented in the data. Brain voxels where reliability was high even though effect size was small have been reported in studies of within-site reliability, where the mismatch between reliability and effect size was attributed to the consistently poor fit of the design model to the acquired time series (Caceres et al., 2009). In support of this hypothesis, the participant in the present study who responded with the most negative response in the region of good reliability and small effect size showed consistently larger standard errors across sites for the recognition probe/scrambled faces contrast than the participant with the largest positive response in this region. The fBIRN group is currently completing an analysis of the between-site consistency of the EPI wave forms generated in the current study to examine more thoroughly reasons for reliability/effect size mismatches. The finding that effect sizes and reliability coefficients might be dissociated at times in reliability studies implies that both effect size and reliability coefficients should be calculated from preliminary studies performed to provide data needed to design large-scale, multisite studies.

The magnitude of the BOLD response can be measured across sites with excellent reliability at voxel and ROI levels of analysis. With appropriate use of experimental control and proper use of quality assurance techniques, functional imaging data collected from between-site fMRI studies can be as consistent as data collected from between-rater studies of behavioral outcomes. These results support the pooling of fMRI data across sites for the task analyzed, though only for some brain regions. An implication of the regional limitations of pooling is that the spatial distribution of correlations between the BOLD response and a covariate, such as a genotype, will reflect how well the reliability map matches the neurobehavioral systems corresponding to the covariate. In regions with poor reliability, individual differences will be small relative to other sources of variation, restricting the size of potential correlations with a covariate (Magnusson 1966). Even when reliability is excellent, accounting for site in the analysis rather than simply pooling data can be useful when it is not possible to balance the enrollment of critical subject groups across sites. Accounting for site in the statistical analysis model would not only reduce the remaining contribution that site differences would otherwise make to error terms in the statistical model, it would also allow investigators to study the interaction of site with subject grouping variables, such as diagnosis. By attending to the determinants of multisite reliability of fMRI data and by using appropriate statistical models, fMRI data from multisite studies are likely to produce important neuroscience findings involving large samples that would be difficult to recruit at a single site.