Diffusion-limited retention of porous particles at density interfaces

Abstract

Downward carbon flux in the ocean is largely governed by particle settling. Most marine particles settle at low Reynolds numbers and are highly porous, yet the fluid dynamics of this regime have remained unexplored. We present results of an experimental investigation of porous particles settling through a density interface at Reynolds numbers between 0.1 and 1. We tracked 100 to 500 μm hydrogel spheres with 95.5% porosity and negligible permeability. We found that a small negative initial excess density 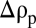relative to the lower (denser) fluid layer, a common scenario in the ocean, results in long retention times of particles at the interface. We hypothesized that the retention time was determined by the diffusive exchange of the stratifying agent between interstitial and ambient fluid, which increases excess density of particles that have stalled at the interface, enabling their settling to resume. This hypothesis was confirmed by observations, which revealed a quadratic dependence of retention time on particle size, consistent with diffusive exchange. These results demonstrate that porosity can control retention times and therefore accumulation of particles at density interfaces, a mechanism that could underpin the formation of particle layers frequently observed at pycnoclines in the ocean. We estimate retention times of 3 min to 3.3 d for the characteristic size range of marine particles. This enhancement in retention time can affect carbon transformation through increased microbial colonization and utilization of particles and release of dissolved organics. The observed size dependence of the retention time could further contribute to improve quantifications of vertical carbon flux.

The settling of particulate organic matter in the ocean is the main vector of carbon export from surface waters toward the deep sea (1, 2). Besides its key role in the oceanic carbon cycle, this particle flux supplies resources to waters below the surface layer, impacting ocean productivity and trophic dynamics (3, 4). The sinking speed of marine particles and their residence time in the epipelagic control the rate at which particulate organic matter is exported from the upper ocean or consumed and remineralized by microbes.

Marine snow particles are 0.5 to 20 mm amorphous aggregates of various origins, both organic and inorganic, bound together by exopolymeric material (5, 6). Their small excess density relative to ambient water [typically <O(1 kg·m⁻³)] (7) results in small sinking speeds (U = 0.01 − 1 mm·s⁻¹) (4). Their Reynolds number, Re = aU/ν (where a is the particle radius and ν the kinematic viscosity of seawater), is O(0.1 − 1), and sinking is thus primarily controlled by viscous, rather than inertial forces.

Marine snow often accumulates at density interfaces (pycnoclines), resulting in layers of highly elevated particle abundance that can persist for days (5, 8, 9). Despite the important effect that this process has on particle sinking rates and local trophic dynamics, the mechanisms responsible for layer formation remain controversial (5, 6).

Marine snow particles are largely composed of seawater (the “interstitial fluid”) trapped in a porous, gel-like matrix. Although porosity ε often exceeds 95% (4), marine snow has been modeled primarily as solid particles, either in a homogeneous (10) or in a stratified (11–13) fluid. Porous particles have been studied exclusively in the context of homogeneous fluids (14). Here we show that the coupling between porosity and stratification leads to a size-dependent retention time at pycnoclines. Marine snow particles are nearly impermeable to flow (15) and exchange of interstitial and ambient solutes proceeds only by diffusion. In this manner, the agent responsible for stratification (“the stratifying agent,” e.g., salt or temperature) can be exchanged between the particle's interior and the surrounding fluid. The diffusive exchange sets the retention time. This process was first proposed by MacIntyre and coworkers (ref. 5, see also refs. 6 and 16) to explain particle accumulations in the ocean, yet the fundamental mechanism has remained untested. Here we demonstrate this mechanism with a combination of laboratory experiments and mathematical modeling.

Because of the large porosity and the small excess density of the solid fraction, the mean density of marine snow particles above the pycnocline often lies between that of the fluid above and below the pycnocline, respectively. When the particle contains fluid from the upper layer, its depth of neutral buoyancy is thus often located at the pycnocline. After sinking through the upper layer, the particle comes to rest at the pycnocline, until diffusive equilibration of the interstitial fluid increases its mean excess density enough for settling to resume in the lower layer. Because diffusive exchange is size dependent, one expects larger particles to have a longer residence time. Here we quantitatively test this prediction by directly measuring the residence time of highly porous particles settling through a pycnocline for a range of particle radii (Fig. 1A). We show that residence time increases quadratically with particle size, consistent with diffusive exchange. These findings suggest that porosity can shape the formation of particle layers often observed in the ocean.

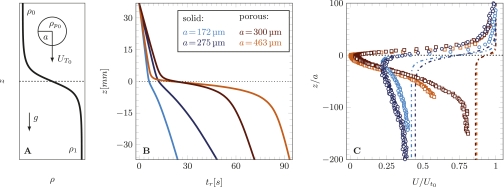
Fig. 1.

(A) Schematic of a particle of radius a approaching a pycnocline ρ(z) with velocity 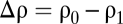. The stratification investigated here was well approximated by a tanh function (see text), connecting a region of lower density (ρ₀) with one of higher density (ρ₁). (B) Representative time series of the vertical position of solid and porous spheres settling in a stratified fluid with a buoyancy frequency of N = 7.2s⁻¹ (at z = 0). The location z = 0 mm corresponds to the center of the pycnocline. The initial excess densities with respect to the lower layer were and +15.8 kg·m⁻³ for porous and solid spheres, respectively. The choice of particle sizes ensured comparable Reynolds numbers during the approach to the pycnocline for porous and solid spheres, 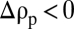(with ν₀ the kinematic viscosity in the upper layer). For the solid spheres Re₀ = 0.6 and 1.9, and for the porous spheres Re₀ = 0.9 and 2.7. (C) Normalized settling velocity profiles corresponding to the cases in B. The dashed-dotted lines represent particle velocities given by Eq. 3, assuming instantaneous exchange of interstitial fluid at each height and no stratification-induced drag enhancement.

Results

Settling Regimes.

Particle settling is largely determined by excess density, the difference between the density of the particle and that of the ambient fluid. For solid particles in a stably stratified fluid, the excess density decreases with depth, because ambient fluid density increases: Particles slow down, until they stop at their depth of neutral buoyancy. Porous particles experience an additional effect: Their mean density (or “soaked density”) is adaptive, as the stratifying agent can be exchanged between interstitial and ambient fluid.

When the particle is in the upper layer (water density ρ₀), its soaked density is

where ρ_s is the density of the solid fraction. To determine the fate of the particle when it encounters the pycnocline, it is useful to distinguish two limiting scenarios on the basis of the initial excess density relative to the lower layer (water density ρ₁), namely

where 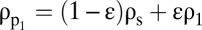is the density jump across the pycnocline. When 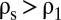, the particle will traverse the pycnocline much like a solid sphere, the buoyancy of the interstitial fluid being largely inconsequential. In contrast, when , the particle is at first too light to cross the pycnocline. A solid sphere with the same excess density would conclude its descent at the pycnocline. However, when a porous particle reaches the pycnocline, diffusive exchange of the stratifying agent with the ambient water increases its soaked density, up to at most . This process enables settling to resume, provided 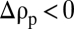, a condition that is typically satisfied for marine particles (8). The retention time of the porous particle at the pycnocline is therefore finite and limited by diffusion.

Retention at the Pycnocline.

To illustrate the effect of porosity on settling, we compared porous spheres with and solid spheres with (solid spheres with 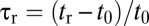would simply stop at the pycnocline indefinitely). These two classes of particles broadly correspond to porous marine snow and to denser, barely porous fecal pellets (4) and aggregates containing mineral ballast (17, 18). Comparison of the trajectories of porous and solid particles revealed that diffusive adaptation of the interstitial fluid can play a prominent role in settling (Fig. 1B). The disturbance exerted by the pycnocline on the descent of solid particles was considerably smaller than that for porous particles. The decrease in settling speed U of porous particles was an order of magnitude larger when compared with that of solid particles (Fig. 1C). Whereas solid particles decelerated to 25% of their upper-layer speed 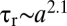, porous particles nearly came to rest at the center of the pycnocline.

A minimum in settling speed at the pycnocline was also observed for solid particles (Fig. 1C), revealing that even in the absence of porosity the settling process is more complex than the simple reduction in excess density resulting from the particle having moved into denser fluid. This velocity minimum is caused by entrainment of lighter fluid (11–13). As it settles, a solid sphere draws a wake of lighter fluid from the upper layer into the lower, denser layer. The buoyancy of the entrained wake temporarily increases the drag of the particle, until the wake is shed.

For porous particles, the minimum in settling speed was considerably more prominent (Fig. 1C). Furthermore, among the two porous spheres in Fig. 1B, the larger one reached the pycnocline ahead of the smaller one, yet left the pycnocline at a later time (Fig. 1B). This result suggests a size dependence of the retention time at the pycnocline, with larger particles retained for a longer time.

Quantification of this size dependence strongly supports the hypothesis that the settling of porous particles is controlled by the diffusion of the stratifying agent into the interstitial fluid. The retention time t_r was quantified as the time spent within the field of view (between the vertical positions z = ±37 mm). This time was normalized by the time t₀ that the sphere would have required to traverse the same distance if it had been settling everywhere at its local terminal velocity. The normalized retention time, 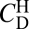, was measured for a range of particle radii, a (Fig. 2). For porous particles, we found . Because the timescale for diffusive exchange of the stratifying agent is 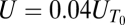, where D is the diffusion coefficient of sodium chloride in water, this result indicates that the retention time of the porous spheres was diffusion limited. In contrast, solid spheres exhibited a slight decrease in retention time with increasing size (Fig. 2).

Fig. 2.

Normalized retention time at the pycnocline as a function of particle radius, a, for solid particles (circles) and porous particles (squares), for N = 7.2s⁻¹ (at z = 0 mm). The solid line represents the best fit and has a slope (2.1) close to 2, suggesting that retention time was determined by diffusive exchange of the stratifying agent.

Quasi-Steady Model.

To support these observations, we developed a quasi-steady model that captures the essential physics. The soaked particle density, ρ_p, was determined by solving the diffusion equation within the sphere as it settled (Methods). The diffusion coefficient of sodium chloride in the interstitial fluid was approximated by its value in pure water (19). The particle velocity, U, was calculated from the balance of inertia, buoyancy, and drag forces, as

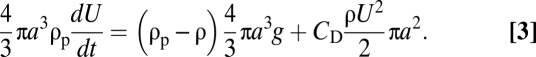The added mass and Basset forces were negligible in the regime under consideration (20). We accounted for the drag increase due to stratification by using the drag coefficient of a sphere in a salt stratification (13),

where is the drag coefficient in a homogeneous fluid, 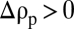is the local Richardson number, N is the local buoyancy frequency, and the ambient density profile was assumed to be locally linear.

The model correctly predicts the shape of the observed velocity profile, including the strong deceleration at the center of the pycnocline (Fig. 3). The minimum velocity predicted by the model, 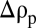, is in close agreement with the measured value. Above and below the center of the pycnocline the model somewhat overpredicts sinking velocity; i.e., it overpredicts the rate of diffusive adaptation. This overprediction can be rationalized by considering that porous spheres entrain a wake of lighter fluid during their descent, as observed for solid spheres (11–13). The wake represents a layer of intermediate density that shields the interstitial fluid from direct diffusive exchange of the stratifying agent with the ambient fluid. This buffer layer delays the relaxation of the concentration profile within the sphere, reducing the settling speed compared with model predictions, consistent with the comparison in Fig. 3. On the other hand, the settling velocity in the central part of the pycnocline was largely unaffected by entrained fluid, likely because the long residence time allowed the wake of lighter fluid to dissipate through a combination of buoyancy and diffusion.

Fig. 3.

Comparison of the settling velocity profile of porous particles from experiments (squares) and model predictions (solid lines). Colors correspond to those in Fig. 1C.

Discussion

We have shown that the retention time of porous particles at pycnoclines in stratified fluids is size dependent, because the timescale for diffusive exchange increases quadratically with particle radius. Studies of solid particles also found a reduction in settling speed, due to a wake of light fluid surrounding the particle (11–13). The two effects are different, but have a common origin: The buoyancy of light fluid entrained by the particle increases the drag on the particle, thereby slowing its descent. For solid particles, the light fluid surrounds the particle, forming a wake (Fig. 4I) attached to the particle by viscosity (11–13). For porous particles, light fluid resides also within the particle. Our results indicate that this interstitial fluid exchanges salt by diffusion with the ambient fluid, leading to a markedly different size dependence of the retention time of porous and solid particles at pycnoclines.

Fig. 4.

Schematic representation of the settling of solid (I) and porous spheres (II) through a pycnocline. See main text for a detailed description.

Retention of solid particles at pycnoclines can also occur by virtue of their buoyancy alone (i.e., independently of entrained wake fluid) when . The retention time for these solid particles is size independent and much greater than that for porous particles (infinite, in fact). Although these conditions undoubtedly occur for some of the many types of marine particles, they are likely not prevalent because natural solid particles typically have (21) and their retention time is thus determined purely by wake effects.

On the basis of these observations, we propose the following conceptual model for the settling of porous particles (Fig. 4II). Descending into the pycnocline from the upper layer (Fig. 4II, a), a particle decelerates due to the increasing ambient density and the entrained fluid (Fig. 4II, b), approaching neutral buoyancy (Fig. 4II, c). In this regime, the descent nearly stalls, allowing time for diffusive exchange of the stratifying agent with the ambient. The settling is here controlled by the diffusive equilibration of the stratifying agent in the interstitial fluid (blue shading of the particle in Fig. 4II). As a result, the timescale for settling across the pycnocline is of the order of the diffusion time, a²/D, and the Péclet number Pe = aU/D, which measures the ratio of diffusive and advective timescales, is of order 1. Once the interstitial fluid has sufficiently adapted, settling resumes (Fig. 4II, d). The particle reaches its new terminal velocity when the interstitial concentration has fully relaxed to the ambient value (Fig. 4II, e).

The strong size dependence of the retention time suggests a preferential accumulation of larger particles at pycnoclines, with a consequently larger effect on vertical fluxes of particulate matter. The inverse dependence on diffusivity further suggests that the effect of porosity will be weaker in temperature stratifications, because temperature diffuses approximately 100-fold faster than salt, likely making thermal relaxation too rapid to cause considerable retention.

It is instructive to consider how marine particles can deviate from the conditions investigated here. First, particle porosities >95% are common in the ocean (4). A greater porosity implies a smaller particle excess density, (Eq. 2), and thus a stronger effect of diffusion on settling. Second, some marine particles are permeable, resulting in reduced retention times, because advection accelerates the equilibration of the interstitial fluid with the ambient, compared with pure diffusion. However, many particles in the ocean have very low permeability (15), making results based on diffusion alone widely applicable.

Typical marine pycnoclines are weaker than the one used in these experiments, with the strongest stratifications in estuaries or fjords characterized by N ≃ 0.2s⁻¹ (22). Particle retention in natural stratifications can be estimated by comparing the timescales of the internal concentration field and the external flow field. Assuming steady diffusion-limited settling within a large-scale stratification, a scaling for the settling velocity U can be obtained by considering the rate of change of interstitial and ambient fluid densities. Neglecting effects of entrainment, the ambient density at the position of the particle varies at a rate

(where g is the acceleration of gravity), whereas diffusive exchange alters the interstitial density, and hence the particle density, at a rate (23)

Settling is steady when the two rates of change balance, i.e., when

The retention time scales inversely with the settling velocity and hence increases with N², a², and 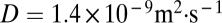. Therefore, although retention time is expected to decrease in weaker stratifications, this can be compensated for by an increase in particle size and porosity. For example, millimeter-sized particles settling in a stratification with N = O(0.1 s⁻¹) experience similar retention times as O(100 μm) particles settling at N = O(1 s⁻¹), and an increase in porosity will further amplify the effect.

These findings support the hypothesis first proposed by MacIntyre et al. (5) that diffusive exchange determines the retention time and therefore the intensity of accumulation of porous particles at pycnoclines. MacIntyre et al. calculated that the particle accumulations they observed in the coastal ocean off central California could be explained by a ≥20% reduction in settling speed (although we note that for a given settling-speed reduction, accumulation is time dependent). They computed that a moderate stratification (N = 0.02 s⁻¹) causes a settling speed reduction of this magnitude for particles with 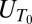and porosity >99%. [Correcting for an error in MacIntyre et al. (5) in the formulation of the drag force, which is linearly rather than quadratically proportional to settling speed in the low Reynolds number regime appropriate for most marine particles, results in an even larger reduction in settling speed, further strengthening their conclusions.] Our results provide a direct experimental demonstration of diffusion-limited retention at pycnoclines and suggest that velocity reductions markedly >20% can be achieved under the appropriate environmental conditions.

Measurements of particle size within layers provide further support for the occurrence of diffusion-limited accumulation in the ocean. Indeed, both the observations that mean aggregate size is larger within particle layers (5, 8) and that smaller particles retained within layers have smaller excess densities (5) are consistent with the predictions from Eq. 7. It is important to note, however, that particle size within layers is affected by additional physical and biological factors. For example, accumulation and differential settling promote aggregation and shift the particle size spectrum toward larger aggregates (24), whereas zooplankton grazing and biotic disintegration (10) have the opposite effect.

By determining the particle residence time at pycnoclines, diffusional exchange does more than affecting particle accumulation. Typical residence times due to diffusion-limited settling can be estimated on the basis of the diffusion relaxation time, 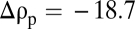, which ranges from 3 min to 3.3 d for particles varying in radius from a = 0.5–20 mm (with at 20 °C) (19). Larger particles will thus experience an increase in solubilization and remineralization at pycnoclines, reducing the amount of carbon exported to greater depths (25). The magnitude of this effect is environment specific, because different environments are characterized by different particle size distributions (26, 27). Importantly, our results indicate that knowledge of particle spectra must be complemented by knowledge of particle porosity to accurately quantify the enhanced retention of carbon at pycnoclines.

Particle retention will also result in the release of copious amounts of dissolved matter and the intensification of biological activity at pycnoclines. Biological activity on and around particles will also be enhanced by the favorable dissolved plume dynamics at pycnoclines. Because the diffusivity of dissolved gases, mineral nutrients, and amino acids (representative of dissolved organic material) is of the same order as that of sodium chloride (15, 28), the concentration field (plume) of these substances will be markedly altered at pycnoclines over the retention timescale. As both numerical models (10) and laboratory experiments (28–30) have shown, the ability of microorganisms to exploit these dissolved plumes and attach to particles is strongly enhanced for low particle settling speeds.

Our results indicate that porosity could play a fundamental role in the vertical distribution and settling rates of particulate matter in the ocean. A full understanding of the hydrodynamics of porous particles in stratified ambients will hinge on the development of models that entirely resolve the coupling between diffusion and settling. Porosity could further influence particle–particle interactions, biological activity on aggregates, and the leakage of dissolved organic matter. Porosity could thus represent an important and understudied property of marine particles, with microscale consequences on biological dynamics and large-scale effects on carbon fluxes.

Materials and Methods

Porous particles were tracked as they settled through the interface between an upper, lighter water layer and a lower, denser water layer, each of homogeneous density.

Porous Particles.

Agarose spheres were prepared by gelation of agarose (Sigma Aldrich) solutions in deionized water, as described previously (29), with the agarose mass concentration c = 45.5 kg·m⁻³. Particle radii a ranged from 100 to 500 μm. During gelation, agarose forms a fibrous microstructure having a fiber volume fraction c/(ωρ_s) = 4.4%, where ρ_s = 1,640 kg·m⁻³ is the dry density of agarose (31) and ω = 0.625 is the mass fraction in a fiber (32), yielding a porosity of ε = 1 − c/(ωρ_s) = 95.6%. The permeability was estimated as O(10⁻¹⁷ m⁻²) (33), indicating that the agarose particles are effectively impermeable to fluid flow. Before experiments, spheres were washed thrice with water taken from the upper layer of the settling chamber (see below) and left to equilibrate overnight in the same fluid. Before being released in the settling chamber, each sphere was imaged at high resolution using an inverted microscope (Nikon TE2000E) with a 10× objective and a 1,280 × 960 pixel CCD camera (XDC-SX90; Sony), to measure a and verify sphericity. Experiments were also performed with (i) a = 125−350 μm solid (i.e., nonporous) polystyrene/divenylbenzene spheres, of density ρ_p = 1,062 kg·m⁻³, in a stratified fluid, and (ii) a = 192 μm solid polystyrene spheres, of density ρ_p = 1,050 kg·m⁻³, in a homogeneous fluid.

Stratification.

Experiments were conducted in a 40-cm-tall settling chamber with a base area of 2.5 × 6.3 cm², using sodium chloride salt as the stratifying agent. Stratifications were established by partially filling the chamber with freshwater (ρ₀ = 999 kg·m⁻³) and then carefully feeding denser, saltier water (ρ₁ = 1,032 kg·m⁻³) underneath. This procedure resulted in a pycnocline between the two layers. To counteract diffusive spreading of the pycnocline, a small amount of fluid (0.2 ml·s⁻¹) was selectively withdrawn from middepth in the pycnocline throughout the experiments with a peristaltic pump, at a location far from the settling path of particles. Withdrawal was compensated for by feeding ρ₀ and ρ₁ fluid at the top and bottom of the chamber, respectively. We tested that the effect of withdrawal on settling, as well as that of any other residual circulation in the chamber, was negligible by ascertaining that particle trajectories were exactly vertical (within the measurement resolution). The density profile, measured before and after the experiments using quantitative synthetic Schlieren (34), was well described by a hyperbolic tangent function (Fig. 1A), ρ(z) = k₁ tanh(−396z) + k₂, (k₁ = 17.9 kg·m⁻³, k₂ = 1,015 kg·m⁻³, z in meters), where z is the vertical coordinate, with origin at the center of the pycnocline and positive upward. The strength of the stratification at the center of the pycnocline, measured in terms of the buoyancy frequency (where g is the acceleration of gravity) averaged over a depth of 5 mm centered at z = 0 mm, was 7.2s⁻¹. Individual porous spheres, each contained within a small volume of water of density ρ₀, were transferred with a pipette and released through a second pipette tip centered within the lid of the settling chamber. The height of the upper layer was sufficient for spheres to reach their terminal velocity . Spheres were imaged using high-resolution time-lapse photography as they settled through the pycnocline, by means of a 1,200 × 1,600 pixel CCD camera (PCO 1600; Cooke) operating at up to 30 frames/s, fitted with a 90-mm macro lens (Nikon; numerical aperture 1.4). To maximize contrast, spheres were illuminated by white light from the side and imaged against a dark background. Calibration with rulers on both the front and the rear walls of the settling chamber showed that resolution was better than 38.5 pixels/mm. Subpixel position resolution was achieved by Gaussian fits to the intensity maximum of the particle image (with five sampling points in the lateral and the vertical direction), which yielded a measurement resolution better than 4 μm for position and 5 μm·s⁻¹ for velocity. Image processing and particle tracking were performed in Matlab (MathWorks).

Validation.

Two sets of experiments were carried out using the same settling chamber and imaging method described above, but in the absence of stratification. In the first set, the terminal velocity of a = 192 μm solid polystyrene spheres was measured and used to compute the drag coefficient C_D from the balance of buoyancy and drag forces (13). C_D agreed to within 5% with the empirical relation of White (20). In the second set, we similarly measured C_D for the agarose spheres in a homogeneous fluid, using the mean particle density to compute the excess density, and found it agreed with White's relation to within 7%. This result is consistent with the prediction of negligible flow through the particle due to its low permeability.

Model.

The quasi-steady model computes the exchange of the stratifying agent, sodium chloride (and hence the mean particle density) and the sphere's settling velocity, at time intervals 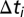, in a fluid having the same stratification as that measured in the experiments. During the settling velocity U_i and the ambient concentration c_i are assumed constant. The sphere accelerates from rest within the homogeneous upper layer and reaches its upper-layer terminal velocity well above the pycnocline. When entering the stratified region, exchange of sodium chloride was determined by integrating the unsteady diffusion equation

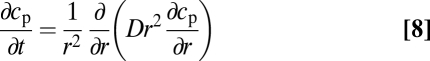inside the sphere (), using the Dirichlet boundary condition on the sphere's surface. The mean sphere density at the following time step, 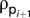, was calculated by converting the mean interstitial concentration of sodium chloride, 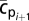, into fluid density, using tabulated sodium chloride data (35), and taking into account particle porosity and solid fraction density according to Eq. 1. Subsequently, the particle's settling speed was determined by solving Eq. 3; i.e.,

where ρ_i is the local ambient fluid density. We then calculated . 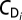was computed by Eq. 4, assuming a locally constant density gradient , i.e., constant Ri. The time increment was adjusted such that , to ensure numerical stability. The model was implemented in Matlab.